一元线性回归分析

回归分析（一元）一、实验目的掌握回归分析的步骤及操作。

二、相关理论知识1.回归分析的步骤： 首先，进行相关分析。

具体应先从定性角度分析变量之间有无相关关系；若存在相关关系，在借助散点图，相关系数等方式，进一步确定相关关系的类型及相关程度，为建立回归模型提供依据。

接下来，以相关分析为基础，进行回归分析。

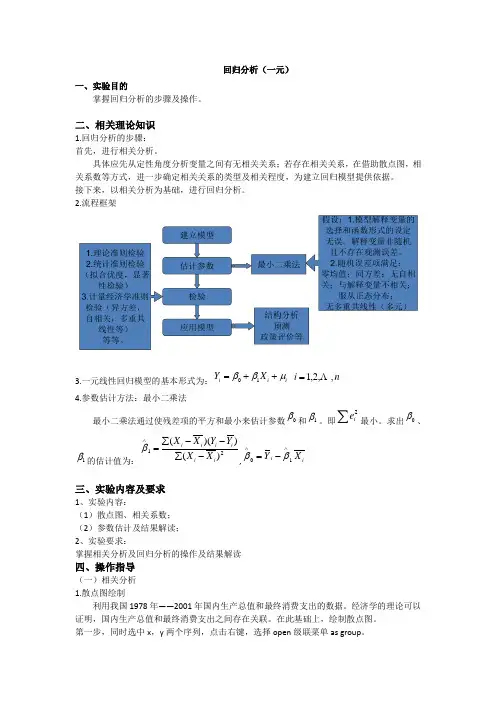
2.流程框架3.一元线性回归模型的基本形式为：i i i X Y μββ++=10 n i ,,2,1 =4.参数估计方法：最小二乘法最小二乘法通过使残差项的平方和最小来估计参数0β和1β。

即∑2i e 最小。

求出0β、1β的估计值为：21)())((i i i i i i X X Y Y X X -∑--∑=∧β,i i X Y 10∧∧-=ββ三、实验内容及要求1、实验内容：（1）散点图、相关系数； （2）参数估计及结果解读； 2、实验要求：掌握相关分析及回归分析的操作及结果解读四、操作指导（一）相关分析 1.散点图绘制利用我国1978年——2001年国内生产总值和最终消费支出的数据。

经济学的理论可以证明，国内生产总值和最终消费支出之间存在关联。

在此基础上，绘制散点图。

第一步，同时选中x ，y 两个序列，点击右键，选择open 级联菜单as group 。

（注意：在选中两个序列时，先选择哪个，打开组后哪个就在前面，作图时默认它就是横轴的变量）第二步，在group窗口，点击view下拉菜单，选择graph——scatter，点确定。

见图1图1表明两者具有很强的线性相关关系。

2.简单相关系数的计算在group窗口选择view下拉菜单中的covariance analysis，将correlation选中，同时将covariance复选框中的√去掉。

然后确定，即可得x和y的简单相关系数矩阵，见图2：图2结果显示x和y之间的简单相关系数为0.999373，两者之间存在高度正线性相关关系。

可建立一元线性回归模型。

一元回归分析1. 简介回归分析是统计学中重要的分析方法之一，用于研究变量之间的关系。

在回归分析中，一元回归是指只涉及一个自变量和一个因变量的分析。

一元回归分析的目的是建立一个数学模型，描述自变量对因变量的影响关系，并通过拟合数据来确定模型的参数。

通过一元回归分析，我们可以研究自变量和因变量之间的线性关系，预测因变量的值，并进行因变量的控制。

2. 原理2.1 线性回归模型一元线性回归模型假设自变量和因变量之间存在线性关系，可以用以下方程来表示：Y = β0 + β1 * X + ε其中，Y 表示因变量，X 表示自变量，β0 和β1 分别表示模型的截距和斜率，ε 表示误差项。

2.2 最小二乘法拟合回归模型的常用方法是最小二乘法。

最小二乘法的目标是通过最小化残差平方和来确定模型的参数。

残差是指观测值与模型预测值之间的差异。

最小二乘法通过计算观测值与回归线之间的垂直距离来确定参数值，使得这些距离的平方和最小化。

3. 回归分析步骤一元回归分析通常包括以下步骤：3.1 数据收集收集与研究问题相关的数据。

数据包括自变量和因变量的观测值。

3.2 模型设定根据问题和数据，选择适当的回归模型。

对于一元回归分析，选择一元线性回归模型。

3.3 模型估计利用最小二乘法估计模型的参数值。

最小二乘法将通过最小化残差平方和来确定参数值。

3.4 模型诊断对拟合的模型进行诊断，检查模型是否满足回归假设。

常见的诊断方法包括检查残差的正态分布性、检查残差与自变量的关系等。

3.5 结果解释解释模型的结果，包括参数估计值、模型拟合程度、因变量的预测等。

3.6 模型应用利用拟合的模型进行预测、推断或决策。

4. 注意事项在进行一元回归分析时，需要注意以下几点：•数据的收集应当尽可能准确和全面，以确保分析的可靠性；•模型的设定应当符合问题的实际情况，并选择合适的函数形式；•模型诊断是确定模型是否可靠的重要步骤，需要进行多种检验；•需要注意回归分析的局限性，不能因为有了一元回归模型就能解释所有的问题。

一元线性回归分析摘要：一元线性回归分析是一种常用的预测和建模技术，广泛应用于各个领域，如经济学、统计学、金融学等。

本文将详细介绍一元线性回归分析的基本概念、模型建立、参数估计和模型检验等方面内容，并通过一个具体的案例来说明如何应用一元线性回归分析进行数据分析和预测。

1. 引言1.1 背景一元线性回归分析是通过建立一个线性模型，来描述自变量和因变量之间的关系。

通过分析模型的拟合程度和参数估计值，我们可以了解自变量对因变量的影响，并进行预测和决策。

1.2 目的本文的目的是介绍一元线性回归分析的基本原理、建模过程和应用方法，帮助读者了解和应用这一常用的数据分析技术。

2. 一元线性回归模型2.1 模型表达式一元线性回归模型的基本形式为：Y = β0 + β1X + ε其中，Y是因变量，X是自变量，β0和β1是回归系数，ε是误差项。

2.2 模型假设一元线性回归模型的基本假设包括：- 线性关系假设：自变量X与因变量Y之间存在线性关系。

- 独立性假设：每个观测值之间相互独立。

- 正态性假设：误差项ε服从正态分布。

- 同方差性假设：每个自变量取值下的误差项具有相同的方差。

3. 一元线性回归分析步骤3.1 数据收集和整理在进行一元线性回归分析之前，需要收集相关的自变量和因变量数据，并对数据进行整理和清洗，以保证数据的准确性和可用性。

3.2 模型建立通过将数据代入一元线性回归模型的表达式，可以得到回归方程的具体形式。

根据实际需求和数据特点，选择适当的变量和函数形式，建立最优的回归模型。

3.3 参数估计利用最小二乘法或最大似然法等统计方法，估计回归模型中的参数。

通过最小化观测值与回归模型预测值之间的差异，找到最优的参数估计值。

3.4 模型检验通过对回归模型的拟合程度进行检验，评估模型的准确性和可靠性。

常用的检验方法包括：残差分析、显著性检验、回归系数的显著性检验等。

4. 一元线性回归分析实例为了更好地理解一元线性回归分析的应用，我们以房价和房屋面积之间的关系为例进行分析。

一元线性回归分析研究实验报告一元线性回归分析研究实验报告一、引言一元线性回归分析是一种基本的统计学方法，用于研究一个因变量和一个自变量之间的线性关系。

本实验旨在通过一元线性回归模型，探讨两个变量之间的关系，并对所得数据进行统计分析和解读。

二、实验目的本实验的主要目的是：1.学习和掌握一元线性回归分析的基本原理和方法；2.分析两个变量之间的线性关系；3.对所得数据进行统计推断，为后续研究提供参考。

三、实验原理一元线性回归分析是一种基于最小二乘法的统计方法，通过拟合一条直线来描述两个变量之间的线性关系。

该直线通过使实际数据点和拟合直线之间的残差平方和最小化来获得。

在数学模型中，假设因变量y和自变量x之间的关系可以用一条直线表示，即y = β0 + β1x + ε。

其中，β0和β1是模型的参数，ε是误差项。

四、实验步骤1.数据收集：收集包含两个变量的数据集，确保数据的准确性和可靠性；2.数据预处理：对数据进行清洗、整理和标准化；3.绘制散点图：通过散点图观察两个变量之间的趋势和关系；4.模型建立：使用最小二乘法拟合一元线性回归模型，计算模型的参数；5.模型评估：通过统计指标（如R2、p值等）对模型进行评估；6.误差分析：分析误差项ε，了解模型的可靠性和预测能力；7.结果解释：根据统计指标和误差分析结果，对所得数据进行解释和解读。

五、实验结果假设我们收集到的数据集如下：经过数据预处理和散点图绘制，我们发现因变量y和自变量x之间存在明显的线性关系。

以下是使用最小二乘法拟合的回归模型：y = 1.2 + 0.8x模型的R2值为0.91，说明该模型能够解释因变量y的91%的变异。

此外，p 值小于0.05，说明我们可以在95%的置信水平下认为该模型是显著的。

误差项ε的方差为0.4，说明模型的预测误差为0.4。

这表明模型具有一定的可靠性和预测能力。

六、实验总结通过本实验，我们掌握了一元线性回归分析的基本原理和方法，并对两个变量之间的关系进行了探讨。

一元线性回归分析的原理
一元线性回归分析是一种用于研究变量之间相互关系的统计分析方法。

它旨在
在一组数据中，以一个线性方程的式子去拟合变量之间的关系。

借此，分析一个独立变量（即自变量）和一个取决变量（即因变量）之间的关系，求出最合适的回归系数。

一元线性回归分析可以用来发现和描述变量之间的复杂方程式，用来估计参数，以及构建预测模型。

具体而言，一元线性回归分析指的是自变量和因变量之间有线性关系的回归分析。

也就是说，自变量和因变量均遵从一元线性方程，也就是y=βx+α，其中y
为因变量，x为自变量，β为系数，α为常数。

通过一元线性回归分析可以精确
的定义出变量之间的关系，从而可以得出最佳的回归系数和常数，并估计每个参数。

一元线性回归分析用于研究很多方面，例如决策科学、经济学和政治学等领域。

例如，在政治学研究中，可以使用一元线性回归分析来分析政府的软性政策是否能够促进社会发展，以及社会福利是否会影响民众的投票行为。

在经济学研究中，则可以使用一元线性回归分析来检验价格是否会影响消费水平，或检验工资水平是否会影响经济增长率等。

总结而言，一元线性回归分析是一种有效的研究变量之间关系的统计分析方法，精确地检验独立变量和取决变量之间的关系，从而求得最合适的回归系数和常数，并用该回归方程式构建预测模型，为决策提供参考。

一元线性回归分析实验报告.doc一、实验目的本实验旨在通过一元线性回归模型，探讨两个变量之间的关系，即一个变量是否随着另一个变量的变化而呈现线性变化。

通过实际数据进行分析，理解一元线性回归模型的应用及其局限性。

二、实验原理一元线性回归是一种基本的回归分析方法，用于研究两个连续变量之间的关系。

其基本假设是：因变量与自变量之间存在一种线性关系，即因变量的变化可以由自变量的变化来解释。

一元线性回归的数学模型可以表示为：Y = aX + b，其中Y是因变量，X是自变量，a是回归系数，b是截距。

三、实验步骤1.数据收集：收集包含两个变量的数据集，用于建立一元线性回归模型。

2.数据预处理：对数据进行清洗、整理和标准化，确保数据的质量和准确性。

3.绘制散点图：通过散点图观察因变量和自变量之间的关系，初步判断是否为线性关系。

4.建立模型：使用最小二乘法估计回归系数和截距，建立一元线性回归模型。

5.模型评估：通过统计指标（如R²、p值等）对模型进行评估，判断模型的拟合程度和显著性。

6.模型应用：根据实际问题和数据特征，对模型进行解释和应用。

四、实验结果与分析1.数据收集与预处理：我们收集了一个关于工资与工作经验的数据集，其中工资为因变量Y，工作经验为自变量X。

经过数据清洗和标准化处理，得到了50个样本点。

2.散点图绘制：绘制了工资与工作经验的散点图，发现样本点大致呈线性分布，说明工资随着工作经验的变化呈现出一种线性趋势。

3.模型建立：使用最小二乘法估计回归系数和截距，得到一元线性回归模型：Y = 50X + 2000。

其中，a=50表示工作经验每增加1年，工资平均增加50元；b=2000表示当工作经验为0时，工资为2000元。

4.模型评估：通过计算R²值和p值，对模型进行评估。

在本例中，R²值为0.85，说明模型对数据的拟合程度较高；p值为0.01，说明自变量对因变量的影响是显著的。

第二节 一元线性回归分析回归是分析变量之间关系类型的方法，按照变量之间的关系，回归分析分为：线性回归分析和非线性回归分析。

本节研究的是线性回归，即如何通过统计模型反映两个变量之间的线性依存关系。

回归分析的主要内容：1. 从样本数据出发，确定变量之间的数学关系式；2. 估计回归模型参数；3. 对确定的关系式进行各种统计检验，并从影响某一特定变量的诸多变量中找出影响显著的变量。

一、一元线性回归模型：一元线性模型是指两个变量x 、y 之间的直线因果关系。

（一）理论回归模型：εββ++=x y 10理论回归模型中的参数是未知的，但是在观察中我们通常用样本观察值),(i i y x 估计参数值10,ββ，通常用10,b b 分别表示10,ββ的估计值，即称回归估计模型：x b b y10ˆ+= 二、模型参数估计：用最小二乘法估计10,b b ：⎪⎩⎪⎨⎧-=--=∑∑∑∑∑xb y b x x n y x xy n b 10221)( 三．回归系数的含义（2）回归方程中的两个回归系数，其中b0为回归直线的启动值，在相关图上变现为x=0时，纵轴上的一个点，称为y 截距；b1是回归直线的斜率，它是自变量（x ）每变动一个单位量时，因变量（y ）的平均变化量。

（3）回归系数b1的取值有正负号。

如果b1为正值，则表示两个变量为正相关关系，如果b1为负值，则表示两个变量为负相关关系。

四．回归方程的评价与检验：当我们得到一个实际问题的经验回归方程后，还不能马上就进行分析与预测等应用，在应用之前还需要运用统计方法对回归方程进行评价与检验。

进行评价与检验主要是基于以下理由：第一，在利用样本数据估计回归模型时，首先是假设变量y 与x 之间存在着线性关系，但这种假设是否存在需要进行检验；第二，估计的回归方程是否真正描述了变量y 与x 之间的统计规律性，y 的变化是否通过模型中的解释变量去解释需要进行检验等。

一般进行检验的内容有：1.经济意义的检验：利用相关的经济学原理及我们所积累的丰富的经验，对所估计的回归方程的回归系数进行分析与判断，看其能否得到合理的解释。

第十三讲简单线性相关（一元线性回归分析）对于两个或更多变量之间的关系，相关分析考虑的只是变量之间是否相关、相关的程度，而回归分析关心的问题是：变量之间的因果关系如何。

回归分析是处理一个或多个自变量与因变量间线性因果关系的统计方法。

如婚姻状况与子女生育数量，相关分析可以求出两者的相关强度以及是否具有统计学意义，但不对谁决定谁作出预设，即可以相互解释，回归分析则必须预先假定谁是因谁是果，谁明确谁为因与谁为果的前提下展开进一步的分析。

一、一元线性回归模型及其对变量的要求（一）一元线性回归模型1、一元线性回归模型示例两个变量之间的真实关系一般可以用以下方程来表示：Y=A+BX+方程中的 A 、B 是待定的常数，称为模型系数，是残差，是以X预测Y 产生的误差。

两个变量之间拟合的直线是：y a bxy 是y的拟合值或预测值，它是在X 条件下 Y 条件均值的估计a 、b 是回归直线的系数，是总体真实直线距，当自变量的值为0 时，因变量的值。

A、B 的估计值， a 即 constant 是截b 称为回归系数，指在其他所有的因素不变时，每一单位自变量的变化引起的因变量的变化。

可以对回归方程进行标准化，得到标准回归方程：y x为标准回归系数，表示其他变量不变时，自变量变化一个标准差单位（ Z XjXj），因变量 Y 的标准差的平均变化。

S j由于标准化消除了原来自变量不同的测量单位，标准回归系数之间是可以比较的，绝对值的大小代表了对因变量作用的大小，反映自变量对Y 的重要性。

（二）对变量的要求：回归分析的假定条件回归分析对变量的要求是：自变量可以是随机变量，也可以是非随机变量。

自变量 X 值的测量可以认为是没有误差的，或者说误差可以忽略不计。

回归分析对于因变量有较多的要求，这些要求与其它的因素一起，构成了回归分析的基本条件：独立、线性、正态、等方差。

（三）数据要求模型中要求一个因变量，一个或多个自变量（一元时为 1 个自变量）。