复利终值与现值、普通年金终值与现值计算器

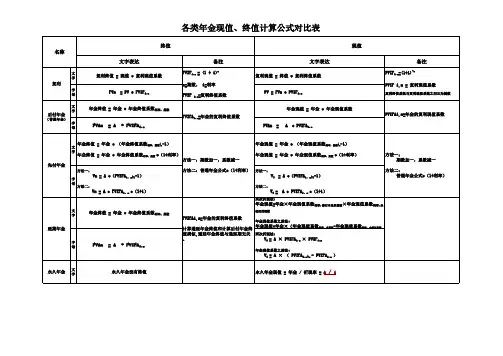
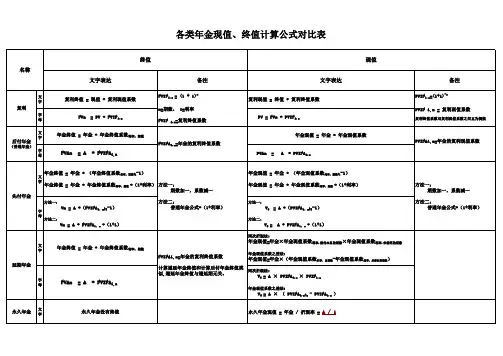
终值F ＝P ＋P ×n ×i ＝P ×（1＋i ×n ）现值P ＝F/(1＋i ×n ）终值F=P ×(1+i)n ＝P ×（F/P ，i ，n ）现值P=F ×(1+i)-n =F ×（P/F ，i ，n ）F=A ×[(1+i)n -1]/i ＝A ×（F/A ，i ，n ）在普通年金终值计算公式中，如果已知年金终值求年金，则求出的年金被称为“偿债基金”。

年偿债基金A=F*i/[(1+i)n -1]=F*(A/F,i,n)即：偿债基金＝普通年金终值×偿债基金系数“偿债基金系数”与“年金终值系数”互为倒数。

P=A ×[1-(1+i)-n ]/i ＝A ×（P/A ，i ，n ）在普通年金现值计算公式中，如果已知年金现值求年金，则求出的年金被称为“资本回收额”。

资本回收额A=P*i/[(1-(1+i)-n ]=P*(A/P,i,n)即：资本回收额＝普通年金现值×资本回收系数“资本回收系数”与“年金现值系数”互为倒数。

F ＝A ×（F/A ，i ，n ）×（1＋i ）＝A ×[（F/A ，i ，n ＋1）-1]P ＝A ×（P/A ，i ，n ）×（1＋i ）＝A ×[（P/A ，i ，n －1）＋1]终值F ＝A ×（F/A ，i ，n ），其中n 是指A 的个数，与递延期无关。

计算方法一：先将递延年金视为n 期普通年金，求出在m 期末普通年金现值，然后再将此年金现值按求复利现值的方法折算到第一期期初。

P ＝A ×（P/A ，i ，n ）×（P/F ，i ，m ）计算方法二：先计算m ＋n 期年金现值，再减去m 期年金现值。

P ＝A ×[（P/A ，i ，m ＋n ）-（P/A ，i ，m ）］计算方法三：先求递延年金终值，再折现为现值。

复利是指利息在每个计息期结束后，都被加入本金中，并以此为基础再次计算下一个计息期的利息。

复利终值是指在一定的时间内，经过连续复利计算后的最终本金和利息总和。

复利终值的计算公式如下：复利终值=P*(1+r/n)^(n*t)其中，P为现值（本金），r为年利率，n为每年计息次数，t为存款年限。

假设我们有以下数据：现值P=1000年利率r=5%每年计息次数n=1存款年限t=5将这些数据代入公式中，计算得到复利终值：复利终值=1000*(1+0.05/1)^(1*5)=1283.68复利的计算过程比简单利息要复杂一些，所以我们可以使用计算器来简化计算过程。

下面是一个复利终值计算器的示例代码：```pythonP = float(input("请输入现值（本金）："))r = float(input("请输入年利率（以小数形式）："))n = int(input("请输入每年计息次数："))t = int(input("请输入存款年限："))FV=P*(1+r/n)**(n*t)print("复利终值为：", FV)```现在我们可以根据输入的数据，计算出复利终值并输出。

用户可以根据需要，输入不同的数据进行计算。

普通年金是指在一定的时间内，每年末等额支付的一系列现金流。

普通年金终值是指存款人在给定的时间内，每年末按固定金额支付的一系列现金流的总和。

普通年金终值的计算公式如下：普通年金终值=C*[((1+r)^n-1)/r]其中，C为每年支付的金额，r为年利率，n为存款年限。

假设我们有以下数据：每年支付的金额C=100年利率r=5%存款年限n=5将这些数据代入公式中，计算得到普通年金终值：普通年金终值=100*[((1+0.05)^5-1)/0.05]=552.56同样地，为了简化计算过程，我们可以使用计算器来计算普通年金终值。

一、单利终值与现值的计算
利息的计算公式为：I = P × i × n
终值的计算公式为F = P + I = P + P × i × n = P × (1 + i × n) 现值的计算公式为：P = F÷(1 + i × n)
二、复利终值与现值的计算
复利终值F = P × (1 + i)n = P × (F/P, i, n)
复利现值P = F/(1 + i)n = F × (P/F，i，n)
三、普通年金的计算（后付年金）
1．普通年金终值（后付年金）
F=A．（F/A，i,n）
2. 普通年金现值
P=A．（Ｐ/A，i,n）
四、先付年金的终值与现值的计算（预付年金或即付年金）
1. 先付年金的终值
★F=Ax（F/A，i,n）x(1+i)
★F=Ax（F/A，i,n）x(1+i)
2. 先付年金的现值
★P=Ax（P/A，i,n）x(1+i)
★P=Ax[（P/A，i,n-1)+1]
五、递延年金终值与现值（延期年金）
1. 递延年金终值
F=A．（F/A，i,n）
2. 递延年金现值（补缺法）
P=Ax[（P/A，i,m+n)-（P/A，I,m,)]
六、永续年金
1.永续年金终值
没有终止时间，因此没有终值2.永续年金现值
P=A/i。

复利终值与现值计算器是一种用来计算复利终值与现值的工具。

复利是指将利息加入本金后再计算下一次的利息的方式，是一种利滚利的方式。

而终值是指一段时间后本金和利息的总和。

现值是指未来要得到的一定金额的现值。

复利终值的计算公式为：FV=PV*(1+r)^n其中，FV表示终值，PV表示现值，r表示年利率，n表示时间。

复利现值的计算公式为：PV=FV/(1+r)^n普通年金终值的计算公式为：FV=P*((1+r)^n-1)/r其中，FV表示终值，P表示每期支付的金额，r表示年利率，n表示时间。

普通年金现值的计算公式为：PV=P*(1-(1+r)^(-n))/r下面是复利终值与现值计算器的示例代码：```#include <iostream>#include <cmath>return PV * pow(1 + r, n);return FV / pow(1 + r, n);double annuityFutureValue(double P, double r, int n) return P * ((pow(1 + r, n) - 1) / r);double annuityPresentValue(double P, double r, int n) return P * (1 - pow(1 + r, -n)) / r;int maidouble PV, FV, r;int n;//输入终值计算复利现值std::cout << "Enter future value: ";std::cin >> FV;std::cout << "Enter interest rate: ";std::cin >> r;std::cout << "Enter number of periods: ";std::cin >> n;//输入现值计算复利终值std::cout << "Enter present value: ";std::cin >> PV;std::cout << "Enter interest rate: ";std::cout << "Enter number of periods: ";std::cin >> n;//输入支付金额计算普通年金终值std::cout << "Enter payment amount: ";std::cin >> P;std::cout << "Enter interest rate: ";std::cin >> r;std::cout << "Enter number of periods: ";std::cin >> n;double annuityFV = annuityFutureValue(P, r, n);std::cout << "Annuity future value: " << annuityFV << std::endl;//输入支付金额计算普通年金现值std::cout << "Enter payment amount: ";std::cin >> P;std::cout << "Enter interest rate: ";std::cin >> r;std::cout << "Enter number of periods: ";double annuityPV = annuityPresentValue(P, r, n);std::cout << "Annuity present value: " << annuityPV << std::endl;return 0;```通过使用上述示例代码，您可以根据需要输入相应的值，计算复利终值与现值以及普通年金终值与现值。

1、复利终值和现值（1）复利终值＝现值×复利终值系数，即s = p×(1+i)n式中(1+i)n称为复利终值系数，记作（s/p,i,n）（2）复利现值＝终值×复利现值系数，即p=s×(1+i)?C n式中(1+i)?C n称为复利现值系数，记作（p/s,i,n）【要点提示】①题目不作特别说明，i均为年利率；一年通常为360天；②题目不作特别指明，均采用复利计算时间价值。

2、普通年金终值和现值年金是指等额、定期的系列收支。

年金有两个特点：一是每次发生的金额相等；二是每次发生的时间间隔相等。

普通年金是指各期期末收付的年金。

（1）普通年金终值普通年金终值＝年金×年金终值系数，即【要点提示】①年金不一定是每年发生一次，也可能是一个月发生一次；年金既可以是款项的支付，也可以是款项的收入。

②在考试中，该系数的具体数值通常会在试卷前面给出，故需要学会如何利用“年金终值系数表”获取具体的数值。

（2）偿债基金实际工作中，往往需要推算年金。

如果已知年金终值，求年金，就是求偿债基金。

计算偿债基金年金的方法实际上是将年金终值折算成年金。

偿债基金年金＝终值×偿债基金系数＝终值÷年金终值系数，即：A=s/(s/A,i,n)=s×(A/s,i,n)式中，(A/s,i,n) 称为偿债基金系数，它是年金终值系数的倒数。

（3）普通年金现值普通年金现值是指为在每期期末取得相等金额的款项，现在需要一次投入的金额；也可以理解为，在未来每期期末取得的相等金额的款项折算为现在的总的价值。

按照终值和现值的关系：现值＝终值/（1＋i）n，故：普通年金现值＝年金×年金现值系数，即p=A×（p/A,i,n）（4）投资回收额如果已知年金现值求年金，就是求投资回收额。

计算投资回收额的方法实际上就是将年金现值折算成年金。

投资回收额＝年金现值×投资回收系数＝年金现值÷年金现值系数即：A= p×(A/p,i,n)= p/(p/A,i,n)式中，(A/p,i,n) 称为投资回收系数，它是年金现值系数的倒数。

例如：本金为50000元，利率或者投资回报率为3％，投资年限为30年，那么，30年后所获得的利息收入，按复利计算公式来计算就是：50000×（1＋3％）30由于，通胀率和利率密切关联，就像是一个硬币的正反两面，所以，复利终值的计算公式也可以用以计算某一特定资金在不同年份的实际价值。

只需将公式中的利率换成通胀率即可。

这均是时间价值问题，简单来讲，今天的100元不等于5年后的100元，那5年后的100元相当于今天的多少呢？这就需要贴现，即用100乘以期限为5，相应利率的复利现值系数,而如果要知道今天的100元相当于5年后的多少呢？则用100乘以复利终值系数，也就是求本利和。

这里的复利终值系数和复利现值系数都是在复利计算下推出的。

（一次性收付款）年金是每隔相同时间就发生相等金额的收付款，比如房租，如果发生时间在每期期末，则称为普通年金，如果以后5年中每年末可以得到100元，相当于今天能得多少（从时间价值考虑，肯定不是500元）就要用100乘以普通年金现值系数 ,反之，比如每年末存银行100元，在复利下5年能得到多少？则用100乘以年金终值系数复利终值系数、复利现值系数是针对一次性收付款，而年金终值系数和年金现值系数是系列收付款，而且是特殊的系列收付款不知道明白没有，最好能看看财务管理中时间价值章节终值的计算终值是指货币资金未来的价值，即一定量的资金在将来某一时点的价值，表现为本利和。

单利终值的计算公式：f＝p（1＋r×n）n复利终值的计算公式：f ＝ p（1＋r）式中f表示终值；p表示本金；r表示年利率；n表示计息年数其中，（1＋r）n称为复利终值系数，记为fvr，n，可通过复利终值系数表查得。

现值的计算现值是指货币资金的现在价值，即将来某一时点的一定资金折合成现在的价值。

单利现值的计算公式：复利现值的计算公式：式中p表示现值；f表示未来某一时点发生金额；r表示年利率；n表示计息年数其中称为复利现值系数，记为pvr，n，可通过复利现值系数表查得。