考虑如下线性规划问题

线性规划问题建模求解实例分析
产品甲 产品乙 产品丙 工时限制 单件铸造工时（小时） 单件机加工工时（小时） 单件装配工时（小时） 自产铸件成本（元/件） 外协铸件成本（元/件） 机加工成本（元/件） 装配成本（元/件） 产品售价（元/件） 5 6 3 3 5 2 3 23 10 4 2 5 6 1 2 18 7 8 2 4 3 2 16 8000 12000 10000
应用EXCEL工具求解线性规划问题
三、线性规划问题解的表现
EXCEL建模求解，其解的结果在“规划 求解结果”对话框中提示： 1、唯一最优解为“找到一个解”
2、无穷多最优解为“满足条件有多个解”
3、无解为“未找到可行解”
线性规划问题建模求解实例分析
（一）生产计划问题 例1：某工厂生产甲、乙、丙三种产品，都要经过铸造、 机加工(包括本场和外包的)和装配三个车间。甲、乙 两种产品的铸件可以外包协作，也可自行生产，但 产品丙必须在本厂铸造才能保证质量。数据见表。 问：公司为了获得最大利润，甲、乙、丙三种产品 应各生产多少件？甲、乙两种产品的铸件应由本公 司铸造和由外包协作各多少件?
方案。一般要求其非负。
约束条件：反映所给问题的客观限制及完成任务的
具体要求，一般表示为一组决策变量的线性等式或
不等式。
目标函数：问题所要达到的目标。一般表示为决策
变量的线性函数，取最大值或最小值。
线性规划问题基本理论及方法

建模步骤：
确定决策变量：根据决策问题，确定 找出约束条件：找出所有的限制条件，写出其
2
n
(, ) b2
…
a x a x ... a x (, )b x , x , x ,...,x 0

线性规划要研究的两类问题中都包含有约束条件和目 标函数。用数学的方式描述，规划的目的就是在给定 的限制条件（或称约束条件）下，求目标函数的极值 问题（包括极小值和极大值）。
2
线性规划的数学模型
3
解： 设产品 的产量为：1 , 产品 的产量为：x2 x
4
5
6
7

配料问题：由若干种不同价格、不同成分含量的原料，用 不同的配比混合调配出一些不同规格的产品，在原料的供 应量限制和保证产品成分含量的前提下，如何进行配料来 获取最大利润或使总成本最低。
15
2.2.3 线性规划求解的可能结局
1、有唯一的最优解
2、有无穷多个最优解 （将目标函数改为 z=4x1+3x2 ）
x2
max z 4 x1 3 x2 x1 2 x2 5 2 x x 4 1 2 s.t. 4 x1 3 x2 9 x1 , x2 0
3x1 2 x2 4 x3 3
3x1 2 x2 4 x3 xs 3
剩余变量
变量xs实际上是原式左端减去右端的差，即 ：
xs 3x1 2 x2 4 x3 3
当约束条件是“ ”型的不等式时，只要将该约 束条件左端减去一个非负的剩余变量即可化为等式。 无论是松弛变量还是剩余变量在决策中都不产生实际价 值，因此它们在目标函数中的系数都应该为零。有时也将松 29 弛变量和剩余变量统称为松弛变量。
2x1+x2=4 D C
x1+2x2=5 B 4x1+3x2=9 O A x1
16
3、无界解
指线性规划问题有可行解，但是 在可行域，目标函数值是无界的， 因而达不到有限最优值。因此线 性规划问题不存在最优解。

• 4.2 两阶段法
• 两阶段法是处理人工变量的另一种方法。其具体做 法是在原约束条件中增加人工变量，构造一个新的 目标函数，其中人工变量的系数为-1，其余变量的 系数为0，这样就产生了如下的最优解有三种情形。 （1）这说明在辅助问题的最优解中，还有人工变量是基变量， 且取值不为0，此时原问题无可行解。 （2）且最优解中人工变量均为非基变量，则把它们划去后就得 到了原问题的一个基本可行解。 （3）但最优解中还有人工变量是基变量，其取值为0。这时， 只要选某个不是人工变量的非基变量进基，把在基中的人工 变量替换出来，则情形同（2）。 第二阶段：对于第一阶段的后两种情形，在第一阶段的最优单 纯形表中划去人工变量所在的列，并把检验数行换成原问题 目标函数（消去基变量以后）的系数，从而得到原问题的初 始单纯形表，再继续迭代求解。
2014-6-19 3
例2（运输问题）
• 设有某种物资要从A1，A2，A3三个仓库运往四个 销售点B1，B2，B3，B4。各发点（仓库）的发货 量、各收点（销售点）的收货量以及 到 的单位运 费如表1-2。问如何组织运输才能使总运费最少？
例3（配料问题）
• 在现代化的大型畜牧业中，经常使用工业生产的饲料。 设某种饲料由四种原料B1，B2，B3 ，B4混合而成，要 求它含有三种成份（如维生素、抗菌素等）A1，A2， A3的數量分別不少于25、36、40个单位（这些单位可 以互不相同），各种原料的每百公斤中含三种成份的数 量及各种原料的单价如表1-3.
1.2 线性规划的数学模型
一、一般形式 上述各例具有下列共同特征： 1．存在一组变量 ，称为决策变量，表示某一方案。通 常要求这些变量的取值是非负的。 2．存在若干个约束条件，可以用一组线性等式或线性 不等式来描述。 3．存在一个线性目标函数，按实际问题求最大值或最 小值。

线性规划常见疑问第一章线性规划常见疑问解答1.线性规划——这一运筹学重要分支的开创者是谁这里，必须谈到两个著名的人物，康托洛维奇和丹捷格。

1939年著名数理经济学者康托洛维奇发表了《生产组织和计划中的数学方法》这一运筹学的先驱性名著，其中已提到类似线性规划的模型和“解乘数求解法”。

但是他的工作直到1960年的《最佳资源利用的经济计算》一书出版后，才得到重视。

1975年，康托洛维奇与T .C . Koopmans 一起获得了诺贝尔经济学奖。

1947年G . B. Dantzig 在研究美国空军军事规划时提出了线性规划的模型和单纯形解法，并很快引起美国著名经济学家Koopmans的注意。

Koopmans为此呼吁当时年轻的经济学家要关注线性规划。

今天，单纯形法及其理论已成为了线性规划的一个重要的部分。

2.线性规划模型的形式是什么目标函数和约束条件都是线性的。

3.线性规划模型的三要素是什么就是资源向量b，价值向量c，系数矩阵A（一般都假设A是满秩的）。

其中，资源向量b表示了稀缺资源的种类和限度；价值向量c反映了单位产品（广义）所创造的收益或形成的成本；而系数矩阵A是现有生产技术、生产工艺、管理水平的具体体现。

只要这三个要素确定了，相应的线性规划模型就确定了。

4.线性规划模型的经济意义何在简言之，线性规划模型对于解决经济学研究的核心问题——资源有效配置有比较重要的意义。

它不仅为宏观或微观的经济研究提供了一个有效的解决问题的平台，而且，（曾经）为经济学家提供了一个解决资源优化配置的新的思路。

不仅如此，线性规划在企业的运作管理、物流管理、财务管理、人力资源管理、战略管理等诸多方面也能为管理者提供科学的决策支持。

5.线性规划的标准形式是怎样的线性规划的标准形式有三个特点：a)约束条件都是等式；b)等式约束的右端项为非负的常数；c)每个变量都要求取非负数值。

下面是线性规划标准形式的一般表达，6.线性规划标准形的向量矩阵形式是怎样的线性规划的标准形式如用向量矩阵形式可简洁表述为：7.在将线性规划的一般形式转化为标准形式时，要注意哪几点要注意两点：一是某一约束条件为“≤”或“≥”形式的不等式时，应“+”一个非负松弛变量或“－”非负松弛变量；二是某个变量不满足非负约束时，这个变量要用一到两个非负的新变量替换，以使标准型中所有的变量均满足非负要求。

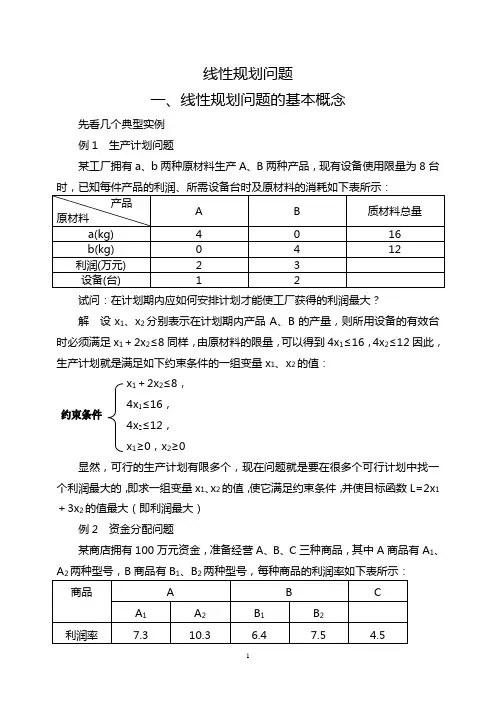
线性规划问题一、线性规划问题的基本概念先看几个典型实例 例1 生产计划问题某工厂拥有a 、b 两种原材料生产A 、B 两种产品，现有设备使用限量为8台时，已知每件产品的利润、所需设备台时及原材料的消耗如下表所示：试问：在计划期内应如何安排计划才能使工厂获得的利润最大？解 设x 1、x 2分别表示在计划期内产品A 、B 的产量，则所用设备的有效台时必须满足x 1＋2x 2≤8同样，由原材料的限量，可以得到4x 1≤16，4x 2≤12因此，生产计划就是满足如下约束条件的一组变量x 1、x 2的值：x1＋2x 2≤8， 4x 1≤16，4x 2≤12， x 1≥0，x 2≥0显然，可行的生产计划有限多个，现在问题就是要在很多个可行计划中找一个利润最大的，即求一组变量x 1、x 2的值，使它满足约束条件，并使目标函数L=2x 1＋3x 2的值最大（即利润最大）例2 资金分配问题某商店拥有100万元资金，准备经营A 、B 、C 三种商品，其中A 商品有A 1、A 2两种型号，B 商品有B 1、B 2两种型号，每种商品的利润率如下表所示：在经营中有以下限制：(1)经营A 或B 的资金各自都不能超过总资金的50%； (2)经营C 的资金不能少于经营B 的资金的25%； (3)经营A 2的资金不能超过经营A 的总资金的60%； 试问应怎样安排资金的使用才能使利润最大？解 设经营A 1、A 2、B 1、B 2、C 的资金分别为x 1，x 2,x 3,x 4，x 5（万元），这一问题的数学模型为求一组变量x 1、x 2，…，x 5的值，使它满足 x 1＋x 2＋…＋x 5=100， x 1＋x 2≤50， x 3＋x 4≤50，025x 3＋0.25x 4－x 5≤0 0.6x 1－0.4x 2≥0，x j ≥0 （j=1，2， (5)并使目标函数L=0.073x 1＋0.103x 2＋0.064x 4＋0.075x 4＋0.045x 5的值最大(利润最大)上面我们建立了几个实际问题的数学模型，虽然实际问题各不相同，但是它们的数学模型却有相同的数学形式，这就是：表示约束条件的数学式子都是线性等式或线性不等式，表示问题最优化指标的目标函数都是线性函数，因为约束条件和目标函数都是线性的，所以把具有这种模型的问题称为线性规划问题。

8）时，直线与原点的距离最近，即z的最小值为12.
解法二：特值验证法
由解法一知，目标函数取得最小值的整点应分布在可行域的 左下侧靠近边界的整点，依次取满足条件的整点A0（0， 15），A1（1，13），A2（2，11），A3（3，9），A4（4， 8），A5（5，8），A6（6，7），A7（7，7），A8（8，7）， A9（9，6），A10（10，6），…，A27（27，0）.
由图可见，当直线z=2x+y经过可行域上的点A时，截距最 大，即z最大.
解方程组 x - 4y 3 0, 3x 5y 25 0
，得A的坐标为(5,2).
∴zmax=2×5+2=12.
当直线z=2x+y经过可行域上的点B时，截距最小，即z
最小.
解方程组
x x
- 4y 1
返回
【解析】设进T 恤x件，运动鞋y双，则有
x 50,y 30,x,y N, x y 40, 36x 48y 2 400,
其目标函数为z=18x+20y. 作出它的可行域如图所示， 由图可知： 当x=50且y=12.5时，z取得最大值1 150. 但x,y∈N*,
（3）由于作图有误差，有时仅由图形不一定就能准确而 迅速地找出最优解，此时可将可能的数逐一检验即可分 晓.
假如你要开一家卖T恤和运动鞋的小商店，由于店面和 资金有限，在你经营时会受到如下限制：①你最多能 进50件T恤；②你最多能进30双运动鞋；③你至少需要 T恤和运动鞋共40件才能维持经营；④已知进货价：T 恤每件36元，运动鞋每双48元.现在你有2 400元资金， 假设每件T恤的利润是18元，每双运动鞋的利润是20元， 问：如何进货可以使你获利最大？

可得改进的基本可行解。
1
B=(P3P5
)=
0
0 1
，基变量
x 3，x 5
非基变量x1,x 2 , x 4 。
X
B
=
x3 x5
,X
N
=
x1 x2 x4
,B=
1 0
1
0 1
,N=
2 5 2
1 3
1
2 -1 2
,
CB =(3,1) CN =(5,2,-1)
,b=
4 3
➢ 若在化标准形式前，m个约束方程都是“≤”的形式， 那么在化标准形时只需在一个约束不等式左端都加上一个松弛变 量xn+i (i=12…m)。
➢ 若在化标准形式前，约束方程中有“≥”不等式， 那么在化标准形时除了在方程式左端减去剩余变量使不等式变 成等式以外，还必须在左端再加上一个非负新变量，称为 人工变量．
➢ 即使系数矩阵Ａ中找到了一个基B，也不能保证该基恰好是可行基。 因为不能保证基变量ＸB=Ｂ-1b≥0。
➢ 为了求得基本可行解
X=
B，01b必 须求基Ｂ的逆阵Ｂ-1。
但是求逆阵Ｂ-1也是一件麻烦的事。
结论：在线性规划标准化过程中设法得到一个m阶单位矩阵I作为初始
可行基Ｂ，
6
为了设法得到一个m阶单位矩阵I作为初始可行基Ｂ，可在性规 划标准化过程中作如下处理：
Ｎ=(Ｐm+1，Pm+2， …Pn)为非基变量xm+1，xm+2， …xn的
系数列向量构成的矩阵。
4
所以约束方程 AX=就b可以表示为
AX=(BN)
XB XN
=BXB
+NXN
=b
用可行基Ｂ的逆阵Ｂ-1左乘等式两端，再通过移项可推得：

互补松弛性孙敏 枣庄学院考虑如下互为对偶的一组线性规划问题⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧+==+=≤=≥+=≤+=≥=⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧+=+=≤=≥+=≥+=≤====nt j c yp t s j c yp s j c yp m q i y q p i y p i y n t j x t s j x s j x m q i b x a q p i b x a p i b x a ybW cx Z j j j j j j i i i j j j i i i i i i ,,1,,,1,,,1,,,1,0,,1,0,,1, s.t. ,,1,,,1,0,,1,0,,1,,,1,,,1, s.t.min max (DP) (LP) 无符号限制无符号限制对偶问题原问题其中[]n m n m R p p p a a a A ⨯∈=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡= 2121。

定理（互补松弛/紧性） 设1*⨯∈n Rx 与mRy ⨯∈1*分别是问题（LP ）与问题（DP ）的可行解，则它们分别是问题（LP ）与问题（DP ）的最优解的充要条件是，对一切m i ,,1 =和一切n j ,,1 =有⎪⎩⎪⎨⎧=-==-=0)(0)(****j j j ji i i i c p y x v y x a b u 证明 首先由1*⨯∈n Rx 与mRy ⨯∈1*分别是问题（LP ）与问题（DP ）的可行解得对一切m i ,,1 =和一切n j ,,1 =有0,0≥≥j i v u 。

定义0,011≥=≥=∑∑==nj j mi i v v u u因此，0=u 当且仅当),,1(0m i u i ==，0=v 当且仅当),,1(0n j v j ==，也就是0=+v u 当且仅当),,1(0),,,1(0n j v m i u j i ====。

于是为了证明命题成立，只需要证明*x 与*y 分别是问题（LP ）与问题（DP ）的最优解的充要条件是0=+v u 。

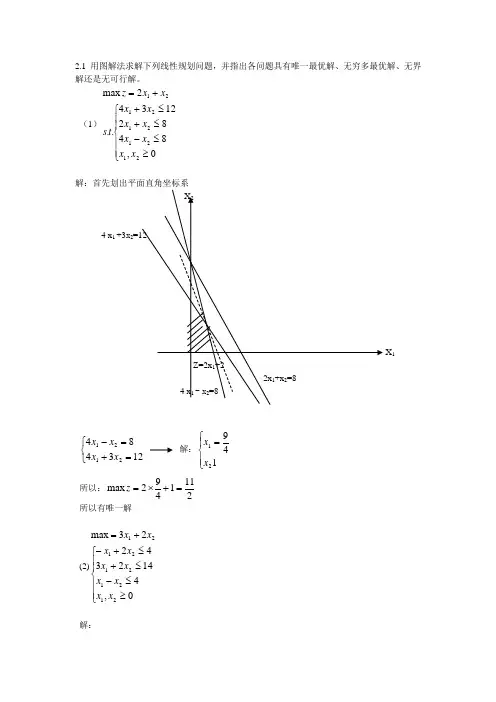
2.1 用图解法求解下列线性规划问题，并指出各问题具有唯一最优解、无穷多最优解、无界解还是无可行解。

（1）⎪⎪⎩⎪⎪⎨⎧≥≤-≤+≤++=0,84821234..2max 2121212121x x x x x x x x t s x x z解：首先划出平面直角坐标系4 x 1 +3x 2X 1⎩⎨⎧=+=-1234842121x x x x 解：⎪⎩⎪⎨⎧=14921x x 所以：2111492max =+⨯=z 所以有唯一解(2)⎪⎪⎩⎪⎪⎨⎧≥≤-≤+≤+-+=0,414234223max 2121212121x x x x x x x x x x 解：2=41⎩⎨⎧=+=+-1423422121x x x x 解得：⎪⎪⎩⎪⎪⎨⎧==4132521x x 所以:144132253max =⨯+⨯=z 因为直线02321=+x x 与直线142321=+x x 平行， 所以有无穷多最优解，max z=14（3） ⎪⎩⎪⎨⎧≥≤+-≤-+=0,432..32max 21212121x x x x x x t s x x z 解：（4）⎪⎩⎪⎨⎧≥-≤-≥-+=0,330..max 21212121x x x x x x t s x x z解：2.2将下列线性规划问题化为标准形式(1) s.t.⎪⎩⎪⎨⎧≥≤≤-+-=++-+-=无约束321321321321,0,0624322min x x x x x x x x x x x x z (2)⎪⎪⎩⎪⎪⎨⎧≤≥-=-+-≤+-≥--+=0,0232132..23min 3213213132321x x x x x x x x x x t s x x x z 无约束， 解：（1）令011≥-=x x )0'','('''33333≥-=x x x x x则上述形式可化为：)'''(32'2m ax 3321x x x x z --+=⎪⎩⎪⎨⎧≥=+--+=-++0,'',',,'6)'''('24)'''('..43321433213321x x x x x x x x x x x x x x t s（2）⎪⎪⎩⎪⎪⎨⎧≤≥-=-+-≤+-≥--+=0,0232132..23min 3213213132321x x x x x x x x x x t s x x x z 无约束， 解：令33'x x -= )0','','(322≥x x x 则上述形式可化为：')'''(23m ax 3221x x x x z ----=⎪⎪⎩⎪⎪⎨⎧≥=---=+--=+---0,,','',',2')'''(321')'''(3')'''(2..543221322153224322x x x x x x x x x x x x x x x x x x t s 2.3. 在下列线性规划问题中，找出所有基解，指出哪些是基可行解并分别代入目标函数，比较找出最优解。

以上约束方程组有无穷多个解，单纯形法就是 确定这些解的过程
.(1)初始单纯形表: X1 x2 x3 x4 x0
x3
x4
3
5
4
4
1
0
0
1
36
40
-32
-30
0
0
0
在初始单纯形表中，横线上以上部分即为约束方程组
的增广矩阵，而横线以下的这一行由目标函数的系数
组成（注意到目标函数中未出现 x3和x4 及常数项，
X1 X3 x1
0
0 1
x2
8 5 4 5
x3
1 0
x4
3 5 1 5
x0 12 8 256
22 5
0
32 5
对这张单纯形表，横线以上部分对应与原 约束方程组同解的方程组，此时等价地将 原规划问题变为如下问题：
22 32 min z 256 x2 x4 . 5 5
第二节:线性规划的解法 一、几个概念
对线性规划问题称满足全部约束条件的解为线 性规划问题的可行解，全部可行解的集合称为 可行域。使目标函数取最小值的可行解，称为 最优解，此时目标函数的最小值称为最优值。 一般讲,线性规划问题可行解有无穷多个,要从中 找出最优解也是很困难的。通常线性规划问题 的可行域的顶点只有有限多个,将这些点的的标 函数值全算出也是可以的.一般对于两个变量线 性规划问题进行图解法。
3x1 4 x 2 x3 36, 5x1 4 x 2 x 4 40;
以上可以得到问题的标准形 min z 32x 30x .
1 2
s.t.
3x1 4 x2 x3 36 5 x1 4 x2 x4 40 x 0 ( j 1,2,3,4) j

线性规划建模步骤
设定决策变量 明确约束条件并用决策变量的线性等式或 不等式表示 用变量的线性函数表示要达到的目标，并 确定是求极小还是求极大 根据变量的物理性质确定变量是否具有非 负性 注：其中最关键是设定决策变量这一步
生产计划问题(1)
某工厂用三种原料生产三种产品，已知的 条件如下表所示，试制订总利润最大的日 生产计划
线性规划问题解的有关概念(2)
基本解：令模型中所有非基变量的值等于零后，由 模型的约束方程组得到的一组解。 基本可行解：满足非负条件的基本解称为基本可行 解。 可行基：对应于基本可行解的基称为可行基。 退化解：基本可行解的非零分量个数小于m时，称 为退化解。 最优基：若对应于基B的基本可行解X是线性规划的 最优解，则称B为线性规划的最优基
人员安排问题(1)
医院护士24小时值班，不同时段需要的护 士人数不等（见下表）。每个护士每天连 续值班8小时，在各时段开始时上班。问最 少需要多少护士？
序号 1 2 3 4 时段 06—10 10—14 14—18 18—22 最少人数 60 70 60 50
5 6
22—02 02—06
20 30
人员安排问题(2)
设xj为第j时段开始值班的护士人数
目标函数为：使人数最少，则有
min f ( X ) x1 x2 x3 x4 x5 x6 x6 x1 60 x x 70 1 2 x2 x3 60 s.t. x3 x4 50 x x 20 5 4 x5 x6 30 x1 , x2 , x3 , x4 , x5 , x6 0且为整数
运筹学
第一章 线性规划问题
本章重点
线性规划建模 线性规划的图解法 线性规划的标准形式 单纯形法 两阶段法 大M法

P11.3（1）将下列线性规划模型化成标准形式：⎩⎨⎧=+≤+--=10352..3max 212121x x x x t s x x z 解：令"2'22"1'11,,'x x x x x x z z -=-=-=，代入上面的线性规划，得标准形式⎪⎩⎪⎨⎧≥=-+-=+-++--++-=0,,,,1033522..33'min 3"2'2"1'1"2'2"1'13"2'2"1'1"2'2"1'1x x x x x x x x x x x x x x t s x x x x z P14:1、用图解法求解下列线性规划问题：⎪⎪⎪⎩⎪⎪⎪⎨⎧≥≥≤-≤-≤+-≤++-=0,013721042242..23min 212121212121x x x x x x x x x x t s x x f 利用图解法：于是得最优解为(4,1),最优值为-10。

P15：2⎪⎪⎩⎪⎪⎨⎧≥≤≤≥-≥+-=06063222..26max 21212121x x x x x x t s x x z 解：利用图解法于是最优解为（6，0），最优值为36。

P15.3⎪⎪⎩⎪⎪⎨⎧≥≥≥+≤+≤+--=0,0121272172..27min 21212121210x x x x x x x x t s x x x 解：利用图解法求得有无穷多最优解，都落在一个线段上，该线段的两个端点是：)3/7,3/7(),0,3()2()1(==x x于是全部的最优解可以表示成)1(x与)2(x的凸组合，即.10,)1()2()1(*≤≤-+=αααx x x最优值都是-21。

P16:1、 解：设ij x 表示第i 台机床加工第j 类产品的产量，于是可得数学模型⎪⎪⎪⎩⎪⎪⎪⎨⎧=≥≤+≤+≤+≤++++++++++++++++=.6,5,4,3,2,1,0900600700850..)(80)(64)(72)(32)(28)(40max 464335322421161514131211461635152414431332122111j x x x x x x x x x x x x x t s x x x x x x x x x x x x f j P16:2、 解：设j x 表示第j 食品的采购量，于是可得数学模型13、某养鸡场有一万只鸡，用动物饲料和谷物饲料混合喂养，每天每只鸡平均吃混合饲料0.5公斤，其中动物饲料占的比例不得少于1/5。

运筹学典型考试试题及答案⼆、计算题（60分）1、已知线性规划（20分）MaxZ=3X1+4X2X1+X2≤52X1+4X2≤123X1+2X2≤8X1,X2≥0其最优解为：基变量X1X2X3X4X5X33/2 0 0 1 -1/8 -1/4X25/2 0 1 0 3/8 -1/4X1 1 1 0 0 -1/4 1/2σj 0 0 0 -3/4 -1/21）写出该线性规划的对偶问题。

2）若C2从4变成5，最优解是否会发⽣改变，为什么？3）若b2的量从12上升到15，最优解是否会发⽣变化，为什么？4）如果增加⼀种产品X6，其P6=(2,3,1)T，C6=4该产品是否应该投产？为什么？解：1)对偶问题为Minw=5y1+12y2+8y3y1+2y2+3y3≥3y1+4y2+2y3≥4y1,y2≥02)当C2从4变成5时，σ4=-9/8σ5=-1/4由于⾮基变量的检验数仍然都是⼩于0的，所以最优解不变。

3）当若b2的量从12上升到15X＝9/829/81/4由于基变量的值仍然都是⼤于0的，所以最优解的基变量不会发⽣变化。

4）如果增加⼀种新的产品，则P6’=(11/8,7/8，－1/4)Tσ6=3/8>0所以对最优解有影响,该种产品应该⽣产2、已知运输问题的调运和运价表如下，求最优调运⽅案和最⼩总费⽤。

（共15分）。

B1B2B3产量销地产地A1 5 9 2 15 A2 3 1 7 11 A3 6 2 8 20 销量18 12 16解：初始解为计算检验数由于存在⾮基变量的检验数⼩于0，所以不是最优解，需调整调整为：重新计算检验数所有的检验数都⼤于等于0，所以得到最优解3、某公司要把4个有关能源⼯程项⽬承包给4个互不相关的外商投标者，规定每个承包商只能且必须承包⼀个项⽬，试在总费⽤最⼩的条件下确定各个项⽬的承包者，总费⽤为多少？各承包商对⼯程的报价如表2所⽰：（15分）项⽬投标者 A B C D 甲 15 18 21 24 ⼄ 19 23 22 18 丙 26 17 16 19 丁 19212317答最优解为：X= 0 1 0 0 1 0 0 0 0 0 1 0 0 0 0 1 总费⽤为504. 考虑如下线性规划问题（24分）B 1 B 2 B 3 产量/t A 1 15 15 A 2 11 11 A 3181 1 20 销量/t 18 1216B 1 B 2 B 3 产量/t A 1 5 13 0 15 A 2 －2 0 0 11 A 30 0 20 销量/t 181216B 1 B 2 B 3 产量/t A 1 15 15 A 2 11 11 A 3 7 12 1 20 销量/t 18 12 16 B 1 B 2 B 3 产量/t A 1 5 13 0 15 A 2 0 2 2 11 A 3 0 0 0 20 销量/t 18 12 16Max z=-5x1+5x2+13x3s.t. -x1+x2+3x3≤2012x1+4x2+10x3≤90x1，x2，x3≥0回答以下问题：1）求最优解2）求对偶问题的最优解3）当b1由20变为45，最优解是否发⽣变化。

设备能力(h)
3 2 0 1500
65 40 75
2.2.1 线性规划的图解法
问题：工厂应如何安排生产可获得最大的 总利润？用图解法求解。
解：设变量xi 为第i种（甲、乙）产品的生 产件数（i＝1，2）。根据前面分析，可 以建立如下的线性规划模型： Max z = 1500 x1 + 2500 x2
2.2.1 线性规划的图解法
(1)建立直角坐标系： 分别取决策变量x1 ,x2 为坐标 向量，建立平面直角坐标系。
2.2.1 线性规划的图解法
（2）绘制可行域： 对每个约束（包括非负约束）条 件，作出其约束半平面（不等式）或 约束直线（等式）。
各半平面与直线交出来的区域若 存在，其中的点为此线性规划的可行 解。称这个区域为可行集或可行域。 然后进行下步。否则若交为空，那么 该线性规划问题无可行解。
线性规划的图解法
2.2.1 线性规划的图解法
对于只有两个决策变量的线性 规划问题，可以二维直角坐标平 面上作图表示线性规划问题的有 关概念，并求解。 图解法求解线性规划问题的步 骤如下：
例题
目标函数 Max z =1500x1+2500x2
约束条件 s.t. 3x1 + 2x2 ≤ 65 2x1 + x2 ≤ 40 3x2 ≤ 75 x1 ,x2 ≥ 0
2.2.1 线性规划的图解法
(3) 绘制目标函数等值线，并移动求解：
目标函数随着取值不同，为一族相 互平行的直线。 首先，任意给定目标函数一个值， 可作出一条目标函数的等值线（直线）； 然后，确定该直线平移使函数值增 加的方向； 最后，依照目标的要求平移此直线。
2.2.1 线性规划的图解法
结果
若目标函数等值线能够移动到 既与可行域有交点又达到最优的位 置，此目标函数等值线与可行域的 交点即最优解（一个或多个），此 目标函数的值即最优值。 否则，目标函数等值线与可行 域将交于无穷远处，此时称无有限 最优解。

9.2.2.2 相关函数介绍linprog函数功能：求解线性规划问题。

数学模型：其中f,x,b,beq,lb和ub为向量，A和Aeq为矩阵。

语法：x = linprog(f,A,b,Aeq,beq)x = linprog(f,A,b,Aeq,beq,lb,ub)x = linprog(f,A,b,Aeq,beq,lb,ub,x0)x = linprog(f,A,b,Aeq,beq,lb,ub,x0,options)[x,fval] = linprog(...)[x,fval,exitflag] = linprog(...)[x,fval,exitflag,output] = linprog(...)[x,fval,exitflag,output,lambda] = linprog(...)描述：x = linprog(f,A,b)求解问题min f'*x，约束条件为A*x <= b。

x = linprog(f,A,b,Aeq,beq)求解上面的问题，但增加等式约束，即Aeq*x = beq。

若没有不等式存在，则令A=[]、b=[]。

x = linprog(f,A,b,Aeq,beq,lb,ub)定义设计变量x的下界lb和上界ub，使得x始终在该范围内。

若没有等式约束，令Aeq=[]、beq=[]。

x = linprog(f,A,b,Aeq,beq,lb,ub,x0)设置初值为x0。

该选项只适用于中型问题，缺省时大型算法将忽略初值。

x = linprog(f,A,b,Aeq,beq,lb,ub,x0,options)用options指定的优化参数进行最小化。

[x,fval] = linprog(...) 返回解x处的目标函数值fval。

[x,lambda,exitflag] = linprog(...)返回exitflag值，描述函数计算的退出条件。

[x,lambda,exitflag,output] = linprog(...) 返回包含优化信息的输出变量output。

（4）等待服务的平均顾客数；
（5）顾客在店内等待时间超过 10 分钟的概率（已知
）。
（10 分）7. 某公司为经营业务的需要，决定要在现有生产条件不变的情况下，生产一种新
产品，现可供开发生产的产品有 I、II、III、IV 四种不同产品，对应的方案为 A1、A2、A3、
A4。由于缺乏相关资料背景，对产品的市场需求只能估计为大、中、小三种状态，而且对
时间
所需售货人员数
星期日
28
星期一
15
星期二
24
星期三
25
星期四
19
星期五
31
星期六
28
（15 分）2. 考虑如下线性规划问题
回答以下问题：
1）请用单纯形法求最优解；
2）直接写出上述问题的对偶问题及其最优解；
3）若问题中列 的系数变为
，问最优解是否有变化？如有变化，将新的解求出；
4）由由 1 变为 2，是否影响最优解？如有影响，将新的解求出。
第1页共3页
宁波大学 2020 年博士研究生招生考试初试试题(A 卷)
(答案必须写在考点提供的答题纸上)
科目代码： 3825 总分值： 100 科目名称：
运筹学
项目 投标者
甲 乙 丙 丁 戊
ABCDE
4 8 7 15 12 7 9 17 14 10 6 9 12 8 7 6 7 14 6 10 6 9 12 10 6
5. （10 分）
为了适应市场需要，某市提出了扩大某种电器生产的两个方案：一个方案是建设大工厂， 另一个方案是建设小工厂，两者的试用期都是 10 年。建设大工厂需要投资 600 万元，建设 小工厂需要投资 280 万元，两个方案的年收益或损失值及自然状态的概率见下表。试用决 策树法做出合理的决策。