微分方程模型--饮酒驾车
- 格式:pdf
- 大小:652.07 KB
- 文档页数:33




微分方程模型在实际问题中,我们很难直接得出变量之间的数量关系,但是有时却很容易写出包括变量的导函数在内的一个方程,这就是微分方程,我们在一般的建模中常涉及常微分方程。
微分方程一般形式为:0),...,'',',,()(=n yy y y x F 或),...,'',',,()1()(-=n n yy y y x f y。
若在某个范围内存在具有n 阶导数的函数)(x y ψ=使得))(,...,')'(,)'(),(,()(=x x x x x F n ψψψψ,则称)(x y ψ=是微分方程的解。
微分方程所解决的问题通常可以分为两类:一类是用微分方程列出变量之间的关系式,求出位置函数的表达式,有时要借助软件进行数值分析;另一类是要了解未知变量或函数的某些性质即可,常需要根据微分方程的定性理论来研究,这两类建模问题我们将在后面进行讨论。
1. 微分方程简介1.1. 简单的微分方程模型一种比较简单的微分方程模型是变量的变化率与函数的即时值成正比,即kyy =',它的解就是kt e y t y 0)(=,这里0y 是初值,k 是待定常量。
通常情况下,如果0>k 称)(t y 指数递增;如果0<k ,称)(t y 指数递减,我们通过几个例子来说明这种事实。
1.1.1. 放射性元素的自然衰变放射性元素的自然衰变是化学上的一个基本事实,它常用于定碳测量,在考古学学上利用该方法测定古生物生存年代。
存活于生物组织中占有确定比例的碳原子是放射性同位素14C ,一旦生物组织死亡,这种14C 不会增加,而会将一定比例的14C 衰变为12C ,并保持一定的速率(14C 的半衰期为5568年)按指数规律下降。
测定它现存的比例并与活的样品比较,就可以求得比例下降了多少,也就得到了被测样品的实际年代。
建立模型:假定)(t y 为t 时刻生物体内14C 原子的个数,经过相同的时间T ,y的值减少为原值的1/2 (指数衰减)。



饮酒驾车的优化模型摘要酒后驾车发生事故给人身安全造成极大的伤害,在全世界引起了广泛的关注。
本文通过分析啤酒中酒精在人体体内胃肠(含肝脏)与体液(含血液)之间的交换机理,分别建立了在短时间内喝酒和长时间喝酒两种情况下,胃肠和体液(含血液)中的酒精含量的微分方程。
对给出的数据,利用非线性最小二乘数据拟合及高斯-牛顿算法,确定了一瓶啤酒中的酒精含量以及酒精从胃肠进入血液的速度系数和酒精从血液渗透出体外的速度系数。
继而,对不同喝酒方式下,血液中酒精浓度进行分析。
该模型不仅能很好地解释大李在中午12:00时喝了一瓶啤酒后,在下午6:00时检查时符合驾车标准,紧接着再喝一瓶啤酒后,在次日凌晨2:00时检查却被判为饮酒驾车这一现象,而且可以预测喝酒后任一时刻血液中的酒精浓度.利用所建立的模型,我们可得到以下结果:1.大李在第一次检查时血液酒精浓度为19.9616毫克/百毫升。
第二次检查时血液酒精浓度为20.2448毫克/百毫升,这是由于第一次喝酒在体液中残留的酒精所导致。
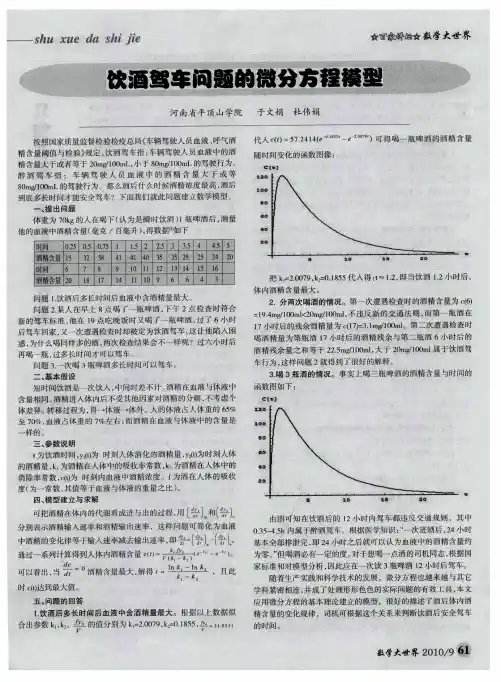
2.在短时间内,喝三瓶啤酒或喝半斤低度白酒分别在12.25小时和13.6小时内驾车会违反驾车新标准规定;在2小时间内喝3瓶啤酒或喝半斤低度白酒分别在13.28小时和14.63小时内驾车会违反驾车新标准规定。
3. 短时间喝酒,无论喝多少酒,血液中的酒精含量达到最高所用时间均为1.3255 小时。
长时间也与所喝酒精的量无关,只与喝酒所持续时间有关,我们得到喝酒持续时间与酒精含量到达最高点的时间的关系如下:4. 如果天天喝酒,只要适当控制好喝酒量与喝酒以后到开车的间隔时间还是可以开车的。
比如:一个70公斤,喝2瓶啤酒需间隔10小时以上。
该模型能较精确的预测时间与血液中酒精浓度的关系,其解具有较好的稳定性,为定量研究饮酒与驾车的关系提供了科学的依据。
同时,它具有很好的推广和应用价值,模型可推广到医学,化学等方面。
一、问题的重述酒后驾车引起的死亡事故占全国交通事故相当大的比例。


饮酒驾车问题模型摘要:关键词:非线性拟合酒后驾车微分方程一.问题重述根据规定,饮酒驾车是车辆驾驶人员血液中的酒精含量大于或者等于20mg/100ml ,小于80mg/100ml 的驾驶行为。
醉酒驾车是车辆驾驶人员血液中的酒精含量大于或者等于80mg/100ml 的驾驶行为。
二.问题分析 三.模型假设1. 人体在新陈代谢过程中不会产生酒精;2. 酒精在进入体液的同时迅速扩散均匀,且肠胃的容积与体液的容积是恒定的;3. 酒精从肠胃中渗透到体液的转移速率只与肠胃中酒精含量成正比;4. 血液中酒精的排除速率只与血液中酒精浓度成正比;5.人所能承受的酒精含量都是一样的,身体无差异性。
四.符号说明0L肠胃中的酒精总量t 时间m 两瓶啤酒中酒精总量0k酒精从肠胃中向血液中的转移速率系数v肠胃中酒精总量的变化速率1L 体液中酒精总量 0V体液的体积 c血液中的酒精含量0c 0t 时血液中的酒精含量1k 酒精从体液中排出的速率系数 1v在一段时间内喝酒的速度五.模型建立酒精从肠胃中进入体液符合渗透原理,分析血液中酒精含量随时间的变化情况,利用微元法对以下两种情况建立微分方程模型。
5.1 酒是在短时间内喝完时血液中酒精含量c 的变化由于酒是在短时间内喝完的,则0t =时肠胃中酒精总量0L 为0(0)L m = (1) 另一方面肠胃中酒精总量0L 的变化速率与其本身成正比,则0L 的变化速率可表示为:00()v t k L =- (2)()dL v t dt= (3) 在体液中,酒精总量1L 的变化速率只与酒精从肠胃中进入血液的速率和从血液中排出的速率有关,由此可得:1110()dL v t k L dt V =--(4) 另外,体液中酒精的浓度c 等于酒精总量与其体积的比值,则有:10()L c t V = (5)当0t =时体液中酒精总量为1L ,则0(0)c c = (6)将(2)(3)(5)代入(4)则可得出酒在短时间内喝完的情况下建立的微分方程模型一:00dL k L dt=- (7) 0(0)L m = (8)0010k L dck c dt V =-+ (9) 0(0)c c = (10)5.2酒是在较长一段时间内喝完时血液中酒精含量c 的变化当人的喝酒速率为恒速1v 时,肠胃中酒精总量在0t =时0(0)0L = (11)此时肠胃中酒精总量0L 的变化速率为001()v t k L v =-+ (12)()dL v t dt= (13) 此时由模型一可得0010k L dck c dt V =-+ (14) 且在0t =时血液中酒精含量为0(0)c c = (15)可以得到当酒在一段时间内喝完的情况下血液中酒精含量关于时间的微分方程模型为001dL k L v dt=-+ (16) 0(0)0L = (17)0010k L dck c dt V =-+ (18) 0(0)c c = (19)六.模型求解利用Matlab 数学软件对所建立的微分方程模型进行求解,并用cftool 工具箱对模型一的曲线进行非线性拟合。
五、饮酒驾车基本思路该问题是微分连续型问题,目的是判断、预测曲线的变化。
做出基本假设,建立微分方程,定义有关参数,利用MATLAB 求解并绘制曲线。
模型建立Ⅰ.假设酒精先以速率0k 进入胃中,然后以速率1()f t 从胃进入体液,再以速率2()f t 从体液中排到体外。
用()x t 与()y t 分别表示酒精在胃、体液中的酒精量,()c t 表示酒精在体液中的浓度。
可以建立如下图所示的带有吸收室的单房室系统,其中胃为吸收室,体液为中心室。
Ⅱ.假设酒精从胃进入体液的速度1()f t 与胃中的酒精量()x t 成正比,速率系数为1k ;酒精从体液中排出的速率2()f t 与体液中的酒精量()y t 成正比,速率系数为2k ,可以建立方程如下。
11()()f t k x t = (1) 22()()f t k y t = (2)01()()dx t k f t dt=- (3) 将(1)式代入(3)式可得01()()dx t k k x t dt=- (4) 通过移项,(4)可以转化为10()()dx t k x t k dt+= (5) 利用一阶线性常微分方程的常数变易法对(5)式求解,可以得到111011110()(0)k t x t c e A k A k c A x x -⎧=+⎪⎪=⎨⎪⎪+==⎩ (6) 又因为11()()f t k x t =,联合(6)式可得111111()K t f t k c e k A -=+11000()k t k x k e k -=-+ (7)Ⅲ.对中心室(即体液)可建立方程组如下。
120()()()(0)dy t f t f t dt y y ⎧=-⎪⎨⎪=⎩ (8) 将(2)式代入(8)式可得12()()()dy t f t k y t dt=- 将(7)其代入上式可得到121000()()()k t dy t k y t k x k e k dt-+=-+ (9) 求解(9)式可得212101002221222()k t k tk t k tk k x k y t c e e k k k c e A B e -----=++-=++ (10)其中022k A k =,100221k x kB k k -=-,2220(0)A B c y y ++==。
五,饮酒驾车问题分析酒精摄入体内直接进入胃中,再由胃中进入体液,由体液排除,不考虑人体其他代谢方式产生的酒精。
他第一次检验时体液中的酒精含量小于20毫克/百毫升,第二次却大于或等于20毫克/百毫升,小于80毫克/百毫升,判断大李第二次检查时中午12点摄入体内的酒精还未代谢完,因而此次检查体液中的酒精含量是两次之和。
所以根据已知条件建立微分方程,得到饮酒后血液中酒精含量m(t)随时间{ EMBED Equation.DSMT4 |t的变化规律,将大李从饮酒到检查的时间间隔代入其中,检验此刻酒精含量是否符合新标准,便可解释大李碰到的情况。
设如下变量:1.,胃和体液的酒精含量;2.:胃和体液的酒精浓度;3.:酒精进入体液的速率;4.:引入的酒精总量5.:胃和体液的体积;6.:酒精从胃进入体液的速率;7.:.酒精从体液排出体外的速率。
模型假设一、酒精从体外进入胃,单向渗入体液,从体液排出体外;二、胃和体液的容积不变;三、酒精在体液的转移速率及向体外排出的速率与体液酒精浓度成正比;模型的建立饮酒者喝酒后,酒精进入胃,单向渗入体液,从体液排出体外,在胃和体液的转移速率和排出速率均不同,所以可得:胃:(1)体液:(2)模型求解与结果分析方程组(1)解得,方程组(2)运用数学软件MATLAB,解得:在现实中每瓶啤酒体积:640ml;啤酒酒精度数:3.6%4.2%;啤酒酒精密度:800mg/l。
取啤酒酒精度数为4%,可得每瓶啤酒酒精含量为20480mg。
人的体液占人的体重的65%至70%,人体体液密度约为mg/100ml,酒精在血液中的含量与在体液中的含量大体一致,体重约为70kg的人在短时间内喝下2瓶啤酒,则为40960mg,(百毫升)。
编写程序如下t=[0.25 0.5 0.75 1 1.5 2 2.5 3 3.5 4 4.5 5 6 7 8 9 10 11 12 13 14 15 16];c=[30 68 75 82 82 77 68 68 58 51 50 41 38 35 28 25 18 15 12 10 7 7 4];k0=[3,0.5];k=lsqcurvefit('test',k0,t,c)Optimization terminated: relative function valuechanging by less than OPTIONS.TolFun.k =2.68580.1474plot(t,c,'*')tt=0:0.1:16;cc=test(k,tt);holdCurrent plot heldplot(tt,cc,'r')拟合图示如下:下面来求解问题我们认为:(1)大李在两次喝酒直到检查时没有服用任何影响体内酒精含量的药物;(2)大李吃晚饭时间为20:00。
饮酒驾车的数学模型摘要本文解决的是一个司机安全驾车与饮酒的问题,目的是通过建立一个数学模型(结合新的国家驾驶员饮酒标准)分析司机如何适量饮酒不会影响正常的安全驾驶。
根据一定合理的假设,建立人体内酒精浓度随时间变化的微分方程模型,并通过拟合曲线对数据进行分析。
在不同饮酒方式下进行分类讨论,得出体内酒精浓度随时间的变化函数。
在讨论过程中,我们得到两个结论:在短时间喝酒形式下,达到最大值的时间为小时,与喝酒量无关;在长时间喝酒形式下,喝酒结束时酒精含量最高。
最后,我们讨论了模型的优缺点,并结合新的国家标准写一篇关于司机如果何适量饮酒的一篇短文。
关键词:微分方程、模型、房室系统。
一、问题重述据报载,2008年全国道路交通事故死亡人数为万,其中饮酒驾车造成的占有相当的比例。
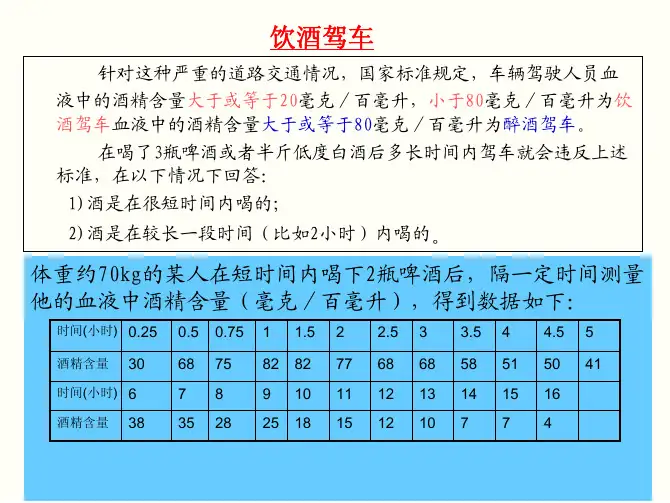
针对这种严重的道路交通情况,国家质量监督检验检疫局2004年5月31日发布了新的《车辆驾驶人员血液呼气酒精含量值与检验》国家标准,新标准规定,车辆驾驶人员血液中的酒精含量大于或等于20毫克/百毫升,小于80毫克/百毫升为饮酒驾车,血液中酒精含量大于或等于80毫克/百毫升为醉酒驾车。
司机大李在中午12点喝下一瓶啤酒,6小时后检查符合新标准,晚饭地其又喝了一瓶啤酒,他到凌晨2点驾车,被检查时定为饮酒驾车,为什么喝相同量的酒,两次结果不一样请你参考下面给出的数据(或自己收集资料)建立饮酒后血液中酒精含量的数学模型,并讨论以下问题:1、对大李碰到的情况做出合理解释;2、在喝三瓶啤酒或半斤白酒后多长时间内驾车会违反标准,在以下情况回答:1)酒食在很短时间内喝的:2)酒食在较长一段时间(比如两小时)内喝的3、怎样估计血液中的酒精含量在什么时间最高;4、根据你的模型论证:如果该司机想天天喝酒,是否还能开车5、根据你做的模型结合新的国家标准写一篇短文,给想喝一点酒的司机如何驾车提出忠告。
二、模型假设1、酒精从胃转移到体液的速率与胃中的酒精浓度成正比。
2、酒精从体液转移到体外的速率与体液中的酒精浓度成正比。
东南大学数学建模实验报告实验内容:酒驾问题一实验目的(1)掌握常微分方程建模问题(2)学会使用Matlab进行常微分方程的求解二实验内容与要求国家质量监督检验检疫局 2004年5月31日发布了新的《车辆驾驶人员血液、呼气酒 精含量阈值与检验》国家标准,新标准规定,车辆驾驶人 员血液中的酒精含量大于或等于20毫克/百毫升,小于80 毫克/百毫升为饮酒驾车(原标准是小于100毫克/百毫 升),血液中的酒精含量大于或等于80毫克/百毫升为醉 酒驾车(原标准是大于或等于100毫克/百毫升 )。
在中某人午12点喝了一瓶啤酒,下午6点检查时符合 新的驾车标准,紧接着他在吃晚饭时又喝了一瓶啤酒,为 了保险起见他呆到凌晨2点才回家,又一次遭遇检查时却 被定为饮酒驾车,这让他懊恼又困惑,为什么喝了同样多 的酒,两次检查结果会不一样呢?请你参考下面的数据建立饮酒后 血液中酒精含量的数学模型,并讨论以下问题: 1、对某人碰到的情况作出解释; 2、假设酒是在很短时间内喝的,在喝了3瓶啤酒或半斤低度白酒后多长时间内驾车就会违反上述标准.3、怎样估计血液中酒精含量在什么时候最高。
4、根据你的模型论证:如果天天喝酒,是否能开车? 以下是某人喝了两瓶啤酒后血液酒精浓度(毫克/百毫升)三 假设及建模假设一:机体分为中心室和周边室,两个室的容积在过程中保持不变。
假设二:药物从一室向另一室的转移速率,及向体外的排除速率,与该室的酒精浓度成正比。
假设三:只在中心室一体外有酒精交换,即酒精从体外进入中心室,最后又从中心室排出体外,与转移和排除的数量相比,酒精的吸收可以忽略。
建模:二室模型的示意图如下图所示:饮酒()t f 0两个房室中酒精量)(),(21t x t x 满足的微分方程。
)(1t x 的变化率由一室向二室的转移112x k -,一室向体外排除113xk -,二室向一室的转移221x k 及酒精)(0t f 组成;)(2t x的变化率由一室向二室的转移112x k 及二室向一室的转移221x k -组成,于是有: )(022********t f x k x k x k dtdx ++--=2211122x k x k dtdx -= (1) )(t x i 与血液中酒精含量)(t c i 、房室容积i V 显然有关系式2,1.................................),........()(==i t c V t x i i i (2)将(2)式代入(1)式可得:2211122121022112113121)()(c k c k V V dt dc V t f c k V Vc k k dt dc -=+++-= (3)喝酒相当于在酒精进入中心室之前先有一个将酒精吸收入血液的过程,可以简化为有一个吸收室,如下图,)(0t x 为吸收室的酒精,酒精由吸收室进入中心室的转移速率系数为01k ,于是)(0t x 满足:00010)0(D x x k dt dx =-= (4)当0)0(,)0(,0)(2110===c V D c t f 时,(3)可以化为: t t Be Ae t c βα--+=)(1四 代码及结果format short g% 题中提供的某人喝了两瓶啤酒后血液酒精浓度随时间变化表t=[ 0.25; 0.5; 0.75; 1; 1.5; 2; 2.5; 3; 3.5; 4; 4.5; 5; 6; 7; 8; 9; 10; 11; 12; 13; 14; 15; 16 ];c=[ 30; 68; 75; 82; 84; 77; 70; 68; 58; 51; 50; 41; 38; 35; 28; 25; 18; 15; 12; 10; 7; 7; 4 ];% 根据此变化表拟合求解相关系数ft =fittype('A1*exp(-a*x)+B1*exp(-b*x)');options = fitoptions('Method','NonlinearLeastSquares');options.StartPoint = [0 -1000 0 0];cfit = fit(t,c,ft,options);plot( cfit, t, c, 'o' );A1=cfit.A1B1=cfit.B1a=cfit.ab=cfit.b由此解得:(数值见右图,拟合曲线见下图)A1 = 110.55B1 = -151.46a = 0.17949b = 2.8243%---1---%%问题:某人中午12点喝了一瓶啤酒,下午6点检查合格,晚饭又喝一瓶,次日凌晨2点检查未通过,请对此情况做出解释。