第1章运筹学基础及应用-第六版

2019工商管理考研最全最详细解读，那些你不得不知的事儿2019考研的小伙伴们已经开始准备了，很多考生选择工商管理专业作为考研的目标，跨考考研老师将针对这一专业从以下几个方面进行分析，为2019考研的考生提供备考的参考。

1.工商管理专业简介工商管理类专业属于管理学中的一个大类，专业的知识范围较广，是一门跨自然科学、工程科学、技术科学以及人文社会科学的综合性交叉科学。

本专业旨在培养适应我国企业改革和发展需要，德、智、体全面发展，具有良好的知识结构，较高的管理素质和较强的创新精神，能独立从事企事业部门管理工作的管理人才。

(1)研究对象。

工商管理学科的研究对象主要是企业的经营管理活动，活动的效率、效果，以及与此相关的各类问题。

这些问题大致包括公司治理、生产运营、物流配送、组织行为与人力资源、财务与会计、市场营销与品牌创建、管理信息系统与互联网技术应用、技术创新管理、战略管理、服务管理等有关管理职能问题;企业产品或服务设计、采购、生产、运营、投资、理财、销售、战略发展等管理决策问题;企业作为一个整体与宏观社会、文化、政治、经济等外部环境之间的关系问题，以及企业创业、成长、危机及衰退等组织演进问题。

(2)学科基础理论。

工商管理学科基础理论主要包括经济学理论、管理学理论、行为科学理论、博弈论与决策论等。

首先，企业经营活动和管理决策在很大程度上受到宏观经济的影响，因此，经济学是工商管理学科的基础理论之一。

其次，经营管理活动和决策的主体是人，而人的个体或群体心理行为会影响企业的经营活动和管理决策，因此，行为科学同样成为工商管理学科的基础理论之一。

最后，本学科研究企业各种职能部门经营管理活动和管理决策，而在企业经营管理中面临复杂的内部代理问题和激烈的外部市场竞争，因此，博弈论和决策论近年来也逐步成为工商管理学科的基础理论之一。

由于工商管理学科内容的复杂性、交叉性、综合性和复杂性特征，各类专业还有自己一些独特的专业理论系统，主要包括财务与会计、生产运营管理、物流与供应链管理、组织行为与人力资源、技术管理、市场营销、企业战略管理等相关理论体系。

运筹学基础及应用P43例13 、混合配料问题:某糖果厂用原料A、B、C加工成三种不同牌号的糖果甲、乙、丙。

已知各种牌号糖果中A、B、C含量，原料成本，各种原料的每月限制用量，三种牌号糖果的单位加工费及售价如表1-19所示。

问该厂每月生产这三种牌号糖果各多少千克，使该厂获利最大。

试建立这个问题的线性规划的数学模型。

表1-19甲乙丙原料成本(元/kg) 每月限制用量(kg) A 2.00 2000 ?60% ?30%B 1.50 2500C 1.00 1200 ?20% ?50% ?60%0.50 0.40 0.30 加工费(元/kg)3.40 2.85 2.25 售价(元/kg)P44例14、投资项目的组合问题:兴安公司有一笔30万元的资金，考虑今后三年内用于下列项目的投资:(1) 三年内的每年年初均可投资，每年获利为投资额的20%，其本利可一起用于下一年投资;(2) 只允许第一年初投入，于第二年末收回，本利合计为投资额的150%，但此类投资限额不超过15万元;(3) 允许于第二年初投入，于第三年末收回，本利合计为投资额的160%，但限额投资20万元;(4) 允许于第三年初投入，年末收回，可获利40%，但限额为10万元。

试为该公司确定一个使第三年末本利和为最大的投资组合方案。

P44例15、生产、库存与设备维修综合计划的安排:红光厂有2台车床，1台钻床，1台磨床，承担4中产品的生产任务(已知生产各种产品所需的设备台时及生产单位产品的售价如表,,20所示(对各种产品今后三个月的市场最大需求(小于最大需求量时即可全部销出)及各产品在今后三个月的生产成本分别如表1,21和表1,22所示(上述设备在1~3月内各需进行一次维修,具体安排为:2台车床于2月份、3月份各维修一台,钻床安排在2月份维修,磨床安排在3月份维修.各设备每月工作22天.每天2班,每班8h,每次维修占用半各月时间.又生产出来的产品当月销售不出去(超过最大需求量)时,可在以后各月销售,但需付每件每月储存费5元.但规定每月底各种产品储存量均不得超过100件.1月初各产品无库存,要求3月底各产品均库存50件.试安排该厂各月的生产计划,使总的利润为最大.表,,20 a值单位:h iji ? ? ? ? j车床 ,., ,., ,.,钻床 ,., ,., ,.,磨床 ,., ,., ,.,售价(元,件) ,, ,, ,, ,,表 1,21 最大需求量单位:件 K ? ? ? ? j1月 200 300 200 200 2月 300 200 0 300 3月 300 100 400 0表,,22 产品成本单位:元,件K ? ? ? ? j,月 ,, ,, ,, ,, ,月 ,, ,, ,, ,, ,月 ,, ,, ,, ,,P81例1、某食品公司经销的主要产品之一是糖果。

一年就这样过去了，内心思绪万千。

一年很短，备考的经历历历在目，一年很长，长到由此改变了一个人的轨迹，并且成就一个梦想。

回忆着一年的历程，总想把它记录下来，希望可以给还在考研道路上奋斗的小伙伴们一点帮助。

考研是一个非常需要坚持的过程，需要你不断坚持和努力才能获得成功，所以你必须要想清楚自己为什么要考研，这一点非常重要，因为只有确认好坚定的动机，才能让你在最后冲刺阶段时能够坚持下来。

如果你只是看到自己周围的人都在考研而决定的考研，自己只是随波逐流没有坚定的信心，那么非常容易在中途就放弃掉了，而且现在考研非常火热，这就意味着竞争也会非常激烈，而且调剂的机会都会非常难得，所以备考时的压力也会比较大，所以大家一定要调整好心态，既不能压力太大，也不能懈怠。

既然选择了，就勇敢的走下去吧。

考研整个过程确实很煎熬，像是小火慢炖，但是坚持下来，你就会发现，原来世界真的是美好的。

文章整体字数较多，大家可视自己情况阅读，在文章末尾我也分享了自己备考过程中的资料和真题，大家可自行下载。

中国矿业大学交通运输的初试科目为：（101）思想政治理论（204）英语二（302）数学二（862）运输运筹学参考书目：1.《运筹学（第4 版）》本科版，《运筹学》教材编写组，清华大学出版社，2013.1；2.《运筹学基础及应用》（第六版），胡运权，高等教育出版社，2014.2；3.《管理运筹学（第4 版）》，韩伯棠，高等教育出版社，2018.6。

关于英语复习的建议考研英语复习建议:一定要多做真题，通过对真题的讲解和练习，在不断做题的过程中，对相关知识进行查漏补缺。

对于自己不熟练的题型，加强训练，总结做题技巧，达到准确快速解题的目的。

虽然准备的时间早但因为各种事情耽误了很长时间，真正复习是从暑假开始的，暑假学习时间充分，是复习备考的黄金期，一定要充分利用，必须集中学习，要攻克阅读，完形，翻译，新题型！大家一定要在这个时间段猛搞学习。

在这一阶段的英语复习需要背单词，做阅读（每篇阅读最多不超过20分钟），并且要做到超精读。

教学基本文件模板课程教学大纲：《运筹学》课程教学大纲课程编号：课程名称：运筹学/Operational Research课程总学时/学分：72/4 （其中理论60学时，实验12学时）适用专业：适用本科四年制信息管理与信息系统专业一、课程简介本课程的授课对象是信息管理与信息系统专业本科生，属管理类专业专业基础必修课。

《运筹学》是以定量分析为主来研究经济管理问题，将工程思想和管理思想相结合，应用系统的、科学的、数学分析的方法，通过建模、检验和求解数学模型获得最优决策方案。

本课程的主要内容包括线性规划、运输问题、整数规划、目标规划、动态规划、网络分析等与经济、管理和工程领域密切相关的运筹学分支的基本模型、方法和应用。

运用科学的模型化方法来描述、求解和分析问题，从而支持决策。

二、教学目的和任务本课程旨在使同学们正确、全面地掌握各级管理工作中已被广泛应用、发展比较成熟的最优化理论与方法，并能运用所学理论和方法解决管理工作中出现的各种优化问题，为后续课程奠定定量分析基础。

在已学过高等数学、微积分、线性代数等课程基础上学习本课程，通过教授、自学、复习、作业练习、辅导、上机等教学环节达到上述目的。

学习中要注意到学科系统性，数学概念和逻辑的严密性、准确性和完整性，但不偏重纯数学方法论证。

注重基本概念、基本思路、基本方法、算法步骤的掌握，了解各种方法特点和实用价值，提高建立模型、分析求解能力和技巧。

应注重实际应用中建立模型，选择可行求解的理论方法，运用计算机工具求解这三方面训练的有机结合。

三、教学基本要求信息管理与信息系统专业的学生应系统地学习《运筹学》的全部内容。

系统掌握线性规划、运输问题、目标规划、整数规划、动态规划、图与网络分析的理论和方法；能借助Excel、Lingo等电子计算手段，运用所学理论和方法解决实际问题。

通过该课程的学习，进一步培养学生的分析问题和解决问题的能力。

四、教学内容与学时分配绪论（2学时）第一节运筹学的定义与发展简史1、运筹学名称的来历；2、运筹学的发展简史。

运筹学第6版参考答案运筹学是一门研究如何有效地利用有限资源来解决实际问题的学科。

它涵盖了数学、统计学、经济学等多个学科的知识，旨在通过建立数学模型和运筹方法来优化决策和规划。

本文将为读者提供《运筹学第6版》的参考答案，帮助他们更好地理解和应用这门学科。

第一章：引论本章主要介绍了运筹学的概念、发展历程以及应用领域。

运筹学的核心思想是通过数学模型和运筹方法来解决实际问题。

它广泛应用于生产、物流、供应链管理、金融等领域，可以帮助企业提高效益、降低成本。

第二章：线性规划线性规划是运筹学中最基础、最常用的方法之一。

它的目标是在给定的约束条件下，最大化或最小化一个线性目标函数。

本章介绍了线性规划的基本概念、模型建立方法以及常用的解法算法，如单纯形法、对偶理论等。

第三章：整数规划整数规划是线性规划的一种扩展形式，它要求决策变量取整数值。

由于整数规划的求解难度较大，本章介绍了常用的整数规划求解方法，如分支定界法、割平面法等，并给出了一些实际问题的案例分析。

第四章：网络优化网络优化是运筹学中的一个重要分支，它研究的是在网络结构中如何选择最优路径、分配资源等问题。

本章介绍了最小生成树、最短路径、最大流等基本概念和算法，并通过实例分析展示了网络优化在交通、通信等领域的应用。

第五章：动态规划动态规划是一种通过递推关系来求解最优化问题的方法。

本章介绍了动态规划的基本思想、模型建立方法以及常见的解法算法，如背包问题、最长公共子序列等。

通过实例分析，读者可以更好地理解动态规划的应用。

第六章：排队论排队论是运筹学中研究排队系统的理论和方法。

本章介绍了排队论的基本概念、模型建立方法以及常用的解法算法，如排队模型、排队规则等。

通过实例分析，读者可以了解如何通过排队论来优化服务质量、提高效率。

第七章：模拟模拟是一种通过构建系统模型进行实验和仿真的方法。

本章介绍了模拟的基本思想、模型建立方法以及常见的模拟技术，如蒙特卡洛方法、离散事件模拟等。

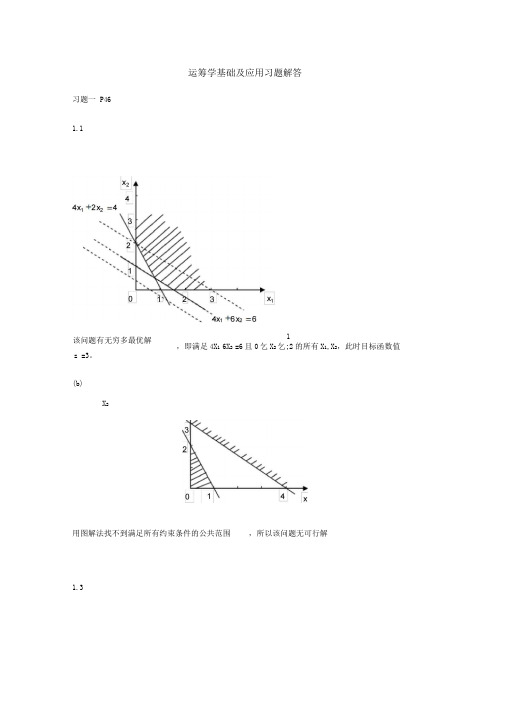
运筹学基础及应用习题解答习题一P461.1该问题有无穷多最优解1，即满足4X1 6X2 =6且0乞X2乞;2的所有X1,X2，此时目标函数值z =3。

(b)X2用图解法找不到满足所有约束条件的公共范围，所以该问题无可行解1.3(1)图解法最优解即为严1 +4x2 -9的解X =h，?丨最大值Zu35 0X1 +2X2 =8 I 2 丿 2 (2)单纯形法首先在各约束条件上添加松弛变量，将问题转化为标准形式max z =10x i 亠5x2 亠0x3 亠0x4丄3为+4X2 +刈=9st.』+2x2+x4=8则f,P4组成一个基。

令x i =x2 =0x = 0,0,9,8c c .「21 8 3■ -2 0, min ,-訂4 2丿2新的单纯形表为C j T10 5 0 0X1 X2 X3 X4C B基 b3 5 35 x 2 —0 12 2 14 1410 X1 1 1 21 07 75 25C j _Z j 0 014 143 * 35 ；「1,；「2 ：：O 表明已找到冋题最优解X1 =1, X2 , X3 =0, X4 =0。

最大值z2 2(b)(1)图解法最优解即为6x1 2x2曲的解X = 7丄,最大值z上:X i +X2 =5 W2 丿 2(2)单纯形法首先在各约束条件上添加松弛变量，将问题转化为标准形式max z =2x1 x2 0x3 0x40疋st. 6x1 2x2 x4=24X i X2 X5 = 5则F3，F4，F5组成一个基。

令x i =X2 =0得基可行解x =[0,0,15,24,5 ，由此列出初始单纯形表Cj T 2 1 0 0 0\C B 基 b X1 X2 X3 X4 X5 \ \0 X 315 0 5 1 0 0X 4 24 ⑹ 2 0 1 00 X 55 1 1 0 0 1C j —Zj2 1 0 0 0日=min( 24 5^=4AO"2。

r 一-6 ‘1丿C j T210 0CB基bX 1X 2 X 3X 4X 5X 351151112X 4436■211X 51〔3」_6111C j 一Zj—33新的单纯形表为C j T21CB基b X 1X 2X 3X 4 X 515 015 15 0X 32 4 2711 2X 4 — 1—— 2 4 231 3 0X 51—■—— 24211 C j -Z j0 01 24二 min15訐,7 15二2 <0,表明已找到问题最优解X. =1 , X2 =2，冷巧，X“°, X. =0。

《运筹学》教案（2014 年2 月）授课班级：2010级农林经济管理教材：《运筹学》，熊伟，机械工业出版社学分：4学分学时：64学时教学过程1.运筹学与线性规划基本概念（10分钟）2.应用模型举例（60分钟）生产计划问题、人员安排问题、合理用料问题、配料问题、投资问题教学过程3•线性规划的一般模型（10分钟）4.课堂练习（10分钟）5.课堂小结（5分钟）6.布置作业教学过程教学过程 1. 引例:（P41）两个模型的对应关系：（20分钟） 2. 线性规划的规范形式（10分钟） 3. 对偶模型（5分钟）4. 对称型对偶关系的一般形式（5分钟）5. 对称型对偶关系的一般形式（三个特点）（10分钟）非对称型对偶关系 对于非对称型且具有对偶关系的两个PL 问题，总结得出:定理：互为对偶的两个PL 问题，如果原问题中第k 个约束条件 是等式，则它的对偶规划中的第k 个变量无非负限制，反之亦然.线性规划的原始问题和对偶问题的对应关系可归纳为下表5. 6. 课堂小结，布置作业教学过程【性质1】（对称性）对偶问题的对偶是原问题。

（5分钟）【性质2】（弱对偶性）设F、r分别为LP（max）与DP （min）的可行解，则CX°<Y°b（10分钟）由性质2可得到下面几个推论：推论1：的任一可行解的目标值是（龙）的最优值下界；（龙）任一可行解的目标是（2乃的最优值的上界；推论2:在互为对偶的两个问题中，若一个问题具有无界解，则另一个问题无可行解；推论3:若原问题可行且另一个问题不可行，则原问题具有无界解。

【性质3］（最优性）设F与尸分别是（2P）与（莎）的可行解，则F、尸是JLP）与（矿）的最优解当且仅当C X0 =卩呢（10分钟）【性质4】（对偶性）若互为对偶的两个问题其中一个有优解，则另一个也有最优解，且最优值相同。

（20分钟）教学过程由性质4还可推出另一结论：若（2P）与（矿）都有可行解，则两者都有最优解；若一个问题无最优解，则另一问题也无最优解。

考研是一项小火慢炖的工程，切不可操之过急，得是一步一个脚印，像走长征那样走下来。

在过去的一年中，我几乎从来没有在12点之前睡去过。

也从来也没有过睡到自然醒的惬意生活，我总是想着可能就因为这一时的懒惰，一切都不同了。

所以，我非常谨小慎微，以至于有时会陷入自我纠结中，像是强迫症那样。

如今想来，这些都是不应该的，首先在心态上尽量保持一个轻松的状态，不要给自己过大的压力。

虽然考研是如此的重要，但它并不能给我们的人生下一个定论。

所以在看待这个问题上不可过于极端，把自己逼到一个退无可退的地步。

而在备考复习方面呢，好多学弟学妹们都在问我备考需要准备什么，在我看来考研大工程，里面的内容实在实在是太多了。

首先当你下定决心准备备考的时候，要根据自己的实际情况、知识准备、心理准备、学习习惯做好学习计划，学习计划要细致到每日、每周、每日都要规划好，这样就可以很好的掌握自己的学习进度，稳扎稳打步步为营。

另外，复试备考计划融合在初试复习中。

在进入复习之后，自己也可以根据自己学习情况灵活调整我们的计划。

总之，定好计划之后，一定要坚持下去。

最近我花费了一些时间，整理了我的一些考研经验供大家参考。

篇幅比较长，希望大家能够有耐心读完，文章结尾处会附上我的学习资料供大家下载。

西华大学交通运输的初试科目为：（101）思想政治理论（204）英语二（302）数学二（812）汽车运用工程或（814）运筹学或（815）交通工程学或（824）高级程序设计语言参考书目：1.《汽车运用工程(第五版)》，许洪国，人民交通出版社，2014年。

2.《运筹学基础及应用》（第六版），胡运权等，高等教育出版社。

3.《交通工程总论》，徐吉谦、陈学武，人民交通出版社；4.《交通规划》，王炜、陈学武，人民交通出版社；5.《交通管理与控制》，罗霞、刘澜，人民交通出版社。

6.《C++程序设计》，谭浩强，清华大学出版社。

关于英语复习的一些小方法英语就是平时一定要做真题，把真题阅读里面不会的单词查出来，总结到笔记上，背诵单词，在考试之前，可以不用大块的时间，但一定要每天都看最起码2小时英语，把英语当做日常的任务，真题一定要做，而且单词要背熟，我在考试之前背了3遍的考研单词，作文可以背诵一些好词好句，在考场灵活运用。

运筹学课后习题答案第六版运筹学是一门应用数学学科，旨在研究如何在有限资源和约束条件下做出最佳决策。

它涉及到决策分析、优化理论、线性规划、整数规划、动态规划等多个领域。

在学习运筹学的过程中，课后习题是巩固知识和提高能力的重要途径。

本文将为大家提供《运筹学课后习题答案第六版》的相关内容。

第一章：决策分析决策分析是运筹学的基础，它主要涉及到决策的目标、决策的环境、决策的准则等方面。

在第一章的习题中，我们需要运用决策树、决策表、决策矩阵等方法来解决实际问题。

比如，一个公司需要决策是否要进军某个新市场，我们可以通过绘制决策树来分析各种可能的结果和概率，从而选择最佳的决策。

第二章：线性规划线性规划是运筹学中的重要工具，它主要涉及到线性目标函数和线性约束条件的最优化问题。

在第二章的习题中，我们需要运用单纯形法、对偶理论等方法来求解线性规划问题。

比如，一个工厂需要决策如何分配有限的资源以最大化利润，我们可以建立一个线性规划模型，然后通过单纯形法来求解最优解。

第三章：整数规划整数规划是线性规划的扩展，它主要涉及到目标函数和约束条件都是整数的最优化问题。

在第三章的习题中，我们需要运用分支定界法、割平面法等方法来求解整数规划问题。

比如，一个物流公司需要决策如何安排货物的配送路线以最小化成本，我们可以建立一个整数规划模型，然后通过分支定界法来求解最优解。

第四章：动态规划动态规划是一种用来解决多阶段决策问题的方法，它主要涉及到状态转移方程和最优子结构的求解。

在第四章的习题中，我们需要运用贝尔曼方程、最短路径算法等方法来求解动态规划问题。

比如，一个投资者需要决策在不同时间点买入和卖出股票以最大化收益，我们可以建立一个动态规划模型，然后通过贝尔曼方程来求解最优解。

第五章：网络优化网络优化是一种用来解决网络流问题的方法，它主要涉及到网络的建模和最大流最小割定理的求解。

在第五章的习题中，我们需要运用最大流算法、最小割算法等方法来求解网络优化问题。

运筹学基础及应用P43例13 、混合配料问题：某糖果厂用原料A、B、C加工成三种不同牌号的糖果甲、乙、丙。

已知各种牌号糖果中A、B、C含量，原料成本，各种原料的每月限制用量，三种牌号糖果的单位加工费及售价如表1-19所示。

问该厂每月生产这三种牌号糖果各多少千克，使该厂获利最大。

试建立这个问题的线性规划的数学模型。

表1-19P44例14、投资项目的组合问题：兴安公司有一笔30万元的资金，考虑今后三年内用于下列项目的投资：（1）三年内的每年年初均可投资，每年获利为投资额的20%，其本利可一起用于下一年投资；（2）只允许第一年初投入，于第二年末收回，本利合计为投资额的150%，但此类投资限额不超过15万元；（3）允许于第二年初投入，于第三年末收回，本利合计为投资额的160%，但限额投资20万元；（4）允许于第三年初投入，年末收回，可获利40%，但限额为10万元。

试为该公司确定一个使第三年末本利和为最大的投资组合方案。

P44例15、生产、库存与设备维修综合计划的安排：红光厂有2台车床，1台钻床，1台磨床，承担4中产品的生产任务．已知生产各种产品所需的设备台时及生产单位产品的售价如表１－20所示．对各种产品今后三个月的市场最大需求（小于最大需求量时即可全部销出）及各产品在今后三个月的生产成本分别如表1－21和表1－22所示．上述设备在1~3月内各需进行一次维修,具体安排为:2台车床于2月份、3月份各维修一台,钻床安排在2月份维修,磨床安排在3月份维修.各设备每月工作22天.每天2班,每班8h,每次维修占用半各月时间.又生产出来的产品当月销售不出去(超过最大需求量)时,可在以后各月销售,但需付每件每月储存费5元.但规定每月底各种产品储存量均不得超过100件.1月初各产品无库存,要求3月底各产品均库存50件.试安排该厂各月的生产计划,使总的利润为最大.表１－20a值单位：h表1－21 最大需求量单位：件P81例1、某食品公司经销的主要产品之一是糖果。