七自由度机器人运动学分析

摘要机器人技术已成为高技术领域内具有代表性的战略性技术之一，它使得传统的工业生产面貌发生巨大的变化，对社会的发展产生深远影响。

机器人运动学是机器人技术重要的组成部分，机器人运动学逆问题的求解是机器人轨迹规划、位置控制和离线编程的主要步骤之一。

本文主要介绍了我国工业机器人的发展以及工业机器人运动学的研究现状，对位姿变换、坐标变换等运动学分析的基础知识进行了简单的描述。

本文通过对Motoman-V A1400型七自由度机器人的结构分析，利用D-H方法建立机器人坐标系简图，确定各关节连杆参数，并在运动学正解的基础上，利用反变换矩阵的方法进行了运动学逆解的计算。

本文简单介绍了虚拟样机技术的概念和应用，虚拟样机技术平台ADAMS软件及其基本模块。

本文最后利用UG对机器人进行三维建模，并导入ADAMS中进行逆运动学的分析及仿真，在已知末端轨迹的情况下，绘出各关节的运动状态曲线，得到仿真结果。

机器人逆运动学研究所取得的任何突破性的进展都将对机器人技术产生重要的影响。

关键词：七自由度，逆运动学，仿真ABSTRACTRobotic technology has become one of representative strategic technology in high-tech field. It makes the traditional industrial production have undergone tremendous changes and have a profound impact on social development. Kinematics is an important part of robotics, and the solution of the robot inverse kinematics is one of the main steps of robot trajectory planning, position control and off-line programming.This article introduces the development of industrial robots and industrial robots research of kinematics, and gives a simple description on the position and orientation transformation, coordinate transformation, kinematics analysis and other basic knowledge. This article analyses the structure of the seven degrees of freedom robot Motoman-V A1400, then establishes the robot coordinate system diagram by D-H method to determine the link parameters of each joint, and the calculations of inverse kinematics by inverse transform matrix method on the basis of kinematics. Then, the article briefly introduces the concept of virtual prototyping technology and applications, virtual prototyping platform, ADAMS, and its basic modules. Finally, the robot using 3D modeling of UG, and in the case of the known end of the track, analyses and simulates the inverse kinematics into ADAMS, draw the simulation results that the state of motion of each joint curves.The progress achieved any breakthrough of inverse kinematics will have a major impact on robotics technology.Key Word: 7 DOF, inverse kinematics, simulation目录摘 要 (I)ABSTRACT (II)第一章 绪论 (1)1.1 工业机器人的发展 (1)1.2 工业机器人运动学研究现状 (2)1.3 虚拟样机技术的应用 (3)1.4 课题来源及选题意义 (4)1.5 本文的主要研究内容 (6)第二章 机器人空间描述与坐标变换矩阵 (7)2.1 MOTOMAN-VA1400机器人简介 (7)2.2 MOTOMAN-VA1400机器人空间描述 (8)2.2.1 机器人坐标系的建立 (8)2.2.2 机器人连杆参数的确定 (10)2.3 MOTOMAN-VA1400机器人坐标变换矩阵 (11)2.3.1 机器人齐次坐标变换 (11)2.3.2 机器人坐标变换矩阵的求解 (12)2.4 本章小结 (15)第三章 机器人逆运动学求解 (17)3.1 逆运动学求解方案的选择 (17)3.2 逆运动学方程最优解的选取 (17)3.3 逆运动学方程的求解过程 (18)3.4 逆运动学求解结果 (21)3.5 本章小结 (25)第四章运动学仿真与分析 (26)4.1 ADAMS基本模块简介 (26)4.2 ADAMS模型仿真 (27)4.2.1 机器人的几何建模 (27)4.2.2 ADAMS环境下生成虚拟样机 (29)4.2.3 样机的约束添加和参数设置 (29)4.2.4 仿真与结果的输出 (32)4.3 仿真结果分析 (34)4.4 本章小结 (36)第五章结论与展望 (37)5.1 结论 (37)5.2 技术经济分析 (37)5.2.1 技术可行性分析 (37)5.2.2 经济优越性分析 (37)5.3 对进一步研究的展望 (38)参考文献 (39)致谢 (41)附录 (42)第一章绪论1.1 工业机器人的发展机器人是一种可编程，通用，有操作和移动能力的自动化机械。

七自由度柔性机械臂机构说明设计目标由于人工成本的不断提升，人们的刚性需求也不断的扩大，生产自动化越来越被人们所重视。

也是社会发展的必然。

让机器人去完成一些高危、肮脏、重复、精度高的工作。

由此，设计一款高精度，高灵活性的机器臂显得更为重要。

设计的目标：高精度仿人工业机器人。

运用先进的仿生理论与柔性设计为基础，设计开发用二次式运动反馈来实现其高精度控制，合理的仿人机构来完成动动。

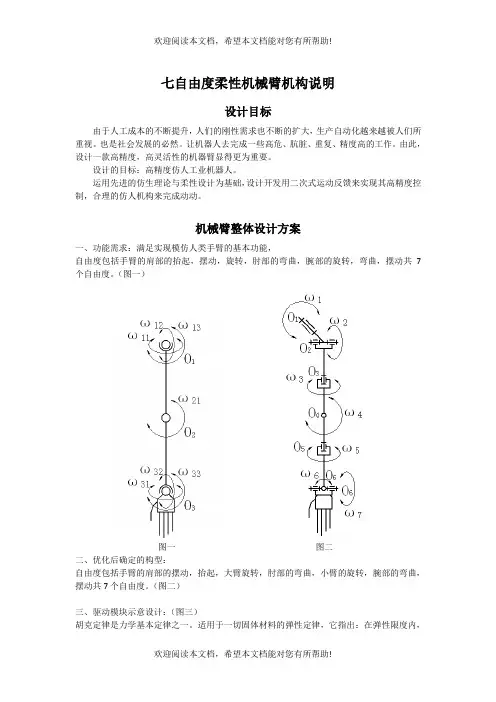
机械臂整体设计方案一、功能需求：满足实现模仿人类手臂的基本功能，自由度包括手臂的肩部的抬起，摆动，旋转，肘部的弯曲，腕部的旋转，弯曲，摆动共7个自由度。

（图一）图一图二二、优化后确定的构型：自由度包括手臂的肩部的摆动，抬起，大臂旋转，肘部的弯曲，小臂的旋转，腕部的弯曲，摆动共7个自由度。

（图二）三、驱动模块示意设计：（图三）胡克定律是力学基本定律之一。

适用于一切固体材料的弹性定律，它指出：在弹性限度内，物体的形变跟引起形变的外力成正比。

这样增加了力的反馈测量。

在弹性材料在弹性限度内形变时，测得其形变量，从而计算出受力与关节下方所处的位置。

1.先进行测试图三四、机械臂的具体设计方案，（图四）五、各关节的受力分析：基本尺寸图（图五）图五L1=426mm，L2=293mm，L3=108mm，L4=442mm。

六、马达的初选谐波减速器的优点：Harmonic减速器结构简单，体积小，重量轻、啮合的齿数多、承载能力大、运动精度高、运动平稳、间隙可以调整、传动效率高、同轴性好、可实现向密闭空间传递运动及动力。

瑞士Maxon电机优点：轴向窜动和径向跳动小、温度范围大、回差小等，并且电机型号全编码器与抱闸与控制器配套全面。

瑞士Maxon电机与日本Harmonic谐波减速器选型需求示例图片：图六马达1：EC90flat 90W扭力：4.67 nm 0.387nm；转速：3190rpm；重量：648g减速器1：CSG-25-160 减速比：1:160；最大扭力：314nm；正常：176nm；重量：420g马达2：EC-4pole max30 200W 扭力：3.18 nm 0.112nm；转速：17000rpm；重量：300g减速器2：CSG-25-160 减速比：1:160；最大扭力：314nm；正常：176nm；重量：420g马达3：EC max40 170W 扭力：2.66nm0.16nm；转速：9840rpm；重量：580g减速器3：CSG-17-120 减速比：1:120；扭力最大：112nm；正常：70nm；重量：150g马达4：EC45flat 70W 扭力：0.82nm0.13nm；转速：4840rpm；重量：110g减速器4：CSG-20-160 减速比：1:160；最大扭力：191nm；正常：120nm；重量：280g马达5：EC-4pole max30 100W 扭力：1.24nm 0.0 63nm；转速：17800rpm；重量：210g减速器5：CSD SHD-17-100 减速比：1:100；最大扭力：71nm；正常：37nm；重量：100g 马达6：EC45flat 70W 扭力：0.13 nm 0.17nm；转速：4840rpm重量：110g减速器6：CSF-11-100 减速比：1:100；最大扭力：25nm；正常：11nm；重量：50g马达7：EC-4pole max30 100W 扭力：1.24nm 0.0 63nm；转速：17800rpm；重量：210g减速器7：CSF-11-100 最大扭力：25nm；正常：11nm；重量：50g说明：EC45flat 70W要更换为EC-I40 70W+MR七、受力分析：有效扭力计算公式：(堵转-连续）*0.3+连续质量分配：设大臂小臂均为，外径D=110mm，假设主体为外壁壁厚为L=5mm的铝壳，长度为H=250mm，则体积为：412cm3，铝的密度2.7g／cm3，外壳质量为1.1kg大臂部分质量有马达3（580g）减速器（150g），外壳（1.1kg）；小臂部分有马达4567（110g，210g，110g，210g），减速器4567（280g，100g，50g，50g），外壳（1.1kg）；手部主要是灵巧手的质量设为1kg；外加假设载荷6kg。

七自由度机械臂逆解方案设计
七自由度机械臂逆解方案设计是指在已知机械臂末端位置和姿态的情况下，求解出机械臂各关节的角度，从而实现机械臂的运动。

以下是一种常用的七自由度机械臂逆解方案设计的步骤：
1. 机械臂建模：确定机械臂的结构和参数，包括关节类型（如旋转关节、滑动关节等）、关节长度和转动轴的方向。

2. 坐标系设定：确定机械臂的坐标系，包括基座的坐标系和末端执行器的坐标系。

通常选择一个固定的参考坐标系作为基座坐标系，然后依次定义各关节坐标系和末端执行器坐标系。

3. 正运动学求解：根据机械臂的结构和参数，使用正运动学方程求解出末端执行器的位置和姿态。

正运动学方程将末端执行器的坐标表示为各关节角度的函数。

4. 逆运动学求解：根据末端执行器的位置和姿态，使用逆运动学方程求解出机械臂的关节角度。

逆运动学方程将关节角度表示为末端执行器的位置和姿态的函数。

5. 解的求解：使用数值方法求解逆运动学方程的解。

由于逆运动学方程往往是非线性的，一般使用数值迭代方法（如牛顿法）求解。

6. 解的优化：对求解得到的关节角度进行优化，以满足机械臂
运动的限制条件，如关节角度限制、关节速度限制等。

7. 控制指令生成：将求解得到的关节角度转化为机械臂的控制指令，发送给机械臂控制系统，实现机械臂的运动。

8. 可视化和验证：将求解得到的关节角度应用到机械臂模型中，进行可视化和验证，确保逆解方案设计的正确性。

以上是一种常用的七自由度机械臂逆解方案设计的步骤，具体的设计过程还需要根据具体的机械臂结构和要求进行调整和优化。

多自由度串联机器人运动学分析与仿真共3篇多自由度串联机器人运动学分析与仿真1多自由度串联机器人运动学分析与仿真随着工业技术的不断发展和普及，机器人系统已经被广泛应用于各个领域，如汽车工业、制造业等。

机器人系统的控制和运动学分析是实现机器人精确控制和操作的重要基础。

本文将介绍多自由度串联机器人的运动学分析以及仿真。

1. 多自由度串联机器人多自由度机器人是指由多个自由度组成的机器人，可以进行更加复杂的操作。

串联机器人是指机器人的多个部分按照一定的顺序连在一起构成的机器人。

多自由度串联机器人是指由多个自由度组成，并且这些自由度按照一定的顺序连在一起构成的机器人。

例如，可以将多个关节连接起来构成一个多自由度关节机器人。

多自由度串联机器人在制造和物流业非常常见。

2. 运动学分析运动学分析是机器人系统控制中非常重要的一部分。

它描述了机器人如何移动和定位，以及如何控制机器人的各个部分进行精确的运动。

运动学分析主要解决以下几个问题：(1) 机器人姿态分析问题。

机器人姿态分析主要是描述机器人末端执行器的空间位置和末端姿态。

(2) 机器人关节角度分析问题。

机器人关节角度分析是指计算机器人各个关节的角度，以确定机器人的运动轨迹。

(3) 机器人轨迹分析问题。

机器人轨迹分析是对机器人运动轨迹进行精确计算和控制，以达到所需的操作目标。

3. 串联机器人的运动学分析多自由度串联机器人的运动学分析可以分为直接运动学和逆运动学两个部分。

(1) 直接运动学直接运动学是一种基于机器人各关节的运动学参数计算出机器人末端执行器姿态和位置的方法。

其公式如下：T_n = T_1 * T_2 * … * T_n-1其中，T_n表示机器人从末端执行器到机器人基座的坐标变换矩阵；T_i表示机器人第i个关节的变换矩阵。

(2) 逆运动学逆运动学是通过机器人末端执行器的姿态和位置计算机器人各关节的角度的方法。

逆运动学公式如下：T_n = T_base * T_tool其中，T_base表示机器人基座的坐标变换矩阵；T_tool表示机器人末端执行器的变换矩阵。

七自由度机械臂逆运动学引言：机械臂是一种重要的工业自动化设备，在许多领域中发挥着重要的作用。

为了实现机械臂的精确控制，我们需要了解机械臂的逆运动学。

本文将介绍七自由度机械臂的逆运动学问题，并探讨其解决方法。

一、机械臂的七自由度七自由度机械臂是指具有七个独立自由度的机械臂。

这意味着机械臂可以在七个不同的方向上进行运动，包括三个平移自由度和四个旋转自由度。

平移自由度使机械臂能够在三维空间中进行定位，而旋转自由度则使机械臂能够在各个方向上进行转动。

二、逆运动学问题的定义逆运动学问题是指已知机械臂的末端位置和姿态，求解机械臂各个关节角度的问题。

通过解决逆运动学问题，我们可以实现对机械臂的精确控制，使其能够达到预定位置和姿态。

三、逆运动学问题的求解方法1. 几何方法几何方法是最常用的求解逆运动学问题的方法之一。

它基于机械臂的几何特性和坐标变换原理，通过解析几何方法求解机械臂的关节角度。

这种方法的优点是简单直观，容易理解和实现。

然而，对于复杂的机械臂结构和运动学模型，几何方法可能会导致复杂的数学计算和多解性问题。

2. 数值方法数值方法是一种基于数值计算的求解逆运动学问题的方法。

它通过迭代计算的方式逼近机械臂的关节角度，直到满足末端位置和姿态的要求。

数值方法的优点是适用于各种复杂的机械臂结构和运动学模型，可以得到较为精确的解。

然而，数值方法的计算量较大，可能需要较长的计算时间。

四、七自由度机械臂逆运动学问题的求解对于七自由度机械臂的逆运动学问题，可以采用几何方法或数值方法进行求解。

其中，几何方法可以通过解析几何的方式求解机械臂的关节角度，而数值方法则可以通过迭代计算的方式逼近机械臂的关节角度。

在具体求解过程中，需要根据机械臂的运动学模型和几何特性建立逆运动学模型。

然后，通过解析几何或数值计算的方法求解机械臂的关节角度。

最后，通过控制器将计算得到的关节角度发送给机械臂，实现对机械臂的精确控制。

五、总结七自由度机械臂的逆运动学是机械臂控制中的重要问题。

基于MATLAB 的七自由度机器人运动学及工作空间仿真徐小龙;高锦宏;王殿君;张立平【摘要】On the basis of the full investigation of advanced welding robot configuration design,designed a 7-DOF weld-ing robot based on UG three-dimensional modeling.The forward equation of kinematics was built based on the D-H matrix according to the body structure and motion features of 7-DOF welding robots.The workspace of manipulator was analyzed by numerical methods for random sampling.The cloud picture was completed based on MATLAB.Simulation results showed that the experimental results indicated that by using numerical methods for random sampling the analysis of weld ro-bot workspace changed smoothly without impact,which confirmed the reasonableness of structural design,and provided the basis for optimal design of robot control system and structural design of the latter.%在充分调研国内外先进机器人构型设计的基础上，设计出一种基于UG三维建模的七自由度机器人。

基于遗传算法的七自由度机器人轨迹规划马丹妮;李传江;张自强【摘要】针对七自由度串联机器人Robai Cyton Gamma 300轨迹规划问题,采用改进遗传算法规划机器人各关节的运动轨迹.利用D-H表示法建立起机器人末端执行器的位姿与参考坐标系之间的齐次变换矩阵,采用遗传算法优化BP神经网络求解机器人的运动学求逆解.利用5次B样条曲线在关节空间构造机器人各关节随时间变化的运动轨迹.在满足运动学约束条件下,对传统遗传算法在编码方式、遗传算子、交叉概率和变异概率等方面进行改进,对机器人各关节运动轨迹进行时间最优规划.运用Matlab对研究进行了仿真实验.结果表明,经改进遗传算法优化后的机器人运动轨迹时间明显缩短,各关节的角速度、加速度和加加速度曲线连续无突变,从而验证了该方法的有效性.【期刊名称】《实验室研究与探索》【年(卷),期】2016(035)009【总页数】5页(P33-37)【关键词】遗传算法;Robai Cyton Gamma 300机器人;Bezier曲线;轨迹优化【作者】马丹妮;李传江;张自强【作者单位】广东省电信规划设计院有限公司,广东广州528000;上海师范大学信息机电学院,上海201418;上海师范大学信息机电学院,上海201418【正文语种】中文【中图分类】TP273机器人轨迹规划是指机器人运动过程中的运动轨迹，即运动时各关节的位移、速度、加速度随时间变化的曲线[1-2]。

机器人的轨迹规划是机器人控制的基础，近年来是机器人领域的研究热点。

轨迹规划的性能指标有很多种，主要分为：时间最优轨迹规划[3]、能量最优轨迹规划[4]、冲击最优轨迹规划[5]以及混合最优轨迹规划[6]。

其中，时间最优轨迹规划对提高机器人工作效率有重要意义，也一直是机器人轨迹规划研究的重点。

国内外针对机器人的时间最优轨迹规划提出了许多不同的规划方法，主要有二次规划法[7]、动态目标规划法[8]、PID控制法[9]、迭代法[10]等。

基金项目:山西省自然科学基金项目(２０１８０１Ｄ１２１１８３)ꎻ山西省重点研发计划项目(２０１８０３Ｄ４２１０２８ꎻ２０１９０３Ｄ４２１０５１)第一作者简介:李冠琦(１９９６ )ꎬ男ꎬ山西吕梁人ꎬ硕士研究生ꎬ研究方向为康复机器人机构ꎮＤＯＩ:１０.１９３４４/ｊ.ｃｎｋｉ.ｉｓｓｎ１６７１－５２７６.２０２２.０１.０２７基于旋量理论的７自由度机械臂运动学建模与分析李冠琦ꎬ武建德ꎬ李瑞琴(中北大学机械工程学院ꎬ山西太原０３００５１)摘㊀要:机械臂模仿人手臂的７自由度会拥有冗余自由度ꎮ基于旋量理论计算７自由度机械臂的正向运动学解ꎬ从数值上验证矩阵指数先分块展开比直接泰勒展开准确ꎮ用Ｎｅｗｔｏｎ－Ｒａｐｈｓｏｎ数值迭代法求逆解ꎮ通过编写Ｍａｔｌａｂ程序对正逆解互相验证ꎮ研究发现逆解的求解有适用范围ꎬ较之传统的Ｄ－Ｈ法ꎬ使用０螺距的螺旋轴ꎬ会使建模更加简洁ꎮ关键词:旋量ꎻ机械臂ꎻＮｅｗｔｏｎ－Ｒａｐｈｓｏｎ数值迭代法中图分类号:ＴＰ２４１㊀㊀文献标志码:Ａ㊀㊀文章编号:１６７１￣５２７６(２０２２)０１￣０１０５￣０３ＫｉｎｅｍａｔｉｃｓＭｏｄｅｌｉｎｇａｎｄＡｎａｌｙｓｉｓｏｆＳｅｖｅｎ－ｄｅｇｒｅｅ－ｆｒｅｅｄｏｍＲｏｂｏｔｉｃＡｒｍＢａｓｅｄｏｎＳｐｉｎｏｒＴｈｅｏｒｙＬＩＧｕａｎｑｉꎬＷＵＪｉａｎｄｅꎬＬＩＲｕｉｑｉｎ(ＩｎｓｔｉｔｕｔｅｏｆＭｅｃｈａｎｉｃａｌＥｎｇｉｎｅｅｒｉｎｇꎬＮｏｒｔｈＵｎｉｖｅｒｓｉｔｙｏｆＣｈｉｎａꎬＴａｉｙｕａｎ０３００５１ꎬＣｈｉｎａ)Ａｂｓｔｒａｃｔ:Ｔｈｅｒｏｂｏｔｉｃａｒｍｍｉｍｉｃｋｉｎｇｔｈｅ７ＤＯＦｏｆｔｈｅｈｕｍａｎａｒｍｗｉｌｌｈａｖｅｒｅｄｕｎｄａｎｔｄｅｇｒｅｅｓｏｆｆｒｅｅｄｏｍ.Ｔｈｅｆｏｒｗａｒｄｋｉｎｅｍａｔｉｃｓｏｌｕｔｉｏｎｏｆｔｈｅｓｅｖｅｎ－ＤＯＦｒｏｂｏｔｉｃａｒｍｉｓｃａｌｃｕｌａｔｅｄｂａｓｅｄｏｎｔｈｅｓｐｉｎｏｒｔｈｅｏｒｙꎬａｎｄｉｔｉｓｖｅｒｉｆｉｅｄｎｕｍｅｒｉｃａｌｌｙｔｈａｔｔｈｅｍａｔｒｉｘｅｘｐｏｎｅｎｔｉａｌｆｉｒｓｔｂｌｏｃｋｅｘｐａｎｓｉｏｎｉｓｍｏｒｅａｃｃｕｒａｔｅｔｈａｎｔｈｅｄｉｒｅｃｔＴａｙｌｏｒｅｘｐａｎｓｉｏｎ.ＴｈｅＮｅｗｔｏｎ－Ｒａｐｈｓｏｎｎｕｍｅｒｉｃａｌｉｔｅｒａｔｉｏｎｍｅｔｈｏｄｉｓｕｓｅｄｔｏｆｉｎｄｔｈｅｉｎｖｅｒｓｅｓｏｌｕｔｉｏｎ.Ｔｈｅｆｏｒｗａｒｄａｎｄｉｎｖｅｒｓｅｓｏｌｕｔｉｏｎｓａｒｅｖｅｒｉｆｉｅｄａｇａｉｎｓｔｅａｃｈｏｔｈｅｒｂｙｗｒｉｔｉｎｇａｍａｔｌａｂｐｒｏｇｒａｍ.Ｉｔｉｓｆｏｕｎｄｔｈａｔｔｈｅｒｅｉｓａｒａｎｇｅｏｆａｐｐｌｉｃａｂｉｌｉｔｙｆｏｒｔｈｅｉｎｖｅｒｓｅｓｏｌｕｔｉｏｎꎬａｎｄｔｈｅｕｓｅｏｆａ０－ｐｉｔｃｈｓｐｉｒａｌａｘｉｓｒｅｓｕｌｔｓｉｎａｍｏｒｅｃｏｎｃｉｓｅｍｏｄｅｌｉｎｇｔｈａｎｔｈｅｔｒａｄｉｔｉｏｎａｌＤ－Ｈｍｅｔｈｏｄ.Ｋｅｙｗｏｒｄｓ:ｓｐｉｎｏｒｔｈｅｏｒｙꎻｒｏｂｏｔｉｃａｒｍꎻＮｅｗｔｏｎ－Ｒａｐｈｓｏｎｎｕｍｅｒｉｃａｌｉｔｅｒａｔｉｖｅｍｅｔｈｏｄ０㊀引言机械臂是机器人技术领域中应用最为广泛的自动化装置ꎬ在工业制造㊁医疗康复等领域都有其应用实例ꎬ拟人化机械臂技术也逐渐成熟[１－４]ꎮ匹兹堡大学生物医学团队在ＢＣＩ机械臂假肢里引入实时触觉反馈ꎬ使完成任务的时间减少一半ꎮ波士顿动力开发Ｓｔｒｅｔｃｈ移动式７Ｒ机械臂已应用于仓库运输ꎮ２０世纪８０年代学者们开始讨论将旋转轴从数学中引入机器人研究的可行性ꎬ旋量理论[５－９]日益成熟ꎬ然而对其的应用介绍却鲜见报道ꎮ本文建模７自由度串联机械臂ꎬ着重对螺旋轴这一单位矢量在运动学的应用加以详细描述ꎮ６自由度逆解有通用公式ꎬ７Ｒ逆解包含３２个实根ꎬ出现虚空间或自运动歧ꎮ７Ｒ逆解可结合Ｎｅｗｔｏｎ－Ｒａｐｈｓｏｎ数值迭代法求解[１０]ꎮ使用Ｍａｔｌａｂ进行正解中的化简与直接展开等运算过程的比较ꎬ并且同时使用开源Ｐｙｔｈｏｎ对结果进行比较ꎮ使用基于空间(ｓｐａｃｅ简称ｓ)坐标系的空间雅可比矩阵ꎬ找出数值迭代法求逆解的适用范围ꎬ基于正解的前提下ꎬ验证逆解的准确性ꎮ１㊀旋量理论螺旋(旋量 旋转向量)理论在正运动学中的应用ꎮ１.１㊀Ｍ矩阵(０位置㊁起始位置)Ｍ矩阵为当所有的关节转角都为０的时候ꎬ操作空间坐标系(ｂｏｄｙ简称ｂ)在ｓ坐标系中的位置和姿态矩阵ꎮ１.２㊀旋转向量Ｓң与指数积公式将每一个转动关节视为０螺距的轴ꎬ假设除了最后一个关节转动θʎ外ꎬ其他关节都是固定的ꎮ在ｓ坐标系里ꎬ关节７上螺旋轴的向量形式如式(１)所示ꎬ在高维度上ꎬＲｎ是ｎ维的欧几里得空间ꎬＳ７ңɪＲ６㊁ω７ңɪＲ３ꎬＶ７ңɪＲ３ꎮ螺旋轴的矩阵形式Ｓ７如式(２)所示ꎮＳ７ң＝ωң７Ｖң７éëêêùûúú(１)Ｓ７＝ω７Ｖң７００éëêêùûúú(２)Ｔ０７＝ｅＳ７θ７Ｍ(３)５０１ 博看网 . All Rights Reserved.特殊正交群是所有有效的３ˑ３旋转矩阵的集合群ＳＯ(３):包括Ｒ㊁ω㊁ｅωθꎮ特殊的欧几里得集合群或刚体运动群或Ｒ３中的同质变换矩阵Ｓｅ(３)表示位姿:包括Ｍ㊁ｅＳθ㊁Ｔ０７ꎮｅＳθ＝Ｉ＋Ｓθ＋Ｓ２θ２２!＋Ｓ３θ３３!＋ ＝ｅωθｆ(θ)ν０１éëêêùûúú(４)式(４)中ꎬ可利用特性ω３＝－ω来化简ꎬ且ｅωθ有Ｒｏｄｒｉｇｕｅｓ公式:ｆ(θ)＝Ｉθ＋(１－ｃｏｓθ)ω＋(θ－ｓｉｎθ)ω２(５)ｅωθ＝Ｉ＋ｓｉｎθω＋(１－ｃｏｓθ)ω２(６)依次解锁一个角度ꎬ往前代值ꎬ得到Ｔ０７＝ｅＳ１θ１ ｅＳ７θ７Ｍ(７)２㊀数值法逆解使用非线性寻根的Ｎｅｗｔｏｎ－Ｒａｐｈｓｏｎ方法ꎬ有寻根㊁不存在根时寻找近似解㊁存在多个解时寻找最优解的优势ꎮ给定一个初始值ꎬ然后代入迭代式求解直到出现误差范围内的解ꎮ设正向运动学函数为ｆ(θｄ)ꎬ末端执行器的位置向量为νꎬ非线性寻根Ｎｅｗｔｏｎ－Ｒａｐｈｓｏｎ是找到目标函数的解ꎮ几何视角如图１所示ꎻ式(８)是解析视角ꎮ式(９)－式(１１)是计算雅可比矩阵ꎮ图１㊀迭代法几何过程Δθ＝Ｊ－１(θ０)[ｖｄ－ｆ(θｉ)](８)ＪＳ(θ)＝ＪＳ１(θ１)ңＪＳ２(θ２)ң ＪＳｎ(θｎ)ң[](９)ＪＳ１(θ１)ң＝Ｓ１ң(１０)ＪＳｉ(θｉ)ң＝[ｅＳ１θ１ ｅＳｉ－１θｉ－１]∗Ｓｉң(１１)式中∗为其伴随矩阵ꎮ对这种算法的进一步改进:１)末端执行器的位置描述ｆ(θｄ)变更为正运动学计算出的矩阵Ｔ０７ꎮ２)误差调整ꎮ用螺旋轴ＳＭＴң两分量的模代替末端执行器每次迭代的位置变化ꎮ３)引进伪逆矩阵Ｊ†避免求解奇异时无解的情况ꎮ在Ｍａｔｌａｂ里编程为ｐｉｎｖ(Ｊ)ꎮ当前基于ｂ坐标系ꎬ变换为基于ｓ坐标系:ＳＭＴｂң＝ｌｏｇ(ＴＭＴ０７(θｉ))(１２)ＳＭＴｓң＝(Ｔｓｂ)∗ＳＭＴｂң(１３)式中:Ｔｓｂ是坐标转移矩阵ꎻ∗为求其伴随矩阵ꎮ改进算法的流程图如图２所示ꎮ图２㊀改进的数值迭代法流程图３㊀验证正逆解３.１㊀正运动学方程㊀绘制三维模型图ꎬ并建立７Ｒ示意图(图３)进行验证ꎮ如图３(ｂ)所示的坐标平面ꎬｙ方向定义为ａ并依次标号ꎬｚ方向定义为ｂ也依次序标号ꎮ标示７个螺距为０的右手螺旋轴Ｓ１ң－Ｓ７ңꎮＭ＝１００００１０２４００００１００００１éëêêêêùûúúúú(１４)Ｓ７ң＝[０㊀０㊀１㊀－ａ７㊀０㊀０]Ｔ＝[０㊀０㊀１㊀－３００㊀０㊀０]Ｔ(１５)U a U 7Rb 7R .图３㊀三维模型图及７Ｒ示意图根据式(３)ꎬ使用矩阵分块后化简的运算过程ꎬ编程并计算结果ꎮＴ(θ)＝ｃ７－ｓ７０－２７００ｓ７ｓ７ｃ７０２７００ｃ７－３００００１０００００éëêêêêùûúúúú(１６)根据式(３)ꎬ发现将矩阵指数直接泰勒展开(采用了３种计算方法:Ｐａｄａ法㊁特征值法㊁６次的泰勒展开)得出的６０１结果虽然一致ꎬ但是它是虚数形式ꎬ增加了计算量ꎮ结果:ＴＭ＿ｐａｄａ(θ)＝ｃ７－ｓ７０－２７００ｓ７ｓ７ｃ７０１３５０ｅ－θ７ｉ＋１３５０ｅθ７ｉ－３００００１００００１éëêêêêùûúúúú(１７)使用先进行矩阵分块然后利用特性化简的运算方法ꎬ该结果更准确㊁后期的运算量更小ꎮ代入式(７)ꎬ使用该方法分别在Ｍａｔｌａｂ和Ｐｙｔｈｏｎ中运算ꎬ得出的结果一致:Ｔ＝ｃ５－６ｃ１２３４ｃ７－ｓ１２３４ｃ７－ｓ１２３４ｃ７－ｃ５－６ｃ１２３４ｓ７－ｓ５－６ｃ１２３４ｒ１ｃ１２３４ｓ７＋ｃ５－６ｓ１２３４ｃ７ｃ１２３４ｃ７－ｃ５－６ｓ１２３４ｓ７－ｓ５－６ｓ１２３４ｒ２ｓ５－６ｃ７－ｓ５－６ｓ７ｃ５－６ｒ３０００１éëêêêêêùûúúúúúｒ１＝１５０ｓ１２３４－５－１３５０ｓ１２３４７－３００ｓ１２３－６７５ｓ１２３４５７－６－６７５ｓ１２３４６７－５－１５０ｓ１２３４５－１３５０ｓ１２３４－７＋６００ｓ１２３４＋３００ｓ１２＋６７５ｓ１２３４５－６－７＋６７５ｓ１２３４６－５－７－３００ｓ１＋７５０ｓ１２３４５－６－７５０ｓ１２３４６－５ｒ２＝１５０ｃ１２３４－５＋１３５０ｃ１２３４７＋３００ｃ１２３＋６７５ｃ１２３４５７－６＋６７５ｃ１２３４６７－５－１５０ｃ１２３４－５＋１３５０ｃ１２３４－７－６００ｃ１２３４－３００ｃ１２－６７５ｃ１２３４５－６－７－６７５ｃ１２３４６－５－７＋３００ｃ１－７５０ｃ１２３４５－６＋７５０ｃ１２３４６－５ｒ３＝２７００ｓ７ｃ５ｓ６－ｓ５ｃ６－１５００ｓ５ｓ６－ｃ５(１５００ｃ６－１５００)－１２００ｃ５＋１２００３.２㊀逆运动学方程１)第一次验证设初始位置为正解的０位置ꎬ转动角度为θｌｉｓｔꎮθｌｉｓｔ＝πꎻπ２ꎻπ３ꎻπ４ꎻπ５ꎻπ６ꎻπ７[]＝[３.１４２ꎻ１.５７１ꎻ１.０４７ꎻ０.７８５ꎻ０.６２８ꎻ０.５２４ꎻ０.４４９]给逆解的初始值[３ꎬ１.５ꎬ１ꎬ０.６ꎬ０.５ꎬ０.４ꎬ０.３]ꎮ解得[３.１６１ꎬ１.５６３ꎬ１.０５９ꎬ０.７６２ꎬ０.６２８ꎬ０.５２３ꎬ０.４４９]ꎮ２)第二次验证因发现误差较大:１)改用角度制ꎻ２)迭代次数增加到１０００次ꎻ３)精度调整为ｅω<０.０００１ꎬｅｖ<０.０００１ꎮ经过多组数据实验发现ꎬ相差３ʎ以内ꎬ位置完全重现ꎻ相差１０ʎ以内ꎬ第一角度有０.１ʎ的偏差ꎻ相差１５ʎ以上的逆运算ꎬ第一个角度有１ʎ以上的偏差ꎮ所以ꎬ该方法求逆解有完全重现的适用范围ꎬ需要把初始解猜测在真实解的附近１５ʎ以内(表１)ꎮ表１㊀正逆解互相验证单位:(ʎ)㊀验证项目θ１θ２θ３θ４θ５θ６θ７Δθ初始角度１０２０３０４０５０６０７０ 猜测角度７１７２７３７４７５７６７计算的逆解１０２０３０４０５０６０７００猜测角度６１６２６３６４６５６６６计算的逆解１０.００１２０.００１２９.９９９３９.９９９５０６０７００.００１猜测角度１１１２１３１４１５１６１计算的逆解１０.０６２０.０３２２９.９４９３９.９５９５０６０７００.０６０猜测角度０１０２０３０４０５０６０计算的逆解１０.１２０.０５３２９.９１６３９.９３２５０６０７００.１００猜测角度－５５１５２５３５４５５５计算的逆解１０.７４２０.４０３２９.３７３３９.４８４５０６０７００.７４０续表１验证项目θ１θ２θ３θ４θ５θ６θ７Δθ猜测角度－６４１４２４３４４４５４计算的逆解１１.０３２０.５６６２９.１２８３９.２７６５０６０７０１.０３０猜测角度－１３－３７１７２７３７４７计算的逆解２６.７２８２４.４６７２４.３７５３４.４２９５０６０７０６.７２８猜测角度－１５－５５１５２５３５４５计算的逆解２４.４６６３３.１０３１８.２５７２４.１７３５０６０７０１４.４６６猜测角度－１６－７４１４２４３４４４计算的逆解６３.４３２－２６.２６４－２２.７２５８５.５５７５０６０７０５３.４３２４㊀结语本文重点介绍了如何使用形如螺旋楼梯的转向量计算正逆解ꎮ结合旋量与Ｎｅｗｔｏｎ－Ｒａｐｈｓｏｎ数值法求逆解ꎮ为涵盖转动机构可能出现的问题ꎬ采用目前串联机构中最复杂的７Ｒ机构并且使机构尽可能复杂ꎬ但是设计中没有涵盖ｈｅｌｉｃａｌ螺旋和ｃｙｌｉｎｄｒｉｃａｌ圆筒等机构ꎮ在比较了不同的运算方法后ꎬ计算正解ꎬ得出先将矩阵分块㊁再利用特性化简的方法更好的结论ꎮ在计算逆解的过程中ꎬ发现当初始猜测的第一个角度超过真实解２０ʎꎬＮｅｗｔｏｎ－Ｒａｐｈｓｏｎ数值法不会重现正解ꎮ验证结果表明旋量形式美观ꎬ建模快捷ꎬ编程明了ꎬ适用于机械臂中的串联机构㊁并联机构㊁转动关节㊁平动关节㊁螺旋关节等的运动学㊁动力学特性建模和分析ꎮ参考文献:[１]ＦＬＥＳＨＥＲＳＮꎬＤＯＷＮＥＹＪＥꎬＷＥＩＳＳＪＭꎬｅｔａｌ.Ａｂｒａｉｎ－ｃｏｍｐｕｔｅｒｉｎｔｅｒｆａｃｅｔｈａｔｅｖｏｋｅｓｔａｃｔｉｌｅｓｅｎｓａｔｉｏｎｓｉｍｐｒｏｖｅｓｒｏｂｏｔｉｃａｒｍｃｏｎｔｒｏｌ[Ｊ].Ｓｃｉｅｎｃｅꎬ２０２１ꎬ３７２(６５４４):８３１￣８３６.[２]ＫＥＶＩＮＭＬꎬＦＲＡＮＫＣＰ.Ｍｏｄｅｒｎｒｏｂｏｔｉｃｓ:ｍｅｃｈａｎｉｃｓｐｌａｎｎｉｎｇａｎｄｃｏｎｔｒｏｌ[Ｍ].Ｉｌｌｉｎｏｉｓ:ＣａｍｂｒｉｄｇｅＵｎｉｖｅｒｓｉｔｙＰｒｅｓｓꎬ２０１７.[３]刘世平ꎬ曹俊峰ꎬ孙涛ꎬ等.基于ＢＰ神经网络的冗余机械臂逆运动学分析[Ｊ].中国机械工程ꎬ２０１９ꎬ３０(２４):２９７４￣２９７７ꎬ２９８５.[４]赵京ꎬ王鑫ꎬ张自强ꎬ等.基于肘部自运动的主从异构７自由度机械臂运动映射及其几何逆解[Ｊ].机械工程学报ꎬ２０２０ꎬ５６(１５):１８１￣１９０.[５]ＹＯＵＷＳꎬＬＥＥＹＨꎬＯＨＨＳꎬｅｔａｌ.Ｄｅｓｉｇｎｏｆａ３Ｄ－ｐｒｉｎｔａｂｌｅꎬｒｏｂｕｓｔａｎｔｈｒｏｐｏｍｏｒｐｈｉｃｒｏｂｏｔｈａｎｄｉｎｃｌｕｄｉｎｇｉｎｔｅｒｍｅｔａｃａｒｐａｌｊｏｉｎｔｓ[Ｊ].ＩｎｔｅｌｌｉｇｅｎｔＳｅｒｖｉｃｅＲｏｂｏｔｉｃｓꎬ２０１９ꎬ１２(１):１￣１６.[６]ＢＩＮＤＵＲＡꎬＮＥＬＯＹＡＡꎬＡＬＡＭＳꎬｅｔａｌ.Ｓｉｇｍａ－３:Ｉｎｔｅｇｒａｔｉｏｎａｎｄａｎａｌｙｓｉｓｏｆａ６ＤＯＦｒｏｂｏｔｉｃａｒｍｃｏｎｆｉｇｕｒａｔｉｏｎｉｎａｒｅｓｃｕｅｒｏｂｏｔ[Ｃ]//２０１９４ｔｈＩｎｔｅｒｎａｔｉｏｎａｌＣｏｎｆｅｒｅｎｃｅｏｎＲｏｂｏｔｉｃｓａｎｄＡｕｔｏｍａｔｉｏｎＥｎｇｉｎｅｅｒｉｎｇ(ＩＣＲＡＥ).Ｓｉｎｇａｐｏｒｅ:ＩＥＥＥꎬ２０１９:６￣１１.[７]常健ꎬ王亚珍ꎬ李斌.基于力/位混合算法的７自由度机械臂精细操控方法[Ｊ].机器人ꎬ２０１６ꎬ３８(５):５３１￣５３９.[８]张昌ꎬ武玉强.基于Ｐ－Ｒｏｂ六自由度机械臂运动学建模与仿真[Ｊ].包装工程ꎬ２０２０ꎬ４１(１１):１６６￣１７３.[９]ＷＩＥＤＭＥＹＥＲＷꎬＡＬＴＯÉＰꎬＡＵＢＥＲＬＥＪꎬｅｔａｌ.Ａｒｅａｌ－ｔｉｍｅ－ｃａｐａｂｌｅｃｌｏｓｅｄ－ｆｏｒｍｍｕｌｔｉ－ｏｂｊｅｃｔｉｖｅｒｅｄｕｎｄａｎｃｙｒｅｓｏｌｕｔｉｏｎｓｃｈｅｍｅｆｏｒｓｅｖｅｎ－ＤｏＦｓｅｒｉａｌｍａｎｉｐｕｌａｔｏｒｓ[Ｊ].ＩＥＥＥＲｏｂｏｔｉｃｓａｎｄＡｕｔｏｍａｔｉｏｎＬｅｔｔｅｒｓꎬ２０２１ꎬ６(２):４３１￣４３８.收稿日期:２０２１０４０１７０１ 博看网 . All Rights Reserved.。