求解一元一次方程导学案

⼀元⼀次⽅程全章导学案第⼀课时 3.1.1⼀元⼀次⽅程（1）学习⽬标1. 了解什么是⽅程，什么事⼀元⼀次⽅程。

2. 体会字母表⽰数的优越性。

重点：知道什么是⽅程，⼀元⼀次⽅程难点：找等关系列⽅程使⽤说明及学法指导：先⾃学课本78—81页内容，独⽴完成学案，然后⼩组讨论交流。

⼀. 导学1. 书中问题⽤算术⽅法解决应怎样列算式：2.含X 的式⼦表⽰关于路程的数量：王家庄距青⼭＿＿＿千⽶，王家庄距秀⽔＿＿＿千⽶。

从王家庄到青⼭⾏车＿＿⼩时，王家庄到秀⽔＿＿⼩时。

3车从王家庄到青⼭的速度为＿＿＿千⽶/⼩时，从王家庄到秀⽔的速度为＿＿＿千⽶/⼩时。

4.车匀速⾏驶，可列⽅程为：5.什么是⽅程？6.什么是⼀元⼀次⽅程？⼆、合作探究1.判断下列式⼦是否是⽅程:(1)5x+3y-6x=7 (2)4x-7 (3)5x >3(4)6x 2+x-2=0 (5)1+2=3 (6) -x5-m=112.下列式⼦哪些是⼀元⼀次⽅程？不是⼀元⼀次⽅程的，要说明理由. (1)9x=2 (2)x+2y=0 (3)x 2-1=0(4) x=0 (5) x3=2 (6) ax=b(a 、b 是常数)3.（1）已知2x m+1 +3=7是⼀元⼀次⽅程，求m 的值；（2）已知关于x 的⽅程mx n-1+2=5是⼀元⼀次⽅程，则m=＿＿,n=＿＿.4、根据下列条件列出⽅程:(1)某数的5倍加上3，等于该数的7倍减去5；（2）某数的3倍减去9，等于该数的三分之⼆加6；（3）某数的8倍⽐该数的5倍⼤12；（4）某数的⼀半加上4，⽐该数的3倍⼩21.（5）某班有x名学⽣，要求平均每⼈展出4枚邮票，实际展出的邮票量⽐要求数多了15枚，问该班共展出多少枚邮票？三、学习⼩结四、作业习题3.1第1、5题。

第⼆课时 3.1.1 ⼀元⼀次⽅程（2）学习⽬标1.根据实际问题中的数量关系，设未知数，列出⼀元⼀次⽅程。

2.知道⽅程的解和解⽅程是两个不同的概念。

___ 年___ 月____日 组长检查： 教师评价：学习内容：3.2.2解一元一次方程（2）移项学习目标：求解数字系数的一元一次方程，经历和体会解一元一次方程中“转化”的思想方法。

学习重点：学会解一元一次方程学习难点：移项学习过程：（阅读教材第88至90页，并完成学前准备的内容）一．学前准备：1．把方程的某一项 后。

从方程的一边移到另一边，这种变形叫做 。

2．移项的理论根据是 ，即在方程的两边同时减去 ，相当于把 ，改变符号后从方程的一边移到另一边。

3．方程2x -5=3x+3变形为2x+3x=3-5的错误原因是 。

4．将方程4x=2x -2，移项，得 ，合并，得 ，方程两边同除以 ，得x= 。

5．将方程2y -11=5，移项，得 ，合并，得 ，方程两边同除以 ，得y= 。

6．将方程2x -1=1-3x ，移项，得 ，合并，得 ，方程两边同除以 ，得x= 。

7．方程2x -4=3x+8移项后正确的是A ． 2x+3x=8+4B ． 2x -3x=-8+4C ． 2x -3x=8+4D ． 2x+3x=8-4二．新知探究：8．解方程（1）32x+4=0 （2）31x+23=0(3) 2x -19=7x+31 (4) 10-2x=x -19．根据下列条件求x 的值。

（1） 25与x 的差是-8； (2) x 的53与8的和是2；10．x 取何值时，4x+2与3x -1的值：（1）相等？（2）互为相反数？三．拓展与应用11．解方程：(1) 6x=24-2x (2) 5.19217-=+x x (3) 6y+7=12y -5-3y(4) 759272911-=+z z (5) 317192+=-m m (6) 3134334-=-x x四．课后巩固：12．若对任意有理数a ，b ，c ，d 规定c ad b =ad-bc ，当3x 42--=2-x 时，求x 。

13．体育馆的某个区域的座位，第一排是20个座位，以后每增加一排，座位就增加2个．如果用字母a n表示每排的座位数，用n表示排数．请填写表格，并回答问题：（2）第10排有_______个座位；（3）第n排有多少个_____________座位；（4）其中某一排的座位是118个，那么它是第几排？五、总结反思。

一元一次方程导学案【学习目标】1、知道什么是方程，会判断一个数学式子是算式还是方程；2、能根据简单的实际问题列一元一次方程，并了解其步骤；3、会判断方程的解。

【学习重点】一元一次方程的含义。

【学习难点】根据简单的实际问题列一元一次方程。

课前自主学习(查阅教材和相关资料,完成下列内容)考点一.方程的概念1、含有的等式叫方程。

考点二.一元一次方程的概念1.只含有个未知数，未知数的次数都是次的方程，叫做一元一次方程。

考点三.列方程遇到实际问题时,要先设字母表示 ,然后根据问题中的 ,最后写出含有未知数的 ,就能列出方程.归纳:列方程解实际问题的步骤:第一步: ,第二步: ,第三步: .考点四.解方程及方程的解的含义解方程就是求出使方程中等号左右两边的的值,这个值就是方程的 .【重要思想】1.类比思想:算式与方程的对比2.转化思想:把实际问题转化为数学问题,特别是方程问题.学练提升问题1:判断下列数学式子X+1, 0.5x-x, 2x-3=7, 3x+2=2x-5 , 2x2+3x-8=0,x+2y=7.是方程有 ,是一元一次方程有【规律总结】【同步测控】1.自己编造两个方程: , .2.自己编造两个一元一次方程: , .问题2.根据问题列方程:1.用一根长24cm的铁丝未成一个正方形,正方形的变长是多少?2.一台计算机已使用1700小时,预计每月再使用150小时,经过多少月这台计算机的使用时间他到规定的检修时间2450小时?【同步测控】根据下列问题,设未知数,列出方程1.环形跑道一周长400m,沿跑道跑多少周,可以跑3000m?2.甲种铅笔每只0.3元,乙种铅笔铅笔每只0.6元,用9元钱买了两种铅笔共20支,两种铅笔各买了多少支?【规律总结】【同步测控】1.一个梯形的下底比上底多2cm,高是5cm,面积是40cm2,求上底.2.x的2倍于10的和等于18;3.比b的一半小7的数等于a与b的和;4.把1400元奖学金按照两种奖项将给22名学生,其中一等奖每人200元,二等奖每人50元,获得一等奖的学生多少人?问题三、判断方程的根1.判断下列各数X=1,x=2,x=-1,x=0.5.那个是方程2x+3=5x-3的解?2.当x= 时,方程3x-5=1 两边相等?等式性质导学案【学习目标】1、了解等式的两条基本性质，并会用数学式子表示；2、能利用等式的基本性质解简单的方程； 【学习重点】理解等式的两条基本性质。

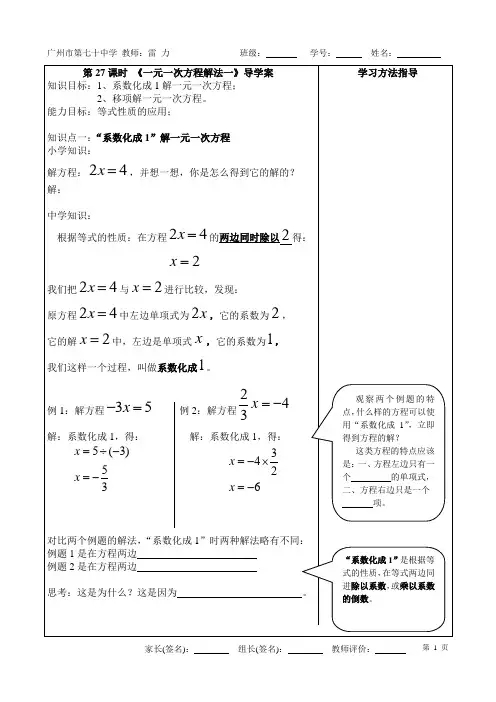
第27课时 《一元一次方程解法一》导学案知识目标：1、系数化成1解一元一次方程； 2、移项解一元一次方程。

能力目标：等式性质的应用； 知识点一：“系数化成1”解一元一次方程 小学知识： 解方程：24x =，并想一想，你是怎么得到它的解的？解：中学知识：根据等式的性质：在方程24x =的两边同时除以2得：2x =我们把24x =与2x =进行比较，发现：原方程24x =中左边单项式为2x，它的系数为2，它的解2x =中，左边是单项式x ，它的系数为1，我们这样一个过程，叫做系数化成1。

例1：解方程35x -= 例2：解方程243x =-解：系数化成1，得： 解：系数化成1，得：5(3)53x x =÷-=-3426x x =-⨯=-对比两个例题的解法，“系数化成1”时两种解法略有不同： 例题1是在方程两边 例题2是在方程两边思考：这是为什么？这是因为 。

学习方法指导观察两个例题的特点，什么样的方程可以使用“系数化成1”，立即得到方程的解？这类方程的特点应该是：一、方程左边只有一个 的单项式，二、方程右边只是一个 项。

“系数化成1”是根据等式的性质，在等式两边同进除以系数，或乘以系数的倒数。

练习：参照以上例题解方程：1、312x =-2、43x -=3、395x -=-4、3445x =- 5、3x -= 知识点二：“移项”解一元一次方程 旧知识： 1、5与 的和为0，3x 与 的和为0，2-与 的和为0， 与4y 的和为0， 与2x -的和为0， 2、两个 之和为0， 两个系数互为 的单项式之和为0 3、等式性质：在等式两边同时加上 ，结果仍是等式。

新知识：“移项”解一元一次方程 根据小学知识，容易知道：35x += 的解为：2x = 下面是用等式性质来解答的，你能理解吗？ 在方程35x +=两边都加上3-，即： x 3+ 3- =5 3-合并两边的同类项得： x =2 详细过程如下： x 3+=5 x 3+ 3- =5 3-x =2系数为整数时，“系数化成1”一般采取除以系数的办法进行。

5.2 .1求解一元一次方程（一）一、教学目标1.知识与能力：通过学生观察、独立思考等过程，培养学生归纳、概括的能力；2.过程与方法：熟悉利用等式的基本性质解一元一次方程的过程，通过具体的例子，归纳移项法则，会用移项法则解方程；3.情感态度价值观：进一步让学生感受并尝试寻找不同的解决问题的方法，激发学生的学习兴趣.二、教学重点和难点重点：移项法则及其应用.难点：移项的同时必须变号.三、教学过程（一）温故知新1．基本知识复习等式的性质1：_______________________________________________。

等式的性质2：___________ _______________。

2.合并同类项：⑴3x-5x=___________ ⑵-3x+7x=__________ ⑶x+5x-2x=_________（二）自主探究新知探究一：阅读教材135页到136页，完成下列问题：1.把原方程中的一项___________后，从方程的一边移动到另一边，这种变形叫做__________。

2.移项的依据是什么？3.解一元一次方程中移项起了什么作用4.移项的过程中，一定要注意___________。

随堂检测1.下列方程的移项是否正确？为什么？（1）由3+x=5,得x=5+3; （2）由23-=x ,得23--=x ;（3）从x ＋5＝7，得到x ＝7＋5 ;（4）从5x ＝2x －4，得到5x －2x ＝－4 .2.下列变形中，属于移项变形的是：（ ）A 、由5x=3，得x=53. B 、由2x+3y-4x,得：2x-4x+3y.C 、由23=x，得x=6. D 、由4x-4=5-x ，得4x+x=5+4.新知探究二：阅读教材135页例1和例2可知，本节课涉及的解一元一次方程的基本步骤：①_________，②__________，③把未知数的系数化为1，最后把方程变成x=a 的形式。

例：解下列方程：（1）5278x x -=+ （2）351322x x -=+ （3）x x 23273-=+ （4）x x 385-=- （5）3 3.5 4.51x x -=- （6）x x x 58.42.13-=--（三）巩固提升1、方程4x-2x ＝6的解是（）A 、5B 、-2C 、3D 、42、解方程1143x =，正确的是（）A 、1143x =，43x =B 、1143x =，112x =C 、1143x =，43x =D 、1143x =，34x = 3、解下列方程：(1) x x 237+=； (2) 13624x x -=；（3）x x 21-=-； （4）x x 355-=- （四）课堂小结：通过这节课的学习你有什么收获?（五）作业布置已知5是关于x 的方程3x-2a=7的解，则a 的值为 。

§6.1 从实际问题到方程科目：七年级数学备课人：王淑轶【教学目标】1.能判断一个数是不是某个方程的解，掌握用尝试检验方法求方程的解的思想方法；2.会列一元一次方程解决一些简单的应用题；3.初步认识方程与现实问题的联系，感受数学的应用价值，激发数学学习兴趣。

【教学重点】能判断一个数是不是某个方程的解，会列一元一次方程解决一些简单的应用题。

【教学难点】会列一元一次方程解决一些简单的应用题。

【教学过程】一、复习回顾，导入新课1.列方程解下面的应用题：一本笔记本1.2元。

小红有6元钱，那么她最多能买到多少本这样的笔记本呢？解：设小红能买到x本笔记本，根据题意得：1.2x＝6解得：x＝5答：小红能买到5本这样的笔记本。

2.结合上题的解答，说说列方程解应用题的一般步骤是什么？有哪些应当注意的问题？二、自主探索1.阅读课本1页“第6章导图”内容，试分别用算术法和方程法解答：一队师生共328人，乘车外出旅游，已有校车可乘64人，如果租用客车，每辆可乘44人，那么还要租多少辆客车？算术法：方程法：(328－64)÷44 解：设需要租用x辆客车，根据题意得：＝264÷44 44x+64＝328＝6(辆) 解得：x＝6答：还要租用6辆客车。

答：还要租用6辆客车。

2.阅读课本2页～3页“问题2”内容，完成下列问题：(1)小敏同学得出答案使用的是什么方法？他的答案正确吗？小敏同学是用“尝试、检验”的方法找出方程的解的。

他的答案是正确的。

(2)你能列方程解答张老师的这道题吗？试一试。

三、合作交流1.你用方程法得到的答案和小敏的答案一样吗？你有什么发现？2.讨论：如果未知数可能取到的数值较多，或者不一定是整数，该从何试起？如果试验根本无法入手又该怎么办呢？四、实践应用1.课本3页“习题6.1”第1～3题。

2.补充练习：(1)检验下列方程后面括号内所列各数是否为相应方程的解。

(a)x-3(x+2)=6+x (x=3,x=-4)(b)2y(y-1)=3 (y=-1,y=32) (c)5(x-1)(x-2)=0 (x=0,x=1,x=2)(2)根据题意，列出相应的方程，不必求解。

第29课时 《一元一次方程解法》3导学案知识目标：1、最小公倍数； 2、等式性质；3、去分母法解方程。

能力目标：转化思想知识点一： 最小公倍数（小学知识）1、2与3的最小公倍数是 ；2、4与6的最小公倍数是 ；3、2、3、4的最小公倍数是 ；4、4、6、10的最小公倍数是 ； 知识点二：等式性质 1、等式的性质是： 2、如果123x =，那么正确的是（ ）A 、23x =B 、12x= C 、13x = D 、32x =3、如果1123x x+-=，那么正确的是（ ） A 、2(1)3(1)x x +=- B 、3(1)2(1)x x +=- C 、112x x +=- D 、113xx -+=4、如果11123x x+-=+，那么正确的是（ ） A 、3(1)2(1)x x +=- B 、31216x x +=⨯-+ C 、3(1)2(1)6x x +=-+ D 、3(1)2(1)2x x +=-+ 学生探究问题知识点三：去分母法解方程11123x x +-=+解法一：方程可化为：111112233x x +=-+合并同类项，得：11412233x x +=- 移项，得：11412332x x +=-合并同类项，得：5566x =系数化成1，得： 1x =解法二： 去分母，得：3(1)2(1)6x x +=-+ 去括号，得：33226x x +=-+ 合并同类项，得：3382x x +=- 移项，得：3283x x +=- 合并同类项，得：55x =系数化成1，得：1x =练习： 1、3x 532x 35-=- 2、2546+=--x x x3、138547=+--x x 4、332121xx -=-+ 作业： 1、2与5的最小公倍数是 ； 2、4与3的最小公倍数是 ； 3、5、3、2的最小公倍数是 ； 4、4、2、5的最小公倍数是 ； 5、方程：124x =去分母后，得到的方程是 6、方程：2323x x+-=去分母后，得到的方程是 7、方程：21223x x-+=+去分母后，得到的方程 是 8、方程：12123x xx -+-=+去分母后，得到的 方程是解下列含分母的方程14223x x +-+=1231337xx -+=-3y 181y 961y 5--+=+51312423x x x -+-=-26135x x x +-+=-()1132152x x --=。

解一元一次方程（去分母）导学案第5课时知识技能目标使学生掌握去分母解方程的方法，并总结解方程的一般步骤；过程性目标1. 经历去分母解方程，进一步体会去分母的规则；2.经历解一元一次方程的过程，领会转化的数学思想．情感态度目标结合实例认清一元一次方程及解题步骤，尝试探索学习的乐趣。

重点、难点重点；解含有分母的一元一次方程的解法。

难点；去分母时注意不能漏乘不含分母的项，不忘添括号。

教学过程一、知识回顾解方程8x =2(x +3)二、创设情境通过上几节课各例的探讨，得出了解一元一次方程的方法，以上所解的各个方程，都有一个共同的特点，未知数的系数都是整数，如果未知数的系数是分数时，怎样来解这种类型的方程呢？三、探究归纳1、解方程：41221x 3-=+x 。

思考:（1）这个方程中含有分母，你有没有办法将它“转化”为不含分母的形式？（2）你认为方程两边应该同时乘以几，就可转化为没有分母的形式？解：方程的两边都同时乘以（ ）得：去掉分母后，得：归纳：什么叫去分母？_________________________________________________________________ _________________________________________________________________四、实践应用例5 解方程：131223x =+--x ．练习.解下列方程：(指名学生台上板书) (1)47815=-a ； (2)15334--=-x x ．五、交流反思通过这节课的学习，说说解一元一次方程的一般步骤有哪些？每步变形时应注意些什么？ __________________________________________________________________________ __________________________________________________________________________六、检测反馈1.指出下列方程求解过程中的错误，并给予纠正（小组讨论）．(1)解方程：1524213+=-x x ． 改正： 解 15x －5 = 8x + 4－1 ，15x －8x = 4－1 + 5 ，7x = 8， x =87．(2)解方程：246231x x x -=+--． 改正： 解 2x －2－x + 2 = 12－3x ，2x －x + 3x = 12 + 2 + 2，4x = 16，x = 4．2、解方程312321x 3--=-+x x。