上服从均匀分布求随机变量的概率密度函数解34页PPT

3章-随机数与随机变量PPT

1
第三章随机数与随机变量
2
①设置仿真钟=0 ②初始化系统状态与统计计数器 ③初始化事件列表
开始
主程序 (0)激活初始化程序
(0) (1)激活时间推进程序 (2)激活事件发生程序i
重复
(1) ①确定下一事件类型，如i ②推进仿真钟
i
(1)更新系统状态 (2)更新统计计数器 (3)产生将来事件并添加到事件列表中
设具有独立同分布的随机变量 X1 , X 2 ,…, X m ，令
Y X1 X2 L Xm
m
Y Y 则的分布函数与 Xi 的分布函数相同，此时称的 i1
分布为 X i 的 m 折卷积。为了生成 Y ，可先独立地
从相应分布函数产生随机变量 X1 , X 2 ,…, X m ，然后
利用上式得到 Y ，这就是卷积法。
14
例：特定供应商提供的发动机次品率为10%，求批量为5的发动机中每批的次品数
❖binomial(0.1,5)
分布列如表
15
3.3 随机数发生器
❖ 对不同的系统或者过程进行仿真时，如果系统或过程本身包含固有的随机组成成分，就需要一定的方法来生成或者获得随机的数值。例如，排队系统中的时间间隔，服务时间，库存系统中的需求量等。在计算机仿真中，能否产生具有一定性能要求的随机数是决定仿真是否可信的重要因素之一。
逆变换法生成随机变量。
5
❖ 随机实验：一个可观察结果的人工或自然过程，所产生的结果可能不止一个，但事先不能确定会产生什么结果。例：骰子
❖ 样本空间：一个随机实验的全部可能出现的结果的集合，记为Ω 。
❖ 随机事件：一个随机实验的一些可能的结果，是样本空间的一个子集
❖ 概率分布：如果样本空间上的所有随机事件都确定了概率，这些概率构成样本空间的一个概率分布

概率密度与随机变量函数的概率分布解读

(2)：规范性若随机变量X的一切可能值都位于区间[a , b]内,则:
P(a X b) 1,即P(a X b) b f ( x)dx 1，且此时认为: a
x a, x b时，f ( x) 0
a
b
b
F () f ( x)dx 0dx f ( x)dx 0dx f ( x)dx 1
f
x
sin
x,
0
x
2
;
0, 其它.
即可.
注意：x
0,
x
2
时f
(x)
0
(2)
sin xdx 2 1,
不是.
0
(3)
当
x
,
3 2
时,
sin x 0,
与 f x 0矛盾, 不是.
第六讲概率密度与随机变量函数的概率分布
例6-1-2 (拉普拉斯分布) 连续随机变量X 的概率密度为
f x Ae x , x .
0
0
注意：x 0时f ( x) 0
指数分布 e 的分布函数为
F(x)
x
f (t)dt
0
0dt
x etdt et x ex 1
0
0
第六讲概率密度与随机变量函数的概率分布
即：
F x
1 e
x,
x 0;
0,
x 0.
f x
F x
1
O
,
x
,
2
x 0; x 0.
讲授下例前，介绍常用的伽玛函数的定义：
x1e x dx 0
0
伽玛函数的性质： 1 ;
(n) (n 1)!
1 .
2
例如：( 3) ( 1 1) 1 (1) 1 0! 1

概率论随机变量的分布函数ppt课件

因此， A 是不可能事件
P{A} 0.
ppt课件
12
例1: 设随机变量X具有概率密度
ke 3 x
x0
f (x)
0 x0
(1)试确定常数k，(2)求F(x)，(3)并求P{X>0.1}。
解: (1)由于
f (x)dx
ke3xdx k 1
，解得k=3.
0
3
于是X的概率密度为
f
(
x)
O
x
(3) 在 x= 处曲线有拐点，且以x轴为渐近线 ;
(4) 对固定的,改变的值,图形沿Ox轴平移;
(5) 对固定的,改变, 越小,图形越尖.
正态分布的分布函数为: F ( x)
ppt课件
1
2
e dt x
(t )2 2 2
28
标准正态分布
当=0, =1时,称X服从标准正态分布,记作X～N(0,1).
例3 设电阻值R是一个随机变量，均匀分布在800欧～1000
欧，求R的概率密度及R落在850欧～950欧的概率.
解: 由题意，R的概率密度为
1 f (r) 1000 800
， 800 r 1000
0
, 其它
950 1
而 P{850 X 950}
dr 0.5
200 ppt课件
850
18
2. 指数分布
注 (4)式及连续性随机变量分布函数的定义表示了分布函数与概率密度间的两个关系．利用这些关系，可以根据分布函数和概率密度中的一个推出另一个．
ppt课件
10
连续型随机变量的分布函数与概率密度的几何意义：
1. F(x)等于曲线f(x)在(-∞,x]上的曲边梯形的面积。

《概率论与数理统计》课件-第2章随机变量及其分布 (1)

则称X服从参数为λ的泊松分布, 记为 X ~ P() .
HAINAN UNIVERSITY
概率论与数理统计
第二五章基随本机极变限量定及理其分布
泊松分布的应用
“稠密性”问题(一段时间内,电话交换中心接到的呼叫次数,公共汽车车站候车的乘客数,售票窗口买票的人数，原子放射的粒子数，保险公司在一定时期内被索赔的次数等)都服从泊松分布.
随机变量的分布函数
1.定义: 设X为一随机变量, x为任意实数, 称函数 F(x)=P{X≤x}为X的分布函数.
注: ① F(x)是一普通函数, 其定义域为 ,; ② F x的值为事件X x的概率; ③ F x可以完全地描述随机变量取值的规律性.
例如: Pa X b PX b PX a
连续型随机变量及概率密度函数
1.定义: 设X ~ F(x), 若存在一个非负可积的函数 f (x),
使 x R, 有
F ( x)
PX
x
x
f
(t)dt
,
则称X为连续型随机变量, f (x) 称为X的概率密度函数或
分布密度函数.
2.几何意义:
HAINAN UNIVERSITY
概率论与数理统计
第二五章基随本机极变限量定及理其分布
二、随机变量的概念
定义：设试验E的样本空间为 , 若对于每个样本
点 , 均有一个实数 X ()与之对应, 这样就得
到一个定义在上的单值函数 X X () , 称X为随
机变量.
X
样本空间
实数
注: ① 随机变量是一个定义在样本空间上的实函数, 它取值的随机性是由样本点的随机性引起的;
x 1
x0
0 x x
不是 (不满足规范性)

随机变量函数的分布密度

y fX
f aX
f aX b
x
第一步，计算aX的密度函数。aX的值域比X的值域大a倍。所以，aX的密度函数是将X的密度函数在x轴方向拉长a倍。但为了使aX的密度函数与x轴围成的面积为1，必须将X的密度函数下拉到原来的1/a. 随机变量aX+b与aX一样,只是将图形平移了b个单位。最后，得到随机变量Y=aX+b的密度函数为：
1 180
30 y 2
6 y2
例设随机变量X的密度函数为
f X (x)
求 Y eX 的密度函数. （教材P65）
1
x2
e2
2
解 y ex 是单调增加的函数，其导函数恒不为零，
值域为y>0，反函数为 x ln y , dx 1
dy y
由定理可得，当 y 0 时，概率密度为
fY ( y)
f X (ln
y) 1 y

1
ln 2 y
e2

1

2
y
1
ln 2 y
e2
2 y
当 y 0 时，Y的概率密度 fY ( y) 0
从而 Y e X 的概率密度为
fY ( y)
1
ln2 y
e 2,
2 y
0,
y0 y0

P(180 y

X)
180 1 FX ( y )
1,若y 180/ 30

1
(180 y

30) /
30,若 180 60

y

180 30
0,若y 180/ 60
0,若y 3

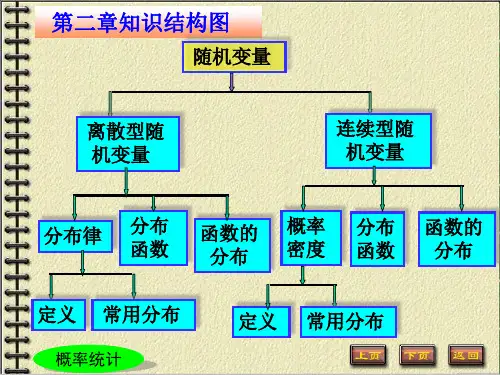
概率论与数理统计图文课件最新版-第2章-随机变量及其分布

一. 连续型随机变量的概率密度 1.定义若对于随机变量 X 的分布函数，存在非负
函数 f ( x)，使得对于任意实数 x 有:
x
F ( x) f (t)dt ( P( X x))
则称 X 为连续型变量，f ( x)为 X 的概率密度函数注 ▲ 连续型随机变量与离散型随机变量的区别
离散型： P( X xk ) 0 连续型：P( X xk ) 0
机
多，而且还不能一一列
变连续型随机变量量
举，而是充满一个区间
例如，“电视机的寿命”，实际中
常遇到的“测量误差”等等.
概率统计
第二章知识结构图
随机变量
离散型随机变量
连续型随机变量
分布律
分布函数
函数的分布
概率密度
分布函数
函数的分布
定义常用分布
概率统计
定义常用分布
第四节连续型随机变量及其概率密度
0 x 0
则称 X 为服从参数的指数分布.
概率统计
二 . 连续型随机变量的分布函数
定义: 若定义在 (, )上的可积函数 f ( x)
满足： (1). f ( x) 0
(2). f ( x)dx 1
f (x)确定了分布函数F(x)，
则称 F ( x)
x
f ( x)dx
f (x)是F(x)的导函数， F(x)是f (x)的一
(2) 某段时间内候车室的旅客数目为 X , 则它也是一个随机变量，它可以取 0 及一切自然数。X 是定义在样本空间，则：
S e {人数人数 0}
X X (e)的值域RX [0, )
概率统计
二. 随机变量的分类离散型随机变量

2-3.连续型随机变量的概率密度函数ppt

X越落平f在(缓xμ),的值表最附明大近X取的值值概为越率分越f 散大.;反之21,当σ越大,则y=f(x)的图形
f (x)
0
x
28
连续型随机变量
（2）分布函数
若 X ~ N ， 2 ，则其分布函数为
x
Fx f tdt
1
x (t )2
e 2 2 dt x
2
若 X ~ N 0， 1，则其分布函数为
该乘客候车时间不超过5分钟的概率．
解：设该乘客于7时X 分到达乘到此客7站:3到0,之达X间此服的站从均的匀区时随间间机是[变0,73量:000]
上的均匀分布．其密度函数为
f
x
1 30
0 x 30
0 其它
令：B={候车时间不超过5分钟 },则
PB P10 X 15 P25 X 30
0
x
25
连续型随机变量
密度函数的验证
xdx
只验证
f
x dx
1
x 2
e 2 2 dx 1
2
作变换：u x ，则 du dx
1
x2
e 2 dx 1
2
则有
见高等数学（下）二重积分
1
x 2
e 2 2 dx
2
x2
( e 2 dx 2 )
1
1
15
1
30
dx
1
dx
1
10 30
25 30
3
20
连续型随机变量
例 6 设随机变量Y 服从区间 1， 3上的均匀分布，
试求方程 4x 2 4Y x (Y 2) 0 有实根的概率．
解

大学概率论均匀分布·指数分布

当 X 在 [a,b] 上服从分布U (a,b) 时，记为: X ~ U (a,b).
概率论与数理统计教程（第四版）
目录
上一页下一页
返回
结束
§2.7 均匀分布 • 指数分布
均匀分布的概率密度与分布函数
(1) 概率密度
在区间[a,b]上概率密度 f (x) C(常数)，于是
b
C d x C(b a) 1 C
P(x1 X x2)
x2 f (x) dx.
x1
f (x)
P(x1 x x2 )
x
O
x1
x2
概率论与数理统计教程（第四版）
目录
上一页下一页
返回
结束
§2.6 连续随机变量的概率密度
[例2] 设连续随机变量 X 的概率密度
f
(x)

A 1 x2
,
x .
求： (1) 常数 A 的值；
x0
x
F(x);
x
(2) F (x) P( X x) f (x) dx.
概率论与数理统计教程（第四版）
目录
上一页下一页
返回
结束
§2.6 连续随机变量的概率密度
[例 1] 设随机变量 X 的概率密度为：
f
(x)

1 2
cos
x,
0,
求 X 的分布函数 F (x).
1 (arctan x π) 1 1 arctan x.
π
2 2π
[柯西(Cauchy)分布]
概率论与数理统计教程（第四版）
目录
上一页下一页
返回
结束

概率论与数理统计--第二章PPT课件

由概率的可列可加性得X的分布函数为
F(x) pk xk x
分布函数F(x)在x xk , 其跳跃值为pk P{X
对k 所1,有2,满足处x有k 跳 x跃的，k求和。
xk }
第26页/共57页
第四节连续型随机变量及其概率密度
定义对于随机变量X的分布函数F(x),如果存在非负函数f (x)，使对于任意实数有
售量服从参数为 10的泊松分布．为了以95%以上的
概率保证该商品不脱销，问商店在月底至少应进该商品多少件？解设商店每月销售该种商品X件，月底的进货量为n件，
按题意要求为 PX n 0.95
由X服附从录的泊1松0的分泊布松表分知布k，140 1则k0！k有e1k0n01k00！k.9e1160 6
可以用泊松分布作近似，即
n
k
pk
1
p
nk
np k
k!
enp , k
0,1, 2,
.
例 4 为保证设备正常工作，需要配备一些维修工.如果各台设备
发生故障是相互独立的，且每台设备发生故障的概率都是 0.01.
试求在以下情况下，求设备发生故障而不能及时修理的概率.
(1) 一名维修工负责 20 台设备.
于是PX I P(B) Pw X (w) I.
随机变量的取值随试验的结果而定，而试验的各个结果出现有一定的概率，因而随机变量的取值有一定的概率.
按照随机变量可能取值的情况，可以把它们分为两类：离散型随机变量和非离散型随机变量，而非离散型随机变量中最重要的是连续型随机变量.因此，本章主要研究离散型及连续型随机变量.
x
x
4. F(x 0) F(x) 即F(x)是右连续的
第23页/共57页

概率论课件：第二章随机变量及其概率分布

π 3π ⎞ ⎛ π 0 ⎟ 22.设随机变量 X 的分布律为 ⎜ 2 2 ⎟ ，求 Y 的分布律： ⎜ ⎝ 0.3 0.2 0.4 0.1 ⎠
（1） Y = ( 2 X − π ) ;
2
（2） Y = cos( 2 X − π ). ⎧2 x , 0 < x < 1 f ( x) = ⎨ ⎩0 , 其它
它意味着第 i 次（ i ≥ k ）成功，且 i − 1 次试验中成功 k − 1 次，设这两个事件分别为A1 ，A2，
则A = A 1 A 2 , 且P(A) = P(A 1 A 2 ) = P(A 1 )P(A 2 )(A 1与A 2 独立 ), 而 P(A 1 ) = p,
1 k −1 1 k −1 i − k P( A2 ) = Cik−− ⋅ q i −1−( k −1) = Cik−− q . 1 p 1 ⋅ p
, ( 2,6),
, (6,1),
例如(6,1) , (6,6)} .这里，
8
5 36
9
4 36
10
3 36
11
2 36
12
1 36
PK
1 36
2 36
3 36
4 36
5 36
6 36
概率 P{X = k }, k = 0,1,2,3.
2、分析：显然 X 服从离散型概率分布，而且 X 的可能取值为 0，1，2，3.问题归结为求
∴ X 的分布律为：
P{X = 0} = P ( A1 ) = 1 / 2; P{X = 1} = P ( A1 A2 ) = 1 / 2 2 ; P{X = 2} = P ( A1 A2 A3 ) = 1 / 2 3 ;
X Pi

2.5 随机变量的函数的分布

推论
若X ~ N ( µ , σ ), 则
2
X −µ
σ
~ N (0, 1)
正态分布的标准化
2010年12月16日星期四中央财经大学《概率统计》课件--孙博第二章第五节 --第18页--
设X ~ N（0，1），其概率密度为（，）其概率密度为：
1 ϕ ( x) = e −∞ < x < +∞ 2π 则 Y = X 2 概率密度函数为：概率密度函数为 1 y − − 1 y 2e 2 , y > 0 fY ( y ) = 2π 0, y ≤ 0
1, 0 < x < 1 fX ( x) = 其它 0,
d(e− y/ 2 ) − y/ 2 − y/ 2 , 0< e <1 fX (e ) fY ( y) = dy 0, 其它 1 − y / 2 得 e , y>0 fY ( y) = 2 0, 其它
服从[19 21]上的均匀分布 [19，上的均匀分布．即 Y 服从[19，21]上的均匀分布
2010年12月16日星期四中央财经大学《概率统计》课件--孙博第二章第五节 --第26页--
设球的半径X 例设球的半径X的概率密度为 6 x(1 − x), x ∈ (0,1) f ( x) = 试求体积的概率密度。试求体积的概率密度。其它 0, 4 Y = π X 3 的分布函数为解体积 3 3y 3y 4 3 FY ( y ) = P π X < y = P X < 3 = FX 3 4π 4π 3 − 2 3 3y 1 3y 3 y 3 y ′ 3 3 3 fY ( y ) = f X ⋅ = fX 3 ⋅ ⋅ ⋅ 4π 4π 4π 3 4π 4π

概率密度函数

而概率 P {Y ≥3 } = ∑k3=03 [C30k pk ( 1 – p)30 – k ]
根据指数分布的分布函数，这个人每次等车时间超过 10 分钟的概率是： p = P { X ＞10 } = 1 – F (10) = 1 – [ 1 – e – 10 / 5 ] = e – 2 ; 每个月等车超过10 分钟的次数 Y ~ B(30,e – 2) ；他至少有三天坐出租车上班的概率就是： P {Y ≥3 } = ∑k3=03 [C30k pk ( 1 – p)30 – k ] = 1 – ∑k=02 [C30k pk ( 1 – p)30 – k ]
假定通过考试的成绩至少要为 d 分，即必须有
P { X ≥ d } ≤ 0.05 P { X ≤ d } ≥ 0.95 。
根据定理 2.4.1， X – 60 ——— ~ N (0,1) 10
因此
d – 60 0.95 ≤P { X ≤ d } = (——— ) 10
查正态分布表，有，
(1.64) = 0.9495 ， (1.65) = 0.9505 ；
1 2
p ( x)
o

x
说明对于同样长度的区间，当参数越大时，X 落在这个区间里的概率将越小，而当参数越小时，X 落在这个区间里的概率将越大。
4. 标准正态分布 X ~ N ( 0 ,1 ) 参数 = 0 ， = 1 的正态分布 (1) 标准正态分布的密度函数
( x)
1 2
e
x2 2
, x
(2) 标准正态分布的分布函数
( x)

x
1 2
e
t2 2
dt , x

概率密度函数 ppt课件

概率密度函数
定义设X为一随机变量，若存在非负实函数 f (x) , 使对任意实数 a < b ，有
b
P{axb}a f(x)dx
则称X为连续型随机变量， f (x) 称为X 的概率密度函数,简称概率密度或密度函数.
x
分布函数 F(x) f (t)dt
P {x1Xx2}xx 12 f(x)dx
(1 x 5)
0 其它
所求概率为 P { 1 } 1f(x)d x f(x)d x2
1
3
指数分布
定义若连续型随机变量X的概率密度为
ex
f(x)
x0(0为常数）
0 x0
则称X服从参数为的指数分布.
X～ E()
分布函数
0
x0
F(x)1ex x0
f(x)和F(x)可用图形表示
f (x)
均匀分布
定义若连续型随机变量X的概率密度为
1 f (x) b a
a xb
0 其它
则称X在区间（a，b）上服从均匀分布．记为 X ~ U (a, b)
分布函数
0,
xa
F
(
x)
x b
a a
,
a xb
1,
b x
意义
0a
b
x
X“等可能”地取区间（a,b）中的值，这里的“等可
能”理解为：X落在区间（a,b)中任意等长度的子区间内
。 P(X a) 1 (a )
例设X~N（1，4），求 P(0<X<1.6)
解
1, 2
P(0X1.6) (1.61)(01)
2
2
(0.3)(0.5)
(0.3)1 (0.5)

随机变量及其分布复习课件.ppt

有
F(x) x f(t)dt，
则称X为连续型随机变量，其中f(x)称为X的概率密度函数，简称概率密度。
（II）概率密度的性质
( 1 ) 非负性： f( x ) 0 ， x R .
(2)规范性：f(x)dx1. 4
( 3 )对于任意实数 a b, 有
P{aXb}abf(x)dx . F(b)F(a)
求这个区间的端点,分二种情形讨论之：
17
（1）区间的一个端点是无穷大，即已知P(X < x) = p1 或P(X > x) = p2，求x .
利用或
然后反查标准正态分布表，即可求出x （2）区间关于μ对称，不妨设为(μ−a,μ+a)，而 P(μ−a<X<μ+a) = p，求a
18
四.随机变量的函数的分布 1.离散型随机变量函数的分布
几种重要的离散型分布
均指正匀数态分分分布布布
二项分布的正态近似
二项分布的泊松近似
二项分布
泊几
松何
分分布布 21
例题选讲
例1 甲、乙、丙3人进行独立射击每人的命中率依次为03 04 06 设每人射击一次试求3人命中总数之概率分布律分析求离散型随机变量的概率分布的步骤为:(1) 写
23
例2 投掷一个均匀骰子n 次，求(1)恰好得到一个6点的概率；(2)至少得到一个6点的概率；(3)为了以0.5的概率保证至少得到一个6点，则至少要投掷几次？
所以至少要投掷4次.
24
例3 设 X 的分布律为 X 1012 1111 p 4444
求 Y X 2 的分布律 .
解 Y 的可能值为 (1)2, 02,12, 22; 即 0, 1, 4.

概率论课件之连续型随机变量及其概率密度PPT课件

如电话通话时间、各种随机服务系统的服务时间、等待时间等.
例某种电子元件的寿命(以小时计) X 服从指数分布,其概率密度为
f
(
x)
1 100
e
x
100
,
x0
0,
其它.
(1) 求元件寿命至少为200小时的概率. (2) 将3只这种元件联接成为一个系统，设系统工作的方式是至少2只元件失效时系统失效，又设3只元件工作相互独立.求系统的寿命至少为200小时的概率.
(4) 若f ( x )在点x 处连续,则有
F ( x) f ( x),
证明
x
F ( x) [ f (t)dt] f ( x).
例设随机变量X
ae x , x 0;
的分布函数为
F ( x) b, 0 x 1; 1 ae x1 , x 1
求(1)a,b的值;(2)X的密度函数;(3)P(X>1\3).
解 (1)由于连续型随机变量的分布函数是连续的
lim F ( x) F (0)
x 0
又 lim F ( x) F (1) x 1
lim ae x b
x 0
b 1 a
故，a b 1 2
ab
(2)X的密度函数
1 2
e
x
,
f ( x) F ( x)
又F ( x)
1
2
,
x 0; 0 x 1;
2 πσ (3) 当 x 时, f ( x) 0; (4)曲线在 x μ σ 处有拐点;
(5) 曲线以 x 轴为渐近线;
(6) 当固定 σ, 改变 μ 的大小时, f ( x) 图形的形状不变 ,只是沿着 x 轴作平移变换;
(7) 当固定 μ, 改变 σ 的大小时, f ( x) 图形的对称轴不变,而形状在改变 , σ 越小,图形越高越瘦,σ越大, 图形越矮越胖 .

例1设随机变量X的概率密度为-PPT精品

1d x l
.
c
c b a b a
若X~U(a, b), 则X具有下述等可能性： X落在区间(a, b)中任意长度相同的子区间里的概率
是相同的. 即X落在子区间里的概率只依赖于子区间的长度, 而与子区间的位置无关.
均匀分布的实际背景
一维几何概型. r.v. X取值在区间(a, b) 上, 并且取值在 (a, b)中任意小区间内的概率与这个小区间的长度成正比, 则X 在(a,b)上服从均匀分布. 如:一段时间内乘客到达车站的时刻、四舍五入引起的误差等一般都服从均匀分布. 例4 秒表最小刻度值为0.01秒. 若计时精度是取最近的刻度值, 求使用该表计时产生的随机误差X 的概率密度, 并计算误差的绝对值不超过0.004秒的概率.
试求:(1)常数a , b ;
(2)
1 P{

X

3 };
(3) X的概率密度.
2
2
例3 已知某型号电子管的使用寿命 X 为连续型r.v., 其
概率密度为
f
( x)

c x2
,
x 1000
(1) 求常数 c;

0,
其它.
(2) 计算 P { X 1 7 0 01 5 0 0 X 2 0 0 0 } ;
例8 3 原理设 X ~ N ( , 2), 求 P{|X|3}
解 P { |X | 3 } P { 3 X 3 }
P{3 X3}
33231
20.998710.9974 【结论】一次试验中, X 落入区间( - 3 , +3 )
f (x)
概率密度
函数图形

已知均匀分布求概率密度函数

已知均匀分布求概率密度函数已知均匀分布求概率密度函数均匀分布是一个经典的概率分布，在数学、物理、经济等领域广泛应用。

当我们知道一个事件发生的范围和事件在范围内发生的概率相同时，可以使用均匀分布求解该事件的概率密度函数。

1. 均匀分布的定义均匀分布是指在一个区间[a, b]内，每个数在该区间内出现的概率都相等，且出现的概率是1/(b-a)。

表示为：X ~ U(a, b)其中，X代表一个随机变量，U表示均匀分布，a和b分别是事件发生的范围。

2. 求解概率密度函数概率密度函数（probability density function，PDF）是指一个随机变量的取值发生的概率密度。

在连续型随机变量中，概率密度函数可以用来描述该随机变量在某个取值范围内的概率密度大小。

对于均匀分布，在[a, b]内任取一点x的概率为1/(b-a)，即P(X=x) = 1/(b-a)为了求解概率密度函数，需要先计算出均匀分布的期望值（expected value）和方差（variance）。

期望值：E(X) = (a+b)/2方差：Var(X) = (b-a)²/12接下来，我们可以使用概率密度函数的定义求解均匀分布的概率密度函数：f(x) = dP(X=x)/dx因为在均匀分布中，X=x的概率为常数1/(b-a)。

那么，在[a, b]内任取x时，P(X<=x) = (x-a)/(b-a)因此，概率密度函数f(x)为：f(x) = dP(X=x)/dx = d/dx (P(X<=x)) = 1/(b-a)综上所述，对于已知均匀分布，求解概率密度函数的步骤如下：1. 求解期望值和方差（用于检验结果）。

2. 根据概率密度函数的定义，计算出X=x的概率密度函数。

3. 将已知的概率密度常数代入概率密度函数中，得到最终的概率密度函数。

总结本文介绍了如何求解已知均匀分布的概率密度函数。

首先，我们需要了解均匀分布的定义，计算出期望值和方差。

分布函数均匀分布指数分布函数演示文档专选课件

(1) P{x1Xx2} P { X x 2 } P { X x 1 } F(x2)F(x1)
(2) P{x1Xx2}P{x1Xx2}P{Xx1} F(x2)F(x1)P{Xx1}
同理，还可以写出P{x1Xx2},P{x1Xx2}
二、分布函数的性质
⑴ 单调不减性：若x1 x2，则 F(x1)F(x2) ⑵ 0F(x)1，且 F( )lim F(x)0,
2
a1,b 1.
2
F(x)可导, f(x)F(x)1
1
1 x2
.
例4、
F(x)
A
x2
Be 2
,
x
0
，求A , B 及 f (x)。
0, x 0
解：F( )A1 A1,B1.
F(0) AB0
F(x)
1
e
x2 2
,
x
0
0, x 0
f
(x)
x
e
x2 2
,
x
0
注：F(x)f(x)的方.法
0, x 0
A(1)e3x 3
0
A 3
1
A3.
P{X 1}
1 3
f (x)dx
3
1
3 3e3xdx e 3 x
0
1
3 0
1e1.
例3、设 X 的分布函数 F ( x ) a b a r c t a n x , 求常数 a,b,
及概率密度函数 f (x)。
解：
F()ab( )0
2
F()a b( ) 1
例2. 已知随机变量X 的分布律为 X 0 1 2
求分布函数 F (x)
pk
1 3
11 62