传热学作业参考答案

传热学习题_建工5版绪 论0-14 一大平板，高3m ，宽2m ，厚0.2m ，导热系数为45()K m W ⋅, 两侧表面温度分别为C t w ︒=1501及C t w ︒=2852，试求热流密度及热流量。

解：根据付立叶定律热流密度为：i dxdt t grad i q xλλ-=-=21212303752015028545m /W .x x t t dx dt q w w x -=-⨯-=---=-=λλ负号表示传热方向与x 轴的方向相反。

通过整个导热面的热流量为：)W (A q 1822502330375=⨯⨯-==Φ0-15 空气在一根内经50毫米，长2.5米的管子内流动并被加热，已知空气的平均温度为85℃，管壁对空气的对流换热系数()K m /W h ⋅=273，热流密度25110m /W q =, 是确定管壁温度及热流量Φ。

解：热流量)W (....)dl (q qA 72005520501435110=⨯⨯⨯===πΦ根据牛顿冷却公式()qA t t hA )dl (h t hA f w =-===π∆Φ管内壁温度为：C A q t t f w ︒=+=+=15573511085第一章 导热理论基础1-1 按20℃时，铜、碳钢（1.5%C ）、铝和黄铜导热系数的大小，排列它们的顺序；隔热保温材料导热系数的数值最大为多少？列举膨胀珍珠岩散料、矿渣棉和软泡沫塑料导热系数的数值。

解：(1)由附录7可知，在温度为20℃的情况下λ铜=398 ()K m W ⋅，λ碳钢＝36()K m W ⋅， λ铝＝237()K m W ⋅，λ黄铜＝109()K m W ⋅.所以,按导热系数大小排列为:λ铜>λ铝>λ黄铜>λ钢(2) 隔热保温材料定义为：温度在350℃以下时，导热系数不超过0.12 ()K m W ⋅的材料。

(3) 由附录8得，当材料的平均温度为20℃时的导热系数:膨胀珍珠岩散料:λ=0.0424+0.t ()K m W ⋅ λ=0.0424+0.×20=0.04514 ()K m W ⋅; 矿渣棉: λ=0.0674+0.t ()K m W ⋅λ=0.0674+0.×20=0.0717 ()K m W ⋅;聚乙烯泡沫塑料在常温下（附录7）3)K m /(W ..⋅-=03800350λ。

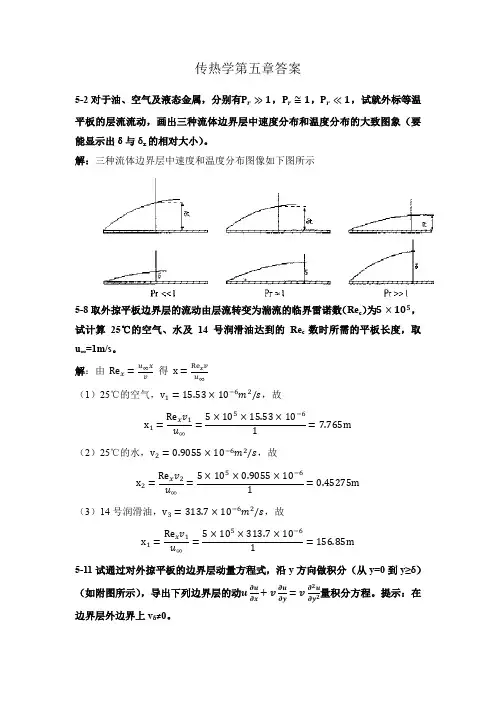
《传热学》第五版部分习题解答第五章5-13 解:本题应指出是何种流体外掠平板，设是水外掠平板。

由60=m t ℃，查附录3 饱和水的热物理性质表得：610478.0-⨯=v m 2/s ，99.2=r p561082.210478.015.09.0Re ⨯=⨯⨯=⋅=-∞v x u x 41.11015.0)1082.2(0.5Re 0.5321521=⨯⨯⨯⨯==---x xδ mm98.099.241.13131=⨯==--rt p δδ mm5-18 解：55230802=+=+=wf m t t t ℃ 由附录2 ，查得空气的热物性参数为：210865.2-⨯=λW/(m.K) 61046.18-⨯=v m 2/s ， 697.0=r p5561051033.41046.188.010Re ⨯<⨯=⨯⨯=⋅=-∞v l u c 所以，此流动换热为层流换热。

923.0101046.18105Re 65=⨯⨯⨯=⋅=-∞u v x c c m46.6)697.0()105(923.010865.2332.0332.03121523121Re =⨯⨯⨯⨯⨯==-r c x h p c c λW/(m 2.K)94.6)697.0()1033.4(8.010865.2332.0332.03121523121Re=⨯⨯⨯⨯⨯==-r lh p l λW/(m 2.K)88.1364.922=⨯==l h h W/(m 2.K)2.555)3080(18.088.13=-⨯⨯⨯=∆=Φt hA W5-23 解： (注意：本题可不做)参考课本p126页（15）到（5-33）式。

2t a by cy =-+；0,w y t t ==；220wd t dy ⎛⎫= ⎪⎝⎭；,t f y t t δ==得到w f w f tt t yt t θθδ-==-，代入速度场和该温度场于能量积分方程()0tf wd t u t t dy a dx y δ⎛⎫∂-= ⎪∂⎝⎭⎰，并且设t δςδ=，略去ς的高阶项，可以得到ς的表达式，进而得到t δ的表达式。

传热学习题答案1-9 一砖墙的表面积为122m ，厚为260mm ，平均导热系数为1.5W/（m.K ）。

设面向室内的表面温度为25℃，而外表面温度为-5℃，试确定次砖墙向外界散失的热量。

解：根据傅立叶定律有：WtA9.207626.05)(25125.1=--⨯⨯=∆=Φδλ1-11 夏天，阳光照耀在一厚度为40mm 的用层压板制成的木门外表面上，用热流计测得木门内表面热流密度为15W/m 2。

外变面温度为40℃，内表面温度为30℃。

试估算此木门在厚度方向上的导热系数。

解：δλtq ∆=，)./(06.0304004.015K m W t q =-⨯=∆=δλ1-12 在一次测定空气横向流过单根圆管的对流换热实验中，得到下列数据：管壁平均温度t w =69℃，空气温度t f =20℃，管子外径 d=14mm ，加热段长 80mm ，输入加热段的功率8.5w ，如果全部热量通过对流换热传给空气，试问此时的对流换热表面传热系数多大？ 解：根据牛顿冷却公式()f w t t rlh q -=π2所以()f w t t d qh -=π＝49.33W/(m 2.k) 1-14 一长宽各为10mm 的等温集成电路芯片安装在一块地板上，温度为20℃的空气在风扇作用下冷却芯片。

芯片最高允许温度为85℃，芯片与冷却气流间的表面传热系数为175 W/(m 2.K)。

试确定在不考虑辐射时芯片最大允许功率时多少？芯片顶面高出底板的高度为1mm 。

解：()()[]⨯⨯⨯+⨯⨯=∆=Φ001.001.0401.001.0./1752max K m W t hA (85℃-20℃) ＝1.5925W1-15 用均匀的绕在圆管外表面上的电阻带作加热元件，以进行管内流体对流换热的实验，如附图所示。

用功率表测得外表面加热的热流密度为3500W/2m ；用热电偶测得某一截面上的空气温度为45℃，内管壁温度为80℃。

设热量沿径向传递，外表面绝热良好，试计算所讨论截面上的局部表面传热系数。

传热学知到章节测试答案智慧树2023年最新青岛理工大学绪论单元测试1.热量传递过程的推动力是温差。

参考答案:对第一章测试1.平板的单位面积导热热阻的计算式应为哪一个?（）参考答案:δ/λ2.导热系数的单位是：（）参考答案:W/(m·K)3.两条不同温度的等温线绝不会彼此相交。

（）参考答案:对4.导热系数的单位是W/(m·K)。

（）参考答案:对5.热流密度q与热流量的关系为（以下式子A为传热面积，λ为导热系数，h为对流传热系数）：（）参考答案:q＝φ/A6.已知某一导热平壁的两侧壁面温差是30℃，材料的导热系数是22 W/(m·K)，通过的热流密度是300 W/m2，则该平壁的壁厚是多少? ( )参考答案:2.2 m7.在稳态传热过程中，传热温差一定，如果希望系统传热量增大，则不能采用下述哪种手段? ( )参考答案:增大系统热阻8.在传热过程中，系统传热量与下列哪一个参数成反比?参考答案:传热热阻9.下列哪几种传热过程不需要有物体的宏观运动?( )参考答案:导热;辐射10.单位时间通过单位面积的热量称为什么?一般用什么符号表示?( )参考答案:热流密度，q第二章测试1.导温系数是材料传播温度变化能力大小的指标。

（）参考答案:对2.工程中很多导热现象，可归结为稳态导热过程，如通过房屋墙壁和长热力管道管壁的导热。

（）参考答案:对3.傅里叶定律是指在各向同性均质的导热物体中，通过某导热面积的热流密度正比于该导热面法向温度变化率。

（）参考答案:对4.肋片效率是指肋片实际散热量与肋片最大可能散热量之比。

（）参考答案:对5.传热过程的热阻等于壁面两侧对流热阻与壁面的导热热阻之和，相当于串联。

（）参考答案:对6.导温系数的物理意义是什么?( )参考答案:反映材料内部温度趋于一致的能力7.温度梯度表示温度场内的某一点等温面上什么方向的温度变化率? ( )参考答案:法线方向8.接触热阻的存在使相接触的两个导热壁面之间产生什么影响?( )参考答案:出现温差9.某热力管道采用两种导热系数不同的保温材料进行保温，为了达到较好的保温效果，应将哪种材料放在内层?( )参考答案:导热系数较小的材料10.物体之间发生热传导的动力是什么?( )参考答案:温差第三章测试1.物体的温度随时间而变化的导热过程称为非稳态导热。

第7章作业7-3把太阳表面近似的看成是T=5800K 的黑体，试确定太阳发出的辐射能中可见光所占的百分数。

解：λ1T=0.38×5800=2204μm.K λ2T=0.76×5800=4408μm.K F b(0-λ1)=10.19% F b(0-λ2)=55.04% F b(λ1-λ2)=44.85%7-7用特定的仪器侧得，一黑体炉发出的波长为0.7μm 的辐射能（在半球范围内）为108w/m 3，试问该黑体炉工作在多高的温度下？在该工况下辐射黑体炉的加热功率为多大？辐射小孔的面积为4×10-4m 2。

解：由普朗特定律(7-6)，得：1)107.0(10742.31062107.0104388.156168−×××=−−××−−−Te所以T=1213.4K该温度下，黑体辐射力E b =5.67×10-8×1213.44=122913w/m 2 辐射炉的加热功率为：4×10-4×122913=49.2w7-17一选择性吸收表面的光谱吸收比随λ变化的特性如图所示，试计算当太阳投入辐射为G=800W/m 2时，该表面单位面积上所吸收的太阳能量与太阳辐射的总吸收比。

解：∫=4.101)5800(9.0λλd E q b∫=4.101)5800()5800(9.0)5800(/λλd E E E q b b b∫∞=4.12)5800(2.0λλd E q bλ1T=1.4×5800=8120μm.K F b(0-λ1)=86.08%F b(λ1-∞)=1-86.08%=13.92% q 1/E b =0.9×0.861=0.775 q 2/E b =0.2×0.139=0.028Q=800×(0.775+0.028)=642.4W 总吸收率642.4/800=80.3%7-19暖房的升温作用可以从玻璃的光谱的穿透比变化特性得到解释。

数值传热学习题答案数值传热学习题答案数值传热学是热力学的一个重要分支，主要研究热量在物质中传递的机理和规律。

在实际工程中，我们经常会遇到各种与传热有关的问题，通过数值计算可以得到准确的答案。

下面我将为大家提供一些数值传热学习题的答案，希望能够帮助大家更好地理解和应用这门学科。

1. 一个铝制热交换器的表面积为10平方米，其表面温度为100摄氏度，环境温度为20摄氏度。

已知铝的导热系数为200 W/(m·K)，求热交换器的传热速率。

答：根据传热定律，传热速率与传热面积、传热系数和温度差之间成正比。

传热速率 = 传热系数× 传热面积× 温度差。

将已知数据代入公式中，可得传热速率= 200 × 10 × (100 - 20) = 160,000 W。

2. 一个房间的尺寸为5米× 5米× 3米，墙壁和天花板的厚度为0.2米，墙壁和天花板的导热系数为0.5 W/(m·K)，室内温度为25摄氏度，室外温度为10摄氏度。

求房间的传热损失。

答：房间的传热损失可以通过计算墙壁和天花板的传热速率来得到。

墙壁和天花板的传热速率 = 传热系数× 传热面积× 温度差。

墙壁和天花板的传热面积 = 2 × (5 × 5) + 2 × (5 × 3) = 70平方米。

将已知数据代入公式中，可得墙壁和天花板的传热速率= 0.5 × 70 × (25 - 10) = 525 W。

因此，房间的传热损失为525瓦特。

3. 一个水箱的体积为1立方米，初始温度为20摄氏度，水的密度为1000千克/立方米，比热容为4186 J/(千克·摄氏度)，水箱的表面积为2平方米，表面温度为100摄氏度。

已知水的传热系数为0.6 W/(m^2·K)，求水箱内水的温度随时间的变化。

绪论思考题与习题（89P -）答案：1． 冰雹落体后溶化所需热量主要是由以下途径得到：Q λ—— 与地面的导热量 f Q ——与空气的对流换热热量注：若直接暴露于阳光下可考虑辐射换热，否则可忽略不计。

6． 夏季：在维持20℃的室内，人体通过与空气的对流换热失去热量，但同时又与外界和内墙面通过辐射换热得到热量，最终的总失热量减少。

（T T 〉外内）冬季：在与夏季相似的条件下，一方面人体通过对流换热失去部分热量，另一方面又与外界和内墙通过辐射换热失去部分热量，最终的总失热量增加。

（T T 〈外内）挂上窗帘布阻断了与外界的辐射换热，减少了人体的失热量。

7．热对流不等于对流换热，对流换热 = 热对流 + 热传导 热对流为基本传热方式，对流换热为非基本传热方式 8．门窗、墙壁、楼板等等。

以热传导和热对流的方式。

9．因内、外两间为真空，故其间无导热和对流传热，热量仅能通过胆壁传到外界，但夹层 两侧均镀锌，其间的系统辐射系数降低，故能较长时间地保持热水的温度。

当真空被破坏掉后，1、2两侧将存在对流换热，使其保温性能变得很差。

10．t R R A λλ= ⇒ 1t R R Aλλ==2218.331012m --=⨯ 11．q t λσ=∆ c o n s t λ=→直线 c o n s t λ≠ 而为λλ=（t ）时→曲线12. i R α 1R λ 3R λ 0R α 1f t −−→ q首先通过对流换热使炉子内壁温度升高，炉子内壁通过热传导，使内壁温度生高，内壁与空气夹层通过对流换热继续传递热量，空气夹层与外壁间再通过热传导，这样使热量通过空气夹层。

（空气夹层的厚度对壁炉的保温性能有影响，影响a α的大小。

） 13．已知：360mm σ=、0.61()Wm K λ=∙ 118f t =℃ 2187()Wh m K =∙210f t =-℃ 22124()Wh m K =∙ 墙高2.8m ，宽3m求：q 、1w t 、2w t 、φ 解：1211t q h h σλ∆=++＝18(10)45.9210.361870.61124--=++2W m111()f w q h t t =-⇒ 11137.541817.5787w f q t t h =-=-=℃222()w f q h t t =-⇒ 22237.54109.7124w f q t t h =+=-+=-℃ 45.92 2.83385.73q A W φ=⨯=⨯⨯=14.已知：3H m =、0.2m σ=、2L m =、45λ=()W m K ∙ 1150w t =℃、2285w t =℃求：t R λ、R λ、q 、φ解：40.27.407104532t K R W A HL λσσλλ-====⨯⨯⨯30.24.4441045t R λσλ-===⨯2m K W ∙ 3232851501030.44.44410t KW q m R λ--∆-==⨯=⨯ 3428515010182.37.40710t t KW R λφ--∆-==⨯=⨯ 15．已知：50i d mm =、 2.5l m =、85f t =℃、273()Wh m K =∙、25110Wq m =求：i w t 、φ()i w f q h t h t t =∆=-⇒iw f qt t h =+51108515573=+=℃0.05 2.551102006.7i Aq d lq Wφππ===⨯⨯=16.已知:150w t =℃、220w t =℃、241.2 3.96()W c m K =∙、1'200w t =℃求： 1.2q 、'1.2q 、 1.2q ∆ 解：12441.2 1.2()()100100w w t t q c ⎡⎤=-⎢⎥⎣⎦44227350273203.96()()139.2100100W m ++⎡⎤=⨯-=⎢⎥⎣⎦12''441.21.2()()100100w w t t qc ⎡⎤=-⎢⎥⎢⎥⎣⎦442273200273203.96()()1690.3100100W m ++⎡⎤=⨯-=⎢⎥⎣⎦'21.2 1.2 1.21690.3139.21551.1Wq q q m ∆=-=-=17．已知：224A m =、215000()Wh m K =∙、2285()Wh m K =∙、145t =℃2500t =℃、'2285()Wk h m K ==∙、1mm σ=、398λ=()Wm K ∙求：k 、φ、∆解：由于管壁相对直径而言较小，故可将此圆管壁近似为平壁 即：12111k h h σλ=++＝3183.5611101500039085-=⨯++2()W m k ∙ 383.5624(50045)10912.5kA t KW φ-=∆=⨯⨯-⨯=若k ≈2h'100k kk-∆=⨯％8583.56 1.7283.56-==％ 因为：1211h h，21h σλ 即：水侧对流换热热阻及管壁导热热阻远小于燃气侧对流换热热阻，此时前两个热阻均可以忽略不记。