【配套K12】八年级数学上册《分式》知识点湘教版
- 格式:doc
- 大小:13.50 KB
- 文档页数:2

湘教版初中八年级数学上册第一章《分式》复习知识点教学目标1 使学生系统了解本章的知识体系及知识内容;2 进一步了解分式的基本性质、分式的运算法则以及整数指数幂,会熟练地进行分式的运算。
重点、难点重点:梳理知识内容,形成知识体系。
难点:熟练进行分式的运算。
教学过程一 知识结构与知识要点1浏览第2章目录,阅读p 61---63 复习与小结 2 这章学习了哪些内容?(学生交流) 教师投影本章知识结构图 3 你还记得下面知识要点吗? (1)什么叫分式?设f 、g 都是整式,且g 中含有字母,我们把f 除以g 所得的商记作f g ,把f g叫做分式。
(2)分式基本性质 设h ≠0,则f f hg g h⋅=⋅即:分式的分子与分母同时乘以一个非零的多项式,所得分式与原分式相等;分式的分子分母同时约去公因式,所得分式与原分式相等。
(3)分式的符号变换法则是什么?,f f f f fg g g g g−−===−−− 形象的理解为:分式的分子分母的符号可以移动 ⎧⎪⎧⎪⎪⎪⎨⎪⎪⎪⎩⎪⎧⎨⎪⎪⎨⎪⎪⎪⎩⎪⎧⎪⎨⎪⎩⎩分式的概念约分分式的性质通分分式的符号变号法则分式乘除法分式的运算乘方加减法分式方程的解法分式方程分式方程的应用(4)分式的运算法则①分式的乘法:f u f ug v g v⋅⋅=⋅可以先把分子、分母分别相乘再约分,也可以先约分再分子、分母分别相乘。
②分式的除法:f u f v f vg v g u g u⋅÷=⋅=⋅,分式除以分式,把被除式的分子分母颠倒位置后,与被除式相乘。
③分式加减法:同分母:f h f hg g g±±=,分母不变,分子相加减。
异分母:先通分,化为同分母的分子然后相加减。
怎样找最简公分母?系数:取各分母的系数最少公倍数。
字母因式:取所有的,指数最高的。
(5)整数指数幂的运算法则①同底数的幂的除法:(n m n m n a a a m −÷=≠、都是正整数,m>n,a 0) ②零次幂和负整数指数幂:01(0)a =≠a ,1(0,n n a a n a−=≠是正整数),11(0a a a−=≠)③整数指数幂有哪些运算法则:设a ≠0,m,n 都是整数,则:()(),nnm n m n m mn n n a a a a a ab a b +⋅===,二 例题精讲w W w .x K b 1.c o M 例1 填空:当x=_____,分式()3(5)(1)2x x x −−+无意义。

八年级数学上册分式知识点(word版可编辑修改) 八年级数学上册分式知识点(word版可编辑修改)编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(八年级数学上册分式知识点(word版可编辑修改))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为八年级数学上册分式知识点(word版可编辑修改)的全部内容。
常见考法考查分式有(无)意义、值为0的条件误区提醒三、约分与通分:1.约分:把一个分式的分子和分母的公因式约去,这种变形称为分式的约分;分式约分:将分子、分母中的公因式约去,叫做分式的约分。
分式约分的根据是分式的基本性质,即分式的分子、分母都除以同一个不等于零的整式,分式的值不变。
约分的方法和步骤包括:(1)当分子、分母是单项式时,公因式是相同因式的最低次幂与系数的最大公约数的积;(2)当分子、分母是多项式时,应先将多项式分解因式,约去公因式。
2.通分:根据分式的基本性质,异分母的分式可以化为同分母的分式,这一过程称为分式的通。
分式通分:将几个异分母的分式化成同分母的分式,这种变形叫分式的通分。
(1)当几个分式的分母是单项式时,各分式的最简公分母是系数的最小公倍数、相同字母的最高次幂的所有不同字母的积;(2)如果各分母都是多项式,应先把各个分母按某一字母降幂或升幂排列,再分解因式,找出最简公分母;(3)通分后的各分式的分母相同,通分后的各分式分别与原来的分式相等;(4)通分和约分是两种截然不同的变形.约分是针对一个分式而言,通分是针对多个分式而言;约分是将一个分式化简,而通分是将一个分式化繁。
注意:(1)分式的约分和通分都是依据分式的基本性质;(2)分式的变号法则:分式的分子、分母和分式本身的符号,改变其中的任何两个,分式的值不变.(3)约分时,分子与分母不是乘积形式,不能约分.3.求最简公分母的方法是:(1)将各个分母分解因式;(2)找各分母系数的最小公倍数;(3)找出各分母中不同的因式,相同因式中取次数最高的,满足(2)(3)的因式之积即为各分式的最简公分母(求最简公分母在分式的加减运算和解分式方程时起非常重要的作用)。


湘教版八年级数学上册知识点总结第1章分式1.1分式1.2分式的乘法和除法1.3整数指数幕1.4分式的加法和减法1.5可化为一元一次方程的分式方程J本章复习与测试第2章三角形2.1三角形2.2命题与证明2.3等腰三角形2.4线段的垂直平分线2.3全等三角形2.6用尺规作三角形本章复习与测试第3章实数3.1平方根3.2立方根3.3实数第4章一元一次不等式(组)4.1不等式4.2不等式的基本性质4.3一元一次不等式的解法4.4一元一次不等式的应用4.5—元一次不等式组本章复习与测试第5章二次根式3.1二次根式3.2二次根式的乘法和除法3.3二次根式的加法和减法本章复习与测试知识点总结第一章:分式一、课前构建:认真阅读教材P IT回顾相关知识:—分式的走义4—分式的概念一—分式的性质2分式_—分式的运算一—分式方程a一分式无意义+j—分式的值为零4—乘’除运算a—整数指数幕的运算A—加、减运算厂二、课堂点拨:知识点一:分式的概念★考点1:分式的定义:f 一个空成/除以一个 ______________ (___________ ),所得的商®叫做分乙1S例1、下列式子竿竽,±⅛叵中,是分式的是__________________ 。
“2x 5 K X姑点2汾式无意义:*jf⅛5>X-屮,当g ______ 时.分Λt⅛⅛: g_______ 时.÷1S例2、令二_____ 亦分式上没有意凫争__________ 陥分式厶有意矢2兀+1 工+1姑点3汾式的值为象亠f⅛5>X-屮,⅛/ ________ JLg ______ 叭分貞的½⅛0BSIY-I例氐若分式J的動岔则询勵_____________ O ÷'A-+1知识点二:分式的性质★考点4:分式的基本性质:分式的分子与分母都乘 _________ ,所得分式与原分式相等。
即 ___________ (其中A ≠ O)分式的分子与分母约去公因式,所得分式与原分式相等。

湘教版初中数学重点知识精选掌握知识点,多做练习题,基础知识很重要!湘教版初中数学和你一起共同进步学业有成!1.2 分式的乘法和除法第1课时 分式的乘除教学目标:1.类比分数的乘除运算法则,探索分式的乘除运算法则。
2.理解分式的乘除运算法则,会进行简单的分式的乘除法运算3.能解决一些与分式有关的简单的实际问题。
4.通过师生讨论、交流,培养学生合作探究的意识和能力。
教学重点:理解分式的乘除运算法则,会进行简单的分式的乘除法运算教学难点:类比分数的乘除运算法则,探索分式的乘除运算法则过程分析第一环节 复习旧知识复习小学学过的分数的乘除法运算。
活动内容1、计算,并说出分数的乘除法的法则:(1) (2); 82174⨯9452÷分数乘以分数,用分子的积做积的分子,分母的积做积的分母;分数除以分数,把除数的分子分母颠倒位置,与被除数相乘. 第二环节 引入新课活动内容97259275,,53425432⨯⨯=⨯⨯⨯=⨯ 279529759275,,435245325432⨯⨯=⨯=÷⨯⨯=⨯=÷ 猜一猜: ; =⨯c d a b =÷cd a b 你能总结分式乘除法的法则吗?与同伴交流。
, c b d a c d b a ⨯⨯=⨯db c a d c b a c d b a ⨯⨯=⨯=÷分式的乘除法的法则:两个分式相乘,把分子相乘的积作为积的分子,把分母相乘的积作为积的分母;两个分式相除,把除式的分子和分母颠倒位置后再与被除式相乘.第三环节 知识运用活动内容 例题1:(1) (2) 226283a y y a ⋅22122a a a a +⋅-+例题2(1) (2) x y xy 2262÷41441222--÷+--a a a a a 活动内容:例题3通常购买同一品种的西瓜时,西瓜的质量越大,花费的钱越多,因此人们希望西瓜瓤占整个西瓜的比例越大越好.假如我们把西瓜都看成球形,并把西瓜瓤的密度看成是均匀的,西瓜的皮厚都是d,已知球的体积公式为(其中R 为球的半径),那么,(1)西瓜瓤与整个西瓜的体积各是多334R V π=少?(2)西瓜瓤与整个西瓜的体积的比是多少?(3)你认为买大西瓜合算还是买小西瓜合算?与同伴交流当分式的分子与分母都是单项式时: (1)乘法运算步骤是,①用分子的积做积的分子,分母的积做积的分母;②把分式积中的分子与分母分别写成分子与分母的分因式与另一个因式的乘积形式,如果分子(或分母)的符号是负号,应把负号提到分式的前面;③约分 (2)除法的运算步骤是,把除式中的分子与分母颠倒位置后,与被除式相乘,其它与乘法运算步骤相同。

第一章 分式分式的概念:一般的,用B A ,表示两个整式,B A ÷就可以表示成BA的形式.如果B 中含有字母,式子BA就叫做分式.其中,A 叫做分式的分子,B 叫做分式的分母.分式和整式通称为有理式. 注意:(1)分母中含有字母是分式的一个重要标志,它是分式与分数、整式的根本区别; (2)分式的分母的值也不能等于零.若分母的值为零,则分式无意义; (3)当分子等于零而分母不等于零时,分式的值才是零. 分式的相关概念:把一个分式的分子与分母的公因式约去,把分式化成最简分式,叫做分式的约分.一个分式约分的方法是:当分子、分母是单项式时,直接约分;当分子、分母是多项式时,把分式的分子和分母分解因式,然后约去分子与分母的公因式.一个分式的分子和分母没有公因式时,叫做最简分式,也叫既约分式.把几个异分母的分式分别化成与原来的分式相等的同分母的分式,叫做分式的通分. 取各分母所有因式的最高次幂的积作公分母,这样的公分母叫做最简公分母. 分式的基本性质:分式的分子和分母都乘以(或除以)同一个不等于零的整式,分式的值不变.用式子表示是:MB MA MB M A B A ÷÷=⨯⨯=(其中M 是不等于零的整式).分式的变号法则:分式的分子、分母与分式本身的符号,改变其中任何两个,分式的值不变.如:BAB A B A B A --=--=--=. 分式的系数化整问题,是利用分式的基本性质,将分子、分母都乘以一个适当的不等于零的数,使分子、分母中的系数全都化成整数.当分子、分母中的系数都是分数时,这个“适当的数”应该是分子和分母中各项系数的所有分母的最小公倍数;当分子、分母中各项系数是小数时,这个“适当的数”一般是n10,其中n 等于分子、分母中各项系数的小数点后最多的位数.例、不改变分式的值,把下列各分式分子与分母中各项的系数都化为整数,且使各项系数绝对值最小.(1)b a b a 41313121-+; (2)22226.0411034.0y x y x -+. 分式的运算法则1、 分式的乘除法则:分式乘以分式,用分子的积做积的分子,分母的积做积的分母;分式除以分式,把除式的分子、分母颠倒位置后,与被除式相乘.用式子表示是:bd ac d c b a =⨯;bcad c d b a d c b a =⨯=÷. 2、 分式的乘方法则:分式乘方是把分子、分母各自乘方.用式子表示是:n n nb a b a =⎪⎭⎫⎝⎛(n 为整数).3、分式的加减法则:①同分母的分式相加减,分母不变,把分子相加减.用式子表示是:cba cbc a ±=±; ②异分母的分式相加减,先通分,变为同分母的分式,然后再加减.用式子表示是:bdbcad d c b a ±=±.分式的混合运算关键是弄清运算顺序,分式的加、减、乘、除混合运算也是先进行乘、除运算,再进行加、减运算,遇到括号,先算括号内的.例、计算78563412+++++-++-++x x x x x x x x . 分析:对于这道题,一般采用直接通分后相加、减的方法,显然较繁,注意观察到此题的每个分式的分子都是一个二项式,并且每个分子都是分母与1的和,所以可以采取“裂项法” . 同底数幂的除法法则:同底数幂相除,底数不变,指数相减.如:nm nmaa a -=÷(n m ,为正整数,0≠a ).注意:10=a (0≠a );p a a app,0(1≠=-为正整数). 科学计数法:把一个数记成na 10⨯±的形式,其中:n a ,101<≤是整数,这种记数法叫做科学记数法.第二章三角形命题、定理、证明命题的概念:判断一件事情的语句,叫做命题.注意:命题的定义包括两层涵义:①命题必须是一个完整的句子;②这个句子必须对某件事情做出判断.例如:“直角都相等” ,“相等的角是对顶角”等都是命题.“连结P 、Q 两点” 、“过点p 作直线l ”等都不是命题. 命题的一般形态:任一个命题都可以写成形式:“如果……,那么…….”如果对应命题的题设(条件)部分,那么对应命题的结论部分。

湘教版分式知识点什么是分式?分式是数学中的一种表示形式,它表示一个数被分为若干等分之一。
分式由分子和分母组成,分子表示被分的数,分母表示分成的等分数。
分式的表示方法我们通常用a/b来表示一个分式,其中a是分子,b是分母。
例如,2/3表示被分成3份中的2份。
分式的概念理解要理解分式的概念,可以通过以下步骤来思考:1.想象一块蛋糕:假设有一块蛋糕,你想将它平均分成若干份。
2.分成几份:你能够将蛋糕分成几份?这个数字就是分母。
3.取其中几份:你要取走多少份蛋糕?这个数字就是分子。
4.计算结果:将取走的份额除以总的份数,就得到了分式表示的结果。
分式的运算分式的加法和减法要进行分式的加法和减法,需要满足分母相同的条件。
具体步骤如下:1.找到分母的最小公倍数:找到所有分式中分母的最小公倍数,记为m。
2.分子的计算:对于每个分式,将分子乘以m/原分母,得到新的分子。
3.分子相加/相减:将新的分子相加/相减,得到结果的分子。
4.结果的分母:结果的分母为最小公倍数m。
分式的乘法要进行分式的乘法,只需要将分子相乘,分母相乘。
具体步骤如下:1.分子相乘:将所有分式的分子相乘,得到结果的分子。
2.分母相乘:将所有分式的分母相乘,得到结果的分母。
分式的除法要进行分式的除法,只需要将第一个分式的分子乘以第二个分式的分母,分母乘以第二个分式的分子。
具体步骤如下:1.分子相乘:将第一个分式的分子乘以第二个分式的分母,得到结果的分子。
2.分母相乘:将第一个分式的分母乘以第二个分式的分子,得到结果的分母。
分式的化简与约分分式可以通过化简和约分来简化表示。
具体步骤如下:1.找到分子和分母的最大公约数:找到分子和分母的最大公约数,记为gcd。
2.分子分母同时除以最大公约数:将分子和分母同时除以gcd,得到化简后的分子和分母。
总结分式是一种表示数被分为若干等分之一的数学形式。
要理解分式,可以通过想象一块蛋糕并将其平均分成若干份来帮助思考。

八年级数学上册期末复习知识点归纳第一章 分式一、分式的判断:分母中含有字母的代数式是分式,注意π不是字母。
二、最简分式:分子分母没有公因式。
三、分式有意义的条件:分母不等于0,分式的值为0 的条件:分子等于0且分母不为0.四、分式的运算:1. 分式的乘法的法则:b a ﹒d c =bdac 2. 分式的除法的法则:b a ÷d c =b a ﹒c d =bcad ) 3. 分式乘除法的运算步骤:当分式的分子、分母中有多项式,①先分解因式;②如果分子与分母有公因式,先约分再计算.③如果分式的分子(或分母)的符号是负号时,应把负号提到分式的前面.最后的计算结果必须是最简分式或整式。
4. 分式的加减:(化简求值)(1)同分母分式加减:分母不变、分子相加减。
(2)异分母分母加减:先通分、再加减。
5. 分式的乘方(选择题判断正误): n nn ba b a =)( 五、整数指数幂:1、零次幂:a 0 =1(a ≠0)2、负整数指数幂:n n a b a )()(b -=3.、科学计数法4.、整数指数幂的运算法则六、分式方程(重点)1. 解分式方程:(1)去分母(不要漏乘、要给分子加括号)(2)去括号(注意变号)(3)移项合并同类项(移向要变号)(4)系数化为1(5)检验:将x 的值代入最简公分母,若值为0,则方程无解;若值不为0,则x=a 是方程的解2. 列分式方程解应用题的步骤:设、列、解、验、答第二章 三角形一、三角形的三边关系:两边之和大于第三边(两条较短两边大于第三边,才能构成三角形 )二、等腰三角形的性质与判断:1. 性质:等边对等角;等角对等边。
2. 判定:两边相等或两角相等的三角形是等腰三角形。
三、全等三角形的判定与性质:1. 判定条件:两角及夹边;两边及夹角;三边;两角及一角对边对应相等。
(考查小题、添加一个条件使三角形全等)2. 尺规作图:(1) 考查小题:考查尺规作图的依据(角平分线SSS ;作一个角等于已知角SSS)(2) 解答题:作角平分线、作一角等于已知角、等腰三角形、等边三角形、高。

第1章分式1.1分式知识点1 分式的概念1.分式的定义:类似地,一个整式f 除以一个非零整式g(g 中含有字母),所得的商记作fg,把代数式f g叫作分式,其中f是分式的分子,g是分式的分母,g≠0. 分式的三要素:(1)形如fg的式子;(2)f为整式,g为非0整式;(3)分母g中含有字母2.分式与分数、整式的关系:(1)分式中分母含有字母,由于字母表示不同的数,因此分式比分数更具有一般性。
分数是分式中字母取特定值时的特殊情况. (2)分式与整式的根本区别是分式的分母中含有字母.知识点2 分式的值存在、不存在的条件1.分式的值存在(分式有意义)的条件:分式的分母表示除数,由于除数不能为0,因此分式的分母不能为即当g≠0时,分式fg才有意义.分式的分母不为0,并不是说分母中的字母不能为0,而是表示分母的整式的值不能为0.2.分式的值不存在(分式无意义)的条件:分式的分母为0,即g=0时,分式fg无有意义.求法:当分式的值不存在时,根据分式中分母的值为0的条件转化为解方程问题.知识点3 分式的值为0的条件分式的值为0的条件:1.当分式的分子等于0且分母不等于0时,分式的值为0.即对于分式fg,当f=0且g≠0时,fg=0.2.对于分式fg,常见的特殊分式值的情况讨论:(1)若fg的值为1,则f=g,且g≠0;反过来若f=g,且g≠0,则fg的值为1.(2)若fg的值为-1,则f=-g,且g≠0;反过来若f=-g,且g≠0,则fg的值为-1.知识点4 分式的基本性质1.分式的基本性质:(1)分式的分子与分母都乘同一个非零整式,所得分式与原分式相等,即对于分式fg,有fg=f·ℎg·ℎ(h≠0).(2)分式得分子与分母都除以他们的一个公因数,所得分式与原分式相等.3.分式的符号法则:分式的分子、分母与分式本身的符号,同时改变其中两个,分式的值不变.用字母表示如下:(1)fg = −f−g= −f−g=−−fg(2)−fg= −−f−g= −fg= f−g知识点5 分式的约分1.分式的约分:根据分式的基本性质,把一个分式的分子与分母的公因式约去(即分子与分母都除以他们的公因式),叫作分式的约分.2.找公因式的方法:(1)当分子、分母都是单项式时,先找分子、分母系数的最大公约数,再找相同字母的最低次幂,它们的积就是公因式.(2)当分子、分母都是多项式时,先把多项式分解因式,再按(1)中的方法找公因式.3.约分的方法(1)若分式的分子、分母都是单项式,就直接约去分子、分母的公因式;(2)若分子或分母含有多项式,应先分解因式,再确定公因式并约去.4.最简分式分子与分母没有公因式的分式叫作最简分式.注意事项:①约分式针对分式的分子和分母整体进行的,而不是针对其中的某些项,因此约分前一定要确认分子和分母都是乘积形式;②约分一定要彻底,其结果必须是最简分式或整式;③注意发现分式的分子与分母的一些隐藏的公因式(如互为相反数的式子)④当分式的分子或分母的系数是负数时,可利用分式的基本性质,把负号提到分式的前面.1.2分式的乘法和除法知识点1分式的乘法1.分式的乘法运算法则:分式乘分式,把分子乘分子、分母乘分母分别作为积的分子、分母.即fg·uv= fugv2.法则的运用方法:(1)若分子、分母都是单项式,可直接利用乘法运算法则运算后再约分;(2)若分子、分母有多项式,可先对分子、分母因式分解,约分后,再进行乘法运算;(3)若分式乘整式,可把整式看成分母为1的“分式”进行运算. (4)运算的结果应为最简分式或整式.3.分式乘法运算的基本步骤:第一步:确定积的符号,写在积中分式的前面.第二步:运用法则,将分子与分母分别相乘,多项式要带扩号;第三步:约分,将结果化成最简分式或正式.知识点2 分式的除法1.分式的除法运算法则:分式除以分式,把除式的分子、分母颠倒位置后,与被除式相乘,即f g÷ u v= f g× v u=fv gu(u ≠0).2. 法则的运用方法:(1)分式的除法需转化成乘法,再利用分式乘法运算法则计算; (2)当除式是整式时,可以将整式看成分母是1的“分式”进行运算.3.分式除法运算的基本步骤:第一步:将分子、分母是多项式的进行因式分解,并约分; 第二步:将除法转化成乘法;第三步:利用分式的乘法运算法则计算。

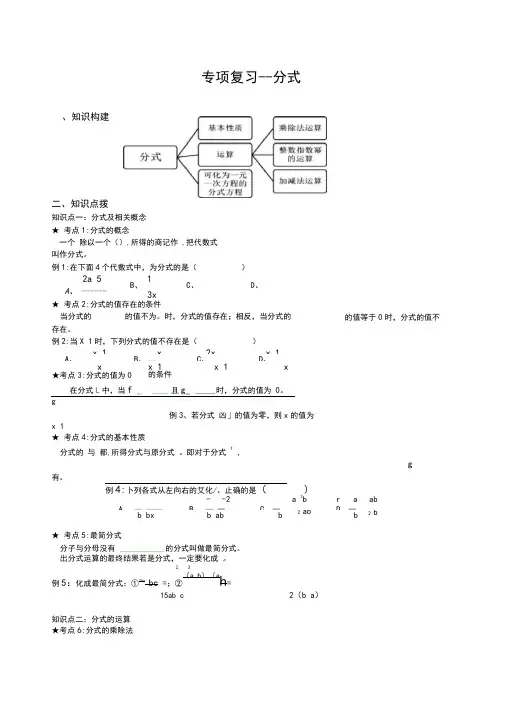
专项复习--分式二、知识点拨知识点一:分式及相关概念 ★ 考点1:分式的概念一个 除以一个(),所得的商记作 ,把代数式 叫作分式。
例1:在下面4个代数式中,为分式的是()★ 考点2:分式的值存在的条件 当分式的 的值不为。
时,分式的值存在;相反,当分式的存在。
例2:当X 1时,下列分式的值不存在是()x 1 x2x x 1A 、B 、 —C 、D 、xx 1x 1x★考点3:分式的值为0的条件在分式L 中,当f _ ____ 且g_ _____ 时,分式的值为 0。
g例3、若分式 凶」的值为零,则x 的值为x 1★ 考点4:分式的基本性质分式的 与 都,所得分式与原分式 。
即对于分式 f,g有。
例4:卜列各式从左向右的艾化/、止确的是() - -2a 2br a abA 、 — ——B 、 — 一C 、一D 、一b bx b abb 2 abb2 b★ 考点5:最简分式分子与分母没有 ___________ 的分式叫做最简分式。
出分式运算的最终结果若是分式,一定要化成 。
2, 3例5:化成最简分式:①25abc =;②(a b )(ah =15ab c2(b a )知识点二:分式的运算 ★考点6:分式的乘除法、知识构建2a 5A 、 ------7 B 、1 3xC 、D 、的值等于0时,分式的值不分式的乘法法则:2例6:计算:①a xf ug v2ay .;分式的除法法则:fby 2 b 2 x ★考点7:分式的乘方 分式的乘方是把分子、分母2②a xy b 2z 2g2 a yz = b 2x 2 ig) 例7、下列运算正确的是(3 6 A 、(斗22 2x 2x ★考点8:整数指数哥 整数指数哥的法则:(1) (2) (3) B 、 ) ■ 2x 同底数骞的乘、骞的乘方法则: 例8:给出的下列等式:a a 3 4■⑦ 2a 3 3a A. 0个6y 6 4x 4 C 、 (卢 2x 9y 64x 4D、(卢 2x9y 64x 4除法法则: 积、商的乘方法则: —L.:③ 22 4;④3 13;⑤ ab3x 21b 1.⑧ 6.510 3 =0, 00065;⑨a 2b ab a 其中正确的个数是B. C.D. 3个 ★考点9:分式的加减法 同分母的分式加减法则: 异分母分式的加减法法则: 例9:计算:①7 x 知识点三:可化为 c ---------- —;②二包 8x 7y 次方程的分式方程 ★考点10:分式方程及相关概念含有未知数的方程叫做分式方程。
湘教版八年级数学上册知识点总结第1章分式1.1 分式1.2 分式的乘法和除法1.3 整数指数幂1.4 分式的加法和减法1.5 可化为一元一次方程的分式方程本章复习与测试第2章三角形2.1 三角形2.2 命题与证明2.3 等腰三角形2.4 线段的垂直平分线2.5 全等三角形2.6 用尺规作三角形本章复习与测试第3章实数3.1 平方根3.2 立方根3.3 实数第4章一元一次不等式(组)4.1 不等式4.2 不等式的基本性质4.3 一元一次不等式的解法4.4 一元一次不等式的应用4.5 一元一次不等式组本章复习与测试第5章二次根式5.1 二次根式5.2 二次根式的乘法和除法5.3 二次根式的加法和减法本章复习与测试知识点总结第一章:分式一、课前构建:回顾相关知识:认真阅读教材P1-40二、课堂点拨:知识点一:分式的概念★考点1:分式的定义:知识点二:分式的性质★考点4:分式的基本性质:分式的分子与分母都乘,所得分式与原分式相等。
即(其中)分式的分子与分母约去公因式,所得分式与原分式相等。
即(其中)分式的变号法则:分式的分子、分母与分式本身的符号,改变其中的任何两个,分式的值不变。
即。
★考点5:最简分式(1)约分:把一个分式的分子与分母的公因式约去,称为分式的约分。
约分的方法:先把分子与分母因式分解,再约去公因式。
(2)最简分式:分子与分母没有分式,叫做最简分式。
知识点三:分式的运算★考点6:分式的加减法①同分母分式相加减,分母,把分子。
即。
②异分母分式相加减,要先,即把各个分式的分子与分母都乘适当的同一个非零多项式,化为同分母的分式,再加减。
即。
①最简公分母的系数是各分母系数的最小公倍数;②最简公分母的字母和式子是各分母的所有字母和式子。
③最简公分母的每个字母或式子的指数是它在各分母中次数最高。
例7、计算的结果是。
★考点7:分式的乘除法乘:分式乘分式,把分子乘分子,分母乘分母,分别作为积的分子、分母,然后约去分子与分母的公因式。
八年级数学上册“第十五章分式”必背知识点一、分式的定义与意义1. 分式的定义:一般地,如果A、B表示两个整式,并且B中含有字母,那么式子A/B叫做分式,A为分子,B为分母。
整式是分母中没有字母的代数式,而分式是分母中含有字母的代数式。
2. 分式有意义的条件:分母不能为0,即B≠0时,分式A/B才有意义。
3. 分式无意义的条件:分母为0,即B=0时,分式A/B无意义。
二、分式的基本性质基本性质:分式的分子与分母同乘 (或除以)一个不等于0的整式,分式的值不变。
用式子表示为:若C≠0,则A/B = A×C / B×C。
约分:根据分式的基本性质,把一个分式的分子与分母的公因式约去,叫做分式的约分。
分子与分母没有公因式的分式叫做最简分式。
通分:根据分式的基本性质,把几个异分母的分式分别化成与原来的分式相等的同分母分式,叫做分式的通分。
最简公分母是取各分母所有因式的最高次幂的积作公分母。
三、分式的运算1. 乘法法则:分式乘分式,用分子的积作为积的分子,分母的积作为积的分母。
即:(a/b) ×(c/d) = ac/bd。
2. 除法法则:分式除以分式,把除式的分子、分母颠倒位置后,与被除式相乘。
即:(a/b) ÷(c/d) = (a/b) ×(d/c) = ad/bc。
3. 乘方法则:分式乘方要把分子、分母分别乘方。
即:(a/b)^n = a^n/b^n (其中n为正整数)。
4. 加减法法则:同分母分式相加减,分母不变,把分子相加减。
即:(a/c) ±(b/c) = (a±b)/c。
异分母分式相加减,先通分,化为同分母的分式,然后再按同分母分式的加减法法则进行计算。
四、分式方程的解法定义:分母中含有未知数的方程叫做分式方程。
解法步骤:1. 去分母:把方程两边同乘以各分母的最简公分母,得到整式方程。
2. 解整式方程:解这个整式方程,得到整式方程的解。
八年级数学上册《分式的乘法与除法》知
识点湘教版
八年级数学上册《分式的乘法与除法》知识点湘教版知识点
1.把一个分式的分子与分母的公因式约去,叫做分式的
约分.
2.分式进行约分的目的是要把这个分式化为最简分式.
3.如果分式的分子或分母是多项式,可先考虑把它分别
分解因式,得到因式乘积形式,再约去分子与分母的公
因式.如果分子或分母中的多项式不能分解因式,此时就不能把分子、分母中的某些项单独约分.
4.分式约分中注意正确运用乘方的符号法则,如
x-y=-(y-x),(x-y)2=(y-x)2,
(x-y)3=-(y-x)3.
5.分式的分子或分母带符号的n次方,可按分式符号法则,变成整个分式的符号,然后再按-1的偶次方为正、奇次方为负来处理.当然,简单的分式之分子分母可直接乘方.
6.注意混合运算中应先算括号,再算乘方,然后乘除,
最后算加减.
7、分式的乘除法法则
两个分式相乘,用分子的积作为积的分子,分母的积作
为积的分母。
两个分式相除,把除式的分子和分母颠倒位置(除数的倒数)后再与被除式相乘。
八年级数学上册《分式》知识点湘教版
知识点
分式的定义:如果A、B表示两个整式,并且B中含有字母,那么式子叫做分式。
分式有意义、无意义的条件:
分式有意义的条件:分式的分母不等于0;分式无意义的条件:分式的分母等于0。
分式值为零的条件:
分式AB=0的条件是A=0,且B≠0.
分式的基本性质:分式的分子与分母同乘一个不等于0的整式,分式的值不变。
用式子表示为,
分式的通分:
和分数类似,利用分式的基本性质,使分子和分母同乘适当的整式,不改变分式的值,把几个异分母分式化成相同分母的分式,这样的分式变形叫做分式的通分。
通分的关键是确定几个式子的最简公分母。
几个分式通分时,通常取各分母所有因式的最高次幂的积作为公分母,这样的分母就叫做最简公分母。
求最简公分母时应注意以下几点:
“各分母所有因式的最高次幂”是指凡出现的字母为底
数的幂选取指数最大的;
如果各分母的系数都是整数时,取它们系数的最小公倍数作为最简公分母的系数;
如果分母是多项式,一般应先分解因式。
分式的约分:
和分数一样,根据分式的基本性质,约去分式的分子和分母中的公因式,不改变分式的值,这样的分式变形叫做分式的约分。
约分后分式的分子、分母中不再含有公因式,这样的分式叫最简公因式。
约分的关键是找出分式中分子和分母的公因式。
约分时注意分式的分子、分母都是乘积形式才能进行约分;分子、分母是多项式时,通常将分子、分母分解因式,然后再约分;
找公因式的方法:
①当分子、分母都是单项式时,先找分子、分母系数的最大公约数,再找相同字母的最低次幂,它们的积就是公因式;
②当分子、分母都是多项式时,先把多项式因式分解。