二次函数综合问题之抛物线与直线交点个数问题

二次函数综合题-中考数学重难点题型二次函数与线段有关的问题（专题训练）1.小聪设计奖杯，从抛物线形状上获得灵感，在平面直角坐标系中画出截面示意图，如图1，杯体ACB 是抛物线的一部分，抛物线的顶点C 在y 轴上，杯口直径4AB =，且点A ，B 关于y 轴对称，杯脚高4CO =，杯高8DO =，杯底MN 在x 轴上．（1）求杯体ACB 所在抛物线的函数表达式（不必写出x 的取值范围）．（2）为使奖杯更加美观，小敏提出了改进方案，如图2，杯体A CB ''所在抛物线形状不变，杯口直径//A B AB ''，杯脚高CO 不变，杯深CD '与杯高OD '之比为0.6，求A B ''的长．2.如图1，隧道截面由抛物线的一部分AED 和矩形ABCD 构成，矩形的一边BC 为12米，另一边AB 为2米．以BC 所在的直线为x 轴，线段BC 的垂直平分线为y 轴，建立平面直角坐标系xOy ，规定一个单位长度代表1米．E （0，8）是抛物线的顶点．(1)求此抛物线对应的函数表达式；(2)在隧道截面内（含边界）修建“”型或“”型栅栏，如图2、图3中粗线段所示，点1P ，4P 在x 轴上，MN 与矩形1234PP P P 的一边平行且相等．栅栏总长l 为图中粗线段12PP ，23P P ，34P P ，MN 长度之和．请解决以下问题：（ⅰ）修建一个“”型栅栏，如图2，点2P ，3P 在抛物线AED 上．设点1P的横坐标为()06m m <≤，求栅栏总长l 与m 之间的函数表达式和l 的最大值；（ⅱ）现修建一个总长为18的栅栏，有如图3所示的修建“”型或“”型栅型两种设计方案，请你从中选择一种，求出该方案下矩形1234P P P P 面积的最大值，及取最大值时点1P 的横坐标的取值范围（1P 在4P 右侧）．3.在平面直角坐标系xoy 中，已知抛物线y ＝－x 2＋bx ＋c 经过点A （－1，0）和点B （0，3），顶点为C ，点D 在其对称轴上，且位于点C 下方，将线段DC 绕点D 按顺时针方向旋转90°，点C 落在抛物线上的点P 处．(1)求抛物线的解析式；(2)求点P 的坐标；(3)将抛物线平移，使其顶点落在原点O ，这时点P 落在点E 的位置，在y 轴上是否存在点M ，使得MP ＋ME 的值最小，若存在，求出点M 的坐标；若不存在，请说明理由．4.如图，在平面直角坐标系中，抛物线223y x x =--与x 轴相交于点A 、B （点A 在点B 的左侧），与y 轴相交于点C ，连接,AC BC ．(1)求线段AC 的长；(2)若点Р为该抛物线对称轴上的一个动点，当PA PC =时，求点P 的坐标；(3)若点M 为该抛物线上的一个动点，当BCM 为直角三角形时，求点M 的坐标．5.如图，已知抛物线2:L y x bx c =++经过点(0,5),(5,0)A B -．（1）求,b c 的值；（2）连结AB ，交抛物线L 的对称轴于点M ．①求点M 的坐标；②将抛物线L 向左平移(0)m m >个单位得到抛物线1L ．过点M 作//MN y 轴，交抛物线1L 于点N ．P 是抛物线1L 上一点，横坐标为1-，过点P 作//PE x 轴，交抛物线L 于点E ，点E 在抛物线L 对称轴的右侧．若10PE MN +=，求m 的值．6.如图，在平面直角坐标系中，四边形ABCD 为正方形，点A ，B 在x 轴上，抛物线2y x bx c =++经过点B ，()4,5D -两点，且与直线DC 交于另一点E ．（1）求抛物线的解析式；（2）F 为抛物线对称轴上一点，Q 为平面直角坐标系中的一点，是否存在以点Q ，F ，E ，B 为顶点的四边形是以BE 为边的菱形．若存在，请求出点F 的坐标；若不存在，请说明理由；（3）P 为y 轴上一点，过点P 作抛物线对称轴的垂线，垂足为M ，连接ME ，BP ．探究EM MP PB ++是否存在最小值．若存在，请求出这个最小值及点M 的坐标；若不存在，请说明理由．7.如图1，在平面直角坐标系xOy 中，抛物线2y ax bx c =++与x 轴分别相交于A 、B 两点，与y 轴相交于点C ，下表给出了这条抛物线上部分点(,)x y 的坐标值：x…1-0123…y …03430…（1）求出这条抛物线的解析式及顶点M 的坐标；（2）PQ 是抛物线对称轴上长为1的一条动线段（点P 在点Q 上方），求AQ QP PC ++的最小值；（3）如图2，点D 是第四象限内抛物线上一动点，过点D 作DF x ⊥轴，垂足为F ，ABD △的外接圆与DF 相交于点E ．试问：线段EF 的长是否为定值？如果是，请求出这个定值；如果不是，请说明理由．8.已知抛物线23y ax bx =+-与x 轴相交于(1,0)A -，(3,0)B 两点，与y 轴交于点C ，点(,0)N n 是x 轴上的动点．（1）求抛物线的解析式；（2）如图1，若3n <，过点N 作x 轴的垂线交抛物线于点P ，交直线BC 于点G ．过点P 作PD BC ⊥于点D ，当n 为何值时，PDG BNG ≌；（3）如图2，将直线BC 绕点B 顺时针旋转，使它恰好经过线段OC 的中点，然后将它向上平移32个单位长度，得到直线1OB ．①1tan BOB ∠=______；②当点N 关于直线1OB 的对称点1N 落在抛物线上时，求点N 的坐标．9.如图，在平面直角坐标系xOy 中，抛物线213442y x x =-++与两坐标轴分别相交于A ，B ，C 三点（1）求证：∠ACB=90°（2）点D 是第一象限内该抛物线上的动点，过点D 作x 轴的垂线交BC 于点E ，交x 轴于点F ．①求DE+BF 的最大值；②点G 是AC 的中点，若以点C ，D ，E 为顶点的三角形与 AOG 相似，求点D 的坐标．10.如图，抛物线(1)()y x x a =+-（其中1a >）与x 轴交于A 、B 两点，交y 轴于点C ．（1）直接写出OCA ∠的度数和线段AB 的长（用a 表示）；（2）若点D 为ABC 的外心，且BCD △与ACO △4，求此抛物线的解析式；（3）在（2）的前提下，试探究抛物线(1)()y x x a =+-上是否存在一点P ，使得CAP DBA ∠=∠若存在，求出点P 的坐标；若不存在，请说明理由．11.如图，二次函数y ＝ax 2+bx+x 的图象过O （0，0）、A （1，0）、B （32，（1）求二次函数的解析式；（2）若线段OB的垂直平分线与y轴交于点C，与二次函数的图象在x轴上方的部分相交于点D，求直线CD的解析式；（3）在直线CD下方的二次函数的图象上有一动点P，过点P作PQ⊥x轴，交直线CD于Q，当线段PQ的长最大时，求点P的坐标．12.如图，抛物线y＝ax2+bx+4交x轴于A（﹣3，0），B（4，0）两点，与y轴交于点C，AC，BC．M为线段OB上的一个动点，过点M作PM⊥x轴，交抛物线于点P，交BC于点Q．（2）过点P作PN⊥BC，垂足为点N．设M点的坐标为M（m，0），请用含m的代数式表示线段PN的长，并求出当m为何值时PN有最大值，最大值是多少？（3）试探究点M在运动过程中，是否存在这样的点Q，使得以A，C，Q为顶点的三角形是等腰三角形．若存在，请求出此时点Q的坐标；若不存在，请说明理由．13.在平面直角坐标系xOy中，直线y=−12x+5与x轴、y轴分别交于点A、B（如图）．抛物线y＝ax2+bx（a≠0）经过点A．（2）如果抛物线y＝ax2+bx经过线段AB上的另一点C，且BC=5，求这条抛物线的表达式；（3）如果抛物线y＝ax2+bx的顶点D位于△AOB内，求a的取值范围．14，若一次函数y＝﹣3x﹣3的图象与x轴，y轴分别交于A，C两点，点B的坐标为（3，0），二次函数y＝ax2+bx+c的图象过A，B，C三点，如图（1）．（1）求二次函数的表达式；（2）如图（1），过点C作CD∥x轴交抛物线于点D，点E在抛物线上（y轴左侧），若BC 恰好平分∠DBE．求直线BE的表达式；（3）如图（2），若点P在抛物线上（点P在y轴右侧），连接AP交BC于点F，连接BP，S△BFP＝mS△BAF．①当m=12时，求点P的坐标；②求m的最大值．15.在平面直角坐标系中，抛物线y＝ax2+bx+3与x轴交于点A（﹣3，0）、B（1，0），交y 轴于点N，点M为抛物线的顶点，对称轴与x轴交于点C．（1）求抛物线的解析式；（2）如图1，连接AM，点E是线段AM上方抛物线上一动点，EF⊥AM于点F，过点E 作EH⊥x轴于点H，交AM于点D．点P是y轴上一动点，当EF取最大值时：①求PD+PC的最小值；②如图2，Q点为y轴上一动点，请直接写出DQ+14OQ的最小值．16.已知抛物线y＝ax2+bx+6（a≠0）交x轴于点A（6，0）和点B（﹣1，0），交y轴于点C．（1）求抛物线的解析式和顶点坐标；（2）如图（1），点P是抛物线上位于直线AC上方的动点，过点P分别作x轴、y轴的平行线，交直线AC于点D，E，当PD+PE取最大值时，求点P的坐标；（3）如图（2），点M为抛物线对称轴l上一点，点N为抛物线上一点，当直线AC垂直平分△AMN的边MN时，求点N的坐标．17.已知抛物线y＝ax2+bx+c与x轴交于A（﹣1，0），B（5，0）两点，C为抛物线的顶点，抛物线的对称轴交x轴于点D，连结BC，且tan∠CBD=43，如图所示．（1）求抛物线的解析式；（2）设P是抛物线的对称轴上的一个动点．①过点P作x轴的平行线交线段BC于点E，过点E作EF⊥PE交抛物线于点F，连结FB、FC，求△BCF的面积的最大值；②连结PB，求35PC+PB的最小值．。

二次函数小综合-二次函数与交点问题例1(2018四调题改)抛物线y ＝x 2－kx －k ，A (1，－2)，B (4，10)，抛物线与线段AB (包含A 、B 两点)有两个交点，那么k 的取值范围为_______．解：线段AB 的解析式是_______(1≤x ≤4)，联立抛物线与直线解析式方程得x 2－4x ＋6＝kx ＋k ，该方程在1≤x ≤4时有两根，此方程可以看作定抛物线_______(1≤x ≤4)，与过定点C (－1，0)的动直线_____．(填写解析式，上同)，有两个交点，画出图像如图． 根据图像回答问题：M 点的坐标为______，N 坐标为______； l 1的k 值为________；l 2的k 值为________．所以，仅有两个交点时，k 的取值范围为_____________．41l 1l 2NMC Oxyy ＝4x －6,y ＝x 2－4x ＋6,y ＝kx ＋k , (1,3),(4,6),k ＝±211－6,k ＝65,－6＋211＜k ≤65. 例2．直线y ＝2x ﹣5m 与抛物线y ＝x 2﹣mx ﹣3在0≤x ≤4范围内只有一个公共点，则m 的取值范围为 ﹣5＜m ≤或m ＝8﹣2．解：联立可得：x 2﹣（m +2）x +5m ﹣3＝0，令y ＝x 2﹣（m +2）x +5m ﹣3，∴直线y ＝2x ﹣5m 与抛物线y ＝x 2﹣mx ﹣3在0≤x ≤4范围内只有一个公共点， 即y ＝x 2﹣（m +2）x +5m ﹣3的图象在0≤x ＜4上只有一个交点， 当△＝0时，即△＝（m +2）2﹣4（5m ﹣3）＝0解得：m ＝8±4，当m ＝8+4时，x ＝＝5+2＞4当m＝8﹣4时，x＝＝5﹣2，满足题意，当△＞0，∴令x＝0，y＝5m﹣3，令x＝4，y＝m+5，∴（m+5）（5m﹣3）＜0，∴﹣5＜m＜令x＝0代入x2﹣（m+2）x+5m﹣3＝0，解得：m＝，此该方程的另外一个根为：，故m＝也满足题意，故m的取值范围为：﹣5＜m≤或m＝8﹣2例3．在平面直角坐标系中，A（﹣2，0），B（1，﹣6），若抛物线y＝ax2+（a+2）x+2与线段AB有且仅有一个公共点，则a的取值范围是﹣5＜a≤1且a≠0或a＝8+4．解：当抛物线过A点，B点为临界，代入A（﹣2，0）则4a﹣2（a+2）+2＝0，解得：a＝1，代入B（1，﹣6），则a+（a+2）+2＝﹣6，解得：a＝﹣5，又a≠0，当a＝﹣5时，抛物线与线段AB有两个交点，所以a的取值范围是﹣5＜a≤1且a≠0．∵直线AB的解析式为y＝﹣2x﹣4，由，消去y得到：ax2+（a+4）x+6＝0，当△＝0时，直线AB与抛物线只有一个交点，∴（a+4）2﹣24a＝0，解得a＝8+4或8﹣4，经检验：当a＝8+4时，切点在线段AB上，符合题意，当a＝8﹣4时，切点不在线段AB上，不符合题意，故答案为﹣5＜a≤1且a≠0或a＝8+4．例4．已知二次函数y＝（m﹣2）x2﹣4mx+2m﹣6的图象与x轴负半轴至少有一个交点，则m的取值范围为（）A．1＜m＜3B．1≤m＜2或2＜m＜3C．m＜1D．m＞3【解答】解：∵二次函数y＝（m﹣2）x2﹣4mx+2m﹣6，∴m﹣2≠0，∴m≠2，当①图象与x轴的交点有两个，原点的两侧各有一个，则，解得2＜m＜3；②图象与x轴的交点都在x轴的负半轴，则，解得：1≤m＜2．综上可得m的取值范围是：1≤m＜2或2＜m＜3 故选：B．例5．已知a、b为y关于x的二次函数y＝（x﹣c）（x﹣c﹣1）﹣3的图象与x轴两个交点的横坐标，则|a﹣c|+|c﹣b|的值为解：当y＝0时，（x﹣c）（x﹣c﹣1）﹣3＝0，（设a＜b），整理得x2﹣（2c+1）x+c2+c﹣3＝0，△＝（2c+1）2﹣4（c2+c﹣3）＝13，x＝，所以a＝c+，b＝c+，所以|a﹣c|+|c﹣b|＝c﹣a+b﹣c＝b﹣a＝c+﹣（c+）＝．故答案为．练习1已知点A ，B 的坐标分别为（1，0），（2，0）．若二次函数y ＝x 2+（a ﹣3）x +3的图象与线段AB 只有一个交点，则a 的取值范围是 ﹣1≤a ＜﹣或a ＝3﹣2 ．解：依题意，应分为两种情况讨论， ①当二次函数顶点在x 轴下方， 若y x ＝1＜0且y x ＝2≥0，即，解得此不等式组无解；若y x ＝2＜0且y x ＝1≥0，即，解得﹣1≤a ＜﹣；②当二次函数的顶点在x 轴上时， △＝0，即（a ﹣3）2﹣12＝0，解得a ＝3±2，而对称轴为x ＝﹣，可知1≤﹣≤2，故a ＝3﹣2．故答案为：﹣1≤a ＜﹣或a ＝3﹣2．2．（2018预测）已知抛物线y ＝x 2－2mx ＋9m －1，当－3≤x ≤3时，使y ＝m 成立的x 的值恰好只有一个，则m 的取值范围是_________________．447m -≤<-或415m =-3．（2018新观察四调模拟卷）已知A （－1，6）、B （4，1）抛物线y ＝x 2＋b 与线段AB 只有唯一公共点，则b 的取值范围是_________________． －15≤b ＜5或214b =4.已知二次函数y ＝x 2+x +c （b ，c 为常数），且当﹣1＜x ＜1时，抛物线与x 轴有且只有一个公共点，求c 的取值范围； ∵对称轴x ＝﹣＝﹣，∴当﹣1＜x ＜1时，抛物线与x 轴有且只有一个公共点，则①此公共点一定是顶点，∴△＝1﹣4c ＝0，即c ＝，②一个交点的横坐标小于等于﹣1，另一交点的横坐标小于1而大于﹣1， ∴1﹣1+c ≤0，1+1+c ＞0，解得﹣2＜c ≤0． 综上所述，c 的取值范围是：c ＝或﹣2＜c ≤0；5．已知a、b为抛物线y＝（x﹣c）（x﹣c﹣d）﹣2与x轴交点的横坐标，a＜b，则|a﹣c|+|c ﹣b|的值为b﹣a．解：当x＝c时，y＝﹣2＜0，由图可知，a＜c＜b，则|a﹣c|+|c﹣b|＝c﹣a+b﹣c＝b﹣a．故答案为b﹣a．6．二次函数y＝x2﹣4mx+1﹣2m，当﹣1＜x＜1时，抛物线与x轴有一个公共点，求m的取值范围．解：∵当﹣1＜x＜1时，抛物线与x轴有一个公共点，∴可得以下几种情况：①，解得m＝．②，解得m＞．③，解得m＜﹣1．∴综上，m＞，m＜﹣1或m＝时当﹣1＜x＜1时，抛物线与x轴有一个公共点．。

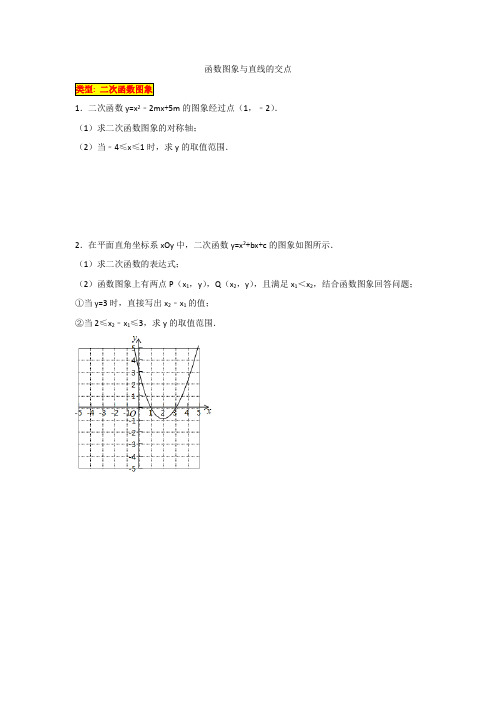
函数图象与直线的交点1．二次函数y=x2﹣2mx+5m的图象经过点（1，﹣2）．（1）求二次函数图象的对称轴；（2）当﹣4≤x≤1时，求y的取值范围．2．在平面直角坐标系xOy中，二次函数y=x2+bx+c的图象如图所示．（1）求二次函数的表达式；（2）函数图象上有两点P（x1，y），Q（x2，y），且满足x1＜x2，结合函数图象回答问题；①当y=3时，直接写出x2﹣x1的值；②当2≤x2﹣x1≤3，求y的取值范围．．已知函数y=x2﹣2mx的顶点为点D．（1）求点D的坐标（用含m的代数式表示）；（2）求函数y=x2﹣2mx的图象与x轴的交点坐标；（3）若函数y=x2﹣2mx的图象在直线y=m的上方，求m的取值范围．2．已知P（﹣3，m）和Q（1，m）是抛物线y=2x2+bx+1上的两点．（1）求b的值；（2）判断关于x的一元二次方程2x2+bx+1=0是否有实数根，若有，求出它的实数根；若没有，请说明理由；（3）将抛物线y=2x2+bx+1的图象向上平移k（k是正整数）个单位，使平移后的图象与x轴无交点，求k的最小值．1．在平面直角坐标系xOy中，二次函数y=mx2﹣（m+n）x+n（m＜0）的图象与y轴正半轴交于A点．（1）求证：该二次函数的图象与x轴必有两个交点；（2）设该二次函数的图象与x轴的两个交点中右侧的交点为点B，若∠ABO=45°，将直线AB 向下平移2个单位得到直线l，求直线l的解析式；（3）在（2）的条件下，设M（p，q）为二次函数图象上的一个动点，当﹣3＜p＜0时，点M关于x轴的对称点都在直线l的下方，求m的取值范围．2．如图，抛物线y=ax2+bx﹣3a经过A（﹣1，0）、C（0，﹣3）两点，与x轴交于另一点B．（1）求此抛物线的解析式；（2）已知点D（m，﹣m﹣1）在第四象限的抛物线上，求点D关于直线BC对称的点D'的坐标．（3）在（2）的条件下，连接BD，问在x轴上是否存在点P，使∠PCB=∠CBD？若存在，请求出P点的坐标；若不存在，请说明理由．1．已知抛物线：y=mx2﹣2mx+m+1（m≠0）．（1）求抛物线的顶点坐标．（2）若直线l1经过（2，0）点且与x轴垂直，直线l2经过抛物线的顶点与坐标原点，且l1与l2的交点P在抛物线上．求抛物线的表达式．（3）已知点A（0，2），点A关于x轴的对称点为点B．抛物线与线段AB恰有一个公共点，结合函数图象写出m的取值范围．2．直线y=﹣3x+3与x轴、y轴分别父于A、B两点，点A关于直线x=﹣1的对称点为点C．（1）求点C的坐标；（2）若抛物线y=mx2+nx﹣3m（m≠0）经过A、B、C三点，求抛物线的表达式；（3）若抛物线y=ax2+bx+3（a≠0）经过A，B两点，且顶点在第二象限．抛物线与线段AC 有两个公共点，求a的取值范围．3．在平面直角坐标系xOy中，抛物线y=x2﹣2mx+m2﹣m+2的顶点为D．线段AB的两个端点分别为A（﹣3，m），B（1，m）．（1）求点D的坐标（用含m的代数式表示）；（2）若该抛物线经过点B（1，m），求m的值；（3）若线段AB与该抛物线只有一个公共点，结合函数的图象，求m的取值范围．4．如图，抛物线y=﹣x2+bx+c经过点A（3，0）和点B（0，3）．（1）求出抛物线y=﹣x2+bx+c的解析式；（2）若直线l⊥x轴，在第一象限内与抛物线交于点M，与直线AB交于点N，设线段MN 的长度为n，请结合函数图象求出n的取值范围．1．已知二次函数y=（t+1）x2+2（t+2）x+在x=0和x=2时的函数值相等（1）求二次函数的解析式，并作图象；（2）若一次函数y=kx+6的图象与二次函数的图象都经过点A（﹣3，m），求m和k的值．2．已知二次函数y=x2﹣2mx+m2+3（m是常数）．（1）求证：不论m为何值，该函数的图象与x轴没有公共点；（2）把该函数的图象沿y轴向下平移多少个单位长度后，得到的函数的图象与x轴只有一个公共点？（3）将抛物线y=x2﹣2mx+m2+3（m是常数）图象在对称轴左侧部分沿直线y=3翻折得到新图象为G，若与直线y=x+2有三个交点，请直接写出m的取值范围．3．在平面直角坐标系xOy中，抛物线y=+2x﹣a+1与y轴交于C点，与x轴交于A，B两点（点A在点B左侧），且点A的横坐标为﹣1．（1）求a的值；（2）设抛物线的顶点P关于原点的对称点为P′，求点P′的坐标；（3）将抛物线在A，B两点之间的部分（包括A，B两点），先向下平移3个单位，再向左平移m（m＞0）个单位，平移后的图象记为图象G，若图象G与直线PP'无交点，求m的取值范围．4．在平面直角坐标系xOy中，抛物线y=﹣x+2与y轴交于点A，顶点为点B，点C与点A关于抛物线的对称轴对称．（1）求直线BC的解析式；（2）点D在抛物线上，且点D的横坐标为4．将抛物线在点A，D之间的部分（包含点A，D）记为图象G，若图象G向下平移t（t＞0）个单位后与直线BC只有一个公共点，求t 的取值范围．5．在平面直角坐标系xOy中，二次函数y=ax2﹣2ax+1（a＞0）的对称轴为x=b，点A（﹣2，m）在直线y=﹣x+3上．（1）求m，b的值；（2）若点D（3，2）在二次函数y=ax2﹣2ax+1（a＞0）上，求a的值；（3）当二次函数y=ax2﹣2ax+1（a＞0）与直线y=﹣x+3相交于两点时，设左侧的交点为P （x1，y1），若﹣3＜x1＜﹣1，求a的取值范围．。

中考数学复习考点知识归类讲解 专题23 二次函数中的交点问题知识对接考点一、直线与抛物线的交点（1）y 轴与抛物线c bx ax y ++=2得交点为(0, c ).（2）与y 轴平行的直线h x =与抛物线c bx ax y ++=2有且只有一个交点(h ,c bh ah ++2).（3）抛物线与x 轴的交点二次函数c bx ax y ++=2的图像与x 轴的两个交点的横坐标1x 、2x ，是对应一元二次方程02=++c bx ax 的两个实数根.抛物线与x 轴的交点情况可以由对应的一元二次方程的根的判别式判定：①有两个交点⇔0>∆⇔抛物线与x 轴相交；②有一个交点（顶点在x 轴上）⇔0=∆⇔抛物线与x 轴相切； ③没有交点⇔0<∆⇔抛物线与x 轴相离. （4）平行于x 轴的直线与抛物线的交点同（3）一样可能有0个交点、1个交点、2个交点.当有2个交点时，两交点的纵坐标相等，设纵坐标为k ，则横坐标是k c bx ax =++2的两个实数根.（5）一次函数()0≠+=k n kx y 的图像l 与二次函数()02≠++=a c bx ax y 的图像G 的交点，由方程组cbx ax y n kx y ++=+=2的解的数目来确定：①方程组有两组不同的解时⇔l 与G有两个交点; ②方程组只有一组解时⇔l 与G 只有一个交点；③方程组无解时⇔l 与G 没有交点.（6）抛物线与x 轴两交点之间的距离：若抛物线c bx ax y ++=2与x 轴两交点为()()0021，，，x B x A ，由于1x 、2x 是方程02=++c bx ax 的两个根，故acx x a b x x =⋅-=+2121,()()a a acb a ca b x x x x x x x x AB ∆=-=-⎪⎭⎫ ⎝⎛-=--=-=-=444222122122121专项训练 一、单选题1．如图，已知抛物线()20y axbx c a =++≠的对称轴为直线1x =，与x 轴的一个交点坐标为()1,0-，其部分图象如图所示．下列结论：①方程20ax bx c ++=的两个根是11x =-，23x =；②0a b c -+=；③80a c +<；④当0y >时，x 的取值范围是13x ．其中结论正确的个数是（）A ．1B ．2C ．3D ．42．将抛物线y ＝x 2+2mx +m 2﹣1向左平移8个单位，平移后的抛物线对称轴为直线x ＝1，则平移后的抛物线与y轴的交点坐标为（）A．(0，0) B．(0，4) C．(0，15) D．(0，16)3．二次函数y＝ax2+bx+c（a≠0）的图象与x轴的两个交点横坐标为﹣2，x0，且满足（a+b+c）（4a+2b+c）＜0，与y轴的负半轴相交，抛物线经过点A（﹣1，y1），B（﹣2，y2），C （1，y3），正确结论是（）A．y3＞y2＞y1B．y3＞y1＞y2C．y1＞y2＞y3D．y1＞y3＞y24．直线y＝x+a不经过第二象限，则关于x的函数y=ax2+2x+1与坐标轴的交点个数是（）A．1个B．2个C．3个D．2个或3个5．如图，已知二次函数y＝ax2+bx+c（a≠0）的图象与x轴交于点A(﹣1，0)，与y轴的交点B在(0，﹣2)和(0，﹣1)之间（不包含这两点），对称轴为直线x＝1．在下列结论中：①abc＞0；②16a+4b+c＜0；③4ac﹣b2＜8a；④13＜a＜23；⑤b＜c．正结论的个数为（）A．1 B．2 C．3 D．46．如图是抛物线y＝ax2+bx+c（a≠0）图象的一部分，抛物线的顶点坐标A(1，3)，与x 轴的一个交点B(4，0)，有下列结论：①2a+b＝0；②abc＞0；③方程ax2+bx+c＝2有两个不相等的实数根；④当y＜0时，﹣2＜x＜4，⑤b2+12a＝4ac．其中正确的个是（）A ．2B ．3C ．4D ．57．如图为某二次函数的部分图像，有如下四个结论：①此二次函数表达式为y ＝14x 2﹣x ＋9：②若点B （﹣1，n ）在这个二次函数图像上，则n ＞m ；③该二次函数图像与x 轴的另一个交点为（﹣4，0）；④当0＜x ＜5.5时，m ＜y ＜8．所有正确结论的序号是（）A ．①③B ．①④C ．②③D ．②④8．已知抛物线()2y a x h k =-+与x 轴有两个交点()1,0A -，()3,0B ，抛物线()2y a x h m k =--+与x 轴的一个交点是()4,0，则m 的值是（） A ．5B ．1-C ．5或1D ．5-或1-9．若抛物线2y x bx c =++与x 轴两个交点间的距离为4．对称轴为2x =，P 为这条抛物线的顶点，则点P 关于x 轴的对称点的坐标是（） A ．()2,4B ．()2,4-C ．()2,4--D ．()2,4-10．如图，抛物线21(6)22y x =--与x 轴交于点A B 、，把抛物线在x 轴及其下方的部分记作1C ，将1C 向左平移得到22,C C 与x 轴交于点B O 、，若直线12y x m =+与12C C 、共有3个不同的交点，则m 的取值范围是（）A ．32m -≤<-B ．4128m -<<- C ．52m -≤<- D ．2528m -<<- 二、填空题11．定义：若抛物线与x 轴有两个交点，且这两个交点与它的顶点所构成的三角形是直角三角形，则把这种抛物线称作“和美抛物线”．如图，一组抛物线的顶点B 1(1，y 1)，B 2(2，y 2)，B 3(3，y 3)，… B n (n ，y n )（n 为正整数）依次是直线y 1134x =+上的点，这组抛物线与x 轴正半轴的交点依次是A 1(a 1，0)，A 2(a 2，0)，A 3(a 3，0)，…A n +1(a n +1，0)（0＜a 1＜1，n 为正整数）．若这组抛物线中存在和美抛物线，则a 1＝___．12．已知二次函数245y x x =-++，它的图象与x 轴的交点坐标为________． 13．已知抛物线()20y axbx c a =++≠与x 轴的一个交点坐标为（3，0），对称轴为直线1x =，则关于x 的一元二次方程()200++=≠ax bx c a 的根是_______．14．我们把一个半圆与抛物线的一部分组成的封闭图形称为“蛋圆”．如图，A 、B 、C 、D 分别是某蛋圆和坐标轴的交点其中抛物线的解析式为y =x 2﹣2x ﹣3，则“蛋圆”的弦CD 的长为____．15．关于抛物线221(0)y ax x a =-+≠，给出下列结论：①当0a <时，抛物线与直线22y x =+没有交点；②若抛物线与x 轴有两个交点，则其中一定有一个交点在点（0，0）与（1，0）之间；③若抛物线的顶点在点（0，0），（2，0），（0，2）所围成的三角形区域内（包括边界），则1a ．其中正确结论的序号是________． 三、解答题16．已知关于x 的二次函数()22410y kx kx k k =-++>，（1）若二次函数的图象与x 轴没有交点，求k 的取值范围；（2）若(),P m n 和()3,q q -是抛物线上两点，且n q <，求实数m 的取值范围； （3）若()1,B c b +和(),C c s 是抛物线上两点，试比较b 和s 的大小．17．定义：若一次函数y ax b =+（0a ≠）与反比例函数c y x=（0c ≠）满足2a c b +=，则我们把函数2y ax bx c =++称为一次函数与反比例函数的“附中函数”．（1）一次函数36y x =+与反比例函数9y x=是否存在“附中函数”？如果存在，写出其“附中函数”，如果不存在，请说明理由．（2）若一次函数y x b =+与反比例函数c y x=（0c ≠）存在“附中函数”，且该“附中函数”的图象与直线27y x =+有唯一交点，求b ，c 的值．（3）若一次函数y ax b =+（0a >）与反比例函数c y x=-（0c ≠）的“附中函数”的图象与x 轴有两个交点分别是A （1x ，0），B （2x ，0），其中3a c a ≤≤，点C （3，4），求△ABC 的面积S △ABC 的变化范围． 18．已知抛物线2122y x x =-．（1）求这个函数的最大值或最小值，并写出函数y 取得最大值或最小值时相应的自变量x 的值．（2）求该抛物线与x 轴的交点坐标，并直接写出当0y >时相应的x 的取值范围． 19．已知抛物线2(21)46y x m x m =--+-．（1）试说明：不论m 取任何实数，该抛物线都经过x 轴上的定点A ；（2）设该抛物线与x 轴的另一个交点为B （A 与B 不重合），顶点为C ，当ABC 为直角三角形时，求m 的值；（3）在（2）的条件下，若点B 在A 的右侧，点(0,3)D ，点E 是抛物线上的一点．问：在x 轴上是否存在一点F ，使得以D ，E ，F 为顶点的三角形是等腰直角三角形，且90EDF ∠=︒，若存在，求F 点的坐标；若不存在，请说明理由．20．已知二次函数24y ax ax b =++与x 轴交于A ，B 两点（其中A 在B 的左侧），且2AB =．（1）抛物线的对称轴是______． （2）求点A 和点B 坐标．（3）点C 坐标为()2.5,4--，()0,4D -．若抛物线24y ax ax b =++与线段CD 恰有一个交点，求a 的取值21．已知抛物线y ＝ax 2＋bx ＋c （a 、b 、c 为常数，且a ≠0）（1）若抛物线的对称轴为x ＝3，若抛物线与x 轴的两个交点的横坐标比为1：2，求这两个交点的坐标；（2）抛物线的顶点为点C ，抛物线与x 轴交点分别为A 、B ，若△ABC 为等边三角形，求证：b 2—4ac ＝12；（3）若当x ＞—1时，y 随x 的增大而增大，且抛物线与直线y ＝ax —1a ＋c 相切于点D ，若ODc 的取值范围．22．如图，抛物线y ＝a （x ﹣2）2+3（a 为常数且a ≠0）与y 轴交于点A （0，53）．（1）求该抛物线的解析式；（2）若直线y ＝kx 23+（k ≠0）与抛物线有两个交点，交点的横坐标分别为x 1，x 2，当x 12+x 22＝10时，求k 的值；（3）当﹣4＜x ≤m 时，y 有最大值43m，求m 的值． 23．现有牌面编码为﹣1，1，2的三张卡片，背面向上，从中随机抽取一张卡片，记其数字为k ，将抽到的卡片背面朝上，放回打乱后，再抽一张记其数字为m ，则事件“关于a 、b的方程组2122a b ka b+=+⎧⎨+=⎩的解满足0≤a﹣b≤1，且二次函数y＝x2﹣2x+m的图象与x轴恰有2个交点”成立的概率为__．。

二次函数与直线的交点问题二次函数与直线的交点问题是数学中的一个经典问题，它既是代数学的重要内容，也是几何学的基础知识。

在解决这类问题时，我们需要用到二次函数和直线的性质和特点，以及相关的数学方法和技巧。

本文将通过对二次函数与直线的交点问题进行分析和解答，探讨它们之间的关系及解题思路。

一、二次函数的定义和性质二次函数指的是形如y=ax^2+bx+c的函数，其中a、b、c为常数，且a≠0。

二次函数的图象一般为抛物线，具有以下性质：1. 对称轴：二次函数的图象关于直线x=-b/2a对称。

2. 顶点坐标：对称轴上的点称为二次函数的顶点，顶点的横坐标为-x/2a，纵坐标为f(-x/2a)。

3. 开口方向：当a>0时，抛物线开口向上；当a<0时，抛物线开口向下。

4. 零点：二次函数与x轴的交点称为二次函数的零点，也就是方程ax^2+bx+c=0的实数解。

二、直线的定义和性质直线是平面上的一种基本几何图形，它具有以下特点：1. 斜率：直线的斜率是指直线在平面上的倾斜程度，斜率为k的直线可以表示为y=kx+b，其中k为斜率，b为截距。

2. 截距：直线与y轴的交点称为直线的y轴截距，可以表示为点(0,b)，其中b为截距。

3. 直线的方程：直线可以通过点斜式、两点式、截距式等形式来表示。

三、在解决二次函数与直线的交点问题时，我们可以将二次函数和直线的方程进行联立，然后求解方程组，从而得到二者的交点坐标。

假设给定的二次函数为y=ax^2+bx+c，直线的方程为y=kx+b。

将二者联立，可得到以下方程组：ax^2+bx+c=kx+b整理后可得：ax^2+(b-k)x+c-b=0接下来就是解二次方程了。

根据二次函数的性质，若该方程有实数解，则说明二次函数与直线有交点；若无实数解，则说明二次函数与直线无交点。

根据一元二次方程求解的公式，可得二次函数与直线的交点坐标。

若方程有两个实数解x1和x2，则交点的坐标为(x1, y(x1))和(x2, y(x2))。

类型一：线段最值问题【经典例题1改编】抛物线y=-x 2+bx +c 与直线y=-x +5一个交点A （2，m ），另一个交点B 在x 轴上，点P 是线段AB 上异于A 、B 的一个动点，过点P 做x 轴的垂线，交抛物线于点E ；（1）求抛物线的解析式；（2）是否存在这样的点P ，使线段PE 长度最大？若存在求出最大值及此时点P 的坐标，若不存在说明理由；（3）在y 轴右侧，当EP 平行于y 轴时，设点E 的横坐标为m ，当点E 到y 轴的距离等于线段EP 的长时，求m 的值；【解析】（1）A(2，-3)，抛物线解析式y=-x 2+6x -5（2）设点P 的横坐标为m ，E(m ，-m 2+6m -5)，P(m ，-m+5)∴EP=y E -y P=(-m 2+6m -5)-(-m +5)=-m 2+7m -10=-(m -27)2+49 当m=27时，EP 长度有最大值49，此时，P(27，23) （3）根据题意分两种情况∴当0<x <2或x >5时，EP=m 2-7m +10，所以m=m 2-7m +10，即m 2-8m +10=0，解得m1=4+6，m2=4-6；∴当2<x<5时，EP=-m2+7m-10，所以m=-m2+7m-10，即m2-6m+10=0，此方程无解。

综上，m1=4+6，m2=4-6【经典例题2】如图所示，抛物线y=ax2+bx-3(a≠0)与x轴交于A(-3，0)，B(1，0)两点，与y轴交于点C，直线y= -x与抛物线交于E，F两点.(1)求抛物线的解析式；(2)P是直线EF下方抛物线上的一个动点，作PH∴EF于点H，求PH的最大值；【解析】(1)抛物线的表达式为：y=a(x+3)(x−1)=a(x2+2x−3)，即−3a=−3，解得：a=1，故抛物线的表达式为：y=x2+2x−3；(2)过点P作PM∴y轴交直线EF于点M，设点P(x ，x 2+2x −3)、点M(x ，−x )，则PH=22PM=22(−x −x 2−2x +3)， 当x =−23时，PH 的最大值为：8221；【经典例题3】已知抛物线l 1:y 1=ax 2−2的顶点为P ，交x 轴于A. B 两点(A 点在B 点左侧)，且sin∴ABP=55. (1)求抛物线l 1的函数解析式；(2)过点A 的直线交抛物线于点C ，交y 轴于点D ，若∴ABC 的面积被y 轴分为1:4两个部分，求直线AC 的解析式；【解析】（1）当x =0时，y 1=ax 2-2=-2∴顶点P （0，-2），OP=2∴∴BOP=90° ∴sin∴ABP=BP OP =55 ∴BP=5OP=25 ∴OB=442022=-=-OP BP∴B （4，0），代入抛物线l 1得：16a -2=0，解得：a =81 ∴抛物线l 1的函数解析式为y 1=81x 2-2 （2）∴知抛物线l 1交x 轴于A 、B 两点∴A 、B 关于y 轴对称，即A （-4，0）∴AB=8设直线AC 解析式：y=kx +b点A 代入得：-4k +b =0∴b =4k∴直线AC ：y=kx +4k ，D （0，4k ）∴S ∴AOD =S ∴BOD =21×4×|4k |=8|k | ∴81x 2-2=kx +4k 整理得：x 2-8kx -32k -16=0∴x 1+x 2=8k∴x 1=-4∴x C =x 2=8k +4，y C =k （8k +4）+4k =8k 2+8k∴C （8k +4，8k 2+8k ）∴S ∴ABC =21AB•|y C |=32|k 2+k | ∴若k >0，则S ∴AOD ：S 四边形OBCD =1：4∴S ∴AOD =51S ∴ABC ∴8k =51×32（k 2+k ） 解得：k 1=0（舍去），k 2=41 ∴直线AC 解析式为y=41x +1 ∴若k <0，则S ∴AOD =S ∴BOD =-8k ，S ∴ABC =-32（k 2+k ）∴-8k =51×[-32（k 2+k ）] 解得：k 1=0（舍去），k 2=41（舍去） 综上所述，直线AC 的解析式为y=41x +1．【经典例题4】如图1，在平面直角坐标系中，直线y=x +4与抛物线y=21-x 2+bx +c (b ，c 是常数)交于A. B 两点，点A 在x 轴上，点B 在y 轴上。

交点个数问题（讲义）知识点睛交点个数问题是确定函数与几何图形是否存在交点及个数的问题，常见问法有交点个数情况、交点是否唯一、存在唯一位置等．处理此类问题的考虑：①交点唯一的情形考虑切点（直线与圆相切）、端点（经过线段端点）、交点（取值范围内唯一）．②多交点问题常建立方程，转化为方程解个数问题．精讲精练1.如图，菱形ABCD的边长为2cm，∠BAD=60°．点P从点A出发，以3cm/s的速度，沿AC向点C作匀速运动；与此同时，点Q也从点A出发，以1cm/s的速度，沿射线AB作匀速运动，当点P运动到点C时，P，Q两点都停止运动．设点P的运动时间为t（s）．（1）当点P异于A，C时，请说明PQ∥BC；（2）以点P为圆心、PQ的长为半径作圆，请问：在整个运动过程中，t为怎样的值时，⊙P与边BC分别有1个公共点和2个公共点？2.如图，在平面直角坐标系中，直线AB与x轴、y轴分别交于点A(6，0)，B(0，8)，点C的坐标为(0，m)，过点C作CE⊥AB于点E，点D为x轴上的一动点，连接CD，DE，以CD，DE为边作□CDEF．（1）当0＜m＜8时，求CE的长（用含m的代数式表示）；（2）点D在整个运动过程中，若存在唯一的位置，使得□CDEF 为矩形，请求出所有满足条件的m的值．3.在平面直角坐标系xOy中，点A的坐标为(0，1)，取一点B(b，0)，连接AB，作线段AB的垂直平分线l1，过点B作x轴的垂线l2，记l1，l2的交点为P．（1）当b=3时，在图1中补全图形（尺规作图，不写作法，保留作图痕迹）．（2）小慧多次取不同数值b，得出相应的点P，并把这些点用平滑的曲线连接起来发现：这些点P竟然在一条曲线L上．①设点P的坐标为(x，y)，试求y与x之间的关系式，并指出曲线L是哪种曲线；②设点P到x轴、y轴的距离分别是d1，d2，求d1+d2的范围，当d1+d2=8时，求点P的坐标；③将曲线L在直线y=2下方的部分沿直线y=2向上翻折，得到一条“W”形状的新曲线，若直线y=kx+3与这条“W”形状的新曲线有4个交点，直接写出k的取值范围．图14.已知二次函数y=ax2-2ax+c（a＜0）的最大值为4，且抛物线过点79()24-，，点P(t，0)是x轴上的动点，抛物线与y轴交点为C，顶点为D．（1）求该二次函数的解析式及顶点D的坐标；（2）求|PC-PD|的最大值及对应的点P的坐标；（3）设Q(0，2t)是y轴上的动点，若线段PQ与函数22y a x a x c=-+的图象只有一个公共点，请直接写出t的取值．【参考答案】1.（1）证明略；（2）当4361332≤，，t t t =-<-=时有一个交点；当4361t -<≤时，有两个交点．2.（1）CE =3(8)5m -；（2）满足条件的m 的值为699607213，，或--．3.（1）作图略；（2）①21122y x =+，抛物线；②P 1(3，5)，P 2(-3，5)；③3333k -<<4.（1）223y x x =-++，D (1，4)；（2）2，P (-3，0)；（3）332t <≤，72t =或3t -≤。

二次函数综合问题之抛物线与直线交点个数1.(201４•北京)在平面直角坐标系xＯy中，抛物线ｙ=2x2+mx＋n经过点Ａ(0,﹣2）,Ｂ（3,４).(1)求抛物线得表达式及对称轴;（2)设点B关于原点得对称点为C,点D就是抛物线对称轴上一动点,记抛物线在A，B之间得部分为图象G（包含A，B两点).若直线CD 与图象Ｇ有公共点,结合函数图象,求点D纵坐标t得取值范围.考点: 待定系数法求二次函数解析式;待定系数法求一次函数解析式;二次函数得最值.专题: 计算题.分析:(1)将A与Ｂ坐标代入抛物线解析式求出m与ｎ得值,确定出抛物线解析式，求出对称轴即可;(２)由题意确定出C坐标,以及二次函数得最小值,确定出D纵坐标得最小值,求出直线BC解析式,令x=１求出ｙ得值,即可确定出t得范围.解答:解:(1）∵抛物线y＝2x2+ｍx+n经过点A（0，﹣2),Ｂ（3,4），代入得:,解得:，∴抛物线解析式为y=2x2﹣4ｘ﹣２,对称轴为直线ｘ=1;(2)由题意得:C（﹣3，﹣4),二次函数y＝2x2﹣4x﹣2得最小值为﹣４,由函数图象得出D纵坐标最小值为﹣4,设直线BC解析式为ｙ=kx+b,将B与C坐标代入得:,解得:k=，ｂ＝0,∴直线BＣ解析式为y=x,当x=1时,y=,则t得范围为﹣4≤ｔ≤.点评:此题考查了待定系数法求二次函数解析式，待定系数法求一次函数解析式,以及函数得最值,熟练掌握待定系数法就是解本题得关键.2.（2011•石景山区二模)已知:抛物线与x轴交于Ａ(﹣２，0)、B(4，0)，与y轴交于C(0,4).（1)求抛物线顶点D得坐标;(２)设直线ＣD交ｘ轴于点Ｅ,过点Ｂ作ｘ轴得垂线,交直线CD于点Ｆ,将抛物线沿其对称轴上下平移,使抛物线与线段EＦ总有公共点.试探究:抛物线向上最多可以平移多少个单位长度，向下最多可以平移多少个单位长度？考点：二次函数图象与几何变换；二次函数得性质;待定系数法求二次函数解析式．专题: 探究型.分析:(1)先设出过A(﹣２,０)、B(4，0）两点得抛物线得解析式为y＝a(ｘ＋2)(x﹣4),再根据抛物线与y轴得交点坐标即可求出a得值,进而得出此抛物线得解析式;(２）先用待定系数法求出直线ＣD解析式，再根据抛物线平移得法则得到(１)中抛物线向下平移m各单位所得抛物线得解析式，再将此解析式与直线CD得解析式联立,根据两函数图象有交点即可求出ｍ得取值范围，进而可得到抛物线向下最多可平移多少个单位;同理可求出抛物线向上最多可平移多少个单位.解答：解：(1）设抛物线解析式为y=a(x+2）（x﹣4),∵C点坐标为(0,4),∴a=﹣，（1分)∴解析式为y=﹣ｘ2+x＋４，顶点Ｄ坐标为（1，);（２分)(2)直线CＤ解析式为y＝kx+b.则，，∴,∴直线ＣD解析式为y=ｘ+４,(3分)∴E（﹣８,０）,F(4,6),若抛物线向下移ｍ个单位,其解析式y＝﹣x2＋x+4﹣m(m>0),由消去y，得﹣x2+x﹣m＝0,∵△＝﹣2m≥０，∴0<m≤,∴向下最多可平移个单位.(５分）若抛物线向上移ｍ个单位,其解析式y=﹣x2+ｘ＋4+m(m＞０),方法一:当ｘ=﹣8时，ｙ＝﹣3６+ｍ,当x=４时,y＝m,要使抛物线与EF有公共点,则﹣36+m≤0或m≤6,∴0<m≤3６;(７分)方法二:当平移后得抛物线过点E(﹣8，0）时，解得m=３6，当平移后得抛物线过点F(４,6）时,m=6,由题意知：抛物线向上最多可以平移36个单位长度,(７分)综上,要使抛物线与ＥＦ有公共点，向上最多可平移3６个单位,向下最多可平移个单位．点评:本题考查得就是二次函数得图象与几何变换,涉及到用待定系数法求一次函数与二次函数得解析式、二次函数与一次函数得交点问题,有一定得难度．３.(2013•丰台区一模）二次函数ｙ=x２＋bx+c得图象如图所示,其顶点坐标为Ｍ（1，﹣4)．（１)求二次函数得解析式；(2）将二次函数得图象在ｘ轴下方得部分沿ｘ轴翻折,图象得其余部分保持不变,得到一个新得图象,请您结合新图象回答:当直线y=x＋n与这个新图象有两个公共点时,求ｎ得取值范围.考点：待定系数法求二次函数解析式;二次函数图象与几何变换.分析:（1）确定二次函数得顶点式，即可得出二次函数得解析式.(2）求出两个边界点,继而可得出n得取值范围.解答:解:(１)因为M(1,﹣4)就是二次函数y=(x+ｍ）2+k得顶点坐标,所以y=(x﹣１)２﹣4=x２﹣2x﹣3,(2)令x2﹣２x﹣３=０,解之得:x１=﹣1，x2=3,故A,B两点得坐标分别为A(﹣１,0),Ｂ(3,0).如图,当直线y＝x+n(ｎ＜1)，经过A点时,可得ｎ=1，当直线y=x＋n经过Ｂ点时,可得n=﹣3，∴ｎ得取值范围为﹣3<n＜1,翻折后得二次函数解析式为二次函数y＝﹣x２+２x+3当直线y＝x＋n与二次函数y=﹣x２+2x+３得图象只有一个交点时,x+n=﹣x2+2x+3，整理得:x2﹣x+n﹣3=0,△=b２﹣4aｃ＝1﹣4(ｎ﹣3)=１3﹣4n=０，解得:n＝,∴n得取值范围为:n>，由图可知,符合题意得ｎ得取值范围为:n＞或﹣3＜n＜１．点评:本题考查了待定系数法求二次函数解析式得知识,难点在第二问,关键就是求出边界点时n得值．4.(2009•北京)已知关于x得一元二次方程2x2＋４ｘ+k﹣1=0有实数根，k为正整数．(1)求k得值;(2)当此方程有两个非零得整数根时,将关于ｘ得二次函数y=2x２+4x+k﹣１得图象向下平移８个单位，求平移后得图象得解析式;(3)在（2)得条件下,将平移后得二次函数得图象在x轴下方得部分沿x轴翻折,图象得其余部分保持不变,得到一个新得图象.请您结合这个新得图象回答:当直线y=x+b(ｂ<k）与此图象有两个公共点时,ｂ得取值范围.考点: 二次函数综合题.专题：综合题.分析：(1）综合根得判别式及k得要求求出ｋ得取值;(2)对ｋ得取值进行一一验证,求出符合要求得k值,再结合抛物线平移得规律写出其平移后得解析式；（３)求出新抛物线与x轴得交点坐标,再分别求出直线y=x+b经过点Ａ、B时得b得取值，进而求出其取值范围.本题第二问就是难点，主要就是不会借助计算淘汰不合题意得ｋ值.解答：解：(１)由题意得,△=1６﹣８(k﹣１)≥0.∴k≤3.∵ｋ为正整数,∴ｋ=1,２,3;(2)设方程２x2+4x+ｋ﹣1=0得两根为x１,x２,则x１＋ｘ２＝﹣２,ｘ１•x２=．当ｋ＝1时,方程2ｘ２+４ｘ+k﹣１=0有一个根为零;当k=2时,x1•x2=,方程２x２+4ｘ+k﹣１=０没有两个不同得非零整数根;当k=３时,方程2x2+4ｘ＋k﹣1=0有两个相同得非零实数根﹣１.综上所述,ｋ＝1与k=２不合题意,舍去,k=3符合题意.当k=3时，二次函数为ｙ=2ｘ２+４x+2,把它得图象向下平移8个单位得到得图象得解析式为y＝2x2＋4x﹣6；(3）设二次函数y=2ｘ2＋4ｘ﹣6得图象与ｘ轴交于Ａ、B两点,则A(﹣3，0),B(１，0).依题意翻折后得图象如图所示.当直线y=x+ｂ经过A点时,可得b=；当直线ｙ=x＋b经过B点时,可得b=﹣．由图象可知,符合题意得b(b＜３)得取值范围为<b＜.（３)依图象得，要图象y=ｘ+ｂ（b小于k)与二次函数图象有两个公共点时，显然有两段.而因式分解得y=2x2＋4x﹣６＝2(x﹣１)(x+３）,第一段,当y=x＋b过（1,0)时,有一个交点,此时b=﹣.当ｙ=x+ｂ过(﹣３,0)时,有三个交点，此时b=.而在此中间即为两个交点,此时﹣＜b＜.第二段,将平移后得二次函数得图象在ｘ轴下方得部分沿ｘ轴翻折后,开口向下得部分得函数解析式为y=﹣２（x﹣1)（x+3）．显然,当y＝x+b与y=﹣2(x﹣1)(ｘ+3）(﹣３＜ｘ＜1)相切时，y=x＋ｂ与这个二次函数图象有三个交点,若直线再向上移,则只有两个交点.因为b<3,而ｙ=ｘ+b(ｂ小于ｋ,k＝3),所以当ｂ＝３时,将y=ｘ+3代入二次函数y=﹣2（ｘ﹣１)（x+3)整理得, 4x2+9x﹣6=0,△>０,所以方程有两根，那么肯定不将有直线与两截结合得二次函数图象相交只有两个公共点.这种情况故舍去.综上,﹣<ｂ＜.点评:考查知识点：一元二次方程根得判别式、二次函数及函数图象得平移与翻折,最后还考到了与一次函数得结合等问题.不错得题目,难度不大,综合性强,考查面广,似乎就是一个趋势或热点.5.(2012•东城区二模）已知关于x得方程(１﹣m)x2+(4﹣m)x+3＝0.(1）若方程有两个不相等得实数根，求ｍ得取值范围;（2)若正整数m满足８﹣2m>2，设二次函数y＝(1﹣ｍ)x２+(4﹣m）x＋3得图象与x轴交于Ａ、Ｂ两点，将此图象在x轴下方得部分沿ｘ轴翻折,图象得其余部分保持不变,得到一个新得图象.请您结合这个新得图象回答:当直线y=k ｘ+3与此图象恰好有三个公共点时,求出ｋ得值（只需要求出两个满足题意得ｋ值即可).考点：二次函数综合题.分析:(1)根据方程有两个不相等得实数根,由一元二次方程得定义与根得判别式可求m得取值范围;(2)先求出正整数m得值,从而确定二次函数得解析式，得到解析式与x轴交点得坐标,由图象可知符合题意得直线y=kx＋3经过点A、B.从而求出k得值．解答:解:(1)△＝(4﹣m)2﹣12（1﹣m)=（ｍ+2)2,由题意得,（m+2）２＞0且1﹣m≠０.故符合题意得m得取值范围就是m≠﹣2且m≠１得一切实数.(2)∵正整数m满足8﹣2ｍ＞2,∴m可取得值为1与2.又∵二次函数ｙ=(1﹣m)x2+(4﹣m)ｘ+3，∴ｍ=2.…（4分)∴二次函数为ｙ＝﹣x2+2x+3.∴A点、B点得坐标分别为(﹣1,0)、(３,０）.依题意翻折后得图象如图所示.由图象可知符合题意得直线y=kｘ＋３经过点Ａ、B.可求出此时ｋ得值分别为3或﹣１.…(7分)注:若学生利用直线与抛物线相切求出k＝2也就是符合题意得答案.点评:本题考查了二次函数综合题.(1)考查了一元二次方程根得情况与判别式△得关系:△＞０⇔方程有两个不相等得实数根.(2)得到符合题意得直线y=kｘ+３经过点A、B就是解题得关键.6.在平面直角坐标系中,抛物线y＝﹣x2+mx＋m2﹣３m+2与ｘ轴得交点分别为原点O与点A,点B(4,n）在这条抛物线上.(1)求B点得坐标;(2）将此抛物线得图象向上平移个单位，求平移后得图象得解析式;(3)在(2)得条件下，将平移后得二次函数得图象在ｘ轴下方得部分沿x轴翻折,图象得其余部分保持不变，得到一个新得图象．请您结合这个新得图象回答:当直线y＝ｘ+b与此图象有两个公共点时,b得取值范围．考点: 二次函数综合题.专题：压轴题.分析：(1）把原点坐标代入抛物线,解关于ｍ得一元二次方程得到m得值,再根据二次项系数不等于0确定出函数解析式,再把点B坐标代入函数解析式求出n得值,即可得解;(2)根据向上平移纵坐标加解答即可;（3)把直线解析式与抛物线解析式联立，消掉y得到关于x得一元二次方程,根据△=0求出ｂ得值，然后令y=０求出抛物线与ｘ轴得交点坐标,再求出直线经过抛物线与x轴左边交点得ｂ值，然后根据图形写出b得取值范围即可.解答：解:(1)∵抛物线经过原点O,∴m2﹣3ｍ+2=0,解得m１＝１，m2=2,当m=１时，﹣＝﹣＝０,∴m=2,∴抛物线得解析式为y＝﹣x2+３ｘ,∵点Ｂ（4,n)在这条抛物线上，∴n=﹣×42+3×４=﹣8+12=４,∴点B（４，4)；（2)∵抛物线得图象向上平移个单位，∴平移后得图象得解析式y=﹣ｘ2+3ｘ+;(3)联立，消掉ｙ得，﹣ｘ2+３ｘ+=x+b,整理得,x2﹣5x+2b﹣７＝0,△=（﹣５)２﹣４×1×(2ｂ﹣7)=0，解得b=,令ｙ=0，则﹣x２＋３ｘ＋＝0,整理得，x2﹣６ｘ﹣７＝0,解得x1=﹣1,x2=7,∴抛物线与x轴左边得交点为（﹣1,０),当直线y=x+b经过点(﹣１,0)时，×(﹣１)+ｂ=0,解得b=,∴当直线y=x+b与此图象有两个公共点时，b得取值范围为b>或ｂ<．点评:本题就是二次函数综合题,主要利用了解一元二次方程，二次函数图象上点得坐标特征,二次函数图象与几何变换,难点在于(３）求出直线与抛物线有三个交点时得b值,作出图形更形象直观.7.关于x得二次函数ｙ=x2＋2ｘ+ｋ﹣1得图象与ｘ轴有交点，k为正整数.（１)求k得值；(2)当关于x得二次函数y＝ｘ2＋２x+k﹣１与x轴得交点得横坐标均就是负整数时,将关于x得二次函数ｙ=ｘ2+２ｘ+k﹣１得图象向下平移4个单位,求平移后得图象得解析式;(3)在(2)得条件下，将平移后得二次函数得图象在x轴下方得部分沿x轴翻折,图象得其余部分保持不变,得到一个新得图象.请您结合这个新得图象回答:当直线y＝（ｂ<3)与此图象有两个公共点时,b得取值范围.考点: 二次函数综合题.分析:（１）综合根得判别式及k得要求,求出k得取值;(2)对k得取值进行一一验证，求出符合要求得k值，再结合抛物线平移得规律写出其平移后得解析式;(3)求出新抛物线与ｘ轴得交点坐标,再分别求出直线y=x+b经过点A、B时得b得取值,进而求出其取值范围. 解答：解:(1)由题意得，△=4﹣4(k﹣1)≥0．∴k≤２.∵ｋ为正整数,∴k=1,2；(2）设方程x2＋2x+k﹣1=０得两根为x1,x2,则ｘ1+x2=﹣2,x１•x２＝k﹣1．当k＝1时,图象y=x２+２x＋k﹣1与x轴有一个交点为(0,0）,不合题意;当k＝２时，图象y=ｘ2+2x+k﹣1与x轴有一个交点为（﹣1,0),符合题意;综上所述,k＝２符合题意.当k=２时,二次函数为y=x２+2ｘ+１，把它得图象向下平移4个单位得到得图象得解析式为:y=x2+2x﹣3；(3)设二次函数y＝x2+2ｘ﹣3得图象与x轴交于A、B两点，则Ａ(﹣3，０）,B(１，0)．依题意翻折后得图象如图所示.当直线y=x+b经过A点时,可得b＝;当直线y=x+ｂ经过B点时,可得b=﹣.由图象可知,符合题意得b(b＜3）得取值范围为:﹣＜b<.点评:此题主要考查了一元二次方程根得判别式、二次函数及函数图象得平移与翻折，最后还考到了与一次函数得结合等问题．不错得题目,难度不大，综合性强．8．（2014•东城区一模)已知:关于ｘ得一元二次方程mx２﹣(4m+1)x+3m+３=０(m>1)．（1)求证:方程有两个不相等得实数根;(2)设方程得两个实数根分别为x１,x2(其中x1>x2),若y就是关于m得函数,且y＝ｘ1﹣3x2,求这个函数得解析式; （３）将(2）中所得得函数得图象在直线ｍ=2得左侧部分沿直线m=２翻折,图象得其余部分保持不变，得到一个新得图象.请您结合这个新得图象回答：当关于m得函数y=2ｍ+b得图象与此图象有两个公共点时,b得取值范围．考点: 一次函数综合题.专题：压轴题．分析:(1)列式表示出根得判别式△,再根据△＞０,方程有两个不相等得实数根证明;（２）利用求根公式法求出ｘ１、x2，然后代入关系式整理即可得解；(３)作出函数图象，然后求出m=2时得函数值与以及m=１时得翻折图象得对应点得坐标，再代入直线解析式求出b值,然后结合图形写出b得取值范围即可.解答:(1)证明：△=(4m+１)2﹣4ｍ(3m＋３)＝４ｍ２﹣4m+1=(２ｍ﹣1)2,∵m>1,∴(2m﹣1)2>0,∴方程有两个不等实根;(2)解：x=,∴两根分别为=３,=1+,∵m>1，∴0＜<1,∴1＜１+＜２,∵x1＞ｘ2,∴x１=3,x２＝1+,∴ｙ=x1﹣3x2,=３﹣３(１+),=﹣,所以,这个函数解析式为y=﹣（ｍ>1);(3)解:作出函数y=﹣(m＞1）得图象，并将图象在直线m=２左侧部分沿此直线翻折,所得新图形如图所示，m=2时,ｙ=﹣,ｍ=1时,y=﹣=﹣3，∴函数图象直线m=2左侧部分翻折后得两端点坐标为(３,﹣3),(２，﹣),当m=3时,2×3+b=﹣3,解得b=﹣9，当m=2时,２×2＋ｂ=﹣，解得ｂ=﹣,所以,此图象有两个公共点时,ｂ得取值范围﹣９＜b<﹣.点评:本题就是一次函数综合题型,主要利用了根得判别式，求根公式法解一元二次方程,一次函数与反比例函数交点问题,难点在于(3)确定出翻折部分得两个端点得坐标以及有两个交点时得b得取值范围，作出图形更形象直观.9.(２０13•门头沟区一模)已知关于x得一元二次方程.(１）求证:无论m取任何实数,方程都有两个实数根;（２)当m<3时，关于x得二次函数得图象与x轴交于A、B两点(点A在点B得左侧),与ｙ轴交于点Ｃ，且２ＡB=3OC，求m得值;(3)在(2)得条件下,过点C作直线ｌ∥x轴，将二次函数图象在y轴左侧得部分沿直线l翻折,二次函数图象得其余部分保持不变,得到一个新得图象,记为G.请您结合图象回答:当直线与图象G只有一个公共点时,b得取值范围．考点: 二次函数综合题.分析:(1)运用根得判别式就可以求出△得值就可以得出结论；(2)先当x=0或y=0就是分别表示出抛物线与ｘ轴与y轴得交点坐标,表示出AB、ＯＣ得值,由2AＢ=3OC建立方程即可求出ｍ得值;（3)把(２)m得值代入抛物线得解析式就可以求出抛物线得解析式与C点得坐标,当直线经过点C时就可以求出b得值,由直线与抛物线只有一个公共点建立方程,根据△＝0就可以求出ｂ得值,再根据图象就可以得出结论.解答：解:(1)根据题意,得△＝(ｍ﹣2)2﹣4××(2m﹣6)=(m﹣4)2,∵无论ｍ为任何数时,都有(m﹣4)2≥0,即△≥0.∴无论m取任何实数,方程都有两个实数根；(２)由题意，得当ｙ=0时,则,解得：ｘ1=6﹣２m,ｘ２=﹣２,∵ｍ<3，点Ａ在点B得左侧,∴A(﹣2,０),B(﹣2m+6,0)，∴ＯA=2,OB=﹣2m+6．当x=０时,ｙ=2m﹣６,∴C(０,2m﹣6),∴OC＝﹣(2ｍ﹣6)=﹣2m+６.∵２AB=3ＯＣ,∴2(2﹣2m+6)=3(﹣2m+6),解得:m＝1;(3)如图,当m=1时,抛物线得解析式为ｙ=ｘ2﹣x﹣4,点C得坐标为(0，﹣４）.当直线y＝x+b经过点C时，可得ｂ＝﹣4,当直线ｙ=ｘ＋ｂ(b＜﹣4）与函数y＝x2﹣ｘ﹣4(ｘ＞０)得图象只有一个公共点时,得x＋b═x２﹣x﹣4．整理得:3ｘ２﹣8x﹣6b﹣24=０,∴△＝(﹣８)２﹣4×3×（﹣6b﹣24)=0,解得：b＝﹣.结合图象可知,符合题意得b得取值范围为ｂ＞﹣4或ｂ<﹣.点评:本题就是一道一次函数与二次函数得综合试题,考查了一元二次方程根得判别式得运用，二次函数与坐标轴得交点坐标得运用,轴对称得性质得运用，解答时根据函数之间得关系建立方程灵活运用根得判别式就是解答本题得关键.。

二次函数的交点问题巧解方法：1、二次函数与x 轴、y 轴的交点：分别令y=0,x=0；2、二次函数与一次、反比例函数或者与其他函数等的相点：联立两个函数表达式，解方程.例1、如图，直线ι经过A （3，0），B （0，3）两点，且与二次函数y=x 2＋1的图象，在第一象限内相交于点C ．求：（1）△AOC 的面积；（2）二次函数图象顶点与点A 、B 组成的三角形的面积．例2、已知抛物线y ＝x 2-2x-8，（1）求证：该抛物线与x 轴一定有两个交点，并求出这两个交点的坐标。

（2）若该抛物线与x 轴的两个交点为A 、B ，且它的顶点为P ，求△ABP 的面积例3、.如图，抛物线2y x bx c =+-经过直线3y x =-与坐标轴的两个交点A 、B ，此抛物线与x 轴的另一个交点为C ，抛物线顶点为D.（1）求此抛物线的解析式；（2）点P 为抛物线上的一个动点，求使APC S ∆：ACD S ∆=5 ：4的点P 的坐标。

例4、已知抛物线y=12x2+x-52．（1）用配方法求它的顶点坐标和对称轴．（2）若该抛物线与x轴的两个交点为A、B，求线段AB的长．例5、已知抛物线y=mx2＋（3－2m）x＋m－2（m≠0）与x轴有两个不同的交点．（1）求m的取值范围；（2）判断点P（1，1）是否在抛物线上；（3）当m=1时，求抛物线的顶点Q及P点关于抛物线的对称轴对称的点P′的坐标，并过P′、Q、P三点，画出抛物线草图．例6．已知二次函数y=x2－（m－3）x－m的图象是抛物线，如图2-8-10．（1）试求m为何值时，抛物线与x轴的两个交点间的距离是3？（2）当m为何值时，方程x2－（m－3）x－m=0的两个根均为负数？（3）设抛物线的顶点为M，与x轴的交点P、Q，求当PQ最短时△MPQ的面积．训练题1．抛物线y=a （x －2）（x ＋5）与x 轴的交点坐标为 ．2．已知抛物线的对称轴是x=－1，它与x 轴交点的距离等于4，它在y 轴上的截距是－6，则它的表达式为 ．3．若a ＞0，b ＞0，c ＞0，△＞0，那么抛物线y=ax 2＋bx ＋c 经过 象限．4．抛物线y=x 2－2x ＋3的顶点坐标是 ．5．若抛物线y=2x 2－（m ＋3）x －m ＋7的对称轴是x=1，则m= ．6．抛物线y=2x 2＋8x ＋m 与x 轴只有一个交点，则m= ．7．已知抛物线y=ax 2＋bx ＋c 的系数有a －b ＋c=0，则这条抛物线经过点 ．8．二次函数y=kx 2＋3x －4的图象与x 轴有两个交点，则k 的取值范围 ．9．抛物线y=x 2－2x ＋a 2的顶点在直线y=2上，则a 的值是 ．10．抛物线y=3x 2＋5x 与两坐标轴交点的个数为（ ）A ．3个B ．2个C ．1个D ．无11．如图1所示，函数y=ax 2－bx ＋c 的图象过（－1，0），则的值是（）A ．－3B ．3C ．D ．－12．已知二次函数y=ax 2＋bx ＋c 的图象如图2所示，则下列关系正确的是（ ）A ．0＜－＜1B ．0＜－＜2C ．1＜－＜2D ．－=113．已知二次函数y=x 2＋mx ＋m －2．求证：无论m 取何实数，抛物线总与x 轴有两个交点．14．已知二次函数y=x 2－2kx ＋k 2＋k －2．（1）当实数k 为何值时，图象经过原点？（2）当实数k 在何范围取值时，函数图象的顶点在第四象限内？a b a ca cbc b a +++++2121a b 2a b 2a b 2a b2函数解析式的求法例一、已知抛物线上任意三点时，通常设解析式为一般式y=ax2+bx+c，然后解三元方程组求解；1．已知二次函数的图象经过A（0，3）、B（1，3）、C（－1，1）三点，求该二次函数的解析式。