二次函数解析式-交点式

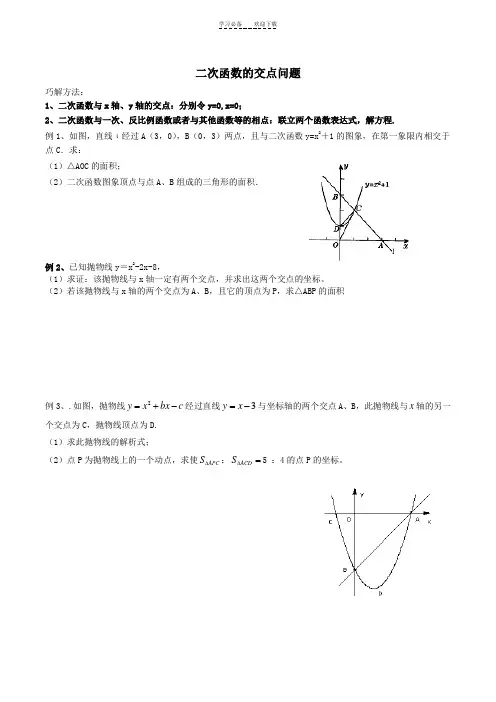
二次函数的交点问题巧解方法：1、二次函数与x 轴、y 轴的交点：分别令y=0,x=0；2、二次函数与一次、反比例函数或者与其他函数等的相点：联立两个函数表达式，解方程.例1、如图，直线ι经过A （3，0），B （0，3）两点，且与二次函数y=x 2＋1的图象，在第一象限内相交于点C ．求：（1）△AOC 的面积；（2）二次函数图象顶点与点A 、B 组成的三角形的面积．例2、已知抛物线y ＝x 2-2x-8，（1）求证：该抛物线与x 轴一定有两个交点，并求出这两个交点的坐标。

（2）若该抛物线与x 轴的两个交点为A 、B ，且它的顶点为P ，求△ABP 的面积例3、.如图，抛物线2y x bx c =+-经过直线3y x =-与坐标轴的两个交点A 、B ，此抛物线与x 轴的另一个交点为C ，抛物线顶点为D.（1）求此抛物线的解析式；（2）点P 为抛物线上的一个动点，求使APC S ∆：ACD S ∆=5 ：4的点P 的坐标。

例4、已知抛物线y=12x2+x-52．（1）用配方法求它的顶点坐标和对称轴．（2）若该抛物线与x轴的两个交点为A、B，求线段AB的长．例5、已知抛物线y=mx2＋（3－2m）x＋m－2（m≠0）与x轴有两个不同的交点．（1）求m的取值范围；（2）判断点P（1，1）是否在抛物线上；（3）当m=1时，求抛物线的顶点Q及P点关于抛物线的对称轴对称的点P′的坐标，并过P′、Q、P三点，画出抛物线草图．例6．已知二次函数y=x2－（m－3）x－m的图象是抛物线，如图2-8-10．（1）试求m为何值时，抛物线与x轴的两个交点间的距离是3？（2）当m为何值时，方程x2－（m－3）x－m=0的两个根均为负数？（3）设抛物线的顶点为M，与x轴的交点P、Q，求当PQ最短时△MPQ的面积．训练题1．抛物线y=a （x －2）（x ＋5）与x 轴的交点坐标为 ．2．已知抛物线的对称轴是x=－1，它与x 轴交点的距离等于4，它在y 轴上的截距是－6，则它的表达式为 ．3．若a ＞0，b ＞0，c ＞0，△＞0，那么抛物线y=ax 2＋bx ＋c 经过 象限．4．抛物线y=x 2－2x ＋3的顶点坐标是 ．5．若抛物线y=2x 2－（m ＋3）x －m ＋7的对称轴是x=1，则m= ．6．抛物线y=2x 2＋8x ＋m 与x 轴只有一个交点，则m= ．7．已知抛物线y=ax 2＋bx ＋c 的系数有a －b ＋c=0，则这条抛物线经过点 ．8．二次函数y=kx 2＋3x －4的图象与x 轴有两个交点，则k 的取值范围 ．9．抛物线y=x 2－2x ＋a 2的顶点在直线y=2上，则a 的值是 ．10．抛物线y=3x 2＋5x 与两坐标轴交点的个数为（ ）A ．3个B ．2个C ．1个D ．无11．如图1所示，函数y=ax 2－bx ＋c 的图象过（－1，0），则的值是（）A ．－3B ．3C ．D ．－12．已知二次函数y=ax 2＋bx ＋c 的图象如图2所示，则下列关系正确的是（ ）A ．0＜－＜1B ．0＜－＜2C ．1＜－＜2D ．－=113．已知二次函数y=x 2＋mx ＋m －2．求证：无论m 取何实数，抛物线总与x 轴有两个交点．14．已知二次函数y=x 2－2kx ＋k 2＋k －2．（1）当实数k 为何值时，图象经过原点？（2）当实数k 在何范围取值时，函数图象的顶点在第四象限内？a b a ca cbc b a +++++2121a b 2a b 2a b 2a b2函数解析式的求法例一、已知抛物线上任意三点时，通常设解析式为一般式y=ax2+bx+c，然后解三元方程组求解；1．已知二次函数的图象经过A（0，3）、B（1，3）、C（－1，1）三点，求该二次函数的解析式。

二次函数解析式交点式
一、表达式形式
二次函数的交点式解析式为：y = k（x-x1）（x-x2），其中（x1，0）和（x2，0）是二次函数与x轴的两个交点的坐标，k为常数。

二、交点坐标
当y=0时，二次函数与x轴交于两点，其横坐标为x1和x2。

三、确定系数
使用交点式时，需要先确定k、x1、x2的值。

通常情况下，可以先将已知的二次函数与x轴的交点坐标代入解析式中，解出k的值，再利用其他条件求出x1和x2的值。

四、适用范围
交点式适用于已知二次函数与x轴的交点坐标和对称轴的情况下，方便求解方程和计算函数值。

五、与一般式比较
二次函数的一般式为y=ax^2+bx+c，交点式在形式上更加简洁，并且能够直接反映二次函数与x轴的交点情况。

相比之下，一般式在求解方程和计算函数值时需要先进行配方或者分解因式等计算步骤。

六、与顶点式比较
二次函数的顶点式为y=a（x-h）^2+k，其中（h，k）为顶点坐标。

相比之下，交点式没有直接包含二次函数的顶点坐标，但可以通过解方程组得到顶点坐标。

同时，在某些情况下，使用交点式可以更加方便地求解方程和计算函数值。

七、应用领域
交点式在数学领域有着广泛的应用，如代数、几何、分析等。

在解决实际问题中，交点式也经常被用来建模和分析数据。

例如，在物理学、工程学、经济学等领域中，交点式被用来描述实验结果、预测模型、分析数据等方面。

求二次函数的解析式的几种方法山东省沂水县高桥镇初级中学 王瑞辉二次函数解析式的求法是二次函数知识的重点，也是中考必考内容。

现在举例，说明求二次函数解析式的常用方法，希望对同学们学习有所帮助。

一、二次函数常见的三种表达式：（1）一般式：y ax bx c a =++≠20()；（2）交点式：y a x x x x =--()()12，其中点(,)()x x 1200，，为该二次函数与x 轴的交点；（3）顶点式：()2()0y a x h k a =-+≠，其中点(),h k 为该二次函数的顶点。

二、利用待定系数法求二次函数关系式(1)、已知二次函数图象上任意三个点的坐标，可设一般式求二次函数的关系式。

例1、已知抛物线2y ax bx c =++，经过点（2，1）、（-1，-8）、（0，-3）．求这个抛物线的解析式． 解：根据题意得421,8,3,a b c a b c c ++=⎧⎪-+=-⎨⎪=-⎩ 解之得1,4,3,a b c =-⎧⎪=⎨⎪=-⎩所以抛物线为243;y x x =-+-说明：用待定系数法求系数a b c 、、需要有三个独立条件，若给出的条件是任意三个点，可设解析式为2(0)y ax bx c a =++≠，然后将三个点的坐标分别代入，组成一次方程组用加减消元法来求解．(2)、已知抛物线与x 轴的两个交点坐标和图象上另一个点坐标，可设交点式求二次函数的关系式。

若知道二次函数与x 轴有两个交点()()1200x x ，，，，则相当于方程20ax bx c ++=有两个不相等的实数根12x x ，，从而212()()ax bx c a x x x x ++=--，故二次函数可以表示为12()()(0)y a x x x x a =--≠．例2、已知一个二次函数的图象经过点A （－1，0），B （3，0），C （0，－3）三点．求此二次函数的解析式．解：根据题设，设此二次函数的解析式为(1)(3)y a x x =+-．又∵该二次函数又过点（0，－3）， ∴(01)(03)3a +-=-． 解得1a =．因此，所求的二次函数解析式为(1)(3)y x x =+-，即223y x x =--．说明：在把函数与x 轴的两个交点坐标代入12()()(0)y a x x x x a =--≠求值时，要注意正确处理两个括号内的符号．(3)、已知抛物线顶点和另外一个点坐标时，设顶点式y =a (x -h )2+k (a ≠0)例3、对称轴与y 轴平行的抛物线顶点是(-2，-1)，抛物线又过(1，0)，求此抛物线的函数解析式。

求二次函数解析式的三种基本方法四川 倪先德二次函数是初中数学的一个重要内容，也是高中数学的一个重要基础。

熟练地求出二次函数的解析式是解决二次函数问题的重要保证。

二次函数的解析式有三种基本形式：1、一般式：y=ax 2+bx+c (a ≠0)。

2、顶点式：y=a(x －h)2+k (a ≠0)，其中点(h,k)为顶点，对称轴为x=h 。

3、交点式：y=a(x －x 1)(x －x 2) (a ≠0)，其中x 1,x 2是抛物线与x 轴的交点的横坐标。

求二次函数的解析式一般用待定系数法，但要根据不同条件，设出恰当的解析式：1、若给出抛物线上任意三点，通常可设一般式。

2、若给出抛物线的顶点坐标或对称轴或最值，通常可设顶点式。

3、若给出抛物线与x 轴的交点或对称轴或与x 轴的交点距离，通常可设交点式。

探究问题，典例指津：例1、已知二次函数的图象经过点)4,0(),5,1(---和)1,1(．求这个二次函数的解析式． 分析：由于题目给出的是抛物线上任意三点，可设一般式y=ax 2+bx+c (a ≠0)。

解：设这个二次函数的解析式为y=ax 2+bx+c (a ≠0)依题意得：⎪⎩⎪⎨⎧=++-=-=+-145c b a c c b a 解这个方程组得：⎪⎩⎪⎨⎧-===432c b a∴这个二次函数的解析式为y=2x 2+3x －4。

例2、已知抛物线c bx ax y ++=2的顶点坐标为)1,4(-，与y 轴交于点)3,0(，求这条抛物线的解析式。

分析：此题给出抛物线c bx ax y ++=2的顶点坐标为)1,4(-，最好抛开题目给出的c bx ax y ++=2，重新设顶点式y=a(x －h)2+k (a ≠0)，其中点(h,k)为顶点。

解：依题意，设这个二次函数的解析式为y=a(x －4)2－1 (a ≠0)又抛物线与y 轴交于点)3,0(。

∴a(0－4)2－1=3 ∴a=41 ∴这个二次函数的解析式为y=41(x －4)2－1，即y=41x 2－2x+3。

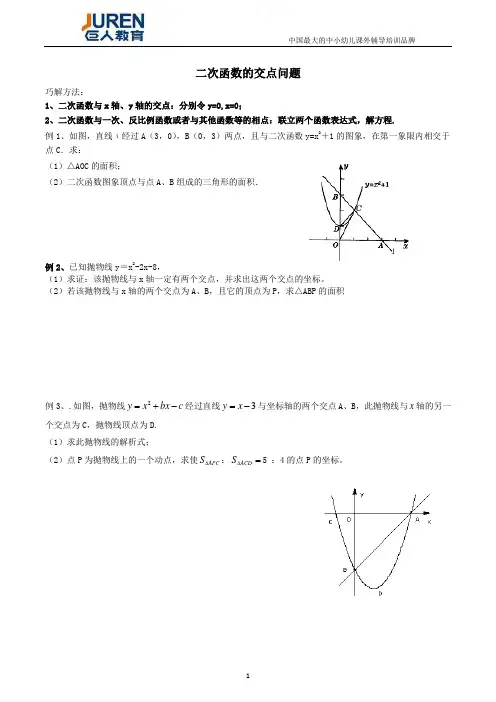
二次函数的交点问题巧解方法：1、二次函数与x 轴、y 轴的交点：分别令y=0,x=0；2、二次函数与一次、反比例函数或者与其他函数等的相点：联立两个函数表达式，解方程.例1、如图，直线ι经过A （3，0），B （0，3）两点，且与二次函数y=x 2＋1的图象，在第一象限内相交于点C ．求：（1）△AOC 的面积；（2）二次函数图象顶点与点A 、B 组成的三角形的面积．例2、已知抛物线y ＝x 2-2x-8，（1）求证：该抛物线与x 轴一定有两个交点，并求出这两个交点的坐标。

（2）若该抛物线与x 轴的两个交点为A 、B ，且它的顶点为P ，求△ABP 的面积例3、.如图，抛物线2y x bx c =+-经过直线3y x =-与坐标轴的两个交点A 、B ，此抛物线与x 轴的另一个交点为C ，抛物线顶点为D.（1）求此抛物线的解析式；（2）点P 为抛物线上的一个动点，求使APC S ∆：ACD S ∆=5 ：4的点P 的坐标。

例4、已知抛物线y=12x2+x-52．（1）用配方法求它的顶点坐标和对称轴．（2）若该抛物线与x轴的两个交点为A、B，求线段AB的长．例5、已知抛物线y=mx2＋（3－2m）x＋m－2（m≠0）与x轴有两个不同的交点．（1）求m的取值范围；（2）判断点P（1，1）是否在抛物线上；（3）当m=1时，求抛物线的顶点Q及P点关于抛物线的对称轴对称的点P′的坐标，并过P′、Q、P三点，画出抛物线草图．例6．已知二次函数y=x2－（m－3）x－m的图象是抛物线，如图2-8-10．（1）试求m为何值时，抛物线与x轴的两个交点间的距离是3？（2）当m为何值时，方程x2－（m－3）x－m=0的两个根均为负数？（3）设抛物线的顶点为M，与x轴的交点P、Q，求当PQ最短时△MPQ的面积．训练题1．抛物线y=a （x －2）（x ＋5）与x 轴的交点坐标为 ．2．已知抛物线的对称轴是x=－1，它与x 轴交点的距离等于4，它在y 轴上的截距是－6，则它的表达式为 ．3．若a ＞0，b ＞0，c ＞0，△＞0，那么抛物线y=ax 2＋bx ＋c 经过 象限．4．抛物线y=x 2－2x ＋3的顶点坐标是 ．5．若抛物线y=2x 2－（m ＋3）x －m ＋7的对称轴是x=1，则m= ．6．抛物线y=2x 2＋8x ＋m 与x 轴只有一个交点，则m= ．7．已知抛物线y=ax 2＋bx ＋c 的系数有a －b ＋c=0，则这条抛物线经过点 ．8．二次函数y=kx 2＋3x －4的图象与x 轴有两个交点，则k 的取值范围 ．9．抛物线y=x 2－2x ＋a 2的顶点在直线y=2上，则a 的值是 ．10．抛物线y=3x 2＋5x 与两坐标轴交点的个数为（ ）A ．3个B ．2个C ．1个D ．无11．如图1所示，函数y=ax 2－bx ＋c 的图象过（－1，0），则的值是（）A ．－3B ．3C ．D ．－12．已知二次函数y=ax 2＋bx ＋c 的图象如图2所示，则下列关系正确的是（ ）A ．0＜－＜1B ．0＜－＜2C ．1＜－＜2D ．－=113．已知二次函数y=x 2＋mx ＋m －2．求证：无论m 取何实数，抛物线总与x 轴有两个交点．14．已知二次函数y=x 2－2kx ＋k 2＋k －2．（1）当实数k 为何值时，图象经过原点？（2）当实数k 在何范围取值时，函数图象的顶点在第四象限内？a b a ca cbc b a +++++2121a b 2a b 2a b 2a b2函数解析式的求法例一、已知抛物线上任意三点时，通常设解析式为一般式y=ax2+bx+c，然后解三元方程组求解；1．已知二次函数的图象经过A（0，3）、B（1，3）、C（－1，1）三点，求该二次函数的解析式。

二次函数交点式：y=a(X-x1)(X-x2) [仅限于与x轴有交点A（x1，0）和B（x2，0）的抛物线][仅限于与x轴有交点A（x1，0）和B（x2，0）的抛物线] 在解决与二次函数的图象和x轴交点坐标有关的问题时，使用交点式较为方便。

y=a(x-x1)(x-x2) 找到函数图象与X轴的两个交点，分别记为x1和x2,代入公式，再有一个经过抛物线的点的坐标，即可求出a的值。

将a、X1、X2代入y=a(x-x1)(x-x2)，即可得到一个解析式，这是y=ax²;+bx+c因式分解得到的，将括号打开，即为一般式。

X1,X2是关于ax²+bx+c=0的两个根。

考点一、平面直角坐标系（3分）1、平面直角坐标系在平面内画两条互相垂直且有公共原点的数轴，就组成了平面直角坐标系。

其中，水平的数轴叫做x轴或横轴，取向右为正方向；铅直的数轴叫做y轴或纵轴，取向上为正方向；两轴的交点O（即公共的原点）叫做直角坐标系的原点；建立了直角坐标系的平面，叫做坐标平面。

为了便于描述坐标平面内点的位置，把坐标平面被x轴和y轴分割而成的四个部分，分别叫做第一象限、第二象限、第三象限、第四象限。

注意：x轴和y轴上的点，不属于任何象限。

2、点的坐标的概念点的坐标用（a，b）表示，其顺序是横坐标在前，纵坐标在后，中间有“，”分开，横、纵坐标的位置不能颠倒。

平面内点的坐标是有序实数对，当时，（a，b）和（b，a）是两个不同点的坐标。

考点二、不同位置的点的坐标的特征（3分）1、各象限内点的坐标的特征点P(x,y)在第一象限：X>0，Y>0点P(x,y)在第二象限：X<0，Y>0点P(x,y)在第三象限：X<0，Y<0点P(x,y)在第四象限：X>0，Y<02、坐标轴上的点的特征点P(x,y)在x轴上，x为任意实数，y=0点P(x,y)在y轴上，y为任意实数，x=0点P(x,y)既在x轴上，又在y轴上x，y同时为零，即点P坐标为（0，0）3、两条坐标轴夹角平分线上点的坐标的特征点P(x,y)在第一、三象限夹角平分线上x与y相等点P(x,y)在第二、四象限夹角平分线上x与y互为相反数4、和坐标轴平行的直线上点的坐标的特征位于平行于x轴的直线上的各点的纵坐标相同。

二次函数交点式求解析式二次函数（quadratic function ）的基本表示形式为y=ax ²+bx+c （a ≠0）。

二次函数最高次必须为二次， 二次函数的图像是一条 对称轴与y 轴平行或重合于y 轴的 抛物线。

二次函数表达式为y=ax ²+bx+c （且a ≠0），它的定义是一个二次 多项式（或单项式）。

如果令y 值等于零，则可得一个 二次方程。

该方程的解称为方程的根或函数的 零点。

基本定义一般地，把形如（a 、b 、c 是 常数）的 函数叫做二次函数，其中a 称为 二次项系数，b 为 一次项系数，c 为 常数项。

x 为 自变量，y 为 因变量。

等号右边自变量的最高次数是2。

顶点坐标交点式 为（ 仅限 于与x 轴有交点的抛物线），与x 轴的交点坐标是和注意：“变量”不同于“自变量”，不能说“二次函数是指变量的最高次数为二次的多项式函数”。

“未知数”只是一个数（具体值未知，但是只取一个值），“变量”可在实数范围内任意取值。

在方程中适用“未知数”的概念（函数方程、微分方程中是未知函数，但不论是未知数还是未知函数，一般都表示一个数或函数——也会遇到特殊情况），但是函数中的字母表示的是变量，意义已经有所不同。

从函数的定义也可看出二者的差别，如同函数不等于函数的关系。

历史大约在公元前480年，古巴比伦人和中国人已经使用配方法求得了二次方程的正根，但是并没有提出通用的求解方法。

公元前300年左右，欧几里得提出了一种更抽象的几何方法求解二次方程。

7世纪印度的婆罗摩笈多是第一位懂得用使用代数方程的人，它同时容许有正负数的根。

11世纪阿拉伯的花拉子密独立地发展了一套公式以求方程的正数解。

亚伯拉罕·巴希亚（亦以拉丁文名字萨瓦索达著称）在他的著作Liber embadorum中，首次将完整的一元二次方程解法传入欧洲。

据说施里德哈勒是最早给出二次方程的普适解法的数学家之一。

但这一点在他的时代存在着争议。