第3章整数规划模型

整数规划的数学模型及解的特点整数规划IP (integer programming)：在许多规划问题中，如果要求一部分或全部决策变量必须取整数。

例如，所求的解是机器的台数、人数、车辆船只数等，这样的规划问题称为整数规划，简记IP 。

松弛问题(slack problem)：不考虑整数条件，由余下的目标函数和约束条件构成的规划问题称为该整数规划问题的松弛问题。

若松弛问题是一个线性规化问题，则该整数规划为整数线性规划(integer linear programming)。

一、整数线性规划数学模型的一般形式∑==nj jj x c Z 1min)max(或中部分或全部取整数n j nj i jij x x x mj ni x b xa ts ,...,,...2,1,...,2,10),(.211==≥=≥≤∑=整数线性规划问题可以分为以下几种类型1、纯整数线性规划(pure integer linear programming)：指全部决策变量都必须取整数值的整数线性规划。

有时，也称为全整数规划。

2、混合整数线性规划(mixed integer liner programming)：指决策变量中有一部分必须取整数值，另一部分可以不取整数值的整数线性规划。

3、0—1型整数线性规划(zero —one integer liner programming)：指决策变量只能取值0或1的整数线性规划。

1 解整数规划问题0—1型整数规划0—1型整数规划是整数规划中的特殊情形，它的变量仅可取值0或1，这时的⎪⎪⎪⎩⎪⎪⎪⎨⎧≥≤+≥+≤-+=且为整数0,5210453233max 2121212121x x x x x x x x x x z变量xi 称为0—1变量，或称为二进制变量。

0—1型整数规划中0—1变量作为逻辑变量(logical variable)，常被用来表示系统是否处于某一特定状态，或者决策时是否取某个方案。

第3章 整数规划3.1 整数规划的数学模型一个规划问题中要求部分或全部决策变量是整数，则这个规划称为整数规划。

当要求全部变量取整数值的，称为纯整数规划(Pure Integer Programming ，IP )，要求一部分变量取整数值的，称为混合整数规划(Mixed Integer Programming ，MIP )，决策变量全部取0或1的规划称为0－1整数规划(Binary Integer Programming ，BIP )，如果模型是线性的，称为整数线性规划（Integer Linear Programming, ILP ）。

本章只讨论整数线性规划。

求解整数规划问题时，如果先不能考虑对变量的整数约束，作为一般线性规划问题来求解，当解为非整数时再用舍入凑整方法寻求最优解，这样得到的解有可能不是整数规划的可行解或是可行解而不是最优解。

【例3.1】某人有一背包可以装10公斤重、0.025m 3的物品。

他准备用来装甲、乙两种物品，每件物品的重量、体积和价值如表3－1所示。

问两种物品各装多少件，所装物品的总价值最大。

表3－1【解】设甲、乙两种物品各装x 1、x 2件，则数学模型为⎪⎩⎪⎨⎧≥≤+≤++=且均取整数,0,255.22108.02.134max 21212121x x x x x x x x Z (3.1)如果不考虑x 1、x 2取整数的约束（称为式（3.1）的松弛问题），线性规划的可行域如图3-1中的阴影部分所示。

图3-1用图解法求得点B 为最优解：X ＝(3.57，7.14)，Z ＝35.7。

由于x 1，x 2必须取整数值，整数规划问题的可行解集只是图中可行域内的那些整数点。

用凑整法求解时需要比较四种组合，但（4，7）、（4，8）（3，8）都不是可行解，（3，7）虽属可行解，代入目标函数得Z =33,并非最优。

实际上问题的最优解是（5，5），Z =35。

即两种物品各装5件，总价值35元。

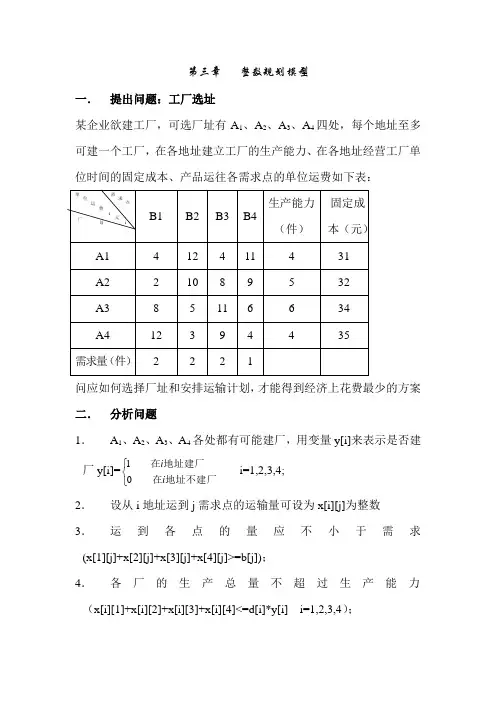
第三章 整数规划模型一． 提出问题：工厂选址某企业欲建工厂，可选厂址有A 1、A 2、A 3、A 4四处，每个地址至多可建一个工厂，在各地址建立工厂的生产能力、在各地址经营工厂单位时间的固定成本、产品运往各需求点的单位运费如下表：问应如何选择厂址和安排运输计划，才能得到经济上花费最少的方案 二． 分析问题 1． A 1、A 2、A 3、A 4各处都有可能建厂，用变量y[i]来表示是否建厂y[i]=⎩⎨⎧地址不建厂在地址建厂在i i 01i=1,2,3,4;2． 设从i 地址运到j 需求点的运输量可设为x[i][j]为整数 3．运到各点的量应不小于需求(x[1][j]+x[2][j]+x[3][j]+x[4][j]>=b[j])； 4．各厂的生产总量不超过生产能力（x[i][1]+x[i][2]+x[i][3]+x[i][4]<=d[i]*y[i] i=1,2,3,4）；5． 运到各需求点的量如何计算b1[j]=x[1][j]+x[2][j]+x[3][j]+x[4][j]j=1,2,3,4; 6． 各厂的生产总量a1[i]= x[i][1]+x[i][2]+x[i][3]+x[i][4]; 7． 目标函数：总费用z=建厂费用+ 运输费用8．运输费用=单位运输费用*运输量（从i 地址运到j 需求点单位运输费用c[i][j]已知，从i 地址运到j 需求点的运输量可设为x[i][j]） 三． 模型建立根据分析建立整数规划模型： 设1(1,2,,4)0i i y i ⎧==⎨⎩ 在处建厂否则，ij x i j 表示从点运到点的货物数量(i,j=1,2,,4)，建立如下整数规划模型：4441114141..(1,2,,4)(1,2,,4)0,0ii ijiji i j iji i j ijj i ij i m in z ay cx s t xd y i xb j x y =====⎧=+⎪⎪⎪≤=⎪⎨⎪⎪≥=⎪⎪≥=⎩∑∑∑∑∑ 或1其中(,1,2,,4)ijc i j i j = 表示从点到点的单位运费，i i a A 为点处建厂经营的单位固定成本(i=1,2,,4)， j b j 表示需求点B 处的需求量(j=1,2,,4)，(1,2,,4)i i d A i = 表示处的生产能力。

整数规划模型整数规划模型是一种数学模型，用于解决优化问题。

在整数规划中，决策变量必须是整数。

这种模型广泛应用于工程、科学、运筹学和管理等领域。

整数规划模型的一般形式如下：\[\text{maximize} \quad c^Tx\]\[\text{subject to} \quad Ax \leq b\]\[x_j \text{整数} , j = 1,2,...,n\]其中，c是一个n维向量，表示目标函数的系数；x是n维向量，表示决策变量；A是m×n维矩阵，表示约束条件的系数矩阵；b是一个m维向量，表示约束条件的上界。

整数规划模型的目标是找到一个满足约束条件的决策变量向量x，使得目标函数值最大或最小。

由于决策变量必须是整数，所以整数规划模型要比普通的线性规划模型更复杂。

整数规划模型可以应用于许多实际问题。

例如，一个公司要决定生产哪种产品以最大化利润，但每种产品有一定的生产限制，需要整数规划模型来确定生产量；一个配送中心要决定如何分配物流资源以最小化成本，但每个分配决策都必须是整数，需要整数规划模型来求解。

求解整数规划模型可以使用多种算法。

例如，分支定界算法通过将问题分解为一个个子问题，并通过剪枝策略来减少搜索空间，最终找到最优解；约简与延迟约束算法通过线性松弛将整数规划转化为一个松弛线性规划问题，并通过迭代加入约束条件来逼近整数解。

整数规划模型的求解过程需要注意一些问题。

首先，由于整数规划是一个NP难问题，没有通用的多项式时间算法可以解决所有情况。

其次，整数规划模型可能有多个最优解，求解算法可能只能找到其中一个最优解。

最后，整数规划模型的求解过程可能需要大量的计算资源和时间。

总之，整数规划模型是一种重要的数学模型，可以用于解决各种实际优化问题。

但由于其复杂性和求解困难，需要合理选择算法和求解策略来获得满意的结果。

第三章数学规划模型第三章数学规划模型数学规划论起始20世纪30年代末，50年代与60年代发展成为⼀个完整的分⽀并受到数学界和社会各界的重视。

七⼋⼗年代是数学规划飞速发展时期，⽆论是从理论上还是算法⽅⾯都得到了进⼀步完善。

时⾄今⽇数学规划仍然是运筹学领域中热点研究问题。

从国内外的数学建模竞赛的试题中看，有近1/4的问题可⽤数学规划进⾏求解。

数学规划模型的⼀般表达式：),,(..),,(min(max)≤βαβαx g t s x ff 为⽬标函数，g 为约束函数，x 为可控变量，α为已知参数，β为随机参数。

本章主要介绍线性规划、整数规划、⾮线性规划的基本概念与基本原理、⽆约束问题的最优化⽅法、约束问题的最优化⽅法、动态规划。

3.1线性规划线性规划模型是运筹学的重要分⽀，是20世纪三四⼗年代初兴起的⼀门学科。

1947年美国数学家丹齐格G.B.Dantzig 及其同事提出的求解线性规划的单纯形法及有关理论具有划时代的意义。

他们的⼯作为线性规划这⼀学科的建⽴奠定了理论基础。

随着1979年前苏联数学家哈奇扬的椭球算法和1984年美籍印度数学家卡玛卡尔H.Karmarkar 算法的相继问世，线性规划的理论更加完备成熟，实⽤领域更加宽⼴。

线性规划研究的实际问题多种多样，如⽣产计划问题、物资运输问题、合理下料问题、库存问题、劳动⼒问题、最优设计问题等。

就模型⽽⾔，线形规划模型类似于⾼等数学中的条件极值问题，只是其⽬标函数和约束条件都限定为线性函数。

线性规划模型的求解⽅法⽬前仍以单纯形法为主要⽅法。

本节介绍的主要内容有：线性规划模型的建⽴以及求解，线性规划的matlab 解法，线性规划问题的建模实例。

3.1.1 线性规划模型的建⽴以及求解⼀、线性规划模型的建⽴例1、某机床⼚⽣产甲、⼄两种机床，每台销售后的利润分别为4000元与3000元。

⽣产甲机床需⽤B A 、机器加⼯，加⼯时间分别为每台2⼩时和1⼩时；⽣产⼄机床需⽤C B A 、、三种机器加⼯，加⼯时间为每台各⼀⼩时。

整数规划模型的构建及求解方法整数规划是一种数学优化问题，其目标是在给定的约束条件下，寻找能够使目标函数最大或最小的整数解。

在实际应用中，整数规划模型常被用于决策问题的求解，如生产计划、物流调度、资源分配等。

本文将介绍整数规划模型的构建方法以及常用的求解方法。

一、整数规划模型的构建方法1.确定决策变量：首先需要确定问题中的决策变量，即可用整数来表示的变量。

这些变量一般代表决策问题中的选择或分配方案。

例如，在生产计划问题中，决策变量可以是不同产品的生产数量。

2.定义目标函数：目标函数是整数规划问题中要最大化或最小化的指标。

根据问题的具体要求，可将目标函数设定为各个决策变量的线性组合或非线性函数。

例如，生产计划问题中，目标函数可以是利润的最大化或成本的最小化。

3.确定约束条件：约束条件用于限制决策变量的取值范围，以满足问题的实际限制。

约束条件可以是等式或不等式。

例如，在物流调度问题中，约束条件可以包括产品的需求量、供应量以及运输容量等。

4.完善模型：为了更准确地描述问题，还需要考虑一些特殊约束条件和问题的具体要求。

例如，某些决策变量可能需要满足某种关系或限制条件，或者需要指定某些变量的取值范围。

二、整数规划模型的求解方法1.穷举法：穷举法是最简单直接的求解方法，即将所有可能的整数解都列举出来，并计算对应的目标函数值，最后选取最优解。

然而，穷举法由于计算复杂度高，只适用于问题规模较小的情况。

2.分支定界法：分支定界法是一种逐步缩小解空间的方法。

通过将整数规划问题分解成若干个子问题，并为每个子问题设定上下界，不断迭代求解，最终找到最优解。

这种方法可以高效地搜索整数解空间，但对于规模较大的问题，计算时间可能会很长。

3.割平面法：割平面法是一种逐步划分解空间的方法。

它通过添加割平面来修正原始线性规划松弛的解，使其成为整数解。

这种方法能够快速收敛到最优解，并且具有较好的计算效率。

4.分枝定界法：分枝定界法是将分支定界法和割平面法相结合的方法。