运筹学——第3章_线性规划问题的计算机求解
- 格式：ppt
- 大小：1.00 MB
- 文档页数：32
下载文档原格式
合集下载
7.2线性规划问题的计算机求解
另一个为： x11 6, x13 3, x23 3, x24 1, x32 5, x34 2 ， 其余都为 0.
19
7.2.3 整数规划 在某些实际问题中，有时还会遇到要求解必须为
整数的情况，例如，所求的解为安排上班的人数、 生产机械的台数等，这就是整数规划问题.
在整数规划中，如果所有的变量都为非负整数， 则称之为纯整数规划问题，如果只有一部分变量 为非负整数，则称之为混合整数规划问题.
35
• 作业P164习题7.2
• 1、 2、 3.
2/16/2014
27
例2
求解下面的混合整数规划问题：
max z 2 x1 x2 3x3
x1 x2 2 x3 4 3 x 4 x 2 2 3 x1 2 x2 3 x3 3 约束条件： x2 1 x1 , x2 , x3 0 x1 , x2为整数
注意：以上有关计算机输出的目标函数系数及约束 条件右边常数项的分析称为灵敏度分析.
2/16/2014
以上的分析都是在其他系数值及约束条件右 边常数项不变，只有一个系数及约束条件右 边常数项变化的基础上得出的，而当有两个 或多个系数变化时，灵敏度分析比较复杂， 请查阅相关资料，这里不详述.
2/16/2014
2/16/2014
第一步
开始
程序
管理运筹学2.0
30
第二步
整数规划
31
第三步
混合整数规划
32
第四步
新建
输入3个变量，3个约束条 件
确定
MAX
输 入 数 据
33
第五步
解决
34
第六步
分析运行结果
19
7.2.3 整数规划 在某些实际问题中，有时还会遇到要求解必须为
整数的情况，例如，所求的解为安排上班的人数、 生产机械的台数等，这就是整数规划问题.
在整数规划中，如果所有的变量都为非负整数， 则称之为纯整数规划问题，如果只有一部分变量 为非负整数，则称之为混合整数规划问题.
35
• 作业P164习题7.2
• 1、 2、 3.
2/16/2014
27
例2
求解下面的混合整数规划问题：
max z 2 x1 x2 3x3
x1 x2 2 x3 4 3 x 4 x 2 2 3 x1 2 x2 3 x3 3 约束条件： x2 1 x1 , x2 , x3 0 x1 , x2为整数
注意：以上有关计算机输出的目标函数系数及约束 条件右边常数项的分析称为灵敏度分析.
2/16/2014
以上的分析都是在其他系数值及约束条件右 边常数项不变，只有一个系数及约束条件右 边常数项变化的基础上得出的，而当有两个 或多个系数变化时，灵敏度分析比较复杂， 请查阅相关资料，这里不详述.
2/16/2014
2/16/2014
第一步
开始
程序
管理运筹学2.0
30
第二步
整数规划
31
第三步
混合整数规划
32
第四步
新建
输入3个变量，3个约束条 件
确定
MAX
输 入 数 据
33
第五步
解决
34
第六步
分析运行结果
管理运筹学作业 韩伯棠第3版高等教育出版社课后答案
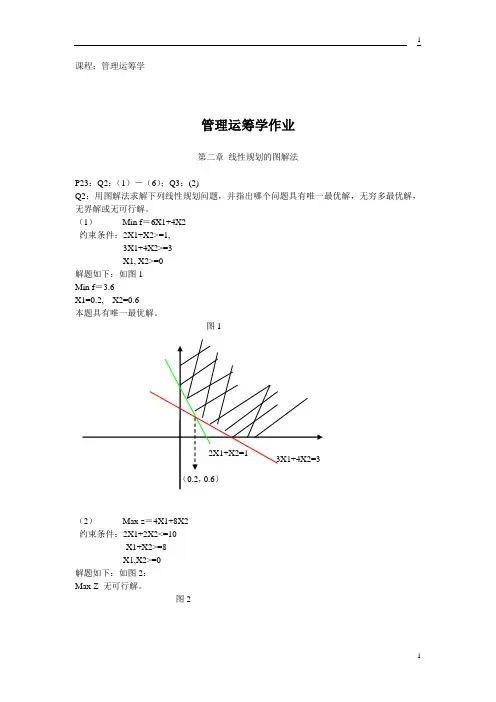
课程：管理运筹学管理运筹学作业第二章线性规划的图解法P23：Q2：（1）－（6）；Q3：(2)Q2：用图解法求解下列线性规划问题，并指出哪个问题具有唯一最优解，无穷多最优解，无界解或无可行解。
（1）Min f＝6X1+4X2约束条件：2X1+X2>=1,3X1+4X2>=3X1, X2>=0解题如下：如图1Min f＝3.6X1=0.2, X2=0.6本题具有唯一最优解。
图1（2）Max z＝4X1+8X2约束条件：2X1+2X2<=10-X1+X2>=8X1,X2>=0解题如下：如图2：Max Z 无可行解。
图2（3） Max z ＝X1+X2 约束条件 8X1+6X2>=24 4X1+6X2>=-12 2X2>=4 X1,X2>=0 解题如下：如图3： Max Z=有无界解。
图3（4） Max Z ＝3X1-2X2 约束条件：X1+X2<=1 2X1+2X2>=4 X1,X2>=0 解题如下：如图4： Max Z 无可行解。
图4(5)Max Z＝3X1+9X2 约束条件：X1+3X2<=22-X1+X2<=4X2<=62X1-5X2<=0X1,X2>=0解题如下：如图5：Max Z =66；X1=4 X2=6本题有唯一最优解。
图5(6)Max Z=3X1+4X2 约束条件：-X1+2X2<=8X1+2X2<=122X1+X2<=162X1-5X2<=0X1,X2>=0解题如下：如图6Max Z =30.669X1=6.667 X2=2.667本题有唯一最优解。
图6Q3：将线性规划问题转化为标准形式（2）min f＝4X1+6X2约束条件：3X1-2X2>=6X1+2X2>=107X1-6X2=4X1,X2>=0解题如下：1）目标函数求最小值化为求最大值：目标函数等式左边min改为max，等式右边各项均改变正负号。
运筹学 第3章 线性规划问题的计算机求解
• 百分之一百法则
• 50
74
• 100
78
• 允许增加量是指该系数在上限范围内的 最大增加量。
• 允许减少量是指该系数在下限范围内的 最大减少量。
c • x1系数的上限为100，故 1的允许增加量为
•
上限-现在值=100-50=50
x c • 而 2的下限为50，故 2的允许减少量为
•
现在值-下限=100-50=50
管理运筹学
朱晓辉 管理科学与工程
第三章 线性规划问题的计算机求解
• 3.1 “管理运筹学软件的操作方法
3.2 “管理运筹学”软件的输出信息分析
• 相差值提供的数值表示相应的决策变量的目 标系数需要改进的数量，使得该决策变量有可能 取正数值，当决策变量已取正数值时相差值为零。
• 在目标函数系数范围一栏中，所谓的上限与 下限是指目标函数的决策变量的系数在此范围内 变化时，其线性规划的最优解不变。
c • 其中bj的允许增加（减少）百分比的定义同 i
的允许增加（减少）百分比一样，为bj的增加量 （减少量）除以bj的允许增加量（减少量）所得
到的值。
• 在使用百分之一百法则进行灵敏度分析时，要 注意以下三点：
• （1）当允许增加量（减少量）为无穷大时，则 对于任一个增加量（减少量），其允许增加（减 少）百分比都看成零。
• 在常数项数范围一栏中，所谓上限与下限是指 当约束条件中的常数项在此范围内变化时，与其 对应的约束条件的对偶价格不变。
• 以上讨论计算机输出的关于目标函数系 数及约束条件中常数项的灵敏度分析都是 基于这样一个重要假设：当一个系数发生 变化时，其他系数保持不变。
• 两个或更多的系数发生变化时，怎么来 进行灵敏度分析？
• 50
74
• 100
78
• 允许增加量是指该系数在上限范围内的 最大增加量。
• 允许减少量是指该系数在下限范围内的 最大减少量。
c • x1系数的上限为100，故 1的允许增加量为
•
上限-现在值=100-50=50
x c • 而 2的下限为50，故 2的允许减少量为
•
现在值-下限=100-50=50
管理运筹学
朱晓辉 管理科学与工程
第三章 线性规划问题的计算机求解
• 3.1 “管理运筹学软件的操作方法
3.2 “管理运筹学”软件的输出信息分析
• 相差值提供的数值表示相应的决策变量的目 标系数需要改进的数量，使得该决策变量有可能 取正数值，当决策变量已取正数值时相差值为零。
• 在目标函数系数范围一栏中，所谓的上限与 下限是指目标函数的决策变量的系数在此范围内 变化时，其线性规划的最优解不变。
c • 其中bj的允许增加（减少）百分比的定义同 i
的允许增加（减少）百分比一样，为bj的增加量 （减少量）除以bj的允许增加量（减少量）所得
到的值。
• 在使用百分之一百法则进行灵敏度分析时，要 注意以下三点：
• （1）当允许增加量（减少量）为无穷大时，则 对于任一个增加量（减少量），其允许增加（减 少）百分比都看成零。
• 在常数项数范围一栏中，所谓上限与下限是指 当约束条件中的常数项在此范围内变化时，与其 对应的约束条件的对偶价格不变。
• 以上讨论计算机输出的关于目标函数系 数及约束条件中常数项的灵敏度分析都是 基于这样一个重要假设：当一个系数发生 变化时，其他系数保持不变。
• 两个或更多的系数发生变化时，怎么来 进行灵敏度分析？
第3章%20线性规划问题的计算机求解pdf
第三章思考题、主要概念及内容“管理运筹学”软件的操作方法“管理运筹学”软件的输出信息分析复习题1.见第二章第7题，设x1为产品Ⅰ每天的产量，x2为产品Ⅱ每天的产量，可以建立下面的线性规划模型：max z=500x1+400x2；约束条件：2x1≤300，3x2≤540，2x1+2x2≤440，1.2x1+1.5x2≤300，x1，x2≥0．使用“管理运筹学”软件，得到的计算机解如图1所示图1根据图3-5回答下面的问题：(1) 最优解即最优产品组合是什么?此时最大目标函数值即最大利润为多少?(2) 哪些车间的加工工时数已使用完?哪些车间的加工工时数还没用完?其松弛变量即没用完的加工工时数为多少?(3) 四个车间的加工工时的对偶价格各为多少?请对此对偶价格的含义予以说明．(4) 如果请你在这四个车间中选择一个车间进行加班生产，你会选择哪个车间?为什么?(5) 目标函数中x1的系数c1，即每单位产品Ⅰ的利润值，在什么范围内变化时，最优产品的组合不变?(6) 目标函数中x2的系数c2，即每单位产品Ⅱ的利润值，从400元提高为490元时，最优产品组合变化了没有?为什么?(7) 请解释约束条件中的常数项的上限与下限．(8) 第1车间的加工工时数从300增加到400时，总利润能增加多少?这时最优产品的组合变化了没有?(9) 第3车间的加工工时数从440增加到480时，从图3-5中我们能否求得总利润增加的数量?为什么?(10) 当每单位产品Ⅰ的利润从500元降至475元，而每单位产品Ⅱ的利润从400元升至450元时，其最优产品组合(即最优解)是否发生变化?请用百分之一百法则进行判断．(11) 当第1车间的加工工时数从300增加到350，而第3车间的加工工时数从440降到380时，用百分之一百法则能否判断原来的对偶价格是否发生变化?如不发生变化，请求出其最大利润．2. 见第二章第8题(2)，仍设xA为购买基金A的数量，xB为购买基金B的数量，建立的线性规划模型如下：max z=5xA+4xB；约束条件：50xA+100xB≤1 200 000，100xB≥300 000，xA，xB≥0．使用“管理运筹学”软件，求得计算机解如图2所示．图2根据图2，回答下列问题：(1) 在这个最优解中，购买基金A和基金B的数量各为多少?这时获得的最大利润是多少?这时总的投资风险指数为多少?(2) 图3-7中的松弛/剩余变量的含义是什么?(3) 请对图3-7中的两个对偶价格的含义给予解释．(4) 请对图3-7中的目标函数范围中的上、下限的含义给予具体说明，并阐述如何使用这些信息．(5) 请对图3-7中的常数项范围的上、下限的含义给予具体说明，并阐述如何使用这些信息．(6) 当投资总金额从1 200 000元下降到600 000元，而在基金B上至少投资的金额从300 000元增加到600 000元时，其对偶价格是否发生变化?为什么?3. 考虑下面的线性规划问题：min z=16x1+16x2+17x3；约束条件：x1+x3≤30， -x2+6x3≥15，05x13x1+4x2-x3≥20，x1，x2，x3≥0．其计算机求解结果如图3所示．图3根据图3，回答下列问题：(1) 第二个约束方程的对偶价格是一个负数(为-3622) ，它的含义是什么? ，它的含义是什么?(2) x2的相差值为0703(3) 当目标函数中x1的系数从16降为15，而x2的系数从16升为18时，最优解是否发生变化?(4) 当第一个约束条件的常数项从30减少到15，而第二个约束条件的常数项从15增加到80时，你能断定其对偶价格是否发生变化吗?为什么?。
线性规划问题的两种求解方式
线性规划问题的两种求解⽅式线性规划问题的两种求解⽅式线性规划是运筹学中研究较早、发展较快、应⽤⼴泛、⽅法较成熟的⼀个重要分⽀，它是辅助⼈们进⾏科学管理的⼀种数学⽅法。
线性规划所研究的是：在⼀定条件下，合理安排⼈⼒物⼒等资源，使经济效果达到最好。
⼀般地，求线性⽬标函数在线性约束条件下的最⼤值或最⼩值的问题，统称为线性规划问题。
解决线性规划问题常⽤的⽅法是图解法和单纯性法，⽽图解法简单⽅便，但只适⽤于⼆维的线性规划问题，单纯性法的优点是可以适⽤于所有的线性规划问题，缺点是单纯形法中涉及⼤量不同的算法，为了针对不同的线性规划问题，计算量⼤，复杂繁琐。
在这个计算机⾼速发展的阶段，利⽤Excel建⽴电⼦表格模型，并利⽤它提供的“规划求解”⼯具，能轻松快捷地求解线性模型的解。
⽆论利⽤哪种⽅法进⾏求解线性规划问题，⾸先都需要对线性规划问题建⽴数学模型，确定⽬标函数和相应的约束条件，进⽽进⾏求解。
从实际问题中建⽴数学模型⼀般有以下三个步骤；1、根据所求⽬标的影响因素找到决策变量；2、由决策变量和所求⽬标的函数关系确定⽬标函数；3、由决策变量所受的限制条件确定决策变量所要满⾜的约束条件。
以下是分别利⽤单纯形法和Excel表格中的“规划求解”两种⽅法对例题进⾏求解的过程。
例题：某⼯⼚在计划期内要安排⽣产I、II两种产品，已知⽣产单位产品所需的设备台时分别为1台时、2台时，所需原材料A分别为4单位、0单位，所需原材料B分别为0单位、4单位，⼯⼚中设备运转最多台时为8台时，原材料A、B的总量分别为16单位、12单位。
每⽣产出I、II产品所获得的利润为2和3，问I、II两种产品的⽣产数量的哪种组合能使总利润最⼤？这是⼀个典型的产品组合问题，现将问题中的有关数据列表1-1如下：表1-1I II 限量设备 1 2 8台时原材料A 4 0 16单位原材料B 0 4 12单位所获利润 2 3⾸先对例题建⽴数学模型。
问题的决策变量有两个：产品I的⽣产数量和产品II的⽣产数量；⽬标是总利润最⼤；需满⾜的条件是：(1)两种产品使⽤设备的台时<= 台时限量值(2) ⽣产两种产品使⽤原材料A、B的数量<= 限量值(3)产品I、II的⽣产数量均>=0。
《管理运筹学》第二版习题答案(韩伯棠教授
x2＋x3＋x4＋x5＋1 ≥ 3
x3＋x4＋x5＋x6＋2 ≥ 3
x4＋x5＋x6＋x7＋1 ≥ 6
x5＋x6＋x7＋x8＋2 ≥ 12
x6＋x7＋x8＋x9＋2 ≥ 12
x7＋x8＋x9＋x10＋1 ≥ 7
x8＋x9＋x10＋x11＋1 ≥ 7
x1，x2，x3，x4，x5，x6，x7，x8，x9，x10，x11≥ 0
第
3章线性规划问题的计算机求解
1、解：
a x1 =
150 x2 =
70 目标函数最优值
103000
b 1，3使用完 2，4没用完 0，330，0，15
c 50，0，200，0
含义： 1车间每增加
1工时，总利润增加
50元
3车间每增加
1工时，总利润增加
约束条件
2：年回报额增加
1个单位，风险系数升高
2.167
c约束条件
1的松弛变量是
0，约束条件
2的剩余变量是
0
约束条件
3为大于等于，故其剩余变量为
700000
d当
c2不变时，
c1在
3.75到正无穷的范围内变化，最优解不变
当
c1不变时，
i=1 i=1
S．T
不变
8 、解：
a 模型：
min f =
8xa +
3xb
50xa +100xb ≤
1200000
5xa +
4xb ≥
60000
100xb ≥
300000
xa , xb ≥
管理运筹学第四版 第三章习题6答案(P35)
《数据、模型和决策》作业一学号：2461604112 姓名：王康兵班级：2016秋MBA2周末班一、第三章线性规划问题的计算机求解习题6 （P35）答：根据图3-10回答问题如下：（1）最优解即最优产品组合是产品Ⅰ每天的产量是150个，产品Ⅱ每天的产量是70个。
此时最大的目标函数即最大利润为103000元。
（2）车间1和车间3的加工工时数已使用完，车间2和车间4的加工工时数还没用完。
车间2的松弛变量即没用完的加工工时数为330工时，车间4的松弛变量即没用完的加工工时数为15工时。
（3）车间1的加工工时的对偶价格为50元，即增加一个工时就可能使总利润增加50元；车间2的加工工时的对偶价格为0元，即增加一个工时不会使总利润有所增加；车间3的加工工时的对偶价格为200元，即增加一个工时就可能使总利润增加200元；车间4的加工工时的对偶价格为0元，即增加一个工时不会使总利润有所增加。
（4）如果要在这四个车间选择一个车间进行加班生产，我会选择车间3。
因为在车间3的加工工时的对偶价格为200元，即每增加一个工时就可能使总利润增加200元，能为公司创造价值。
（5）目标函数中x1的系数c1，即每单位产品Ⅰ的利润值，当c1在400与+∞之间变化时，最优产品组合不变。
（6）目标函数中x2的系数c2，即每单位产品Ⅱ的利润值，当c2从400元提高到490元时，最优产品组合没有变化。
因为当c2=490元时，0《490《500，仍在c2的系数变化范围内，所以其最优产品组合没有变化。
（7）约束条件中的常数项的现在值由图3-10可知，b1=300，b2=540，b3=440，b4=300。
所谓常数项的上限和下限是指当约束条件中的常数项在此范围内变化时，与其对应的约束条件的对偶价格不变。
具体地说，当车间1的加工工时数在200到440的范围内时，其对偶价格都为50元；当车间2的加工工时数在210到+∞范围内时，其对偶价格为零；当车间3的加工工时数在300到460范围内时，其对偶价格都为200元；当车间4的加工工时数在285到+∞范围内时，其对偶价格为零。
《管理运筹学》第三版(韩伯棠 )课后习题答案 高等教育出版社
x1＝8，x2＝0，x3＝1，x4＝1，x5＝0，x6＝4，x7＝0，x8＝6，x9＝0， x10＝0，x11＝0 最优值为 320。
a、 在满足对职工需求的条件下，在 10 时安排 8 个临时工，12 时新安排 1 个临时工，13 时新安排 1 个临时工，15 时新安排 4 个临时工，17 时新 安排 6 个临时工可使临时工的总成本最小。
50xa + 100xb ≤ 1200000 5xa + 4xb ≥ 60000 100xb ≥ 300000 xa , xb ≥ 0 基金 a,b 分别为 4000，10000。 回报率：60000
b 模型变为： max z = 5xa + 4xb
50xa + 100xb ≤ 1200000 100xb ≥ 300000 xa , xb ≥ 0
xi ≥ 0, yi ≥ 0 i=1,2,…,11
稍微变形后，用管理运筹学软件求解可得：总成本最小为 264 元。 安排如下：y1=8（ 即在此时间段安排 8 个 3 小时的班），y3=1，y5=1，y7=4，x8=6 这样能比第一问节省：320-264=56 元。
x2＋x3＋x4＋x5＋1 ≥ 3 x3＋x4＋x5＋x6＋2 ≥ 3 x4＋x5＋x6＋x7＋1 ≥ 6 x5＋x6＋x7＋x8＋2 ≥ 12 x6＋x7＋x8＋x9＋2 ≥ 12 x7＋x8＋x9＋x10＋1 ≥ 7 x8＋x9＋x10＋x11＋1 ≥ 7 x1，x2，x3，x4，x5，x6，x7，x8，x9，x10，x11≥ 0 用管理运筹学软件我们可以求得此问题的解为：
b、 这时付给临时工的工资总额为 80 元，一共需要安排 20 个临时工的班 次。
约束 -------
1 2 3 4 5 6 7 8 9 10 11
a、 在满足对职工需求的条件下，在 10 时安排 8 个临时工，12 时新安排 1 个临时工，13 时新安排 1 个临时工，15 时新安排 4 个临时工，17 时新 安排 6 个临时工可使临时工的总成本最小。
50xa + 100xb ≤ 1200000 5xa + 4xb ≥ 60000 100xb ≥ 300000 xa , xb ≥ 0 基金 a,b 分别为 4000，10000。 回报率：60000
b 模型变为： max z = 5xa + 4xb
50xa + 100xb ≤ 1200000 100xb ≥ 300000 xa , xb ≥ 0
xi ≥ 0, yi ≥ 0 i=1,2,…,11
稍微变形后，用管理运筹学软件求解可得：总成本最小为 264 元。 安排如下：y1=8（ 即在此时间段安排 8 个 3 小时的班），y3=1，y5=1，y7=4，x8=6 这样能比第一问节省：320-264=56 元。
x2＋x3＋x4＋x5＋1 ≥ 3 x3＋x4＋x5＋x6＋2 ≥ 3 x4＋x5＋x6＋x7＋1 ≥ 6 x5＋x6＋x7＋x8＋2 ≥ 12 x6＋x7＋x8＋x9＋2 ≥ 12 x7＋x8＋x9＋x10＋1 ≥ 7 x8＋x9＋x10＋x11＋1 ≥ 7 x1，x2，x3，x4，x5，x6，x7，x8，x9，x10，x11≥ 0 用管理运筹学软件我们可以求得此问题的解为：
b、 这时付给临时工的工资总额为 80 元，一共需要安排 20 个临时工的班 次。
约束 -------
1 2 3 4 5 6 7 8 9 10 11
管理运筹学知识
5筹学在国内或国外的推广前景是非常广阔的运筹学在国内或国外的推广前景是非常广阔的工商企业对运筹学应用和需求是很大的工商企业对运筹学应用和需求是很大的在工商企业推广运筹学方面有大量的工作要做在工商企业推广运筹学方面有大量的工作要做844如何学习运筹学如何学习运筹学mba学员学习运筹学要把重点放在结合实际的应用上不要被一些概念理论的困难吓倒要用好计算机这个强有力的工具
0 c1 100 • 假设产品甲的利润 50 元不变，即 c1 = 50 ，代到式（*）并整理得
50 c2 +
• 假若产品甲、乙的利润均改变，则可直接用式（*）来判断。
• 假设产品甲、乙的利润分别为60元、55元，则
- 2 - (60 / 55) - 1
那麽，最优解为 z = x1 + x2 和 z = 2 x1 + x2 的交点 x1 = 100，x2 = 200 。
• 工商企业对运筹学应用和需求是很大的 • 在工商企业推广运筹学方面有大量的工作要做
8
§4如何学习运筹学
• MBA学员学习运筹学要把重点放在结合实际的应用上，不要 被一些概念、理论的困难吓倒，要用好计算机这个强有力的工 具。
• MBA学员学习运筹学要充分发挥自己实践经验丰富和理论联系实际 能力强的优势。
*** 设备维修、更新，项目选择、评价，工程优化设计与管理等
5
运筹学方法使用情况(美1983)
70 60 50 40 30 20 10
0
从不使用 有时使用 经常使用
6
统计 计算机模拟
网络计划 线性规划
排队论 非线性规划
动态规划 对策论
运筹学方法在中国使用情况(随机抽样)
90 80 70 60 50 40 30 20 10
0 c1 100 • 假设产品甲的利润 50 元不变，即 c1 = 50 ，代到式（*）并整理得
50 c2 +
• 假若产品甲、乙的利润均改变，则可直接用式（*）来判断。
• 假设产品甲、乙的利润分别为60元、55元，则
- 2 - (60 / 55) - 1
那麽，最优解为 z = x1 + x2 和 z = 2 x1 + x2 的交点 x1 = 100，x2 = 200 。
• 工商企业对运筹学应用和需求是很大的 • 在工商企业推广运筹学方面有大量的工作要做
8
§4如何学习运筹学
• MBA学员学习运筹学要把重点放在结合实际的应用上，不要 被一些概念、理论的困难吓倒，要用好计算机这个强有力的工 具。
• MBA学员学习运筹学要充分发挥自己实践经验丰富和理论联系实际 能力强的优势。
*** 设备维修、更新，项目选择、评价，工程优化设计与管理等
5
运筹学方法使用情况(美1983)
70 60 50 40 30 20 10
0
从不使用 有时使用 经常使用
6
统计 计算机模拟
网络计划 线性规划
排队论 非线性规划
动态规划 对策论
运筹学方法在中国使用情况(随机抽样)
90 80 70 60 50 40 30 20 10
运筹学——第3章_线性规划问题的计算机求解
变量 下限 当前值 上限
x1
0
50
100
x2
50
100 无上限
从上面可知目标函数中X1的系数的上限为100，故C1
允许增加量为： 上限-现在值=100-50=50；
而X2的下限为50，故C2的允许减少量为： 现在值-下限=100-50=50。
定义Ci 的允许增加(减少)百分比为：Ci 的增加量 (减少量)除以Ci 的允许增加量(允许减少量)的值。
在上题中C1 的允许增加百分比与C2 的允许减 少百分比之和为92％不超过100％，所以当每件产 品Ⅰ利润从50元增加到74元，每件产品Ⅱ利润从 100元减少到78元时，此线性规划最优解仍然为Ⅰ 产品生产50件， Ⅱ产品生产250件(即x1= 50， x2=250)，此时有最大利润为:
74× 50+78× 250=3700＋19500=23200(元)。
为50元，即增加了一个台时数就可使总利润增加50元；
原料A还有50千克没有使用，原料A的对偶价格当然为零，
即增加1千克A原料不会使总利润有所增加；原料B全部使
用完，原料B的对偶价格为50元，即增加一千克原料B就
可使总利润增加50元。
在目标函数系数范围一栏中，所谓的当前值是指在目标函数 中决策变量的当前系数值。如x1的系数值为50，x2的系数值为100。 所谓的上限与下限值是指目标函数的决策变量的系数（其它决策 变量的系数固定在当前值）在此范围内变化时，其线性规划的最 优解不变。例如当c1= 80时，因为0≤80≤100，在x1的系数变化范 围内，所以其最优解不变（此时要固定c2=100)，也即当x1=50， x2=250时，有最大利润。当然由于产品Ⅰ的单位利润由50变为80 了，其最大利润也增加了(最优值变了)，
第三章 线性规划问题的求解07.9
输入部分： 2. 输入部分：
（1）线性规划、整数规划的目标函数和约束的输 线性规划、 入必须按由小到大的序号顺序输入， 入必须按由小到大的序号顺序输入，同时约 束变量必须放在运算符的左侧。 束变量必须放在运算符的左侧。如（x1+x2x3=0，不能输为x2-x3+x1=0；x1-x2+x3=0， ， ； ， 不能输为x1+x3=x2） （2）输入的约束中不包括" ≥ "或"≤"，而是用 输入的约束中不包括 或 ，而是用">“ 代替， 或“<”代替，这不会影响求解。如 对于约束 代替 这不会影响求解。 X1 ≥ 2,则输入 X1>2,而不是 1 ≥ 2。 而不是X 则输入 而不是 。 （3）当所有的约束条件输入完了之后，在下一个 ）当所有的约束条件输入完了之后， 约束条件中输入“ 约围：
当前值——指bj的现在值 指 当前值 上限值和下限值——指bj在此范围内变化时，则与 上限值和下限值 指 在此范围内变化时， 其对应的约束条件的对偶价格不变。 其对应的约束条件的对偶价格不变。
三、百分之一百法则及其应用
1、允许增加量：允许△ = 上限 – 现在值 、允许增加量： 2、允许减少量：允许△ = 现在值 – 下限 、允许减少量： 3、允许增加（减少）百分比： 、允许增加（减少）百分比：
输出部分： 4. 输出部分：
（1）线性规划和整数规划子程序没有把运算结 果存储到文本文件的功能， 果存储到文本文件的功能，其它子程序都 可以实现。 可以实现。 （2）若不通过运行Main.exe进入各子问题，而 若不通过运行Main.exe进入各子问题， Main.exe进入各子问题 是直接运行各子程序，系统会默认当前目 是直接运行各子程序， 录为存储目录。 录为存储目录。
运筹学本科版答案
运筹学本科版答案【篇一：运筹学课后习题答案】xt>1．用xj（j=1.2…5）分别代表5中饲料的采购数，线性规划模型： minz?0.2x1?0.7x2?0.4x3?0.3x4?0.8x5st.3x1?2x2?x3?6x4+18x5?700x1?0.5x2?0.2x3+2x4?x5?300.5x1?x2?0.2x3+2x4?0.8x5?1002.解：设x1x2x3x4x5x6x表示在第i个时期初开始工作的护士人数，z表示所需的总人数，则minz?x1?x2?x3?x4?x5?x6st.x1?x6?60x?x2?701x2?x3?60x3?x4?50x4?x5?20x5?x6?30xj(j?1,2,3,4,5,6)?03．解：设用i=1，2，3分别表示商品a，b，c，j=1，2，3分别代表前，中，后舱，xij表示装于j舱的i种商品的数量，z表示总运费收入则：maxz?1000(x11?x12?x13)?700(x21?x22?x23)?600(x31?x32?x3 3)st.x11?x12?x13?600x21?x22?x23?1000x31?x32?x33?80010x11?5x21?7x31?40010x12?5x22?7x32?540010x13?5x23?7x33?15008x11?6x21?5x31?20008x12?6x22?5x32?30008x13?6x23?5x33?15008x?6x21?5x3111?0.158x12?6x22?5x328x?6x23?5x3313?0.158x12?6x22?5x328x?6x21?5x3111?0.18x13?6x23?5x33xij?0(i?1,2.3.j?1,2,3)xi(i?1,2.3.4.5.6)?05. （1）z = 4（2）maxz?x1?x2st.6x1?10x2?120x1?x2?705?x1?10解：如图：由图可得：x?(10,6)；z*t*3?x2?8?16*即该问题具有唯一最优解x?(10,6)t（3）无可行解(4)maxz?5x1?6x2st.2x1?x2?2?2x1?3x2?2 x1,x2?0如图：由图知，该问题具有无界解。
兰州大学运筹学——线性规划问题的计算机求解 课后习题题解
第四章 线性规划问题的计算机求解4.1 有以下线性规划数学问题： max Z=2x l +3 x 2 S.T. x l + x 2≤10 2x l + x 2≥4x l +3 x 2≤24 2x l + x 2≤16x l 、 x 2≥01、 用EXCEL 线性规划求解模板求解该数学模型。
2、 本问题的最优解是什么？此时最大目标函数值是多少？3、 四个约束条件中，哪些约束条件起到了作用？各约束条件的剩余量或松弛量及对偶价格是多少？4、 目标函数中各变量系数在什么范围内变化时，最优解不变？5、 确定各给定条件中的常数项的上限和下限。
解： 1、2、最优解：（3，7），最优值：273、 可变单元格约束对于求最大化的问题，对偶价格=阴影价格松弛量/剩余量对偶价格x l+ x2≤10 0 1.52x l+ x2≥4 9 0x l+3 x2≤24 0 0.52x l+ x2≤16 13 0 因第一、第三个约束条件的松弛量/剩余量为0 ，所以这两个约束条件起到了约束作用。
4、目标函数中各变量系数1≤C1≤32≤C1≤65、常数项8≤b1≤9.2无限≤b2≤1318≤b3≤3013≤b4≤无限4.2 有以下线性规划数学问题：min f=8x l+3 x2S.T. 500x l+100 x2≤12000005x l+4 x2≥60000100x l≥300000x l 、x2≥01、用EXCEL线性规划求解模板求解该数学模型。
2、本问题的最优解是什么？此时最大目标函数值是多少？3、各约束条件的剩余量或松弛量及对偶价格是多少？分别解释其含义。
4、目标函数中各变量系数在什么范围内变化时，最优解不变？5、确定各给定条件中的常数项的上限和下限。
解：本问题无解。
4.3 有以下线性规划数学问题：max Z=x l+2 x2+3 x3- x4S.T. x l+2 x2+3 x3≤152x l+ x2+5 x3≤20x l+2 x2+ x3+ x4≤10x l 、x2、x3、x4≥01、用EXCEL线性规划求解模板求解该数学模型。
运筹学实验报告(一)线性规划问题的计算机求解
运筹学实验报告实验课程:运筹学实验日期: 2020年4月4日任课教师:杨小康班级：数学1802 姓名：王超学号：2501180224一、实验名称: 简单线性规划模型的求解与Lingo软件的初步使用二、实验目的：了解Lingo软件的基本功能和简单线性规划模型的求解的输入和输出结果。
熟悉Lingo 软件在运筹学模型求解中的作用，增强自身的动手能力，提高实际应用能力三、实验要求:1、熟悉Lingo软件的用户环境，了解Lingo软件的一般命令2、给出Lingo中的输入，能理解Solution Report中输出的四个部分的结果。
4、能给出最优解和最优值；5、能给出实际问题的数学模型，并利用lingo求出最优解四、报告正文（文挡，数据，模型，程序，图形）:1.在Lingo中求解下面的线性规划数学模型;(1)12132412512345 max2543..28,,,,0z x xx xx xs tx x xx x x x x=++=⎧⎪+=⎪⎨++=⎪⎪≥⎩(2)12121212max2343..28,0z x xxxs tx xx x=+≤⎧⎪≤⎪⎨+≤⎪⎪≥⎩(3)12121212max243..28,0z x xxxs tx xx x=+≤⎧⎪≤⎪⎨+≤⎪⎪≥⎩(4)12121212max324 ..3,0z x xx xs t x xx x=+-≤⎧⎪-+≤⎨⎪≥⎩(5)1212121212max102401.530.50,0z x xx xx xs tx xx x=++≤⎧⎪+≤⎪⎨+≥⎪⎪≥⎩2、某工厂利用三种原料生产五种产品，其有关数据如下表。
原料可利用数（千克）每万件产品所用材料数（千克）A B C D E甲10 1 2 1 0 1 乙24 1 0 1 3 2 丙21 1 2 2 2 2 每万件产品的利润（万元）8 20 10 20 21 (l)建立该问题的运筹学模型。
（2）利用lingo 软件求出最优解，得出最优生产计划解：（1）设xi（i=1,2...,5）为所用材料生产的件数则数学模型,,,,21 2222242 3102;212010208max543215 43215431532154321≥≤++++≤+++≤+++++++ =xxxxxx xxxxt xxxx xxxxsxxxxxz （2）结果为220.3：现有15米长的钢管若干，生产某产品需4米、5米、7米长的钢管各为100、150、120根，问如何截取才能使原材料最省？（建立线性规划模型并利用lingo软件求解）解：方案4米5米7米剩余量截取长度1 3 0 0 32 2 1 0 23 2 0 1 04 1 2 0 15 0 3 0 06 0 1 1 37 0 0 2 14人力资源分配问题某昼夜服务的公交线路每天各时间段内所需司机和乘务人员人数如表1所示。
《管理运筹学》第4版课后习题解析(韩伯棠)
3x1 x2 s1 6 x1 2 x2 s2 10 7 x1 6 x2 4 x1 , x2 , s1 , s2 ≥ 0
（3）标准形式
2 x2 2 x2 0 s1 0 s2 min f x1
5 x2 s1 70 3x1 5 x2 5 x2 5 x2 50 2 x1 2 x2 2 x2 s2 30 3x1 , x2 , x2 , s1 , s2 ≥ 0 x1
4．解： 标准形式
max z 10 x1 5 x2 0 s1 0 s2
3x1 4 x2 s1 9 5 x1 2 x2 s2 8 x1 , x2 , s1 , s2 ≥ 0
松弛变量（0，0） 最优解为 x1 =1，x2=3/2。 5．解： 标准形式
min f 11x1 8 x2 0 s1 0 s2 0 s3
8
《管理运筹学》第四版课后习题解析
韩伯棠
第 3 章 线性规划问题的计算机求解
1．解： ⑴甲、乙两种柜的日产量是分别是 4 和 8，这时最大利润是 2720 ⑵每多生产一件乙柜，可以使总利润提高 13.333 元 ⑶常数项的上下限是指常数项在指定的范围内变化时， 与其对应的约束条件的对偶价格不变。 比如油漆时间变为 100，因为 100 在 40 和 160 之间，所以其对偶价格不变仍为 13.333 ⑷不变，因为还在 120 和 480 之间。 2．解： ⑴不是，因为上面得到的最优解不为整数解，而本题需要的是整数解 ⑵最优解为 (4，8) 3 ．解： ⑴农用车有 12 辆剩余 ⑵大于 300 ⑶每增加一辆大卡车，总运费降低 192 元 4．解： 计算机得出的解不为整数解，平移取点得整数最优解为(10，8) 5．解： 圆桌和衣柜的生产件数分别是 350 和 100 件，这时最大利润是 3100 元 相差值为 0 代表，不需要对相应的目标系数进行改进就可以生产该产品。 最优解不变，因为 C1 允许增加量 20-6=14；C2 允许减少量为 10-3=7，所有允许增加百分比 和允许减少百分比之和（7.5-6）/14+（10-9）/7〈100%，所以最优解不变。 6．解： （1） x1 150 ， x2 70 ；目标函数最优值 103 000。 （2）1、3 车间的加工工时数已使用完；2、4 车间的加工工时数没用完；没用完的加工工时 数为 2 车间 330 小时，4 车间 15 小时。 （3）50，0，200，0。 含义：1 车间每增加 1 工时，总利润增加 50 元；3 车间每增加 1 工时，总利润增加 200 元； 2 车间与 4 车间每增加一个工时，总利润不增加。 （4）3 车间，因为增加的利润最大。 （5）在 400 到正无穷的范围内变化，最优产品的组合不变。 （6）不变，因为在 0,500 的范围内。 （7）所谓的上限和下限值指当约束条件的右边值在给定范围内变化时，约束条件 1 的右边 值在 200,440 变化，对偶价格仍为 50（同理解释其他约束条件） 。 （8）总利润增加了 100×50=5 000，最优产品组合不变。 （9）不能，因为对偶价格发生变化。
管理运筹学复习提纲
管理运筹学》复习提纲第一章绪论（P1-P9）1. 决策过程（解决问题的过程）（1）认清问题。
（2）找出一些可供选择的方案。
（3）确定目标或评估方案的标准。
（4）评估各个方案：解的检验、灵敏性分析等。
（5）选出一个最优的方案：决策。
（6）执行此方案：回到实践中。
（7）进行后评估：考察问题是否得到圆满解决。
其中：（1）（2）（3）形成问题。
（4）（5）分析问题：定性分析与定量分析，构成决策2. 运筹学的分支：线性规划、整数线性规划、动态规划、图与网络模型、存储论、排队论、排序与统筹方法、决策分析、对策论、预测、目标规划，此外，还有多目标规划、随机规划、模糊规划等。
3. 运筹学在工商管理中的应用1）生产计划：生产作业的计划、日程表的编排、合理下料、配料问题、物料管理等，追求利润最大化和成本最小化。
2）库存管理：多种物资库存量的管理，某些设备的库存方式、库存量等的确定。
3）运输问题：确定最小成本的运输线路、物资的调拨、运输工具的调度以及建厂地址的选择等。
4）人事管理：对人员的需求和使用的预测，确定人员编制、人员合理分配，建立人才评价体系等。
5）市场营销：广告预算、媒介选择、定价、产品开发与销售计划制定等。
6）财务和会计：预测、贷款、成本分析、定价、证券管理、现金管理等。
此外，还有设备维修、更新，项目选择、评价，工程优化设计与管理等。
3. 学习管理运筹学必须使用相应的计算机软件，必须注重学以致用的原则。
第二章线性规划的图解法（P10-P26）1. 一些典型的线性规划在管理上的应用合理利用线材问题：如何在保证生产的条件下，下料最少；配料问题：在原料供应量的限制下如何获取最大利润；投资问题：从投资项目中选取方案，使投资回报最大；产品生产计划：合理利用人力、物力、财力等，使获利最大；劳动力安排：用最少的劳动力来满足工作的需要；运输问题：如何制定调运方案，使总运费最小。
2. 线性规划的组成目标函数：max f 或min f ；约束条件：. (subject to) ，满足于；决策变量：用符号来表示可控制的因素。
运筹学实验报告(一)线性规划问题的计算机求解-(1)
运筹学实验报告(一)线性规划问题的计算机求解-(1)-CAL-FENGHAI.-(YICAI)-Company One1运筹学实验报告实验课程:运筹学实验日期: 任课教师:王挺第五种方案0 3 0 0第六种方案0 1 1 3第七种方案0 0 2 1设：第i种方案需要的钢管为Xi根（其中i=1，2...6）,可得:minz=X1+X2+X3+X4+X5+X6+X7解：model:min= X1+X2+X3+X4+X5+X6+X7;3*X1+2*X2+2*X3+X4>=100;X2+2*X4+3*X5+X6>=150;X3+X6+2*X7>=120;endObjective value: 135.0000Infeasibilities: 0.000000Total solver iterations: 2Variable Value Reduced CostX1 0.000000 0.2500000X2 0.000000 0.1666667X3 50.00000 0.000000X4 0.000000 0.8333333E-01X5 50.00000 0.000000X6 0.000000 0.1666667X7 35.00000 0.0000004人力资源分配问题某昼夜服务的公交线路每天各时间段内所需司机和乘务人员人数如表1所示。
班次时间所需人数班次时间所需人数1 6:00~10:00 60 4 18:00~22:00 502 10:00~14:00 70 5 22:00~2:00 203 14:00~18:00 60 6 2:00~6:00 30设司机和乘务人员分别在各时间段开始时上班，并连续工作8小时，问该公交线路应怎样安排司机和乘务人员，既能满足工作需要，又使配备司机和乘务人员的人数最少？5投资计划问题某地区在今后三年内有四种投资机会，第一种是在3年内每年年初投资，年底可获利润20%，并可将本金收回。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第三章 线性规划问题的 计算机求解
如何求解？
本章将介绍如何使用计算机软件包求解线性规划问题。 解决线性规划问题的软件包分两种，一种是大规模 的软件包，它可以用来解决复杂的包含数千个决策变量 和数千个约束条件的大型的线性规划的问题，重点掌握 国内外常用软件：由芝加哥大学LinusE．Schrage开发 的lindo6.1软件，此软件包可解决32000个变量(3200整 型变量）16000个约束方程的运筹学问题。 另一种是用于微机的软件包，它们有很好的界面， 使用方便，由科研机构和小软件公司为解决包含数百个 决策变量的线性规划问题而开发的。本章介绍的是与本 书配套的名为“管理运筹学”2.0软件包就是属于这种 软件，此软件包可解决100个变量50个约束方程的管理 运筹学问题。 本章的重点放在如何读懂“管理运筹学”软件包的 计算机输出结果——关于线性规划问题的求解和灵敏度 分析的信息，解决工商管理中的实际问题。
喂！相差值是什么意思？
我知道：如果决策变量取正数值，则相差值一般为零。 则此时目标函数的系数无法再改变使目标函数值变得更 好。 如果决策变量取0值，则相差值可能不为0（比如说 相差值为正a，也有可能为0)。则此时目标函数的系数可 以在原来基础上增加a（而当目标函数是求最小值时， 减少a)，则可能才能使此决策变量变为非零（即生产该 种产品），才有可能使目标函数值变得更好。 也可以这样理解：在相差值内,价值系数增加就不会影 响原来的最优基，但当价值系数增加大于等于相差值时, 最优基就会发生变x2≤300，（台时数） 2 x1+x2≤400，（原料A） x2≤250, （原料B） 在约束条件、松弛／剩余变量、对偶价格这栏中，可 知设备的台时数全部使用完，每个设备台时的对偶价格 为50元，即增加了一个台时数就可使总利润增加50元； 原料A还有50千克没有使用，原料A的对偶价格当然为零， 即增加1千克A原料不会使总利润有所增加；原料B全部使 用完，原料B的对偶价格为50元，即增加一千克原料B就 可使总利润增加50元。
输入目标函数系数
在这输入约束条件，在输 入约束条件时注意清0，还 要注意不等号的方向。
一般地变量的非负性不必 修改。
输完模型后就可以选择要进行的操作， 如：保存、解决（求解）等。下面是例 1的输入结果。
输完模型后，苦要修 改模型点这里
解决后得到如下结果。
如果选择保存，就弹出保存路 径的对话框。
设备 原料A 原料B
所谓当前值是指约束条件右边值的现在值，可知b1=300；b2=400， b3=250。所谓上限值与下限值是指当约束条件的右边值在此范围 内变化时，则与其对应的约束条件的对偶价格不变，不能保证最 优解不变。从可由对偶价格判断增加某约束条件的常数项值是否 能使目标函数值变得更好（前提条件是其它常数项保持不变）。 当设备台时数在250→325的范围内，其对偶价格都为50元，说 明增加设备台时数可使目标函数值变大，每增加1个台时数可增加 利润50元。当原料A的公斤数在350到+∞范围内，其对偶价格都为 零；增加原料A对目标函数值无影响。当原料B的千克数在200到 300的范围内，其对偶价格都为50元。例如设备台时数和原料A的 数量不变，即b1=300；b2=400，原料B变为280千克，由于 200≤280≤300，原料B的对偶价格仍为50元，故新的最大利润值应 为： 27500+(280-250)×50=29000元。这里50是对偶价格。
下面以第二章的例1为例说明 此软件的用法
max Z=50x1+100x2， 约束条件：x1+x2≤300， 2 x1+x2≤400， x2≤250, x1≥0, x2≥0. 选择了线性规划后，就出现的界面，然后点 新建。得到如下对话框：
然后新建清零，下面就可以 输入模型了。
先输入变量个数、约束个数和 MAX或Min，然后点确定后， 才能输入模型。
“管理运筹学”的软件包
§3.1“管理运筹学”软件的操作方法 下面用运筹学软件2.0来解决例1的线性规划问题。
从开始→程序→管理运筹学2.0，这样就打开此软件，如下 图：
然后就 根据需 要选择 运筹学 的各个 分枝
1．输入的系数可以是整数、小数， 但不能是分数，要把分数先化为小数再输入。 2．输入前先要合并同类项。 3、此软件的一个最大缺点是变量只有一组X， 不能有Y和Z等，而且下标不能是二维下标如： X12是错的（看作是一维）。还有X1A等也是错 误的，其次模型的修改比较麻烦。
在目标函数系数范围一栏中，所谓的当前值是指在目标函数 中决策变量的当前系数值。如x1的系数值为50，x2的系数值为100。 所谓的上限与下限值是指目标函数的决策变量的系数（其它决策 变量的系数固定在当前值）在此范围内变化时，其线性规划的最 优解不变。例如当c1= 80时，因为0≤80≤100，在x1的系数变化范 围内，所以其最优解不变（此时要固定c2=100)，也即当x1=50， x2=250时，有最大利润。当然由于产品Ⅰ的单位利润由50变为80 了，其最大利润也增加了(最优值变了)， 变为80×50 +100×250 =29000(元)。 但是如果c1=110元时，由于110>100，所以原来的最优解就可 能不再是最优解了。 同样从上图可知，当c2 在50与＋∞之间变化时（此时要固定 c1=50) ，原来的最优解依然是其最优解。
输入文件名，然后 点保存即可，以后 可以点打开调出模 型。
如何读懂输出结果？
§3.2软件输出信息分析
从上面变量、最优解、相差值一栏中，知道例1的最优解为生 产Ⅰ产品50单位；生产Ⅱ产品250单位。相差值的数值表示相应的 决策变量的目标系数需要改进的数量，使得该决策变量有可能取 正数值，一般地，当决策变量已取正数值时则相差值为零。如果 决策变量取0值，则相差值可能不为0。对例1来说由于x1=50， x2=250，都是正值，所以它们的相差值都为零。如果x1的值为0； x1 的相差值为20；则就知道，只有当产品I 的利润再提高20元，即 达到50+20=70元时（这里的50是表示X1的利润，不是X1的最优 解）， 产品I 才可能生产，即x1才可能大于零。对于目标函数求最 小值的线性规划问题，那么所谓的改进就应该使其对应的决策变 量的系数减少其相差值。这在以后还要说明。
如何求解？
本章将介绍如何使用计算机软件包求解线性规划问题。 解决线性规划问题的软件包分两种，一种是大规模 的软件包，它可以用来解决复杂的包含数千个决策变量 和数千个约束条件的大型的线性规划的问题，重点掌握 国内外常用软件：由芝加哥大学LinusE．Schrage开发 的lindo6.1软件，此软件包可解决32000个变量(3200整 型变量）16000个约束方程的运筹学问题。 另一种是用于微机的软件包，它们有很好的界面， 使用方便，由科研机构和小软件公司为解决包含数百个 决策变量的线性规划问题而开发的。本章介绍的是与本 书配套的名为“管理运筹学”2.0软件包就是属于这种 软件，此软件包可解决100个变量50个约束方程的管理 运筹学问题。 本章的重点放在如何读懂“管理运筹学”软件包的 计算机输出结果——关于线性规划问题的求解和灵敏度 分析的信息，解决工商管理中的实际问题。
喂！相差值是什么意思？
我知道：如果决策变量取正数值，则相差值一般为零。 则此时目标函数的系数无法再改变使目标函数值变得更 好。 如果决策变量取0值，则相差值可能不为0（比如说 相差值为正a，也有可能为0)。则此时目标函数的系数可 以在原来基础上增加a（而当目标函数是求最小值时， 减少a)，则可能才能使此决策变量变为非零（即生产该 种产品），才有可能使目标函数值变得更好。 也可以这样理解：在相差值内,价值系数增加就不会影 响原来的最优基，但当价值系数增加大于等于相差值时, 最优基就会发生变x2≤300，（台时数） 2 x1+x2≤400，（原料A） x2≤250, （原料B） 在约束条件、松弛／剩余变量、对偶价格这栏中，可 知设备的台时数全部使用完，每个设备台时的对偶价格 为50元，即增加了一个台时数就可使总利润增加50元； 原料A还有50千克没有使用，原料A的对偶价格当然为零， 即增加1千克A原料不会使总利润有所增加；原料B全部使 用完，原料B的对偶价格为50元，即增加一千克原料B就 可使总利润增加50元。
输入目标函数系数
在这输入约束条件，在输 入约束条件时注意清0，还 要注意不等号的方向。
一般地变量的非负性不必 修改。
输完模型后就可以选择要进行的操作， 如：保存、解决（求解）等。下面是例 1的输入结果。
输完模型后，苦要修 改模型点这里
解决后得到如下结果。
如果选择保存，就弹出保存路 径的对话框。
设备 原料A 原料B
所谓当前值是指约束条件右边值的现在值，可知b1=300；b2=400， b3=250。所谓上限值与下限值是指当约束条件的右边值在此范围 内变化时，则与其对应的约束条件的对偶价格不变，不能保证最 优解不变。从可由对偶价格判断增加某约束条件的常数项值是否 能使目标函数值变得更好（前提条件是其它常数项保持不变）。 当设备台时数在250→325的范围内，其对偶价格都为50元，说 明增加设备台时数可使目标函数值变大，每增加1个台时数可增加 利润50元。当原料A的公斤数在350到+∞范围内，其对偶价格都为 零；增加原料A对目标函数值无影响。当原料B的千克数在200到 300的范围内，其对偶价格都为50元。例如设备台时数和原料A的 数量不变，即b1=300；b2=400，原料B变为280千克，由于 200≤280≤300，原料B的对偶价格仍为50元，故新的最大利润值应 为： 27500+(280-250)×50=29000元。这里50是对偶价格。
下面以第二章的例1为例说明 此软件的用法
max Z=50x1+100x2， 约束条件：x1+x2≤300， 2 x1+x2≤400， x2≤250, x1≥0, x2≥0. 选择了线性规划后，就出现的界面，然后点 新建。得到如下对话框：
然后新建清零，下面就可以 输入模型了。
先输入变量个数、约束个数和 MAX或Min，然后点确定后， 才能输入模型。
“管理运筹学”的软件包
§3.1“管理运筹学”软件的操作方法 下面用运筹学软件2.0来解决例1的线性规划问题。
从开始→程序→管理运筹学2.0，这样就打开此软件，如下 图：
然后就 根据需 要选择 运筹学 的各个 分枝
1．输入的系数可以是整数、小数， 但不能是分数，要把分数先化为小数再输入。 2．输入前先要合并同类项。 3、此软件的一个最大缺点是变量只有一组X， 不能有Y和Z等，而且下标不能是二维下标如： X12是错的（看作是一维）。还有X1A等也是错 误的，其次模型的修改比较麻烦。
在目标函数系数范围一栏中，所谓的当前值是指在目标函数 中决策变量的当前系数值。如x1的系数值为50，x2的系数值为100。 所谓的上限与下限值是指目标函数的决策变量的系数（其它决策 变量的系数固定在当前值）在此范围内变化时，其线性规划的最 优解不变。例如当c1= 80时，因为0≤80≤100，在x1的系数变化范 围内，所以其最优解不变（此时要固定c2=100)，也即当x1=50， x2=250时，有最大利润。当然由于产品Ⅰ的单位利润由50变为80 了，其最大利润也增加了(最优值变了)， 变为80×50 +100×250 =29000(元)。 但是如果c1=110元时，由于110>100，所以原来的最优解就可 能不再是最优解了。 同样从上图可知，当c2 在50与＋∞之间变化时（此时要固定 c1=50) ，原来的最优解依然是其最优解。
输入文件名，然后 点保存即可，以后 可以点打开调出模 型。
如何读懂输出结果？
§3.2软件输出信息分析
从上面变量、最优解、相差值一栏中，知道例1的最优解为生 产Ⅰ产品50单位；生产Ⅱ产品250单位。相差值的数值表示相应的 决策变量的目标系数需要改进的数量，使得该决策变量有可能取 正数值，一般地，当决策变量已取正数值时则相差值为零。如果 决策变量取0值，则相差值可能不为0。对例1来说由于x1=50， x2=250，都是正值，所以它们的相差值都为零。如果x1的值为0； x1 的相差值为20；则就知道，只有当产品I 的利润再提高20元，即 达到50+20=70元时（这里的50是表示X1的利润，不是X1的最优 解）， 产品I 才可能生产，即x1才可能大于零。对于目标函数求最 小值的线性规划问题，那么所谓的改进就应该使其对应的决策变 量的系数减少其相差值。这在以后还要说明。