【区级联考】黑龙江省哈尔滨市平房区2021届九年级中考调研测试(一)数学试题

第23题图2021年平房区中考调研测试(一)数学答案一、选择题12345678910AC B A C BD D B C 二、填空题11. . × 12. ≠ 13.2 14. ( − ) 15.-2;16.(-1,-3)17. ≤ <18.319.10或620. 三、解答题21.解：3331)3)(3()2(223+=++-++⨯+-=x x x x x x x 原式......4分3313232-=⨯-⨯=x ∵......2分33333-33==+=∴原式......1分22.（1）正确画图......3分（2）正确画图......3分5EF =......1分23.解：(1)36÷45%=80（人）......2分答：本次调查学生的总人数为80人.......1分(2)80-36-14-10=20（人）......1分补全图形......1分(3)1200×1480=210（人）......2分答：估计有210人最喜欢“线上答题”的方式。

......1分24.（1）证明：∵四边形ABCD 是平行四边形∴AD=BC,AD∥BC ∴∠ADE=∠CBD∵EA⊥AD，EC⊥BC∴∠EAD=∠FCB=90°∴△EAD≌△FCB ......2分∴EA=FC,∠AED=∠CFB ∴EA∥FC......1分∴四边形AECF 是平行四边形.......1分（2）△ABE、△ADE、△BCF、△DCE......4分25．（1）解：设篮球每个为x 元,足球每个为y 元⎩⎨⎧=+=+550350032y x y x ......3分解得⎩⎨⎧==100150y x ......1分答:篮球每个是150元,足球每个是100元......1分2177m 7mBD CD ==（2）解：设购买篮球m 个2200)20(100%80150≤-+⨯m m ......3分解得：10≤m ......1分答:最多购买10个篮球......1分26.（1）设∠DBC=α，则∠BAC=2α∵BD⊥AC ∴∠BDC=90°∴∠BCD=90°-α.......1分∴∠ABC=180°-∠BAC-∠ACB=90°-α.......1分∴∠ABC=∠ACB ∴AB=AC .......1分（2）延长CF 交☉O 于点M，交AB 于点N∵∠ECF=∠BAC ∴AN=NC∵∴∠BAC=∠BMC ∵AM=AM∴∠ABM=∠ACM ∴∠NMB=∠NBM∴MN=NB ∴AN+BN=CN+NM ∴AB=CM.......1分∵∠CMB=∠ACM ∴BM∥AC ∵点F 为BE 中点∴BF=EF ∴△BFM≌△EFC.......1分∴CF=FM=CM ∴AB=2CF.......1分（3）连接ME，∵BM∥CE 且BM=CE ∴四边形MBCE 为平行四边形∴ME=BC，∠AEM=∠ACB连接AM，∵四边形AMBC 为圆内接四边形∴∠MAC+∠MBC=180°∵∠ACB+∠MBC=180°∴∠ACB=∠MAC ∴∠MAE=∠AEM∴AM=ME.......1分过点M 作MR⊥AE ∴AR=RE ∵BC=ME，∠AEM=∠DCB，∠MRE=∠BDC=90°∴△MRE≌△BDC ∴DC=RE=AR ∵AH=AH∴∠ABD=∠ACK 又∵∠K=∠ADB,AB=AC∴△ABD≌△ACK ∴∠CAK=∠BAD=2α∵AB=AB ∴∠AGB=∠ACB=90°-α∴∠AEG=90°-α=∠BEC=∠ECB∴BE=BC ∵BD⊥EC ∴DE=DC∴AE=EC 设CD=m 则AD=3mAB=4m 在Rt△ABD 中，222ADAB BD -=m 7m 9m 16BD 22=-=∴tan∠DBC=.......1分连接OA、OC，∵E 为AC 中点∴OE⊥AC BC=BC77AE 774AE OE ==∵AC=AC ∴∠OAE=α=∠DBC=∠DBE 连接AH ∵GH=GH ∴tan∠OAE=tan∠DBC=∴AE=4.......1分∴AD=AE+DE=6分27.x 轴∴OB=OC=3........1分点B 的坐标是（-3，0）........1分（2）过点D 作DQ⊥x 轴,可证△DFQ≌△EFH,得到DQ=EH，FQ=FH,3-t+d-6=OQ+t ........1分,OQ=d-2t-3,BQ=3-OQ=6+2t-d再证△DBQ≌△ECH,得BQ=CH,即6+2t-d=d-6........1分∴d=6+t........1分（3）过点K 作KN⊥y 轴交y 轴于点N,∵CE=AK，∵EH∥OA ∴∠HEC=∠OAC,AB=AC∴∠BAO=∠OAC=∠NAK=∠HEC,∠KNA=∠CHE,△NAK≌△HEC,CH=NK,∵d=6+t,BC=6,CH=OF=t,∴NK=OF,NK∥OF,∠KNA=90°∴四边形OFKN 是矩形∴∠KFO=90°........1分∵BM∥KF,∠KFC=∠MBO=90°,∠BMG=∠FKC分∴tan∠ABO=3由勾股可得AB=5∴BM=8∴∠ABM=∠AMB,AM=AB=AC,DM∥CK,∠AMD=∠ACK,∠DAM=∠KAC∴△DAM≌△KAC分,∠QDG=∠BMG ∴直线GK 分。

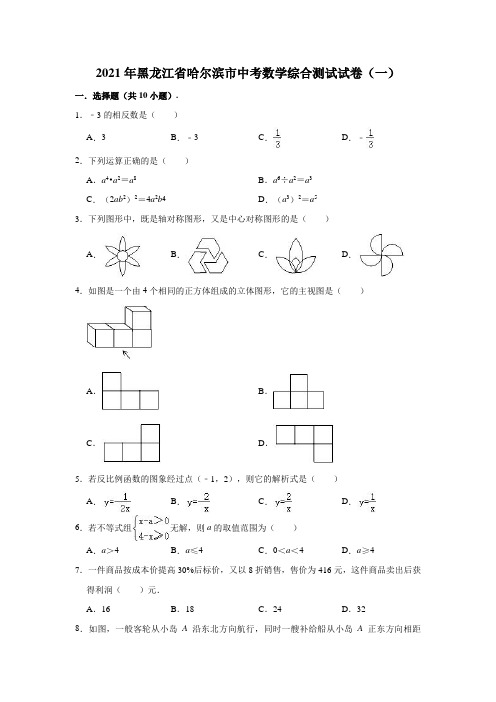
2021年黑龙江省哈尔滨市中考数学综合测试试卷（一）一．选择题（共10小题）.1．﹣3的相反数是（）A．3B．﹣3C．D．﹣2．下列运算正确的是（）A．a4•a2＝a8B．a6÷a2＝a3C．（2ab2）2＝4a2b⁴D．（a3）2＝a53．下列图形中，既是轴对称图形，又是中心对称图形的是（）A．B．C．D．4．如图是一个由4个相同的正方体组成的立体图形，它的主视图是（）A．B．C．D．5．若反比例函数的图象经过点（﹣1，2），则它的解析式是（）A．B．C．D．6．若不等式组无解，则a的取值范围为（）A．a＞4B．a≤4C．0＜a＜4D．a≥47．一件商品按成本价提高30%后标价，又以8折销售，售价为416元，这件商品卖出后获得利润（）元．A．16B．18C．24D．328．如图，一般客轮从小岛A沿东北方向航行，同时一艘补给船从小岛A正东方向相距（100+100）海里的港口B出发．沿北偏西60°方向航行，与客轮同时到达C处给客轮进行补给，则客轮与补给船的速度之比为（）A．：2B．：1C．：2D．：19．如图，在△ABC中，点D、E分别在BC、AB边上、DF∥AB，交AC边于点H，EF∥BC，交AC边于点G．则下列结论中错误的是（）A．B．C．D．10．如图是甲、乙两车在某时段速度随时间变化的图象，下列结论错误的是如图是甲、乙两车在某时段速度随时间变化的图象，下列结论错误的是（）A．两车到第3秒时行驶的路程相等B．在4至8秒内甲的速度都大于乙的速度C．乙前4秒行驶的路程为48米D．在0到8秒内甲的速度每秒增加4米/秒二．填空题（满分30分，每小题3分）11．人的血管首尾相连的长度大约可达96000千米，96000千米用科学记数法表示为米．12．函数y＝的自变量x的取值范围是．13．两个最简二次根式与相加得6，则a+b+c＝．14．分解因式：2x2﹣8x+8＝．15．已知二次函数y＝x2﹣4x+3，当自变量满足﹣1≤x≤3时，y的最大值为a，最小值为b，则a﹣b的值为．16．一位小朋友在粗糙不打滑的“Z”字形平面轨道上滚动一个半径为10cm的圆盘，如图所示，AB与CD是水平的，BC与水平面的夹角为60°，其中AB＝60cm，CD＝40cm，BC＝40cm，那么该小朋友将圆盘从A点滚动到D点其圆心所经过的路线长为cm．17．在一个不透明的盒子中装有8个白球，若干个黄球，它们除颜色不同外，其余均相同．若从中随机摸出一个球，它是白球的概率为，则黄球的个数为个．18．如图，在以O为圆心的两个同心圆中，大圆的弦AB是小圆的切线，P为切点，如果AB＝8cm，小圆直径为6cm，那么大圆半径为cm．19．如图，在矩形ABCD中，AD＝6，AB＝4，∠BAD的平分线交BC于点E，则DE ＝．20．如图，在△ABC中，DE∥BC，若AD＝3，DB＝2，则S△ADE：S△ABC＝．三．解答题（共7小题，满分60分）21．先化简，再求代数式（）的值，其中a＝2sin45°tan30°．22．图①、图②、图③均是6×6的正方形网格，每个小正方形的顶点称为格点，点A、B、C、D、E、F均在格点上．只用无刻度的直尺按下列要求在给定的网格中画图，所画图形的顶点均在格点上，不要求写画法．（1）在图①中以线段AB为一腰画一个等腰锐角三角形ABP；（2）在图②中以线段CD为底画一个等腰直角三角形CDM；（3）在图③中画等腰钝角三角形EFN．23．校文学社在全校范围内随机抽取一部分读者对社刊中最感兴趣的文学栏目进行了投票．每人一张选票，每张选票只能投给一个栏目，经统计无弃权票，根据投票结果绘制的条形统计图如下：（1）这次参加投票的总人数为．（2）若全校有3000名读者，估计其中对“写作指导”最感兴趣的人数．（3）在全校3000名读者中，若对某个栏目最感兴趣的人数少于300人将会影响社刊的销售，这个栏目就需要被撤换．请通过计算判断，“新书上架”栏目是否需要被撤换．24．菱形ABCD的边长为6，∠D＝60°，点E在边AD上运动．（1）如图1，当点E为AD的中点时，求AO：CO的值；（2）如图2，F是AB上的动点，且满足BF+DE＝6，求证：△CEF是等边三角形．25．某县要修筑一条长为6000米的乡村旅游公路，准备承包给甲、乙两个工程队来合作完成，已知甲队每天筑路的长度是乙队的2倍，前期两队各完成了400米时，甲比乙少用了5天．（1）求甲、乙两个工程队每天各筑路多少米？（2）若甲队每天的工程费用为1.5万元，乙队每天的工程费用为0.9万元，要使完成全部工程的总费用不超过120万元，则至少要安排甲队筑路多少天？26．如图1，扇形AOB的半径为6，弧长为2π．（1）求圆心角∠AOB的度数；（2）如图2，将扇形AOB绕点O逆时针旋转60°，连接AB，BC．①判断四边形OABC的形状并证明：②如图3，若∠POQ＝60°，将∠POQ绕点O旋转，与AB，BC分别交于点M，N（点M，N与点A，B，C均不重合），判断MB+NB的值是否为定值．如果是定值请求出；如果不是，请说明理由27．如图，已知抛物线y＝ax2+bx+c（a≠0）与x轴交于点A（1，0）和点B（﹣3，0），与y轴交于点C，且OC＝OB．（1）求点C的坐标和此抛物线的解析式；（2）若点E为第二象限抛物线上一动点，连接BE，CE，BC，求△BCE面积的最大值；（3）点P在抛物线的对称轴上，若线段PA绕点P逆时针旋转90°后，点A的对应点A′恰好也落在此抛物线上，求点P的坐标．参考答案一．选择题（满分30分，每小题3分）1．﹣3的相反数是（）A．3B．﹣3C．D．﹣【分析】根据相反数的意义，只有符号不同的两个数为相反数．解：﹣3的相反数是3．故选：A．2．下列运算正确的是（）A．a4•a2＝a8B．a6÷a2＝a3C．（2ab2）2＝4a2b⁴D．（a3）2＝a5【分析】分别根据同底数幂的乘法法则，同底数幂的除法法则，积的乘方运算法则以及幂的乘方运算法则逐一判断即可．解：A．a4•a2＝a6，故本选项不合题意；B．a6÷a2＝a4，故本选项不合题意；C．（2ab2）2＝4a2b4，正确；D．（a3）2＝a6，故本选项不合题意；故选：C．3．下列图形中，既是轴对称图形，又是中心对称图形的是（）A．B．C．D．【分析】根据轴对称图形与中心对称图形的概念求解．解：A、是轴对称图形，也是中心对称图形，故此选项正确；B、不是轴对称图形，也不是中心对称图形，故此选项错误；C、是轴对称图形，不是中心对称图形，故此选项错误；D、不是轴对称图形，是中心对称图形，故此选项错误；故选：A．4．如图是一个由4个相同的正方体组成的立体图形，它的主视图是（）A．B．C．D．【分析】找到从正面看所得到的图形即可，注意所有的看到的棱都应表现在主视图中．解：该立体图形主视图的第1列有1个正方形、第2列有1个正方形、第3列有2个正方形，故选：C．5．若反比例函数的图象经过点（﹣1，2），则它的解析式是（）A．B．C．D．【分析】首先设出反比例函数解析式，再把（﹣1，2）代入解析式可得k的值，进而得到答案．解：设反比例函数解析式为y＝，∵反比例函数的图象经过点（﹣1，2），∴k＝﹣1×2＝﹣2，∴反比例函数解析式为y＝﹣，故选：B．6．若不等式组无解，则a的取值范围为（）A．a＞4B．a≤4C．0＜a＜4D．a≥4【分析】不等式组整理后，根据不等式组无解确定出a的范围即可．解：不等式组整理得：，由不等式组无解，得到a≥4．故选：D．7．一件商品按成本价提高30%后标价，又以8折销售，售价为416元，这件商品卖出后获得利润（）元．A．16B．18C．24D．32【分析】此题可设原价为x元，提高30%后标价，实际上是按原价的130%标价，又以8折销售是以原价的80%销售，根据题意列方程解答即可．解：设原价为x元，根据题意列方程得：x×（1+30%）×80%＝416解得x＝400，416﹣400＝16（元）．答：这件商品卖出后获得利润16元．故选：A．8．如图，一般客轮从小岛A沿东北方向航行，同时一艘补给船从小岛A正东方向相距（100+100）海里的港口B出发．沿北偏西60°方向航行，与客轮同时到达C处给客轮进行补给，则客轮与补给船的速度之比为（）A．：2B．：1C．：2D．：1【分析】过C作CD⊥AB于D，设AD＝x，根据特殊三角形的性质，分别用含x的代数式表示出CD，BD，根据AB的长求出x，再根据勾股定理求出AC，BD，即可得到答案．解：过C作CD⊥AB于D，设AD＝x，由题意得∠CAD＝45°，∠NBC＝60°，在Rt△ACD中，∠ACD＝90°﹣45°＝45°，∴∠ACD＝∠CAD，∴CD＝AD＝x，∴AC＝＝x，在Rt△BCD中，∠CBD＝90°﹣60°＝30°，∴BC＝2CD＝2x，∴BD＝＝x，∵AB＝100+100，∴AD+BD＝x+x＝100+100，∴（1+）x＝100（1+），∴x＝100，即AD＝100海里，∴AC＝100海里，BC＝200海里，∵时间一定时速度与路程成正比，∴客轮与补给船的速度之比为100：200＝：2，故选：A．9．如图，在△ABC中，点D、E分别在BC、AB边上、DF∥AB，交AC边于点H，EF∥BC，交AC边于点G．则下列结论中错误的是（）A．B．C．D．【分析】根据平行线分线段成比例即可得到答案．解：∵DF∥AB，EF∥BC，∴四边形EBDF是平行四边形，BE＝DF，EF＝BD，A、∵EF∥BC，∴，故A不符合题意，B、∵DF∥AB，∴，故B不符合题意，C、∵DF∥AB，∴，故C不符合题意，D、∵DF∥AB，∴＝，∴，∴，故D符合题意，故选：D．10．如图是甲、乙两车在某时段速度随时间变化的图象，下列结论错误的是如图是甲、乙两车在某时段速度随时间变化的图象，下列结论错误的是（）A．两车到第3秒时行驶的路程相等B．在4至8秒内甲的速度都大于乙的速度C．乙前4秒行驶的路程为48米D．在0到8秒内甲的速度每秒增加4米/秒【分析】结合速度与时间的变化图象，作出判断即可．解：A、由于甲的图象是过原点的直线，所以可得v＝4t（v、t分别表示速度、时间），将v＝12m/s代入v＝4t得t＝3s，则t＝3s前，甲的速度小于乙的速度，所以两车到第3秒时行驶的路程不相等，符合题意；B、在4至8秒内甲的速度图象一直在乙的上方，所以甲的速度都大于乙的速度，不符合题意；C、根据图象可得，乙前4秒的速度不变，为12米/秒，则行驶的路程为12×4＝48米，不符合题意；D、根据图象得：在0到8秒内甲的速度是一条过原点的直线，即甲的速度从0均匀增加到32米/秒，则每秒增加（32÷8）＝4（米/秒），不符合题意，故选：A．二．填空题（满分30分，每小题3分）11．人的血管首尾相连的长度大约可达96000千米，96000千米用科学记数法表示为9.6×107米．【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n 的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值≥10时，n是正整数；当原数的绝对值＜1时，n是负整数．解：96000千米＝96000000＝9.6×107（米）．故答案为：9.6×107．12．函数y＝的自变量x的取值范围是x＜2．【分析】根据分式有意义的条件、二次根式有意义的条件列出不等式，解不等式即可．解：由题意得，2﹣x＞0，解得，x＜2，故答案为：x＜2．13．两个最简二次根式与相加得6，则a+b+c＝11．【分析】两个最简二次根式可以合并，说明它们是同类二次根式，根据合并的结果即可得出答案．解：由题意得，与是同类二次根式，∵与相加得6，∴a+c＝6，b＝5，则a+b+c＝11．故答案为：11．14．分解因式：2x2﹣8x+8＝2（x﹣2）2．【分析】先提公因式2，再用完全平方公式进行因式分解即可．解：原式＝2（x2﹣4x+4）＝2（x﹣2）2．故答案为2（x﹣2）2．15．已知二次函数y＝x2﹣4x+3，当自变量满足﹣1≤x≤3时，y的最大值为a，最小值为b，则a﹣b的值为9．【分析】根据题目中的函数解析式和二次函数的性质，可以得到自变量满足﹣1≤x≤3时，x＝﹣1时取得最大值，x＝2时取得最小值，然后即可得到a、b的值，从而可以求得a﹣b的值，本题得以解决．解：∵二次函数y＝x2﹣4x+3＝（x﹣2）2﹣1，∴该函数图象开口向上，对称轴为直线x＝2，∵当自变量满足﹣1≤x≤3时，y的最大值为a，最小值为b，∴当x＝﹣1时，取得最大值，当x＝2时，函数取得最小值，∴a＝1+4+3＝8，b＝﹣1，∴a﹣b＝8﹣（﹣1）＝8+1＝9，故答案为：9．16．一位小朋友在粗糙不打滑的“Z”字形平面轨道上滚动一个半径为10cm的圆盘，如图所示，AB与CD是水平的，BC与水平面的夹角为60°，其中AB＝60cm，CD＝40cm，BC＝40cm，那么该小朋友将圆盘从A点滚动到D点其圆心所经过的路线长为（）cm．【分析】A点滚动到D点其圆心所经过的路线在点B处少走了一段，在点C处又多求了一段弧长，所以A点滚动到D点其圆心所经过的路线＝（60+40+40）﹣+＝（cm）．解：A点滚动到D点其圆心所经过的路线＝（60+40+40）﹣+＝（cm）．故答案为：（）．17．在一个不透明的盒子中装有8个白球，若干个黄球，它们除颜色不同外，其余均相同．若从中随机摸出一个球，它是白球的概率为，则黄球的个数为4个．【分析】根据白球个数除以小球总数进而得出得到白球的概率，进而得出答案．解：∵在一个不透明的盒子中装有8个白球，从中随机摸出一个球，它是白球的概率为，设黄球有x个，根据题意得出：∴＝，解得：x＝4．故答案为：4．18．如图，在以O为圆心的两个同心圆中，大圆的弦AB是小圆的切线，P为切点，如果AB＝8cm，小圆直径为6cm，那么大圆半径为5cm．【分析】连接OA，由切线的性质可知OP⊥AB，由垂径定理可知AP＝PB，在Rt△OAP 中，利用勾股定理可求得OA的长．解：如图，连接OP，AO，∵AB是小圆的切线，∴OP⊥AB，∵OP过圆心，∴AP＝BP＝AB＝4cm，∵小圆直径径为6cm，∴OP＝3cm，在Rt△AOP中，由勾股定理可得OA＝＝5（cm），即大圆的半径为5cm，故答案为：5．19．如图，在矩形ABCD中，AD＝6，AB＝4，∠BAD的平分线交BC于点E，则DE＝2．【分析】过点E作EF⊥AD于点F，根据矩形性质和角平分线定义证明矩形ABEF是正方形，再根据勾股定理即可求出DE的长．解：如图，过点E作EF⊥AD于点F，在矩形ABCD中，∠B＝∠BAD＝90°，∵EA是∠BAD的平分线，∴∠DAB＝∠EAF＝45°，∴∠AEB＝45°，∴AB＝BE，∴矩形ABEF是正方形，∴AB＝BE＝EF＝AF＝4，∴DF＝AD﹣AF＝6﹣4＝2，∴DE＝＝＝2．故答案为：2．20．如图，在△ABC中，DE∥BC，若AD＝3，DB＝2，则S△ADE：S△ABC＝9：25．【分析】由线段的和差，已知AD＝3，DB＝2的长度，求出AB＝5，相似三角形的判定与性质得△ADE∽△ABC，其性质相似三角形的面积之比等于相似比的平方，求出S△ADE：S△ABC的值为9：25．解：如图所示：∵AD+DB＝AB，AD＝3，DB＝2，∴AB＝5，又∵DE∥BC，∴△ADE∽△ABC，∴，∴＝，故答案为9：25．三．解答题（共7小题，满分60分）21．先化简，再求代数式（）的值，其中a＝2sin45°tan30°．【分析】原式括号中两项通分并利用同分母分式的减法法则计算，同时利用除法法则变形，约分得到最简结果，把a的值代入计算即可求出值．解：原式＝[﹣]•＝（﹣）•＝•＝，当a＝2×+2×＝+2时，原式＝＝．22．图①、图②、图③均是6×6的正方形网格，每个小正方形的顶点称为格点，点A、B、C、D、E、F均在格点上．只用无刻度的直尺按下列要求在给定的网格中画图，所画图形的顶点均在格点上，不要求写画法．（1）在图①中以线段AB为一腰画一个等腰锐角三角形ABP；（2）在图②中以线段CD为底画一个等腰直角三角形CDM；（3）在图③中画等腰钝角三角形EFN．【分析】（1）根据等腰三角形的定义画出图形即可．（2）根据等腰直角三角形的定义画出图形即可．（3）根据等腰钝角三角形的定义画出图形即可．解：（1）如图①中，△ABP或△ABP′即为所求作．（2）如图②中，△CDM或△CDM′即为所求作．（3）如图③中，△EFN即为所求作．23．校文学社在全校范围内随机抽取一部分读者对社刊中最感兴趣的文学栏目进行了投票．每人一张选票，每张选票只能投给一个栏目，经统计无弃权票，根据投票结果绘制的条形统计图如下：（1）这次参加投票的总人数为500．（2）若全校有3000名读者，估计其中对“写作指导”最感兴趣的人数．（3）在全校3000名读者中，若对某个栏目最感兴趣的人数少于300人将会影响社刊的销售，这个栏目就需要被撤换．请通过计算判断，“新书上架”栏目是否需要被撤换．【分析】（1）将统计图中所有数据相加即可得到总人数；（2）用总人数乘以写作感兴趣的比例即可得到答案；（3）求出新书上架的人数与300比较即可得到答案．解：（1）投票总人数＝76+88+97+42+60+111+26＝500人；（2）3000×＝360人；（3）∵3000×＝252＜300∴这个栏目将被撤换．24．菱形ABCD的边长为6，∠D＝60°，点E在边AD上运动．（1）如图1，当点E为AD的中点时，求AO：CO的值；（2）如图2，F是AB上的动点，且满足BF+DE＝6，求证：△CEF是等边三角形．【分析】（1）先由菱形的性质得BC＝AD＝6，AD∥BC，再证△AOE∽△COB，即可得出答案；（2）先证△ABC是等边三角形，得AC＝BC，∠ACB＝60°，再证△ACE≌△BCF（SAS），得CE＝CF，∠ACE＝∠BCF，然后证∠ECF＝∠ACB＝60°，即可得出结论．【解答】（1）解：∵四边形ABCD是菱形，∴BC＝AD＝6，AD∥BC，∵点E为AD的中点，∴AE＝AD＝3，∵AD∥BC，∴△AOE∽△COB，∴＝＝＝；（2）证明：∵四边形ABCD是菱形，∴AB＝BC，AD∥BC，∠B＝∠D＝60°，∴∠CAE＝∠ACB，△ABC是等边三角形，∴AC＝BC，∠ACB＝60°，∴∠EAC＝60°＝∠B，∵AE+DE＝AD＝6，BF+DE＝6，∴AE＝BF，在△ACE和△BCF中，，∴△ACE≌△BCF（SAS），∴CE＝CF，∠ACE＝∠BCF，∴∠ACE+∠ACF＝∠BCF+∠ACF＝∠ACB＝60°，即∠ECF＝60°，∴△CEF是等边三角形．25．某县要修筑一条长为6000米的乡村旅游公路，准备承包给甲、乙两个工程队来合作完成，已知甲队每天筑路的长度是乙队的2倍，前期两队各完成了400米时，甲比乙少用了5天．（1）求甲、乙两个工程队每天各筑路多少米？（2）若甲队每天的工程费用为1.5万元，乙队每天的工程费用为0.9万元，要使完成全部工程的总费用不超过120万元，则至少要安排甲队筑路多少天？【分析】（1）设乙队每天筑路x米，则甲每天筑路2x米．由题意列出分式方程，解方程即可；（2）设甲筑路t天，则乙筑路天数为（150﹣2t）天，由题意列出不等式，解不等式即可．解：（1）设乙队每天筑路x米，则甲每天筑路2x米．依题意，得：，解得：x＝40，经检验：x＝40是原分式方程的解，则2x＝80答：甲每天筑路80米，乙每天筑路40米；（2）设甲筑路t天，则乙筑路天数为＝（150﹣2t）天，依题意：1.5t+0.9（150﹣2t）≤120，解得：t≥50，∴甲至少要筑路50天．26．如图1，扇形AOB的半径为6，弧长为2π．（1）求圆心角∠AOB的度数；（2）如图2，将扇形AOB绕点O逆时针旋转60°，连接AB，BC．①判断四边形OABC的形状并证明：②如图3，若∠POQ＝60°，将∠POQ绕点O旋转，与AB，BC分别交于点M，N（点M，N与点A，B，C均不重合），判断MB+NB的值是否为定值．如果是定值请求出；如果不是，请说明理由【分析】（1）根据弧长公式即可得到答案；（2）①证明△OAB与△OBC是等边三角形，可得四边形OABC得四边相等，从而证明四边形OABC是菱形；②证明△OMA≌△ONB得MA＝NB，从而可得MB+NB＝AB，是定值6．解：（1）∵扇形AOB的半径为6，弧长为2π．∴＝2π，∴n＝60，∴圆心角∠AOB＝60°；（2）①四边形OABC是菱形，理由如下：在扇形AOB中，OA＝OB，∠AOB＝60°，∴△AOB是等边三角形，∴OA＝OB＝AB，∵扇形AOB绕点O逆时针旋转60°，∴△COB是等边三角形，∴OA＝AB＝BC＝OC，∴四边形OABC是菱形；②MB+NB是定值，由①知△OAB与△OBC是等边三角形，∴∠OBC＝∠OAB＝∠AOB＝60°，∵∠POQ＝60°，∴∠AOB＝∠POQ，∴∠AOB﹣∠BOM＝∠POQ﹣∠BOM，即∠AOM＝∠BON，又OA＝OB，∠OAB＝∠OBC＝60°，∴△OMA≌△ONB（ASA），∴MA＝NB，∴MB+NB＝MB+MA＝AB＝6，∴MB+NB为定值6．27．如图，已知抛物线y＝ax2+bx+c（a≠0）与x轴交于点A（1，0）和点B（﹣3，0），与y轴交于点C，且OC＝OB．（1）求点C的坐标和此抛物线的解析式；（2）若点E为第二象限抛物线上一动点，连接BE，CE，BC，求△BCE面积的最大值；（3）点P在抛物线的对称轴上，若线段PA绕点P逆时针旋转90°后，点A的对应点A′恰好也落在此抛物线上，求点P的坐标．【分析】（1）已知抛物线过A、B两点，可将两点的坐标代入抛物线的解析式中，用待定系数法即可求出二次函数的解析式；（2）如图2，连接BC，过点E作EF⊥x轴于点F，设E（a，﹣a2﹣2a+3）（﹣3＜a＜0），可得EF＝﹣a2﹣2a+3，BF＝a+3，OF＝﹣a，根据S△BEC＝S四边形BOCE﹣S△BOC，构建二次函数，利用二次函数的性质求解即可．（3）由P在抛物线的对称轴上，设出P坐标为（﹣1，m），如图所示，过A′作A′N ⊥对称轴于N，由旋转的性质得到一对边相等，再由同角的余角相等得到一对角相等，根据一对直角相等，利用AAS得到△A′NP≌△PMA，由全等三角形的对应边相等得到A′N＝PM＝|m|，PN＝AM＝2，表示出A′坐标，将A′坐标代入抛物线解析式中求出相应m的值，即可确定出P的坐标．解：（1）∵抛物线y＝ax2+bx+c（a≠0）与x轴交于点A（1，0）和点B（﹣3，0），∴OB＝3，∵OC＝OB，∴OC＝3，∴c＝3，∴，解得：，∴所求抛物线解析式为：y＝﹣x2﹣2x+3，C（0，3）．（2）如图2，连接BC，过点E作EF⊥x轴于点F，设E（a，﹣a2﹣2a+3）（﹣3＜a＜0），∴EF＝﹣a2﹣2a+3，BF＝a+3，OF＝﹣a，∴S△BEC＝S四边形BOCE﹣S△BOC＝BF•EF+（OC+EF）•OF﹣•OB•OC＝（a+3）•（﹣a2﹣2a+3）+（﹣a2﹣2a+6）•（﹣a）﹣＝﹣a2﹣a＝﹣（a+）2+，∴当a＝﹣时，S△BEC最大，且最大值为．（3）∵抛物线y＝﹣x2﹣2x+3的对称轴为x＝﹣1，点P在抛物线的对称轴上，∴设P（﹣1，m），∵线段PA绕点P逆时针旋转90°后，点A的对应点A′恰好也落在此抛物线上，①当m≥0时，∴PA＝PA′，∠APA′＝90°，如图3，过A′作A′N⊥对称轴于N，设对称轴于x轴交于点M，∴∠NPA′+∠MPA＝∠NA′P+∠NPA′＝90°，∴∠NA′P＝∠NPA，在△A′NP与△PMA中，，∴△A′NP≌△PMA（AAS），∴A′N＝PM＝m，PN＝AM＝2，∴A′（m﹣1，m+2），代入y＝﹣x2﹣2x+3得：m+2＝﹣（m﹣1）2﹣2（m﹣1）+3，解得：m＝1，m＝﹣2（舍去），②当m＜0时，要使P2A＝P2A2，由图可知A2点与B点重合，∵∠AP2A2＝90°，∴MP2＝MA＝2，∴P2（﹣1，﹣2）．∴满足条件的点P的坐标为P（﹣1，1）或（﹣1，﹣2）．。

2021年平房区中考调研测试（一）综合试卷考生须知：1．本试卷满分为140分，考试时间为120分钟。

2．答题前，考生先将自己的“姓名”、“考号”、“考场”、“座位号”在答题卡上填写清楚，将“条形码”准确粘贴在条形码区域内。

3．请按照题号顺序在答题卡各题目的答题区域内作答，超出答题区域书写的答案无效，在草稿纸、试题纸上答题无效。

4．选择题必须使用2B 铅笔填涂；非选择题必须使用0.5毫米黑色字迹的签字笔书写，字迹工整、笔迹清楚。

5．保持卡面整洁，不要折叠、不要弄脏、不要弄皱，不准使用涂改液、修正带、刮纸刀。

可能用到的相对原子质量：H －1C －12N －14O －16Na －23Mg －24S －32Ba －137一、选择题（1—27题，每题2分，共54分,每题只有一个正确选项）1.哈尔滨市第二十四中学新校区近日于平房区破土动工，下列有关叙述错误的是（）A ．新校区的硬件设施将全面满足选课走班的要求，提升区域教育实力B ．施工使用的挖掘机铲斗是由主要成分为铁、锰、碳的锰钢制成C ．新建教学楼使用的钢筋混凝土属于金属材料D ．新建化学实验室的下水管道使用了具有密度小、耐腐蚀等性能的PVC2.下列实验操作正确的是……………………………………………………………（）A ．向试管中加入锌粒B ．稀释浓硫酸C ．测定溶液pH D ．过滤3.下列过程中只发生物理变化的是…………………………………………………（）A ．食物为人体提供能量B ．用铁矿石炼铁C ．塑料餐盒降解D ．不锈钢制成餐具4.下列物质的用途错误的是…………………………………………………………（）锌粒镊子A ．纯碱用于蒸馒头B ．氮气用于霓虹灯C ．NaOH 用于制肥皂D ．CO 2用于光合作用5.下列生活中的做法正确的是………………………………………………………（）A ．用喷漆的方法防止自行车车架生锈B ．酒精着火，使用水基型灭火器降低酒精的着火点，将火扑灭C ．化学农药对农业的高产丰收有重要作用，大量使用不会带来对环境的污染D ．燃气灶火焰呈现黄色或橙色，可以调小进风口6.下列实验现象描述正确的是………………………………………………………（）A ．白色固体燃烧，放热，产生白烟B ．银白色液体变为红色固体C ．溶液由紫色变为红色D ．产生蓝紫色火焰，放热7.下列应用、相应的原理(用化学方程式表示)及基本反应类型均正确的是………（）A ．工业制二氧化碳CaCO 3高温CO 2↑+CaO 分解反应B ．用稀硫酸洗去附着在试管壁上的铜Cu +H 2SO 4CuSO 4+H 2↑置换反应C ．用氢氧化钠溶液吸收二氧化硫2NaOH +SO 2Na 2SO 4+H 2O 复分解反应D ．铁丝在氧气中燃烧4Fe+3O 2点燃2Fe 2O 3化合反应8.下列有关健康的说法正确的是……………………………………………………（）A ．幼儿缺碘会影响生长发育，引起食欲不振B ．老年人缺少钙元素会患佝偻病，容易骨折，可服用大量补钙药品C ．纤维素属于糖类，但不能被人体消化，所以无需摄入D ．香烟的烟气中含有尼古丁、焦油等有害物质，青少年一定不要吸烟9.有机玻璃是由甲基丙烯酸甲酯(C 5H 8O 2)聚合而成的，下列关于甲基丙烯酸甲酯的说法正确的是……………………………………………………………………………（）A ．甲基丙烯酸甲酯是有机高分子化合物B ．甲基丙烯酸甲酯分子中碳、氢原子个数比为5:8C ．甲基丙烯酸甲酯是由碳、氢、氧三个元素组成的D ．甲基丙烯酸甲酯分子中氢元素的质量分数最小10.下列有关资源和能源的叙述正确的是……………………………………………（）甲基丙烯酸甲酯分子结构模型拉瓦锡研究空气组成实验加热通入二氧化碳的石蕊溶液甲烷燃烧A ．空气是一种宝贵的资源，其中氮气和氧气约占空气体积的99%B ．地球上的淡水资源有限，可利用的淡水约占全球水储量的30.4%C ．废旧金属的回收利用，是保护金属资源的唯一途径D ．汽油、柴油、煤焦油等是石油加热炼制得到的产品制成的11.对下列事实的微观解释错误的是…………………………………………………（）选项事实解释A 香水要密封保存分子在不断运动B 金刚石、石墨性质存在明显的差异碳原子的排列方式不同C 碳酸钠溶液是混合物由不同种分子构成D 白醋、盐酸能使紫色石蕊溶液变红溶液中都含有氢离子12.在实验室区分下列各组物质所用的两种方法都可行的是……………………（）两种固体物质（不含结晶水）的溶解度曲线如右图，下列叙述正确的是……（）A ．t 1℃时，a 的溶解度大于b 的溶解度B ．t 2℃时，a 的溶液降温到t 1℃，一定能得到a 的饱和溶液C ．t 2℃时，a 、b 饱和溶液的溶质质量分数一定相等D ．b 中含少量a ，可用冷却热饱和溶液的方法提纯b 14.除去下列物质中的少量杂质，所选用的试剂和操作方法均正确的是…………（）15.向一定质量的氢氧化钠和硝酸钠组成的样品中加入100g 稀硫酸，恰好完全反应，得到116g 溶液，再向所得溶液中加入200g 某质量分数的硝酸钡溶液，恰好完全反应，过滤，将滤液蒸干得到25g 晶体，则该样品中氢氧化钠的含量为………………………（）A ．12.5%B ．25%C ．50%D ．75%16．对常见物理量估计错误的是……………………………………………………（）A ．人感觉最舒适的气温是40℃B ．成年人正常步行的速度约为1.2m/s C ．教室课桌的高度约为80cm D ．一个鸡蛋的质量约为50g方案二通过灼热的氧化铜，观察现象放在石棉网上灼烧，观察触摸，比较手感溶解，滴加无色酚酞溶液，观察选项物质少量杂质所用试剂和操作方法A氨气水蒸气通过足量浓硫酸，干燥B氯化钙碳酸钙适量的稀盐酸，过滤、洗涤、干燥C 水植物油适量的洗涤剂，振荡D硫酸钠氢氧化钠加水溶解，加适量的硫酸铜溶液，过滤、蒸发结晶a b17．下列关于物态变化的知识说法错误的是…………………………………………（）A ．冰雪消融是熔化现象B ．冰熔化时吸热，温度升高C ．露珠是水蒸气液化形成的D ．雾凇是水蒸气凝华形成的18．关于光现象的说法正确的是……………………………………………………（）A ．甲图是光的漫反射现象，因反射光线射向各个方向，故漫反射不遵循光的反射定律B ．乙图中人通过镜子能看到视力表的像，利用了光沿直线传播的知识C ．丙图中小聪和小猫通过平面镜可以互相看到对方，说明在反射时光路是可逆的D ．丁图中小猫没有叉到鱼，是因为光从空气射入水中发生了折射的缘故19．下列有关声音的说法正确的是…………………………………………………（）A ．敲击鼓面，鼓面振动产生的声音可以像电磁波一样在真空中传播B ．在交通道路上设置的噪声强度显示仪可以减弱噪声C ．直尺伸出桌面的长度越短，拨动时发出的声音音调越高，说明音调由振幅决定D ．扬声器发声使烛焰晃动，说明声音可以传递能量20．能源是能量的来源，为人类提供多种形式的能量。

2021年哈尔滨市中考数学试题及答案解析版一、选择题（每小题3分，共计30分）1．﹣6的绝对值是（）A．﹣6 B．6 C．D．﹣2．下列运算正确的是（）A．a2•a3=a6B．（a2）3=a5C．（﹣2a2b）3=﹣8a6b3D．（2a+1）2=4a2+2a+13．下列图形中，既是轴对称图形又是中心对称图形的是（）A．B．C．D．4．点（2，﹣4）在反比例函数y=的图象上，则下列各点在此函数图象上的是（）A．（2，4）B．（﹣1，﹣8）C．（﹣2，﹣4）D．（4，﹣2）5．五个大小相同的正方体搭成的几何体如图所示，其主视图是（）A．B．C．D．6．不等式组的解集是（）A．x≥2 B．﹣1＜x≤2 C．x≤2 D．﹣1＜x≤17．某车间有26名工人，每人每天能够生产800个螺钉或1000个螺母，1个螺钉需要配2个螺母，为使每天生产的螺钉和螺母刚好配套．设安排x名工人一辈子产螺钉，则下面所列方程正确的是（）A．2×1000（26﹣x）=800x B．1000（13﹣x）=800xC．1000（26﹣x）=2×800x D．1000（26﹣x）=800x8．如图，一艘轮船位于灯塔P的北偏东60°方向，与灯塔P的距离为30海里的A处，轮船沿正南方向航行一段时刻后，到达位于灯塔P的南偏东30°方向上的B处，则现在轮船所在位置B处与灯塔P之间的距离为（）A．60海里B．45海里C．20海里D．30海里9．如图，在△ABC中，D、E分别为AB、AC边上的点，DE∥BC，BE与CD相交于点F，则下列结论一定正确的是（）A．=B．C．D．10．明君社区有一块空地需要绿化，某绿化组承担了此项任务，绿化组工作一段时刻后，提高了工作效率．该绿化组完成的绿化面积S（单位：m2）与工作时刻t（单位：h）之间的函数关系如图所示，则该绿化组提高工作效率前每小时完成的绿化面积是（）A．300m2B．150m2C．330m2D．450m2二、填空题（每小题3分，共计30分）11．将5700 000用科学记数法表示为．12．函数y=中，自变量x的取值范畴是．13．运算2﹣的结果是．14．把多项式ax2+2a2x+a3分解因式的结果是．15．一个扇形的圆心角为120°，面积为12πcm2，则此扇形的半径为cm．16．二次函数y=2（x﹣3）2﹣4的最小值为．17．在等腰直角三角形ABC中，∠ACB=90°，AC=3，点P为边BC的三等分点，连接AP，则AP的长为．18．如图，AB为⊙O的直径，直线l与⊙O相切于点C，AD⊥l，垂足为D，AD交⊙O于点E，连接OC、BE．若AE=6，OA=5，则线段DC的长为．19．一个不透亮的袋子中装有黑、白小球各两个，这些小球除颜色外无其他差别，从袋子中随机摸出一个小球后，放回并摇匀，再随机摸出一个小球，则两次摸出的小球差不多上白球的概率为．20．如图，在菱形ABCD中，∠BAD=120°，点E、F分别在边AB、BC上，△BEF与△GEF关于直线EF 对称，点B的对称点是点G，且点G在边AD上．若EG⊥AC，AB=6，则FG的长为．三、解答题（其中21-22题各7分，23-24题各8分，25-27题各10分，共计60分）21．先化简，再求代数式（﹣）÷的值，其中a=2sin60°+tan45°．22．图1、图2是两张形状和大小完全相同的方格纸，方格纸中每个小正方形的边长均为1，线段AC的两个端点均在小正方形的顶点上．（1）如图1，点P在小正方形的顶点上，在图1中作出点P关于直线AC的对称点Q，连接AQ、QC、CP、PA，并直截了当写出四边形AQCP的周长；（2）在图2中画出一个以线段AC为对角线、面积为6的矩形ABCD，且点B和点D均在小正方形的顶点上．23．海静中学开展以“我最喜爱的职业”为主题的调查活动，围绕“在演员、教师、大夫、律师、公务员共五类职业中，你最喜爱哪一类？（必选且只选一类）”的问题，在全校范畴内随机抽取部分学生进行问卷调查，将调查结果整理后绘制成如图所示的不完整的统计图，请你依照图中提供的信息回答下列问题：（1）本次调查共抽取了多少名学生？（2）求在被调查的学生中，最喜爱教师职业的人数，并补全条形统计图；（3）若海静中学共有1500名学生，请你估量该中学最喜爱律师职业的学生有多少名？24．已知：如图，在正方形ABCD中，点E在边CD上，AQ⊥BE于点Q，DP⊥AQ于点P．（1）求证：AP=BQ；（2）在不添加任何辅助线的情形下，请直截了当写出图中四对线段，使每对中较长线段与较短线段长度的差等于PQ的长．25．早晨，小明步行到离家900米的学校去上学，到学校时发觉眼镜忘在家中，因此他赶忙按原路步行回家，拿到眼镜后赶忙按原路骑自行车返回学校．已知小明步行从学校到家所用的时刻比他骑自行车从家到学校所用的时刻多10分钟，小明骑自行车速度是步行速度的3倍．（1）求小明步行速度（单位：米/分）是多少；（2）下午放学后，小明骑自行车回到家，然后步行去图书馆，假如小明骑自行车和步行的速度不变，小明步行从家到图书馆的时刻不超过骑自行车从学校到家时刻的2倍，那么小明家与图书馆之间的路程最多是多少米？26．已知：△ABC内接于⊙O，D是上一点，OD⊥BC，垂足为H．（1）如图1，当圆心O在AB边上时，求证：AC=2OH；（2）如图2，当圆心O在△ABC外部时，连接AD、CD，AD与BC交于点P，求证：∠ACD=∠APB；（3）在（2）的条件下，如图3，连接BD，E为⊙O上一点，连接DE交BC于点Q、交AB于点N，连接OE，BF为⊙O的弦，BF⊥OE于点R交DE于点G，若∠ACD﹣∠ABD=2∠BDN，AC=5，BN=3，tan∠ABC=，求BF的长．27．如图，在平面直角坐标系中，O为坐标原点，抛物线y=ax2+2xa+c通过A（﹣4，0），B（0，4）两点，与x轴交于另一点C，直线y=x+5与x轴交于点D，与y轴交于点E．（1）求抛物线的解析式；（2）点P是第二象限抛物线上的一个动点，连接EP，过点E作EP的垂线l，在l上截取线段EF，使EF=EP，且点F在第一象限，过点F作FM⊥x轴于点M，设点P的横坐标为t，线段FM的长度为d，求d与t之间的函数关系式（不要求写出自变量t的取值范畴）；（3）在（2）的条件下，过点E作EH⊥ED交MF的延长线于点H，连接DH，点G为DH的中点，当直线PG通过AC的中点Q时，求点F的坐标．2021年黑龙江省哈尔滨市中考数学试卷参考答案与试题解析一、选择题（每小题3分，共计30分）1．﹣6的绝对值是（）A．﹣6 B．6 C．D．﹣【考点】绝对值．【分析】依照负数的绝对值是它的相反数，可得答案．【解答】解：﹣6的绝对值是6．故选：B．2．下列运算正确的是（）A．a2•a3=a6B．（a2）3=a5C．（﹣2a2b）3=﹣8a6b3D．（2a+1）2=4a2+2a+1【考点】幂的乘方与积的乘方；同底数幂的乘法；完全平方公式．【分析】分别利用幂的乘方运算法则以及合并同类项法则以及完全平方公式、同底数幂的乘法运算法则、积的乘方运算法则分别化简求出答案．【解答】解：A、a2•a3=a5，故此选项错误；B、（a2）3=a6，故此选项错误；C、（﹣2a2b）3=﹣8a6b3，正确；D、（2a+1）2=4a2+4a+1，故此选项错误；故选：C．3．下列图形中，既是轴对称图形又是中心对称图形的是（）A．B．C．D．【考点】中心对称图形；轴对称图形．【分析】依据轴对称图形的定义和中心对称图形的定义回答即可．【解答】解：A、是轴对称图形，但不是中心对称图形，故A错误；B、是轴对称图形，也是中心对称图形，故B正确；C、是中心对称图形，但不是轴对称图形，故C错误；D、是轴对称图形，但不是中心对称图形，故D错误．故选：B．4．点（2，﹣4）在反比例函数y=的图象上，则下列各点在此函数图象上的是（）A．（2，4）B．（﹣1，﹣8）C．（﹣2，﹣4）D．（4，﹣2）【考点】反比例函数图象上点的坐标特点．【分析】由点（2，﹣4）在反比例函数图象上结合反比例函数图象上点的坐标特点，即可求出k值，再去验证四个选项中横纵坐标之积是否为k值，由此即可得出结论．【解答】解：∵点（2，﹣4）在反比例函数y=的图象上，∴k=2×（﹣4）=﹣8．∵A中2×4=8；B中﹣1×（﹣8）=8；C中﹣2×（﹣4）=8；D中4×（﹣2）=﹣8，∴点（4，﹣2）在反比例函数y=的图象上．故选D．5．五个大小相同的正方体搭成的几何体如图所示，其主视图是（）A．B．C．D．【考点】简单组合体的三视图．【分析】依照从正面看得到的图形是主视图，可得答案．【解答】解：从正面看第一层是三个小正方形，第二层右边是两个小正方形，故选：C．6．不等式组的解集是（）A．x≥2 B．﹣1＜x≤2 C．x≤2 D．﹣1＜x≤1【考点】解一元一次不等式组．【分析】分别求出每一个不等式的解集，依照口诀：同大取大确定不等式组的解集．【解答】解：解不等式x+3＞2，得：x＞﹣1，解不等式1﹣2x≤﹣3，得：x≥2，∴不等式组的解集为：x≥2，故选：A．7．某车间有26名工人，每人每天能够生产800个螺钉或1000个螺母，1个螺钉需要配2个螺母，为使每天生产的螺钉和螺母刚好配套．设安排x名工人一辈子产螺钉，则下面所列方程正确的是（）A．2×1000（26﹣x）=800x B．1000（13﹣x）=800xC．1000（26﹣x）=2×800x D．1000（26﹣x）=800x【考点】由实际问题抽象出一元一次方程．【分析】题目差不多设出安排x名工人一辈子产螺钉，则（26﹣x）人一辈子产螺母，由一个螺钉配两个螺母可知螺母的个数是螺钉个数的2倍从而得出等量关系，就能够列出方程．【解答】解：设安排x名工人一辈子产螺钉，则（26﹣x）人一辈子产螺母，由题意得1000（26﹣x）=2×800x，故C答案正确，故选C8．如图，一艘轮船位于灯塔P的北偏东60°方向，与灯塔P的距离为30海里的A处，轮船沿正南方向航行一段时刻后，到达位于灯塔P的南偏东30°方向上的B处，则现在轮船所在位置B处与灯塔P之间的距离为（）A．60海里B．45海里C．20海里D．30海里【考点】勾股定理的应用；方向角．【分析】依照题意得出：∠B=30°，AP=30海里，∠APB=90°，再利用勾股定理得出BP的长，求出答案．【解答】解：由题意可得：∠B=30°，AP=30海里，∠APB=90°，故AB=2AP=60（海里），则现在轮船所在位置B处与灯塔P之间的距离为：BP==30（海里）故选：D．9．如图，在△ABC中，D、E分别为AB、AC边上的点，DE∥BC，BE与CD相交于点F，则下列结论一定正确的是（）A．=B．C．D．【考点】相似三角形的判定与性质．【分析】依照平行线分线段成比例定理与相似三角形的对应边成比例，即可求得答案．【解答】解；A、∵DE∥BC，∴，故正确；B、∵DE∥BC，∴△DEF∽△CBF，∴，故错误；C、∵DE∥BC，∴，故错误；D、∵DE∥BC，∴△DEF∽△CBF，∴，故错误；故选：A．10．明君社区有一块空地需要绿化，某绿化组承担了此项任务，绿化组工作一段时刻后，提高了工作效率．该绿化组完成的绿化面积S（单位：m2）与工作时刻t（单位：h）之间的函数关系如图所示，则该绿化组提高工作效率前每小时完成的绿化面积是（）A．300m2B．150m2C．330m2D．450m2【考点】一次函数的应用．【分析】依照待定系数法可求直线AB的解析式，再依照函数上点的坐标特点得出当x=2时，y的值，再依照工作效率=工作总量÷工作时刻，列出算式求出该绿化组提高工作效率前每小时完成的绿化面积．【解答】解：如图，设直线AB的解析式为y=kx+b，则，解得．故直线AB的解析式为y=450x﹣600，当x=2时，y=450×2﹣600=300，300÷2=150（m2）．答：该绿化组提高工作效率前每小时完成的绿化面积是150m2．二、填空题（每小题3分，共计30分）11．将5700 000用科学记数法表示为 5.7×106．【考点】科学记数法—表示较大的数．【分析】科学记数法的表示形式为a×10n的形式．其中1≤|a|＜10，n为整数，确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞10时，n是正数；当原数的绝对值＜1时，n是负数．【解答】解：5700 000=5.7×106．故答案为：5.7×106．12．函数y=中，自变量x的取值范畴是x≠．【考点】函数自变量的取值范畴．【分析】依照分母不为零是分式有意义的条件，可得答案．【解答】解：由题意，得2x﹣1≠0，解得x≠，故答案为：x≠．13．运算2﹣的结果是﹣2．【考点】二次根式的加减法．【分析】先将各个二次根式化成最简二次根式，再把同类二次根式进行合并求解即可．【解答】解：原式=2×﹣3=﹣3=﹣2，故答案为：﹣2．14．把多项式ax2+2a2x+a3分解因式的结果是a（x+a）2．【考点】提公因式法与公式法的综合运用．【分析】第一提取公因式a，然后将二次三项式利用完全平方公式进行分解即可．【解答】解：ax2+2a2x+a3=a（x2+2ax+a2）=a（x+a）2，故答案为：a（x+a）215．一个扇形的圆心角为120°，面积为12πcm2，则此扇形的半径为6cm．【考点】扇形面积的运算．【分析】依照扇形的面积公式S=即可求得半径．【解答】解：设该扇形的半径为R，则=12π，解得R=6．即该扇形的半径为6cm．故答案是：6．16．二次函数y=2（x﹣3）2﹣4的最小值为﹣4．【考点】二次函数的最值．【分析】题中所给的解析式为顶点式，可直截了当得到顶点坐标，从而得出解答．【解答】解：二次函数y=2（x﹣3）2﹣4的开口向上，顶点坐标为（3，﹣4），因此最小值为﹣4．故答案为：﹣4．17．在等腰直角三角形ABC中，∠ACB=90°，AC=3，点P为边BC的三等分点，连接AP，则AP的长为或．【考点】等腰直角三角形．【分析】①如图1依照已知条件得到PB=BC=1，依照勾股定理即可得到结论；②如图2，依照已知条件得到PC=BC=1，依照勾股定理即可得到结论．【解答】解：①如图1，∵∠ACB=90°，AC=BC=3，∵PB=BC=1，∴CP=2，∴AP==，②如图2，∵∠ACB=90°，AC=BC=3，∵PC=BC=1，∴AP==，综上所述：AP的长为或，故答案为：或．18．如图，AB为⊙O的直径，直线l与⊙O相切于点C，AD⊥l，垂足为D，AD交⊙O于点E，连接OC、BE．若AE=6，OA=5，则线段DC的长为4．【考点】切线的性质．【分析】OC交BE于F，如图，有圆周角定理得到∠AEB=90°，加上AD⊥l，则可判定BE∥CD，再利用切线的性质得OC⊥CD，则OC⊥BE，原式可判定四边形CDEF为矩形，因此CD=EF，接着利用勾股定理运算出BE，然后利用垂径定理得到EF的长，从而得到CD的长．【解答】解：OC交BE于F，如图，∵AB为⊙O的直径，【分析】依据题意先用列表法或画树状图法分析所有等可能的显现结果，然后依照概率公式求出该事件的概率即可．【解答】解：列表得，黑1 黑2 白1 白2黑1 黑1黑1 黑1黑2 黑1白1 黑1白2黑2 黑2黑1 黑2黑2 黑2白1 黑2白2白1 白1黑1 白1黑2 白1白1 白1白2白2 白2黑1 白2黑2 白2白1 白2白2∵由表格可知，不放回的摸取2次共有16种等可能结果，其中两次摸出的小球差不多上白球有4种结果，∴两次摸出的小球差不多上白球的概率为：=，故答案为：．20．如图，在菱形ABCD中，∠BAD=120°，点E、F分别在边AB、BC上，△BEF与△GEF关于直线EF 对称，点B的对称点是点G，且点G在边AD上．若EG⊥AC，AB=6，则FG的长为3．【考点】菱形的性质．【分析】第一证明△ABC，△ADC差不多上等边三角形，再证明FG是菱形的高，依照2•S△ABC=BC•FG 即可解决问题．【解答】解：∵四边形ABCD是菱形，∠BAD=120°，∴AB=BC=CD=AD，∠CAB=∠CAD=60°，∴△ABC，△ACD是等边三角形，∵EG⊥AC，∴∠AEG=∠AGE=30°，∵∠B=∠EGF=60°，∴∠AGF=90°，∴FG⊥BC，∴2•S△ABC=BC•FG，∴2××（6）2=6•FG，∴FG=3．故答案为3．三、解答题（其中21-22题各7分，23-24题各8分，25-27题各10分，共计60分）21．先化简，再求代数式（﹣）÷的值，其中a=2sin60°+tan45°．【考点】分式的化简求值；专门角的三角函数值．【分析】先算括号里面的，再算除法，最后把a的值代入进行运算即可．【解答】解：原式=[﹣]•（a+1）=•（a+1）=•（a+1）=•（a+1）=，当a=2sin60°+tan45°=2×+1=+1时，原式==．22．图1、图2是两张形状和大小完全相同的方格纸，方格纸中每个小正方形的边长均为1，线段AC的两个端点均在小正方形的顶点上．（1）如图1，点P在小正方形的顶点上，在图1中作出点P关于直线AC的对称点Q，连接AQ、QC、CP、PA，并直截了当写出四边形A QCP的周长；（2）在图2中画出一个以线段AC为对角线、面积为6的矩形ABCD，且点B和点D均在小正方形的顶点上．【考点】作图-轴对称变换．【分析】（1）直截了当利用网格结合勾股定理得出符合题意的答案；（2）直截了当利用网格结合矩形的性质以及勾股定理得出答案．【解答】解：（1）如图1所示：四边形AQCP即为所求，它的周长为：4×=4；（2）如图2所示：四边形ABCD即为所求．23．海静中学开展以“我最喜爱的职业”为主题的调查活动，围绕“在演员、教师、大夫、律师、公务员共五类职业中，你最喜爱哪一类？（必选且只选一类）”的问题，在全校范畴内随机抽取部分学生进行问卷调查，将调查结果整理后绘制成如图所示的不完整的统计图，请你依照图中提供的信息回答下列问题：（1）本次调查共抽取了多少名学生？（2）求在被调查的学生中，最喜爱教师职业的人数，并补全条形统计图；（3）若海静中学共有1500名学生，请你估量该中学最喜爱律师职业的学生有多少名？【考点】条形统计图；用样本估量总体；扇形统计图．【分析】（1）用条形图中演员的数量结合扇形图中演员的百分比能够求出总调查学生数；（2）用总调查数减去其他几个职业类别就能够得到最喜爱教师职业的人数；（3）利用调查学生中最喜爱律师职业的学生百分比可求出该中学中的相应人数．【解答】解：（1）12÷20%=60，答：共调查了60名学生．（2）60﹣12﹣9﹣6﹣24=9，答：最喜爱的教师职业人数为9人．如图所示：（3）×1500=150（名）答：该中学最喜爱律师职业的学生有150名．24．已知：如图，在正方形ABCD中，点E在边CD上，AQ⊥BE于点Q，DP⊥AQ于点P．（1）求证：AP=BQ；（2）在不添加任何辅助线的情形下，请直截了当写出图中四对线段，使每对中较长线段与较短线段长度的差等于PQ的长．【考点】正方形的性质；全等三角形的判定与性质．【分析】（1）依照正方形的性质得出AD=B A，∠BAQ=∠ADP，再依照已知条件得到∠AQB=∠DPA，判定△AQB≌△DPA并得出结论；（2）依照AQ﹣AP=PQ和全等三角形的对应边相等进行判定分析．【解答】解：（1）∵正方形ABCD∴AD=BA，∠BAD=90°，即∠BAQ+∠DAP=90°∵DP⊥AQ∴∠ADP+∠DAP=90°∴∠BAQ=∠ADP∵AQ⊥BE于点Q，DP⊥AQ于点P∴∠AQB=∠DPA=90°∴△AQB≌△DPA（AAS）∴AP=BQ（2）①AQ﹣AP=PQ②AQ﹣BQ=PQ③DP﹣AP=PQ④DP﹣BQ=PQ25．早晨，小明步行到离家900米的学校去上学，到学校时发觉眼镜忘在家中，因此他赶忙按原路步行回家，拿到眼镜后赶忙按原路骑自行车返回学校．已知小明步行从学校到家所用的时刻比他骑自行车从家到学校所用的时刻多10分钟，小明骑自行车速度是步行速度的3倍．（1）求小明步行速度（单位：米/分）是多少；（2）下午放学后，小明骑自行车回到家，然后步行去图书馆，假如小明骑自行车和步行的速度不变，小明步行从家到图书馆的时刻不超过骑自行车从学校到家时刻的2倍，那么小明家与图书馆之间的路程最多是多少米？【考点】分式方程的应用；一元一次不等式的应用．【分析】（1）设小明步行的速度是x米/分，依照题意可得等量关系：小明步行回家的时刻=骑车返回时刻+10分钟，依照等量关系列出方程即可；（2）依照（1）中运算的速度列出不等式解答即可．【解答】解：（1）设小明步行的速度是x米/分，由题意得：，解得：x=60，经检验：x=60是原分式方程的解，答：小明步行的速度是60米/分；（2）小明家与图书馆之间的路程最多是y米，依照题意可得：，解得：y≤240，答：小明家与图书馆之间的路程最多是240米．26．已知：△ABC内接于⊙O，D是上一点，OD⊥BC，垂足为H．（1）如图1，当圆心O在AB边上时，求证：AC=2OH；（2）如图2，当圆心O在△ABC外部时，连接AD、CD，AD与BC交于点P，求证：∠ACD=∠APB；（3）在（2）的条件下，如图3，连接BD，E为⊙O上一点，连接DE交BC于点Q、交AB于点N，连接OE，BF为⊙O的弦，BF⊥OE于点R交DE于点G，若∠ACD﹣∠ABD=2∠BDN，AC=5，BN=3，tan∠ABC=，求BF的长．【考点】圆的综合题．【分析】（1）OD⊥BC可知点H是BC的中点，又中位线的性质可得AC=2OH；（2）由垂径定理可知：，因此∠BAD=∠CAD，由因为∠ABC=∠ADC，因此∠ACD=∠APB；（3）由∠ACD﹣∠ABD=2∠BDN可知∠AND=90°，由tan∠ABC=可知NQ和BQ的长度，再由BF⊥OE和OD⊥BC可知∠GBN=∠ABC，因此BG=BQ，连接AO并延长交⊙O于点I，连接IC后利用圆周角定理可求得IC和AI的长度，设QH=x，利用勾股定理可求出QH和HD的长度，利用垂径定理可求得ED的长度，最后利用tan∠OED=即可求得RG的长度，最后由垂径定理可求得BF的长度．【解答】解：（1）∵OD⊥BC，∴由垂径定理可知：点H是BC的中点，∵点O是AB的中点，∴OH是△ABC的中位线，∴AC=2OH；（2）∵OD⊥BC，∴由垂径定理可知：，∴∠BAD=∠CAD，∵，∴∠ABC=∠ADC，∴180°﹣∠BA D﹣∠ABC=180°﹣∠CAD﹣∠ADC，∴∠ACD=∠APB，（3）连接AO延长交于⊙O于点I，连接IC，AB与OD相交于点M，∵∠ACD﹣∠ABD=2∠BDN，∴∠ACD﹣∠BDN=∠ABD+∠BDN，∵∠ABD+∠BDN=∠AND，∴∠ACD﹣∠BDN=∠AND，∵∠ACD+∠ABD=180°，∴∠ABD+∠BDN=180°﹣∠AND，∴∠AND=180°﹣∠AND，∴∠AND=90°，∵tan∠ABC=，BN=3，∴NQ=，∴由勾股定理可求得：BQ=，∵∠BNQ=∠QHD=90°，∴∠ABC=∠QDH，∵OE=OD，∴∠OED=∠QDH，∵∠ERG=90°，∴∠OED=∠GBN，∴∠GBN=∠ABC，∵AB⊥ED，∴BG=BQ=，GN=NQ=，∵AI是⊙O直径，∴∠ACI=90°，∵tan∠AIC=tan∠ABC=，∴=，∴IC=10，∴由勾股定理可求得：AI=25，连接OB，设QH=x，∵tan∠ABC=tan∠ODE=，∴，∴HD=2x，∴OH=OD﹣HD=﹣2x，BH=BQ+QH=+x，由勾股定理可得：OB2=BH2+OH2，∴（）2=（+x）2+（﹣2x）2，解得：x=或x=，当QH=时，∴QD=QH=，∴ND=QD+NQ=6，∴MN=3，MD=15∵MD，∴QH=不符合题意，舍去，当QH=时，∴QD=QH=∴ND=NQ+QD=4，由垂径定理可求得：ED=10，∴GD=GN+ND=∴EG=ED﹣GD=，∵tan∠OED=，∴，∴EG=RG，∴RG=，∴BR=RG+BG=12∴由垂径定理可知：BF=2BR=24．27．如图，在平面直角坐标系中，O为坐标原点，抛物线y=ax2+2xa+c通过A（﹣4，0），B（0，4）两点，与x轴交于另一点C，直线y=x+5与x轴交于点D，与y轴交于点E．（1）求抛物线的解析式；（2）点P是第二象限抛物线上的一个动点，连接EP，过点E作EP的垂线l，在l上截取线段EF，使EF=EP，且点F在第一象限，过点F作FM⊥x轴于点M，设点P的横坐标为t，线段FM的长度为d，求d与t之间的函数关系式（不要求写出自变量t的取值范畴）；（3）在（2）的条件下，过点E作EH⊥ED交MF的延长线于点H，连接DH，点G为DH的中点，当直线PG通过AC的中点Q时，求点F的坐标．【考点】二次函数综合题．【分析】（1）利用待定系数法求二次函数的解析式；（2）如图1，作辅助线构建两个直角三角形，利用斜边PE=EF和两角相等证两直角三角形全等，得PA′=EB′，则d=FM=OE﹣EB′代入列式可得结论，但要注意PA′=﹣t；（3）如图2，依照直线EH的解析式表示出点F的坐标和H的坐标，发觉点P和点H的纵坐标相等，则PH与x轴平行，依照平行线截线段成比例定理可得G也是PQ的中点，由此表示出点G的坐标并列式，求出t的值并取舍，运算出点F的坐标．【解答】解：（1）把A（﹣4，0），B（0，4）代入y=ax2+2xa+c得，解得，因此抛物线解析式为y=﹣x2﹣x+4；（2）如图1，分别过P、F向y轴作垂线，垂足分别为A′、B′，过P作PN⊥x轴，垂足为N，由直线DE的解析式为：y=x+5，则E（0，5），∴OE=5，∵∠PEO+∠OEF=90°，∠PEO+∠EPA′=90°，∴∠EPA′=∠OEF，∵PE=EF，∠EA′P=∠EB′F=90°，∴△PEA′≌△EFB′，∴PA′=EB′=﹣t，则d=FM=OB′=OE﹣EB′=5﹣（﹣t）=5+；（3）如图2，由直线DE的解析式为：y=x+5，∵EH⊥ED，∴直线EH的解析式为：y=﹣x+5，∴FB′=A′E=5﹣（﹣t2﹣t+4）=t2+t+1，∴F（t2+t+1，5+t），∴点H的横坐标为：t2+t+1，y=﹣t2﹣t﹣1+5=﹣t2﹣t+4，∴H（t2+t+1，﹣t2﹣t+4），∵G是DH的中点，∴G（，），∴G（t2+t﹣2，﹣t2﹣t+2），∴PH∥x轴，∵DG=GH，∴PG=GQ，∴=t2+t﹣2，t=，∵P在第二象限，∴t＜0，∴t=﹣，∴F（4﹣，5﹣）．。

九年级中考调研测试数学试卷（一）一、单选题1.如果冰箱冷藏室的温度是5℃，冷冻室的温度是-3℃，则冷藏室比冷冻室高（）A.8℃B.-8℃C.-2℃D.2℃【答案】A【考点】有理数的减法【解析】【解答】解：5﹣（﹣3）=5+3=8．故答案为：A．【分析】求冷藏室比冷冻室温度高多少，就用冰箱冷藏室的温度减去冷冻室的温度，根据有理数的减法即可得出答案。

2.下列图形中,不是轴对称图形的是()A. B. C. D.【答案】D【考点】轴对称图形【解析】【解答】解：A．是轴对称图形，故不符合题意；B．是轴对称图形，故不符合题意；C．是轴对称图形，故不符合题意；D．不是轴对称图形，故符合题意．故答案为：D．【分析】把一个图形沿着某条直线折叠，直线两旁的部分能完全重合的图形就是轴对称图形；根据定义一一判断即可。

3.下列运算中，正确的是（）A.x·x2= x2B.（xy）2=xy2C.D.x2+x2=2x4【答案】C【考点】同底数幂的乘法，幂的乘方与积的乘方，合并同类项法则及应用【解析】【解答】A.x·x2=x3 ，故不符合题意；B.（xy）2=x2y2，故不符合题意；C. 符合题意；D.x2+x2=2x2，故不符合题意；故答案为：C.【分析】根据同底数幂的乘法，底数不变指数相加；积的乘方，等于把积中的每一个因式分别乘方，再把所得的幂相乘；合并同类项法则，只把系数相加减，字母和字母的指数都不变；幂的乘方，底数不变，指数相乘；根据法则一一判断即可。

4.如左图是由几个相同的小正方体搭成的一个几何体，它的左视图是（）A. B. C. D.【答案】B【考点】简单组合体的三视图【解析】【解答】解：从左向右看第一列是两个正方体，第二列式一个正方体，故答案为：B．【分析】求简单几何体的左视图，就是从左向右看得到的正投影，从左向右看第一列是两个正方体，第二列式一个正方体从而得出答案。

5.反比例函数(k为常数,k≠0)的图象位于()A.第一、二象限B.第一、三象限C.第二、四象限D.第三、四象限【答案】C【考点】反比例函数的图象【解析】【解答】解：∵k≠0，∴k2＞0，∴﹣k2＜0，∴反比例函数（k为常数，k≠0）的图象位于第二、四象限．故答案为：C．【分析】根据偶次方的非负性及已知条件可知：k2＞0，故﹣k2＜0，根据双曲线的比例系数小于0，则图像位于第二、四象限．即可得出答案。

数 学 试 卷（考试时间共100分钟，满分120分）准考证号：__________ 姓名：________ 座位号：___________{请同学们保持良好的心态，认真审真，认真答题，切不可马虎应付}一、选择题(每小题3分,共30分)1.如果冰箱冷藏室的温度是5℃，冷冻室的温度是-3℃，则冷藏室比冷冻室高（ ）A.8℃ B.-8℃ C.-2℃ D.2℃2.下列图形中,不是轴对称图形的是( )3.下列运算中,正确的是（ ）A.2a 6a 2a 3=• B.()532a a = C.426a a -a =D.ab 8b 5a 3=+ 4.如图,是由几个相同的小正方体搭成的一个几何体,它的左视图是( )A B C D5.反比例函数x k -y 2=(k 为常数,k ≠0)的图象位于( )A.第一、二象限 B.第一、三象限 C.第二、四象限 D.第三、四象限6.如图,飞机在空中B 处探测到它的正下方地面上目标C,此时飞行高度BC=1200米,从飞机上看地面指挥台A 的俯角α的正切值为43则飞机与指挥台之间AB 的距离为( )米A.1200B.1600C.1800D.2000 7.将抛物线y=x 2向左平移2个单位,再向下平移3个单位,得到的抛物线解析式是( ）A.()3-2-x y 2=B.()32-x y 2+=C.()3-2x y 2+=D.()32x y 2++=8.如图,在菱形ABCB 中,点E 在AD 边上,EF ∥CD,交对角线BD 于点F,则下列结论中错误的是( )第8题 第9题 第10题A.BF DF AE DE = B.DB DF AD EF = C.BF DF AD EF = D.DB DF CD EF =9.如图,△ABC 为等边三角形,将△ABC 绕点A 逆时针旋转75°,得到△AED,过点E 作EF ⊥AC,垂足为点F,若AC=8,则AF 的长为( ）A.4 B.3C.64D.2410.在一次越野赛中,甲选手匀速跑完全程,乙选手1.5小时后速度为每小时10千米,两选手的行程y(千米)随时间x(小时）变化的图像（全程）如图所示，则乙比甲晚到（ ）小时。

2021年平房区中考调研测试(一)英语试卷考生须知：1.本试卷满分为100分，考试时间为100分钟。

2．答题前，考生先将自己的"姓名"、"考号"、"考场"、"座位号"在答题卡上填写清楚，将条形码准确粘贴在条形码区域内。

3.请按照题号顺序在答题卡各题目的答题区域内作答，超出答题区域书写的答案无效;在草稿纸、试题纸上答题无效。

4.选择题必须使用2B铅笔填涂;非选择题必须使用0.5毫米黑色字迹的签字笔书写，字体工整、笔迹清楚。

5.保持卡面整洁，不要折叠、不要弄脏、不要弄皱，不准使用涂改液、修正带、刮纸刀。

第I 卷一、单项选择(本题共20分, 每小题1分)选择最佳答案。

1. Which pair of the words with the underlined letters has the same sound?A. down allowB. above goldC. treat great2. In the following words, which underlined letters have a different sound from the others?A machine B. cheap C. change3. Which of the following words doesn’t have the same stress as the others?A. Effort.B. Attract.C. Supply.4. No matter how small __________ star is, it shines in the darkness. Have confidence in yourself and try your best.A. theB. aC. an5. Chinese time-travel comedy Hi. Mom entered the world's top 100 _________March, 2021 with the ticket sales of 5. 15 billion(十亿) yuan.A. at B in C. on6. Keep calm! A good grade depends on good behavior and hard work. If you believe in yourself, success will belong to ____________.A. yourB. youC. yours7, —Ben is a really hard-working student.—He studies so hard ___________ he wants to enter No. 3 High School.A. that B because C. if8, —The cinemas in Harbin are open now. Let's go to the movies.—Really? The news really __________ everyone.A. cheers upB. puts upC. fixes up9. A home without books is like a house without windows. Books, which guide us to the bright future, are great ___________ in our daily life.A. treasureB. balanceC. emotion10. Communist Party of China(中国共产党)will celebrate its __________ birthday on July 1st, 202 l . We will never forget that the peaceful and happy life is worth protecting with blood and lives.A. 100B. 100thC. the 100th11. —Which do you enjoy ___________the coming summer vacation, staying at home or going on vacation on the beach?—I prefer staying at home to have a rest.A. spendingB. to spendC. spend12. —To make our school more beautiful, we _________ throw the rubbish on the ground. —Everyone should play an important part in doing it.A. needn't B mustn't C. may not13. —Look! Somebody ______________the light in our classroom.—Well, it wasn't me. I didn't do that.A. is turning off B was turning off C. has turned off)14. With the development of the society and technology, smart phones seem to be __________ popular. However, we students should use them in a correct way.A. less and lessB. fewer and fewerC. more and more15. —Who is the lady ___________ is talking with your mom over there?—Oh, it's Mrs. Wang, our new English teacher.A. thatB. whichC. who16. ―Could you tell me __________________?—I am not sure. But the Internet says it is 100 yuan for one person.A. how much did you pay for Harbin Ice and Snow WorldB. what the price of Harbin Ice and Snow World wasC. how much I should pay for Harbin Ice and Snow World17. —At present, one of the best ways to study is working in groups.—Yes. In groups, more chances ___________to the students to learn from each other.A. offerB. are offeredC. have offered18. The World Trade Center in _________ was taken down by terrorists on September 11, 2001, which has meaning to most Americans.A. BerlinB. New YorkC. London19. It's convenient to use some apps to call for a car. To keep safe, you should .①call your parents or friends to let them know the license plate number(车牌号)②talk about your personal information with the driver③use some apps that meet the standards of the law④accept the driver's invitation without telling others⑤turn on your GPS and share it with your parents or friendsA. ①③⑤B①③④ C. ②③⑤20. Many students like doing different things on holiday. We made a survey among 200 students in Sunshine Middle School. According to the table, s tudents like traveling.A. 60B. 90C. 110二、完形填空(本题共10分, 每小题1分)Saint Nicholas was very rich and liked to help others. He also cared for the 21 very much. He often brought many kinds of gifts, money and other useful things to their houses. He did this at night secretly so that no one knew, because he wanted no praise and just wanted to help others.At that time, there were three poor kids in a family in his town. 22 of their parents died. They could hardly make enough money to make a living. Nicholas felt sorry for them and decided to do 23 to help them._24 the night before Christmas, when everyone was asleep, Nicholas walked through the streets to the house where the three kids lived. Quietly, he climbed onto the roof (屋顶)and dropped three bags of gold into the chimney(烟囱). It so happened that the three kids had _25_ their stockings(长筒袜)before they went to bed. The stockings had been hung by the fire to dry. When Nicholas dropped the gold, each bag fell into a stocking.The three kids were excited to find the three bags of gold in their stockings the next morning. And all of them couldn't help 26 "What a great wonder!" Now they didn't have to worry about their meals. Soon, the story began to get around. Other 27 began to hang up stockings on that day in the hope of 28 bags of gold when they woke up the next morning.Over the years. Saint Nicholas was 29 Christmas. The 30 of hanging stockings up by the chimney on Christmas Eve was known all over the world. And Santa Claus became the most popular guest on Christmas Day.根据短文内容选择最佳答案。

2021年平房区中考调研测试（一）综 合 试 卷考生须知：1．本试卷满分为140分，考试时间为120分钟。

2．答题前，考生先将自己的“姓名”、“考号”、“考场”、“座位号”在答题卡上填写清楚，将 “条形码”准确粘贴在条形码区域内。

3．请按照题号顺序在答题卡各题目的答题区域内作答，超出答题区域书写的答案无效，在草 稿纸、试题纸上答题无效。

4．选择题必须使用2B 铅笔填涂；非选择题必须使用0.5毫米黑色字迹的签字笔书写，字迹工 整、笔迹清楚。

5．保持卡面整洁，不要折叠、不要弄脏、不要弄皱，不准使用涂改液、修正带、刮纸刀。

可能用到的相对原子质量：H －1 C －12 O －16 Na －23 Mg －24 Cl －35.5 Ca －40一、选择题（1—27题，每题2分，共54分,每题只有一个正确选项）1. 哈尔滨市被确定为国家地下综合管廊建设试点城市，哈南新区全力组织地下综合管廊建设，下列有关叙述错误的是……………………………………………………（ ）A ．地下综合管廊避免了城市道路出现“拉链式修补”的弊端B ．管廊内设置溢水沟，坑壁采用的钢筋混凝土是复合材料C ．管廊工程内各类管线均以耐腐蚀的纯铁制成D ．建造管廊时对废旧金属进行回收可减少对环境的污染2.下列过程中发生化学变化的是……………………………………………………（ ）3.下列叙述正确的是…………………………………………………………………（） A ．农业和园林浇灌最好采用喷灌和漫灌B ．生活中常用蒸馏的方法来降低水的硬度C ．贵重设备、精密仪器失火可用水基型灭火器灭火D ．发现家中燃气泄漏不能立即打开吸油烟机4.下列实验操作错误的是……………………………………………………………（ ）5.下列物质的用途正确的是…………………………………………………………（ ）A ．用铁合金制造人造骨B ．氧气用于医疗急救C ．炉具清洁剂除餐具油污D ．石墨净水 A ．石油炼制 各种产品B ．浓盐酸罐车翻 倒产生白雾C ． 碳铵放出氨味D ．用稀有气体制航标灯 A ．稀释浓硫酸 B ．液体的量取 C ．给液体加热 D ．往试管里送入固体粉末6.下列实验现象描述正确的是………………………………………………………（）A．检验电解水实验负极产生的气体：产生蓝紫色火焰，放热B．氧化铁与足量稀硫酸反应：红棕色固体逐渐减少至消失，溶液由无色变成黄色C．加热氢氧化钠溶液与硫酸铜溶液反应后的物质：蓝色固体变成黑色的氧化铜D．向氢氧化镁中加入无色酚酞溶液：无色酚酞溶液变成红色7.下列叙述、对应的化学方程式、所属基本反应类型都正确的是…………………（）A．用磁铁矿炼铁的反应：Fe2O3+ 3CO高温3CO2+ 2Fe 还原反应B．实验室用高锰酸钾制氧气：2KMnO4△ K2MnO2+MnO2 +O2↑分解反应C．用氢氧化钠溶液吸收三氧化硫：2NaOH+SO3Na2SO4 +H2O复分解反应D．探究铜和银的活动性：Cu+2AgNO32Ag+ Cu(NO3)2置换反应8.人体健康与化学关系密切，下列叙述正确的是…………………………………（）A．玉米霉变产生黄曲霉毒素对人体有害，但蒸煮后可以食用B．用pH试纸测得血浆的pH为7.4，此人一定健康C．长期食用添加过量亚硝酸钠的食品有害人体健康D．铁、锌、钙是对人体有益的微量元素9.维生素C（化学式为C6H8O6）是人体必须的营养物质，能提高免疫力，预防癌症，保护牙龈等。