第一类曲线积分的计算
- 格式:docx
- 大小:152.75 KB
- 文档页数:5

第一类曲线积分的计算第一类曲线积分的计算1、定义定义1 :设L 为平面上可求长度的曲线段,)y ,x (f 为定义在L 上的函数.对曲线L 作分割T ,它把L 分成n 个可求长度的小曲线段)n ,,2,1i (L i ,i L 的弧长记为i s ,分割T 的细度为i ni 1s max T ,在i L 上任取一点(i ,).n ,,2,1i )(i 若存在极限J s ),(f lim i i n1i i 0T且J 的值与分割T 及点),(i i 的取法无关,则称此极限为)y ,x (f 在L 上的第一型曲线积分,记作 .ds )y ,x (f L (1) 定义2: 若L 为空间可求长曲线段,)y ,x (f 为定义在L 上的函数,则可类似地定义)z ,y ,x (f 在空间曲线L 上的第一型曲线积分为J s ),,(f lim i i i n1i i 0T ,(此处i s 为i L 的弧长,i n i 1s max T ,J 为一常数),并且记作 L .ds )z ,y ,x (f (2) 2、物理意义(1)设某物体的密度函数f (P )是定义在 上的连续函数.当 是直线段时,应用定积分就能计算得该物体的质量。
现在研究当 是平面上某一可求长度的曲线段时物体的质量的计算问题.首先对 作分割,把 分成n 个可求长度的小曲线段i (i=1,2,…,n),并在每一个i 上任取一点P i由于f (P )为 上的连续函数,故当i 的弧长都很小时,每一小段i 的质量可近似地等于f (P i)i ,其中 i 为小曲线段i 的长度.于是在整个 上的质量就近似地等于和式i n1i i )P (f 当对 的分割越来越细密时,上述和式的极限就应是该物体的质量。
(2)空间曲线L 的重心坐标为(,,)(,,)yz LLx x y z dlM x Mx y z dl,(,,)(,,)zx LLy x y z dlM y Mx y z dl,(,,)(,,)xy LLz x y z dlM z Mx y z dl(3) 曲线L 的绕z 轴(x, y 轴)的转动惯量是22()(,,)z LJ x y x y z dl3、几何意义1) 当被积函数为1时, 积分的值恰为曲线的长度。

第一型曲线积分的定义第一型曲线积分,是微积分中的一种重要概念与计算方法,它涉及曲线和向量场之间的积分。
本文将介绍第一型曲线积分的定义、性质和计算方法。
一、第一型曲线积分的定义第一型曲线积分,也称为曲线的线积分,是指在曲线上某个有向长度元素$\mathrm{d}s$上的函数值与该长度元素的乘积$d\boldsymbol{s}$在整个曲线上的积分。
设$C$是曲线,其参数方程为$\boldsymbol{r}(t)=(x(t), y(t), z(t)), t\in[a,b]$,则$C$的长度由公式:$$ L(C)=\int_{C}\mathrm{d}s=\int_{a}^{b}\left[\ left(x^{\prime}(t)\right)^{2}+\left(y^{\prime}(t)\r ight)^{2}+\left(z^{\prime}(t)\right)^{2}\right]^{\f rac{1}{2}} \mathrm{d}t $$计算曲线$C$上的一个标量函数$f(x,y,z)$在曲线上的第一型曲线积分,即为:$$ \int_{C} f(x, y, z) \mathrm{d}s=\int_{a}^{b}f\left(\boldsymbol{r}(t)\right)\left[\left(x^{\prim e}(t)\right)^{2}+\left(y^{\prime}(t)\right)^{2}+\left(z^{\prime}(t)\right)^{2}\right]^{\frac{1}{2}}\mathrm{d}t $$若积分路径可以看成向量值函数$\boldsymbol{r}(t)$的积分,第一型曲线积分就可以写作:$$ \int_{\boldsymbol{r}}\boldsymbol{F}(\boldsymbol{r}) \cdot \mathrm{d}\boldsymbol{r}=\int_{a}^{b}\boldsymbol{F}\left(\boldsymbol{r}(t)\right) \cdot \boldsymbol{r}^{\prime}(t) \mathrm{d}t=\int_{a}^{b} \boldsymbol{F} \cdot \mathrm{d}\boldsymbol{s} $$其中$\boldsymbol{F}(\boldsymbol{r})$是向量场,$\mathrm{d}\boldsymbol{r}$表示一个有向长度元素,$\cdot$表示向量内积运算,$\mathrm{d}\boldsymbol{s}=\boldsymbol{r}^{\prime}(t ) \mathrm{d} t$表示线元素。


第一类曲线积分计算公式曲线积分是微积分学中的重要概念之一,在物理学、工程学、统计学等方面有着广泛的应用。
曲线积分又分为第一类曲线积分和第二类曲线积分,本文将为大家介绍第一类曲线积分的计算公式以及其在实际应用中的具体运用。
第一类曲线积分是指对于参数曲线C,取定其上的一个向量场F,对其在曲线C上的积分。
第一类曲线积分的计算公式为:∫CF·dr=∫abF(x(t),y(t))·r'(t)dt其中,a和b为曲线C的参数范围,x(t)和y(t)为曲线C上点的参数方程,r(t)为C上对应点的位置向量,r'(t)为其对应点在曲线上的切向量,F(x,y)为一个二元向量函数。
需要注意的是,由于不同的参数方程对应的切向量r'(t)不同,因此在实际应用中可能需要通过对曲线进行参数化来确定正确的积分范围和积分方向。
第一类曲线积分在实际应用中具有广泛的应用。
例如,在物理学中,它可以用来计算电场或磁场在曲线上的沿程积分;在工程学中,它可以用来计算流体在曲线上的流量或者力对物体的作用积分等等。
因此,掌握第一类曲线积分的计算公式以及其在实际应用中的具体运用是非常重要的。
除了以上所介绍的第一类曲线积分,还有第二类曲线积分。
第二类曲线积分是指对参数曲线C,取定其上的标量函数f(x,y)和向量函数F(x,y),对其在曲线C上的积分。
第二类曲线积分的计算公式为:∫CF·ds=∫abF(x(t),y(t))·r'(t)ds其中,ds表示曲线C上的线元素。
第二类曲线积分在实际应用中同样具有广泛的应用,例如在工程学中可以用来计算物体在曲线上的质心;在物理学中可以用来计算质点或者非定常电荷在曲线上的沿程积分。
总之,曲线积分在各个学科中都有着重要的应用,而第一类曲线积分的计算公式对于理解曲线积分的本质以及在实际运用中的具体应用都至关重要。
因此,我们建议大家认真学习并掌握这方面的知识,为以后的学习和工作打下坚实的基础。

曲线积分与曲面积分曲线积分与曲面积分是微积分中重要的概念和计算方法,它们在物理、工程和其他科学领域中的应用广泛。
本文将重点介绍曲线积分和曲面积分的概念、计算方法和应用。
一、曲线积分曲线积分是对曲线上的函数进行积分运算的方法。
它可以用来计算曲线上的物理量或者曲线周围的环量。
曲线积分可以分为第一类曲线积分和第二类曲线积分。
1. 第一类曲线积分第一类曲线积分也叫标量场的曲线积分,是对曲线上函数的积分。
设曲线C为参数方程r(t) = {x(t), y(t), z(t)},函数f(x, y, z)在曲线C上有定义,则第一类曲线积分的计算公式为:∫[C]f(x, y, z)ds = ∫[a,b]f(x(t), y(t), z(t))|r'(t)|dt其中ds表示曲线上的长度元素,|r'(t)|表示参数方程的导数的模。
2. 第二类曲线积分第二类曲线积分也叫矢量场的曲线积分,是对曲线上的矢量场进行积分。
设曲线C为参数方程r(t) = {x(t), y(t), z(t)},矢量场F(x, y, z)在曲线C上有定义,则第二类曲线积分的计算公式为:∫[C]F(x, y, z)•dr = ∫[a,b]F(x(t), y(t), z(t))•r'(t)dt其中•表示矢量的点积运算。
二、曲面积分曲面积分是对曲面上的函数进行积分运算的方法。
曲面积分可以分为第一类曲面积分和第二类曲面积分。
1. 第一类曲面积分第一类曲面积分也叫标量场的曲面积分,是对曲面上函数的积分。
设曲面S为参数方程r(u, v) = {x(u, v), y(u, v), z(u, v)},函数f(x, y, z)在曲面S上有定义,则第一类曲面积分的计算公式为:∬[S]f(x, y, z)dS = ∬[D]f(x(u, v), y(u, v), z(u, v))|ru × rv|dudv其中dS表示曲面上的面积元素,D为参数化区域,ru和rv分别为参数方程r(u, v)对u和v的偏导数,ru × rv表示它们的叉积。


曲线积分的计算曲线积分是微积分中的一个重要概念,用于计算沿曲线的函数的积分。
在本文中,我们将介绍曲线积分的概念、计算方法以及一些常见的应用。
一、什么是曲线积分曲线积分是指沿曲线对一个函数进行积分的过程。
它在物理学、工程学和计算机图形学等领域中都有广泛的应用。
二、曲线积分的类型曲线积分分为第一类曲线积分和第二类曲线积分。
第一类曲线积分是沿曲线对一个标量场进行积分,常用符号为∮f(s)ds。
第二类曲线积分是沿曲线对一个向量场进行积分,常用符号为∮F⋅dr。
三、第一类曲线积分的计算计算第一类曲线积分的方法有很多,其中一种常见的方法是参数化曲线。
设曲线C的参数方程为x = x(t)、y = y(t),则曲线积分的计算步骤如下:1. 根据参数方程求得曲线C的切线向量r'(t);2. 计算函数f(x, y)在曲线上的取值f(x(t), y(t));3. 将r'(t)与f(x(t), y(t))相乘,得到积分被积函数;4. 确定积分的上下限,并按照常规积分的方法进行计算。
四、第二类曲线积分的计算对于第二类曲线积分,常用的计算方法有格林公式和斯托克斯定理。
格林公式适用于平面内的有向曲线,而斯托克斯定理适用于有向曲面的边界曲线。
1. 格林公式的计算设曲线C的参数方程为x = x(t)、y = y(t),向量场为F = P(x, y)i +Q(x, y)j。
则曲线积分的计算步骤如下:1. 根据参数方程求得曲线C的切线向量r'(t);2. 将向量场F与r'(t)进行点积运算,得到积分被积函数;3. 确定积分的上下限,并按照常规积分的方法进行计算。
2. 斯托克斯定理的计算对于有向曲面S的边界曲线C,设有向曲面的法向量为n,向量场为F = P i + Q j + R k。
则曲线积分的计算步骤如下:1. 计算曲线C的方向与曲面S的法向量的点积,得到积分被积函数;2. 确定积分的上下限,并按照常规积分的方法进行计算。


第一类曲线积分的三种计算方式1.参数方程法参数方程法是最常用的计算第一类曲线积分的方法之一、它利用参数方程将曲线分成若干小段,然后计算每一小段上的积分,最后将所有小段上的积分相加得到整个曲线上的积分值。
具体步骤如下:1.将曲线的参数方程表示为x=f(t),y=g(t),z=h(t),其中t的取值范围为[a,b]。
2.求出曲线的切线向量T(t)和曲率向量K(t)。
3.将向量场F(x,y,z)表示为F(x,y,z)=P(x,y,z)i+Q(x,y,z)j+R(x,y,z)k。
4. 计算曲线段的长度ds=sqrt(dx^2+dy^2+dz^2),其中dx=f'(t)dt,dy=g'(t)dt,dz=h'(t)dt。
5.将向量场在曲线上的投影F·T计算出来。
6. 将F·T乘以ds,再积分得到曲线上的积分。
参数方程法的优点是适用于任意形状的曲线,缺点是当曲线的参数方程比较复杂时,计算较为繁琐。
2.向量场法向量场法是计算第一类曲线积分的另一种常见方法。
它直接利用向量场在曲线上的投影与曲线段的长度相乘然后积分,而无需转化为参数方程。
具体步骤如下:1.将向量场F(x,y,z)表示为F(x,y,z)=P(x,y,z)i+Q(x,y,z)j+R(x,y,z)k。
2.将曲线表示为r(t)=x(t)i+y(t)j+z(t)k,其中t的取值范围为[a,b]。
3. 计算向量场在曲线上的投影F·dr,其中dr=dx i+dy j+dz k,dx=x'(t)dt,dy=y'(t)dt,dz=z'(t)dt。
4. 将F·dr积分得到曲线上的积分。
向量场法的优点是计算较为简单直接,而无需转化为参数方程,缺点是不适用于复杂的曲线形状。
3.微积分基本定理法微积分基本定理法是计算第一类曲线积分的另一个重要方法。
它利用微积分基本定理将曲线积分转化为定积分,从而简化计算过程。
第一型曲线积分计算公式:第一型曲线积分也称为路径积分或弧长积分,用于计算向量场沿着曲线的积分。
其计算公式如下:∫C F · dr其中,C 是曲线,F 是向量场,dr 是曲线上的微元弧长向量。
以下是两个实例:实例1:考虑曲线C,由参数方程r(t) = (cos(t), sin(t)),其中0 ≤ t ≤ π/2。
向量场F(x, y) = (x, y)。
我们可以首先计算曲线的切向量r'(t) = (-sin(t), cos(t))。
然后计算F · dr:F · dr= (x, y) · (dx, dy) = (x, y) · (dx/dt, dy/dt) dt [使用链式法则将dr 转换为dt] = (cos(t), sin(t)) · (-sin(t), cos(t)) dt = -sin(t)cos(t) + sin(t)cos(t) dt = 0由于F · dr = 0,因此该曲线上的第一型曲线积分为0。
实例2:考虑曲线C,由参数方程r(t) = (t, t^2),其中0 ≤ t ≤ 1。
向量场F(x, y) = (y, x)。
首先计算曲线的切向量r'(t) = (1, 2t)。
然后计算F · dr:F · dr = (y, x) · (dx, dy) = (y, x) · (dx/dt, dy/dt) dt = (t^2, t) · (1, 2t) dt = t^2 + 2t^2 dt = 3t^2 dt要计算第一型曲线积分,我们需要将积分限从参数t 转换为实际的曲线长度。
曲线长度由下式给出:s = ∫[a, b] ||r'(t)|| dt计算曲线长度:s = ∫[0, 1] ||r'(t)|| dt = ∫[0, 1] ||(1, 2t)|| dt = ∫[0, 1] sqrt(1^2 + (2t)^2) dt = ∫[0, 1] sqrt(1 + 4t^2) dt = ∫[0, 1] sqrt(4t^2 + 1) dt现在我们可以计算第一型曲线积分:∫C F · dr = ∫[0, 1] 3t^2 dt = 3∫[0, 1] t^2 dt = 3[t^3/3] [0, 1] = 1因此,该曲线上的第一型曲线积分为1。
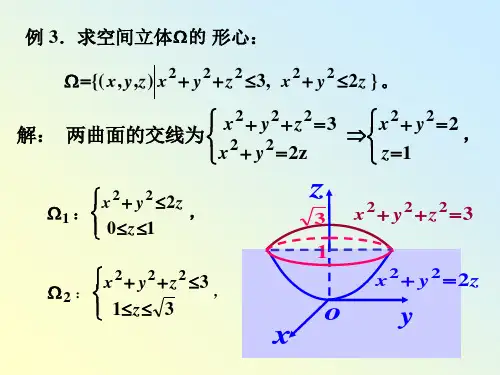
第一类曲线积分的计算
1、定义
定义1 :设L 为平面上可求长度的曲线段,)y ,x (f 为定义在L 上的函数.对曲线L 作分割T ,它把L 分成n 个可求长度的小曲线段)n ,,2,1i (L i ,i L 的弧长记为i s ,分割T 的细度为i n
i 1s max T ,在i L 上任取一点(i ,
).n ,,2,1i )(i 若存在极限J s ),(f lim i i n
1
i i 0T
且J 的值与分割T 及点),(i i 的取法无关,则称此极限为)y ,x (f 在L 上的第一型曲线积分,记作 .ds )y ,x (f L (1) 定义2: 若L 为空间可求长曲线段,)y ,x (f 为定义在L 上的函数,则可类似地
定义)z ,y ,x (f 在空间曲线L 上的第一型曲线积分为J s ),,(f lim i i i n
1
i i 0T ,
(此处i s 为i L 的弧长,i n
i 1s max T , J 为一常数),并且记作 L .ds )z ,y ,x (f (2)
2、物理意义
(1)设某物体的密度函数f (P )是定义在 上的连续函数.当 是直线段时,应用定积分就能计算得该物体的质量。
现在研究当 是平面上某一可求长度的曲线段时物体的质量的计算问题.首先对 作分割,把 分成n 个可求长度的小曲线段i (i=1,2,…,n),并在每一个i 上任取一点P i
由于f (P )为 上的连续函数,故当i 的弧长都很小时,每一小段i 的质量可近似地等于f (P i
)
i ,其中 i 为小曲线段i 的长度.于是在整个 上的质量就近似地等于和式
i n
1
i i )P (f
当对 的分割越来越细密时,上述和式的极限就应是该物体的质量。
(2)空间曲线L 的重心坐标为
(,,)(,,)yz L
L
x x y z dl
M x M
x y z dl
,
(,,)(,,)zx
L
L
y x y z dl
M y M
x y z dl
,
(,,)(,,)xy L
L
z x y z dl
M z M
x y z dl
(3) 曲线L 的绕z 轴(x, y 轴)的转动惯量是
22()(,,)z L
J x y x y z dl
3、几何意义
1) 当被积函数为1时, 积分的值恰为曲线的长度。
(2) 当.ds )y ,x (f ,0)y ,x (f L 表示以L 为准线,以平行于z 轴的线为母线的曲柱面的面积。
4、 性质
第一型曲线积分具有下述一些重要性质:
(1)若 k ,,2,1i ds y ,x f L i 存在, k ,,2,1i c i 为常数,则
ds y ,x f c i L k 1i i 也存在,且 .ds y ,x f c ds y ,x f c L i k
1
i i i L k 1i i (2)若曲线段L 由曲线k 21L ,,L ,L 首尾相接而成,且
i (ds y ,x f i
L )k ,,2,1 都存在,则 ds y ,x f L 也存在,且 ds y ,x f ds y ,x f k
1
i L L I。
(3)若 ds y ,x f L 与 ds y ,x g L 都存在,且在L 上 ,y ,x g y ,x f 则
ds y ,x g ds y ,x f L L 。
(4)若 ds y ,x f L 存在,则 .ds y ,x f L 也存在,且 ds y ,x f ds y ,x f L L 。
(5)若 ds y ,x f L 存在,L 的弧长为s ,则存在常数c,使得 ,cs ds y ,x f L
这里 y ,x f sup c y ,x f inf L
L。
5、 第一型曲线积分的计算 定理1 设有光滑曲线 L : ,,t ,
t y ,
t x
函数 y ,x f 为定义在L 上的连
续函数,则 .dt t t t ,t f ds y ,x f 2'2'L
(3) 定理2 当曲线L 由方程 b ,a x ,x y 给出,且 x 在 b ,a 上有连续导函数
时, dx x 1x ,x f ds y ,x f 2'b a
L (5) 定理3 当曲线L 由方程 d ,c y ,y x 给出,且 y 在 d ,c 上有连续导函数
时, L d c
2'.dy y 1y ,y f ds y ,x f (6) 定理4 设函数)y ,x (f 在光滑曲线上有定义且连续,曲线的方程为
0x x t y y t t t T z z t
则
,,,,T
l
t f x y z ds f x t y t z t。
定理5 设函数)y ,x (f 在光滑曲线上有定义且连续,曲线的方程为
12(,,)0
(,,)0
x y z x y z
则可化为以x 为参数的参数方程。
然后化为定理4的形式。
,,,,T
l
t f x y z ds f x y x z x。
定理6 设函数)y ,x (f 在光滑曲线上有定义且连续,曲线的的方程为
12(,)
(,)z g x y z g x y
则在一定的条件下可化为以z 为参数的参数方程,再化为定理4的形式。
,,,,T
l
t f x y z ds f x z y z z z。
历年真题
1、计算 L 2ds x ,其中L 为球面2222a z y x 被平面0z y x 所截得的圆周。
【解析】
由对称性知 L
L
22L
2ds z ds y ds x
所以.a 32ds 3a ds )z y x (31ds x 3L 2L 2
22L
2
2、求 L
ds )zx yz xy (,其中L 是球面2222a z y x 与平面0z y x 的
交线。
【解析】
L
ds )zx yz xy (
L
ds )zx yz xy (221
L
2
222ds )]z y x ()z y x [(21 L
2
22ds )z y x (21
L 32a ds 2a 3、已知曲线2x 0(x y :L 2 ,则 L xds
(2009,数一,4分)
【解析】
6
13)x 41(d x 4181dx x 41x xds 2202202L 4、已知曲线2x 1y :L ,则曲线积分 L 2
2ds )y x (
(1989,数一,3分)
【解析】
将积分曲线方程2x 1y 即)0y (1y x 22 代入被积函数,得
L L 2
2ds 1ds )y x (
5、设L 为椭圆13
y 4x 2
2 ,其周长为a ,则 L 22ds )y 4x 3xy 2(
(1998,数一,3分)
【解析】
将积分曲线方程13
y 4x 2
2 即12y 4x 322 代入被积函数,得 a 12ds 12ds )y 4x 3(L L 2
2
由于L 关于x 轴对称,函数xy 2关于变量y 为奇函数,所以0xyds 2L 所以a 12ds )y 4x 3xy 2(L 22。