下载文档原格式
《最高考系列 高考总复习》2014届高考数学总复习（考点引领+技巧点拨）选修4－2 矩阵与变换第1课时 线性变换、二阶矩阵及其乘法1. (选修42P 34习题第1题改编)求点A(2，0)在矩阵⎣⎢⎡⎦⎥⎤1 00－2对应的变换作用下得到的点的坐标．解：矩阵⎣⎢⎡⎦⎥⎤1 00－2表示横坐标保持不变，纵坐标沿y 轴负方向拉伸为原来的2倍的伸压变换，故点A(2，0)变为点A′(2，0)2. 点(－1，k)在伸压变换矩阵⎣⎢⎡⎦⎥⎤m 001之下的对应点的坐标为(－2，－4)，求m 、k 的值．解：⎣⎢⎡⎦⎥⎤m 001⎣⎢⎡⎦⎥⎤－1 k ＝⎣⎢⎡⎦⎥⎤－2－4，⎩⎪⎨⎪⎧－m ＝－2，k ＝－4. 解得⎩⎪⎨⎪⎧m ＝2，k ＝－4.3. 已知变换T 是将平面内图形投影到直线y ＝2x 上的变换，求它所对应的矩阵． 解：将平面内图形投影到直线y ＝2x 上，即是将图形上任意一点(x ，y)通过矩阵M 作用变换为(x ，2x)，则有⎣⎢⎡⎦⎥⎤a 0b 0⎣⎢⎡⎦⎥⎤x y ＝⎣⎢⎡⎦⎥⎤x 2x ，解得⎩⎪⎨⎪⎧a ＝1，b ＝2， ∴ T ＝⎣⎢⎡⎦⎥⎤1020.4. 求曲线y ＝x 在矩阵⎣⎢⎡⎦⎥⎤0110作用下变换所得的图形对应的曲线方程．解：设点(x ，y)是曲线y ＝x 上任意一点，在矩阵⎣⎢⎡⎦⎥⎤0110的作用下点变换成(x′，y ′)，则⎣⎢⎡⎦⎥⎤0110⎣⎢⎡⎦⎥⎤x y ＝⎣⎢⎡⎦⎥⎤x′y′，所以⎩⎪⎨⎪⎧x′＝y y′＝x .因为点(x ，y)在曲线y ＝x 上，所以x′＝y′，即x ＝y.5. 求直线x ＋y ＝5在矩阵⎣⎢⎡⎦⎥⎤0011 对应的变换作用下得到的图形．解：设点(x ，y)是直线x ＋y ＝5上任意一点，在矩阵⎣⎢⎡⎦⎥⎤0011的作用下点变换成(x′，y ′)，则⎣⎢⎡⎦⎥⎤0011⎣⎢⎡⎦⎥⎤x y＝⎣⎢⎡⎦⎥⎤x′y′，所以⎩⎪⎨⎪⎧x′＝0y′＝x ＋y .因为点(x ，y)在直线x ＋y ＝5上，所以y′＝x ＋y ＝5，故得到的图形是点(0，5)．1. 变换一般地，对于平面上的任意一个点(向量)(x ，y)，若按照对应法则T ，总能对应唯一的一个平面点(向量)(x′，y ′)，则称T 为一个变换，简记为T ：(x ，y )→(x′，y ′)或T ：⎣⎢⎡⎦⎥⎤x y →⎣⎢⎡⎦⎥⎤x′y′. 一般地，对于平面向量的变换T ，如果变换规则为T ：⎣⎢⎡⎦⎥⎤x y →⎣⎢⎡⎦⎥⎤x′y′＝⎣⎢⎡⎦⎥⎤ax ＋by cx ＋dy ，那么根据二阶矩阵与列向量的乘法规则，可以改写为⎣⎢⎡⎦⎥⎤x y →⎣⎢⎡⎦⎥⎤x′y′＝⎣⎢⎡⎦⎥⎤a b c d ⎣⎢⎡⎦⎥⎤x y (a 、b 、c 、d∈R )的矩阵形式，反之亦然．2. 几种常见的平面变换(1) 当M ＝⎣⎢⎡⎦⎥⎤1001时，则对应的变换是恒等变换．(2) 由矩阵M ＝⎣⎢⎡⎦⎥⎤k 001或M ＝⎣⎢⎡⎦⎥⎤100k(k>0)确定的变换T M 称为(垂直)伸压变换． (3) 反射变换是轴对称变换、中心对称变换的总称．(4) 当M ＝⎣⎢⎡⎦⎥⎤cos θ－sin θsin θ cos θ时，对应的变换叫旋转变换，即把平面图形(或点)逆时针旋转θ角度．(5) 将一个平面图投影到某条直线(或某个点)的变换称为投影变换．(6) 由矩阵M ＝⎣⎢⎡⎦⎥⎤1k 01或⎣⎢⎡⎦⎥⎤10k 1确定的变换称为切变变换．3. 变换的复合与矩阵的乘法(1) 一般情况下，AB ≠BA ，即矩阵的乘法不满足交换律． (2) 矩阵的乘法满足结合律，即(AB )C ＝A (BC )． (3) 矩阵的乘法不满足消去律． [备课札记]题型1 求变换前后的曲线方程例1 设椭圆F ：x 22＋y24＝1在(x ，y )→(x′，y ′)＝(x ＋2y ，y)对应的变换下变换成另一个图形F′，试求F′的解析式．解：变换矩阵为⎣⎢⎡⎦⎥⎤1201，任取椭圆上一点(x 0，y 0)，则⎣⎢⎡⎦⎥⎤1201⎣⎢⎡⎦⎥⎤x 0y 0＝⎣⎢⎡⎦⎥⎤x 0＋2y 0y 0，令⎩⎪⎨⎪⎧x′＝x 0＋2y 0，y ′＝y 0， 则⎩⎪⎨⎪⎧x 0＝x′－2y′，y 0＝y′. 又点(x 0，y 0)在椭圆F 上，故（x′－2y′）22＋y′24＝1，所以2x′2－8x′y′＋9y′2－4＝0，即F′的解析式为2x 2－8xy ＋9y 2－4＝0. 变式训练设M ＝⎣⎢⎡⎦⎥⎤1002，N ＝⎣⎢⎢⎡⎦⎥⎥⎤12001，试求曲线y ＝sinx 在矩阵MN 变换下的曲线方程． 解：MN ＝⎣⎢⎡⎦⎥⎤1002⎣⎢⎢⎡⎦⎥⎥⎤12001＝⎣⎢⎢⎡⎦⎥⎥⎤12002， 设(x ，y)是曲线y ＝sinx 上的任意一点，在矩阵MN 变换下对应的点为(x′，y ′)． 则⎣⎢⎢⎡⎦⎥⎥⎤12002⎣⎢⎡⎦⎥⎤xy ＝⎣⎢⎡⎦⎥⎤x′y′， 所以⎩⎪⎨⎪⎧x′＝12x ，y ′＝2y ，即⎩⎪⎨⎪⎧x ＝2x′，y ＝12y′，代入y ＝sinx 得12y ′＝sin2x ′，即y′＝2sin2x ′.即曲线y ＝sinx 在矩阵MN 变换下的曲线方程为y ＝2sin2x. 备选变式（教师专享）已知矩阵M ＝⎣⎢⎡⎦⎥⎤1 00 2，N ＝⎣⎢⎢⎡⎦⎥⎥⎤12 00 1，矩阵MN 对应的变换把曲线y ＝12sin 12x 变为曲线C ，求曲线C 的方程．解： MN ＝⎣⎢⎡⎦⎥⎤1 00 2⎣⎢⎢⎡⎦⎥⎥⎤12001＝⎣⎢⎢⎡⎦⎥⎥⎤12002， 设P(x ，y)是所求曲线C 上的任意一点，它是曲线y ＝sinx 上点P 0(x 0，y 0)在矩阵MN 变换下的对应点，则有⎣⎢⎡⎦⎥⎤x y ＝⎣⎢⎢⎡⎦⎥⎥⎤12002⎣⎢⎡⎦⎥⎤x 0y 0，即⎩⎪⎨⎪⎧x ＝12x 0，y ＝2y 0，所以⎩⎪⎨⎪⎧x 0＝2x ，y 0＝12y.又点P(x 0，y 0)在曲线y ＝12sin 12x 上，故y 0＝12sin 12x 0，从而12y ＝12sinx.所求曲线C 的方程为y ＝sinx.题型2 根据变换前后的曲线方程求矩阵例2 二阶矩阵M 对应变换将(1，－1)与(－2，1)分别变换成(5，7)与(－3，6)． (1) 求矩阵M ；(2) 若直线l 在此变换下所变换成的直线的解析式l′：11x －3y －68＝0，求直线l 的方程．解：(1) 不妨设M ＝⎣⎢⎡⎦⎥⎤a b c d ，则由题意得⎣⎢⎡⎦⎥⎤a b c d ⎣⎢⎡⎦⎥⎤ 1－1＝⎣⎢⎡⎦⎥⎤57，⎣⎢⎡⎦⎥⎤a b c d ⎣⎢⎡⎦⎥⎤－2 1＝⎣⎢⎡⎦⎥⎤－3 6，所以⎩⎪⎨⎪⎧a ＝－2，b ＝－7，c ＝－13，d ＝－20，故M ＝⎣⎢⎡⎦⎥⎤－2－7－13－20. (2) 取直线l 上的任一点(x ，y)，其在M 作用下变换成对应点(x′，y ′)，则⎣⎢⎡⎦⎥⎤－2－7－13－20⎣⎢⎡⎦⎥⎤x y ＝⎣⎢⎡⎦⎥⎤－2x －7y －13x －20y ＝⎣⎢⎡⎦⎥⎤x′y′， 即⎩⎪⎨⎪⎧x′＝－2x －7y ，y ′＝－13x －20y ，代入11x －3y －68＝0，得x －y －4＝0，即l 的方程为x －y －4＝0.变式训练在平面直角坐标系xOy 中，直线l ：x ＋y ＋2＝0在矩阵M ＝⎣⎢⎡⎦⎥⎤1a b 4对应的变换作用下得到直线m ：x －y －4＝0，求实数a 、b 的值．解：(解法1)在直线l ：x ＋y ＋2＝0上取两点A(－2，0)，B(0，－2)，A 、B 在矩阵M 对应的变换作用下分别对应于点A′、B′，因为⎣⎢⎡⎦⎥⎤1a b 4⎣⎢⎡⎦⎥⎤－2 0＝⎣⎢⎡⎦⎥⎤－2－2b ，所以A′的坐标为(－2，－2b)； ⎣⎢⎡⎦⎥⎤1a b 4⎣⎢⎡⎦⎥⎤ 0－2＝⎣⎢⎡⎦⎥⎤－2a －8，所以B′的坐标为(－2a ，－8)．由题意A′、B′在直线m ：x －y －4＝0上，所以⎩⎪⎨⎪⎧（－2）－（－2b ）－4＝0，（－2a ）－（－8）－4＝0，解得a ＝2，b ＝3.(解法2)设直线l ：x ＋y ＋2＝0上任意一点(x ，y)在矩阵M 对应的变换作用下对应于点(x′，y ′)．因为⎣⎢⎡⎦⎥⎤1a b 4⎣⎢⎡⎦⎥⎤x y ＝⎣⎢⎡⎦⎥⎤x′y′，所以x′＝x ＋ay ，y ′＝bx ＋4y.因为(x′，y ′)在直线m 上，所以(x ＋ay)－(bx ＋4y)－4＝0，即(1－b)x ＋(a －4)y －4＝0.又点(x ，y)在直线x ＋y ＋2＝0上，所以1－b 1＝a －41＝－42，解得a ＝2，b ＝3.题型3 平面变换的综合应用例3 已知M ＝⎣⎢⎡⎦⎥⎤1101，N ＝⎣⎢⎢⎡⎦⎥⎥⎤10012，向量α＝⎣⎢⎡⎦⎥⎤34. (1) 验证：(MN )α＝M (N α)；(2) 验证这两个矩阵不满足MN ＝NM .解：(1) 因为MN ＝⎣⎢⎡⎦⎥⎤1101⎣⎢⎢⎡⎦⎥⎥⎤10012＝⎣⎢⎢⎡⎦⎥⎥⎤112012，所以(MN )α＝⎣⎢⎢⎡⎦⎥⎥⎤112012⎣⎢⎡⎦⎥⎤34＝⎣⎢⎡⎦⎥⎤52. 因为N α＝⎣⎢⎢⎡⎦⎥⎥⎤10012⎣⎢⎡⎦⎥⎤34＝⎣⎢⎡⎦⎥⎤32，所以M (N α)＝⎣⎢⎡⎦⎥⎤1101⎣⎢⎡⎦⎥⎤32＝⎣⎢⎡⎦⎥⎤52，所以(MN )α＝M (N α)．(2) 因为MN ＝⎣⎢⎢⎡⎦⎥⎥⎤112012，NM ＝⎣⎢⎢⎡⎦⎥⎥⎤11012， 所以这两个矩阵不满足MN ＝NM . 备选变式（教师专享）在直角坐标系中，已知△ABC 的顶点坐标为A ()0，0，B ()－1，2，C ()0，3.求△ABC在矩阵⎣⎢⎡⎦⎥⎤0－110作用下变换所得到的图形的面积．解：因为⎣⎢⎡⎦⎥⎤0－11 0⎣⎢⎡⎦⎥⎤00＝⎣⎢⎡⎦⎥⎤00，⎣⎢⎡⎦⎥⎤0－11 0⎣⎢⎡⎦⎥⎤－1 2＝⎣⎢⎡⎦⎥⎤－2－1，⎣⎢⎡⎦⎥⎤0－11 0⎣⎢⎡⎦⎥⎤03＝⎣⎢⎡⎦⎥⎤－3 0，所以A ()0，0，B ()－1，2，C ()0，3在矩阵⎣⎢⎡⎦⎥⎤0 －11 0作用下变换所得到的三个顶点坐标分别为A′()0，0，B ′()－2，－1，C ′()－3，0.故S △A ′B ′C ′＝12A ′C ′|y B ′|＝32.1. 在直角坐标系中，△OAB 的顶点坐标O(0，0)、A(2，0)，B(1，2)，求△OAB 在矩阵MN 的作用下变换所得到的图形的面积，其中矩阵M ＝⎣⎢⎡⎦⎥⎤100－1，N ＝⎣⎢⎢⎡⎦⎥⎥⎤12222. 解：由题设得MN ＝⎣⎢⎢⎡⎦⎥⎥⎤1220－22，∴ ⎣⎢⎢⎡⎦⎥⎥⎤1 220－22·⎣⎢⎡⎦⎥⎤00＝⎣⎢⎡⎦⎥⎤00， ⎣⎢⎢⎡⎦⎥⎥⎤1 220－22·⎣⎢⎡⎦⎥⎤20＝⎣⎢⎡⎦⎥⎤20， ⎣⎢⎢⎡⎦⎥⎥⎤1 220－22·⎣⎢⎡⎦⎥⎤12＝⎣⎢⎡⎦⎥⎤ 2－1. 可知O 、A 、B 三点在矩阵MN 作用下变换所得的点分别为O′(0，0)、A′(2，0)、B′(2，－1)．可得△O′A′B′的面积为1.2. 已知矩阵M ＝⎣⎢⎡⎦⎥⎤0110，N ＝⎣⎢⎡⎦⎥⎤0－11 0，在平面直角坐标系中，设直线2x －y ＋1＝0在矩阵MN 对应的变换作用下得到的曲线F ，求曲线F 的方程．解：由题设得MN ＝⎣⎢⎡⎦⎥⎤0110⎣⎢⎡⎦⎥⎤0－11 0＝⎣⎢⎡⎦⎥⎤1 00－1.设(x ，y)是直线2x －y ＋1＝0上任意一点，点(x ，y)在矩阵MN 对应的变换作用下变为(x′，y ′)，则有⎣⎢⎡⎦⎥⎤1 00－1⎣⎢⎡ ⎦⎥⎤x y ＝⎣⎢⎡⎦⎥⎤x′y′，即⎣⎢⎡⎦⎥⎤ x －y ＝⎣⎢⎡⎦⎥⎤x′y′， 所以⎩⎪⎨⎪⎧x ＝x′，y ＝－y′.因为点(x ，y)在直线2x －y ＋1＝0上，从而2x′－(－y′)＋1＝0，即2x′＋y′＋1＝0.所以曲线F 的方程为2x ＋y ＋1＝0.3. (2013·福建)已知直线l ：ax ＋y ＝1在矩阵A ＝⎣⎢⎡⎦⎥⎤1201对应的变换作用下变为直线l′：x ＋by ＝1.(1) 求实数a 、b 的值；(2) 若点P(x 0，y 0)在直线l 上，且A ⎣⎢⎡⎦⎥⎤x 0y 0＝⎣⎢⎡⎦⎥⎤x 0y 0，求点P 的坐标．解：(1) 设直线l ：ax ＋y ＝1上任意一点M(x ，y)在矩阵A 对应的变换作用下的象是M′(x′，y ′)，由⎣⎢⎡⎦⎥⎤x′y′＝⎣⎢⎡⎦⎥⎤1201⎣⎢⎡⎦⎥⎤x y ＝⎣⎢⎡⎦⎥⎤x ＋2y y ， 得⎩⎪⎨⎪⎧x′＝x ＋2y ，y ′＝y. 又点M′(x′，y ′)在l′上， 所以x′＋by′＝1，即x ＋(b ＋2)y ＝1.依题意⎩⎪⎨⎪⎧a ＝1.b ＋2＝1，解得⎩⎪⎨⎪⎧a ＝1，b ＝－1. (2) 由A ⎣⎢⎡⎦⎥⎤x 0y 0＝⎣⎢⎡⎦⎥⎤x 0y 0，得⎩⎪⎨⎪⎧x 0＝x 0＋2y 0，y 0＝y 0，解得y 0＝0.又点P(x 0，y 0)在直线l 上，所以x 0＝1，故点P 的坐标为(1，0)． 4. 在线性变换⎣⎢⎡⎦⎥⎤x′y′＝⎣⎢⎡⎦⎥⎤1122⎣⎢⎡⎦⎥⎤x y 下，直线x ＋y ＝k(k 为常数)上的所有点都变为一个点，求此点坐标．解：由⎣⎢⎡⎦⎥⎤x′y′＝⎣⎢⎡⎦⎥⎤1122⎣⎢⎡⎦⎥⎤x y ，得⎩⎪⎨⎪⎧x′＝x ＋y ，y ′＝2x ＋2y ，而x ＋y ＝k ，所以⎩⎪⎨⎪⎧x′＝k ，y ′＝2k (k 为常数)，所以直线x ＋y ＝k(k 为常数)上的所有点都变为一个点(k ，2k)．1. 如图所示，四边形ABCD 和四边形AB′C′D 分别是矩形和平行四边形，其中各点的坐标分别为A(－1，2)、B(3，2)、C(3，－2)、D(－1，－2)、B′(3，7)、C′(3，3)．求将四边形ABCD 变成四边形AB′C′D 的变换矩阵M .解：该变换为切变变换．设矩阵M ＝⎣⎢⎡⎦⎥⎤10k 1，由图知，C ――→MC ′，则⎣⎢⎡⎦⎥⎤10k 1⎣⎢⎡⎦⎥⎤3－2＝⎣⎢⎡⎦⎥⎤33.所以3k －2＝3，解得k ＝53.所以，M ＝⎣⎢⎢⎡⎦⎥⎥⎤10531.2. 已知矩阵M ＝⎣⎢⎡⎦⎥⎤－1－2－34，向量α＝⎣⎢⎡⎦⎥⎤57，β＝⎣⎢⎡⎦⎥⎤68.(1) 求向量3α＋12β在T M 作用下的象；(2) 求向量4M α－5M β.解：(1) 因为3α＋12β＝3⎣⎢⎡⎦⎥⎤57＋12⎣⎢⎡⎦⎥⎤68＝⎣⎢⎡⎦⎥⎤1521＋⎣⎢⎡⎦⎥⎤34＝⎣⎢⎡⎦⎥⎤1825，所以M ⎝ ⎛⎭⎪⎫3α＋12β＝⎣⎢⎡⎦⎥⎤－1－2－34⎣⎢⎡⎦⎥⎤1825＝⎣⎢⎡⎦⎥⎤－6846.(2) 4M α－5M β＝M (4α－5β)＝⎣⎢⎡⎦⎥⎤－1－2－34⎣⎢⎡⎦⎥⎤－10－12＝⎣⎢⎡⎦⎥⎤34－18. 3. 二阶矩阵M 对应的变换将点(1，－1)与(－2，1)分别变换成点(－1，－1)与(0，－2)．设直线l 在变换M 作用下得到了直线m ：2x －y ＝4，求l 的方程．解：设M ＝⎣⎢⎡⎦⎥⎤a b c d ，则有⎣⎢⎡⎦⎥⎤a b c d ⎣⎢⎡⎦⎥⎤1－1＝⎣⎢⎡⎦⎥⎤－1－1，⎣⎢⎡⎦⎥⎤a b c d ⎣⎢⎡⎦⎥⎤－21＝⎣⎢⎡⎦⎥⎤0－2，∴ ⎩⎪⎨⎪⎧a －b ＝－1c －d ＝－1， 且⎩⎪⎨⎪⎧－2a ＋b ＝0－2c ＋d ＝－2，解得⎩⎪⎨⎪⎧a ＝1b ＝2和⎩⎪⎨⎪⎧c ＝3d ＝4 ，∴ M ＝⎣⎢⎡⎦⎥⎤1234， ∵ ⎣⎢⎡⎦⎥⎤x′y′＝⎣⎢⎡⎦⎥⎤1234⎣⎢⎡⎦⎥⎤x y ＝⎣⎢⎡⎦⎥⎤x ＋2y 3x ＋4y ，且m ：2x′－y′＝4， ∴ 2(x ＋2y)－(3x ＋4y)＝4，即x ＋4 ＝0，∴ 直线l 的方程为x ＋4 ＝0.4. 二阶矩阵M 对应的变换将点(1，－1)与(－2，1)分别变换成点(－1，－1)与(0，－2)．(1) 求矩阵M ；(2) 设直线l 在变换M 作用下得到了直线m ：x －y ＝4，求l 的方程．解：(1) 设M ＝⎣⎢⎡⎦⎥⎤a b c d ，则有⎣⎢⎡⎦⎥⎤a b c d ⎣⎢⎡⎦⎥⎤1－1＝⎣⎢⎡⎦⎥⎤－1－1，⎣⎢⎡⎦⎥⎤a b c d ⎣⎢⎡⎦⎥⎤－21＝⎣⎢⎡⎦⎥⎤0－2，所以⎩⎪⎨⎪⎧a －b ＝－1，c －d ＝－1， 且⎩⎪⎨⎪⎧－2a ＋b ＝0，－2c ＋d ＝－2，解得⎩⎪⎨⎪⎧a ＝1，b ＝2，c ＝3，d ＝4，所以M ＝⎣⎢⎡⎦⎥⎤1234. (2) 因为⎣⎢⎡⎦⎥⎤x′y′＝⎣⎢⎡⎦⎥⎤1234⎣⎢⎡⎦⎥⎤x y ＝⎣⎢⎡⎦⎥⎤x ＋2y 3x ＋4y 且m ：x′－y′＝4，所以(x ＋2y)－(3x ＋4y)＝4，即x ＋y ＋2＝0，即直线l 的方程为x ＋y ＋2＝0.几种特殊的变换：反射变换：M ＝⎣⎢⎡⎦⎥⎤1 00－1：点的变换为(x ，y )→(x，－y)，变换前后关于x 轴对称；M ＝⎣⎢⎡⎦⎥⎤－10 01：点的变换为(x ，y )→(－x ，y)，变换前后关于y 轴对称；M ＝⎣⎢⎡⎦⎥⎤－1 0 0－1：点的变换为(x ，y )→(－x ，－y)，变换前后关于原点对称； M ＝⎣⎢⎡⎦⎥⎤0110：点的变换为(x ，y )→(y，x)，变换前后关于直线y ＝x 对称． 投影变换：M ＝⎣⎢⎡⎦⎥⎤1000：将坐标平面上的点垂直投影到x 轴上，点的变换为(x ，y )→(x，0)； M ＝⎣⎢⎡⎦⎥⎤0001：将坐标平面上的点垂直投影到y 轴上，点的变换为(x ，y )→(0，y)； M ＝⎣⎢⎡⎦⎥⎤1010：将坐标平面上的点垂直于x 轴方向投影到y ＝x 上，点的变换为(x ，y )→(x，x)；M ＝⎣⎢⎡⎦⎥⎤0101：将坐标平面上的点平行于x 轴方向投影到y ＝x 上，点的变换为(x ，y )→(y，y)；M ＝⎣⎢⎢⎡⎦⎥⎥⎤12121212：将坐标平面上的点垂直于y ＝x 方向投影到y ＝x 上，点的变换为(x ，y )→⎝⎛⎭⎪⎫x ＋y 2，x ＋y 2.请使用课时训练（A ）第1课时（见活页）.。
矩阵的变换与运算矩阵的乘法与逆矩阵矩阵的变换与运算：矩阵的乘法与逆矩阵矩阵在数学中扮演着重要的角色，它可以用于描述线性变换或者表示线性系统的方程组。
本文将讨论矩阵的变换与运算，重点介绍矩阵的乘法与逆矩阵两个关键概念。
一、矩阵的乘法（Matrix Multiplication）矩阵的乘法是矩阵运算中的一种基本运算，表示为A * B，其中A 和B分别为两个矩阵。
在进行矩阵乘法时，需要满足乘法的条件：A 矩阵的列数等于B矩阵的行数。
矩阵乘法的计算方法是将A矩阵的每一行与B矩阵的每一列进行内积运算，并将结果填入一个新的矩阵C中。
具体计算过程如下：C[i][j] = A[i][1]*B[1][j] + A[i][2]*B[2][j] + ... + A[i][n]*B[n][j]其中，C[i][j]表示矩阵C中第i行第j列的元素，A[i][k]表示矩阵A 中第i行第k列的元素，B[k][j]表示矩阵B中第k行第j列的元素。
矩阵乘法的重要性在于可以描述线性变换的复合效果，同时也有利于解决线性方程组。
在实际应用中，矩阵乘法广泛运用于计算机图形学、信号处理、最优化等领域。
二、逆矩阵（Inverse Matrix）逆矩阵是指对于一个可逆矩阵A，存在一个矩阵B，使得A * B = B * A = I，其中I为单位矩阵。
逆矩阵的存在与否与矩阵的行列式密切相关。
判断矩阵A是否可逆的条件是行列式不等于零，即|A| ≠ 0。
若矩阵A可逆，则可以通过一系列行变换将其转化为单位矩阵，对应的变换矩阵为逆矩阵。
逆矩阵的计算可以使用伴随矩阵法或者初等行变换法。
例如，对于一个2x2的矩阵A：A = [a b][c d]若|A| ≠ 0，即ad - bc ≠ 0，则A的逆矩阵存在，并可表示为：A^-1 = 1/(ad - bc) * [d -b][-c a]逆矩阵的应用广泛，例如求解线性方程组、计算矩阵的行列式与秩、求解微分方程等。
三、矩阵的变换（Matrix Transformation）矩阵的变换是指通过矩阵的乘法，对向量进行线性变换。
2.2 二项分布一、教学目标：1、知识与技能：理解n 次独立重复试验的模型及二项分布，并能解答一些简单的实际问题。
2、过程与方法：能进行一些与n 次独立重复试验的模型及二项分布有关的概率的计算。
3、情感、态度与价值观：承前启后，感悟数学与生活的和谐之美 ,体现数学的文化功能与人文价值。
二、教学重点：理解n 次独立重复试验的模型及二项分布，并能解答一些简单的实际问题。
教学难点：能进行一些与n 次独立重复试验的模型及二项分布有关的概率的计算。
三、教学方法：讨论交流，探析归纳四、教学过程（二）、探析新课：1 独立重复试验的定义：指在同样条件下进行的，各次之间相互独立的一种试验2．独立重复试验的概率公式：一般地，如果在1次试验中某事件发生的概率是P ，那么在n 次独立重复试验中这个事件恰好发生k 次的概率k n k k n n P P C k P --=)1()(．它是[](1)nP P -+展开式的第1k +项 3.离散型随机变量的二项分布:在一次随机试验中，某事件可能发生也可能不发生，在n 次独立重复试验中这个事件发生的次数ξ是一个随机变量．如果在一次试验中某事件发生的概率是P ，那么在n 次独立重复试验中这个事件恰好发生k 次的概率是k n k k n n q p C k P -==)(ξ，（k ＝0,1,2,…，n ，p q -=1）． 于是得到随机变量ξ的概率分布如下：由于k n k k n q p C -恰好是二项展开式011100)(q p C q p C q p C q p C p q n n n k n k k n n n n n n +++++=+--中的各项的值，所以称这样的随机变量ξ服从二项分布（binomial distribution )，记作ξ～B (n ，p )，其中n ，p 为参数，并记k n k k n q p C -＝b (k ；n ， p )．例1．某射手每次射击击中目标的概率是0 . 8.求这名射手在 10 次射击中，(1)恰有 8 次击中目标的概率； (2)至少有 8 次击中目标的概率．（结果保留两个有效数字．)例2．某气象站天气预报的准确率为80%，计算（结果保留两个有效数字）：（1）5次预报中恰有4次准确的概率；（2）5次预报中至少有4次准确的概率例3．某车间的5台机床在1小时内需要工人照管的概率都是14，求1小时内5台机床中至少2台需要工人照管的概率是多少？（结果保留两个有效数字）例4．某人对一目标进行射击，每次命中率都是0.25，若使至少命中1次的概率不小于0.75，至少应射击几次？例5．重复抛掷一枚筛子5次得到点数为6的次数记为ξ，求P(ξ>3)．（四）、课堂练习：1.．十层电梯从低层到顶层停不少于3次的概率是多少？停几次概率最大？2．实力相等的甲、乙两队参加乒乓球团体比赛，规定5局3胜制（即5局内谁先赢3局就算胜出并停止比赛）．（1）试分别求甲打完3局、4局、5局才能取胜的概率．（2）按比赛规则甲获胜的概率．精美句子1、善思则能“从无字句处读书”。
二阶矩阵乘法矩阵（Matrix）又称数字矩形，是一种以数字字符构成的二维表格，是数学中重要的概念。
每一个矩阵都可以表示为一个m*n矩阵，m行n列。
二阶矩阵乘法是计算矩阵乘积的通用方法，它可以直接应用于计算两个矩阵乘积，也可以用于计算更高阶乘积。
一阶矩阵乘法是在二维空间中比较简单的乘法运算，而二阶矩阵乘法则需要处理三维或更高维的数据。
首先，它涉及的操作是将两个二维矩阵的每一个元素相乘，再加总，这样就可以得到一个二维新矩阵。
如果将矩阵A和矩阵B分别表示为$A = begin{bmatrix}a_{11} & a_{12}a_{21} & a_{22}end{bmatrix},B = begin{bmatrix}b_{11} & b_{12}b_{21} & b_{22}end{bmatrix}$，则二阶矩阵乘法的结果为：$C = begin{bmatrix} a_{11} * b_{11} + a_{12} * b_{21} & a_{11} * b_{12} + a_{12} * b_{22}a_{21} * b_{11} + a_{22} * b_{21} & a_{21} * b_{12} + a_{22} * b_{22}end{bmatrix}$有，$C=AB$二阶矩阵乘法的计算其实是一个典型的线性变换的过程，因为结果矩阵的每一个元素都符合线性变换的性质，即每一个元素都是由原矩阵乘以一个常数得到的。
因此，在做二阶矩阵乘法之前，需要了解一些线性变换的概念，例如缩放、位移、旋转等。
在实际应用中，二阶矩阵乘法可以用来计算两个矩阵之间的乘积，也可以用来计算矩阵与向量之间的乘积，甚至可以用来计算更高阶的矩阵乘积。
在工程性计算中，二阶矩阵乘法的应用非常多，例如矩阵运算、图像处理、数据挖掘、推荐系统、机器学习等。
总之，二阶矩阵乘法是一种非常有用的运算方法，它可以用来计算矩阵的乘积，从而帮助我们更好的理解线性变换的原理，也可以用于计算机视觉与机器学习等领域。
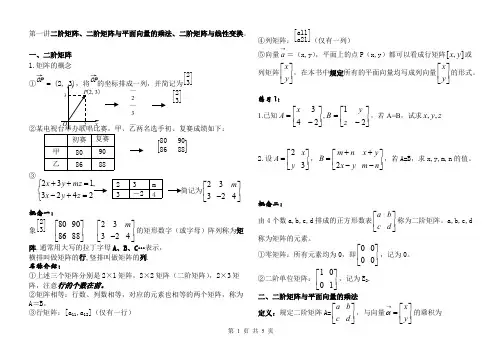
第一讲二阶矩阵、二阶矩阵与平面向量的乘法、二阶矩阵与线性变换。
一、二阶矩阵1.矩阵的概念① =OP → →[23][23]初赛复赛甲8090乙8688③概念一：象 的矩形数字（或字母）阵列称为矩[23]80908688⎡⎤⎢⎥⎣⎦23324m ⎡⎤⎢⎥-⎣⎦阵.通常用大写的拉丁字母A 、B 、C…表示， 横排叫做矩阵的行,竖排叫做矩阵的列.名称介绍：①上述三个矩阵分别是2×1矩阵，2×2矩阵（二阶矩阵），2×3矩阵，注意行的个数在前。
②矩阵相等：行数、列数相等，对应的元素也相等的两个矩阵，称为A ＝B 。
③行矩阵：[a 11,a 12]（仅有一行）④列矩阵：（仅有一列）[a11a21]⑤向量＝（x,y ），平面上的点P （x,y ）都可以看成行矩阵或a →[,]x y 列矩阵，在本书中规定所有的平面向量均写成列向量的形式。
x y ⎡⎤⎢⎥⎣⎦x y ⎡⎤⎢⎥⎣⎦练习1：1.已知,，若A=B ，试求⎥⎦⎤⎢⎣⎡-=243x A ⎥⎦⎤⎢⎣⎡-=21z y B z y x ,,2.设，，若A=B ，求x,y,m,n 的值。
23x A y ⎡⎤=⎢⎥⎣⎦2m n x y B x y m n ++⎡⎤=⎢⎥--⎣⎦概念二：由4个数a,b,c,d 排成的正方形数表称为二阶矩阵。
a,b,c,d a b c d ⎡⎤⎢⎥⎣⎦称为矩阵的元素。
①零矩阵：所有元素均为0，即，记为0。
0000⎡⎤⎢⎥⎣⎦②二阶单位矩阵：，记为E 2.1001⎡⎤⎢⎥⎣⎦二、二阶矩阵与平面向量的乘法定义：规定二阶矩阵A=，与向量的乘积为a b c d ⎡⎤⎢⎥⎣⎦x y α→⎡⎤=⎢⎥⎣⎦23m 3－24—2—3—[80 9086 88]23324x y mz x y z ++=⎧⎨-+=⎩23324m ⎡⎤⎢⎥-⎣⎦，即＝＝ax by A cx dy α→+⎡⎤=⎢⎥+⎣⎦A α→a b c d ⎡⎤⎢⎥⎣⎦x y ⎡⎤⎢⎥⎣⎦ax by cx dy +⎡⎤⎢⎥+⎣⎦练习2：1.（1）＝⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡-131021（2） ＝⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡-3110212.=，求⎥⎦⎤⎢⎣⎡2101⎥⎦⎤⎢⎣⎡y x ⎥⎦⎤⎢⎣⎡-11⎥⎦⎤⎢⎣⎡y x 三、二阶矩阵与线性变换1.旋转变换问题1:P （x,y ）绕原点逆时针旋转180o 得到P ’(x ’,y ’),称P ’为P在此旋转变换作用下的象。
