spss判别分析
- 格式:ppt
- 大小:1.20 MB
- 文档页数:81





判别分析的SPSS实现判别分析(Discriminant Analysis)是一种统计分析方法,用于识别和分类不同群体之间的差异。
它通过建立数学模型来寻找最佳判别函数,将样本划入事先定义好的不同类别中。
SPSS是一种流行的统计软件,可以用于进行多种数据分析,包括判别分析。
在SPSS中进行判别分析的步骤如下:1.导入数据:打开SPSS软件,并导入需要进行判别分析的数据集。
选择“文件”-“打开”-“数据”命令,找到数据文件并点击“打开”按钮。
2. 选择变量:从数据文件中选择需要用于判别的变量。
在数据视图中,点击变量名旁边的方框来选定变量。
可以按住Ctrl键并单击多个变量来进行选择。
3.运行判别分析:选择“分析”-“分类”-“判别分析”命令,打开判别分析对话框。
在对话框的“变量”选项卡中,将选择的变量移入“输入变量”框中。
如果有分类变量,可以选择将其移入“说明变量”框中。
4.设置判别函数模型:在对话框的“选项”选项卡中,可以设置判别分析的具体模型。
可以选择线性判别函数或二次判别函数,并设置解释变量和额外变量。
5.运行分析:点击对话框底部的“确定”按钮,运行判别分析。
SPSS将计算出最佳的判别函数,并用于分类和预测。
6.解释结果:判别分析完成后,可以查看结果并进行解释。
SPSS将输出各个变量的判别系数、判别函数结果、群体统计信息等。
可以根据这些结果来理解不同变量对分类的重要性。
7.进行预测:判别分析还可以用于对新样本进行分类和预测。
在对话框的“选项”选项卡中,选择“保存变量”选项,并指定一个新的变量名。
运行分析后,可以查看新变量的值,以得到新样本的分类结果。
8.检验结果:可以使用SPSS提供的各种统计方法来检验判别分析结果的显著性。
例如,可以进行方差分析来检验不同群体之间的差异性。
判别分析是一种有效的统计方法,可以用于各种不同的研究领域。
在SPSS中,通过简单的几个步骤就可以实现判别分析,并得到结果。
同时,SPSS还提供了丰富的数据可视化和结果解释功能,可以帮助用户更好地理解和解释判别分析的结果。

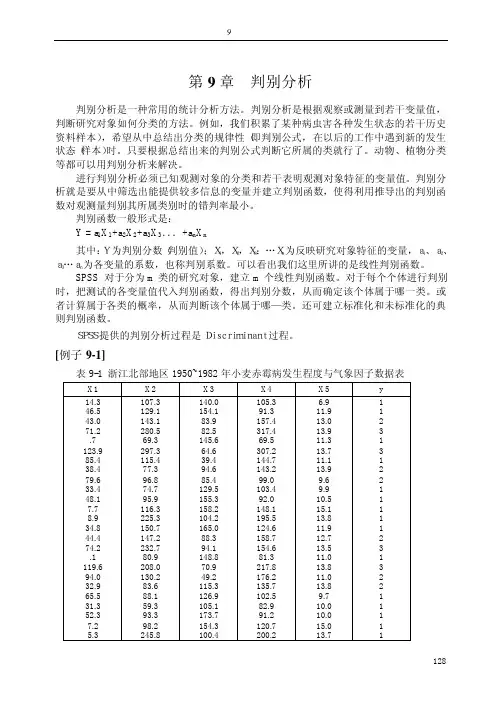

判别分析1.基本理解判别分析用于处理已知分类情况的数据集,将未知分类数据归入已知的分类中。
判别分析过程基于对变量的函数组合,变量应能够充分地体现各个类别之间的差异。
从已知变量类别的样本中拟合判别函数,后根据判别函数将新样本进行类别归类。
在P维空间中,有K个相关已知类别的总体G1,G2,G3,....Gk,单个的预测样本记为Xi =(Xi1,Xi2,Xi3,....,Xip),i=1,2,3,....n,样本属于K个总体的一个,P个变量为判别指标,判别函数就是确定样本属于哪一类别。
判别函数的两种判别方法:(1)贝叶斯判别:是一种概率型的判别函数,开始需要知道各个类别的先验概率或分布密度,后计算每个样本属于某个类别的最大概率或最小错判损失,并以此归类。
类别概率计算公式:P(Gi|D)=P(D|Gi)P(Gi)/ΣP(D|Gi)P(Gi),其中P(Gi)为属于i类的先验概率,P(D|Gi)为在第i类中得D分的条件概率,而P(Gi|D)为在第i类中得D分的后验概率。
(2)Fisher判别:是一种依据方差分析原理建立的判别方法,基本思路为投影。
对P维空间中的点Xi =(Xi1,Xi2,Xi3, (X)in),i=1,2,3,....,n,找到一组线性函数Ym (Xi)=×B,m=1,2,3,....,m,一般m<p,依据组间均方差与组内均方差之比最大的原则,选择最优的线性函数。
判别分析的一般步骤:(1):依据已知类别的观测集建立分类规则或判别规则。
(2):运用所建规则对样本进行分类检验,得到各样本的判别准确率。
(3):选择拥有较高准确率的判别规则,应用于新样本的类别判断。
2.判别分析操作步骤判别函数第一步:首先将已确定分类情况的数据到spss软件中,点击分析、分类、判别式。
图1第一步第二步:进入判别分析勾选框后首先将变量列表中的变量放入右侧的变量框中,将因变量(已知分组情况变量)放入分组变量框并定义好范围,点击继续,将自变量放入自变量框中。

判别分析的SPSS实现判别分析是一种常用的统计方法,也是一种分类的机器学习方法。
它的目的是使用已知的分类信息来训练一个分类模型,然后根据这个模型来预测新的未知实例的分类。
SPSS是一种常用的统计软件,提供了方便易用的界面来进行判别分析。
下面将介绍如何在SPSS中进行判别分析。
首先,打开SPSS软件并加载要进行判别分析的数据。
可以通过"File"->"Open"来打开数据文件,或者直接将数据文件拖动到SPSS界面中。
然后,选择"Analyze"->"Classify"->"Discriminant",进入判别分析的界面。
在界面中,需要选择要进行判别分析的变量,包括一个或多个预测变量和一个分类变量。
预测变量是判别分析模型的输入,而分类变量是判别分析模型的输出。
可以使用鼠标将变量从"Available"列表拖动到"Predictors"和"Target"列表中。
接下来,可以点击"Statistics"按钮来选择统计量。
在判别分析中,有几个常用的统计量可以选择。
例如,可以选择"Wilks' lambda"来衡量判别分析模型的预测准确率,或者选择"Group centroids"来了解不同分类的均值差异。
然后,点击"Options"按钮来设置其他选项。
在"Options"界面中,可以选择是否标准化变量,即将变量标准化为均值为0和标准差为1的形式。
标准化可以使得不同变量的尺度一致,有助于提高判别分析的性能。
此外,还可以选择输出判别函数的系数和判别函数值,以及设定分类概率的阈值等。
最后,点击"OK"按钮开始进行判别分析。

判别分析方法与SPSS判别分析(Discriminant Analysis)是一种常用的统计方法,用于分析两个或多个已知样本分类的特征,确定如何将新样本分配到已知分类中的方法。
该方法通常用于判别样本的所属类别或进行预测分类,并且可以应用于多个学科领域,如市场研究、医学、生物学等。
SPSS(Statistical Package for the Social Sciences)是一种常用的统计软件,广泛应用于社会科学领域的数据分析。
SPSS提供了丰富的统计方法和数据分析工具,包括描述统计、相关分析、回归分析等,同时也提供了判别分析方法。
在SPSS中,进行判别分析需要先导入数据集并选择“分类”方法。
在分类方法中,可以选择“线性鉴别法”或者“二次鉴别法”,通常选择线性鉴别法。
选择线性鉴别法后,可以选择“反向排序”和“选择必备输入变量”。
反向排序是指将判别函数的变量排序方式从最大向最小递减排序的方式转变为最小向最大递增排序。
选择必备输入变量是指程序会自动选择在判别分析中具有最大判别力的变量。
在SPSS中执行判别分析后,可以得到一些结果,其中最重要的是判别函数。
判别函数用于预测未知样本的类别,可以提供样本的判别得分,判别得分越高表示属于该类别的可能性越大。
判别分析的结果也包括统计指标,如Wilks' Lambda、标准化判别函数系数等。
Wilks' Lambda是判别分析的一个重要统计量,用于衡量所有判别函数的总效应,其值介于0和1之间,越接近0表示判别函数越有效。
标准化判别函数系数用于表示各个变量对判别函数的贡献,系数绝对值越大表示对判别函数的影响越大。
总之,判别分析是一种常用的统计方法,可用于分类和预测。
SPSS 是一种常用的统计软件,提供了判别分析方法和相关的数据分析工具,可以方便地进行判别分析并解释结果。

判别分析的一般步骤及SPSS实现判别分析是一种用于分类变量的统计方法,它可以用于确定一个或多个预测变量对于区分不同组之间差异的程度。
判别分析由一系列步骤组成,包括问题的定义、数据的准备、模型的建立、模型的评估和结果的解释。
以下是判别分析的一般步骤以及如何在SPSS中实现这些步骤的详细说明。
第一步:问题的定义在进行判别分析之前,需要明确研究的目的和问题。
例如,我们可能希望根据顾客的一些特征(如性别、年龄、收入等)来预测顾客是否购买一些产品。
这样的问题可以通过判别分析解决。
第二步:数据的准备在进行判别分析之前,需要确保数据满足分析的要求。
数据应包括一个或多个预测变量和一个分类变量。
如果数据中存在缺失值,需要进行缺失值的处理。
如果数据中存在异常值,可以选择忽略或进行适当的修正。
第三步:模型的建立在SPSS中,可以使用“分类函数”来建立判别分析模型。
选择“分析”菜单中的“分类”选项,然后选择“判别”子菜单。
在“判别”对话框中,选择一个或多个预测变量,并将分类变量指定为“因变量”。
此外,还可以选择是否进行卡方检验以及是否使用交叉验证等选项。
卡方检验可以用于评估预测变量与分类变量之间的关联性,而交叉验证可以用于评估模型对于不同样本的预测效果。
第四步:模型的评估在SPSS中,判别分析的模型评估结果可以在“判别”输出中找到。
主要关注以下几个指标:1.方差贡献表:可以查看每个预测变量对于判别函数的贡献程度,以及它们之间的相关性。
2.群组描述:可以查看不同组之间的平均值,以确定最能区分不同组的预测变量。
3.准确性表:可以查看模型的整体分类准确率以及每个组的分类准确率。
4.标准化系数表:可以查看每个预测变量对于判别函数的贡献程度,使用标准化系数来比较不同预测变量的影响。
第五步:结果的解释对于判别分析的结果进行解释是非常重要的,以帮助我们理解预测变量如何影响分类变量,并从中得出有用的结论。
可以通过参考判别函数的系数、标准化系数和方差贡献来解释结果。
判别分析实验报告 SPSS一、实验目的判别分析是一种用于分类和预测的统计方法。
本次实验旨在通过使用 SPSS 软件,掌握判别分析的基本原理和操作流程,能够运用判别分析方法对实际数据进行分类,并对分类结果进行评估和解释。
二、实验数据本次实验使用的数据集包含了两个类别(类别 A 和类别 B)的样本,每个样本具有若干个特征变量,如年龄、收入、教育程度等。
数据集共有 200 个样本,其中类别 A 有 100 个样本,类别 B 有 100 个样本。
三、实验步骤1、数据导入首先,打开 SPSS 软件,选择“文件”菜单中的“打开”选项,将实验数据文件导入到 SPSS 中。
2、变量定义在 SPSS 数据视图中,对各个变量进行定义,包括变量名称、变量类型、变量标签等。
3、判别分析操作选择“分析”菜单中的“分类”子菜单,然后点击“判别分析”选项。
在弹出的判别分析对话框中,将类别变量选入“分组变量”框中,将其他特征变量选入“自变量”框中。
4、选择判别方法SPSS 提供了多种判别方法,如费希尔判别法、贝叶斯判别法等。
本次实验选择费希尔判别法。
5、模型评估在判别分析结果中,查看判别函数的系数、判别函数的显著性检验、分类结果的准确性等指标,以评估模型的性能。
四、实验结果与分析1、判别函数系数判别函数的系数反映了各个自变量对判别函数的贡献程度。
通过查看系数的大小和符号,可以了解各个变量在区分不同类别中的重要性。
例如,年龄变量的系数为正,说明年龄越大,越有可能属于某个类别;而收入变量的系数为负,说明收入越低,越有可能属于另一个类别。
2、判别函数的显著性检验通过对判别函数的显著性检验,可以判断判别函数是否能够有效地区分不同的类别。
如果检验结果显著,说明判别函数具有统计学意义,可以用于分类。
3、分类结果SPSS 会给出每个样本的分类结果,以及分类的准确性。
通过比较实际类别和预测类别,可以评估模型的分类效果。
如果分类准确性较高,说明模型能够较好地对样本进行分类;如果分类准确性较低,则需要进一步分析原因,可能是数据质量问题、变量选择不当或者判别方法不合适等。
判别分析的SPSS操作判别分析(Discriminant Analysis)是一种用于确定样本所属类别的统计分析方法。
它通过构建线性方程来将样本分类到不同的组中,该线性方程称为判别函数。
在进行判别分析之前,首先需要收集关于不同类别的样本数据,并且这些样本必须是可信的、有代表性的。
SPSS是一种常用的统计软件,可以进行判别分析。
下面将介绍使用SPSS进行判别分析的步骤。
一、数据准备在进行判别分析之前,需要针对每个样本收集一些特征变量的数据。
这些特征变量可以是连续变量或者分类变量。
同时,还需要收集样本的类别信息,类别信息必须是分类变量。
将这些数据输入到SPSS中的数据文件中。
二、进行判别分析1. 打开 SPSS 软件,在主界面点击 "Analyze"(分析),然后选择"Classify"(分类),再点击 "Discriminant"(判别)。
2. 在 "Discriminant Function"(判别函数)对话框中,选择"Variables"(变量)。
将所有的特征变量移动到 "Predictors"(预测变量)列表中,将类别信息移动到 "Grouping Variable"(分组变量)中。
3. 在 "Options"(选项)中,可以选择 "Statistics"(统计量)和"Save classification results"(保存分类结果)。
4.单击"OK"开始进行判别分析。
三、结果解读1. 判别分析将给出一些统计结果,其中最重要的是 "Canonical Discriminant Function Coefficients"(标准化判别系数)和"Structure Matrix"(结构矩阵)。
SPSS判别分析SPSS(Statistical Package for the Social Sciences)是一款广泛使用的统计分析软件,也提供了强大的判别分析功能。
本文将介绍SPSS中判别分析的步骤、应用以及结果的解读。
一、判别分析的步骤1.数据准备:首先,将已知类别的样本数据录入SPSS中,每个样本对应一个实例,每个实例有一组预测变量和一个类别变量。
2.变量选择:选择要作为预测变量的特征或属性,并将其加入模型。
通常,只有连续型或分类型的自变量(预测变量)可以用于判别分析。
3.数据分割:将已知类别的样本数据分为训练集和测试集,一般按照70%的比例划分。
4.判别模型:使用SPSS中的判别分析功能建立判别模型。
在SPSS中,可以通过路径“分析-分类-判别”打开判别分析对话框。
5.模型评估:使用测试集来评估模型的准确性和性能。
可以查看分类结果的混淆矩阵,计算预测准确率、召回率、F1值等指标。
6.结果解读:根据模型的解读提示,分析各个预测变量对判别结果的重要性,找出主要影响判别的变量。
二、判别分析的应用领域判别分析广泛应用于各个领域,包括社会科学、医学、市场营销等。
以下是几个常见的应用案例:1.疾病诊断:通过患者的生物特征(如血液检测结果、基因表达谱等)来判断是否患有其中一种疾病。
2.风险评估:用于评估贷款申请者的信用风险,根据一些个人特征(如年龄、收入、居住地等)来预测违约概率。
3.市场细分:根据消费者的特征(如年龄、性别、购买行为等)将市场区分为不同的细分市场,以制定更精准的市场营销策略。
4.情感识别:通过分析文本数据(如社交媒体评论、产品评论等)来判断用户的情感倾向,以评估产品或服务的满意度。
三、结果解读判别分析的结果包括判别函数、判别系数和预测结果。
判别函数可以看作是一组线性加权的预测变量,用于将实例划分到不同的类别中。
判别系数表示了每个预测变量对判别结果的贡献程度,可以用于解释影响判断的主要变量。
SPSS数据的判别分析判别分析(Discriminant Analysis)是一种统计分析方法,用于确定一组变量如何能够最好地区分或判别不同的群体。
该方法可以用于解决分类问题,即将多个已知类别的观测对象分配到新的未知类别中。
SPSS是一种功能强大的统计软件,可以进行各种统计分析,包括判别分析。
在SPSS中,进行判别分析的步骤如下:1.打开SPSS软件并导入数据集。
2.选择“分析”菜单下的“判别分析”选项。
3.在弹出的对话框中,将要分类的变量(被解释变量)放入“因子”框中,用于判别的变量(解释变量)放入“变量”框中。
点击“分类图”按钮可以选择是否绘制分类图表。
4.点击“确定”按钮,进行判别分析。
判别分析的目标是找到一个线性组合,能够最好地将样本区分开来。
在SPSS的结果中,输出了多种统计量,包括判别系数,判别函数的系数,标准化判别函数系数等信息。
这些统计量可以帮助我们理解分类问题的解释力和判别函数的重要性。
判别函数是判别分析的核心输出,它可以根据变量的值来预测被解释变量的分类。
判别函数通常以线性函数的形式表示,例如:D = a1X1 + a2X2 + ... + anXn + b其中,D是判别函数的值,X1, X2, ..., Xn是解释变量的值,a1,a2, ..., an是判别函数的系数,b是常数项。
通过计算判别函数的值,就可以将新的观测对象分配到相应的分类中。
在SPSS中,可以使用“分类评估”功能来检验判别函数的准确性。
该功能可以计算被正确分类的对象的百分比,以及各个分类中的正确分类的百分比。
同时,SPSS还提供了一些可视化工具来帮助我们理解判别分析的结果。
例如,通过绘制分类图表,可以直观地了解不同分类之间的分隔情况。
此外,还可以通过散点图来展示解释变量和被解释变量之间的关系,以及如何影响判别函数的值。
判别分析在实际应用中具有广泛的应用。
例如,在医学领域,可以使用判别分析将患者分为不同的疾病分类,以便进行诊断和治疗。
用SPSS软件来实现判别分析判别分析是一种统计模型和机器学习方法,可用于研究两个或更多群体之间的差异。
通过使用SPSS软件,我们可以对数据进行判别分析,并评估自变量的贡献程度,以及如何使用这些自变量来预测因变量。
要进行判别分析,首先需要准备数据。
在SPSS中,数据应该被整理为一个数据框,每一行代表一个样本,每一列代表一个特征或变量。
在判别分析中,我们需要明确选择一个因变量和若干个自变量。
在SPSS软件中,进行判别分析的步骤如下:步骤1:导入数据在SPSS中,首先需要导入我们的数据集。
点击“文件(File)”选项卡,选择“打开(Open)”,然后选择数据文件。
确保数据文件是一个包含正确数据格式的数据框。
如果数据集过大,可以选择只导入部分数据进行分析,可以通过“变量视图(Variable View)”进行选择。
步骤2:选择判别分析方法点击“分析(Analyze)”选项卡,选择“描述统计(Descriptive Statistics)”,选择“判别(Discriminant)”。
步骤3:设置因变量和自变量在弹出的“判别函数(Discriminant Function)”对话框中,将被解释的变量(因变量)从左边的“因变量(Dependent)”栏拖到右边的“因变量(Dependent)”栏。
然后,将讲自变量(特征)从左边的“自变量(Independent(s))”栏拖到右边的“自变量(Independent(s))”栏。
函数使用的哪些变量将取决于数据中可用的变量数。
步骤4:选择分类方法在“类型(Method)”选项中,选择判别分析的分类方法。
SPSS提供了两种方法:“协方差矩阵相等(Covariance matrices equal)”和“协方差矩阵不等(Covariance matrices not equal)”。
前者使用默认参数,即假设所有群体具有相同的协方差矩阵。
后者提供了更具灵活性的选项,可以允许不同群体拥有不同的协方差矩阵。