解决问题找单位一全面

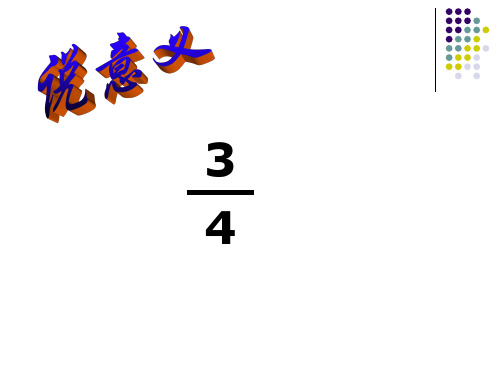
《利用单位“1”解决问题》教学设计姓名：曾毅所在单位：广西壮族自治区南宁市江南区江南小学联系电话：1576161641所属版本：《义务教育课程标准实验教科书•数学》（人教版）【教学内容】《义务教育课程标准实验教科书•数学》（人教版）人教版六年级上册数学第42-43页例7、做一做及相关练习。

【教材分析】新课程倡导“用教材教而不是教教材”，教学设计应坚持以学生发展为本。

《工程问题》这部分内容是九年义务教育小学数学第十一册第三单元分数除法的最后一部分内容。

工程问题应用是分数应用题中的一个特例，它是学生在学习了整数工程问题的基础上进行教学的。

这类应用题的数量关系和解题思路与整数工程应用题基本相同，不同之处在于它是利用分数知识中的单位“1”来理解和解决有关工作总量、工作时间和工作效率之间相互关系的数学问题。

解题时要把工作总量抽象成一个整体,用单位“1”表示,把单位时间内完成工作总量的几分之一表示为工作效率。

由于计算的不是具体的数量,学生往往感到抽象、不易理解。

这既是对过去列方程解决问题的扩展，也为后面解决百分数的实际问题做准备。

通过教学,使学生理解工程问题的实际意义,掌握它的解题方法,培养学生的分析,对比能力和综合、概括能力,提高他们的解题能力,发展他们的智力。

【学情分析】六年级的学生已初步具备了抽象思维能力，对于学习工程应用题在思想上已经做好准备。

学生已经在三、四年级学习了工作总量、工作效率、工作时间三者之间的关系；六年级第三单元学习分数除法应用题，学生已经掌握了相关的分数应用题的知识，在教学过程中，学生已具备了结合相关的数量关系进行独立解题的能力。

这些都为学生学习工程应用题做好了充分的知识准备。

因此激活这些基础知识，让工程应用题建构在已有知识经验之上，显得尤为重要。

依据本单元教材特点和学生认知规律，本课采用的素材是工程问题，借此让学生经历自主探究，解决问题的过程，掌握假设、验证等方法解决问题的基本策略，让学生体会数学模型思想。

谈用分数解决问题中如何找单位“1”的量作者：侯曙霞来源：《学周刊》2018年第29期摘要：在分数应用题的解答过程当中，能否找准单位“1”的量非常重要，它是解答分数应用题的关键。

在平时的课堂教学当中，必须立足根本，从“意义’入手找单位“1”；也可以从部分与整体的比较中找到单位“1”；还可以从原数量与现数量的比较分析中找到单位“1”，从而抓住问题的本质，提高学生分析问题、解决问题的能力。

关键词：分数；解决问题；单位“1”；分率中图分类号：G62 文献标识码：A 文章编号：1673-9132（2018）29-0069-02DOI：10.16657/ki.issn1673-9132.2018.29.042单位“1”也称整体“1”，它是一个标准量，是相对于比较量（几分之几）来说的。

所以比较量和标准量是一组相互依存的概念。

有时在同一道题中往往会出现一个或多个单位“1”的量，只有把握准单位“1”的量，才能使学生更轻松地解题。

一、从“分数的意义”入手分数是指把单位“1”均分成若干份，表示这样一份或几份的数。

教材中明确指出“一个物体，一个计量单位，或者是许多物体组成的一个整体”都可以用单位“1”表示。

所以单位“1”与分数的意义紧密相连。

从而理解把谁平均分，谁就是单位“1”。

例如；国家一级保护动物野生丹顶鹤，2001年全世界约有2000只，我国占其中的1/4，我国约有多少只？教师可先引导学生动手画图，在分析“我国占其中的1/4”，就是指把2000只丹顶鹤平均分成4份，我国的丹顶鹤数量占这样的1份。

要把2000只丹顶鹤平均分，所以“2000只丹顶鹤”是单位“1”的量。

二、在分率句子中出现两种数量的比较找出关键的分率句子中的“的”“相当于”“是”“比”“占”等字词，让学生明白这些字词对单位“1”的判断很重要。

孩子们在平时的练习中，经常会遇到像这样的含分率的句子：一个果园里有600棵果树，苹果树是全部果树的2/5；一个果园里，苹果树是梨树的1/2；一个果园里，苹果树相当于梨树的1/2；一个果园里，苹果树占梨树的1/2；一个果园里，苹果树比梨树多1/2。

解决问题单位“1”是关键作者：陈魏群来源：《教育·教学科研》2018年第12期解决问题是小学数学中的一个重要组成部分，对学生思维能力的培养有很重要的作用。

在小学数学教学中，教师普遍认为，分数的应用与解决问题是教学的重点，而对于小学生来说这也是一大难点，如何能够让教师成功地将应用题这部分知识传授给学生，而学生也能够轻松地掌握，是当前小学数学教师需要认真思考的问题。

教科书中对于分数的意义有一个详细的概述，教学中始终在强调把一个整体看作单位“1”。

分数在应用与解决问题中与其他类型的问题相比，涉及单位“1”，显得更为抽象，学习难度也相对较大，解题方法更加独特。

而小学生在解决分数问题时，常常理不清该用乘法还是除法，以下是分数乘除法单元中几类典型问题的分析和整理。

“几分之几”的问题探讨例题：东东家养了7只鹅，10只鸭，鹅的只数是鸭的几分之几？阅读理解：“鹅的只数是鸭的几分之几”是什么意思？就是求7只是10只的几分之几。

分析解答：把10只看做单位“1”，平均分成10份，每份1只，7只就是这个整体的 ;，根据分数与除法的关系，求7只是10只的几分之几，可以用7÷10解决。

总结：关于“求一个数是（占、相当于、正好是）另一个数的几分之几”的问题可以根据分数的意义以及分数与除法的关系用“一个数÷另一个数”的方法解决问题。

把问题带进生活，走进班级，发现班级人数这一信息可是非常适用于分数的应用和解决问题。

班里有46个同学，其中男生25人，女生21人，男生比女生多全班的几分之几？男生比女生多几分之几？乍一看，部分同学会有意见“老师，这两问题不是一样的吗？”这时候可就得反复斟酌了，最后个别熟知分数意义的同学觉悟了，原来单位“1”发生了改变。

“男生比女生多全班的几分之几”求的是男生比女生多的人数是全班的几分之几，这里把全班人数当做单位“1”，也就是求（25-21）是46的几分之几？用算式（25-21）÷46解决。

巧用单位“1”解决问题沂源县悦庄二中阮阳在应用分数乘法、除法，百分数的乘法、除法解决问题时，很多同学不能正确的找到单位“1”，不会应用单位“1”解决问题，在此，就单位“1”的问题做一下研究。

一、找单位“1”的方法。

一般情况下，题目都会告诉我们“一个量的几分之几，一个量的百分之几。

”这里的一个量就是本题的单位“1”，我们要弄清楚这里的“几分之几、百分之几”是那个量的，只要找出这个量，就找出了单位“1”。

例：1、鸡是鸭的16。

这里的16指的是“鸭只数的16”，由此，我们可以说：鸭的只数就是本题的单位“1”。

2、男生比女生多30%。

是与女生比较，比女生多30%，就是指男生比女生多女生的30%，由此我们可以知道：女生人数就是本题的单位“1”。

3、水结成冰，体积增加111。

我们知道，水结成冰后，体积就变大了。

因此，题目中的“体积增加111”可以叙述为“冰的体积比水的体积增加水体积的111”。

由此，可以断定：水的体积是本题的单位“1”。

二、正确分析单位“1”是已知量还是未知量，确定解决方法在一道题目中，如果单位“1”是已知量，该题用“乘法”做，如果单位“1”是未知量，该题用“除法”解决。

例：1、某超市运来白菜1500kg，运来的土豆是白菜的35，超市运来土豆多少千克？解析：本题的关键句是“运来的土豆是白菜的35”，由这句话可知：白菜的数量是单位“1”，第一句话又告诉了“白菜有1500kg”，故单位“1”是已知的量，本题用乘法解决。

可列式为：1500×35=900kg。

2、某超市运来白菜1500kg，是运来的土豆的35，超市运来土豆多少千克？解析：本题的关键句是“是运来土豆的35”，由这句话可知：土豆的数量是单位“1”，题中的1500kg是白菜的数量，不是土豆的，故单位“1”是未知的量，本题用除法解决。

可列式为：1500÷35=1500×53=2500kg。

3、某养殖场养鸡480只，养的鸭是鸡的56，又是鹅的47，该养殖场养鹅多少只？解析：由“养的鸭是鸡的56”可知，鸡的数量是单位“1”，又知鸡有480只。

180分数乘除法问题的解决策略★ 任广慧在我们的小学数学的学习过程中，分数乘除法解决问题是其中的重点，又是难点。

它不仅在小学数学中起到非常重要的作用，也是初中深层次知识学习的基础，它对逻辑思维能力和解题能力都有很高的要求，所以很多同学在遇到这类问题时，经常混淆计算方法，找不到解题思路。

下面老师就来介绍几种解决策略，帮助大家突破难点，化繁为简。

一、找准单位“1”是基础找单位“1”是解决分数乘除法问题的基础，只有找准了单位“1"，才能明确题目的数量关系，找到解决问题的方法。

那怎样来找单位“1"呢?单位“1”都藏在含有分率的句子中，我们把这个句子叫关键句。

它可以分为以下三种情况：1、标准句式直接找2、一般在“的”字前，“是”、“占”、“比”、“相当于”等字词后面的量是单位“1”。

这几个字叫关键字。

3、省略句式补充找如：现价降低4/7，没有关键字，我们就要根据这句话的意思补充成“现价（比原价）降低4/7"，这时就回到了前面说的标准句式，“比”后面是“原价”就是单位“1”。

4、特殊句式慎重找5、有些关键句比较特殊，就像“吃去的比剩下的多总量的2/ 5”，这个关键句中，既出现了“的”，又出现了“比”，这就要仔细思考了。

当“比”和“的”都出现时，以“的”优先，所以单位“1”是总量，而不是剩下的量。

二、分清类型是关键找准单位“1”，就进入了解决问题的重要环节，分清类型，根据类型写出数量关系式，确定解题方法。

通过学习，我们知道分数乘除法解决问题可以分为三大类型，把它整理在下表格中。

通过表格，我们就可以看出第一种类型是分数乘法，后两种是分数除法，它们都有三个量单位“1”、比较量和对应分率，并已知其中两个量，求第三个。

那如何才能区分类型，确定方法呢？老师有妙招，只要区分问题，就能确定方法。

三、多种策略要灵活在解决实际问题时，除了上面的策略，还得学会从不同的方法入手，灵活解题。

1、从“量率对应”入手找出解题方法分数乘除法解决问题中，有“量率对应”的明显特点，对一个单位“1”来说，每个分率都对应着一个具体的数量，而每一个具体的数量，也同样对应着一个分率，因此，正确确定“量率对应”是解题的关键。

在分数混合运算解决问题中怎样突出单位“1”分数问题可分为两类，一类是基本分数问题，此类问题中单位“1”比较容易找。

另一类是分数混合运算问题，这类问题中既有整数问题中的数量关系，又有分数问题中的数量关系，混合交错出现，因此正确找出单位“1”至关重要。

就需要交给学生一些找单位“1”的方法和技巧。

一利用分数的意义找单位“1”。

把单位“1”平均分成几份或若干份，表示这样一份或几份的数叫分数。

单位“1”可以是一个物体，可以是一个计数单位，还可以是一个整体。

把谁平均分谁就是标准，谁就是单位“1”。

再搞清楚要求的问题或已知数量占单位“1”的几分之几，选择合适的方法解决。

例1 一个发电厂有煤2500吨，用去3/5，还剩多少吨？分析：这道题中把原有煤的总吨数平均分成5份，因此原有煤的总吨数作为单位“1”。

求的是还剩的吨数？找出还剩的分率是1-3/5，单位“1”已知用乘法可求。

算式：2500*（1-3/5）例2 修一条公路，已经修了3/4, 还剩6千米没有修。

这条公路长多少米？分析：题中是把整条公路平均分成4份，修了的占3份，剩下的占1份。

是把整条公路平均分，因此公路总长度是单位“1”。

剩下的6千米对应的分率是1-3/4，单位“1”未知用除法。

算式：6/（1-3/4）例3 一件工程，甲队单独完成要20天，乙队单独完成要15天。

两队合作完成要多少天？分析：这道题中没有给出具体的工作量和工作效率。

从“甲队单独完成要20天”可理解为把这件工程平均分为20份，1份是1/20，“乙队单独完成要15天”可理解为把这件工程平均分为15份，1份是1/15。

由此可见是把这件工程平均分，因此把工作总量看作单位“1”。

甲、乙两队合作每天完成全工程的（1/20+1/15）。

根据“工作总量/工作效率=工作时间”关系式求出。

算式：1/(1/20+1/15)二在隐含中找单位“1”。

单位“1”的量有时不明显，要从题中找出隐含的单位“1”。

仔细读题，正确理解题意，搞清楚谁和谁比，这两个量中后一个量作比较标准，就是单位“1”。

四解决问题一、“求一个数的几分之几(或百分之几)是多少”的实际问题1.“已知一个部分量是总量的几分之几,求另一个部分量是多少”的实际问题的解题方法。

(1)单位“1”的量-单位“1”的量×一个部分量占单位“1”的几分之几=另一个部分量。

(2)单位“1”的量×(1-一个部分量占单位“1”的几分之几)=另一个部分量。

2.“已知一个数比另一个数多几分之几,求这个数”的实际问题的解题方法。

(1)单位“1”的量+单位“1”的量×一个数比单位“1”的量多的几分之几=这个数。

(2)单位“1”的量×(1+一个数比单位“1”的量多的几分之几)=这个数。

3.“已知一个数比另一个数少几分之几,求这个数”的解题思路与“已知一个数比另一个数多几分之几,求这个数”的解题思路相同,只不过在列式时把加法换成减法。

二、“已知一个数的百分之几(或几分之几)是多少,求这个数”的实际问题1.简单的“已知一个数的百分之几是多少,求这个数”的问题的解题方法。

(1)方程法。

①找出单位“1”,设单位“1”的量为x。

②找出题中的等量关系。

③列出方程并解答。

(2)算术法。

①找出单位“1”。

②找出己知量和己知量占单位“1”的百分之几。

③列除法算式解决问题。

2.稍复杂的“已知一个数的几分之几是多少,求这个数”的问题的解题方法。

(1)找出题中的等量关系,设单位“1”的量为x,列出方程并解“已知一个部分量占总量的百分之几,求另一个部分量是多少”的实际问题的解题方法与“已知一个部分量占总量的几分之几,求另一个部分量是多少”的实际问题的解题方法相同。

“已知一个数比另一个数多百分之几,求这个数”的解题方法与“已知一个数比另一个数多几分之几,求这个数”的解题方法相同。

易错点:在解答百分数问题时,一定要找准单位“1”,单位“1”的量未知,可以用除法求出单位“1”的量。

举例:李强六月份的生活费为255元,比计划节省了15%,节省了多少钱?错解:255×15%=38.25(元)答:节省了38.25元。

正确找准单位“1”解决应用题正确找准单位“1”，是解答小学六年级分数（百分数）应用题的关键。

每一道分数应用题中总是有关键句（含有分数率的句子）。

如何从关键句中找准单位“1”，我觉得可以从以下这些方面进行考虑：一、 解决问题的基本思路：分数的意义，“把单位1平均分成若干份，表示这样的一份或几份的数，叫分数”。

所以单位1的判定，就是看把谁平均分了，就把谁看作单位1.二、找单位“1”的具体方法：（一）、部分和总体：在同一整体中，部分和总体作比较关系时，部分通常作为比较量，而总体则作为标准量，那么总体就是单位“1”。

例如：我国人口约占世界人口的1/5，世界人口是总数，我国人口是部分数，所以，世界人口就是单位“1”。

再如，食堂买来100千克白菜，吃了52，吃了多少千克？在这里，食堂一共买来的白菜是总数，吃掉的是部分数，所以100千克白菜就是单位“1”。

解答这类分数应用题，一般有两种方法：：一种是先求出已知量是总量的几分之几的部分量，在用总量减去这个部分量，求出另一个量；另一种是先求出要求的部分量占总量的几分之几，再根据分数乘法的意义求出这个部分量是多少。

例如：食堂里有540千克大米，第一周吃掉总数的31，第二周吃掉总数的21，第二周比第一周多吃去多少千克？分析：把540千克看做单位“1”，单位“1”的数量是已知的，所以用乘法计算，要求“第二周比第一周多吃去多少千克”所以用减法。

即：540×21－540×31＝270－180＝90千克（二）、两种数量比较：分数应用题中，两种数量相比的关键句非常多。

有的是“比”字句，有的则没有“比”字，而是带指向性特征的“占”、“是”、“相当于”。

在含有“比”字的关键句中，比后面的那个数量通常就作为标准量，也就是单位“1”。

例如：六（2）班男生比女生多21。

就是以女生人数为标准（单位“1”），男生比女生多的人数作为比较量。

在另外一种没有比字的两种量相比的时候，我们通常找到分率，看“占”谁的，“相当于”谁的，“是”谁的几分之几。

有些同学在解决问题时，往往不注意单位名称，因此常常出现错误。

所以我们在审题时，先要全面理解题意，特别要看清单位名称，相互比较，统一单位，分析数量关系后，再形成解题计划。

例1：一台脱粒机每小时可以脱粒35吨，4台这样的脱粒机40分钟可以脱粒多少吨？分析与解分析与解：：题目中告诉了单一量“一台脱粒机每小时可以脱粒35吨”，其中时间单位是小时，而另一个条件却是40分钟，单位不一致，因此要统一单位，把40分钟化成40÷60=23小时。

35×4×23=85（吨）答：4台这样的脱粒机40分钟可以脱粒85吨。

例2：王叔叔家阁楼上的窗玻璃是梯形的，上底、下底和高分别是35米、45米、7.5分米。

这块玻璃的面积是多少平方厘米？
分析与解分析与解：：首先条件中上底、下底和高的长度单位不同，要先统一后才能列式计算，并且问题中的单位也和条件中的不一致，所以最后还要与问题中的单位相统一。

7.5分米=34米（35+45）×34÷2=2140（平方米）2140平方米=5250（平方厘米）答：这块玻璃的面积是5250平方厘米。

也可以先把条件中的单位与问题中的相统一。

35米=60厘米、45米=80厘米、7.5分米=75厘米。

然后列式计算：
（60+80）×75÷2=5250（平方厘米）
◎相子凡
答 Copyright©博看网 . All Rights Reserved.。

“单位一”专项解析及习题单位“1”问题贯穿了整个六年级数学的学习内容，从分数乘法到分数除法，从比例到百分数，基本上所有的计算类题目、解决问题都有着单位“1”的影子出现。

因此找单位“1”也就成了解分数等一类问题的基础与关键，只有找准了单位“1”，才能明确题目的数量关系，找到解决问题的方法。

那怎样来找单位“1”呢？一、标准句式直接找（1）找“的”字。

如“看了全书的1/5”，有“的”字，那单位“1”就是“的”前面的量，即全书的页数。

但也要注意，不是所有的“的”字前面就是单位“1”，这个“的”字既要在关键句中，又得紧挨在分数前面，否则就会找错单位“1”了！（2）找“比”字。

在题目的关键句中找“比”字，单位“1”就是比“字”后面的量。

如“小明比小红高1/8”，单位“1”就是小红的身高。

二、省略句式补充找如“现价降低4/7”，先补充成“现价（比原价）降低4/7”，“原价”就是单位“1”的量。

三、特殊句式慎重找有些关键句比较特殊，就像“吃去的比剩下的多总量的2/5”这个关键句中，既出现了“的”，又出现了“比”，怎么办?这就要仔细思考了。

当“比”和“的”都出现时，以“的”优先，所以单位“1”是总量，而不是剩下的量。

解题小技巧：1、解决问题或列式计算等问题中，式子的列法：首先审题找到单位“1”、“已知量”、“未知量（要求的量）”，然后看单位“1”是已知量还是未知量，是已知量用乘，是未知量用除。

最后确定已知量与未知量间的直接的分数关系（谁是谁的几分之几），列式。

已知量×/÷直接分数关系题目中，有时候单位“1”是固定的，有时候确是变化的，做题时一定要注意这一点！2、“谁比谁多几分之几，谁比谁少几分之几”问题解法：这类问题中有的时候给的数量是具体数，有的时候给的是比例或分数关系，这时候在求解“谁比谁多几分之几，谁比谁少几分之几”要区别对待：对于给的是具体数的题目，我们直接用具体数去做，反之则可以用“赋值（代数）法”去做。

巧用单位“1”解决分数、百分数问题分数、百分数的解题方法，大致是相同的。

步骤如下：一、寻找单位“1”1、表示数量关系的分数或百分数前面的量，就是单位“1”。

例如：“儿子的年龄比爸爸年龄的多4岁”，单位“1”是前的量“爸爸的年龄”；“男生60人，女生80人，男生人数比女生多百分之几？”单位“1”是“百分之几前的量：女生人数。

2、如果叙述比较简洁，需根据题意将句子补充完整。

例如：解决“8月份用水100吨，10月份节约15%，10月份用水多少吨？”时，把“10月份节约15%”补充成“10月份比8月份节约15%”。

单位“1”就是15%前的量：8月份的用水量。

解决“一种手机原价1200元，现在降低了，现价多少钱？”时，需将“现在降低了”补充成“现价比原价降低了” ，单位“1”就是前面的量：原价。

二、选择合适的方法。

（一）不求单位“1”1、分数，百分数前有多，增加等字样，用乘加。

例如：五年级师生向希望小学捐书150本，六年级比五年级多捐20% 。

六年级师生捐书多少本？分析：单位“1”是五年级师生捐书数。

不求单位“1”，前有“多”，用乘加。

列式150×（1+20% ）2、分数，百分数前有少，降低，短等字样，用乘减。

例如：五年级师生向希望小学捐书150本，六年级比五年级少捐20%。

六年级师生捐书多少本？分析：单位“1”是五年级师生捐书数。

不求单位“1”，20%前有“少”，用乘减。

列式150×（1-20% ）3、分数，百分数前无多无少。

直接用乘法。

例如：五年级师生向希望小学捐书150本，六年级捐书数是五年级的80%。

六年级师生捐书多少本？分析：单位“1”是五年级师生捐书数。

不求单位“1”，80%前无多无少字样，直接用乘法。

列式150×80%（二）求单位“1”1、分数，百分数前有多，增加等字样，用除加。

例如：图书馆有科技书400本，比故事书多20% ，故事书有多少本？分析：单位“1”是故事书册数，求单位“1”。

一、分数乘法的解决问题
（如果单位1是已知的, 要求它的几分之几，就用乘法）
1、找单位“1”：在分率句中分率的前面；或“占”、“是”、“比”的后面
2、求一个数的几倍：一个数×几倍；
求一个数的几分之几是多少：一个数×几分之几。

3、写数量关系式技巧：
（1）“的”相当于“×”
“占”、“是”、“比”相当于“= ”
（2）分率前是“的”：单位“1”的量×分率=分率对应量
（3）分率前是“多或少”的意思：单位“1”的量×（1 +/ - 分率）=分率对应量
二、分数除法解决问题
（已知单位“1”的几分之几是多少，单位“1”的量是要求的问题。

就用除法）
1、数量关系式和分数乘法解决问题中的关系式相同：
（1）分率前是“的”：单位“1”的量×分率=分率对应量
（2）分率前是“多或少”的意思：单位“1”的量×（1 +/-分率）=分率对应量
2、解法：（建议：最好用方程解答）
（1）方程：根据数量关系式设未知量为x，用方程解答。

（2）算术（用除法）：分率对应量÷对应分率= 单位“1”的量
3、求一个数是(占)另一个数的几分之几：
一个数÷另一个数
4、求一个数比另一个数多（少）几分之几：
①求多几分之几：大数÷小数–1 或①求多几分之几(大数-小数)÷比后面的数（单位“1”）
②求少几分之几：1-- 小数÷大数或②求少几分之几(大数-小数)÷比后面的数（单位“1”）。