当前位置：文档之家 › 工程力学范钦珊第二版7、8复习弯曲强度与弯曲变形

工程力学范钦珊第二版7、8复习弯曲强度与弯曲变形

  • 格式：ppt
  • 大小：1.40 MB
  • 文档页数：40

下载文档原格式

  / 40

合集下载

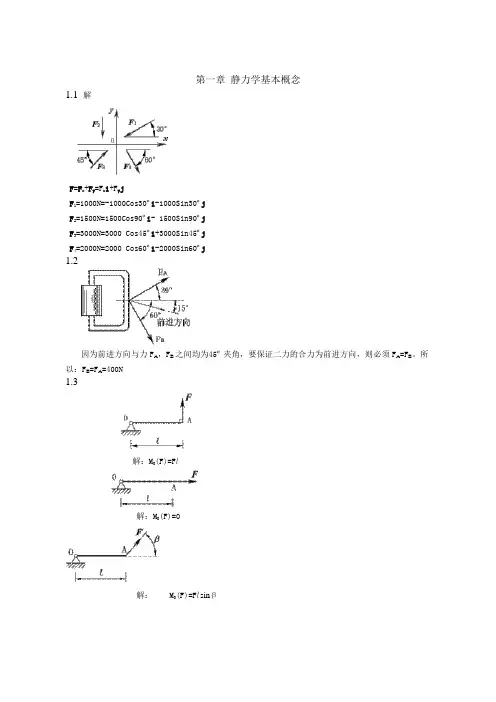
工程力学课后答案(第二版少学时)

工程力学课后答案(第二版少学时)

第一章静力学基本概念1.1 解F=F x+F y=F x i+F y jF1=1000N=-1000Cos30ºi-1000Sin30ºjF2=1500N=1500Cos90ºi- 1500Sin90ºjF3=3000N=3000 Cos45ºi+3000Sin45ºjF4=2000N=2000 Cos60ºi-2000Sin60ºj1.2因为前进方向与力F A，F B之间均为45º夹角，要保证二力的合力为前进方向，则必须F A=F B。

所以：F B=F A=400N1.3解：M O(F)=F l解：M O(F)=0解： M O(F)=F l sinβ解： M O(F)=F l sinθ解： M O(F)= -F a解：M O(F)= F(l＋r)解:1.4解:1.5解：1位置：M A(G)=02位置：M A(G)=-G l sinθ3位置：M A(G)=-G l1.6解：M O(F n)=-F n cosθ·D/2=-75.2N·m 1.71.8第二章平面力系2.1 力系简化解：（1）主矢大小与方位：F/R x＝∑F x＝F1cos45º+F3+F4cos60º＝100Ncos45º+200N+250cos60º＝395.7N F/R y＝∑F y＝F1sin45º-F2-F4sin60º＝100Nsin45º-150N-250sin60º＝-295.8N（2）主矩大小和转向：M O＝∑M O(F)＝M O(F1)+M O(F2)+M O(F3)+M O(F4)+m＝0-F2×0.3m+F3×0.2m+F4sin60×0.1m+F×0.1m＝0-150N×0.3m+200N×0.2m+250Nsin60×0.1m+50N×0.1m ＝21.65N·m( )向O点的简化结果如图所示。

工程力学第2版教学配套课件刘思俊8弯曲8

工程力学第2版教学配套课件刘思俊8弯曲8


M= M(x)
2.剪力图和弯矩图—剪力方程和弯矩方程表示的函数图象。
例8-3 图示台钻手柄杆AB用螺纹固定在 转盘上，已知l、F，试建立手柄杆AB的剪
力、弯矩方程，并画其剪力、弯矩图。
MA
A FA
x
l
FQ
F
M
-Fl
F
B
解 :1.建AB杆悬臂梁模型，求出约束力 FA=F， MA=Fl。
2.列剪力方程和弯矩方程
称平面内，梁轴线弯成一条平面曲线。
二、梁的力学模型 梁的力学模型包括了梁的简化、载荷的简化和支座的简化。
静定梁的基本力学模型分为简支梁、外伸梁、悬臂梁。 三、弯曲内力—剪力FQ和弯矩M
弯曲内力的正负规定：剪力左上右下为正，反之为负。弯矩 左顺右逆为正，反之为负。
求梁横截面内力的简便方法： FQ (x)= 左(或右)段梁上外力的代数和，左上右下为正。
x
FQ（x）= FA=F
（0<x<l)
Ｍ（x）= FAx-MA=-F（l-x） (0<x<l)
3. 建立坐标画剪力图和弯矩图
x 剪力图为平行于x 轴的水平线，弯矩图为
斜直线6，/12 |Ｍ|max= Fl 。
尚尚辅辅教网学sh配ang套fuw课ang件
MA
A FA
x
l
FQ
F
F B
x
M
x
-Fl
从上例8-3可以得出
6/12
三、弯曲内力—剪力FQ尚和尚辅弯辅教矩网学Msh配ang套fuw课ang件
1.用截面法求剪力和弯矩 图示悬臂梁，在A端作用一集中力F。
用画梁m-的m将受梁力分图求为其两约段束，力求F任B、意约x 束力偶A矩MB。
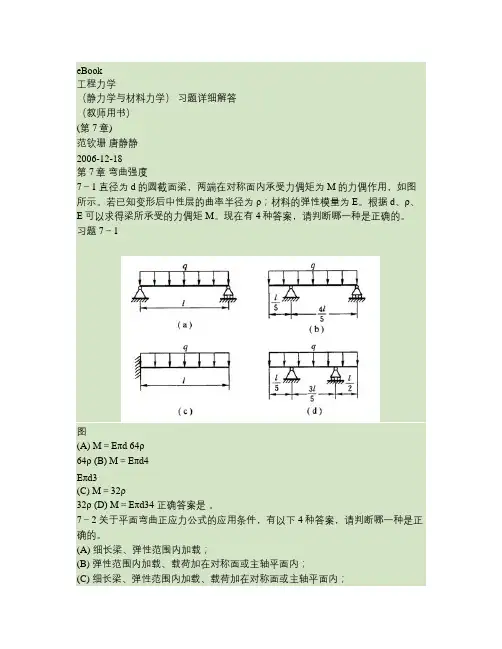
工程力学(静力学和材料力学)第2版课后习题答案 范钦珊主编 第10章 组合受力与变形杆件的强度计算

工程力学(静力学和材料力学)第2版课后习题答案 范钦珊主编 第10章 组合受力与变形杆件的强度计算


解：危险截面在 A 处，其上之内力分量为： 弯矩： M y = FP1 a ， M z = FP2 H 扭矩： M x = FP2 a 轴力： FNx = FP1 在截面上垂直与 M 方向的垂直线 ab 与圆环截 求得 M y 与 M z 的矢量和 M 过截面中心， 面边界交于 a、b 两点，这两点分别受最大拉应力和最大压应力。但由于轴向压力的作用，最 大压应力值大于最大拉应力值，故 b 点为危险点，其应力状态如图所示。 10－7 试求图 a 和 b 中所示之二杆横截面上最大正应力及其比值。 解： （a）为拉弯组合
7
y
y
A
O
0.795
B
14.526
+13.73MPa
z
(a)
O O
+14.43MPa
(b)
C
y
A
C
B B
y
A
O O
B
z
12.6mm
14.1mm
zC
−15.32MPa
16.55MPa
zC
z
(c)
(d)
习题 10－9 解图
∴
+ σ max
= 14.526 − 0.795 = 13.73 MPa
− σ max = −14.526 − 0.795 = −15.32 MPa
Ebh
由此得
2 FP 6e
e=
10－9
ε1 − ε 2 h × ε1 + ε 2 6
图中所示为承受纵向荷载的人骨受力简图。试：
1．假定骨骼为实心圆截面，确定横截面 B－B 上的应力分布； 2．假定骨骼中心部分(其直径为骨骼外直径的一半)由海绵状骨质所组成，忽略海绵状承受 应力的能力，确定横截面 B－B 上的应力分布；
工程力学课后习题答案_范钦珊(合订版)

工程力学课后习题答案_范钦珊(合订版)


(a)
(b)
习题 1－1 图
解：图（a）： F = F cosα i1 + F sinα j1 分力： Fx1 = F cosα i1 ， Fy1 = F sinα j1
投影： Fx1 = F cosα ， Fy1 = F sinα
讨论： ϕ = 90°时，投影与分力的模相等；分力是矢量，投影是代数量。
∴ ϕ2 = 29°51′ 由 A 平衡： FNA = 1⋅ cosϕ1 = 0.092N
由 B 平衡： FNB = 2 ⋅ cosϕ 2 = 1.73N
（4） （5）
返回总目录 下一章
11
eBook
工程力学
（静力学与材料力学）
习题详细解答
（教师用书） (第 2 章)
范钦珊 唐静静
2006-12-18
y
FTA
FR
α
FTB
x
FTC
习题 2－3 图
习题 2－3 解图
解：（1）由题意知 FTA = FTB = FTC = 5kN 。
由习题2－3解图，作用于大船上的合力在x、y轴上的投影的大小分别为：
FAx
A
C FC' x
FAy
FC' y
习题 1－5b 解 3 图
FC C
FB'
B
D FD' FD
FAx
A
D
FE FE'
E
E
B
FAy
FB
习题 1－5c 解图
1—6 图示刚性构件 ABC 由销钉 A 和拉杆 D 所悬挂，在构件的 C 点作用有一水力 F。 如果将力 F 沿其作用线移至 D 点或 E 点处（如图示），请问是否会改变销钉 A 和 D 杆的受 力？
工程力学第8章 梁弯曲时的强度计算

工程力学第8章 梁弯曲时的强度计算


A
E
6
B
E
CF
D
6kN·m
8.2.4 按叠加原理作弯矩图
叠加原理：当梁在载荷作用下发生微小变形时，其跨长 的改变可以略去不计，因此在求梁的约束力、剪力和弯 矩时，均可按其原始尺寸进行计算，而所得的结果均与 梁上荷载成线性关系。在这种情况下，当梁上受几种荷 载共同作用时，某一横截面上的弯矩就等于梁在各项荷 载单独作用下同一横截面上弯矩的代数和。
F
1
2
A
C
200
1265
F FB
3
D
B
115
CD段 FSC右 FA F 1.7kN
+ 23.6kN
DB段 FSD右 FB 27kN
1.7kN
27kN
FSB右 0kN
FSmax 27kN
每段梁的弯矩图均为斜直
线，且梁上无集中力偶. FA
MA 0
A
M C FA 0.2 4.72kNm
q(x)、FS(x)图、M（x）图三者间的关系
1.梁上某段无分布荷载即q(x) = 0 剪力图为一条水平直线，弯矩图 为一斜直线.剪力图是正号，弯矩图为斜向上的直线;剪力图是负 号，弯矩图为斜向下的直线；剪力图为零，弯矩图为水平线。
2.梁上某段有均布荷载。剪力图为斜直线，弯矩图为二次抛物线。
q(x) > 0，剪力图为斜向上的直线，弯矩图为向上凸的二次抛物线；
例题8 一简支梁受两个力F作用,如图所示.已知 F= 25.3kN, 有关尺寸如图所示.试作剪力图和弯矩图.
解：（1）求梁的支反力
FA 23.6kΝ FB 27 kN
FA
F
1
2
A
工程力学(静力学和材料力学)第2版课后习题答案 范钦珊主编 第8章 弯曲刚度

工程力学(静力学和材料力学)第2版课后习题答案 范钦珊主编 第8章 弯曲刚度


课
后 答
案
网
解：由挠度表查得：
FP al 180° × 3 EI π Wal 180° = ⋅ 3 EI π 20000 × 1 × 2 × 64 180° = ⋅ 3 × 200 × 109 × π d 4 π ≤ 0 .5 ° d ≥ 0.1117 m，取 d = 112mm。
θB =
ww w
6 ( 246 + 48) ×10 × 200 ×10 × π × 32 × 10−12
2
co
m
8—3 具有中间铰的梁受力如图所示。试画出挠度曲线的大致形状，并说明需要分几段 建立微分方程，积分常数有几个，确定积分常数的条件是什么？（不要求详细解答）
习题 8－3 图
后 答
案
网
习题 8－4 图
课
习题 8－4a 解图
解： (a)题 1.
wA = wA1 + wA 2
wA1 =
⎛l⎞ q⎜ ⎟ ⎝2⎠
87图示承受集中力的细长简支梁在弯矩最大截面上沿加载方向开一小孔若不考虑应力集中影响时关于小孔对梁强度和刚度的影响有如下论述试判断哪一种是正确的
eBook
工程力学
（静力学与材料力学）
习题详细解答
(第 8 章) 范钦珊 唐静静
课
后 答
案
网
2006-12-18
ww w
1
.k hd
aw .
co
m
（教师用书）
−3 9 4
(
.k hd
解：由挠度表查得 F ba 2 wC = P l − a 2 − b2 6lEI
(
)
习题 8－9 图
8
aw .
)
工程力学基础课件：第8章 弯曲强度

工程力学基础课件：第8章 弯曲强度


A
C
横力弯曲：横截面上既有 弯矩，又有切力。
a F
F
D
B
a
F
M
zM
Fa
Fa
O
dA x
dA
y
梁横截面上的弯矩
z M ydA 直接导出弯曲正应力
y
A
1、几何关系
（1）变形现象
（a）各纵向线段弯成弧线，且部分纵向线段伸长， 部分纵向线段缩短。
（b）各横向线相对转过了一个角度，仍保持为直线。 （c）变形后的横向线仍与纵向弧线垂直。
平面弯曲
梁的弯曲平面（即弯曲前与弯曲后梁轴线所确定的 平面）与载荷平面（即梁上载荷所在平面）重合 （或平行）的这种弯曲，称为平面弯曲。
通过梁轴线和截面对称轴的平面，称为纵向对称面。 当梁上载荷（含支座反力）位于纵向对称面内时，将 发生平面弯曲。
纵向对称面
最基本常见的弯曲问题
——对称弯曲
纵对称面
将应力表达式代入第二式，得
A z
dA
E
yzdA 0
A
此即保证梁为平面弯曲的条件。
E y
M z ydA M 3
A
将应力表达式代入第三式，得
M ydA E y2 dA
A
A
A y2 dA IZ
1 M
E Iz
中性层曲率半径的确定 也即梁弯曲变形的基本公式
纯弯曲时横截面上弯曲正应力的计算公式
中性轴
中性层
z
横截面
（4）应变变化规律
O
b1'b2' ydq
b1b2 dx O1O2 O1'O2' dq
( y)dq dq y
dq
M
工程力学(静力学和材料力学)第2版课后习题答案 范钦珊主编 .

工程力学(静力学和材料力学)第2版课后习题答案 范钦珊主编 .

eBook工程力学（静力学与材料力学）习题详细解答（教师用书）(第7章)范钦珊唐静静2006-12-18第7章弯曲强度7－1 直径为d的圆截面梁，两端在对称面内承受力偶矩为M的力偶作用，如图所示。

若已知变形后中性层的曲率半径为ρ；材料的弹性模量为E。

根据d、ρ、E可以求得梁所承受的力偶矩M。

现在有4种答案，请判断哪一种是正确的。

习题7－1图(A) M＝Eπd 64ρ64ρ (B) M＝Eπd4Eπd3(C) M＝32ρ32ρ (D) M＝Eπd34 正确答案是。

7－2 关于平面弯曲正应力公式的应用条件，有以下4种答案，请判断哪一种是正确的。

(A) 细长梁、弹性范围内加载；(B) 弹性范围内加载、载荷加在对称面或主轴平面内；(C) 细长梁、弹性范围内加载、载荷加在对称面或主轴平面内；(D) 细长梁、载荷加在对称面或主轴平面内。

正确答案是 C _。

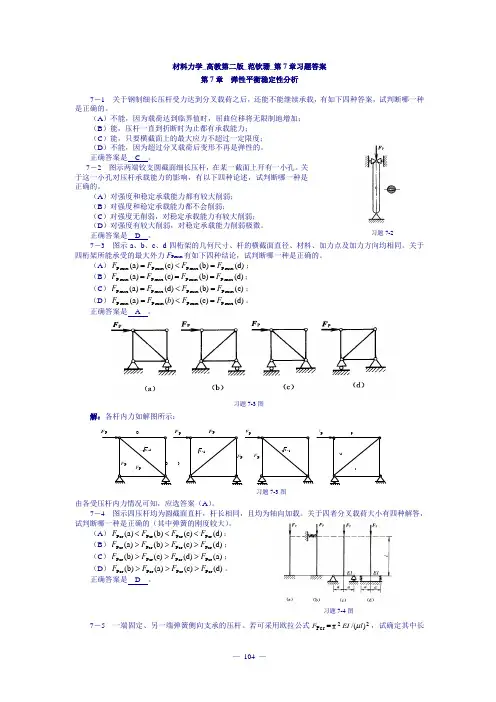
7－3 长度相同、承受同样的均布载荷q作用的梁，有图中所示的4种支承方式，如果从梁的强度考虑，请判断哪一种支承方式最合理。

l 5习题7－3图正确答案是7－4 悬臂梁受力及截面尺寸如图所示。

图中的尺寸单位为mm。

求：梁的1－1截面上A、 2B两点的正应力。

习题7－4图解：1. 计算梁的1－1截面上的弯矩：M=−⎜1×10N×1m+600N/m×1m×2. 确定梁的1－1截面上A、B两点的正应力：A点：⎛⎝31m⎞=−1300N⋅m 2⎟⎠⎛150×10−3m⎞−20×10−3m⎟1300N⋅m×⎜2My⎝⎠×106Pa=2.54MPa(拉应力)σA=z=3Iz100×10-3m×150×10-3m()12B点：⎛0.150m⎞1300N⋅m×⎜−0.04m⎟My⎝2⎠=1.62×106Pa=1.62MPa(压应力)σB=z=3Iz0.1m×0.15m127－5 简支梁如图所示。

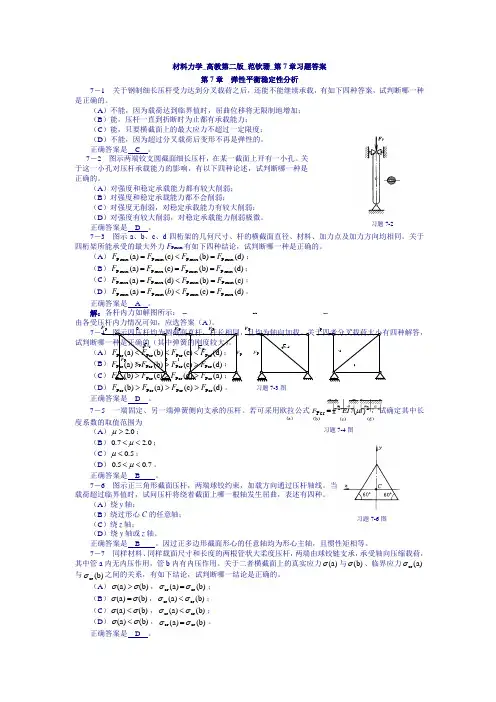
材料力学高教第二范钦珊第7章习题答案

材料力学高教第二范钦珊第7章习题答案

习题7-4图 材料力学_高教第二版_范钦珊_第7章习题答案第7章 弹性平衡稳定性分析7－1 关于钢制细长压杆受力达到分叉载荷之后，还能不能继续承载，有如下四种答案，试判断哪一种是正确的。

（A ）不能，因为载荷达到临界值时，屈曲位移将无限制地增加； （B ）能，压杆一直到折断时为止都有承载能力；（C ）能，只要横截面上的最大应力不超过一定限度； （D ）不能，因为超过分叉载荷后变形不再是弹性的。

正确答案是 C 。

7－2 图示两端铰支圆截面细长压杆，在某一截面上开有一小孔。

关于这一小孔对压杆承载能力的影响，有以下四种论述，试判断哪一种是正确的。

（A ）对强度和稳定承载能力都有较大削弱； （B ）对强度和稳定承载能力都不会削弱；（C ）对强度无削弱，对稳定承载能力有较大削弱；（D ）对强度有较大削弱，对稳定承载能力削弱极微。

正确答案是 D 。

7－3 图示a 、b 、c 、d 四桁架的几何尺寸、杆的横截面直径、材料、加力点及加力方向均相同。

关于四桁架所能承受的最大外力F Pmax 有如下四种结论，试判断哪一种是正确的。

（A ）)d ()b ()c ()a (max P max P max P max P F F F F =<=； （B ）)d ()b ()c ()a (max P max P max P max P F F F F ===； （C ）)c ()b ()d ()a (max P max P max P max P F F F F =<=；（D ）)d ()c ()()a (max P max P max P max P F F b F F =<=。

正确答案是 A 。

正确答案是 D 。

7－5 一端固定、另一端弹簧侧向支承的压杆。

若可采用欧拉公式22Pcr )/(πl EI F μ=，试确定其中长度系数的取值范围为（A ）0.2>μ；（B ）0.27.0<<μ；（C ）5.0<μ；（D ）7.05.0<<μ。

工程力学(静力学和材料力学)第2版课后习题答案 范钦珊主编 第7章 弯曲强度

工程力学(静力学和材料力学)第2版课后习题答案 范钦珊主编 第7章 弯曲强度


[ ]
[]
0.5 x 0.4125
M(kN.m)
7
习题 7－10 图
解：画弯矩图如图所示： 对于梁：
M max = 0.5q M 0.5q σ max = max ≤ [σ ] , ≤ [σ ] W W [σ ]W = 160 ×106 × 49 ×10−6 = 15.68 ×103 N/m=15.68kN/m q≤ 0.5 0.5
A
B
W
a + Δa
W + ΔW
B
A
a图
b图
整理后得
Δa =
ΔW (l − a ) (W + ΔW )
此即为相邻跳水者跳水时，可动点 B的调节距离 Δa 与他们体重间的关系。 7－ 14 利用弯曲内力的知识，说明为何将标准双杠的尺寸设计成 a=l/4。
9
习题 7－14 图
解：双杠使用时，可视为外伸梁。 其使用时受力点应考虑两种引起最大弯矩的情况。如图a、b所示。
[ ]＋
[σ ]－ ＝120 MPa。试校核梁的强度是否安全。
6
30 x 10 M(kN.m) C 截面
+ = σ max － σ max
40
习题 7－9 图
30 ×103 N ⋅ m × 96.4 ×10−3 m = 28.35 × 106 Pa=28.35 MPa 1.02 ×108 ×10−12 m 4 30 ×103 N ⋅ m ×153.6 ×10−3 m = = 45.17 ×106 Pa=45.17 MPa 1.02 ×108 × 10−12 m 4 40 ×103 N ⋅ m ×153.6 ×10−3 m = 60.24 ×106 Pa=60.24 MPa> [σ ] 8 −12 4 1.02 ×10 × 10 m 40 ×103 N ⋅ m × 96.4 × 10−3 m = = 37.8 × 106 Pa=37.8 MPa 8 −12 4 1.02 × 10 × 10 m
材料力学_高教第二版_范钦珊_第7章习题答案

材料力学_高教第二版_范钦珊_第7章习题答案

习题7-3图习题7-4图材料力学_高教第二版_范钦珊_第7章习题答案第7章 弹性平衡稳定性分析7－1 关于钢制细长压杆受力达到分叉载荷之后，还能不能继续承载，有如下四种答案，试判断哪一种是正确的。

（A ）不能，因为载荷达到临界值时，屈曲位移将无限制地增加； （B ）能，压杆一直到折断时为止都有承载能力；（C ）能，只要横截面上的最大应力不超过一定限度； （D ）不能，因为超过分叉载荷后变形不再是弹性的。

正确答案是 C 。

7－2 图示两端铰支圆截面细长压杆，在某一截面上开有一小孔。

关于这一小孔对压杆承载能力的影响，有以下四种论述，试判断哪一种是正确的。

（A ）对强度和稳定承载能力都有较大削弱； （B ）对强度和稳定承载能力都不会削弱；（C ）对强度无削弱，对稳定承载能力有较大削弱；（D ）对强度有较大削弱，对稳定承载能力削弱极微。

正确答案是 D 。

7－3 图示a 、b 、c 、d 四桁架的几何尺寸、杆的横截面直径、材料、加力点及加力方向均相同。

关于四桁架所能承受的最大外力F Pmax 有如下四种结论，试判断哪一种是正确的。

（A ）)d ()b ()c ()a (max P max P max P max P F F F F =<=； （B ）)d ()b ()c ()a (max P max P max P max P F F F F ===； （C ）)c ()b ()d ()a (max P max P max P max P F F F F =<=；（D ）)d ()c ()()a (max P max P max P max P F F b F F =<=。

正确答案是 A 。

7－4 图示四压杆均为圆截面直杆，杆长相同，且均为轴向加载。

关于四者分叉载荷大小有四种解答，试判断哪一种是正确的（其中弹簧的刚度较大）。

（A ）)d ()c ()b ()a (Pcr Pcr Pcr Pcr F F F F <<<；（B ）)d ()c ()b ()a (Pcr Pcr Pcr Pcr F F F F >>>； （C ）)a ()d ()c ()b (Pcr Pcr Pcr Pcr F F F F >>>； （D ）)d ()c ()a ()b (Pcr Pcr Pcr Pcr F F F F >>>。

工程力学 第二版 (范钦珊 唐静静 著) 高等教育出版社 课后答案 第10章 组合受力与变形杆件的强度计算


网
FP a2
ww w
5
.k hd
b
m
上表面
∴
σa 4 = σb 3
习题 10－7 图
和 ε 2 。证明偏心距 e与 ε1 、 ε 2 之间满足下列关系：
FP
网
ww w
e=
ε1 − ε 2 h × ε1 + ε 2 6
课
后 答
案
FP
M = FP e
习题 10－8 图
解：1，2 两处均为单向应力状态，其正应力分别为： 1 处：
第10章
组合变形与变形杆件的强度计算
10－1 根据杆件横截面正应力分析过程， 中性轴在什么情形下才会通过截面形心？试分析 下列答案中哪一个是正确的。 （A）My = 0 或 Mz = 0， FN ≠ 0 ； （B）My = Mz = 0， FN ≠ 0 ； （C）My = 0，Mz = 0， FN ≠ 0 ； （D） M y ≠ 0 或 M z ≠ 0 ， FN = 0 。 正确答案是 D 。 解：只要轴力 FN x ≠ 0 ， 则截面形心处其拉压正应力一定不为零， 而其弯曲正应力一定为零， 这样使其合正应力一定不为零，所以其中性轴一定不通过截面形心，所以答案选（D） 。 关于中性轴位置，有以下几种论述，试判断哪一种是正确的。 （A）中性轴不一定在截面内，但如果在截面内它一定通过形心； （B）中性轴只能在截面内并且必须通过截面形心； （C）中性轴只能在截面内，但不一定通过截面形心； （D）中性轴不一定在截面内，而且也不一定通过截面形心。 正确答案是 D 。 解：中性轴上正应力必须为零。由上题结论中性轴不一定过截面形心；另外当轴力引起的 拉（压）应力的绝对值大于弯矩引起的最大压（拉）应力的绝对值时，中性轴均不在截面内， 所以答案选（D） 。 并且垂 10－3 图示悬臂梁中， 集中力 FP1 和 FP2 分别作用在铅垂对称面和水平对称面内， 直于梁的轴线，如图所示。已知 FP1＝1.6 kN，FP2＝800 N，l＝1 m，许用应力 σ ＝160 MPa。 试确定以下两种情形下梁的横截面尺寸： 1．截面为矩形，h＝2b； 2．截面为圆形。

工程力学(静力学与材料力学)弯曲强度(剪力图与弯矩图)-PPT文档资料


第7章A 弯曲强度(1)－剪力图与弯矩图
梁的内力及其与外力的相互关系
所谓剪力和弯矩变化规律是指表示剪力和弯矩变 化的函数或变化的图线。这表明，如果在两个外力 作用点之间的梁上没有其他外力作用，则这一段梁 所有横截面上的剪力和弯矩可以用同一个数学方程 或者同一图线描述。
第7章A 弯曲强度(1)－剪力图与弯矩图
范钦珊教育与教学工作室
工程力学(静力学与材料力学）
课堂教学软件
返回总目录
工程力学（静力学与材料力学）
材料力学
弯曲强度－剪力图与弯矩图
返回总目录
第7章A 弯曲强度－剪力图与弯矩图
杆件承受垂直于其轴线的外力或位于其轴线所在平面 内的力偶作用时，其轴线将弯曲成曲线，这种受力与变形 形式称为 弯曲 （ bending ）。主要承受弯曲的杆件称为 梁 （beam）。 在外力作用下，梁的横截面上将产生剪力和弯矩两种 内力。
第7章A 弯曲强度(1)－剪力图与弯矩图
工程中的弯曲构件 梁的内力及其与外力的相互关系
剪力方程与弯矩方程
载荷集度、剪力、弯矩之间的微分关系 剪力图与弯矩图
结论与讨论
返回总目录
第7章A 弯曲强度(1)－剪力图与弯矩图
工程中的弯曲构件
返回
第7章A 弯曲强度(1)－剪力图与弯矩图
在很多情形下，剪力和弯矩沿梁长度方向的分布不是 均匀的。 对梁进行强度计算，需要知道哪些横截面可能最先发 生失效，这些横截面称为危险面。弯矩和剪力最大的横截 面就是首先需要考虑的危险面。研究梁的变形和刚度虽然 没有危险面的问题，但是也必须知道弯矩沿梁长度方向是 怎样变化的。
第7章A 弯曲强度(1)－剪力图与弯矩图
返回
第7章A 弯曲强度(1)－剪力图与弯矩图

工程力学教程篇(第二版)习题第7章答案

第7章 刚体的平面运动习题7-1 直杆AB 长为l ，两端分别沿着水平和铅直方向运动，已知点A 的速度A υ为常矢量，试求当 60=θ时，点B 的速度和杆AB 的角速度。

（a ） （b ）解法一（如图a ）1.运动分析：杆AB 作平面运动。

2.速度分析：A B A B v v v +=，作速度矢量合成图 IA AB υυυ360tan == A A BA υυυ260cos /==A BAlAB υυω2==解法二（如图b ）1.运动分析：杆AB 作平面运动。

2.速度分析：杆AB 的速度瞬心是点I 。

ωυ⨯=AP A A All υυω260cos ==A AB ll BP υυωυ3260sin =⨯⨯=⨯=s rad /6=ω，试求图示位置时，滑块B 的速度以及连杆AB 的角速度。

解：1.运动分析：杆AB 均作一般平面运动，滑块作直线运动，杆OA 作定轴转动。

2.速度分析：对杆AB ，s m OA A /12=⨯=ωυA B A B v v v +=或AB B AB A v v ][][=30cos B A υυ=s m B /38=υs m A BA /3430tan =⨯=υυ s rad ABBAAB /2==υω7-3 图示机构，滑块B 以s m /12的速度沿滑道斜向上运动，试求图示瞬时杆OA 与杆AB 的角速度。

解：AB 杆运动的瞬心为I 点。

AB B BP ωυ⨯= s r a d BAB /325.043=⨯=υωs m AP AB A /2.7323.043=⨯⨯=⨯=ωυ 4.0⨯=OA A ωυ s rad OA /184.02.7==ω 或利s /m .B A 2753==υυOA=2m ，，圆轮半径为2m ，s rad /60=ω，试求图示位置时，轮心的速度，圆轮的角速度及连杆AB 的角速度。

解：1.运动分析：圆轮和杆AB 均作一般平面运动。

杆OA 作定轴转动。

清华出版社工程力学答案-第7章 圆轴扭转时的强度与刚度计算

解：τ (ρ) = M x ρ Ip 在推导时利用了等截面圆轴受扭后，其横截面保持平面的假设，同时 推导过程中还应用了剪切胡克定律，要求在线弹性范围加载。所以正确答案是 A 。
7－2 两根长度相等、直径不等的圆轴承受相同的扭矩受扭后，轴表面上母线转过相同 的角度。设直径大的轴和直径小的轴的横截面上的最大剪应力分别为 τ1max 和 τ 2max ，剪切弹 性模量分别为 G1 和 G2。试判断下列结论的正确性。
解： τ 轴max
=
Mx Wp1
= T1 πd 3
≤ 60 ×106
16
T1
≤
60 ×106
× π× 663 16
× 10 −9
=
3387 N·m
τ 套 max
= Mx Wp2
=
T2 πd 3 ⎜⎛1 − ( 68 )4 ⎟⎞
≤ 60 ×106
16 ⎝ 80 ⎠
T2
≤
60 ×106
× π× 803 16
8
7－12 功率为 150kW、转速为 15.4r/s(转/秒)的电机轴如图所示。其中 d1=135mm， d2=75mm，d3=90mm，d4=70mm，d5=65mm。轴外伸端装有胶带轮。试对轴的扭转强度进行 校核。
Me
Me
d5 d2 d1 d3 d4
电机轴
习题 7－12 图
解：1. 求外力偶矩
（A） τ 1max ＞ τ 2 max ； （B） τ 1max ＜ τ 2 max ； （C）若 G1＞G2，则有 τ1max ＞ τ 2 max ； （D）若 G1＞G2，则有 τ1max ＜ τ 2 max 。
解：因两圆轴等长，轴表面上母线转过相同角度，指切应变相同，即 γ1 = γ 2 = γ 由剪切 胡克定律 τ = Gγ 知 G1 > G2 时， τ1max > τ2 max 。因此，正确答案是 C 。

工程力学范钦珊第二版7、8复习弯曲强度与弯曲变形

一、弯曲应力的公式推导
aP
Pa
纯弯曲(Pure Bending):
A
B
FQ
某段梁的内力只有弯矩 没有剪力时，该段梁的变 形称为纯弯曲。如AB段。
x
x
M
2020/9/19
2
由纯弯曲推导梁横截面上的正应力
平面假设：横截面
纵向对称面 中性层
变形后仍为平面，只 中性轴 是绕中性轴发生转动，
距中性轴等高处，变
-4kNm
x
M 2.5kNm
A1
A3
y1 G
y2
A2
y2 G y 2020/9/19 1
A4 A3
A4
A2LM IC zy272.5 6 18 30 882.2 8MPa
A3LM IBzy1746 5 3 12 082.72MPa
A4y
MBy2 Iz
746 8 3 18 084.62MPa
校核强度
1 Mz EI z
… …(3)
（对称面） EIz 杆的抗弯刚度。
2020/9/19
x
My Iz
...... (4)
5
4、最大正应力：
max
M Wz
… …(5)
W z yIm zax 抗 弯 截 面 模 量 。
5、惯性矩
Iz
y2dA
A
圆截面Iz： 6D44
y z
圆 环 W zyIm z a x 3D32(14)
2020/9/19
bcmaxW MFAN
13
四、弯曲变形
1、度量梁变形的两个基本位移量
1.挠度：横截面形心沿垂直于轴线方向的线位移。用w表示。
与
w
同向为正，反之为负。 q

材料力学第2版 课后习题答案 第7章 弯曲变形


解：查自重得：
q = 587.02 N / m
J = 15760cm4 Pl 3 5ql 4 f =− − 48EJ 384EJ −176 × 103 × 113 = 48 × 210 × 109 × 15760 × 10−8 × 4 −587.02 × 5 × 114 + 385 × 210 × 109 × 15760 × 10−8 × 4 = 0.0377 m = 3.77cm
(d) 解：
D A P P E
' yC = y E + θ B ia + y C
C B P
− P ( 2a ) − Pa 3 − Pa3 = − − 3EJ 3EJ 3EJ 3 −10 Pa = 3EJ
3
252
7-5 门式起重机横梁由4根36a工字钢组成如图所示， 梁的两端均可视为铰支， 钢的弹 性模量E=210Gpa。试计算当集中载荷P＝176 kN作用在跨中并考虑钢梁自重时，跨中截面 C的挠度yC。
x=l
∴y =−
'
∴D = 0
y=0
∴C =
− M 0l 6
M 0l 2 ⎛ x x 3 ⎞ ⎜ − ⎟ 6 EJ ⎝ l l 3 ⎠
M 0l 2 ⎛ 1 3 x 2 ⎞ ∴θ = y = − ⎜ − ⎟ 6 EJ ⎝ l l 3 ⎠
− M 0l 2 l ；此时挠度最大 f = 3 9 3EJ 2 ⎛ l ⎞ − M 0l 中点挠度 y ⎜ ⎟ = ⎝ 2 ⎠ 16 EJ − M 0l Ml θA = θB = 0 6 EJ 3EJ （b）解： 设中点为C点，则分析CB段
''
C2 = −
D2 = −
a4 24
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2020/11/3
4
2、物理关系：
x
E x
Ey
...... (2)
3、静力学关系：
FN x
dA
A
Ey dA E
A
ydA ESz 0
A
Sz 0 z (中性)轴过形心
M z
(dA) y
A
Ey 2
E
dA
A
y 2dA EI z M
A
M y
(dA)z
A
Eyz dA E
B
挠度。
解、载荷分解如图
由梁的简单载荷变形表，
B
查简单载荷引起的变形。
q
PA
Pa 2 4EI
wPC
Pa 3 6EI
q
B
q
qA
qa3 3EI
wqC
5qL4 24 EI
26
A C
a
a
P
A
A
2020/11/3
+
=
q B
q
PA
Pa 2 4EI
wPC
Pa 3 6EI
q
qA
qa3 3EI
5qL4 wqC 24 EI
一、弯曲应力的公式推导
aP
Pa
纯弯曲(Pure Bending):
A
B
FQ
某段梁的内力只有弯矩 没有剪力时，该段梁的变 形称为纯弯曲。如AB段。
x
x
M
2020/11/3
2
由纯弯曲推导梁横截面上的正应力
平面假设：横截面
纵向对称面 中性层
变形后仍为平面，只 中性轴 是绕中性轴发生转动，
距中性轴等高处，变
FAy
wm ax
x1
x2
w
a
b
EIq2
Fb 2l
x22
F 2
( x2
a)2
Fb 6l
(l 2
b2 )
B qB x
FBy
EIw2
Fb 6l
x23
F 6
( x2
a)3
Fb 6l
(l 2
b2 )x2
2020/11/3
23
6）确定最大转角和最大挠度
令 dq 0
dx
得，
l a x
l,qmax
qB
Fab 6EIl
弧度,试核此杆的刚度。
=+ =+
L=400mm a=0.1mP
A
D
B
C
A
D
B
200mm P1=1kN
C P2=2kN
A
D
B
C
P1=1kN
P2
a
B
C
P2
P2 M
A
D
B
C
A
D
B
2020/11/3
P2=2kN
C
31
L=400mm a=0.1mP
A
D
B
2f00mm P1=1kN
Cx P2=2kN
=+ +
A
D1 D2 0
2020/11/3
F
A
qA
DC
FAy
wm ax
x1
x2
w
a
b
B qB x
FBy
22
5）确定转角方程和挠度方程
AC 段： 0 x1 a
F
EIq1
Fb 2l
x2 1
Fb 6l
(l 2
b2 )
A
qA
DC
EIw1
Fb 6l
x3 1
Fb 6l
(l 2
b2 )x1
CB 段： a x2 l
dx
w''(x) 0 w
x
在小变形条件下， ddx2w2
2
1，故忽略。
w
M<0 w''(x) 0
2020/11/3
1
d 2w dx 2
d 2w(x) M (x)
dx
EI 16
积分一次得转角方程为：
EI
dw dx
EIq
M (x)dx
C
再积分一次得挠度方程为：
EIw M (x)dxdx Cx D
-4kNm
x
M 2.5kNm
A1
A3
y1 G
y2
A2
y2 G y 2020/11/3 1
A4 A3
A4
A2L
M C y2 Iz
2.5 88 763 10 8
28.2MPa
A3L
MB Iz
y1
4 52 763108
27.2MPa
A4 y
M B y2 Iz
4 88 763108
46.2MPa
x
A
D
B
C
f 200mm P1=1kN P2=2kN
=+ +
A
D
B
图1
P1=1kN
图2
B
C
a C
P2
图3
A
D
2020/11/3
P2 M
B
C
叠加求复杂载荷下的变形
q
B
P1L2 16 EI
P2 La 3EI
wC
P1L2a 16 EI
P2a3 3EI
P2 a 2 L 3EI
I (D4d 4 )
D
B
图1
P1=1kN B
图2
C
a C
P2
P2 M
A
D
B
C
2020/11/3
图3
解：结构变换，查表求简单 载荷变形。
q1B
P1L2 16 EI
w1C
q1Ba
P1L2a 16 EI
q2B 0
w2C
P2a3 3EI
q
3B
ML 3EI
LaP2 3EI
w3C
q3Ba
P2 La 2 3EI
32
L=400mm a=0.1mP
积分常数C、D 的确定：
位移边界条件
光滑连续条件
~
~
~
~
AA
A AA A A A AAA A
~ ~~ ~~
~ ~~~ ~ ~
~
~
A AAAA A AAA A
A A AA A
~~
~
wA 0 2020/11/3
wA 0
qA 0
wA
－弹簧变形
wAL wAR
q AL q AR
wAL wAR
17
19
例 求梁的转角方程和挠度方程，并求最大转角和最大挠度，
梁的EI已知，l=a+b，a>b。
解 1）由梁整体平衡分析得：
F
FAx
0, FAy
Fb l
,
FBy
Fa l
2）弯矩方程
A
qA
FAy x1
DC
B qB x
wm ax
FBy
AC 段：
x2
M x1 FAy x1
Fb l x1,0
x1 a
2020/11/3
Wz
Iz ymax
D3
32
(1 4)
b
矩形截面： I z
bh3 12
6
二、梁的强度设计
1、危险面与危险点分析：
一般截面，最大正应力发生在弯矩绝对值最大的截面的上下边 缘上.
当横截面不对称，或是压缩许用应力与拉伸许用应力不同，或 是弯矩出现正号负号时应两者都取。要特别注意符号
M
2、正应力和剪应力强度条件：
MPa，其截面形心位于C点， y1=52mm， y2=88mm， Iz=763cm4 ，试校核此梁的强度。 并说明T字梁怎样放置更合理？
解：画弯矩图并求危面内力 RA 2.5kN ; RB 10.5kN M C 2.5kNm (下拉、上压 ) M B 4kNm（上拉、下压）
画危面应力分布图，找危1险0 点
x3 1
C1x1
D1
CB 段：
a x2 l
F
A
qA
DC
FAy
wm ax
x1
x2
w
a
b
EI
d 2w2 dx22
M (x2 )
Fb l
x2
F (x2
a)
EI dw2 dx2
EIw2
EIq (x2 )
Fb 2l
x2 2
Fb 6l
x3 2
F 6
( x2
a)3
F 2
( x2
a)2
C2 x2 D2
L2
P 等价
B
L2 C
L2
P 等价
w L1
P L2
B
刚化BC段
A w
C
M
P Bx
w1
Bx
29
w2
六、梁的刚度设计
刚度条件： 应用：
wmax w
qmax q
、校核刚度：
、设计截面尺寸；
、设计载荷。
2020/11/3
30
例7 下图为一空心圆杆，内外径分别为：d=40mm、D=80mm，
杆的E=210GPa，工程规定C点的[f/L]=0.00001,B点的q]=0.001
C2
2020/11/3
B qB x
FBy
21
4）由边界条件确定积分常数
位移边界条件
x1 0, w1(0) 0 x2 l, w2 (l) 0
光滑连续条件
x1 x2 a, q1(a) q2 (a)