车辆动力学模型

vtd 动力学模型VTD 动力学模型是一种用于描述和分析车辆运动行为的数学模型。

它基于车辆动力学原理，通过考虑车辆的质量、惯性、摩擦力等因素，来预测车辆在不同驾驶条件下的运动状态和行驶性能。

本文将详细介绍 VTD 动力学模型的原理和应用。

一、VTD 动力学模型的原理VTD（Vehicle Test Dynamic）动力学模型是一种基于物理原理的模型，它通过对车辆的力学特性进行建模，来模拟车辆的运动行为。

VTD 模型的核心是基于牛顿第二定律和运动学方程，结合车辆的质量、惯性、车轮力等参数，来描述车辆的加速度、速度和位置变化。

1. 车辆的加速度模型VTD 模型中，车辆的加速度可以通过考虑各种力的作用来计算。

其中，牵引力、阻力、制动力、侧向力等是影响车辆加速度的重要因素。

牵引力主要由车辆的发动机输出扭矩和传动系统的效率决定；阻力包括空气阻力、滚动阻力等，它们与车辆的速度和行驶状态有关；制动力与刹车系统的性能相关；侧向力主要由车辆的操控性能和轮胎的附着力决定。

2. 车辆的速度和位置模型在 VTD 模型中，车辆的速度和位置可以通过车辆的加速度和初始条件来计算。

根据牛顿第二定律和运动学方程，可以得到车辆速度和位置的变化规律。

通过积分计算，可以得到车辆在不同时间段内的速度和位置。

二、VTD 动力学模型的应用VTD 动力学模型在车辆工程领域有着广泛的应用。

下面将介绍几个典型的应用场景。

1. 车辆性能评估VTD 动力学模型可以用于评估车辆的加速性能、制动性能、悬挂系统性能等。

通过模拟车辆在不同驾驶条件下的运动行为，可以分析车辆的动力学特性，评估车辆的性能指标，并为改进车辆设计提供依据。

2. 驾驶辅助系统开发VTD 动力学模型可以用于开发和测试驾驶辅助系统，如车道保持系统、自适应巡航系统等。

通过模拟车辆的运动行为，可以评估驾驶辅助系统的控制策略和性能，验证系统的可靠性和安全性。

3. 燃料经济性分析VTD 动力学模型可以用于分析车辆的燃料经济性。

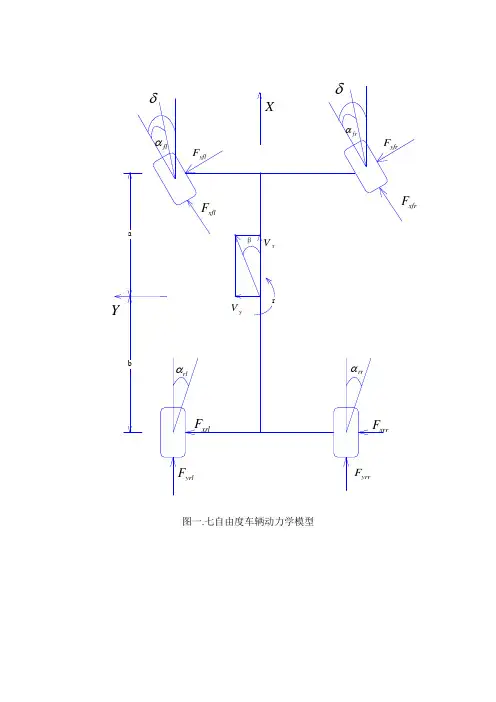
图一.七自由度车辆动力学模型纵向力平衡方程：()()cos ()sin x y xfl xfr yfl yfr xrl xrr m V r V F F F F F F δδ•-⋅=+-+++ ①侧向力平衡方程：()()sin ()cos y x xfl xfr yfl yfr yrl yrr m V r V F F F F F F δδ•+⋅=+++++ ②绕Z 轴力矩平衡方程：12[()sin ()cos ][()cos ()sin ]2()()2w z xfl xfr yfl yfr xfr xfl yfl yfr w xrr xrl yrl yrr t I r F F F F a F F F F t F F F F b δδδδ•⋅=++++-+-+--+ ③四个车轮的力矩平衡方程：tw w xi bi di I R F T T i w •⋅=-⋅-+ ④上述方程中：δ为前轮转角；Vx ，Vy 分别为纵向、横向车速；β为质心侧偏角；γ为横摆角速度；Fxi 、Fyi 、Fzi 分别为轮胎纵向力、侧向力、垂向力；i=左前轮fl 、右前轮fr 、左后轮rl 、右后轮rr ，为分别对应的车轮；m 为整车质量；ms 为悬挂质量；a 、b 为前后轴到质心的距离；l=a+b 为前后轴距;tw1为前轴轮距；tw2为后轴轮距； Iz 为整车绕Z 轴的转动惯量；hg 为质心到地面的距离；各轮胎垂向载荷公式：_1_1_1_122222222gg z fl x y w gg z fr x y w gg z rl x y w gg z rr x y w h h b b F mg mV mV l l t l h h b b F mg mV mV l l t lh h aa F mg mV mV l l t lh h a a F mg mV mV l l t l••••••••=--⋅=-+⋅=+-⋅=++⋅⑤各轮胎侧偏角公式：11222222arctan()arctan()arctan()arctan()wwww y fl t x y fr t x y rl t x y rr t x V arV rV arV rV brV rV br V rαδαδαα+=--+=-+-=---=-+ ⑥各车轮轮心在车轮坐标系下的纵向速度：1_1_2_2_()cos ()sin 2()cos ()sin 222w t fl x y w t fr x y w t rl x w t rr x t V V r V ar tV V r V ar t V V rtV V rδδδδ=-++=+++=-=+ ⑦其中_t fl V 、_t fr V 、_t rl V 、_t rr V 为轮胎坐标系下的轮胎纵向速度。

汽车二自由度动力学模型
汽车二自由度动力学模型是一种用于描述汽车运动的简化模型。

它考虑了两个自由度，通常是车辆的纵向（前进方向）和侧向（横向）运动。

在这个模型中，车辆被视为一个质量集中的刚体，通过两个自由度来描述其运动状态。

这两个自由度通常是车辆的速度（纵向）和横摆角速度（侧向）。

汽车二自由度动力学模型的建立基于一些基本的物理原理，如牛顿第二定律、动量守恒定律和刚体动力学。

通过对这些原理的应用，可以得到描述车辆运动的微分方程。

这些方程通常包括车辆的加速度、驱动力或制动力、转向力矩以及车辆的惯性参数等。

通过求解这些微分方程，可以预测车辆在不同工况下的运动响应，例如加速、制动、转弯等。

汽车二自由度动力学模型在车辆动力学研究、驾驶模拟器、自动驾驶系统等领域有广泛应用。

它可以帮助工程师和研究人员了解车辆的基本运动特性，评估车辆的操控稳定性、行驶安全性等方面的性能。

然而，需要注意的是，二自由度模型是一种简化的模型，它忽略了许多实际情况中的复杂因素，如悬挂系统、轮胎特性、空气动力学等。

在实际应用中，可能需要使用更复杂的多自由度模型或考虑更多的因素来更准确地描述汽车的运动。

总的来说，汽车二自由度动力学模型提供了一个简单而有用的工具，用于初步研究和理解汽车的运动行为，但在具体应用中，需要根据实际需求进行适当的修正和扩展。

如果你对汽车动力学模型有更深入的问题或需要进一步的讨论，我将很愿意提供帮助。

车辆动力学模型推导概述及解释说明1. 引言1.1 概述本文旨在介绍车辆动力学模型推导的相关内容。

车辆动力学模型是研究汽车运动时所遵循的物理规律的数学表达式，通过建立和分析这些模型，可以深入了解车辆运动过程中涉及的各种参数和因素，并且为设计、控制和优化车辆性能提供有效依据。

1.2 文章结构本文共包括五个部分。

引言部分对文章进行概述，并介绍各部分内容安排。

第二部分将探讨车辆动力学模型推导的理论基础、参数定义以及模型假设。

第三部分将详细描述动力学模型的数学建立与推导过程，包括前提假设与约束条件说明、基本方程推导过程以及对动力学模型的解释与说明。

第四部分将通过实例分析介绍具体应用场景，并进行可行性分析和结果对比评估。

最后一部分是结论与展望，总结研究内容重点，展望未来研究方向以及对成果应用前景进行分析。

1.3 目的目前，随着社会科技的不断发展和人们对汽车性能的不断追求，对于车辆动力学模型推导的需求日益增加。

本文的目的是系统地介绍车辆动力学模型推导的相关理论和方法，以帮助读者更好地理解和应用这些模型。

此外，通过实例分析与应用场景探讨，也旨在展示动力学模型在实际问题中的应用价值，并提供未来研究方向和成果应用前景的思考。

2. 车辆动力学模型推导:2.1 理论基础：车辆动力学是研究车辆在不同路况条件下的运动规律的一门学科。

它主要涉及到车辆的加速度、速度和位移等运动参数。

在车辆动力学模型推导中，我们需要建立一组数学方程来描述车辆运动的规律性和物理特性。

2.2 动力学参数定义：在推导车辆动力学模型之前，首先需要定义一些重要的参数。

这些参数包括车辆质量、惯性矩阵、轮胎摩擦系数以及驱动力等。

这些参数对于建立准确的车辆动力学模型非常重要，并且可以通过实验或者工程估算得到。

2.3 模型假设：在推导车辆动力学模型时，通常会做出一定的假设，以简化问题并减少计算复杂度。

例如，我们可能会假设车辆是刚体、忽略空气阻力、平均考虑轮胎与地面之间的接触等。

商用车车辆开发动力学模型1. 引言随着科技的进步和交通运输行业的发展，商用车车辆的开发与设计面临着越来越高的要求。

为了满足这些要求，开发出更加高效、安全和环保的商用车，动力学模型在车辆设计中的作用越来越重要。

本文将深入探讨商用车车辆开发动力学模型的基本原理、特性、开发流程、验证与评估以及应用场景与优势。

2. 动力学模型的基本原理动力学模型是一种数学模型，用于描述物体运动的状态和行为。

在车辆动力学中，这种模型被用来模拟和分析车辆在不同工况下的运动特性，包括纵向、横向和横摆运动等。

基于牛顿第二定律和相关运动学关系，动力学模型能够预测车辆在不同路面条件、行驶状态和外部干扰下的响应。

3. 商用车车辆动力学特性商用车，如重型卡车和大型客车，具有独特的动力学特性。

这些特性包括较大的质量、较高的重心位置、复杂的悬挂系统和特定的驾驶室布局等。

这些因素都显著影响着商用车在行驶过程中的稳定性、操纵性和乘坐舒适性。

因此，在建立商用车动力学模型时，必须充分考虑这些特性。

4. 模型的开发流程开发商用车车辆动力学模型通常遵循以下步骤：首先，通过实验和测量获取车辆的详细参数，包括质量、质心位置、转动惯量等；其次，基于这些参数和车辆的运动方程建立数学模型；随后，通过编程实现模型，并进行初步验证；最后，通过实车试验对比模型预测与实际表现，进行必要的调整和优化。

5. 模型的验证与评估模型的验证与评估是确保其准确性和可靠性的关键环节。

这通常涉及到对比模型的预测结果与实际测试数据。

评估指标包括预测的准确性、稳定性以及与实际工况的符合程度等。

在评估过程中，还需要对模型在不同工况下的表现进行充分测试，以确保其在各种情况下的可靠性。

6. 模型的应用场景与优势商用车车辆开发动力学模型的应用场景广泛，主要包括新车型的开发与设计、现有车型的改进与优化以及智能化控制等。

在开发阶段，模型能够预测新车型的性能表现，为设计决策提供依据；在优化阶段，通过对模型的调整和改进，可以显著提高现有车型的性能；在智能化控制方面，动力学模型为自动驾驶、智能导航和车辆协同提供了强大的支持。

车辆动力学模型python车辆动力学模型是描述车辆运动状态变化的数学模型。

在车辆动力学模型中，常见的模型包括简化的自行车模型、单轮模型、两轮车模型、四轮车模型等。

以下是一个简化的两轮车辆动力学模型的Python示例代码：pythonimport mathimport numpy as npimport matplotlib.pyplot as plt# 车辆参数m = 1000 # 质量(kg)Iz = 1000 # 车辆绕Z轴的转动惯量(kg*m^2)lf = 1.1 # 车辆重心到前轴的距离(m)lr = 1.2 # 车辆重心到后轴的距离(m)Caf = 80000 # 前轴轮胎的纵向刚度(N/rad)Car = 120000 # 后轴轮胎的纵向刚度(N/rad)Vx = 10 # 车辆前进速度(m/s)# 初始状态X0 = 0Y0 = 0Psi0 = 0del0 = 0beta0 = 0def two_wheeled_vehicle_model(x, t):# 状态变量X, Y, Psi, del_, beta = x# 计算车辆参数Faf = Caf * math.atan2((beta + lf * Psi), Vx)Far = Car * math.atan2((beta - lr * Psi), Vx)# 计算状态变化率X_dot = Vx * math.cos(Psi + beta)Y_dot = Vx * math.sin(Psi + beta)Psi_dot = Vx * math.sin(beta) / lrdel_dot = 0 # 假设方向盘转角保持不变beta_dot = (lf * Faf * math.cos(del_) - lr * Far) / (m * Vx) - Psi_dot return [X_dot, Y_dot, Psi_dot, del_dot, beta_dot]# 模拟车辆运动T = np.arange(0, 10, 0.01) # 时间范围X = np.zeros(len(T)) # X坐标Y = np.zeros(len(T)) # Y坐标Psi = np.zeros(len(T)) # 车辆航向角del_ = np.zeros(len(T)) # 方向盘转角beta = np.zeros(len(T)) # 滑移角# 设置初始条件X[0] = X0Y[0] = Y0Psi[0] = Psi0del_[0] = del0beta[0] = beta0# 模拟车辆运动for i in range(1, len(T)):# 使用Euler方法（欧拉方法）进行数值积分x = [X[i-1], Y[i-1], Psi[i-1], del_[i-1], beta[i-1]] dx = two_wheeled_vehicle_model(x, T[i-1])X[i] = X[i-1] + dx[0] * (T[i] - T[i-1])Y[i] = Y[i-1] + dx[1] * (T[i] - T[i-1])Psi[i] = Psi[i-1] + dx[2] * (T[i] - T[i-1])del_[i] = del_[i-1] + dx[3] * (T[i] - T[i-1])beta[i] = beta[i-1] + dx[4] * (T[i] - T[i-1])# 绘制车辆轨迹plt.plot(X, Y)plt.xlabel('X')plt.ylabel('Y')plt.title('Vehicle Trajectory')plt.axis('equal') # 保持坐标轴比例一致plt.show()这个示例代码使用欧拉方法对车辆动力学模型进行数值积分，模拟车辆在一段时间内的运动轨迹，并绘制出车辆的轨迹图。

二自由度车辆动力学模型一自由度车辆动力学模型和二自由度车辆动力学模型是当前车辆动力学研究的重要部分。

一自由度车辆动力学模型只有一个转动扭矩，而二自由度车辆动力学模型则是加入了驱动车辆惯性转动扭矩和启动车辆非惯性转动扭矩。

在安全驾驶领域，二自由度车辆动力学模型可以更准确地模拟真实车辆的驾驶行为，这在事故分析和行车安全方面具有重要意义。

二自由度车辆动力学模型描述了建立汽车动力学模型所必需的参数，这些参数表征了汽车的运动特性。

根据不同的车辆结构，二自由度车辆动力学模型可以分为简化模型和综合模型，其中简化模型只包括车辆惯性特性和质量结构，而综合模型则需要将不同的惯性项和质量参数、转向设置参数和车轴系数包含在动力学模型中。

二自由度车辆动力学模型的总体模型如下：\begin{matrix}M_{1}\ddot{X}+D_{1}\dot{X}+U_{1}=K*F_{1}+U_{2} \\\M_{2}\ddot{Y}+D_{2}\dot{Y}+U_{3}=F_{2}\end{matrix}其中，$M_1$和$M_2$分别表示横向与纵向的动力质量；$D_1$和$D_2$分别表示横向与纵向的阻尼系数；$U_1$、$U_2$和$U_3$分别表示横向惯性扭矩、横向转动非惯性扭矩和纵向弹性力；$K$表示倾斜系数，用于模拟车轮对地面的抓地力；$F_1$和$F_2$表示制动转动非惯性扭矩和纵向弹性力。

通过二自由度车辆动力学模型可以计算汽车的动态行为，从而分析安全驾驶问题。

此外，这一模型也可以用于驾驶辅助系统的设计和仿真，帮助提高汽车的驾驶安全然而，二自由度车辆动力学模型实际上是基于简化参数建立的，模型参数与真实参数之间会存在一定程度的误差，因此当需要更加精确地模拟车辆行为时，这一模型可能不够准确。

另外，这种模型的可靠性也受到模型参数的设置和计算过程的限制，因此在实际应用中还需要对其进行适当的修正。

高速列车车辆动力学模型与仿真随着科技的不断进步，高速列车已经成为现代交通运输的重要组成部分。

高速列车的设计和运行必须经过严格的测试和仿真，以确保其安全性、稳定性和可靠性。

在这个过程中，车辆动力学模型和仿真技术起到了至关重要的作用。

本文将介绍高速列车车辆动力学模型的基本原理和仿真技术的应用。

一、高速列车车辆动力学模型的基本原理1. 刚体动力学模型高速列车可以近似地看作是一个刚体系统，因此刚体动力学模型是描述高速列车运动的基本原理。

刚体动力学模型基于牛顿的力学定律，通过分析列车各个部件之间的力学关系，可以推导出列车的运动方程。

这些方程可以描述列车的加速度、速度和位移与力的关系，从而揭示出列车的整体运动特性。

2. 多体系统模型除了刚体动力学模型外，高速列车还可以被看作是一个多体系统。

多体系统模型考虑了列车车体、轮轴、车轮等多个部件之间的运动关系，精确地描述了列车的动力学行为。

根据刚体动力学模型的基础上，多体系统模型进一步考虑了车体的变形和部件间的相互作用，使得列车的仿真结果更加准确和可靠。

3. 车辆-轨道相互作用在高速列车的运行过程中，车辆与轨道之间的相互作用是不可忽视的。

车辆-轨道相互作用模型考虑了列车与轨道之间的接触、摩擦和力的传递等因素，进一步提高了仿真结果的准确性。

通过车辆-轨道相互作用模型，可以模拟列车在不同运行条件下的动力学特性，包括转向性能、悬挂系统动态响应等。

二、高速列车车辆动力学模型的仿真技术应用1. 系统分析和设计优化高速列车车辆动力学模型的仿真技术可以用于系统分析和设计优化。

通过建立准确的车辆动力学模型，可以对列车的运行性能进行全面评估，包括加速度、速度、稳定性等方面。

仿真结果可以提供给设计师，用于优化列车的结构和参数，以满足运行要求和乘客舒适度等方面的需求。

2. 运行条件预测和评估高速列车的安全运行需要对各种运行条件进行预测和评估。

仿真技术可以模拟不同的运行条件，包括曲线行驶、坡道行驶、刹车等。

高速列车车辆动力学模型分析高速列车作为现代铁路运输的主要形式之一，其运行速度快、效率高，受到了人们的广泛关注。

但是，在高速列车的设计和运行中，需要考虑诸多因素。

其中，车辆动力学模型是其中一个重要的方面。

车辆动力学模型是指对车辆在不同速度和工况下的运动特性进行研究和分析的理论模型。

通过车辆动力学模型，可以更好地掌握车辆的运行规律，为车辆的设计、运行和维护提供可靠的理论依据。

在高速列车的车辆动力学模型分析中，可以考虑以下几个方面。

一、车辆运动方程车辆运动方程是车辆动力学模型的核心内容之一。

其基本思想是在考虑到车辆运动和外界因素的影响下，建立车辆位置、速度和加速度之间的关系。

车辆运动方程的具体形式可以采用牛顿第二定律，即F=ma。

其中，F为作用在车辆上的合力，m为车辆质量，a为车辆加速度。

在高速列车的车辆动力学模型中，需要考虑多种因素对车辆运动方程的影响。

例如，列车曲线通过半径、曲率、超高等参数的影响，车桥耦合效应对车辆运动的影响，以及车辆轮对与轨道之间的摩擦力等因素。

二、车辆减震系统高速列车行驶时，车辆在轨道中遇到各种不平顺，如平交道、曲线、道岔、坡度、车站等，会产生强烈的振动。

因此，车辆减震系统的设计和运行显得尤为重要。

车辆减震系统一般包括弹簧、减震器、橡胶元件等。

其中，减震器是最主要的部件之一，负责吸收车辆振动的能量。

在车辆动力学模型分析中，需要考虑减震器对车辆振动的影响，从而为减震系统的设计和优化提供理论依据。

三、车辆悬挂系统车辆悬挂系统也是一个重要的方面。

其主要作用是保证列车的稳定性和平稳性，在车辆行驶时减少车辆与轨道之间的相互作用力，从而有效地减少了车辆与轨道之间的动态摩擦。

车辆悬挂系统的技术含量很高，需要考虑多种因素的影响，比如车辆轴距、悬挂物长度、弹簧刚度、减震器参数等等。

在车辆动力学模型中，需要对这些因素进行综合分析，从而优化车辆悬挂系统的设计和运行。

四、车辆轮对车辆轮对是高速列车的重要组成部分。

车辆动力学模型及控制算法研究综述概述：车辆动力学模型及控制算法是车辆工程领域的重要研究内容之一，它涉及到汽车的运动学、动力学以及相应的控制算法。

本篇综述将围绕此主题进行介绍，重点分析车辆动力学模型的发展历程、常用的控制策略和未来的发展趋势。

一、动力学模型的发展历程1. 基本假设和数学原理车辆动力学模型的研究基于几个基本假设和数学原理，包括刚体运动学、力学平衡原理、动力学平衡原理等。

这些基本原理在车辆动力学模型的发展中起到了重要的指导作用。

2. 经典车辆模型经典车辆模型是车辆动力学模型的基础，主要包括单轴模型、双轴模型和多轴模型。

这些模型考虑了车辆的基本运动特性和力学特性，对于分析车辆的运动行为提供了基本框架。

3. 拓展模型为了更精确地描述车辆的动力学行为，研究者们提出了一些拓展模型，如包括悬挂系统的模型、非线性模型和多体动力学模型等。

这些拓展模型在实际应用中能更准确地预测车辆的运动行为。

二、常用的控制策略1. PID控制策略PID控制是最常用的一种控制策略，它基于车辆动力学模型和误差反馈，通过不断调整控制量来使车辆的运动行为满足期望。

PID控制策略简单有效，广泛应用于车辆的轨迹跟踪、速度控制等方面。

2. 模型预测控制策略模型预测控制策略是一种基于车辆动力学模型的优化控制方法，它通过解决动态优化问题来得到最优控制量。

模型预测控制策略具有较好的鲁棒性和适应性，适用于复杂的控制场景。

3. 最优控制策略最优控制策略是以最优调整控制量为目标的控制方法，通过求解变分问题得到最优控制方案。

最优控制策略对车辆动力学模型的准确性要求较高，但可以获得更好的控制效果。

三、未来的发展趋势1. 深度学习在车辆动力学模型和控制算法中的应用随着深度学习的快速发展，它在车辆动力学模型和控制算法中的应用逐渐展开。

深度学习算法可以从大量的数据中学习车辆的动力学模型和控制策略，提高模型的准确性和控制效果。

2. 非线性控制算法的进一步研究车辆动力学模型和控制算法的研究中，非线性控制算法起着重要的作用。

在建立车辆动力学模型时，我们对其做如下假设：1.汽车行驶在水平公路上，道路无起伏；2.忽略空气阻力和滚动阻力的影响；3.忽略汽车的俯仰、侧倾和垂向运动；4.各个轮胎的机械特性相同；5.不考虑载荷转移，汽车质量均匀地分布在每个车轮上。

1.车辆动力学模型（整车）由图1可得车辆动力学方程为车辆运动方程：F vM -= . （1） 车轮运动方程：b T FR I -=ω. （2） 车辆纵向摩擦力：N F μ=. （3）式中:M 为1/4车辆的质量(kg),v 为车辆行驶速度(m/s),F 为纵向摩擦力(N),I 为车轮的转动惯量(2m kg ⋅),ω为车轮角速度(rad/s),R 为车轮行驶半径(m),b T 为制动器制动力矩(N ·m),μ为纵向附着系数,N 为地面支持力(N)。

图1 车辆受力分析图根据式(1)、(2)和(3) 建立Simulink 仿真模型,输入为制动力和纵向附着系数, 输出为车辆速度、车轮转速及制动距离, 仿真模型如图2所示图2 车辆动力学仿真模型2.轮胎模型轮胎模型是指制动过程中轮胎附着力和其它各种参数之间的函数关系式，通常用轮胎附着系数与各种参数的函数关系式来表示。

而影响附着系数的因素很多，如前所述．除滑移率外，道路的材料、路面的状况与轮胎的结构、胎面花纹、材料以及汽车运动速度等都是影响因素。

但在实际应用中，很难得出上述多种变量对附着系数影响的关系式，而较为实际与合理的办法则是只考虑对附着系数影响较大的因素，建立附着系数的计算表达式。

经典的轮胎模型有魔术公式轮胎模型、双线性模型、Dugoff轮胎模型和Burckhardt轮胎模型等，这里采取应用比较广泛的双线性模型。

图3 纵向附着系数μ 与滑移率S 的关系曲线根据上图，推导出双线性轮胎模型的数学表达式为：................................................................................................................11h opt opt hg opt h g optopt opt S S S S S S S S S S μμμμμμμ⎧=⋅≤⎪⎪⎨-⋅-⎪=-⋅>⎪--⎩（4）基于本课题的研究目的，我们采用双线性模型分别模拟三种典型路面的 曲线，并应用于汽车防抱制动系统的控制仿真模型中。

汽车横向动力学模型推导过程
汽车横向动力学模型是研究汽车在行驶过程中的侧向运动特性的数学模型。

它通过描述车辆的侧向运动方程，来分析车辆在转弯、横向加速等情况下的行驶性能。

下面将从车辆的侧向力、横向加速度和车辆的稳定性等方面，来介绍汽车横向动力学模型的推导过程。

一、车辆的侧向力
车辆在转弯或横向加速时，轮胎与地面之间会产生侧向力。

侧向力可以分为横向力和法向力两个分量。

横向力是垂直于车辆的运动方向的力，它使车辆产生侧向加速度；法向力是垂直于地面的力，它支撑着车辆的重力。

二、横向加速度
横向加速度是描述车辆在横向运动时的加速度大小，它与车辆的侧向力和车辆的质量有关。

根据牛顿第二定律，车辆的横向加速度等于车辆的侧向力除以车辆的质量。

三、车辆的稳定性
车辆的稳定性是指车辆在转弯或横向加速时保持平衡的能力。

车辆的稳定性与车辆的质心高度、轴距、重心位置等因素有关。

当车辆的质心高度较低、轴距较大、重心位置较低时，车辆的稳定性较好。

四、车辆的横向动力学模型
汽车横向动力学模型是基于上述车辆的侧向力、横向加速度和车辆
的稳定性等因素建立起来的数学模型。

它可以描述车辆在转弯或横向加速时的运动特性。

汽车横向动力学模型是通过分析车辆的侧向力、横向加速度和车辆的稳定性等因素，来推导出车辆在转弯或横向加速时的运动特性的数学模型。

这个模型可以帮助我们更好地理解车辆的横向运动特性，为汽车设计和操控提供参考。

图一.七自由度车辆动力学模型纵向力平衡方程：()()cos ()sin x y xfl xfr yfl yfr xrl xrr m V r V F F F F F F δδ∙-⋅=+-+++ ① 侧向力平衡方程：()()sin ()cos y x xfl xfr yfl yfr yrl yrr m V r V F F F F F F δδ∙+⋅=+++++ ② 绕Z 轴力矩平衡方程：12[()sin ()cos ][()cos ()sin ]2()()2w z xfl xfr yfl yfr xfr xfl yfl yfr w xrr xrl yrl yrr t I r F F F F a F F F F t F F F F b δδδδ∙⋅=++++-+-+--+ ③四个车轮的力矩平衡方程：tw w xi bi di I R F T T i w ∙⋅=-⋅-+ ④上述方程中：δ为前轮转角；Vx ，Vy 分别为纵向、横向车速；β为质心侧偏角；γ为横摆角速度；Fxi 、Fyi 、Fzi 分别为轮胎纵向力、侧向力、垂向力；i=左前轮fl 、右前轮fr 、左后轮rl 、右后轮rr ，为分别对应的车轮；m 为整车质量；ms 为悬挂质量；a 、b 为前后轴到质心的距离；l=a+b 为前后轴距;tw1为前轴轮距；tw2为后轴轮距； Iz 为整车绕Z 轴的转动惯量；hg 为质心到地面的距离；各轮胎垂向载荷公式：_1_1_1_122222222g g z fl x y w gg z fr x y w gg z rl x y w gg z rr x y w h h b bF mg mV mV l l t l h h b b F mg mV mV l l t lh h aa F mg mV mV l l t lh h a a F mg mV mV l l t l∙∙∙∙∙∙∙∙=--⋅=-+⋅=+-⋅=++⋅⑤各轮胎侧偏角公式：112222arctan()arctan()arctan()arctan()www wy fl t x y fr t x y rl t x y rr t x V arV rV arV rV br V r V brV rαδαδαα+=--+=-+-=---=-+ ⑥各车轮轮心在车轮坐标系下的纵向速度：1_1_2_2_()cos ()sin 2()cos ()sin 222w t fl x y w t fr x y w t rl x w t rr x t V V r V ar tV V r V ar t V V rtV V rδδδδ=-++=+++=-=+ ⑦ 其中_t fl V 、_t fr V 、_t rl V 、_t rr V 为轮胎坐标系下的轮胎纵向速度。

unicycle动力学模型
unicycle动力学模型是描述单轮车运动的数学模型。

该模型可以用来研究单轮车的稳定性、控制和动力学行为。

一般来说，unicycle动力学模型可以分为两个主要部分：车辆的运动学模型和车辆的动力学模型。

1. 运动学模型：
运动学模型描述了车辆的运动状态和姿态。

常见的运动学模型包括车辆的位置、速度、加速度以及车辆前进方向的角度等。

在unicycle模型中，通常假设车辆沿着一个平面运动，因此可以用二维坐标系来描述车辆的位置。

车辆的姿态可以用车辆前进方向的角度来表示。

2. 动力学模型：
动力学模型描述了车辆的运动是如何受到外部力和力矩的影响的。

在unicycle模型中，主要考虑的外部力是重力和地面对车轮的支持力。

此外，还需要考虑车辆的惯性和摩擦等因素。

动力学模型可以用欧拉-拉格朗日方程或牛顿定律来描述车辆的运动。

根据运动学和动力学模型，可以通过数学方法求解车辆的运动轨迹、稳定性和控制策略。

这对于设计和控制unicycle车辆具有重要的意义，例如在自动驾驶车辆或机器人中的应用。

车辆动力学的建模与仿真研究作为一种机械装置，汽车的动态特性是其重要的性能之一。

而车辆动力学的研究就是评估车辆在不同路况、不同外界因素的影响下运动过程所表现出来的物理特征，并进一步探究车辆的操纵性、稳定性、安全性等方面的问题。

本文将介绍车辆动力学建模与仿真的基本概念及方法。

1. 车辆动力学模型车辆动力学模型是指描述汽车在运动过程中受到的外界力和热力学效应的一组数学方程，可以通过对不同因素如路况、车速、气温影响的分析，进行预测汽车在特定情况下的行驶特性。

一般情况下，车辆动力学模型包括整车模型、轮胎模型和路面模型三部分。

1.1 整车模型整车模型是车辆动力学模型的基础，主要包括车辆质量、发动机参数、车辆动力学变量等。

其中，车辆重量、车轮半径等物理量是最基本的整车模型参数。

此外，车辆的悬挂系统、转向系统和传动系统也可以在整车模型中考虑，以使模拟效果更为精确。

1.2 轮胎模型轮胎模型描述了轮胎在地面上所受的力和变形等特性。

轮胎的物理参数不同，对车速、车辆稳定性、制动距离等方面的影响也不同。

轮胎模型的建立主要考虑轮胎的纵向力、侧向力和滚转阻力等因素。

1.3 路面模型路面模型描述了车辆在路面上所受的阻力和摩擦等特性。

道路的不同纹理和材质对于车辆运动状态的影响是十分显著的。

路面模型的建立不仅需要考虑路面形状、材质等因素，还需要考虑气温、降雨等实际环境影响因素。

2. 车辆动力学仿真车辆动力学仿真是指利用计算机软件对车辆动力学模型进行算法模拟，以预测车辆在运行过程中的动态特性。

车辆动力学仿真是一种非常重要的手段，它可以用于评估车辆的操纵稳定性、驾驶员的驾驶技能水平、车辆零部件的设计优化等方面。

车辆动力学仿真的流程如下：第一步，选择车辆动力学模型、配备路面模型，设定仿真环境参数和运行路线，确定模拟致动方式。

第二步，设定车辆初始化信息，包括车速、转向角、初始位置等实际情况下的信息。

第三步，对车辆整车、轮胎和路面进行建模和仿真，并预测车辆在运动过程中的动态特性和行驶轨迹等。

车辆动力学模型的建立与仿真分析引言随着汽车工业的发展，车辆的动力学特性成为了工程师们关注的重点之一。

为了研究和改善车辆性能，建立车辆动力学模型并进行仿真分析成为了必不可少的工具。

本文将介绍车辆动力学模型的建立方法，并应用仿真分析技术对其进行探索。

一、车辆动力学模型的建立1.车辆运动学建模车辆动力学模型的第一步是建立车辆的运动学模型。

这包括车辆的位置、速度和加速度等关键参数的表达与计算。

通常，车辆运动学模型可以采用经典的运动学方程来描述，如牛顿第二定律和牛顿运动定律。

此外，还可以利用机械臂法和转角法等方法推导车辆的运动学模型。

2.车辆力学建模在车辆动力学模型的建立过程中，力学建模也是重要的一步。

力学建模旨在描述车辆受到的力和力矩等动力学特性。

常见的力学模型包括车辆的质量、重心高度、车轮滚动阻力、制动力和驱动力等。

通过建立准确的力学模型，可以更好地了解车辆的运动特性和动力特性。

3.车辆轮胎力学建模在车辆动力学中，轮胎力学模型是一个至关重要的组成部分。

轮胎对车辆运动和操纵性能的影响很大。

常用的轮胎力学模型有Magic Formula模型和Tire model等。

通过对轮胎的力学特性进行建模，可以在仿真分析中更准确地模拟车辆的行为。

二、车辆动力学模型的仿真分析1.悬挂系统仿真分析在车辆动力学模型的仿真分析中，悬挂系统是一个重要的部分。

悬挂系统可以影响到车辆的驾驶舒适性、操控性能和行驶稳定性等。

通过对悬挂系统进行仿真分析，可以评估并优化车辆的悬挂调校。

2.转向系统仿真分析车辆的转向系统是影响车辆操纵性能的另一个关键部分。

通过对转向系统进行仿真分析，可以评估车辆在转向时的稳定性和灵活性。

此外，还可以通过仿真分析来改进转向系统的设计和调校。

3.刹车系统仿真分析刹车系统是车辆安全性的关键因素之一。

通过仿真分析刹车系统可以评估车辆制动性能，包括制动距离、制动稳定性和制动力分布等。

这对于改进刹车系统的设计和优化具有重要意义。

商用车车辆开发动力学模型
商用车车辆开发动力学模型是一种用于描述商用车辆运动和受力影响的物理模型。

这个模型考虑了车辆的动力学特性，包括力的作用、车辆质量、惯性和摩擦等因素。

通过对这些因素进行建模和分析，可以预测车辆的运动性能、燃油消耗和排放等相关数据。

商用车车辆开发动力学模型通常基于牛顿力学原理，并考虑以下几个方面的因素：
1. 动力系统模型：包括发动机、传动系统和驱动轴等组成部分。

这部分模型主要用于描述车辆的动力输出和驱动方式。

2. 负载模型：考虑到商用车常常需要携带货物或乘客，模型还需要考虑负载对车辆的影响。

负载模型一般通过考虑车辆承载能力和重心位置来建立。

3. 轮胎模型：车辆在行驶过程中受到轮胎与地面之间的摩擦力的影响。

轮胎模型通常考虑轮胎与地面之间的摩擦系数、轮胎变形以及轮胎与地面之间的相互作用等因素。

4. 空气动力学模型：商用车在高速行驶时还需要考虑空气阻力对车辆的影响。

空气动力学模型通常考虑车辆的空气阻力系数、车身形状以及车辆运动速度等因素。

通过对以上因素进行建模和分析，商用车车辆开发动力学模型可以预测车辆的加速度、最高速度、燃油消耗和排放等数据。

这些数据对于商用车辆的设计、优化和性能评估具有重要的价值。