12.13函数补充作业(黄磊)

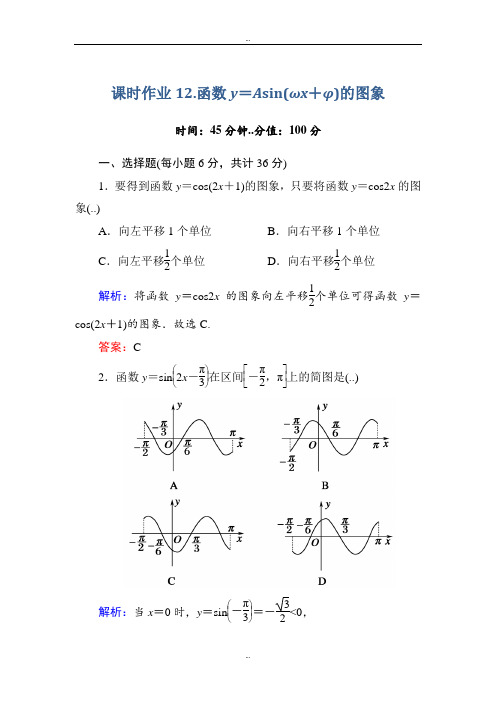
课时作业12.函数y ＝A sin(ωx ＋φ)的图象时间：45分钟..分值：100分一、选择题(每小题6分，共计36分)1．要得到函数y ＝cos(2x ＋1)的图象，只要将函数y ＝cos2x 的图象(..)A ．向左平移1个单位B ．向右平移1个单位C ．向左平移12个单位D ．向右平移12个单位解析：将函数y ＝cos2x 的图象向左平移12个单位可得函数y ＝cos(2x ＋1)的图象．故选C.答案：C2．函数y ＝sin ⎝ ⎛⎭⎪⎫2x －π3在区间⎣⎢⎡⎦⎥⎤－π2，π上的简图是(..)解析：当x ＝0时，y ＝sin ⎝ ⎛⎭⎪⎫－π3＝－32<0，故可排除B ，D.当x ＝π6时，sin ⎝ ⎛⎭⎪⎫2×π6－π3＝sin0＝0，排除C ，故选A.答案：A3．要得到函数y ＝sin 12x 的图象，只需将函数y ＝sin(12x －π3)的图象(..)A ．向左平移π3个单位 B ．向右平移π3个单位 C ．向左平移2π3个单位D ．向右平移2π3个单位解析：可求由y ＝sin 12x 怎么得到y ＝sin(12x －π3)，再逆推回去， ∵y ＝sin(12x －π3)＝sin[12(x －23π)]的图象错误!y ＝sin 错误!x 的图象，故选C.答案：C4．把函数y ＝cos2x ＋1的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变)，然后向左平移1个单位长度，再向下平移1个单位长度，得到的图象是(..)解析：由题意，y ＝cos2x ＋1的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变)，得解析式为y ＝cos x ＋1，向左平移一个单位为y ＝cos(x ＋1)＋1，向下平移一个单位为y ＝cos(x ＋1)，显然点(π2－1,0)在函数图象上．故选A.答案：A5．设函数f (x )＝cos ωx (ω>0)，将y ＝f (x )的图象向右平移π3个单位长度后，所得的图象与原图象重合，则ω的最小值等于(..)A.13 B ．3 C ．6D ．9解析：将y ＝f (x )的图象向右平移π3个单位长度后得到y ＝cos[ω(x －π3)]，所得图象与原图象重合，所以cos(ωx －π3ω)＝cos ωx ，则－π3ω＝2k π， 得ω＝－6k (k ∈Z )．又ω>0， 所以ω的最小值为6，故选C. 答案：C6．(2013·福建卷)将函数f (x )＝sin(2x ＋θ)(－π2<θ<π2)的图象向右平移φ(φ>1)个单位长度后得到函数g (x )的图象，若f (x )，g (x )的图象都经过点P (0，32)，则φ的值可以是(..)A.5π3B.5π6C.π2D.π6解析：将函数f (x )的图象向右平移φ个单位长度，得g (x )＝sin[2(x－φ)＋θ]，由题意得⎩⎨⎧sin θ＝32，sin (θ－2φ)＝32，解得θ＝π3，φ＝－k π或－π6－k π(k ∈Z )，结合选项取得φ＝5π6.答案：B二、填空题(每小题8分，共计24分)7．把函数y ＝3sin(2x ＋π3)的图象向右平移π6个单位长度，再向下平移1个单位长度，则得到的函数的解析式是________．解析：函数y ＝3sin(2x ＋π3)的图象向右平移π6个单位长度得函数y ＝3sin[2(x －π6)＋π3]＝3sin2x ，再向下平移1个单位长度得y ＝3sin2x －1.答案：y ＝3sin2x －18．将函数f (x )的图象向右平移π3个单位长度后，再向上平移1个单位长度得函数y ＝2sin(4x －π4)的图象，则f (x )＝________.解析：将y ＝2sin(4x －π4)的图象向左平移π3个单位长度，得函数y＝2sin[4(x ＋π3)－π4]＝2sin(4x ＋13π12)的图象，再向下平移一个单位长度，得函数y ＝2sin(4x ＋13π12)－1的图象，即f (x )＝2sin(4x ＋13π12)－1.答案：2sin(4x ＋13π12)－19．已知函数f (x )＝sin ⎝⎛⎭⎪⎫ωx ＋π4(x ∈R ，ω>0)的最小正周期为π，为了得到函数g (x )＝2sin ⎝⎛⎭⎪⎫x ＋π4的图象，只需将y ＝f (x )的图象上________．答案：各点的纵坐标变为原来的2倍，横坐标变为原来的2倍 三、解答题(共计40分，其中10题10分，11、12题各15分) 10．由函数y ＝sin x 的图象如何得到y ＝2cos x 的图象？ 解：由y ＝sin x ＝cos(π2－x )＝cos(x －π2)，则由y ＝cos(x －π2)的图象得到y ＝2cos x 的图象可由以下方法得到：11．已知函数f (x )＝3sin(2x ＋φ)⎝ ⎛⎭⎪⎫φ∈⎝ ⎛⎭⎪⎫0，π2，其图象向左平移π6个单位长度后，关于y 轴对称．(1)求函数f (x )的解析式．(2)说明其图象是由y ＝sin x 的图象经过怎样的变换得到的． 解：(1)将函数f (x )＝3sin(2x ＋φ)图象上的所有点向左平移π6个单位长度后，所得图象的函数解析式为y ＝3sin[2(x ＋π6)＋φ]＝3sin(2x ＋π3＋φ)． 因为图象平移后关于y 轴对称， 所以2×0＋π3＋φ＝k π＋π2(k ∈Z )，所以φ＝k π＋π6(k ∈Z )．因为φ∈(0，π2)，所以φ＝π6.所以f (x )＝3sin(2x ＋π6)．(2)将函数y ＝sin x 的图象上的所有点向左平移π6个单位长度，所得图象的函数解析式为y ＝sin(x ＋π6)，再把所得图象上各点的横坐标缩短到原来的12倍(纵坐标不变)，得函数y ＝sin(2x ＋π6)的图象，再把图象上各点的纵坐标伸长到原来的3倍(横坐标不变)，即得函数y ＝3sin(2x ＋π6)的图象．12．已知函数f (x )＝2sin ⎝⎛⎭⎪⎫2x －π4＋1.(1)求函数y ＝f (x )的周期、最大值和对称中心； (2)在直角坐标系中画出y ＝f (x )在[－π2，π2]上的图象．解：(1)周期T ＝2πω＝2π2＝π，∵－1≤sin ⎝⎛⎭⎪⎫2x －π4≤1，∴f (x )的最大值是1＋ 2.由2x －π4＝k π(k ∈Z )．得x ＝k π2＋π8(k ∈Z )，∴对称中心为(k π2＋π8，1)(k ∈Z )． (2)列表如下：函数y ＝f (x )在⎣⎢⎦⎥⎤－π2，π2上的图象如下图所示．。

八年级数学下册4.5.2《一次函数的应用（二）》课时作业（新版）湘教版编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（八年级数学下册4.5.2《一次函数的应用（二）》课时作业（新版）湘教版）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为八年级数学下册4.5.2《一次函数的应用（二）》课时作业（新版）湘教版的全部内容。

《一次函数的应用（二）》1、某蔬菜基地要把一批新鲜蔬菜运往外地,有两种运输方式可供选择，主要参考数据如下： 运输方式 运输速度（h km /） 装卸费用（元）途中综合费用（元/h ） 汽车60 200 270 火车 100 410 240⑴请分别写出汽车、火车运输的总费用1y （元）、2y （元）与运输路程x (km ）之间的函数关系；⑵你能说出用哪种运输方式较好吗？2、某公司准备与汽车租赁公司签订租车合同，以每月用车路程xkm 计算,甲汽车租赁公司的月租费是1y 元,乙汽车租赁公司的月租费是2y 元，如果1y 、2y 与x 之间的关系如图所示，那么:（1）月用车路程是多少时，租用两家汽车租赁公司的车所需费用相同?⑵每月用车路程在什么范围内,租用甲汽车租赁公司的车所需要费用较少？⑶如果每月用车的路程约为2300km ，那么租用哪家的车所需费用较少？3、某种摩托车的油箱最多可储油10升，加满油后，油箱中的剩余油量y （升）与摩托车行驶路程x (千米)之间的关系如图，根据图象回答下列问题：（1）一箱汽油可供摩托车行驶多少千米？ （2）摩托车每行驶100千米消耗多少升汽油？(3）油箱中的剩余油量小于1升时, 摩托车 将自动报警。

课时作业(五十五) 函数y ＝A sin(ωx ＋φ)[练基础]1．函数y ＝sin ⎝⎛⎭⎫2x －π3在区间⎣⎡⎦⎤－π2，π上的简图是( )2．为了得到函数y ＝cos(3x －1)的图象，只需把y ＝cos 3x 的图象上的所有点( ) A ．向左平移1个单位 B ．向右平移1个单位C ．向左平移13个单位D ．向右平移13个单位3．已知函数f (x )＝A cos(ωx ＋φ)的图象如图所示，f ⎝⎛⎭⎫π2＝－23，则f (0)＝( )A ．－23B ．－12C.23D.124．为了得到函数y ＝3sin ⎝⎛⎭⎫2x ＋π3的图象，只需把y ＝3sin x 上所有的点( ) A ．先把横坐标伸长到原来的2倍，然后向左平移π6个单位B ．先把横坐标伸长到原来的2倍，然后向左平移π3个单位C ．先把图象向右平移π3个单位，然后横坐标缩短到原来的12倍D ．先把图象向左平移π3个单位，然后横坐标缩短到原来的12倍5．将函数f (x )＝12sin ⎝⎛⎭⎫2x －π3的图象上每一个点向左平移π3个单位，得到函数g (x )的图象，则函数g (x )的单调递增区间为( )A.⎣⎡⎦⎤k π－π4，k π＋π4，k ∈Z B.⎣⎡⎦⎤k π＋π4，k π＋3π4，k ∈Z C.⎣⎡⎦⎤k π－2π3，k π－π6，k ∈ZD.⎣⎡⎦⎤k π－5π12，k π＋π12，k ∈Z 6．(多选)要得到函数y ＝sin ⎝⎛⎭⎫2x ＋π3的图象，只要将函数y ＝sin x 的图象( ) A ．每一点的横坐标扩大到原来的2倍(纵坐标不变)，再将所得图象向左平移π3个单位长度B ．每一点的横坐标缩短到原来的12(纵坐标不变)，再将所得图象向左平移π6个单位长度C ．向左平移π3个单位长度，再将所得图象每一点的横坐标缩短到原来的12(纵坐标不变)D ．向左平移π6个单位长度，再将所得图象每一点的横坐标缩短到原来的12(纵坐标不变)7．若函数f (x )＝2sin(ωx ＋φ)(ω>0)的图象的相邻两条对称轴的距离是π，则ω的值为________．8．函数f (x )＝A sin(ωx ＋φ)(A ＞0，ω＞0，－π＜φ＜0)的部分图象如图所示，则f ⎝⎛⎭⎫π4的值为________．9．用“五点法”画出函数y ＝2sin ⎝⎛⎭⎫x 2＋π6图象．10．已知函数f (x )＝A sin(ωx ＋φ)(A ＞0，ω＞0，|φ|＜π2)的部分图象如图所示．(1)求函数f (x )的解析式；(2)若将函数f (x )的图象上所有点的横坐标变为原来的2倍，纵坐标不变；再把所得函数图象向左平移π3个单位长度，得到函数g (x )的图象．求函数g (x )在[0,2π]上的单调递增区间．[提能力]11．要得到函数y ＝2cos x 的图象，只需将函数y ＝2sin ⎝⎛⎭⎫2x ＋π4图象上的所有点的( )A ．横坐标缩短到原来的12(纵坐标不变)，再向左平行移动π8个单位长度B ．横坐标缩短到原来的12(纵坐标不变)，再向右平行移动π4个单位长度C ．横坐标伸长到原来的2倍(纵坐标不变)，再向左平行移动π4个单位长度D ．横坐标伸长到原来的2倍(纵坐标不变)，再向右平行移动π8个单位长度12．(多选)已知函数f (x )＝A sin(ωx ＋φ)(A ＞0，ω＞0，0＜φ＜π)的部分图象如图所示，则下列正确的是( )A ．f (x )＝2sin ⎝⎛⎭⎫2x ＋2π3 B ．f (2021π)＝1C ．函数y ＝|f (x )|为偶函数D ．∀x ∈R ，f ⎝⎛⎭⎫π6＋x ＋f ⎝⎛⎭⎫π6－x ＝013．函数y ＝cos(2x ＋φ)(－π≤φ<π)的图象向右平移π2个单位后，与函数y ＝sin ⎝⎛⎭⎫2x ＋π3的图象重合，则φ＝________.14.函数f (x )＝sin(ωx ＋φ)⎝⎛⎭⎫ω>0，|φ|<π2的部分图象如图所示，则φ＝________；将函数f (x )的图象沿x 轴向右平移b (0<b <π2)个单位后，得到一个偶函数的图象，则b ＝________.15．已知函数f (x )＝sin (2x ＋φ)(0＜φ＜π2)，函数y ＝f ⎝⎛⎭⎫x －π12为奇函数． (1)求函数f (x )的单调递增区间；(2)将函数y ＝f (x )的图象向右平移π6个单位，然后将所得图象上的各点的横坐标缩小到原来的12倍(纵坐标不变)得到函数g (x )的图象，证明：当x ∈⎣⎡⎦⎤0，π4时，2g 2(x )－g (x )－1≤0.[培优生]16．已知函数f (x )＝2sin ωx ，其中常数ω>0.(1)若y ＝f (x )在⎣⎡⎦⎤－π4，2π3上单调递增，求ω的取值范围； (2)令ω＝2，将函数y ＝f (x )的图象向左平移π6个单位长度，再向上平移1个单位长度，得到函数y ＝g (x )的图象，区间[a ，b ](a ，b ∈R 且a <b )满足：y ＝g (x )在[a ，b ]上至少含有30个零点，在所有满足上述条件的[a ，b ]中，求b －a 的最小值．课时作业(五十五) 函数y ＝A sin(ωx ＋φ)1．解析：当x ＝0时，y ＝sin ⎝⎛⎭⎫－π3＝－32<0，排除B 、D ；当x ＝π6时，sin ⎝⎛⎭⎫2×π6－π3＝sin 0＝0，排除C.故选A. 答案：A2．解析：只需把y ＝cos 3x 的图象上的所有点向右平移13个单位，即可得到函数y ＝cos(3x －1)的图象， 故选D. 答案：D3．解析：由图象可知函数f (x )的周期为23π，故ω＝3.将⎝⎛⎭⎫11π12，0代入解析式得114π＋φ＝π2＋2k π(k ∈Z )，所以φ＝－π4＋2(k －1)·π(k ∈Z )．令φ＝－π4，代入解析式得f (x )＝A cos ⎝⎛⎭⎫3x －π4，又f ⎝⎛⎭⎫π2＝－A cos π4＝－23，故A ＝223.所以f (0)＝223cos ⎝⎛⎭⎫－π4＝223cos π4＝23. 故选C. 答案：C4．解析：只需把y ＝3sin x 上所有的点先把图象向左平移π3个单位，然后横坐标缩短到原来的12倍，即可得到函数y ＝3sin ⎝⎛⎭⎫2x ＋π3的图象， 故选D. 答案：D5．解析：由题意可知平移后的解析式：g (x )＝12sin ⎝⎛⎭⎫2x ＋π3 函数y ＝g (x )的单调递增区间：2k π－π2≤2x ＋π3≤2k π＋π2，k ∈Z解得：k π－5π12≤x ≤k π＋π12，k ∈Z故选D. 答案：D6．解析：(1)先伸缩后平移时：每一点的横坐标缩短到原来的12(纵坐标不变)，再将所得图象向左平移π6个单位长度，所以A 选项错误，B 选项正确．(2)先平移后伸缩时：向左平移π3个单位长度，再将所得图象每一点的横坐标缩短到原来的12(纵坐标不变)，所以C 选项正确，D 选项错误． 故选BC. 答案：BC7．解析：因为函数f (x )＝2sin(ωx ＋φ)(ω>0)的图象的相邻两条对称轴的距离是π，所以T 2＝π⇒T ＝2π＝2πω⇒ω＝1. 答案：18．解析：由图象得：A ＝2，T 2＝π3－⎝⎛⎭⎫－π6＝π2， 故T ＝π，故ω＝2ππ＝2，由f ⎝⎛⎭⎫π3＝2sin ⎝⎛⎭⎫2×π3＋φ＝2， 故2π3＋φ＝π2，解得：φ＝－π6， 故f (x )＝2sin ⎝⎛⎭⎫2x －π6，f ⎝⎛⎭⎫π4＝2sin ⎝⎛⎭⎫2×π4－π6＝2sin π3＝2×32＝ 3. 答案：39．解析：令t ＝x 2＋π6，列表如下10．解析：(1)根据函数f (x )＝A sin(ωx ＋φ)(A ＞0，ω＞0，|φ|＜π2)的部分图象，可得 A ＝2，12×2πω＝5π6－π3，∴ω＝2.再根据五点法作图，2×π3＋φ＝π2，∴φ＝－π6，∴f (x )＝2sin ⎝⎛⎭⎫2x －π6. (2)将函数f (x )的图象上所有点的横坐标变为原来的2倍，纵坐标不变，可得y ＝2sin⎝⎛⎭⎫x －π6的图象； 再把所得函数图象向左平移π3个单位长度，得到函数g (x )＝2sin ⎝⎛⎭⎫x ＋π6的图象． 令2k π－π2≤x ＋π6≤2k π＋π2，求得2k π－2π3≤x ≤2k π＋π3，可得g (x )的增区间为⎣⎡⎦⎤2k π－2π3，2k π＋π3，k ∈Z . 故函数g (x )在[0,2π]上的单调递增区间为⎣⎡⎦⎤0，π3，⎣⎡⎦⎤4π3，2π. 11．解析：∵y ＝2cos x ＝2sin ⎝⎛⎭⎫x ＋π2， ∴y ＝2sin ⎝⎛⎭⎫2x ＋π4――――――――――――→纵坐标不变横坐标伸长到原来的2倍y ＝2sin ⎝⎛⎭⎫x ＋π4y ＝2sin ⎝⎛⎭⎫x ＋π2. 故选C.答案：C12．解析：由图象知：A ＝2，T ＝2⎣⎡⎦⎤5π12－⎝⎛⎭⎫－π12＝π， 故ω＝2πT ＝2ππ＝2，故f (x )＝2sin(2x ＋φ)，∵f (x )的图象过点⎝⎛⎭⎫－π12，2， ∴2sin ⎝⎛⎭⎫－π6＋φ＝2，故sin ⎝⎛⎭⎫－π6＋φ＝1， ∴－π6＋φ＝π2＋2k π，k ∈Z ，故φ＝2π3＋2k π，k ∈Z ，∵0＜φ＜π，故φ＝2π3，故f (x )＝2sin ⎝⎛⎭⎫2x ＋2π3， 对于A ：f (x )＝2sin ⎝⎛⎭⎫2x ＋2π3，故A 正确； 对于B ：f (2021π)＝2sin ⎝⎛⎭⎫2·2021π＋2π3＝2sin 2π3＝3，故B 错误； 对于C ：∵⎪⎪⎪⎪f ⎝⎛⎭⎫－π3＝⎪⎪⎪⎪2sin ⎝⎛⎭⎫－2π3＋2π3 ＝0，⎪⎪⎪⎪f ⎝⎛⎭⎫π3＝⎪⎪⎪⎪2sin ⎝⎛⎭⎫2π3＋2π3＝3， 故⎪⎪⎪⎪f ⎝⎛⎭⎫－π3 ≠⎪⎪⎪⎪f ⎝⎛⎭⎫π3，故|f (x )|不是偶函数，故C 错误； 对于D ：∵f ⎝⎛⎭⎫π6＋x ＝2sin ⎝⎛⎭⎫π3＋2x ＋2π3＝2sin(π＋2x )＝－2sin 2x ， f ⎝⎛⎭⎫π6－x ＝2sin ⎝⎛⎭⎫π3－2x ＋2π3＝2sin (π－2x )＝2sin 2x ， 故f ⎝⎛⎭⎫π6＋x ＋f ⎝⎛⎭⎫π6－x ＝－2sin 2x ＋2sin 2x ＝0，故D 正确，故选AD. 答案：AD13．解析：因为y ＝cos(2x ＋φ)＝cos (－2x －φ)＝sin ⎣⎡⎦⎤π2－()－2x －φ＝sin ⎝⎛⎭⎫2x ＋π2＋φ，图象向右平移π2个单位后为y ＝sin ⎝⎛⎭⎫2x －π2＋φ，与y ＝sin ⎝⎛⎭⎫2x ＋π3重合，所以φ－π2＝π3，解得φ＝5π6.答案：5π614．解析：根据函数的图象可得14T ＝3π8－π8＝π4，所以T ＝π，所以2πω＝π，所以ω＝2，又因为f ⎝⎛⎭⎫π8＝1，所以sin ⎝⎛⎭⎫2×π8＋φ＝1，所以φ＋π4＝2k π＋π2，k ∈Z ， 所以φ＝2k π＋π4，k ∈Z ，因为|φ|<π2，所以φ＝π4.所以f (x )＝sin(2x ＋π4)，将f (x )的图象沿x 轴向右移b 个长度单位得函数y ＝sin ⎣⎡⎦⎤2()x －b ＋π4＝sin ⎝⎛⎭⎫2x ＋π4－2b 的图象，因为函数y ＝sin ⎝⎛⎭⎫2x ＋π4－2b 是偶函数，所以π4－2b ＝k π＋π2，k ∈Z ， 所以b ＝－k π2－π8，k ∈Z ，因为0<b <π2，所以k ＝－1，b ＝3π8.答案：π4 3π815．解析：(1)f ⎝⎛⎭⎫x －π12＝sin ⎝⎛⎭⎫2x －π6＋φ， 因为其为奇函数，所以－π6＋φ＝k π，k ∈Z ，解得φ＝k π＋π6，k ∈Z ，因为0＜φ＜π2，所以φ＝π6，所以f (x )＝sin ⎝⎛⎭⎫2x ＋π6， 令－π2＋2k π≤2x ＋π6≤π2＋2k π，k ∈Z ，解得－π3＋k π≤x ≤π6＋k π，k ∈Z ，可得函数f (x )的单调递增区间⎣⎡⎦⎤－π3＋k π，π6＋k π，k ∈Z . (2)证明：函数y ＝f (x )的图象向右平移π12个单位，得到函数y ＝sin ⎣⎡⎦⎤2⎝⎛⎭⎫x －π12＋π6＝sin 2x 的图象，再将所得图象各点的横坐标缩短为原来的12倍，纵坐标不变，得到函数g (x )＝sin 4x 的图象，因为x ∈⎣⎡⎦⎤0，π4时，g (x )∈[0,1]， 所以2g 2(x )－g (x )－1＝[2g (x )＋1][g (x )－1]≤0，得证．16．解析：(1)因为ω>0，根据题意有⎩⎨⎧－π4ω≥－π2，2π3ω≤π2解得0<ω≤34.所以ω的取值范围为⎝⎛⎦⎤0，34. (2)由题意知f (x )＝2sin 2x ，g (x )＝2sin ⎣⎡⎦⎤2⎝⎛⎭⎫x ＋π6＋1＝2sin ⎝⎛⎭⎫2x ＋π3＋1， 由g (x )＝0得，sin ⎝⎛⎭⎫2x ＋π3＝－12，解得x ＝k π－π4或x ＝k π－712π，k ∈Z ，即g (x )的零点相离间隔依次为π3和2π3，故若y ＝g (x )在[a ，b ]上至少含有30个零点，则b －a 的最小值为14×2π3＋15×π3＝43π3.。

【成才之路】2014-2015学年高中数学 2.1 函数课后强化作业北师大版必修1一、选择题1．谚语“瑞雪兆丰年”说明( )A．下雪与来年的丰收具有依赖关系B．下雪与来年的丰收具有函数关系C．下雪是丰收的函数D．丰收是下雪的函数[答案] A[解析] 积雪层对越冬作物具有防冻保暖的作用，大雪可以防止土壤中的热量向外散发，又可阻止外界冷空气的侵入，具有增墒肥田的作用．所以下雪与来年的丰收具有依赖关系，但不是函数关系．2．已知变量x，y满足y＝|x|，则下列说法错误的是( )A．x，y之间有依赖关系B．x，y之间有函数关系C．y是x的函数D．x是y的函数[答案] D[解析] 当y取一个正值时，有两个x与它对应，故D错．3．下图是反映某市某一天的温度随时间变化情况的图像．由图像可知，下列说法中错误的是( )A．这天15时的温度最高B．这天3时的温度最低C．这天的最高温度与最低温度相差13℃D．这天21时的温度是30℃[答案] C[解析] 这天的最高温度与最低温度相差为36－22＝14℃，故C错．4．下列两个变量之间的关系，不是函数关系的是( )A．多边形的边数和它的内角和B．正方形的边长和面积C．球的体积和半径D．人的体重和身高[答案] D5．张大明种植了10亩小麦，每亩施肥x千克，小麦总产量y千克，则( )A．x，y之间有依赖关系B．x，y之间有函数关系C．y是x的函数D．x是y的函数[答案] A[解析] 虽然小麦总产量y与每亩施肥量x之间存在依赖关系，但小麦总产量y还受气候、管理等其他因素的影响，所以x，y之间无函数关系．6．星期天，小明从家出发，出去散步，图中描述了他散步过程中离家的距离s(m)与散步所用的时间t(min)之间的函数关系，根据图像，下面的描述符合小明散步情况的是( )A．从家出发，到一个公共阅报栏，看了一会儿报，就回家了B．从家出发，到一个公共阅报栏，看了一会儿报后，继续向前走了一段，然后回家了C．从家出发，散了一会儿步(没有停留)，然后回家了D．从家出发，散了一会儿步，就找同学去了，18min后才回家[答案] B[解析] 像线段表明小明离家的距离始终是300米，然后离家距离达到500米，说明小明从家出发后，到一个公共阅报栏，看了一会儿报后，继续向前走了一段，然后回家了．故答案为B.二、填空题7．从市场中了解到，饰用K金的含金量如下表：饰用K．[答案] 函数越高8.右图表示一位骑自行车者和一位骑摩托车者在相距80km的两城镇间旅行时，路程和时间的函数图像，由图可知，骑自行车者用了6小时(含途中休息的1小时)，骑摩托车者用了2小时，有人根据这个函数图像，提供了这两个旅行者的如下信息，其中正确信息的序号是________．①骑自行车者比骑摩托车者早出发3小时，晚到1小时②骑自行车者是变速运动，骑摩托车者是匀速运动③骑摩托车者在出发1.5小时后追上了骑自行车者[答案] ①[解析] 由图像可以看出骑自行车者早出发3个小时，而晚到1小时，速度是先快后慢，然后再快，是变速运动．骑摩托车者也是变速运动，但速度变化不大．骑摩托车者在出发1小时后追上骑自行车者．所以正确的序号是①.三、解答题9．下图的曲线表示一人骑自行车离家的距离s(千米)与时间t(时)的关系．骑车者9时离开家，15时回家．根据这个曲线图，请你回答下列问题：(1)最初到达离家最远的地方是什么时间？离家多远？(2)何时开始第一次休息？休息多长时间？(3)第一次休息时，离家多远？到他骑了多少千米？(5)他在～和～的平均速度分别是多少？(6)他在哪段时间里停止前进并休息用午餐？[解析] (1)最初到达离家最远的地方的时间是12时，离家30千米．开始第一次休息，休息了半小时．(3)第一次休息时，离家17千米．至，他骑了13千米． ～的平均速度是10千米/时；～的平均速度是14千米/时．(6)从12时到13时停止前进，并休息用午餐.一、选择题1．如图，将一个“瘦长”的圆柱钢锭经过多次锻压成一个“矮胖”的圆柱钢锭(不计损耗)，则在锻压过程中，圆柱体积与高的关系可用图像表示为( )[答案] B[解析] 圆柱钢锭的体积不随高的变化而变化．2．向高为H 的水瓶中注水，注满为止．如果注水量V 与水深h 的函数关系的图像如图所示，那么水瓶的形状是图中的( )[答案] B[解析] 观察图像，根据图像的特点，发现取水深h ＝H 2，注水量V >V 02，即水深为一半时，实际注水量大于水瓶总量V 0的一半，A 项中V <V 02，C 项、D 项中V ＝V 02，故排除选项A ，C，D.∴应选B.二、填空题3．某公司生产某种产品的成本为1 000元，以1 100元的价格批发出去，随生产产品数量的增加，公司收入________，它们之间是________关系．[答案] 增加函数4．圆柱的高为10cm，当圆柱底面半径变化时，圆柱的体积也随之发生变化，在这个变化过程中，________是自变量，________是因变量．设圆柱底面半径为r(cm)，圆柱的体积V(cm3)与r(cm)的关系式为________，当底面半径从2cm变化到5cm时，圆柱的体积由________(cm3)变化到________(cm3)．[答案] 圆柱底面半径圆柱体积V＝10πr240π250π[解析] 圆柱的体积为V＝πr2h(其中r表示圆柱的底面半径，h表示圆柱的高)．三、解答题5．向平静的湖面投一块石子，便会形成以落水点为圆心的一系列同心圆．(1)在这个变化过程中，有哪些变量？(2)若圆的面积用S表示，半径用R表示，则S和R的关系是什么？它们是常量还是变量？(3)若圆的周长用C表示，半径用R表示，则C与R的关系式是什么？[解析] (1)形成的一系列同心圆的半径、周长、面积都是变量．(2)圆的面积S与半径R存在着依赖关系，对于半径R的每一个取值，都有唯一的面积S与之对应，所以圆的面积S是半径R的函数，其函数关系式是S＝πR2.圆的面积S、半径R都是变量．(3)C＝2πR.6．在工作的状态下，饮水机会通过自动对水加热使机中水的温度保持在一定范围内．下图表示在饮水机的水温达到最高后，饮水机处于工作状态中的水的温度的变化情况：根据右图，设计一个问题，并解答所设计的问题.[解析] 设计问题就是从图像中获取有关信息．例如，提出下列问题：问题1：饮水机中水的最高温度是多少？最低温度是多少？解：水的最高温度为96℃，最低温度为91℃，问题2：水温上升到最高温度后，再经过10分钟饮水机中水的温度多高？35分钟时水的温度多高？解：10分钟后水的温度约93℃高，35分钟时水的温度约95℃高．问题3：哪段时间水的温度在不断下降？哪段时间水的温度在持续上升？解：约从开始到27分钟时水的温度在不断下降，从27分钟到32分钟时水的温度在不断上升，后面又一个相同的下降与上升的过程．7．一辆汽车在某段路程中的行驶速度与时间的关系如图所示．(1)试求图中阴影部分的面积，说明面积的实际含义，并分析面积与时间是否构成函数关系？(2)假设汽车里程表在行驶这段路程前的读数为a km，当1<t≤2时，试建立汽车里程表的读数s(km)与时间t(h)的函数关系式．[解析] (1)阴影部分的面积为S＝50＋80＋90＋70＋60＝350，阴影部分的面积表示汽车在这5个小时内行驶的总路程为350km.由于对于时间t的每一个取值，都有唯一的面积的值与之对应，因此面积与时间构成函数关系．(2)根据图像可得，s＝80(t－1)＋a＋50.。

【成才之路】2014-2015学年高中数学 2.1.3 第2课时 函数的单调性的应用课后强化作业 新人教B 版必修1一、选择题1．已知函数f (x )＝3x，则在下面区间内f (x )不是递减函数( )A ．(0，＋∞)B ．(－∞，0)C ．(－∞，0)∪(0，＋∞)D ．(1，＋∞) [答案] C[解析] f (x )＝3x在(0，＋∞)上和(－∞，0)上都是减函数，故A 、B 、D 正确，但在(0，＋∞)∪(－∞，0)上不是减函数．2．已知函数f (x )＝x 2－4x ，x ∈[1,5]，则函数f (x )的值域是( ) A ．[－4，＋∞) B ．[－3,5] C ．[－4,5] D ．(－4,5][答案] C[解析] ∵f (x )＝x 2－4x ＝(x －2)2－4，∴函数f (x )的图象是开口向上的抛物线，对称轴为x ＝2，又∵x ∈[1,5]， 故当x ＝2时，f (x )取最小值－4， 当x ＝5时，f (x )取大值5，故选C.3．在区间(0，＋∞)上不是增函数的是( ) A ．y ＝3x －2 B ．y ＝3x 2－1 C ．y ＝2x 2＋3x D ．y ＝2x－1[答案] D[解析] 函数y ＝3x －2在(0，＋∞)上是增函数；函数y ＝3x 2－1的图象是开口向上的抛物线，对称轴为x ＝0，故在(0，＋∞)上是增函数；函数y ＝2x 2＋3x 的图象是开口向上的抛物线，对称轴为x ＝－34，故在(0，＋∞)上是增函数；函数y ＝2x －1在(0，＋∞)上为减函数，故选D.4．函数f (x )＝⎩⎪⎨⎪⎧2x ＋61≤x ≤2x ＋7－1≤x ≤1，则f (x )的最大值、最小值分别为( )A ．10,6B ．10,8C ．8,6D ．以上都不对[答案] A[解析] 函数f (x )在区间[－1,2]上是增函数，∴函数f (x )的最大值为f (2)＝10，最小值为f (－1)＝6.5．已知函数f (x )＝ax 2＋2ax ＋4(a >0)．若x 1<x 2，x 1＋x 2＝0，则( ) A ．f (x 1)>f (x 2) B ．f (x 1)＝f (x 2) C ．f (x 1)<f (x 2)D ．f (x 1)与f (x 2)的大小不能确定 [答案] C[解析] f (x 1)－f (x 2)＝ax 21＋2ax 1＋4－ax 22－2ax 2－4＝a (x 1－x 2)(x 1＋x 2)＋2a (x 1－x 2) ∵a >0，x 1<x 2，x 1＋x 2＝0， ∴f (x 1)－f (x 2)＝2a (x 1－x 2)<0， ∴f (x 1)<f (x 2)．6．已知函数f (x )在其定义域R 上单调递增，则满足f (2x －2)<f (2)的x 的取值范围是( )A ．(－∞，0)B ．(2，＋∞)C ．(－∞，0)∪(2，＋∞)D ．(－∞，2)[答案] D[解析] ∵函数f (x )在其定义域R 上单调递增， ∴2x －2<2，∴x <2，故选D. 二、填空题7．函数y ＝－a x在(0，＋∞)上是减函数，则y ＝－2x 2＋ax 在(0，＋∞)上的单调性为________．[答案] 单调递减[解析] ∵函数y ＝－a x在(0，＋∞)上是减函数，∴a <0.又函数y ＝－2x 2＋ax 的图象是开口向下的抛物线，对称轴为x ＝a4<0，∴函数y ＝－2x 2＋ax 在(0，＋∞)上单调递减．8．函数y ＝|x －3|＋2的递增区间为________，递减区间为________． [答案] [3，＋∞) (－∞，3][解析] y ＝|x －3|＋2＝⎩⎪⎨⎪⎧x －1x ≥35－x x <3，其图象如图所示，由图象知，其递增区间为[3，＋∞)，递减区间为(－∞，3]． 三、解答题9．用函数单调性的定义证明：f (x )＝x ＋ax ＋b(a >b >0)在(－b ，＋∞)上是减函数． [解析] 设x 1、x 2∈(－b ，＋∞)，且x 1<x 2，则Δx ＝x 2－x 1>0. Δy ＝f (x 2)－f (x 1)＝x 2＋a x 2＋b －x 1＋ax 1＋b＝x 2－x 1b －ax 2＋b x 1＋b，由x 1、x 2∈(－b ，＋∞)得x 1>－b ，x 2>－b ， ∴x 1＋b >0，x 2＋b >0， 又a >b >0，∴b －a <0， 又x 2－x 1>0，∴Δy <0. ∴f (x )＝x ＋ax ＋b(a >b >0)在(－b ，＋∞)上是减函数.一、选择题1．函数y ＝|x |在(－∞，a ]上是减函数，则a 的取值范围是( ) A ．a >0 B ．a ≥0 C ．a <0 D ．a ≤0[答案] D[解析] 如图所示：∴函数y ＝|x |的单调减区间为(－∞，0]， 要使y ＝|x |在(－∞，a ]上是减函数，则有a ≤0.2．设(a ，b )，(c ，d )都是f (x )的单调增区间，且x 1∈(a ，b )，x 2∈(c ，d )，x 1<x 2，则f (x 1)与f (x 2)的大小关系为( )A ．f (x 1)<f (x 2)B ．f (x 1)>f (x 2)C ．f (x 1)＝f (x 2)D ．不能确定[答案] D[解析] 根据函数单调性的定义，所取两个自变量必须在同一单调区间内，才能由该区间上函数的单调性来比较函数值的大小，而x 1，x 2分别在两个单调增区间，故f (x 1)与f (x 2)的大小不能确定，选D.3．下列函数中，满足“对任意x 1，x 2∈(0，＋∞)，都有ΔyΔx>0”的是( ) A ．f (x )＝2xB ．f (x )＝－3x ＋1C ．f (x )＝x 2＋4x ＋3 D ．f (x )＝x ＋1x[答案] C [解析]Δy Δx >0⇔f x 2－f x 1x 2－x 1>0⇔f (x )在(0，＋∞)上为增函数，而f (x )＝2x及f (x )＝－3x ＋1在(0，＋∞)上均为减函数，故A ，B 错误；f (x )＝x ＋1x在(0,1)上递减，在[1，＋∞)上递增，故D 错误；f (x )＝x 2＋4x ＋3＝x 2＋4x ＋4－1＝(x ＋2)2－1，所以f (x )在[－2，＋∞)上递增，故选C.4．函数f (x )＝4x 2－mx ＋5在区间[－2，＋∞)上是增函数，则有( ) A ．f (1)≥25B ．f (1)＝25C ．f (1)≤25D ．f (1)>25[答案] A[解析] ∵f (x )＝4x 2－mx ＋5的图象是开口向上的抛物线，对称轴为x ＝m8，由f (x )在区间[－2，＋∞)上为增函数，∴m8≤－2，即m ≤－16.又f (1)＝4－m ＋5＝9－m ≥25.二、填空题5．已知函数y ＝ax 和y ＝bx在(0，＋∞)上都是减函数，则y ＝ax 2＋bx ＋c 在(－∞，0)上是__________函数．[答案] 增[解析] ∵y ＝ax 和y ＝b x在(0，＋∞)上都是减函数，∴a <0，b >0，结合二次函数图象可得，函数y ＝ax 2＋bx ＋c 在(－∞，0)上是增函数．6．设函数f (x )满足；对任意的x 1，x 2∈R ，都有(x 1－x 2)·[f (x 1)－f (x 2)]>0，则f (－3)与f (－π)的大小关系是________．[答案] f (－3)>f (－π)[解析] (x 1－x 2)[f (x 1)－f (x 2)]>0，可得函数为增函数． ∵－3>－π，∴f (－3)>f (－π)． 三、解答题7．已知f (x )是定义在[－2,1]上的增函数，若f (t －1)<f (1－3t )，求t 的取值范围． [解析] ∵函数f (x )是定义在[－2,1]上的增函数，且f (t －1)<f (1－3t )，∴⎩⎪⎨⎪⎧－2≤t －1≤1－2≤1－3t ≤1t －1<1－3t，∴⎩⎪⎨⎪⎧－1≤t ≤20≤t ≤1t <12，即0≤t <12.故t 的取值范围为0≤t <12.8．已知函数f (x )对任意x ∈R ，都有f (2＋x )＝f (2－x )，且当x >2时， f (x )为增函数，试比较f (1)、f (4)、f (－2)的大小．[解析] ∵x ∈R ，都有f (2＋x )＝f (2－x )， ∴f (x )的图象关于直线x ＝2对称，又x >2时，f (x )为增函数，∴x <2时，f (x )为减函数，则在x 轴上距离对称轴x ＝2越远的数，其函数值越大，∴f (－2)>f (4)>f (1)． 9．已知函数f (x )对任意x 、y ∈R ，总有f (x )＋f (y )＝f (x ＋y )，且当x >0时，f (x )<0，f (1)＝－23.(1)求证：f (x )是R 上的单调递减函数； (2)求f (x )在[－3,3]上的最小值．[解析] (1)证明：设x 1和x 2是任意的两个实数，且x 1<x 2，则Δx ＝x 2－x 1>0，∵x >0时，f (x )<0，∴f (x 2－x 1)<0，又∵x 2＝(x 2－x 1)＋x 1，∴f (x 2)＝f [(x 2－x 1)＋x 1]＝f (x 2－x 1)＋f (x 1)， ∴f (x 2)－f (x 1)＝f (x 2－x 1)<0，∴f (x 2)<f (x 1)． ∴f (x )是R 上的单调递减函数．(2)解：由(1)可知f (x )在R 上是减函数， ∴f (x )在[－3,3]上也是减函数， ∴f (x )在[－3,3]上的最小值为f (3)．而f (3)＝f (1)＋f (2)＝3f (1)＝3×⎝ ⎛⎭⎪⎫－23＝－2. ∴函数f (x )在[－3,3]上的最小值是－2.。

《函数图像》练习
一、变式训练
（1）、已知函数12sin(4)53y x π=+
的图象为C ，为了得到函数22sin(4)3
y x π=+的图象，只需把C 的所有点（ ） （2）、已知函数12sin(4)53
y x π=+的图象为C ，为了得到函数12sin()53
y x π=+的图象，只需把C 的所有点（ ） （3）、已知函数12sin(4)53
y x π=+的图象为C ，为了得到函数1sin 45
y x =的图象，只需把C 的所有点（ ） （4）、将正弦曲线上各点向左平移3y π
=个单位，再把横坐标伸
长到原来的2倍，纵坐标不变，则所得图象的解析式为( )
二、巩固作业
1、画出下列函数在长度为一个周期的闭区间上的简图，并说明函数的图象由正（余）弦曲线经过怎样的变化得出。

①1sin(2)36y x π
=- ②12cos()24
y x π
=+ 2、函数f(x)的横坐标伸长到原来的两倍，再向左平移2
π个单位，所得到的曲线是1sin 2y x =的图象，试求函数()y f x =的解析式。

20.4函数的初步应用补充习题（二）一、单项方法题1．向高为h的水瓶中注水，注满为止。

如果注水量V与水深h的关系如图21-11所示，那么水瓶的形态是（）。

2．不经过第二象限的直线是（）。

A．2 y x =-B．21 y x=-C．21 y x=+D．21 y x=-+3．如图21-12所示，函数2y hx=-中，y 随x的增大而减小，则它的图象是（）。

4．若点P（a，b）在第二象限内，则直线y=ax+b不经过的象限是（）。

A．第一象限B．第二象限C．第三象限D．第四象限5．直线1122y x=+上到x轴或y轴距离为1的点有（）。

A．1个B．2个C．3个D ．4个6．若A（2，-3）B（4，3）C（5，a）三点共线，则a等于（）。

A．6B．-6C．±6D．6或37．函数y=2x+b的图象过点（1，-3），则b=_____。

三、综合方法题8．如图21-13，OA、BA分别表示甲、乙两人的运动图象，请根据图象回答下列问题。

（1）用t表示时间，s表示路程，则甲的速度为_____千米/时。

（2）乙的速度是_____千米/时。

（3）两人同时出发。

，相遇时甲比乙多走_____千米。

9．如图21-14，表明小明上学的时间和离家的距离之间的函数关系，看图回答下面问题：（1）学校到小明家的路程是多少？（2）小明上学是几点出发，路上用了多长时间？（3）小明在学校的时间是多少，几点返回家中？（4）小明上学和放学回家行走的速度哪个快些？答案：1．B2．B3．C4．C5．C6．A7．-58．（1）4 （2）3 （3）59．（1）4000米（2）7点出发,用了1小时（3）9小时 19点（4）上学快。

高三数学一轮复习函数的图像专项提升练习在数学中，函数f的图形(或图象)指的是所有有序对(x, f(x))组成的集合，以下是查字典数学网整理的函数的图像专项提升训练，期望对考生有关心。

1、(2021山东卷)函数y=xcos x+sin x的图象大致为().解析函数y=xcos x+sin x在x=时为负，排除A;易知函数为奇函数，图象关于原点对称，排除B;再比较C，D，不难发觉当x取接近于0的正数时y0，排除C.答案D函数y=xsin x在[-]上的图象是().解析容易判定函数y=xsin x为偶函数，可排除D.当0答案A3、函数y=x+cos x的大致图象是().y=1-sin x0，函数y=x+cos x为增函数，排除C.又当x=0时，y=1，排除A，当x=时，y=，排除D，故选B.B4、函数y=log2(|x|+1)的图象大致是().解析当x0时，y=log2(x+1)，先画出y=log2x的图象，再将图象向左平移1个单位，最后作出关于y轴对称的图象，得与之相符的图象为B.答案B已知函数f(x)=|x2-4x+3|.(1)求函数f(x)的单调区间，并指出其增减性;(2)求集合M={m|使方程f(x)=m有四个不相等的实根}.解f(x)=作出函数图象如图.(1)函数的增区间为[1,2]，[3，+函数的减区间为(-，1]，[2,3].(2)在同一坐标系中作出y=f(x)和y=m的图象，使两函数图象有四个不同的交点(如图).由图知0M={m|0.(2021青岛一模)函数y=21-x的大致图象为().解析y=21-x=x-1，因为01，因此y=x-1为减函数，取x=0时，则y=2，故选A.答案A.(2021福建卷)函数f(x)=ln(x2+1)的图象大致是().解析函数f(x)=ln(x2+1)的定义域为(-，+)，又因为f(-x)=f(x)，故f(x)为偶函数且f(0)=ln 1=0，综上选A.答案A.(2021日照一模)函数f(x)=lg(|x|-1)的大致图象是().解析易知f(x)为偶函数，故只考虑x0时f(x)=lg(x-1)的图象，将函数y =lg x图象向x轴正方向平移一个单位得到f(x)=lg(x-1)的图象，再依照偶函数性质得到f(x)的图象.答案B.函数y=(x-1)3+1的图象的对称中心是________.解析y=x3的图象的对称中心是(0,0)，将y=x3的图象向上平移1个单位，再向右平移1个单位，即得y=(x-1)3+1的图象，因此对称中心为(1,1).答案(1,1).已知函数f(x)=且关于x的方程f(x)-a=0有两个实根，则实数a的范畴是________.解析当x0时，01，因此由图象可知要使方程f(x)-a=0有两个实根，即f(x)=a有两个交点，因此由图象可知0答案(0,1].已知函数f(x)=.(1)画出f(x)的草图;(2)指出f(x)的单调区间.解(1)f(x)==1-，函数f(x)的图象是由反比例函数y=-的图象向左平移1个单位后，再向上平移1个单位得到，图象如图所示.(2)由图象能够看出，函数f(x)的单调递增区间为(-，-1)，(-1，+).1.设函数f(x)=x+的图象为C1，C1关于点A(2,1)对称的图象为C2，C2对应的函数为g(x).(1)求g(x)的解析式;(2)若直线y=m与C2只有一个交点，求m的值和交点坐标.解(1)设点P(x，y)是C2上的任意一点，则P(x，y)关于点A(2,1)对称的点为P(4-x,2-y)，代入f(x)=x+，可得2-y=4-x+，即y=x-2+，g(x)=x-2+.(2)由消去y得x2-(m+6)x+4m+9=0，= [-(m+6)]2-4(4m+9)，直线y=m与C2只有一个交点，=0，解得m=0或m=4.当m=0时，经检验合理，交点为(3,0);当m=4时，经检验合理，交点为(5,4)..函数f(x)是定义在[-4,4]上的偶函数，其在[0,4]上的图象如图所示，那么不等式0的解集为().A.B.C.D.{x|-1解析当x(0,1)时，cos x0，f(x)当x时，cos x0，f(x)当x时，cos x0，f(x)0，当x(-1,0)时，cos x0，f(x)当x时，cos x0，f(x)当x时，cos x0，f(x)0.故不等式0的解集为.答案C4.已知函数f(x)=|x2-4x+3|.若关于x的方程f(x)-a=x至少有三个不相等的实数根，求实数a的取值范畴.解f(x)=作出图象如图所示.原方程变形为|x2-4x+3|=x+a.因此，设y=x+a，在同一坐标系下再作出y=x+a的图象.如图.则当直线y=x+a过点(1,0)时a=-1;当直线y=x+a与抛物线y=-x2+4x-3相切时，由x2-3x+a+3=0.与当今“教师”一称最接近的“老师”概念，最早也要追溯至宋元时期。

函数y ＝Asin （ωx ＋φ）的图象及应用课时作业1．(2019·河南周口二模)将函数y ＝sin ⎝ ⎛⎭⎪⎫x ＋π6的图象上所有的点向左平移π4个单位长度，再把图象上各点的横坐标扩大到原来的2倍(纵坐标不变)，则所得图象的解析式为( )A ．y ＝sin ⎝⎛⎭⎪⎫2x ＋5π12B ．y ＝sin ⎝ ⎛⎭⎪⎫x 2＋5π12C ．y ＝sin ⎝ ⎛⎭⎪⎫x 2－π12 D ．y ＝sin ⎝ ⎛⎭⎪⎫x 2＋5π24 答案 B解析 将函数y ＝sin ⎝⎛⎭⎪⎫x ＋π6的图象上所有的点向左平移π4个单位长度，可得y ＝sin ⎝ ⎛⎭⎪⎫x ＋π4＋π6＝sin ⎝ ⎛⎭⎪⎫x ＋5π12的图象，再把所得图象上各点的横坐标扩大到原来的2倍(纵坐标不变)，可得y ＝sin ⎝ ⎛⎭⎪⎫12x ＋5π12的图象，故选B.2．如图所示，函数y ＝3tan ⎝ ⎛⎭⎪⎫2x ＋π6的部分图象与坐标轴分别交于点D ，E ，F ，则△DEF的面积为( )A.π4B ．π2C ．πD ．2π答案 A解析 在y ＝3tan ⎝ ⎛⎭⎪⎫2x ＋π6中，令x ＝0可得D (0,1)；令y ＝0解得x ＝k π2－π12(k ∈Z )，故E ⎝ ⎛⎭⎪⎫－π12，0，F ⎝ ⎛⎭⎪⎫5π12，0.所以△DEF 的面积为12×π2×1＝π4.3．已知ω＞0,0＜φ＜π，直线x ＝π4和x ＝5π4是函数f (x )＝sin(ωx ＋φ)图象的两条相邻的对称轴，则φ＝( )A.π4 B ．π3C.π2D ．3π4答案 A解析 由题意得周期T ＝2⎝⎛⎭⎪⎫5π4－π4＝2π，∴2π＝2πω，即ω＝1，∴f (x )＝sin(x ＋φ)，∴f ⎝ ⎛⎭⎪⎫π4＝sin ⎝ ⎛⎭⎪⎫π4＋φ＝±1.∵0＜φ＜π，∴π4＜φ＋π4＜5π4，∴φ＋π4＝π2， ∴φ＝π4.4．(2019·山东青岛模拟)将函数y ＝sin(2x ＋φ)的图象沿x 轴向左平移π8个单位后，得到一个偶函数的图象，则φ的一个可能取值为( )A.3π4B ．π4C ．0D ．－π4答案 B解析 把函数y ＝sin(2x ＋φ)的图象向左平移π8个单位后，得到的图象的解析式是y ＝sin ⎝ ⎛⎭⎪⎫2x ＋π4＋φ，该函数是偶函数的充要条件是π4＋φ＝k π＋π2，k ∈Z ，根据选项检验可知φ的一个可能取值为π4.5．如图是周期为2π的三角函数y ＝f (x ) 的图象，那么f (x )可以写成( )A ．sin(1＋x )B ．sin(－1－x )C ．sin(x －1)D ．sin(1－x ) 答案 D解析 设y ＝sin(x ＋φ)，∵点(1,0)为五点法作图的第三点，∴sin(1＋φ)＝0⇒1＋φ＝π，φ＝π－1，∴y ＝sin(x ＋φ)＝sin(1－x )．6．如图所示，为了研究钟表与三角函数的关系，建立如图所示的坐标系，设秒针针尖位置P (x ，y )．若初始位置为P 0⎝⎛⎭⎪⎫32，12，当秒针从P 0(注：此时t ＝0)正常开始走时，那么点P 的纵坐标y 与时间t 的函数关系为( )A ．y ＝sin ⎝⎛⎭⎪⎫π30t ＋π6B ．y ＝sin ⎝ ⎛⎭⎪⎫－π60t －π6C ．y ＝sin ⎝ ⎛⎭⎪⎫－π30t ＋π6D ．y ＝sin ⎝ ⎛⎭⎪⎫－π30t －π3答案 C解析 由题意可得，函数的初相位是π6，排除B ，D.又函数周期是60秒且秒针按顺时针方向旋转，即T ＝2π|ω|＝60，所以|ω|＝π30，所以ω＝－π30，故y ＝sin ⎝ ⎛⎭⎪⎫－π30t ＋π6.7．已知函数f (x )＝2sin ⎝⎛⎭⎪⎫ωx －π6(ω>0)的部分图象如图所示，则ω的值可能为( )A ．1B ．2C ．3D ．4答案 B解析 由图可知T 4<π3，∴T <4π3，∴ω＝2πT >32，把⎝ ⎛⎭⎪⎫π3，2代入函数表达式得2sin ⎝ ⎛⎭⎪⎫π3ω－π6＝2，∴π3ω－π6＝2k π＋π2(k ∈Z )，解得ω＝6k ＋2(k ∈Z )．故选B.8．已知函数f (x )＝A sin(ωx ＋φ)(A ，ω，φ均为正常数)的最小正周期为π，当x ＝2π3时，函数f (x )取得最小值，则下列结论正确的是( )A ．f (2)<f (－2)<f (0)B ．f (0)<f (2)<f (－2)C ．f (－2)<f (0)<f (2)D ．f (2)<f (0)<f (－2)答案 A解析 由题意知函数在⎣⎢⎡⎦⎥⎤2π3－π2，2π3，即⎣⎢⎡⎦⎥⎤π6，2π3上单调递减．f (－2)＝f (π－2)，f (0)＝f ⎝ ⎛⎭⎪⎫π3，而π3<π－2<2，且π3，π－2,2∈⎣⎢⎡⎦⎥⎤π6，2π3，所以f ⎝ ⎛⎭⎪⎫π3>f (π－2)>f (2)，即f (0)>f (－2)>f (2)．故选A.9．(2019·昆明质检)已知函数f (x )＝sin ⎝ ⎛⎭⎪⎫ωx ＋π6(0＜ω＜2)满足条件：f ⎝ ⎛⎭⎪⎫－12＝0，为了得到函数y ＝f (x )的图象，可将函数g (x )＝cos ωx 的图象向右平移m (m ＞0)个单位长度，则m 的最小值为( )A ．1B ．12 C.π6D ．π2答案 A解析 由题意，得sin ⎝ ⎛⎭⎪⎫－12ω＋π6＝0，即－12ω＋π6＝k π(k ∈Z )，则ω＝π3－2k π(k∈Z )，结合0＜ω＜2，得ω＝π3，所以f (x )＝sin ⎝ ⎛⎭⎪⎫π3x ＋π6＝cos ⎝ ⎛⎭⎪⎫π2－π3x －π6＝cos ⎣⎢⎡⎦⎥⎤π3(x －1)，所以只需将函数g (x )＝cos π3x 的图象向右至少平移1个单位长度，即可得到函数y ＝f (x )的图象，故选A.10．将函数f (x )＝sin(2x ＋φ)⎝⎛⎭⎪⎫|φ|<π2的图象向左平移π6个单位长度后关于原点对称，则函数f (x )在⎣⎢⎡⎦⎥⎤0，π2上的最小值为( )A ．－32B ．－12C.12 D ．32答案 A解析 将函数f (x )＝sin(2x ＋φ)的图象向左平移π6个单位长度后，得到f (x )＝sin ⎝ ⎛⎭⎪⎫2x ＋π3＋φ的图象．再根据所得图象关于原点对称，可得π3＋φ＝k π(k ∈Z )，所以φ＝k π－π3(k ∈Z )．又|φ|<π2，所以φ＝－π3，所以f (x )＝sin ⎝ ⎛⎭⎪⎫2x －π3，因为x ∈⎣⎢⎡⎦⎥⎤0，π2，所以2x －π3∈⎣⎢⎡⎦⎥⎤－π3，2π3.当2x －π3＝－π3时，f (x )取得最小值，为－32.11．(2019·全国卷Ⅲ)设函数f (x )＝sin ⎝ ⎛⎭⎪⎫ωx ＋π5(ω>0)，已知f (x )在[0,2π]有且仅有5个零点，下述四个结论：①f (x )在(0,2π)有且仅有3个极大值点； ②f (x )在(0,2π)有且仅有2个极小值点；③f (x )在⎝ ⎛⎭⎪⎫0，π10单调递增；④ ω的取值范围是⎣⎢⎡⎭⎪⎫125，2910.其中所有正确结论的编号是( ) A ．①④ B ．②③ C ．①②③ D ．①③④答案 D解析已知f (x )＝sin ⎝ ⎛⎭⎪⎫ωx ＋π5(ω>0)在[0,2π]有且仅有5个零点，如图，其图象的右端点的横坐标在[a ，b )上，此时f (x )在(0,2π)有且仅有3个极大值点，但f (x )在(0,2π)可能有2或3个极小值点，所以①正确，②不正确；当x ∈[0,2π]时，ωx ＋π5∈⎣⎢⎡⎦⎥⎤π5，2πω＋π5，由f (x )在[0,2π]有且仅有5个零点可得5π≤2πω＋π5<6π，得ω的取值范围是⎣⎢⎡⎭⎪⎫125，2910，所以④正确；当x ∈⎝ ⎛⎭⎪⎫0，π10时，π5<ωx ＋π5<πω10＋π5<49π100<π2，所以f (x )在⎝ ⎛⎭⎪⎫0，π10单调递增，所以③正确．故选D.12．将函数f (x )＝sin2x 的图象向右平移φ⎝ ⎛⎭⎪⎫0＜φ＜π2个单位后得到函数g (x )的图象．若对满足|f (x 1)－g (x 2)|＝2的x 1，x 2，有|x 1－x 2|min ＝π3，则φ＝( )A.5π12 B ．π3C.π4D ．π6答案 D解析 由已知得g (x )＝sin(2x －2φ)，满足|f (x 1)－g (x 2)|＝2，不妨设此时y ＝f (x )和y ＝g (x )分别取得最大值与最小值，又|x 1－x 2|min ＝π3，令2x 1＝π2，2x 2－2φ＝－π2，此时|x 1－x 2|＝|π2－φ|＝π3，又0＜φ＜π2，故φ＝π6.选D.13．(2020·北京海淀模拟)去年某地的月平均气温y (℃)与月份x (月)近似地满足函数y＝a ＋b sin ⎝ ⎛⎭⎪⎫π6x ＋π6(a ，b 为常数)．若6月份的月平均气温约为22 ℃，12月份的月平均气温约为4 ℃，则该地8月份的月平均气温约为________℃.答案 31解析 将(6,22)，(12,4)代入函数，解得a ＝13，b ＝－18，所以y ＝13－18sin ⎝ ⎛⎭⎪⎫π6x ＋π6.当x ＝8时，y ＝13－18sin ⎝ ⎛⎭⎪⎫π6×8＋π6＝31.14．已知函数y ＝sin(ωx ＋φ)(ω>0，－π≤φ<π)的图象如图所示，则φ＝________.答案9π10解析 由题图可知ω＝45，当x ＝2π时，y ＝1，∴45×2π＋φ＝π2＋2k π，k ∈Z . ∵－π≤φ<π，∴φ＝9π10.15．(2019·厦门模拟)已知x ∈(0，π]，关于x 的方程2sin ⎝⎛⎭⎪⎫x ＋π3＝a 有两个不同的实数解，则实数a 的取值范围为________．答案 (3，2)解析 令y 1＝2sin ⎝⎛⎭⎪⎫x ＋π3，x ∈(0，π]，y 2＝a ，作出y 1的图象如图所示．若2sin ⎝⎛⎭⎪⎫x ＋π3＝a 在(0，π]上有两个不同的实数解，则y 1与y 2的图象应有两个不同的交点，所以3<a <2.16．(2019·临沂模拟)已知函数f (x )＝A cos(ωx ＋φ)的图象如图所示，f ⎝ ⎛⎭⎪⎫π2＝－23，则f ⎝ ⎛⎭⎪⎫－π6＝________. 答案 －23解析 由题图知T 2＝11π12－7π12＝π3，∴T ＝2π3，即ω＝3，当x ＝7π12时，f (x )＝0，即3×7π12＋φ＝2k π－π2，k ∈Z ，∴φ＝2k π－9π4，k ∈Z ，取k ＝1，则φ＝－π4，∴f (x )＝A cos ⎝ ⎛⎭⎪⎫3x －π4. ∵f ⎝ ⎛⎭⎪⎫π2＝－23，∴A cos ⎝⎛⎭⎪⎫3π2－π4＝－23，解得A ＝223，∴f (x )＝223cos ⎝⎛⎭⎪⎫3x －π4，故f ⎝ ⎛⎭⎪⎫－π6＝223cos ⎝ ⎛⎭⎪⎫－π2－π4＝－23.17．如图，某地一天6～14时的温度变化曲线近似满足y ＝A sin(ωt ＋φ)＋b (A >0，ω>0,0<φ<π)．(1)求解析式；(2)若某行业在当地需要的温度在区间[20－52，20＋52]之间为最佳营业时间，那么该行业在6～14时，最佳营业时间为多少小时？解 (1)由题图知A ＝10，12·2πω＝14－6，所以ω＝π8，所以y ＝10sin ⎝⎛⎭⎪⎫πt 8＋φ＋b .①因为y max ＝10＋b ＝30，所以b ＝20. 把t ＝6，y ＝10代入①得φ＝3π4，所以解析式为y ＝10sin ⎝ ⎛⎭⎪⎫π8t ＋3π4＋20，t ∈[6,14]．(2)由题意，得20－52≤10sin ⎝ ⎛⎭⎪⎫π8t ＋3π4＋20≤20＋52， 即－22≤sin ⎝ ⎛⎭⎪⎫π8t ＋3π4≤22， 所以k π－π4≤π8t ＋3π4≤k π＋π4，k ∈Z .即8k －8≤t ≤8k －4，因为t ∈[6,14]，所以k ＝2，所以8≤t ≤12， 所以最佳营业时间为12－8＝4小时．18．已知函数f (x )＝3sin(ωx ＋φ)⎝ ⎛⎭⎪⎫ω＞0，－π2≤φ＜π2的图象关于直线x ＝π3对称，且图象上相邻两个最高点的距离为π.(1)求ω和φ的值；(2)当x ∈⎣⎢⎡⎦⎥⎤0，π2时，求函数y ＝f (x )的最大值和最小值．解 (1)因为f (x )的图象上相邻两个最高点的距离为π，所以f (x )的最小正周期T ＝π，从而ω＝2πT＝2.又f (x )的图象关于直线x ＝π3对称， 所以2×π3＋φ＝k π＋π2，k ∈Z ，由－π2≤φ＜π2得k ＝0，所以φ＝π2－2π3＝－π6.综上，ω＝2，φ＝－π6.(2)由(1)知f (x )＝3sin ⎝ ⎛⎭⎪⎫2x －π6， 当x ∈⎣⎢⎡⎦⎥⎤0，π2时，－π6≤2x －π6≤5π6，∴当2x －π6＝π2，即x ＝π3时，f (x )最大＝3；当2x －π6＝－π6，即x ＝0时，f (x )最小＝－32.19．已知某海滨浴场海浪的高度y (m)是时间t (0≤t ≤24，单位：h)的函数，记作：y ＝f (t )，下表是某日各时的浪高数据：(1)根据以上数据，求函数y ＝A cos ωt ＋b 的最小正周期T ，振幅A 及函数表达式； (2)依据规定，当海浪高度高于1.25 m 时才对冲浪爱好者开放，请依据(1)的结论，判断一天内有多长时间可供冲浪者进行运动．解 (1)由题意，知T ＝12，所以ω＝2πT ＝2π12＝π6.由t ＝0，y ＝1.5得A ＋b ＝1.5；由t ＝3，y ＝1.0得b ＝1.0，所以A ＝0.5，所以y ＝12cosπ6t ＋1，t ∈[0,24]．(2)由题意，知，当y >1.25时才可对冲浪者开放， 所以12cos π6t ＋1>1.25，cos π6t >12.所以2k π－π3<π6t <2k π＋π3，k ∈Z ，即12k －2<t <12k ＋2，k ∈Z .①因为0≤t ≤24，故可令①中k 分别为0,1,2， 得0≤t <2或10<t <14或22<t ≤24.所以有8个小时的时间可供冲浪者进行运动．20．(2019·湖北襄阳模拟)某同学用“五点法”画函数f (x )＝A sin(ωx ＋φ)⎝⎛⎭⎪⎫ω>0，|φ|<π2在某一个周期内的图象时，列表并填入了部分数据，如下表：(1)请将上表数据补充完整，并直接写出函数f (x )的解析式；(2)将y ＝f (x )图象上所有点向左平移θ(θ>0)个单位长度，得到y ＝g (x )的图象．若y ＝g (x )图象的一个对称中心为⎝⎛⎭⎪⎫5π12，0，求θ的最小值．解 (1)根据表中已知数据，解得A ＝5，ω＝2，φ＝－π6.数据补全如下表：且函数表达式为f (x )＝5sin ⎝ ⎛⎭⎪⎫2x －6. (2)由(1)知f (x )＝5sin ⎝ ⎛⎭⎪⎫2x －π6， 得g (x )＝5sin ⎝⎛⎭⎪⎫2x ＋2θ－π6.因为函数y ＝sin x 图象的对称中心为(k π，0)，k ∈Z .令2x ＋2θ－π6＝k π，k ∈Z ，解得x ＝k π2＋π12－θ，k ∈Z . 由于函数y ＝g (x )的图象关于点⎝ ⎛⎭⎪⎫5π12，0成中心对称，令k π2＋π12－θ＝5π12，k ∈Z ，解得θ＝k π2－π3，k ∈Z . 由θ>0可知，当k ＝1时，θ取得最小值π6.。