当前位置：文档之家 › 准双曲面齿轮参数化计算程序

准双曲面齿轮参数化计算程序

  • 格式：pdf
  • 大小：810.22 KB
  • 文档页数：4

下载文档原格式

  / 4

合集下载

基于Excel、Matlab与UG的准双曲面齿轮精确建模研究

基于Excel、Matlab与UG的准双曲面齿轮精确建模研究

基于Excel、Matlab与UG的准双曲面齿轮精确建模研究准双曲面齿轮是一种特殊的齿轮，在机械传动领域中广泛使用。

准双曲面齿轮的特点是具有精确的啮合性能、传动能力强等优点。

因此，如何精确地建模准双曲面齿轮对于机械设计非常重要。

本文将介绍使用Excel、Matlab和UG软件进行准双曲面齿轮精确建模的研究。

首先，我们在Excel中建立了准双曲面齿轮的基本几何参数模型，包括齿轮的模数、齿数、压力角、齿宽等参数。

然后，通过Matlab编写程序，利用几何算法生成齿面曲线。

在程序中，我们使用了双曲线函数来描述准双曲面齿轮的齿面曲线。

通过调整参数，可以得到精确的齿面曲线。

接下来，我们将生成的齿轮齿面曲线导入到UG软件中进行建模。

首先，我们生成一个旋转体，即齿轮的基本体形。

然后，在基本体形上使用齿轮齿面曲线进行网格划分，从而得到具有精确齿形的齿轮模型。

通过使用Excel、Matlab和UG软件进行准双曲面齿轮精确建模，我们成功地解决了传统建模方法中难以精确建模的问题。

这种方法具有如下优点：1. 精度高。

利用双曲线函数生成齿面曲线，可以得到精确的齿形。

通过将齿面曲线导入到UG软件中，可以获得具有高精度的齿轮模型。

2. 灵活性好。

齿轮的基本几何参数模型可以根据需求灵活调整。

齿面曲线也可以通过调整参数进行优化，得到更加精确的齿形。

3. 使用方便。

本方案基于Excel、Matlab和UG软件，这些软件都是非常常用的工具。

因此，使用本方案进行准双曲面齿轮建模相对于其他方法更加容易上手。

综上所述，通过Excel、Matlab和UG软件进行准双曲面齿轮精确建模，可以得到具有高精度、灵活性好和使用方便等优点的齿轮模型。

这种方法可以被广泛应用于机械设计和制造领域。

数据分析是对已有数据进行收集、处理、分析、解释、推断以及展示等一系列过程的总称，是在统计学和数据挖掘等领域中常用的方法。

在现代社会，各行各业都需要利用数据分析来支持决策和管理。

齿轮的参数化建模操作实例

齿轮的参数化建模操作实例


主要参数：
可在模型中编辑局部参数。例如，在系统中 定义的尺寸参数。
2.外部参数：在当前模型外面创建的并 用于控制模型某些方面的参数。不能在模型 中修改外部参数。例如，可在“布局”模式 下添加参数以定义某个零件的尺寸。
1.局部参数：当前模型中创建的参数。
3.用户定义参数：可连接几何的其它信息。 可将用户定义的参数添加到组件、零件、特 征或图元。例如，可为组件中的每个零件创 建 COST 参数。然后，可将 COST 参数包括 在“材料清单”中以计算组件的总成本。 4.系统参数：由系统定义的参数，例如， “质量属性”参数。这些参数通常是只读的。 可在关系中使用它们，但不能控制它们的值。 5.注释元素参数：为“注释元素”定义的 参数。
步骤八：镜像渐开线 步骤九：创建实体特征
采用拉伸的方式创建该实体，将拉伸的高度与齿宽B关联起来。
镜像的渐开线
步骤十：倒角ห้องสมุดไป่ตู้
拉伸的实体特征
在圆柱体的上下边棱处创建1.5× 45º 的倒角
步骤十一：创建单个齿槽
通过去材料的方式创建一个齿槽。
步骤十二：阵列齿槽
齿槽轮廓
创建的单个齿槽
通过轴阵列的方式创建其它齿，并将齿 轮的齿数与参数Z通过关系式联系起来。
2.关系式中使用的数学函数
3．关系式中使用的运算符
4. 关系式错误的检查与修改
执行对话框中的【实用工具】→【校验】菜 单击 （校核）按钮，系统会自动检查 单命令或 关系式的有效性，如果发现错误，则提示出错， 编辑区错误的关系式下方打上标记。 并在显示 常见的错误类型有： 1）横列超过80个字符。此时应应用反斜线“\” 把其分成两行。 2）参数名称超过31个字符。 3）语法错误，出现没有定义的参数或函数。
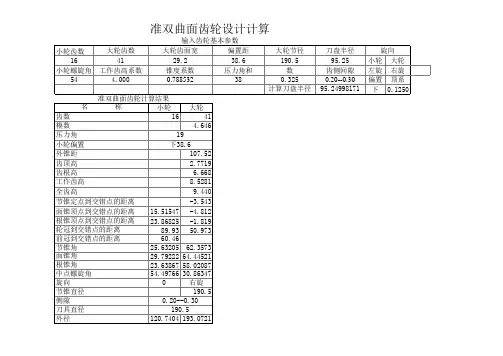
准双曲面齿轮设计计算

准双曲面齿轮设计计算


19 下38.6 107.52 2.7719 6.668 8.5281 9.440 -3.543 15.51547 -4.812 23.86825 -1.819 89.93 50.973 60.46 25.63205 62.3573 29.79222 64.44521 23.63867 58.02087 54.49766 30.86347 0 右旋 190.5 0.20--0.30 190.5 120.7404 193.0721
准双曲面齿轮设计计算
小轮齿数 16 小轮螺旋角 54 大轮齿数 41 工作齿高系数 4.000 输入齿轮基本参数 大轮齿面宽 偏置距 29.2 38.6 锥度系数 压力角和 0.788532 38 大轮节径 刀盘半径 190.5 95.25 大轮齿顶高系数 齿侧间隙 0.325 0.20--0.30 计算刀盘半径 95.24998171 旋向 小轮 大轮 左旋 右旋 偏置双曲面齿轮计算结果 称 小轮 16
大轮 41 4.646
齿数 模数 压力角 小轮偏置 外锥距 齿顶高 齿根高 工作齿高 全齿高 节锥定点到交错点的距离 面锥顶点到交错点的距离 根锥顶点到交错点的距离 轮冠到交错点的距离 前冠到交错点的距离 节锥角 面锥角 根锥角 中点螺旋角 旋向 节锥直径 侧隙 刀具直径 外径
驱动桥准双曲面齿轮的建模与分析

驱动桥准双曲面齿轮的建模与分析


XF
, X1
2
准双曲面齿轮的实体模型
鉴于准双曲面齿轮齿面形状的复杂性，本文决定
[5]
αP
rC 1
Yt1 YP
OP sP θP ZP Z t1 X t1
XP
研究了在安装误 差下准双曲面齿轮的啮合性能，
比较了直齿锥齿轮和准双曲面齿轮对安装误差的敏感 性，文献 [6] 研究了接触区偏移对螺旋锥齿轮齿根弯曲 强度的影响，得出不同工况对接触区的要求。 综合上述考虑，本文决定从齿轮副的建模和有限 元分析两个方面入手，建立该齿轮的精确的数学模型 和实体模型，比较在具有安装误差情况下，大端接触、 小端接触和中点接触三个不同接触区的应力状态以及 发生边缘接触时的载荷，提高齿轮传动可靠性。
准双曲面齿轮能够传递两相交轴或交错轴之间的 运动和动力，具有重合度大、承载能力高、传动平稳等 优点，广泛应用于车辆和工程机械的驱动桥传动中
[1,2]
面方程，过程如下 ： 图 1 是小轮的刀盘坐标系，在刀盘坐标系 SP 中，
。 表示刀盘的切削面方程和法线方程如下 ：
准双曲面齿轮具有非常复杂的齿面形状，无法实 现直接建模和参数化建模 ；在加工方面，国内外普遍 采用 HFT(hypoid gear formate tilt)[3] 法，这种方法较 为成熟，目前，国外学者提出一种新的加工方法—全 工序法 [4]，但该方法尚处于研究阶段，对加工机床的 要求过高，需要对机床加以改造 ； 准双曲面齿轮作为驱 动桥的主要部件，其接触强度和弯曲强度对齿轮的使 用寿命和可靠性具有重要意义 ；安装误差对齿轮副的 接触路径以及传动性能具有很大的影响，鉴于此，文 献
式中 ： rc1 —刀尖半径 ；
（2）
H FT 法加工，大轮的数学模型较为简单，具体可参照 文献 ，鉴于篇幅，本文以左旋小轮为例，推导其齿
准双曲面齿轮的设计 ppt

准双曲面齿轮的设计 ppt


准双曲面齿轮
弧齿锥齿轮
图 2.1 准双曲面齿轮与弧齿锥齿轮对比
同等条件下准双曲面小轮比弧齿锥齿轮小 轮大得多。
2. 准双曲面齿轮概述
优点： 优点： 3) 比弧齿锥齿轮传动的重叠系数更大，传 动更加平稳，而且齿面所受的正压力小。 4) 轴线位置的偏置，使传动在空间的布置 具有了更大的自由度。如下偏可以用于降 低汽车的重心增加平稳性；也可以用来增 加车身的高度，增加汽车的越野性。
小 相 等 、符 号 相 反 。为 了 使 极 限 曲 率 半 径 符 合 标 准 刀 盘 尺 寸 ，可 以 改 变 原 设 的 大 轮 偏 置 角 ε值 。
5.准双曲面齿轮的设计过程
• 如果螺旋角不满足要求，通过改变r1 如果螺旋角不满足要求，通过改变r 来满足 • 如果极限曲率半径不符合标准刀盘 尺寸，通过改变小轮轴截面偏置角η 尺寸，通过改变小轮轴截面偏置角η 来满足 • 过程通常由计算机叠代完成
cos β 2 R1 sin δ 1 z2 r1 z2 = × = × cos β1 R2 sin δ 2 z1 r2 z1
r1 、r2 确定之后，不同的螺 旋角可以适应不同的传动比, 因此对于给定的传动比准双 曲面齿轮的节锥并不唯一， 轮齿法线可以在任意方向垂 直于轮齿切线，因此压力角 可以自由选取。
E tgη1 = ' ' r2 (tgδ2 sinΣ + cosΣ) + r1
给定大轮刀盘半径 r0=d2/(2sinδ2’)
三.准双曲面齿轮的初始参数的选取
•齿坯设计需输入的初始参数
1. 齿数的选取
• 对于准双曲面齿轮，虽然齿数可任意选定，但在一 般情况下，小轮的齿数不得小于5，小轮与大轮的 齿数和应不小于40，且大轮齿数应与小轮齿数之间 避免有公约数。表2.1为格里森推荐的不同传动比 下小轮的最少齿数。若是设计汽车用的准双曲面齿 轮，则小轮齿数可以选得较小。对于格里森调整卡 和计算程序都作了以上限制，突破上述范围将不能 进行设计计算。也有突破以上齿数限制设计的方法， 比如“非零变位”设计，小轮齿数可小到2~3齿的。
摆线齿准双曲面齿轮模拟加工系统软件的开发

摆线齿准双曲面齿轮模拟加工系统软件的开发

《装备制造技术）２０１６年第 ０３期
摆 线齿准双 曲面齿轮模Байду номын сангаас 加工 系统软件 的开发
祁 倩
（江 门职 业 技术 学 院机 电系 ，广 东 江 门 ５２９０９０）
摘 要 ：简单介绍摆线 齿准双 曲面齿轮模 拟加 工 系统软件 的组 成、界 面设计原 则 ，详 细描述摆 线齿 准双 曲面齿轮模拟加 工 系统的界 面 内容 ，包括界 面启动、数据输入 、齿轮参数设 计、可行性检验 、强度校核 、数据结果输 出、系统帮助和提 示。利 用 摆 线 齿 准 双 曲 面 齿轮 模 拟 加 工 系统 软 件 进 行 三 维 建 模 ，通 过 观 察 刀 具 和 齿 坯 的 实体 模 型 可进 行 刀盘 干 涉 、齿 面刮 伤及 槽 底 留埂 的检 验 分 析 ，为摆 线 齿 准 双 曲 面齿 轮 的优 化 设 计 和加 工提 供 理 论 基 础 。 关 键 词 ：摆 线 齿 准 双 曲 面 齿轮 ；模 拟 加 工 系统软 件 ；三 维 建模 ；界 面设 计 ；干 涉检 验
中图分类号 ：ＴＨ１３２．４１４
文献标识码 ：Ａ
文章编号 ：１６７２—５４５Ｘ（２０１６）０３—０２２９—０４
与 弧 齿 准 双 曲 面齿 轮 相 比 ，摆 线 齿 准 双 曲 面齿 算 、强度 校 核 、铣 齿 调 整 计 算 及 数 据输 出 、齿 轮模 拟
轮 虽 与其 属 同 一 类 ，具有 相 同 的特 点 、功 能 ，但 是 摆 加 工 、系统 专 用数 据 库 等模 块 ，摆 线 齿 准 双 曲面 模 拟
线 齿 准 双 曲 面齿 轮 具 有 生 产效 率 高 、易 于干 切 屑 、啮 合性能佳等 特点 ，在航空 、车辆 工程 、重型矿 山和煤 炭 设 备 中 已得 到 广泛 应用 【ｌ＿２１。根 据铣 齿 机 和 铣 齿 刀 具 不 同 ，摆 线 齿准 双 曲面 齿 轮分 为 两 种 齿制 ：一 种 是 奥 利 康 制 ，采 用 ＣＤＳ（Ｃｏｎｔｒｏｌｌｅｄ Ｄｉｓｋ Ｓｙｓｔｅｍ）软 件 进 行 几 何 设 计 嘲；另 一 种 是 克 林 根 贝 尔 格 制 （简 称 “克 ”制 ），按 Ｋｌｉｎｇｅｌｎｂｅｒｇ公 司 的 ＫＮ３０２９标准 进 行 几 何 设计 Ｉ ６】。上述 两 种齿 制 的共 同点 是采 用 连续 分 度 双 面铣齿 法 ，同时 冠轮 齿 线为 长 幅外 摆线 。
准双曲面齿轮和螺旋锥齿轮设计的统一算法

准双曲面齿轮和螺旋锥齿轮设计的统一算法

准双曲面齿轮和螺旋锥齿轮设计的统一算法准双曲面齿轮传动是锥齿轮传动中的普遍形式，螺旋锥齿轮是它的一种特殊情况.当准双曲面齿轮的偏置距E12=0时，就成为螺旋锥齿轮传动.在外形和加工方法上，准双曲面齿轮与螺旋锥齿轮无本质区别，切齿计算方法差别也不大［1，2］.在实际设计中，它们的几何计算方法却不相同.当偏置距E12趋近于零时，现行的准双曲面齿轮的几何计算公式误差增大，甚至失效.因此螺旋锥齿轮设计的几何计算不能采用准双曲面齿轮几何计算公式和计算方法.在CAD软件开发中必须对这两种锥齿轮分别进行处理. 作者提出一种适合于准双曲面齿轮和螺旋锥齿轮设计的统一几何计算方法，其特点是当偏置距E12较大时，它与准双曲面齿轮现行计算结果一致；当偏置距E12为零时，得到正确的螺旋锥齿轮几何参数；当E12较小时，计算误差很小.因此在锥齿轮CAD软件开发中，可将这两种锥齿轮甚至包括直齿锥齿轮统一处理.1 分度锥参数基本公式准双曲面齿轮与螺旋锥齿轮几何计算中最大的区别在于分度锥参数的确定方法.分析现行准双曲面齿轮几何计算公式可知，当偏置距E12趋近于零时，齿轮的偏置角η，ε，ε′也趋近于零，因而导致公式计算误差增大甚至失效.作者在分析过程中发现，虽然E12趋近于零时，齿轮的偏置角η，ε，ε′也趋近于零，但它们属于同阶无穷小.即极限和存在.令式中e1和e2为偏置角系数.根据偏置角系数，可给出分度锥参数基本公式为式中k为放大系数；上面这组基本公式不仅适合于准双曲面齿轮，也适合于螺旋锥齿轮，不会因E12=0而失效.2 分度锥参数的求解上面给出的基本公式是一组非线性方程组，其中有5个参数是在几何计算前确定的.根据传动和强度等要求先确定齿轮的偏置距E12，轴交角ζ=90°-Σ，齿轮齿数z1和z2，大齿轮中点端面模数mt2，小齿轮中点螺旋角β1.则上面基本公式中的已知参数为i12=z2/z1, r2=mt2z2/2,及E12，ζ，β1. 由于基本公式是非线性方程组，在此采用迭代法求解.即初选k和e1值，按下面步骤进行迭代：若｜k*-k｜≤ξ(由计算精度确定的某一小量)，则可进行下面的迭代；否则改变k初值重新迭代.式中rc为刀盘半径. 若｜k0-kc｜＞ξ，则改变e1初值重新迭代，直到｜k0-kc｜≤ξ为止.迭代完毕，便得到了所有的分度锥参数.然后根据齿宽、齿高系数、变位系数和齿根倾斜类型，按准双曲面齿轮的方法进行其它所有几何尺寸参数的计算.3 算例作者采用上面的统一公式和算法分别对准双曲面齿轮和螺旋锥齿轮两种情况进行了大量的计算分析.表1是偏置距E12=0的螺旋锥齿轮算例结果；表2是偏置距E12=30mm的准双曲面齿轮算例结果.大量的计算分析结果表明：当E12=0时，上面方法所确定的分度锥参数与现行螺旋锥齿轮几何计算结果一致；当E12≠0时，上面方法与现行准双曲面齿轮几何计算结果一致；特别是当E12非常小时，本方法所得结果比较精确.因此，可用上面方法将这两种锥齿轮的几何计算方法统一起来.这对CAD软件开发特别有利.表1 螺旋锥齿轮参数表2 准双曲面齿轮参数4 统一设计中的问题现行准双曲面齿轮和螺旋锥齿轮的标准参数，如模数、齿高系数、变位系数等都定义在大端.这对准双曲面齿轮会导致理论啮合节点偏离齿宽中点而与螺旋锥齿轮不同.因此建议将标准参数定义在齿宽中点，这样也可以与强度计算方法一致［3］.此外，现行准双曲面齿轮标准参数中的螺旋角是小齿轮螺旋角，而标准参数中的模数是大齿轮端面模数.建议标准参数取大齿轮螺旋角和法向模数，这样更合理.5 结论大量算例和实际应用表明，作者提出的几何计算方法是可行的.作者已经根据此原理开发了CAD应用软件，并用于实际设计中.这样就使准双曲面齿轮和螺旋锥齿轮甚至直齿锥齿轮设计中的几何计算方法的统一有了依据.结果也在一定程度上揭示了准双曲面齿轮和螺旋锥齿轮理论上的本质联系.对锥齿轮的标准化、系列化和CAD技术也有一定的意义.。

准双曲面齿轮的加工

准双曲面齿轮的加工

• 大轮轮坯旋转后，大轮轴线与机床平面之间的 夹角，即根锥角将发生变化；螺旋角切线方向 e1与水平方向的夹角，即螺旋角也将发生变化。
13
二.成形法加工大轮
14
二.成形法加工大轮
成形法加工大轮的基本数据： • 轮坯安装角dM2 • 轴向轮位修正值X2 • 水平刀位 H • 垂直刀位V *刀盘两侧齿形角也可取不同的值，但之和
1. 大轮成形法基本数据：
• 轮坯安装角： 66.85104（根锥角 67.839099）
• 垂直刀位：
103.21999
• 水平刀位：
60.13623
• 轴向轮位修正值：3.4682 （0.413569）
• 机床:
No.609
• 线性量规A:186.90455
• 线性量规B:395.31999
• 线性量规C:79.41406
27
三.刀倾法加工小轮
5.机床刀倾角（I）—影响被切齿面的压力角 6.机床刀转角（J）—影响到摇台角调整，在接触区修正
时，代替摇台角来适应偏心角的改变。
i
sin I x
sin 2
2 sin150
J
2
1800 左旋 j 00 右旋
28
三.刀倾法加工小轮
7.水平轮位X1 —或称轴向轮位修正量，是指摇台中心到 工件箱主轴断面的距离，其中X1还要考虑工件的夹具 尺寸和小轮的安装距，三者之和即为机床实际的水平 轮位。可修正被切齿轮的压力角。
必须等于2倍的平均压力角。
15
二.成形法加工大轮
No.609拉齿机调整示意图
16
1.什么是传统机械按键设计？
传统的机械按键设计是需要手动按压按键触动PCBA上的 开关按键来实现功能的一种设计方式。
基于Excel_Matlab与UG的准双曲面齿轮精确建模研究_王红芳

基于Excel_Matlab与UG的准双曲面齿轮精确建模研究_王红芳

PreciseModelingStudyofHypoidGearsBasedonMatlab, ExcelandUG
WANG Hongfang Abstract:ThisarticlefirstexactlydesignsthehypoidgeargeometryparametersbyusingtheExcelspreadsheet, thenestablishesthe toothprofileequationafteranalyzingthemathematicalmodelofhypoidgeartoothprofilesection.Atlast, bytheapplicationofthenumerical computingofMatlab, inaccordingtotheequationgeartoothprofile, obtainsthecoordinatesofdiscretepoints.discrerethepointsintothedata fileofUGenvironment, completesthetoothsurfaceandhypoidgearsofthethree-demensionalsolidmodelingbyusingthepowerfulsurfaceand solidmodelingcapabilitiesofUG. Keywords:hypoidgear;toothprofileequation;UG;MatlabExcel
面的任一径向直线与瞬时回转轴之间的夹角 ;ε为基锥角 。
(2)大端齿顶圆弧方程
x=Rsinωαcosλα y=Rsinωαsinλα
z=Rcosωα 式中 :λα为根锥角 , 也就是矢径与 Z轴的夹角 ;ωα为矢径在 XOY平面的投影与 X轴夹角 ,通过与大端齿顶圆与齿根圆之
汽车主减速器双曲面齿轮几何尺寸C计算程序

汽车主减速器双曲面齿轮几何尺寸C计算程序

/*圆弧齿双曲面齿轮的几何尺寸计算*/#include<math.h>#include<stdio.h>#define pi 3.141592654#define PF printfmain(){double s[150];double z1=7,z2=46,f2=55,e=38,d2=322,rd=114.3,beta1=44;doubles67l,s67r,s68l,s68r,s123l,s123r,s124l,s124r,s125l,s125r,s126l,s126r;int i;double O2,Q2,Qs,TR,QTR,O2T,Q2T;PF("\n圆弧齿双曲面齿轮的几何尺寸计算\n\n");s[1]=z1;s[2]=z2; PF("主动锥齿轮齿数 z1=7 从动锥齿轮齿 z2=46\n");s[3]=s[1]/s[2];s[4]=43.4; PF("大齿轮齿面宽 F2=55\n");s[5]=28; PF("小齿轮轴线偏移距 E=38\n");s[6]=280; PF("大齿轮分度圆直径 d2=322\n");s[7]=152.4; PF("刀盘名义半径 rd=114.3\n");s[8]=beta1*pi/180; PF("小齿轮螺旋角预选值 beta1=44\n");s[9]=tan(s[8]);s[10]=1.2*s[3];s[11]=sin(atan(1/s[10]));s[12]=(s[6]-s[4]*s[11])/2.0;s[13]=s[5]*s[11]/s[12];s[14]=cos(asin(s[13]));s[15]=s[14]+s[9]*s[13];s[16]=s[3]*s[12];s[17]=s[15]*s[16];s[18]=1.300;s[19]=s[12]/s[10]+s[17];s[20]=s[5]/s[19];s[21]=sqrt(1+s[20]*s[20]);s[22]=s[20]/s[21];s[23]=asin(s[22]);s[24]=(s[5]-s[17]*s[22])/s[12];s[25]=tan(asin(s[24]));s[27]=cos(atan(s[26]));s[28]=s[24]/s[27];s[29]=cos(asin(s[28]));s[30]=(s[15]-s[29])/s[28];s[31]=s[28]*(s[9]-s[30]);s[32]=s[3]*s[31];s[33]=s[24]-s[22]*s[32];s[34]=tan(asin(s[33]));s[35]=s[22]/s[34];s[36]=atan(s[35]); PF("小齿轮节锥角 r1=%f\n",s[36]*180/pi);s[37]=cos(s[36]);s[38]=s[33]/s[37];s[39]=asin(s[38]);s[40]=cos(s[39]);s[41]=(s[15]+s[31]-s[40])/s[38];s[42]=atan(s[41]); PF("小齿轮中点螺旋角 beta1=%f\n",s[42]*180/pi);s[43]=cos(s[42]);s[44]=s[42]-s[39]; PF("大齿轮中点螺旋角 beta2=%f\n",s[44]*180/pi);s[45]=cos(s[44]);s[46]=tan(s[44]);s[47]=s[22]/s[33];s[48]=atan(1/s[47]);PF("大齿轮节锥角 r2=%f\n",s[48]*180/pi);s[49]=sin(s[48]);s[50]=cos(s[48]);s[51]=(s[17]+s[12]*s[32])/s[37];s[52]=s[12]/s[50];s[53]=s[51]+s[52];s[54]=s[12]*s[45]/s[49];s[55]=s[43]*s[51]/s[35];s[56]=(s[41]*s[55]-s[46]*s[54])/s[53];s[57]=atan(s[56]);s[58]=cos(s[57]);s[59]=s[41]*s[56]/s[51];s[60]=s[46]*s[56]/s[52];s[61]=s[54]*s[55];s[62]=(s[54]-s[55])/s[61];s[63]=s[59]+s[60]+s[62];s[64]=(s[41]-s[46])/s[63];s[65]=s[64]/s[58];s[66]=s[7]/s[65];s67r=1-s[3];s68l=s[5]/s[34]-s[17]*s[35];s68r=s[35]*s[37];s[69]=s[37]+s[40]*s67l;s[70]=s[49]*s[51];s[71]=s[12]*s[47]-s[70]; PF("大齿轮节锥顶点到小齿轮轴线的距离Z=%f\n",s[71]);s[72]=s[12]/s[49];s[73]=0.5*s[6]/s[49]; PF("大锥齿轮节距 A0=%f\n",s[73]);s[74]=s[73]-s[72];s[75]=4*s[12]*s[45]/s[2];s[76]=s[12]*s[46]/s[7];s[77]=s[49]/s[45]-s[76];s[78]=pi*42.5/180;s[79]=sin(s[78]);s[80]=s[78]/2;s[81]=cos(s[80]);s[82]=tan(s[80]);s[83]=s[77]/s[82];s[84]=10560*s[83]/s[2];s[85]=0.170;s[86]=1.150-s[85];s[87]=s[75]*s[85];s[88]=s[75]*s[86]+0.05;O2=3438*s[87]/s[72];Q2=3438*s[88]/s[72];Qs=O2+Q2;TR=s[84]/Qs-s[18];if(TR>0){QTR=s[18]*Qs/60*pi/180; PF("TR=%f 为倾根锥母线收缩齿\n",TR);} else{QTR=s[84]/60*pi/180; PF("TR=%f 为双重收缩齿\n",TR);}O2T=s[85]*QTR;Q2T=QTR-O2T;s[89]=O2T; PF("大齿轮齿顶角 O2=%f\n",s[89]*180/pi*60);s[90]=sin(s[89]);s[91]=Q2T; PF("大齿轮齿根角 Q2=%f\n",s[91]*180/pi*60);s[92]=sin(s[91]);s[93]=s[87]+s[74]*s[90]; PF("大齿轮齿顶高 hd2=%f\n",s[93]);s[94]=s[88]+s[74]*s[92]; PF("大齿轮齿根高 hg2=%f\n",s[94]);s[95]=0.15*s[75]+0.05; PF("径向间隙 C=%f\n",s[95]);s[96]=s[93]+s[94]; PF("大齿轮齿全高 h=%f\n",s[96]);s[97]=s[96]-s[95]; PF("大齿轮齿工作高 hg=%f\n",s[97]);s[98]=s[48]+s[89]; PF("大齿轮面锥角 r02=%f\n",s[98]*180/pi);s[99]=sin(s[98]);s[100]=cos(s[98]);s[101]=s[48]-s[91]; PF("大齿轮根锥角 rR2=%f\n",s[101]*180/pi); s[102]=sin(s[101]);s[103]=cos(s[101]);s[104]=1/tan(s[101]);s[105]=s[93]*s[50]/0.5+s[6]; PF("大齿轮外圆直径 do2=%f\n",s[105]);s[106]=s[70]+s[74]*s[50];s[107]=s[106]-s[93]*s[49]; PF("大齿轮外缘至小齿轮轴线的距离Xo2=%f\n",s[107]);s[108]=(s[72]*s[90]-s[87])/s[99];s[109]=(s[72]*s[92]-s[88])/s[102];s[110]=s[71]-s[108]; PF("大齿轮面锥顶点到小齿轮轴线的距离Zo=%f\n",s[110]);s[111]=s[71]+s[109]; PF("大齿轮根锥顶点到小齿轮轴线的距离ZR=%f\n",s[111]);s[112]=s[12]+s[70]*s[104];s[113]=s[5]/s[112];s[114]=sqrt(1-s[113]*s[113]);s[115]=s[113]/s[114];s[116]=s[103]*s[114];s[117]=asin(s[116]); PF("小齿轮面锥角 ro1=%f\n",s[117]*180/pi);s[118]=cos(s[117]);s[119]=tan(s[117]);s[120]=(s[102]*s[111]+s[95])/s[103];s[121]=(s[5]*s[113]-s[120])/s[114]; PF("小齿轮面锥顶点到大齿轮轴线的距离 Go=%f\n",s[121]);s[122]=s[38]*s67l/s[69];s123l=atan(s[122]);s123r=cos(s123l);s124l=s[39]-s123l;s124r=cos(s124l);s125l=s[117]-s[36];s125r=cos(s125l);s126l=s[113]*s67r-s68r;s126r=-s[113]*s67r-s68r;s[127]=s123r/s124r;s[128]=s68l+s[87]*s68r;s[129]=s[118]/s125r;s[130]=s[74]*s[127];s[131]=s[128]+s[130]*s[129]+s[75]*s126l; PF("小齿轮外缘到大齿轮轴线的距离 BR=%f\n",s[131]);s[132]=s[4]*s[127]-s[130];s[133]=s[128]-s[132]*s[129]+s[75]*s126r; PF("小齿轮前缘至大齿轮轴线的距离 B1=%f\n",s[133]);s[134]=s[121]+s[131];s[135]=s[119]*s[134]/0.5; PF("小齿轮的外圆直径 do1=%f\n",s[135]);s[136]=s[70]*s[100]/s[99]+s[12];s[137]=s[5]/s[136];s[138]=asin(s[137]);s[139]=cos(s[138]);s[140]=(s[99]*s[110]+s[95])/s[100];s[141]=(s[5]*s[137]-s[140])/s[139]; PF("小齿轮根锥顶点到大齿轮轴线的距离 GR=%f\n",s[141]);s[142]=s[100]*s[139];s[143]=asin(s[142]); PF("小齿轮根锥角 rR1=%f\n",s[143]*180/pi);s[144]=cos(s[143]);s[145]=tan(s[143]);s[146]=0.239894; PF("最小齿侧间隙允许值 Bmin=0.239894\n");s[147]=0.324936; PF("最大齿侧间隙允许值 Bmax=0.324936\n");s[148]=s[90]+s[92];s[149]=s[96]-s[4]*s[148];s[150]=s[73]-s[4];PF("计算完毕!!!\n\n");/*用来检查每个数的数值*/for(i=1;i<151;i++){PF("\ns[%d]=%f\n",i,s[i]);}PF("%f,%f,%f,%f,%f,%f,%f,%f,%f,%f,%f,%f\n",s67l,s67r,s68l,s68r,s123l,s12 3r,s124l,s124r,s125l,s125r,s126l,s126r);}。

弧齿准双曲面齿轮CAD集成系统开发

弧齿准双曲面齿轮CAD集成系统开发


文章编号 ：１７—５９（ ０ ６ ０ —０ ０ ４ ６ ３１４ ２０ ） ２０６ — ０
弧齿准双 曲面齿轮 Ｃ Ｄ集成 系统开发 Ａ
胡 莲君 ，宋 弘
（ 四川理工学院机 电工程 系，四川 自贡 ６３ ０ ） ４ ００
摘 要 ：介 绍 了运 用 ＶＣ ． Ｏｂｅｔ ”６０与 ｊｃ ＡＲＸ２ ０ ０ ０开发 弧 齿 准双 曲面 齿轮 ＣＡ 集成 系统 的过程 与 方 Ｄ
象技术实现。这样就使 Ｏ ｊ ｔＲ ２０ 二次开发的 Ａ ｔ Ａ ｂｅ Ａ Ｘ ０ ０ ｃ ｕ Ｃ Ｄ绘 ｏ
图程序与 Ｖ ” Ｃ 开发 的应用程序在同一水平上实现系统集成。 系统主要 由 ４大模块组成 ：齿轮几何设计模块 ，确定齿轮
的基本参数 和几何尺寸 ；齿轮 的强度设计模块 ，完成轮齿的弯
迫切要求加速设计 、绘 图以及切削加工计算过程 。利用 Ｏ ｊ ｔＲ ｂ ｃ Ｘ与可视化编程语言 Ｖｓａ Ｃ ＋ ．相 ｅＡ ｉ ｌ ＋６ ｕ ０ 结合 ， 所开发出的参数化设计与绘图系统可以很方便的解决这些问题并提高设计质量 ， 是齿轮制造企业
设计 人员的好帮手 。
１系统 分析 与 总体 结 构设 计
２２强度校核模块 ． 本模块利用美 国 Ａ Ｍ 强度标准及准双曲面齿轮强度校核公式对准双 曲面齿轮在特定的使用条件 Ｇ Ａ 下， 进行齿轮的接触强度和弯 曲强度的校核 ， 以保证其满足实际的使用要求。 本模块根据齿轮设计功率、
转速的大小 ，考虑 了各种使用条件 ，针对齿轮的不同材料 、精度和齿形 ，以下拉表组合框（Ｃ ｍ ｏ ｏ Ｃ ｏ ｂＢ ｘ 类） 的形式 ，让用户选择输入 ，判断强度是否符合要求。由于准双曲面齿轮强度校核公式计算复杂 ，涉 及与图表有关的系数数量多， 为了避免人工繁琐查 阅， 把它们做程序化处理 。 对简单有规律的图表直接 用多项值处理 ； 对复杂的图表 ， 则采用分段多项式插值拟合的方法 ， 用多个插值多项式代表 ， 然后把多 项式编入程序 ， 代替人工查询。 强度校核未通过时 ， 程序会给出提示重新选取有关初始参数 。 强度校核

基于ANSYS的准双曲面齿轮建模及有限元分析_马雪洁

摘 要 针对传统悬臂梁理论计算轮齿弯曲应力的不足 , 本文在 ANSYS 软件中采用 从低级到高 级的建 模方法对准双曲面齿轮进行三维实体建模 , 并对齿轮进行分析 , 收敛计 算到足够的 精确度 , 得到了满 意的结 果 。 文中采用了合理的分割方法对轮齿 进行切块 、选 用六面 体单元划 分网格 , 根 据赫兹理 论对 齿面瞬 时接 触椭圆 施加半椭球分布压力 , 分析 结果更准 确 。 该建 模方法 易于实现 参数化 建模 , 为复杂 零件 的三维 实体 建模提供了一个思路 。
假设齿轮与轴是刚性联接的 , 对齿轮安装孔 表面的节点进行零位移约束 。 不考虑齿轮的制 造误差与安装误差 。
本文采用无限体的赫兹理论来近似确定轮
齿接触区的压力接触节点的载荷 。根据弹性理 论[ 4 、5] , 两光滑 曲面接触时 , 在接触点附 近可近
似处理成两个密切抛物曲面接触 。施加载荷后 在接触点处形成一瞬时接触椭圆 , 压力按照半椭 球分布[ 6] 。 瞬时接触区形 状图见图 4 。 根据圣
接触椭圆的法向可由曲面特性求得 , 本文在
ANSYS 软件中取齿面两相邻节点坐标差得叉积
为法向 。
ANSYS 软 件中 能 施加 沿 着坐 标 轴方 向 的 力 。要在齿面法向施加载荷 , 有两种方法 :一是 创建局部坐标系 , 使其一轴沿齿面法线方向 ;另 一种方法就是计算出力沿全局坐标各轴的分量 ,
图 5 齿面节点施加负载 后的示意图
图 6 小齿轮节点变形和节点应力
7
《 重型机械科技》2004 年第 3 期
用 ANSYS 有限元分析软件分析准双曲面齿 轮 , 可以处理复杂的边界条件及多种实际工况 , 能够求得更加接近实际情况的应力场和轮齿变 形情况 。
参考文献

锥齿轮和准双曲面齿轮

锥齿轮和准双曲面齿轮锥齿轮和准双曲面齿轮锥齿轮和准双曲面齿轮术语基本尺寸参数(GB12370-90) 6基本尺寸参数6.1锥距6.1.1外锥距(锥距)分锥顶点沿分锥母线至背锥的距离。

6.1.2内锥距分锥顶点沿分锥母线至前锥的距离。

6.1.3中点锥距分低度顶点沿分锥母线至轮齿齿宽中点的距离。

6.1.4背锥距背锥顶点沿背锥母线至分锥的距离。

6.2直径6.2.1分度圆直径分度圆的直径6.2.2齿顶圆直径(顶圆直径) 齿顶圆的直径。

6.2.3齿根圆直径(根圆直径) 齿根圆的直径。

6.2.4节圆直径节圆的直径。

6.3齿高6.3.1齿离齿顶圆至齿根圆之间沿背锥母线度量的距离。

6.3.2齿顶高齿顶圆至分度圆之间沿背锥母线度量的距离。

6.3.3齿根高分度圆至齿根圆之间沿背锥母线度量的距离。

6.3.4工作高度一对锥齿轮相互啮合时，两者的齿顶圆与两背锥的公共母线各有一个交点，这两个交点之间沿上述化共母线度量的最短距离。

同义词工作齿高6.4齿距、齿厚和齿宽6.4.1齿距两个相邻的同侧齿面之间的分度圆弧长。

6.4.2齿厚一个轮齿的两侧面之间的分度圆弧长。

6.4.3弦齿厚齿厚所对的弦长。

6.4.4齿槽宽(槽宽)在锥齿轮上，一个齿槽的两侧齿面之间的分度圆弧长。

6.4.5齿宽锥齿轮的轮齿沿分锥母线度量的宽度。

6.5其他线性参数6.5.1齿线偏差量斜齿锥齿轮的产形冠轮的齿线与锥顶(或冠轮轴线)之间的距离。

6.5.2顶隙锥齿传输线的齿顶圆锥面与它的配对齿轮齿根圆锥面之间，沿着两背锥的公共母线度量的距离。

6.5.3侧隙侧隙是在工作节圆上，齿槽宽度大于相啮合轮齿齿厚的量。

6.5.4圆周侧隙在一对相啮合的锥齿轮中，固定其中一个齿轮，另一个齿轮所能转过的节圆弧长的最大值。

6.5.5法向侧隙两个锥齿轮，当其一侧齿面处于接触状态时，另一侧齿面之间在背锥上量度的最短距离。

6.6圆锥角6.6.1分度圆锥角(分锥角)锥齿轮轴线与分锥母线之间的夹角，根锥母线位于此角之内。

准双曲面齿轮运动参数和曲率特性的研究

准双曲面齿轮运动参数和曲率特性的研究赵志忠;闵晓勇;杨荣松【摘要】文中根据机床加工调整参数,推导了准双曲面齿轮的齿面数学表达式,建立了准双曲面齿轮的三维模型,并通过数值迭代方法求解了准双曲面齿轮点接触弹流润滑分析所需的相对运动速度、卷吸速度以及瞬时接触椭圆长短轴方向的曲率等参数,为准双曲面齿轮弹流润滑分析奠定了基础.【期刊名称】《机械工程师》【年(卷),期】2014(000)004【总页数】3页(P20-22)【关键词】准双曲面齿轮;三维模型;相对运动速度;卷吸速度;曲率【作者】赵志忠;闵晓勇;杨荣松【作者单位】四川大学制造科学与工程学院,成都610065;四川科技职工大学,成都610101;四川大学制造科学与工程学院,成都610065【正文语种】中文【中图分类】TP391.7准双曲面齿轮的齿面是复杂的空间曲面，其齿面形状决定于机床的加工调整参数。

我们把能够得到希望的传动误差、接触区形状及V/H调整值的机床加工调整参数作为“标准加工参数”，把由“标准加工参数”决定的齿面作为弧齿锥齿轮和准双曲面齿轮的“基准齿面”［1－2］。

为了得到准双曲面齿轮的“基准齿面”形状，需要根据机床的加工调整参数建立齿面数学模型求解齿面形状［3］。

此外，对于高质量的准双曲面齿轮在设计过程中还必须考虑润滑特性。

本研究根据机床加工调整参数，建立准双曲面齿轮的齿面数学模型，并通过数值迭代方法求解准双曲面齿轮点接触弹流润滑分析所需的相对运动速度、卷吸速度以及瞬时接触椭圆长短轴的方向的曲率等参数，为准双曲面齿轮弹流润滑分析奠定基础。

准双曲面齿轮的机床加工调整参数决定之后，其齿面形状也就随之确定了。

齿面接触分析求解过程中［1］使用齿面在固定空间坐标系的数学表达式进行求解。

为了得到齿面的形状，需要求得齿面和工件固定的坐标系中的数学表达式。

1．1 齿面加工啮合点首先以左旋齿轮作为研究对象，加工左旋齿轮的机床加工调整参数和坐标系如图1所示。

准双曲线盆齿轮加工参数的测量方法

准双曲线盆齿轮加工参数的测量方法Wang Huiwen;Sun Xiaojuan;Wang Enze;Wang Jiajie【摘要】提出了准双曲线盆齿轮加工时机床设置参数的测量方法,首先建立了刀具刃面和盆齿轮齿面的数学模型,然后利用三维坐标测量仪在准双曲线盆齿轮的齿面上进行多点测量,通过最小二乘法分析求出与坐标值相适应的准双曲线盆齿轮实际齿面机床加工参数.通过接触轨迹检测可知,利用这组实际齿面机床加工参数得到的准双曲线盆齿轮的接触轨迹和原配对接触轨迹几乎相同,证明利用该组机床加工设定参数可以在一台或多台机床上加工出与准双曲线角齿轮良好接触的准双曲线盆齿轮.这种方法基本实现了准双曲线齿轮加工互换性,也避免了准双曲线齿轮加工中反复调试的麻烦.【期刊名称】《东北林业大学学报》【年(卷),期】2018(046)012【总页数】3页(P112-114)【关键词】准双曲线盆齿轮;三维坐标测量仪;加工参数;径向滑移量;接触轨迹【作者】Wang Huiwen;Sun Xiaojuan;Wang Enze;Wang Jiajie【作者单位】【正文语种】中文【中图分类】TG61;TH161.5准双曲线齿轮可以实现交叉传动，并且啮合时的重合度较大、承载能力强，传动平稳噪声小，在汽车后桥减速器和需要传动扭矩较大的交叉传动场合广泛使用。

由于准双曲线齿面线形复杂，难以在普通齿轮加工机床上准确加工，基本使用格里森机床或数控铣床，根据齿轮齿面各点计算值编制程序进行多点加工成型。

因为缺乏精确的机构学分析，齿面各点的坐标值计算并不准确，另外由于机床定位精度、刀具加工精度和磨损等原因很难得到理想啮合状态和互换性的准双曲线齿轮。

为了提高配对齿轮的啮合面积，提高承载能力，在齿轮加工时要多次测量配对齿轮的齿面接触轨迹，适当地调整机床加工设定参数。

因此有必要研究用格里森机床加工时准双曲线齿轮齿面加工参数的确定方法。

本研究选择一个与角齿轮齿面接触最好的准双曲线盆齿轮，用三维坐标测量仪测量盆齿轮齿面坐标值，通过数据分析计算得到机床切削加工实际设置参数。

准双曲面锥齿轮传动计算

1小轮齿数Z1：6.00002大轮齿数Z2：38.00003齿数比的倒数Z1/Z2：0.4大轮齿面宽b2：62.00005偏置距E：35.00006大轮节圆直径de2：384.940007刀盘名义半径rb：152.400008初选小轮螺旋角βm1c：35.00009βm1c正切值tanβm1c：0.10初选大轮节锥角之余切值cotδ2c：0.11δ2c之正弦值sinδ2c：0.12初定大轮中点分圆半径rm2c：162.13大、小轮螺旋角差角正弦值sinΔβc：0.14Δβc之xx值cosΔβc：0.15初定小轮扩大系数Kc：1.16小轮中点分度圆半径换算值rm1H：25.17初定小轮中点分圆半径rm1c：28.18轮齿收缩系数H：1.1800019近似计算公法线K1K2在大轮轴线上的投影(截距)Q：883.20大轮轴线在小轮回转平面内偏置角正切tan纾?0.21偏置角余割sec纾?1.22偏置角正弦sin纾?0.03944723大轮轴线在小轮回转平面内偏置角纾? 2.24初算大轮回转平面内偏置角正弦sin錭：0.25an錭：0.26初算小轮节锥角正切tan?1c：0.27?1c角xxcos?1c：0.28第一次校正螺旋角差值拟'的正弦sin拟'：0.29拟'角xxcos拟'：0.30第一次校正小轮螺旋角正切tan?'m1：0.31扩大系数的xx量腒：0.32大轮扩大系数xx量的换算值腒H：0.00224133校正后大轮偏置角的正弦值sinxx?0.34anxx?0.35校正后小轮节锥角正切tan洌?0.36小轮节锥角?1：10.37?1角的xxcos?1：0.38第二次校正后的螺旋角差值的正弦sin拟：0.39拟值拟：12.40拟xxcos拟：0.41第二次校正后小轮螺旋角的正切值tan鈓1：0.42小轮中点螺旋角鈓1：35.00756743鈓1xxcos鈓1：0.44大轮中点螺旋角鈓2：22.45鈓2xxcos鈓2：0.46鈓2正切tan鈓2：0.41883247大轮节锥角余切cot?2：0.48大轮节锥角?2：79.49?2正弦sin?2：0.50?2xxcos?2：0.51 B1c：29.52 B2c：874.53两背锥之和B12：903.54大轮锥距在螺旋线中点切线方向投影T2：152.55小轮锥距在螺旋线中点切线方向投影T1：130.56极限齿形角正切负值-tana0：0.03881357极限齿形角负值-a0：1.58腶0的xxcos腶0：0.59 B59：0.60 B60：0.00145661 B61：19,795.62 B62：0.63 B63：64 B64：152.65齿线中点曲率半径r'0：152.66比较r'0与rb比值V：0.99894967 A67：0.68 A68：158.69 A69：1.70 rm2圆心至轴线交叉点距离Am2：28.71大轮节锥顶点至小轮轴线的距离A02，正数表示节锥顶点越过了小齿轮的轴线，负值表示节锥顶点在大轮与轴线之间：1.72大轮节锥上中点锥距Rm2：164.73大轮节锥上外锥距(节锥距)R2：74大轮节锥上齿宽之半0.5bm：30.75大轮在平均锥距上工作齿高h'm：13.76 A76：0.77 A77：0.78两侧压力角总和ac：20.000079 ac角正弦值sinac：0.34201480平均压力角a：10.000081 a角xxcosa：0.82 a角正弦tana：0.83 A83：84齿顶角与齿根角总和栌：16.85大轮齿顶高系数ha*2：0.1100086大轮齿根高系数hf*2：1.0400087大轮中点齿顶高ham2：1.88大轮中点齿根高hfm2：14.89大轮齿顶角鑑2：0.90鑑2角正弦sin鑑2：0.91大轮齿根角鑖2：4.92鑖2角正弦sin鑖2：0.93大轮大端齿顶高hae2：1.94大轮大端齿根高hfe2：17.95径向间隙c：2.96大轮大端齿全高he2：18.97大轮大端工作齿高h'e2：16.98大轮顶锥角(面锥角)鋋2：79.99鋋2角正弦sin鋋2：0.100鋋2角xxcos鋋2：0.101大轮根锥角鋐2：74.102鋐2角正弦sin鋐2：0.103鋐2角xxcos鋐2：0.104鋐2角余切cot鋐2：0.105大轮大端齿顶圆直径dae2：385.106大端节圆中心至轴线交叉点距离Akm2：34.107大轮轮冠至轴线交叉点距离Ake2：32.108大端顶圆齿顶与节圆处齿高之差膆am：-0.006485109大端节圆处与根圆处齿高之差膆mf：-0.110大轮面锥顶点到小轮轴线的距离Aoa2(参考71）：1.111大轮根锥顶点到小轮轴线的距离Aof2(参考71）：1.112 A112：170.113修正后小轮轴线在大轮回转平面内的偏置角正弦sin澹?0.114偏置角xxcosxx?0.115偏置角正切tanxx?0.116小轮顶锥角正弦sin鋋1：0.117小轮顶锥角(面锥角)鋋1：15.118顶锥角xxcos鋋1：0.119顶锥角正切tan鋋1：0.273884120 A120：13.121小轮顶锥顶点到轴线交叉点的距离Aoa1(参考71）：-6. 122 A122：0.123 A123：0.124 A124：11.125 A125：4.126 A126：-0.127 A127：1.128 A128：158.129 A129：0.130 A130：31.131小轮轮冠到轴线交叉点的距离Ake1：189.132：31.133小轮前轮冠到轴线交叉点的距离Aki1：123.134：182.135小轮大端齿顶圆直径dae1：99.136：167.137在大轮回转平面内偏置角正弦sin澹?138偏置角xx?12.139偏置角xxcosxx?0.140：21.141小轮根锥顶点到轴线交叉点的距离Aof1(参考71）：-14. 142：0.143小轮根锥角鋐1：9.144 cos鋐1：0.145 tan鋐1：0.146允许的最小侧隙jnmin：0.203200147允许的最大侧隙jnmax：0.279400148：149：12.150大轮内锥距Ri：133.。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

为计算小轮节圆中点分度圆半径需要先按式
(5)确定小轮扩大系数 K c 。
10
机电技术 K c cos ' sin ' tan m10 小轮节圆中点分度圆半径按照式(6)确定:
2012 年 12 月
(5)
tan 2
sin cos tan sin tan
K c cos ' 1 cos '
2.2
刀盘半径核算子程序
m11 arctan
(11)
准双曲面齿轮副设计时大轮和小轮之间需要 满足啮合方程 , 在基本参数输入子程序中初步选 定了刀盘名义半径,当刀盘名义半径不合适时,大 轮和小轮之间是无法满足啮合方程的 , 为此需要 进行刀盘半径核算。要求计算出的刀盘半径和选 定的刀盘名义半径之间误差不超过 1%,通过计算 齿线中点曲率半径与名义刀盘半径进行比较 , 根 据比较结果决定计算流程。
(13)
z1 , z 2 , b2 , E
d e2 r0
(14)
计算出 1 后可以进行第二次修正 , 第二次修 正时小轮螺旋角 m12 为: K K cos ' m12 arctan c sin '
Z1 和大轮齿数 Z 2 。大轮齿宽 b2 一般选择为小于
等于外锥距的30%。 大轮分度圆直径 d e 2 参考文献 [2] 按照齿面接触强度和齿根抗弯强度有关式子 确定。选定大轮分度圆直径后,可以按照设计手册 选取刀盘名义半径 r0 。 大轮分锥角按式(1)初选:
1
Pro/Toolkit应用程序开发简介
2
几何参数计算程序
1 2 '
sin ' E sin 2 rm 2
(3) (4)
通过对格里森制准双曲面齿轮设计过程的分 析 , 本文把格里森制准双曲面齿轮几何参数计算 程序分为以下几个部分:基本参数计算子程序､刀 盘半径核算子程序､大轮轮齿计算子程序､小轮轮
作者简介:王琳(1972-),女,工程师,硕士研究生,研究方向:数控技术｡
1 (1) 1.2i 大轮节圆中点分度圆半径 rm 2 按照式(2)确定。
2 arctan
rm 2
d e 2 b2 sin 2 2
(2)
为保证齿轮有合适的重合度 , 大轮和小轮都 要有一定的螺旋角。准双曲面齿轮副大轮螺旋角 和小轮螺旋角应该满足式(3)。一般初选小轮节圆 中点螺旋角 m10 为 50°,此时可以按照式(4)确定 准双曲面齿轮副大轮和小轮之间的偏置角 ' ( 或 大小轮螺旋角的差值)。
齿计算子程序和主程序。 2.1 基本参数计算子程序 基本参数计算子程序用于确定大轮分锥角 ､ 小轮分锥角 ､ 大轮分度圆半径 ､ 小轮分度圆半径 ､ 轮齿收缩系数､刀盘名义半径等。 准双曲面齿轮副 设计时轴交角 ､传动比 i ､小轮旋转方向､大轮旋 转方向和偏置距离 E 是事先给定的 , 根据齿轮副 的传动要求 ､ 传动比和轴交角可以确定小轮齿数
修正后小轮轴线在大轮回转面内的夹角 为:
z1 sin ' (tan m1 tan m ) (12) 1 2 z 2 1 tan 1
arcsin
根据重新计算的 计算小轮分锥角 1 : sin 1 arctan tan 根据重新计算的 计算大轮分锥角 2 : sin 2 arctan tan
Pro/Toolkit 是 PTC 公司为 Pro/Engineer 软件提 供的二次开发包 , 其主要目的在于让用户或第三 方 通 过 C 程 序 代 码 扩 充 Pro/Engineer 软 件 的 功 能,Pro/Toolkit采用Microsoft Visual C++6.0作为编 译器和连接器,可以在Microsoft Visual C++6.0集 成环境下完成应用程序的设计､调试和编译[3]。 Pro/Toolkit应用程序有两种运行模式:同步模 式和异步模式。 在同步模式下Pro/Toolkit应用程序 和 Pro/Engineer 产 生 各 自 的 进 程 。 在 异 步 模 式 下,Pro/Toolkit应用程序和Pro/Engineer通过远程调 用进行交互。 考虑到Pro/Toolkit应用程序一般离不 开Pro/Engineer,因此一般情况下都采用同步模式, 本文应用程序开发即采用同步模式。
第6期
机电技术
9
准双曲面齿轮参数化计算程序研究
王 琳 1,2 谢明红 1
(1.华侨大学机电及自动化学院,福建 厦门 361021;2.集美大学计算机工程学院,福建 厦门 361021) 摘 要:准双曲面齿轮副设计计算过程非常复杂,为简化设计计算过程,基于三维造型软件Pro/Engineer wildfire 5.0二
(10)
rm1 K c i rm 2 (6) 准双曲面齿轮副一般采用齿根收缩法进行设 计,齿轮收缩系数H按照设计手册选取[2],至此基本 参数已经确定,其子程序流程图如图1所示。
在基本参数输入框中 , 小轮螺旋角是初步选 定的,为此需要经过至少两次修正。第一次修正时 小轮螺旋角 m11 为:
次开发接口Pro/Toolkit开发了格里森制准双曲面齿轮副几何参数计算程序,该程序能辅助准双曲面齿轮副三维参数化建 模,提高准双曲面齿轮副设计效率。 关键词:格里森;准双曲面齿轮;参数计算程序; 中图分类号:TH132.41 文献标识码:A 文章编号:1672-4801ห้องสมุดไป่ตู้2012)06-009-04
格里森制准双曲面齿轮设计计算过程非常复 杂,主要参数计算时需要使用150多个公式,其中47 个公式至少需要迭代三次 , 并且许多公式和参数 意义不明显[1,2]。采用手工计算,计算过程繁琐､计 算量大, 当初始参数发生变化时,整个计算过程需 要重新进行。虽然市面上已有格里森齿轮专家设 计系统,但是由于该系统价格昂贵,大量普通用户 仍然无法利用该系统。实际上这种计算过程完全 可以通过自主开发程序实现。为此本文研究如何 通过三维造型软件Pro/Engineer wildfire5.0二次开 发接口 Pro/Toolkit 进行格里森制准双曲面齿轮几 何参数计算,以减轻设计工作量。