田忌赛马与对策论
- 格式:ppt
- 大小:254.50 KB
- 文档页数:9

《田忌赛马——对策问题》说课稿(2)一、背景介绍田忌赛马的故事在中国可谓家喻户晓,其故事情节虽然简单,却内含丰富的策略管理思想。
今天,我们将一起探讨田忌赛马所体现的对策问题,以深入理解这一古老故事的智慧。
二、深入分析1. 田忌赛马的规则田忌赛马的规则是以马匹的速度为竞逐标准,快马对快马,慢马对慢马。
这一规则在当时的社会背景下,无疑是一种创新的竞赛方式,它打破了常规的比赛模式,使策略的运用变得尤为重要。
2. 田忌的对策在比赛中,田忌采用了两种策略:一是用上等马对上等马,二是用下等马对上等马。
这两种策略的运用,使得田忌能够在总体实力不如齐王的情况下,仍然能够在比赛中占据优势。
三、田忌赛马中的管理智慧1. 知己知彼,百战不殆在比赛中,田忌对齐王的马匹情况有深入的了解,他清楚地知道齐王的马匹优势在哪里,自己的马匹优势又在哪里。
因此,他能够针对性地制定对策,使自己的马匹能够在比赛中占据优势。
2. 策略制定需灵活变通在比赛中,田忌并没有固守一种策略,而是根据比赛情况灵活变通。
当发现齐王采用了一种新的策略时,他能够迅速调整自己的策略,使自己的马匹能够在比赛中继续占据优势。
四、田忌赛马对企业管理的启示1. 资源有限的情况下,如何通过合理的调配和利用,发挥出最大的效益。
田忌在比赛中,由于自己整体实力不如齐王,因此他必须通过合理的调配和利用,使自己的马匹能够在比赛中占据优势。
同样,企业在资源有限的情况下,也需要通过合理的调配和利用,使企业能够在市场竞争中占据优势。
2. 策略的制定需要考虑全局。
田忌在比赛中,并没有只关注一匹马的表现,而是考虑到了全局。
同样,企业在制定策略时,也需要考虑全局,而不仅仅是一个部门或者一个产品的表现。
只有从全局出发,才能制定出有效的策略。
3. 策略制定需要具有灵活性和创新性。
田忌在比赛中,能够根据比赛情况灵活变通。
同样,企业在制定策略时,也需要具有灵活性和创新性。
市场变化莫测,企业需要能够根据市场变化灵活调整策略。


田忌赛马中的数学知识
“田忌赛马所用的数学知识是“博弈论”。
这是一种专门研究斗争的方法,后来被称为“对策论”,或者叫做“博弈论”。
田忌所代表的一方的上、中、下三批马,每个层次的质量都劣于齐王的马。
但是,田忌用完全没有优势的下马对齐王有完全优势的上马,再用拥有相对比较优势上、中马对付齐王的中、下马,结果稳赢。
大输、小赢、小赢→ 输少赢多,是博弈论最早的例子之一。
明明田忌每个等级的马都比齐王略差,最后为什么能够反败为胜呢?
按照常规思路,用上等马对上等马,下等马对下等马。
其实这样的应对方案属于下策,明明比对手略逊一筹还硬碰硬,最后三场全败。
而获胜的方案在齐王出上等马的时候,田忌居然出下等马应对,你知道这是什么策略?为什么这么安排?
因为在齐王出上等马的时候,不管田忌出什么马应对,都属于必输的结局。
反正是必输那就用自己最差的下等马应对,输得彻彻底底。
但是这局比赛后局势完全转变。
原来齐王的三匹马都比田忌略胜一筹,但是第一局田忌以最差的下等马应对齐王的最强的上等马后,田忌剩下的是上等马和中等马,齐王剩下的是中等马和下等马。
这样原来是齐王略胜一筹,现在是田忌略胜一筹,情况发生了大逆转。
因为有实力更有底气,在接下来的比赛中,田忌就可以全力出击,和齐王硬碰硬了,而且连胜两场,最终以三局两胜获胜,扭转了连输三场的败局,做到了反败为胜,田忌赛马也成为了最后策略的代名词。


田忌赛马——对策问题一、教学内容:四年级上册数学广角例4田忌赛马二、教学目标:1、通过田忌赛马的故事让学生体会对策论方法在实际中的应用,感受对策在生活中的重要作用。
2、在活动中让学生认识到解决问题策略的多样性,形成寻找解决问题最优方案的意识,同时培养学生详细分析,周密思考的思维品质。
3、让学生受到数学思想方法的熏陶,形成探索数学问题的兴趣与欲望,逐步发展数学思维能力,培养学生的应用意识和解决实际问题的能力。
三:教学重难点:重点:根据具体的情况,制定不同的对策,体会优化的思想。
难点:寻找解决问题最优方案,提高学生解决问题的能力。
课前交流(比大小游戏):师:孩子们,喜欢玩游戏吗?好,咱们来玩一个用“扑克牌比大小”的游戏(出示课件),怎么样?师:老师这里有两组扑克牌,它们分别是10、7、5和8、6、1。
请看游戏规则:(屏幕出示游戏规则)双方每次各出一张牌比大小,每张牌只能出一次,比赛采用“3局2胜”制。
师:游戏规则大家都清楚了吗?如果让你选一组牌和我比大小,你会选哪一组呢?(一起说)为什么?师:用你们的10、7、5和老师的8、6、1比大小,你有没有信心获胜?好,谁敢上来和我比试比试?其余同学,你们都是小裁判,负责宣布每场比赛获胜的是谁,行吗?(请学生上台)请出牌!(生输了)师:想说点什么?师:还有谁想来和我PK一下?请出牌。
谁还想来?师:孩子们,想一想:老师为什么总能赢呢?其实,老师之所以能赢,是因为我用到了一个小小的对策,想知道吗?好,就让我们一起在待会儿的数学课上来揭秘吧!一、创新情境,导入新课。
师:孩子们,老师为你们带来了一个故事,想听吗?故事的名字叫《田忌赛马》(板书课题:田忌赛马)师讲故事:齐国的大将田忌很喜欢赛马。
有一回他和齐王约定,进行一次比赛。
比赛采用三战两胜。
比赛前,他们把各自的马分成上、中、下三等。
但是,齐王每个等级的马都比田忌的强。
比赛时,田忌用上等马对齐王的上等马,中等马对中等马,下等马对下等马。


第8单元数学广角—优化第3课时策略问题【教学内容】教材P106例3。
【教学目标】1.在活动过程中体会对策论方法在解决实际问题中的应用,认识解决问题策略的多样性,形成从多种方案中寻找最优方案的意识。
2.在独立思考、合作交流的探究过程中,尝试用数学的方法解决生活中的简单问题,提升观察概括、分析思考和解决问题的能力。
3.在研究过程中激发兴趣、开阔眼界,感悟对策论与日常生活的密切联系及重要性,让学生进一步学会用数学眼光观察生活,提高应用意识。
【重点难点】重点:探寻最优的应对策略。
难点:感悟运用对策获胜的运筹思想。
【教学过程】一、新课导入师:小朋友,你听过“田忌赛马”的故事吗?谁能给大家讲讲。
指名学生讲或教师讲述“田忌赛马”的故事。
师:田忌到底用了什么方法赢了齐王?同学们知道吗?其实呀,这其中也蕴藏着很深奥的数学问题,今天这节课我们就一起来探究。
(板书课题:策略问题)二、探究新知1.讨论:田忌是怎样赢了齐王的?田忌取胜的策略:2.提问设疑。
(1)田忌所用的这种策略是不是唯一能赢齐王的方法?(2)田忌到底有多少种可以采用的应对策略呢?结果是怎样的呢?学生独立思考后,记录赛马的方法和结果,完成后和同桌说一说,再全班交流。
3.组织学生进一步思考,体会“唯一”的意义。
学生汇报完毕后,引导学生将这些策略进行有序整理,呈现下表:第一场第二场第三场获胜方齐王上等马中等马下等马田忌1 上等马中等马下等马齐王田忌2 上等马下等马中等马齐王田忌3 中等马上等马下等马齐王田忌4 中等马下等马上等马齐王田忌5 下等马上等马中等马田忌田忌6 下等马中等马上等马齐王师:仔细观察这张表格,你发现了什么?【学情预设】学生会发现一共有6种策略,齐王赢了5次,田忌只赢了1次,所以这种方法就是唯一方法,也就是最优策略。
4.举一反三。
师:请同学们想一想,田忌的这种策略在生活中还有哪些应用?学生自由发言。
师:现在我们来实际应用一下,完成教材P106“做一做”。

《对策问题——田忌赛马》一等奖创新教案对策问题——田忌赛马学情分析一、教材分析《田忌赛马》是新人教版四年级上册第八单元“数学广角”的教学内容,包含例题及一个游戏和一个在生活中应用的习题。
教材从故事“田忌赛马”引入对策论的应用问题,通过故事,激发学生的学习兴趣,引导学生采用列表的方法,探究田忌获胜的策略。
在探究田忌获胜策略的过程中,体会有序思考及优化思想,研究田忌获胜的策略,渗透“对策思想”,提高学生解决问题的策略意识。
教材编排了“对策思想”在生活中的应用,教材编排让学生体会到对策论的方法在生活、比赛中的重要性。
结合实际情境,激发学生的思维,开阔视野,启迪心智,提高策略意识,增强解决问题的能力。
二、学生分析“田忌赛马”对策问题,是日常生活中的实际问题,学生平时都有接触这个故事,但只是停留在表面上,没有深层次地体会其中所蕴含的数学思想。
是在学生学习了有序思考,合理安排等问题,初步具备了优化意识,有解决问题的策略意识的基础上进行教学的。
学生有了一定的探究问题的能力,兴趣会很浓。
在独立思考、小组讨论交流的基础上将会进一步提高分析问题和解决问题的能力和策略意识,体会对策思想在生活中的应用。
教学工具PPT课件、视频软件、扑克牌和自制纸片等教学目标教学目标:1. 在玩游戏和听故事等活动中,让学生探究获胜的策略,体验策略的重要性。
2. 让学生在运用有序思考、列举列表等数学方法解决问题的过程中,积累数学活动经验。
3. 引导学生在自主探究中感悟“运筹思想”:知己知彼、全盘考虑达到以弱胜强的结果,初步体会运筹思想的应用价值。
4.培养学生冷静思考,沉着“应战”的心理品质。
教学重难点教学重点:运用数学方法探寻最优的应对策略。
教学难点:感悟运用对策获胜的“运筹思想”。
教学方法讨论法、谈话法、讲授法、自主学习法、合作探究法等。
教学过程教学过程:一、游戏导入,初步感知1. 师生谈话,明确规则。
师(出示扑克牌):认识这个吧?玩过扑克牌吗?玩过什么游戏?今天我们玩用扑克牌“比大小”的游戏。

战国时期,齐威王与大将田忌赛马,齐威王和田忌各有三匹好马:上马,中马与下马。
比赛分三次进行,每赛马以千金作赌。
由于两者的马力相差无几,而齐威王的马分别比田忌的相应等级的马要好,所以一般人都以为田忌必输无疑。
但是田忌采纳了门客孙膑(著名军事家)的意见,用下马对齐威王的上马,用上马对齐威王的中马,用中马对齐威王的下马,结果田忌以2比1胜齐威王而得千金。
这是我国古代运用对策论思想解决问题的一个范例。
下面有一个两人做的游戏:轮流报数,报出的数不能超过8(也不能是0),把两个人报出的数连加起来,谁报数后使和为88,谁就获胜。
如果让你先报数,你第一次应该报几才能一定获胜?
分析:因为每人每次至少报1,最多报8,所以当某人报数之后,另一人必能找到一个数,使此数与某所报的数之和为9.依照规则,谁报数后使和为88,谁就获胜,于是可推知,谁报数后和为79(=88-9),谁就获胜。
88=99+7,依次类推,谁报数后使和为16,谁就获胜。
进一步,谁先报7,谁就获胜。
于是得出先报者的取胜对策为:先报7,以后若对方报K(1K8),你就报(9-K)。
这样,当你报第10个数的时候,就会取得胜利。
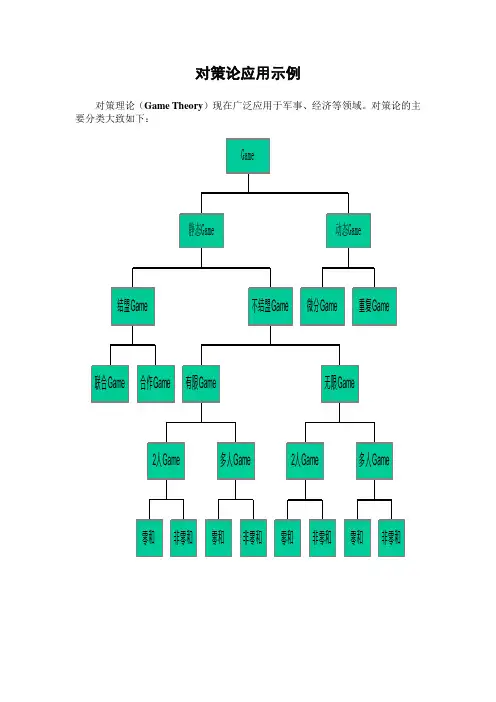
对策论应用示例对策理论(Game Theory)现在广泛应用于军事、经济等领域。
对策论的主要分类大致如下:§1 对策论应用举例例1 齐王与田忌赛马(孙膑对策)传说齐威王与大臣田忌赛马,每人都以上等马、中等马、下等马比赛,三局两胜制,胜者得1千金。
齐王的同等马优于田忌的同等马,田忌总输。
后来军事家孙膑为田忌出主意:田忌用上等马赢齐王的中等马、用中等马赢齐王的下等马,最后以下等马输给齐王一局,这样田忌就以总分3:2获胜。
对局图如下:齐王的马田忌的马上等马上等马中等马中等马下等马下等马在这个对策中,双方对于对方的情况十分熟悉,事先也知道比赛规则,这在对策论中叫做双方全信息的对策。
另外,在这个对策中,一方用计谋和策略,另一方不用,这不是现代意义下的对策。
现代意义下的对策,对局双方都用计谋和策略,并且双方都选择对自己有利的策略,这在对策论中叫理智的局中人(经济对策中叫理性的消费者)。
例2 1943年2月,由于战争的失败,日本舰队打算从新不列颠岛撤退到伊里安岛(如图)。
美国西南太平洋空军奉命轰炸这支日本舰队。
北日本舰队的可能撤退航线有两条:南线与北线,航程都是3天。
气象预报:未来3天,北线阴雨、南线晴天。
日本人应该选择哪一条撤退航线呢?美军的选择是重点搜索的方向:(1)非重点搜索:派少量搜索飞机,发现目标后派大量飞机轰炸;(2)重点搜索:派大量搜索飞机,发现目标后再派大量飞机轰炸。
根据气象预报,未来3天,北线阴雨,能见度很差,不利于侦察飞机巡航侦察(二战时,主要依靠飞行员目测侦察);南线晴天,能见度好,有利于侦察机巡航侦察。
美军应该把搜索重点放在北边还是南边呢?表中第一行第一列的-2/3表示:日方若选择北线撤退,美军的重点搜索方向也在北线,日本舰队在3天中大约能安全行走一天,然后被美军侦察机发现,招来大批轰炸机,在未来2天被轰炸。
下面讨论双方应该选择的较好的策略。
日本方面:北边的损失向量(-2/3,-1/3)≥南边的损失向量(-2/3,-3/3),表示北线损失比南线小,日方司令官若是理智的决策者就应选北线作为航线。

从田忌赛马谈到对策论从田忌赛马谈到对策论第二次世界大战前后,由于军事上的需要,一门研究斗争的新的数学分支“对策论”出现了。
当然,不少人认为“对策论”起源于更早一些的“博奕论”(博,指赌博;弃,指下棋)。
但查阅历史,“对策论”的始祖却是我国战国时代著名的军事家孙膑。
孙膑(约公元前360—前330年)是战国时代的齐国(今山东一带)人,是春秋末期杰出的军事家孙武的后代。
他曾在齐国将领田忌手下当门客。
田忌常和齐威王(公元前356—320年在位)及诸公子以赛马赌博。
田忌的马有上、中、下三等;齐王的马也有上、中、下三等,但每一等都比田忌同等的马好,于是田忌屡赛屡输。
这次他俩又下了1000两黄金的赌注,田忌一筹莫展。
就在这时,孙膑对田忌说:“您尽管同他赛,我有办法让您赢。
” 比赛又开始了。
齐王令出上马,孙膑让田忌先出下马,给齐王舒舒服服、轻而易举地赢了第一场;然后齐王令出中马,孙膑让田忌出上马,经过激烈比赛,田忌的马赢了;最后齐王出下马,孙膑让田忌出中马,田忌的马又赢了。
3场比赛,田忌以2:1取胜,“卒得王千金”。
这次比赛有以下特点:知己知彼,避敌锋芒,后发制人,以弱胜强。
这里包含着许多辩证的军事思想,并且成功地应用了数学(数学决不单单是计算)。
田忌反败为胜,使齐王大为惊讶。
于是田忌向齐王孙膑。
齐王准奏,任命孙膑为军师。
此后孙膑屡建战绩。
而“田忌赛马”则成为脍炙人口的一个故事,数学家爱说它,政治家、哲学家、军事家也爱说它。
同学们看过《三国演义》吧?在《三国演义》中有许多极其精彩的战例,其中就包含着“对策论”的思想。
让我们以著名的“赤壁大战”为例,以胜方周瑜、诸葛亮为主方来评价这次战争。
一、孙(权)、刘(备)联盟,共御曹操。
这是根本的战略方针;没有这一条,就会被曹操各个击破。
二、统一思想,战必胜、降必亡。
诸葛亮舌战群儒、周瑜力谏孙权,都是为了克服投降或主和思想,做到上下一心,群威群胆,同仇敌汽。
这是取胜的政治因素。
教学案例--《田忌赛马》按:下面的案例中指出:“适切的材料是学生探究活动能否成功的关键。
探究材料必须具备以下特点:有结构,保证探究过程的丰厚;承载核心问题,保证探究活动的方向;学生容易理解和表达,保证探究活动的效度;探究空间大,促进思维提升。
”探究材料的设计是本案例最大的亮点。
案例中又指出:“我们经常会说,要设计有挑战性的问题,让学生自主探究,但是问题的难度系数往往会影响探究进程,如果挑战性太大,学生将无从入手。
因此探究问题的适度分解或分层,降低探究的门槛,让更多学生参与探究,应该是教师指导中需要考虑的问题。
”探究坡度的设计,成为本案例第二大亮点。
对学生探究方案的反馈与指导,在学生探究中遭遇思维搁浅时教师的及时提示,也是本探究案例中教师指导上的亮点。
《田忌赛马》探究教学案例一、基本情况分析《田忌赛马》是人教版四年级上册第七单元“数学广角”例4的教学内容。
从故事“田忌赛马”引入对策论的应用问题,对策论研究的是竞争的双方各自采取什么对策才能够战胜对手,让学生体会到对策论的方法在生活、比赛中的重要性。
本节课教师在对学生自主探究进行指导时,需要注意如下几点。
(一)引导学生通过探究活动学习有序思考。
田忌所用的这种策略是不是唯一能赢齐王的方法?学生的探究方法是把所有可以采用的策略列出来,发现田忌可以采用的策略一共有6种,但其中只有一种也就是他所使用的方法是唯一可以获胜的。
教师应在学生探究应对方案时有针对性的引导学生理解,有序思考能够做到不重复不遗漏,可以更快地寻找到应对的策略(二)给学生创设更具探究空间的学习情境。
“田忌赛马”获胜的必要条件有哪些?“田忌赛马”不仅仅是一个故事,而是一种策略。
这一策略并不是“必胜宝典”,还是需要一定的前提。
但学生对田忌赛马故事内容熟悉,在教学中如果仅依赖“田忌赛马”的故事本身,不利于学生从对策论的角度进行探究。
因此,教学中教师可以提供与“田忌赛马”同样结构的探究材料,以便于学生不断尝试、比较、发现、概括、归纳。