【k12小学同步资源】2018-2019学年第二学期北京市海淀区某名校期末真题测试卷

2018-2019学年北京市海淀区八一学校七年级（下）期末数学试卷一、选择题（每小题3分，共30分）1．（3分）已知三角形的两边a＝3，b＝5，第三边是c，则c的取值范围是（）A．3＜c＜5B．2＜c＜8C．2＜c＜5D．3＜c＜82．（3分）下列调查中，适合用全面调查方式的是（）A．了解一批IP AD的使用寿命B．了解电视栏目《朗读者》的收视率C．了解某班学生对国家“一带一路”战略的知晓率D．了解某鱼塘中鱼的数量3．（3分）下列邮票中的多边形中，内角和等于540°的是（）A．B．C．D．4．（3分）如图，天平左盘中物体A的质量为m g，天平右盘中每个砝码的质量都是1g，则m的取值范围在数轴上可表示为（）A．B．C．D．5．（3分）若m＜n，则下列不等式中，正确的是（）A．m﹣4＞n﹣4B．＞C．﹣3m＜﹣3n D．2m+1＜2n+16．（3分）若△ABC中，∠A＝90°，且∠B﹣∠C＝30°，那么∠C的度数为（）A．30°B．40°C．50°D．60°7．（3分）如图所示，已知AC∥ED，∠C＝30°，∠CBE＝40°，则∠BED的度数是（）A．60°B．80°C．70°D．50°8．（3分）如图，已知∠1＝∠2，AC＝AD，要使△ABC≌△AED，还需添加一个条件，那么在①AB＝AE，②BC＝ED，③∠C＝∠D，④∠B＝∠E，这四个关系中可以选择的是（）A．①②③B．①②④C．①③④D．②③④9．（3分）小文同学统计了某小区部分居民每周使用共享单车的时间，并绘制了统计图，如图所示．下面有四个推断：①小文此次一共调查了100位小区居民②每周使用时间不足15分钟的人数多于45﹣60分钟的人数③每周使用时间超过30分钟的人数超过调查总人数的一半④每周使用时间在15﹣30分钟的人数最多根据图中信息，上述说法中正确的是（）A．①④B．①③C．②③D．②④10．（3分）如图，AB∥CD，∠BAC与∠ACD的平分线相交于点G，EG⊥AC于点E，F为AC中点，GH⊥CD于H，∠FGC＝∠FCG．下列说法正确的是（）①AG⊥CG；②∠BAG＝∠CGE；③S△AFG＝S△GFC；④若∠EGH：∠ECH＝2：7，则∠AFG＝150°．A．①③④B．②③C．①②③D．①②③④二、填空题（本题共14分，每小题2分）11．（2分）写出一个解为的二元一次方程是．12．（2分）在生活中，我们常常看到在电线杆的两侧拉有两根钢线用来固定电线杆（如图所示），这样做的数学原理是．13．（2分）《九章算术》中记载：“今有大器五、小器一容三斛；大器一、小器五容二斛．问大、小器各容几何？”其大意是：今有大容器5个，小容器1个，总容量为3斛；大容器1个，小容器5个，总容量为2斛．问大容器、小容器的容积各是多少斛？设大容器的容积为x斛，小容器的容积为y斛，根据题意，可列方程组为（斛：古量器名，容量单位）．14．（2分）一个多边形的内角和是外角和的2倍，则这个多边形的边数为．15．（2分）关于x的不等式2x﹣a≤﹣3的解集如图所示，则a的值是．16．（2分）如图，BE是∠ABD的平分线，CF是∠ACD的平分线，BE与CF交于G，若∠BDC＝140°，∠BGC＝110°，则∠A的度数为°．17．（2分）某公园划船项目收费标准如下：船型两人船（限乘两人）四人船（限乘四人）六人船（限乘六人）八人船（限乘八人）每船租金（元/小时）90100130150某班18名同学一起去该公园划船，若每人划船的时间均为1小时，则租船的总费用最低为元．三、解答题：（共56分，18-21题每题4分，22，23，24，26题每题5分，25题6分，27题7分，28题7分）18．（4分）解方程组19．（4分）解不等式＜3﹣x，并把它的解集在数轴上表示出来．20．（4分）解不等式组并写出它的所有非负整数解．21．（4分）如图，已知△ABC中，AB＝9，BC＝12，AC＝5．（1）画出△ABC的高AD和BE；（2）画出△ABC的中线CF；（3）计算的值是．22．（5分）如图，△ABC中，CD是∠ACB的角平分线，DE∥AC，交BC于点E，∠B＝20°，∠ADC＝44°，求△DEC各内角的度数．23．（5分）已知关于x，y的二元一次方程组的解满足x＜y，求m的取值范围．24．（5分）如图，在△ABC中，D是边AB上一点，E是边AC的中点，作CF∥AB交DE 的延长线于点F．（1）证明：△ADE≌△CFE；（2）若∠B＝∠ACB，CE＝5，CF＝7，求DB．25．（6分）某汽车专卖店销售A，B两种型号的新能源汽车．上周售出1辆A型车和3辆B 型车，销售额为96万元；本周已售出2辆A型车和1辆B型车，销售额为62万元．（1）求每辆A型车和B型车的售价各为多少万元．（2）甲公司拟向该店购买A，B两种型号的新能源汽车共6辆，且A型号车不少于2辆，购车费不少于130万元，则有哪几种购车方案？26．（5分）某综合实践小组为了了解本校学生参加课外读书活动的情况，随机抽取部分学生，调查其最喜欢的图书类别，并根据调查结果绘制成如下不完整的统计表与统计图：图书类别画记人数百分比文学类艺体类正5科普类其他14合计a100%请结合图中的信息解答下列问题：（1）随机抽取的样本容量a为；（2）在扇形统计图中，“艺体类”所在的扇形圆心角应等于度；（3）补全条形统计图；（4）已知该校有600名学生，估计全校最喜欢文学类图书的学生有人．27．（7分）定义：对任意一个两位数a，如果a满足个位数字与十位数字互不相同，且都不为零，那么称这个两位数为“迥异数”．将一个“迥异数”个位数字与十位数字对调后得到一个新的两位数，把这个新两位数与原两位数的和与11的商记为f（a）．例如：a＝12，对调个位数字与十位数字得到新两位数21，新两位数与原两位数的和为21+12＝33，和与11的商为33÷11＝3，所以f（12）＝3．根据以上定义，回答下列问题：（1）填空：①下列两位数：20，21，22中，“迥异数”为．②计算：f（35）＝，f（10m+n）＝．（2）如果一个“迥异数”b的十位数字是k，个位数字是2（m+1），且f（b）＝9；另一个“迥异数”c的十位数字是m+4，个位数字是2k﹣1，且f（c）＝11，请求出“迥异数”b和c．（3）如果一个“迥异数”m的十位数字是x，个位数字是x﹣3，另一个“迥异数”n的十位数字是x﹣4，个位数字是2，且满足f（m）﹣f（n）＜7，请直接写出满足条件的所有x的值．28．（7分）如图，在直角三角形ABC中，∠ACB＝90°，∠BAC＝45°．点P是直线AC 上一个动点（点P不与点A，C重合），连接BP，在线段BC的延长线上取一点D，使得∠BPC＝∠DPC．过点B作BE⊥DP，交直线DP于点E．（1）如图1，当点P在线段AC上时，若∠BPC＝60°，则∠ABE＝；（2）当点P在线段CA的延长线上时，在图2中依题意补全图形，并判断∠ABE与∠ABP 有怎样的数量关系，写出你的结论，并证明；（3）在点P运动的过程中，直接写出∠ABE与∠ABP的数量关系为．。

2018-2019学年北京市海淀区八一学校七年级（下）期末数学试卷一卷一．选择题（共10小题）1．已知三角形的两边a＝3，b＝5，第三边是c，则c的取值范围是（）A．3＜c＜5B．2＜c＜8C．2＜c＜5D．3＜c＜82．下列调查中，适合用全面调查方式的是（）A．了解一批IP AD的使用寿命B．了解电视栏目《朗读者》的收视率C．了解某班学生对国家“一带一路”战略的知晓率D．了解某鱼塘中鱼的数量3．下列邮票中的多边形中，内角和等于540°的是（）A．B．C．D．4．如图，天平左盘中物体A的质量为m g，天平右盘中每个砝码的质量都是1g，则m的取值范围在数轴上可表示为（）A．B．C．D．5．若m＜n，则下列不等式中，正确的是（）A．m﹣4＞n﹣4B．＞C．﹣3m＜﹣3n D．2m+1＜2n+16．若△ABC中，∠A＝90°，且∠B﹣∠C＝30°，那么∠C的度数为（）A．30°B．40°C．50°D．60°7．如图所示，已知AC∥ED，∠C＝30°，∠CBE＝40°，则∠BED的度数是（）A．60°B．80°C．70°D．50°8．如图，已知∠1＝∠2，AC＝AD，要使△ABC≌△AED，还需添加一个条件，那么在①AB ＝AE，②BC＝ED，③∠C＝∠D，④∠B＝∠E，这四个关系中可以选择的是（）A．①②③B．①②④C．①③④D．②③④9．小文同学统计了某小区部分居民每周使用共享单车的时间，并绘制了统计图，如图所示．下面有四个推断：①小文此次一共调查了100位小区居民②每周使用时间不足15分钟的人数多于45﹣60分钟的人数③每周使用时间超过30分钟的人数超过调查总人数的一半④每周使用时间在15﹣30分钟的人数最多根据图中信息，上述说法中正确的是（）A．①④B．①③C．②③D．②④10．如图，AB∥CD，∠BAC与∠ACD的平分线相交于点G，EG⊥AC于点E，F为AC中点，GH⊥CD于H，∠FGC＝∠FCG．下列说法正确的是（）①AG⊥CG；②∠BAG＝∠CGE；③S△AFG＝S△GFC；④若∠EGH：∠ECH＝2：7，则∠AFG＝150°．A．①③④B．②③C．①②③D．①②③④二．填空题（共7小题）11．写出一个解为的二元一次方程是．12．在生活中，我们常常看到在电线杆的两侧拉有两根钢线用来固定电线杆（如图所示），这样做的数学原理是．13．《九章算术》中记载：“今有大器五、小器一容三斛；大器一、小器五容二斛．问大、小器各容几何？”其大意是：今有大容器5个，小容器1个，总容量为3斛；大容器1个，小容器5个，总容量为2斛．问大容器、小容器的容积各是多少斛？设大容器的容积为x 斛，小容器的容积为y斛，根据题意，可列方程组为（斛：古量器名，容量单位）．14．一个多边形的内角和是外角和的2倍，则这个多边形的边数为．15．关于x的不等式2x﹣a≤﹣3的解集如图所示，则a的值是．16．如图，BE是∠ABD的平分线，CF是∠ACD的平分线，BE与CF交于G，若∠BDC＝140°，∠BGC＝110°，则∠A的度数为°．17．某公园划船项目收费标准如下：船型两人船（限乘两人）四人船（限乘四人）六人船（限乘六人）八人船（限乘八人）每船租金（元/小时）90100130150某班18名同学一起去该公园划船，若每人划船的时间均为1小时，则租船的总费用最低为元．一．解答题（共11小题）1．解方程组2．解不等式＜3﹣x，并把它的解集在数轴上表示出来．3．解不等式组并写出它的所有非负整数解．4．如图，已知△ABC中，AB＝9，BC＝12，AC＝5．（1）画出△ABC的高AD和BE；（2）画出△ABC的中线CF；（3）计算的值是．5．如图，△ABC中，CD是∠ACB的角平分线，DE∥AC，交BC于点E，∠B＝20°，∠ADC＝44°，求△DEC各内角的度数．6．已知关于x，y的二元一次方程组的解满足x＜y，求m的取值范围．7．如图，在△ABC中，D是边AB上一点，E是边AC的中点，作CF∥AB交DE的延长线于点F．（1）证明：△ADE≌△CFE；（2）若∠B＝∠ACB，CE＝5，CF＝7，求DB．8．某汽车专卖店销售A，B两种型号的新能源汽车．上周售出1辆A型车和3辆B型车，销售额为96万元；本周已售出2辆A型车和1辆B型车，销售额为62万元．（1）求每辆A型车和B型车的售价各为多少万元．（2）甲公司拟向该店购买A，B两种型号的新能源汽车共6辆，且A型号车不少于2辆，购车费不少于130万元，则有哪几种购车方案？9．某综合实践小组为了了解本校学生参加课外读书活动的情况，随机抽取部分学生，调查其最喜欢的图书类别，并根据调查结果绘制成如下不完整的统计表与统计图：图书类别画记人数百分比文学类艺体类正5科普类其他14合计a100%请结合图中的信息解答下列问题：（1）随机抽取的样本容量a为；（2）在扇形统计图中，“艺体类”所在的扇形圆心角应等于度；（3）补全条形统计图；（4）已知该校有600名学生，估计全校最喜欢文学类图书的学生有人．10．定义：对任意一个两位数a，如果a满足个位数字与十位数字互不相同，且都不为零，那么称这个两位数为“迥异数”．将一个“迥异数”个位数字与十位数字对调后得到一个新的两位数，把这个新两位数与原两位数的和与11的商记为f（a）．例如：a＝12，对调个位数字与十位数字得到新两位数21，新两位数与原两位数的和为21+12＝33，和与11的商为33÷11＝3，所以f（12）＝3．根据以上定义，回答下列问题：（1）填空：①下列两位数：20，21，22中，“迥异数”为．②计算：f（35）＝，f（10m+n）＝．（2）如果一个“迥异数”b的十位数字是k，个位数字是2（m+1），且f（b）＝9；另一个“迥异数”c的十位数字是m+4，个位数字是2k﹣1，且f（c）＝11，请求出“迥异数”b和c．（3）如果一个“迥异数”m的十位数字是x，个位数字是x﹣3，另一个“迥异数”n的十位数字是x﹣4，个位数字是2，且满足f（m）﹣f（n）＜7，请直接写出满足条件的所有x的值．11．如图，在直角三角形ABC中，∠ACB＝90°，∠BAC＝45°．点P是直线AC上一个动点（点P不与点A，C重合），连接BP，在线段BC的延长线上取一点D，使得∠BPC＝∠DPC．过点B作BE⊥DP，交直线DP于点E．（1）如图1，当点P在线段AC上时，若∠BPC＝60°，则∠ABE＝；（2）当点P在线段CA的延长线上时，在图2中依题意补全图形，并判断∠ABE与∠ABP 有怎样的数量关系，写出你的结论，并证明；（3）在点P运动的过程中，直接写出∠ABE与∠ABP的数量关系为．。

海淀区 2019-2019 学年八年级第二学期期末练习数学（分数： 100 分时间： 90 分钟）2019.7学校班级姓名成绩一、选择题：（本题共30 分，每小题 3 分）在下列各题的四个备选答案中，只有一个是正确的．．．．．1．下列各式中，运算正确的是A．( 2)22B．2810C．284D．2222．如图，在△ABC 中， AB 3， BC6， AC4，点 D，E分别是边AB，CB的中点，那么 DE 的长为AA ．1.5B ． 2C． 3 D ．4DB EC 3．要得到函数y 2x 3 的图象，只需将函数y2x 的图象A ．向左平移 3 个单位B．向右平移 3 个单位C．向上平移 3 个单位D．向下平移 3 个单位．在 Rt△ABC中, D 为斜边AB的中点，且 BC 3， AC 4 ，则线段 CD 的长是4A ．2B．3C．5D．5 25．已知一次函数y (k 1)x .若 y 随 x 的增大而增大，则k 的取值范围是A ．k1B．k1C．k0D．k06 ．如图，在△ABC 中, AB5， BC 6 ， BC 边上的中线AD 4 ，那么 AC 的长是A ．5B．6C．34D．2 13AB D C7．如图，在点 M , N , P, Q 中，一次函数y kx 2 (k 0) 的图象不可能经过的点是A．M B．N C．P D．QyM2N- 2O 2x Q - 2P8．如图是某一天北京与上海的气温T （单位： C ）随时间t（单位：时）变化的图象.根据图中信息，下列说法错误的是．．A ．12 时北京与上海的气温相同B ．从 8 时到 11 时，北京比上海的气温高C．从 4 时到 14 时，北京、上海两地的气温逐渐升高D ．这一天中上海气温达到 4 C 的时间大约在上午 10时9．如图，在平面直角坐标系xOy 中，正方形ABCD的顶点D在y轴上，且 A(3,0) ，B (2, b ) ，则正方形ABCD 的面积是yDA ．13B．20C．25D．34CA O x10．已知两个一次函数y1， y2的图象相互平行，它们的部分自变量与相B 应的函数值如下表：x m02y143ty26n- 1则 m 的值是1B ．31D ．5A ．C．32二、填空题：（本题共18 分，每小题 3 分）11．x 2 在实数范围内有意义，那么x 的取值范围是．12．已知 2 x (y 1)20 ，那么y x的值是．13．如图，两张等宽的纸条交叉叠放在一起，若重合部分构成的四边形ABCD中，AB 3 ， AC 2 ，则BD的长A B为．D C144的正方形ABCD四条边上的点，．如图， E, F,M, N 分别是边长为EA B且AE BF CM DN .那么四边形 EFMN 的面积的最小值N 是．15．第 24 届冬季奥林匹克运动会，将于2022 年 2 月在北京市和张家口市联合举行 . 某校寒假期间组织部分滑雪爱好者参加冬令营集训. 训练期间，冬令营的同学们都参加了“单板滑雪” 这个项目40 次的训练测试，每次测试成绩分别为 5 分，4 分， 3 分， 2 分，1 分五档 .甲乙两位同学在这个项目的测试成绩统计结果如图所示.F D M C根据上图判断，甲同学测试成绩的众数是；乙同学测试成绩的中位数是；甲乙两位同学中单板滑雪成绩更稳定的是．16．已知一次函数y kx b 的图象过点( 1,0) 和点 (0,2) . 若 x(kx b) 0 ，则 x 的取值范围是．三、解答题：（本题共22 分，第 17— 19 题每小题 4 分，第 20— 21 题每小题 5 分）317．计算：12 6 ．218．如图，在Y ABCD中，点E，F分别在边AD ， BC 上，AE CF ，求证：BE DF .A E D19．已知x5 1，求x2BFC 2x 的值.20．在平面直角坐标系xOy 中，已知点A(0, 3) 、点 B(3, 0) ，一次函数y 2x 的图象与直线AB交于点 M ．（1）求直线AB的函数解析式及M点的坐标；（2）若点N是x轴上一点，且△MNB的面积为 6，求y 54 3 2点 N 的坐标．1- 5 - 4 - 3 - 2 - 1O 1234 5 x-1-2-3-4-521．如图，在△ABC中，点D，E，F分别是边AB ， AC ，ABC 的中点，且 BC2AF .（ 1）求证：四边形ADFE为矩形；D E（2）若 C 30， AF 2 ，写出矩形ADFE的周长.B CF四、解答题：（本题共14分，第 22题 8 分，第 23题 6 分）22．阅读下列材料：2019 年人均阅读16 本书！2019 年 4 月 23 日“世界读书日” 之前，国际网络电商亚马逊发布了“亚马逊中国2019全民阅读报告”．报告显示，大部分读者已养成一定的阅读习惯，阅读总量在10 本以上的占 56%，而去年阅读总量在10 本以上的占48%．京东图书也发布了2019 年度图书阅读报告．根据京东图书文娱业务部数据统计，2019年销售纸书人均16 册，总量叠在一起相当于15000 个帝国大厦的高．（1）在亚马逊这项调查中，以每年有效问卷 1.4 万份来计， 2019 年阅读量十本以上的人数比去年增加了人；（2）小雨作为学校的图书管理员，根据初二年级每位同学本学期的借书记录，对各个班借阅的情况作出了统计，并绘制统计图表如下：初二年级图书借阅分类统计扇形图初二年级各班图书借阅情况统计表班级1234人数35353436借阅总182165143数（本）中位数5655①全年级140名同学中有科技社团成员40 名，他们人均阅读科普类书籍1.5 本，年级其他同学人均阅读科普类书籍 1.08 本，请你计算全年级人均阅读科普类书籍的数量，再通过计算补全统计表；②在①的条件下，若要推荐初二某个班级为本学期阅读先进集体，你会推荐哪个班，请写出你的理由．23．在四边形中，一条边上的两个角称为邻角. 一条边上的邻角相等，且这条边的对边上的邻角也相等，这样的四边形叫做 IT 形 . 请你根据研究平行四边形及特殊四边形的方法，写出 IT形的性质，把你的发现都写出来 .五、解答题：（本题共16分，第 24题 8 分，第 25题 8 分）24．如图，四边形ABCD是正方形，E是CD垂直平分线上的点，点 E 关于 BD 的对称点是 E'，直线 DE 与直线 BE'交于点 F .A B（1）若点E是CD边的中点，连接AF ，则FAD ＝；E'F（2）小明从老师那里了解到，只要点 E 不在正方形的中心，则直线 AF 与 AD 所夹锐角不变．他尝试改变点 E 的位置，计算相应角度，验证老师的说法．①如图，将点 E 选在正方形内，且△ EAB为等边三角形，求出直线AF 与AD 所夹锐角的度数；D CEA B E'E②请你继续研究这个问题，可以延续小明的想法，也可用其它方法 .D C F我想沿用小明的想法，把点 E 选在CD 垂直平分线上的另一个特殊位置，我选择的位置是⋯⋯我没有沿用小明的想法，我的想法是⋯⋯我选择小明的想法；（填“用”或“不用”）并简述求直线度数的思路．AF与AD 所夹锐角A BD C 25．对于正数 x ，用符号 [ x] 表示 x 的整数部分，例如： [0.1] 0 ，[2.5] 2 ，[3] 3 ．点 A(a ,b)在第一象限内，以 A 为对角线的交点画一个矩形，使它的边分别与两坐标轴垂直. 其中垂直于y 轴的边长为 a ，垂直于 x 轴的边长为 [ b] 1，那么，把这个矩形覆盖的区域叫做点 A 的矩形域．例如：点(3, 3 ) 的矩形域是一个以2(3, 3 ) 为对角线交点，长为23，宽为 2 的矩形所覆盖的区域，如图 1 所示，它的面积是6．y321- 1O 1234 5 x- 1y7654321- 1O 12345x- 1图 1图 2根据上面的定义，回答下列问题：（ 1）在图 2 所示的坐标系中画出点(2, 7) 的矩形域，该矩形域的面积是；2（7),Q( a,70) 的矩形域重叠部分面积为1，求 a 的值；2）点 P(2,)(a22（ 3）已知点 B(m, n )(m0)在直线 y x 1上，且点 B 的矩形域的面积S满足 4S 5 ，那么 m 的取值范围是．（直接写出结果）八年级第二学期期末练习数学答案2019.7一、选择题（本题共30 分，每小题3 分）题号12345678910答案C B C C B A D D D A 二、填空题（本题共18 分，每小题 3 分）11． x212．113． 4214．815．3；3；乙同学16． 1 x 0说明：第15 题每空1分，共 3分.三、解答题（本题共22 分，第17— 19 题每小题 4 分，第 20— 21 题每小题 5 分）17．解：原式＝2333 ------------------------------3分＝53 ------------------------------4分18．证明：∵四边形ABCD是平行四边形，∴AD∥BC，AD BC.------------------------------1分∵AE CF，A E D ∴ DE BF .------------------------------2分EBFD 是B F C∴ 四边形平行四边形 .------------------------------ 3 分∴ BE DF .------------------------------ 4 分证法二：∵四边形ABCD是平行四边形，∴ AB DC， A C.------------------------------1分A E D ∵ AE CF .------------------------------2分∴ VBAE VDCF .------------------------------3分∴ BE DF .------------------------------4分B F C 19．解法一：∵x51，∴ x1 5 .∴ x22x x22x 1 1 (x 1)2 1------------------------------ 2 分( 5)2 14 .解法二：∵ x5 1，∴ x 22x x(x 2) ( 5 1)( 5 1 2)( 5)21------------------------------4分------------------------------2 分4 .------------------------------ 4分注：结论错，有对根式计算正确的部分给1 分。

2018-2019学年北京市海淀区高一第二学期期末复习测试数学试题一、单选题1．不等式2230x x +-<的解集为（ ） A ．{|3x x <-或1}x > B ．{|1x x <-或3}x > C ．{|13}x x -<< D ．{|31}x x -<<【答案】D【解析】根据不含参数的一元二次不等式的解法，可直接求出结果. 【详解】由2230x x +-<得(3)(1)0x x +-<，解得31x -<<. 故选D 【点睛】本题主要考查一元二次不等式，熟记不含参数的一元二次不等式的解法即可，属于基础题型.2．若等差数列{}n a 中，33a =，则{}n a 的前5项和5S 等于（ ） A ．10 B ．15C ．20D ．30【答案】B【解析】根据等差数列的性质，得到535S a =，进而可求出结果. 【详解】因为等差数列{}n a 中，33a =， 则{}n a 的前5项和15535()5152a a S a +===. 故选B 【点睛】本题主要考查等差数列，熟记等差数列的性质即可，属于基础题型. 3．当3,5,7a b c ===时，执行如图所示的程序框图，输出的m 值为（ ）A ．12B ．12-C．2D． 【答案】B【解析】根据框图，逐步执行，即可得出结果. 【详解】执行程序框图如下： 输入3,5,7a b c ===，则22219254915z a b c =+-=+-=-，2223530z ab ==⨯⨯=，则12151302z m z ==-=-， 输出12m =-. 故选B 【点睛】本题主要考查程序框图，分析框图的作用，逐步执行即可，属于常考题型. 4．设,,a b c ∈R 且a b >，则下列不等式成立的是（ ） A ．c a c b -<- B ．22ac bc >C ．11a b< D ．1b a< 【答案】A【解析】 A 项，由a b >得到a b -<-，则c a c b -<-，故A 项正确；B 项，当0c =时，该不等式不成立，故B 项错误；C 项，当1a =，2b =-时，112>-，即不等式11a b <不成立，故C 项错误；D项，当1a =-，2b =-时，21b a =>，即不等式1b a<不成立，故D 项错误． 综上所述，故选A ．5．若向面积为2的ABC ∆内任取一点P ，并连接PB ，PC ，则PBC ∆的面积小于1的概率为（ ） A ．14B ．12C ．23D ．34【答案】D【解析】记事件A={△PBC 的面积小于1}，基本事件空间是三角形ABC 的面积,(如图)事件A 的几何度量为图中阴影部分的面积(DE 是三角形的中位线)，因为阴影部分的面积是整个三角形面积的34，所以P(A)=34.本题选择D 选项.点睛：数形结合为几何概型问题的解决提供了简捷直观的解法．用图解题的关键：用图形准确表示出试验的全部结果所构成的区域，由题意将已知条件转化为事件A 满足的不等式，在图形中画出事件A 发生的区域，据此求解几何概型即可.6．某小型服装厂生产一种风衣，日销售量x （件）与单价P （元）之间的关系为1602P x =-，生产x 件所需成本为C （元），其中50030C x =+元，若要求每天获利不少于1300元，则日销量x 的取值范围是（ ） A ．2030x ≤≤ B ．2045x ≤≤ C ．1530x ≤≤ D ．1545x ≤≤【答案】B【解析】设该厂每天获得的利润为y 元，则2(1602)(50030)2130500y x x x x x =-⋅-+=-+-，(080)x <<，根据题意知，221305001300x x -+-≥，解得：2045x ≤≤， 所以当2045x ≤≤时，每天获得的利润不少于1300元，故选B ．点睛：考查了根据实际问题分析和解决问题的能力，以及转化与化归的能力，对于函数的应用问题：（1）函数模型的关键是找到一个影响求解目标函数的变量，以这个变量为自变量表达其他需要的量，综合各种条件建立数学模型；（2）在实际问题的函数模型中要特别注意函数的定义域，它是实际问题决定的，不是由建立的函数解析式决定的．7．在ABC ∆中，,,A B C ∠∠∠所对应的边分别为a,b,c 若30,C a ︒∠==，则B Ð等于（ ）A ．45︒B ．105︒C ．15︒或105︒D ．45︒或135︒【答案】C【解析】根据题中条件，结合正弦定理，先求出A ∠，再由三角形内角和为180︒，即可求出结果. 【详解】因为在ABC ∆中，30,C a ︒∠==，由正弦定理可得sin sin a c A C =，所以sin 1sin 22a C A c ===， 所以45A ∠=或135，因此1804530105B ∠=--=或1801353015B ∠=--=. 故选C 【点睛】本题主要考查解三角形，熟记正弦定理即可，属于常考题型.8．某校为了了解学生近视的情况，对四个非毕业年级各班的近视学生人数做了统计，每个年级都有7个班，如果某个年级的每个班的近视人数都不超过5人，则认定该年级为“学生视力保护达标年级”，这四个年级各班近视学生人数情况统计如下表： 初一年级 平均值为2，方差为2 初二年级 平均值为1，方差大于0 高一年级 中位数为3，众数为4 高二年级 平均值为3，中位数为4从表中数据可知：一定是“学生视力保护达标年级”的是（ ） A ．初一年级B ．初二年级C ．高一年级D ．高二年级【答案】A【解析】根据平均值、方差、中位数以及众数的实际意义，即可得出结果. 【详解】能反应“学生视力保护达标年级”的是平均值和方差；平均值反应数据的平均水平，方差反应数据的波动大小，方差越大，波动越大.高一年级，知道中位数与众数，不能判断出是否达标，高二年级知道平均数与中位数，也不能判断是否达标；故排除CD ；初二年级，方差大于0，但不确定具体取值，因此初二年级也不能判断是否达标； 初一年级，平均数和方差均为2，满足题意，因为若有一个数据大于5，方差必然大于2. 故选A 【点睛】本题主要考查平均数、方差、中位数、众数等，熟记其实际意义即可，属于基础题型.二、填空题9．若实数a ， b 满足02a <<， 01b <<，则a b -的取值范围是__________． 【答案】()1,2-【解析】01,10b b <<∴-<-<，02,12a a b <<∴-<-<，故答案为()1,2-.10．公比为2的等比数列{}n a 中，若123a a +=，则34a a +的值为_______. 【答案】12【解析】根据23412()a a q a a +=+，结合题中条件，即可求出结果.【详解】因为等比数列{}n a 公比为2，且123a a +=，所以23412()12a a q a a +=+=.故答案为12 【点睛】本题主要考查等比数列，熟记等比数列的性质即可，属于基础题型. 11．如图，若5N =，则输出的S 值等于_______【答案】56【解析】根据程序框图，逐步执行，即可得出结果. 【详解】 执行框图如下：输入5N =，初始值1,0k S ==； 第一步：110122S =+=⨯，15<，进入循环； 第二步：112112,2233k S =+==+=´，25<，进入循环；第三步：213213,3344k S =+==+=´，35<，进入循环；第四步：314314,4455k S =+==+=´，45<，进入循环；第五步：415415,5566k S =+==+=´，结束循环，输出56S =；故答案为56【点睛】本题主要考查程序框图，分析框图的作用，逐步执行即可，属于常考题型.12．函数24()(0)x x f x x x-+-=>的最大值为______,此时x 的值为______.【答案】-3 2【解析】先将原式化为4()()1f x x x=-++，再由基本不等式，即可求出结果. 【详解】因为244()()1x x f x x x x-+-==-++，又0x >，所以44x x+≥=，当且仅当2x =时取等号； 此时244()()1413x x f x x x x-+-==-++≤-+=-.即()f x 最大值为3-，此时2x =. 【点睛】本题主要考查求函数的最值，熟记基本不等式即可，属于常考题型.13．高一某研究性学习小组随机抽取了100名年龄在10岁到60岁的市民进行问卷调查，并制作了频率分布直方图（如图），从图中数据可知a =__,现从上述年龄在20岁到50岁的市民中按年龄段采用分层抽样的方法抽取30人，则在[20,30)年龄段抽取的人数应为__【答案】0.035 10【解析】根据频率之和为1，结合频率分布直方图中数据，即可求出a 的值；根据分层抽样确定抽样比，进而可求出抽取的人数. 【详解】由题意可得，(0.0050.0150.0200.025)101a ++++⨯=，解得0.035a =； 因为在20岁到50岁的市民中按年龄段采用分层抽样的方法抽取30人，20岁到50岁的市民中20岁到30岁所占比例为0.02510.0250.0350.0153=++，故在[20,30)年龄段抽取的人数应为130103⨯=.故答案为(1). 0.035 (2). 10 【点睛】本题主要考查频率分布直方图，会分析频率分组直方图即可，属于基础题型.14．设数列{}n a 使得10a =，且对任意的*n ∈N ，均有1n n a a n +-=，则3a 所有可能的取值构成的集合为：___,64a 的最大值为__. 【答案】{3,1,1,3}-- 2016【解析】根据1n n a a n +-=，10a =，逐步计算，即可求出3a 所有可能的取值；由1n n a a n +-=，要使n a 取最大值，只需{}n a 为增数列，得到1n n n a a +-=，由累加法求出n a ，进而可求出结果. 【详解】因为数列{}n a 使得10a =，且对任意的*n ∈N ，均有1n n a a n +-=， 所以211a a -=，因此21a =或21a =-；又322a a -=，所以322a a -=±，因此312a =±或312a =-±， 即3a 所有可能的取值为3,1,1,3--，故3a 所有可能的取值构成的集合为{3,1,1,3}--； 若n a 取最大值，则{}n a 必为增数列，即10n n a a +->， 所以有1n n n a a +-=，因此211a a -=，322a a -=，…，11n n n a a -=--， 以上各式相加得112...(1)n n a a =+++--， 所以(1)12...(1)2n n n n a -=+++-=，因此64636420162a ⨯==. 故答案为 (1). {3,1,1,3}-- (2). 2016 【点睛】本题主要考查数列的应用，由数列的递推公式求解即可，属于常考题型.三、解答题15．已知公差不为零的等差数列{}n a 满足11a =，2a 是1a 与5a 的等比中项 （I ）求数列{}n a 的通项公式；（II ）设2n an b =，判断数列{}n b 是否为等比数列。

2018-2019学年北京市海淀区八一学校七年级（下）期末数学试卷一、选择题（每小题3分，共30分）1．（3分）已知三角形的两边3a =，5b =，第三边是c ，则c 的取值范围是( )A ．35c <<B ．28c <<C ．25c <<D ．38c <<2．（3分）下列调查中，适合用全面调查方式的是( )A ．了解一批IPAD 的使用寿命B ．了解电视栏目《朗读者》的收视率C ．了解某班学生对国家“一带一路”战略的知晓率D ．了解某鱼塘中鱼的数量3．（3分）下列邮票中的多边形中，内角和等于540︒的是( )A ．B ．C ．D ．4．（3分）如图，天平左盘中物体A 的质量为m g ，天平右盘中每个砝码的质量都是1g ，则m 的取值范围在数轴上可表示为( )A ．B ．C ．D ．5．（3分）若m n <，则下列不等式中，正确的是( )A ．44m n ->-B ．55m n >C ．33m n -<-D ．2121m n +<+6．（3分）若ABC ∆中，90A ∠=︒，且30B C ∠-∠=︒，那么C ∠的度数为( )A ．30︒B ．40︒C ．50︒D ．60︒7．（3分）如图所示，已知//AC ED ，30C ∠=︒，40CBE ∠=︒，则BED ∠的度数是( )A ．60︒B ．80︒C ．70︒D ．50︒8．（3分）如图，已知12∠=∠，AC AD =，要使ABC AED ∆≅∆，还需添加一个条件，那么在①AB AE =，②BC ED =，③C D ∠=∠，④B E ∠=∠，这四个关系中可以选择的是( )A ．①②③B ．①②④C ．①③④D ．②③④9．（3分）小文同学统计了某小区部分居民每周使用共享单车的时间，并绘制了统计图，如图所示．下面有四个推断：①小文此次一共调查了100位小区居民②每周使用时间不足15分钟的人数多于4560-分钟的人数③每周使用时间超过30分钟的人数超过调查总人数的一半④每周使用时间在1530-分钟的人数最多根据图中信息，上述说法中正确的是( )A ．①④B ．①③C ．②③D ．②④10．（3分）如图，//AB CD ，BAC ∠与ACD ∠的平分线相交于点G ，EG AC ⊥于点E ，F 为AC 中点，GH CD ⊥于H ，FGC FCG ∠=∠．下列说法正确的是( )①AG CG ⊥；②BAG CGE ∠=∠；③AFG GFC S S ∆∆=；④若:2:7EGH ECH ∠∠=，则150AFG ∠=︒．A ．①③④B ．②③C ．①②③D ．①②③④二、填空题（本题共14分，每小题2分）11．（2分）写出一个解为11x y =⎧⎨=-⎩的二元一次方程是 ． 12．（2分）在生活中，我们常常看到在电线杆的两侧拉有两根钢线用来固定电线杆（如图所示），这样做的数学原理是 ．13．（2分）《九章算术》中记载：“今有大器五、小器一容三斛；大器一、小器五容二斛．问大、小器各容几何？”其大意是：今有大容器5个，小容器1个，总容量为3斛；大容器1个，小容器5个，总容量为2斛．问大容器、小容器的容积各是多少斛？设大容器的容积为x 斛，小容器的容积为y 斛，根据题意，可列方程组为 （斛：古量器名，容量单位）．14．（2分）一个多边形的内角和是外角和的2倍，则这个多边形的边数为 ．15．（2分）关于x 的不等式23x a --的解集如图所示，则a 的值是 ．16．（2分）如图，BE是ABD∠的平分线，CF是ACD∠的平分线，BE与CF交于G，若140BDC∠=︒，110BGC∠=︒，则A∠的度数为︒．17．（2分）某公园划船项目收费标准如下：船型两人船（限乘两人）四人船（限乘四人）六人船（限乘六人）八人船（限乘八人）每船租金（元/小时）90100130150某班18名同学一起去该公园划船，若每人划船的时间均为1小时，则租船的总费用最低为元．三、解答题：（共56分，18-21题每题4分，22，23，24，26题每题5分，25题6分，27题7分，28题7分）18．（4分）解方程组451 23x yx y-=-⎧⎨+=⎩19．（4分）解不等式2133xx-<-，并把它的解集在数轴上表示出来．20．（4分）解不等式组3221152x xx x-⎧⎪++⎨<⎪⎩并写出它的所有非负整数解．21．（4分）如图，已知ABC∆中，9AB=，12BC=，5AC=．（1）画出ABC∆的高AD和BE；（2）画出ABC∆的中线CF；（3）计算ADBE的值是．22．（5分）如图，ABC∆中，CD是ACB∠的角平分线，//DE AC，交BC于点E，20B∠=︒，44ADC∠=︒，求DEC∆各内角的度数．23．（5分）已知关于x，y的二元一次方程组2231x y mx y m-=⎧⎨+=-⎩的解满足x y<，求m的取值范围．24．（5分）如图，在ABC∆中，D是边AB上一点，E是边AC的中点，作//CF AB交DE 的延长线于点F．（1）证明：ADE CFE∆≅∆；（2）若B ACB∠=∠，5CE=，7CF=，求DB．25．（6分）某汽车专卖店销售A，B两种型号的新能源汽车．上周售出1辆A型车和3辆B 型车，销售额为96万元；本周已售出2辆A型车和1辆B型车，销售额为62万元．（1）求每辆A型车和B型车的售价各为多少万元．（2）甲公司拟向该店购买A，B两种型号的新能源汽车共6辆，且A型号车不少于2辆，购车费不少于130万元，则有哪几种购车方案？26．（5分）某综合实践小组为了了解本校学生参加课外读书活动的情况，随机抽取部分学生，调查其最喜欢的图书类别，并根据调查结果绘制成如下不完整的统计表与统计图：图书类别画记 人数 百分比 文学类艺体类正 5 科普类其他14 合计 a 100%请结合图中的信息解答下列问题：（1）随机抽取的样本容量a 为 ；（2）在扇形统计图中，“艺体类”所在的扇形圆心角应等于 度；（3）补全条形统计图；（4）已知该校有600名学生，估计全校最喜欢文学类图书的学生有 人．27．（7分）定义：对任意一个两位数a ，如果a 满足个位数字与十位数字互不相同，且都不为零，那么称这个两位数为“迥异数”．将一个“迥异数”个位数字与十位数字对调后得到一个新的两位数，把这个新两位数与原两位数的和与11的商记为f （a ）．例如：12a =，对调个位数字与十位数字得到新两位数21，新两位数与原两位数的和为211233+=，和与11的商为33113÷=，所以(12)3f =．根据以上定义，回答下列问题：（1）填空：①下列两位数：20，21，22中，“迥异数”为 ．②计算：(35)f = ，(10)f m n += ．（2）如果一个“迥异数” b 的十位数字是k ，个位数字是2(1)m +，且f （b ）9=；另一个“迥异数” c 的十位数字是4m +，个位数字是21k -，且f （c ）11=，请求出“迥异数” b 和c ．（3）如果一个“迥异数” m 的十位数字是x ，个位数字是3x -，另一个“迥异数” n 的十位数字是4x -，个位数字是2，且满足()()7f m f n -<，请直接写出满足条件的所有x 的值 ．28．（7分）如图，在直角三角形ABC 中，90ACB ∠=︒，45BAC ∠=︒．点P 是直线AC 上一个动点（点P 不与点A ，C 重合），连接BP ，在线段BC 的延长线上取一点D ，使得BPC DPC ∠=∠．过点B 作BE DP ⊥，交直线DP 于点E ．（1）如图1，当点P 在线段AC 上时，若60BPC ∠=︒，则ABE ∠= ；（2）当点P 在线段CA 的延长线上时，在图2中依题意补全图形，并判断ABE ∠与ABP ∠有怎样的数量关系，写出你的结论，并证明；（3）在点P 运动的过程中，直接写出ABE ∠与ABP ∠的数量关系为 ．2018-2019学年北京市海淀区八一学校七年级（下）期末数学试卷参考答案与试题解析一、选择题（每小题3分，共30分）1．（3分）已知三角形的两边3a =，5b =，第三边是c ，则c 的取值范围是( )A ．35c <<B ．28c <<C ．25c <<D ．38c <<【解答】解：三角形的两边3a =，5b =，第三边是c ，5353c ∴-<<+，28c ∴<<．故选：B ．2．（3分）下列调查中，适合用全面调查方式的是( )A ．了解一批IPAD 的使用寿命B ．了解电视栏目《朗读者》的收视率C ．了解某班学生对国家“一带一路”战略的知晓率D ．了解某鱼塘中鱼的数量【解答】解：A 、了解一批IPAD 的使用寿命，适合用抽样调查方式；B 、了解电视栏目《朗读者》的收视率，适合用抽样调查方式；C 、了解某班学生对国家“一带一路”战略的知晓率，适合用全面调查方式；D 、了解某鱼塘中鱼的数量，适合用抽样调查方式；故选：C ．3．（3分）下列邮票中的多边形中，内角和等于540︒的是( )A ．B ．C ．D ．【解答】解：设这个多边形的边数为n ，则(2)180540n -︒=︒，解得5n =．故选：B ．4．（3分）如图，天平左盘中物体A 的质量为m g ，天平右盘中每个砝码的质量都是1g ，则m 的取值范围在数轴上可表示为( )A ．B ．C ．D ．【解答】解：根据题意得：12m m >⎧⎨<⎩， 解得：12m <<，故选：D ．5．（3分）若m n <，则下列不等式中，正确的是( )A ．44m n ->-B ．55m n >C ．33m n -<-D ．2121m n +<+【解答】解：已知m n <，A 、44m n -<-，故A 选项错误；B 、55m n <，故B 选项错误； C 、33m n ->-，故C 选项错误；D 、2121m n +<+，故D 选项正确．故选：D ．6．（3分）若ABC ∆中，90A ∠=︒，且30B C ∠-∠=︒，那么C ∠的度数为( )A ．30︒B ．40︒C ．50︒D ．60︒【解答】解：90A ∠=︒，90B C ∴∠+∠=︒，30∠-∠=︒，B C∠=︒，C∴∠=︒，30B60故选：A．7．（3分）如图所示，已知//∠的度数是()CBE∠=︒，则BED∠=︒，40AC ED，30CA．60︒B．80︒C．70︒D．50︒【解答】解：30CBE∠=︒，∠=︒，40CCAE C CBE∴∠=∠+∠=︒，70AC ED，//∴∠=∠=︒，70BED CAE故选：C．8．（3分）如图，已知12∠=∠，AC AD∆≅∆，还需添加一个条件，那=，要使ABC AED么在①AB AE∠=∠，这四个关系中可以选择的是=，②BC ED=，③C D∠=∠，④B E()A．①②③B．①②④C．①③④D．②③④【解答】解：12∠=∠，EAB EAB∴∠+∠=∠+∠，12即CAB DAE∠=∠，①加上条件AB AE=可利用SAS定理证明ABC AED∆≅∆；②加上BC ED∆≅∆；=不能证明ABC AED③加上C D∆≅∆；∠=∠可利用ASA证明ABC AED④加上B E∠=∠可利用AAS证明ABC AED∆≅∆；故选：C．9．（3分）小文同学统计了某小区部分居民每周使用共享单车的时间，并绘制了统计图，如图所示．下面有四个推断：①小文此次一共调查了100位小区居民②每周使用时间不足15分钟的人数多于4560-分钟的人数 ③每周使用时间超过30分钟的人数超过调查总人数的一半 ④每周使用时间在1530-分钟的人数最多 根据图中信息，上述说法中正确的是( )A ．①④B ．①③C ．②③D ．②④【解答】解：①小文此次调查的小区居民的人数为10602010100+++=（位)，此结论正确；②由频数直方图知，每周使用时间不足15分钟的人数与4560-分钟的人数相同，均为10人，此结论错误；③每周使用时间超过30分钟的人数占调查总人数的比例为2010310010+=，此结论错误； ④每周使用时间在1530-分钟的人数最多，有60人，此结论正确； 故选：A ．10．（3分）如图，//AB CD ，BAC ∠与ACD ∠的平分线相交于点G ，EG AC ⊥于点E ，F 为AC 中点，GH CD ⊥于H ，FGC FCG ∠=∠．下列说法正确的是( )①AG CG ⊥；②BAG CGE ∠=∠；③AFG GFC S S ∆∆=；④若:2:7EGH ECH ∠∠=，则150AFG ∠=︒．A ．①③④B ．②③C ．①②③D ．①②③④【解答】解：//AB CD ，180BAC ACD ∴∠+∠=︒，BAC ∠与DCA ∠的平分线相交于点G ，11118090222GAC GCA BAC ACD ∴∠+∠=∠+∠=⨯︒=︒，180GAC GCA AGC ∠+∠+=∠︒， 90AGC ∴∠=︒， AG CG ∴⊥，故①正确；90AGE EGC ∠+∠=︒，90AGE GAE ∠+∠=︒， CGE GAC ∴∠=∠，故BAG CGE ∠=∠，故②正确；F 为AC 中点，AF CF ∴=，AFG CFG S S ∆∆∴=，故③正确；④中，根据题意，得：在四边形GECH 中，180EGH ECH ∠+∠=︒． 又:2:7EGH ECH ∠∠=， 2180409EGH ∴∠=︒⨯=︒，71801409ECH ∠=︒⨯=︒． CG 平分ECH ∠， 1702FCG ECH ∴∠=∠=︒，AG CG ⊥，F 为AC 中点， FG FC ∴=，70FGC FCG ∴∠=∠=︒， 140AFG ∴∠=︒，故④错误．故选：C ．二、填空题（本题共14分，每小题2分）11．（2分）写出一个解为11x y =⎧⎨=-⎩的二元一次方程是 0x y += ．【解答】解：根据题意得：0x y +=． 故答案为：0x y +=12．（2分）在生活中，我们常常看到在电线杆的两侧拉有两根钢线用来固定电线杆（如图所示），这样做的数学原理是三角形的稳定性．【解答】解：结合图形，为了防止电线杆倾倒，常常在电线杆上拉两根钢筋来加固电线杆，所以这样做根据的数学道理是三角形的稳定性．故答案是：三角形的稳定性．13．（2分）《九章算术》中记载：“今有大器五、小器一容三斛；大器一、小器五容二斛．问大、小器各容几何？”其大意是：今有大容器5个，小容器1个，总容量为3斛；大容器1个，小容器5个，总容量为2斛．问大容器、小容器的容积各是多少斛？设大容器的容积为x斛，小容器的容积为y斛，根据题意，可列方程组为5352x yx y+=⎧⎨+=⎩（斛：古量器名，容量单位）．【解答】解：设大容器的容积为x斛，小容器的容积为y斛，根据题意得：5352x yx y+=⎧⎨+=⎩，故答案为：5352x yx y+=⎧⎨+=⎩．14．（2分）一个多边形的内角和是外角和的2倍，则这个多边形的边数为6．【解答】解：多边形的外角和是360度，多边形的内角和是外角和的2倍，则内角和是720度，72018026÷+=，∴这个多边形的边数为6．故答案为：6．15．（2分）关于x 的不等式23x a --的解集如图所示，则a 的值是 1 ．【解答】解：23x a --， 32a x-∴， 1x -，1a ∴=．故答案为：1．16．（2分）如图，BE 是ABD ∠的平分线，CF 是ACD ∠的平分线，BE 与CF 交于G ，若140BDC ∠=︒，110BGC ∠=︒，则A ∠的度数为 80 ︒．【解答】解：连接BC ， 140BDC ∠=︒，18014040DBC DCB ∴∠+∠=︒-︒=︒， 110BGC ∠=︒，18011070GBC GCB ∴∠+∠=︒-︒=︒， 704030GBD GCD ∴∠+∠=︒-︒=︒，BE 是ABD ∠的平分线，CF 是ACD ∠的平分线，30ABG ACG GBD GCD ∴∠+∠=∠+∠=︒，在ABC ∆中，180********A ∠=︒-︒-︒-︒=︒． 故A ∠的度数为80︒．17．（2分）某公园划船项目收费标准如下：某班18名同学一起去该公园划船，若每人划船的时间均为1小时，则租船的总费用最低为380元．【解答】解：共有18人，当租两人船时，1829∴÷=（艘)，每小时90元，∴租船费用为909810⨯=元，当租四人船时，1844÷=余2人，∴要租4艘四人船和1艘两人船，四人船每小时100元，∴租船费用为100490490⨯+=元，当租六人船时，1863÷=（艘)，每小时130元，∴租船费用为1303390⨯=元，当租八人船时，1882÷=余2人，∴要租2艘八人船和1艘两人船，8人船每小时150元，∴租船费用150290390⨯+=元当租1艘四人船，1艘6人船，1艘8人船，100130150380++=元而810490390380>>>，∴当租1艘四人船，1艘6人船，1艘8人船费用最低是380元，故答案为：380．三、解答题：（共56分，18-21题每题4分，22，23，24，26题每题5分，25题6分，27题7分，28题7分）18．（4分）解方程组451 23x yx y-=-⎧⎨+=⎩【解答】解：45123x yx y-=-⎧⎨+=⎩①②，①+②5⨯得：1414x=，解得：1x=，把1x=代入②得：1y=，则方程组的解为11x y =⎧⎨=⎩．19．（4分）解不等式2133x x -<-，并把它的解集在数轴上表示出来．【解答】解：去分母，得2193x x -<-． 移项，得2391x x +<+． 合并，得510x <． 系数化1，得2x <．不等式的解集是在数轴上表示如下：20．（4分）解不等式组3221152x x x x -⎧⎪++⎨<⎪⎩ 并写出它的所有非负整数解．【解答】解：3221152x x x x -⎧⎪⎨++<⎪⎩①②，解不等式①得1x ， 解不等式②得3x >-，∴不等式组的解集是：31x -<． ∴不等式组的非负整数解为0，1．21．（4分）如图，已知ABC ∆中，9AB =，12BC =，5AC =． （1）画出ABC ∆的高AD 和BE ； （2）画出ABC ∆的中线CF ； （3）计算AD BE 的值是 512．【解答】解：如图，（1）AD和BE即为所求；（2）CF即为所求；（3）AD和BE是ABC∆的高，∴1122BC AD AC BE=，125AD BE∴=，∴ADBE的值是512．故答案为：512．22．（5分）如图，ABC∆中，CD是ACB∠的角平分线，//DE AC，交BC于点E，20B∠=︒，44ADC∠=︒，求DEC∆各内角的度数．【解答】解：CD是ACB∠的角平分线，ACD BCD∴∠=∠，//DE AC，CDE ACD∴∠=∠，CDE DCE∴∠=∠，∴设ACD DCE x∠=∠=，2ACB x∴∠=，180180202A B ACB x∴∠=︒-∠-∠=︒-︒-，44ADC∠=︒，44180202180x x∴︒+︒-︒-+=︒，24x∴=︒，24CDE DCE∴∠=∠=︒，1802424132CED ∴∠=︒-︒-︒=︒．23．（5分）已知关于x ，y 的二元一次方程组2231x y mx y m -=⎧⎨+=-⎩的解满足x y <，求m 的取值范围．【解答】解：解二元一次方程组2231x y m x y m -=⎧⎨+=-⎩得1727x m y ⎧=-⎪⎪⎨⎪=-⎪⎩，x y <，1277m ∴-<-， 解得17m <-．所以m 的取值范围是17m <-．24．（5分）如图，在ABC ∆中，D 是边AB 上一点，E 是边AC 的中点，作//CF AB 交DE 的延长线于点F ．（1）证明：ADE CFE ∆≅∆；（2）若B ACB ∠=∠，5CE =，7CF =，求DB ．【解答】（1）证明：E 是边AC 的中点，AE CE ∴=．又//CF AB ，A ACF ∴∠=∠，ADF F ∠=∠，在ADE ∆与CFE ∆中， ADF F A ACF AE CE ∠=∠⎧⎪∠=∠⎨⎪=⎩()ADE CFE AAS ∴∆≅∆．（2）解：ADE CFE ∆≅∆，7CF =， 7CF AD ∴==，又B ACB ∠=∠， AB AC ∴=，E 是边AC 的中点，5CE =，210AC CE ∴==． 10AB ∴=，1073DB AB AD ∴=-=-=．25．（6分）某汽车专卖店销售A ，B 两种型号的新能源汽车．上周售出1辆A 型车和3辆B 型车，销售额为96万元；本周已售出2辆A 型车和1辆B 型车，销售额为62万元． （1）求每辆A 型车和B 型车的售价各为多少万元．（2）甲公司拟向该店购买A ，B 两种型号的新能源汽车共6辆，且A 型号车不少于2辆，购车费不少于130万元，则有哪几种购车方案？【解答】解：（1）每辆A 型车和B 型车的售价分别是x 万元、y 万元． 则396262x y x y +=⎧⎨+=⎩，解得1826.x y =⎧⎨=⎩，答：每辆A 型车的售价为18万元，每辆B 型车的售价为26万元；（2）设购买A 型车a 辆，则购买B 型车(6)a -辆，则依题意得 1826(6)130a a +-， 解得134a1234a ∴．a是正整数，2a∴=或3a=．共有两种方案：方案一：购买2辆A型车和4辆B型车；方案二：购买3辆A型车和3辆B型车；26．（5分）某综合实践小组为了了解本校学生参加课外读书活动的情况，随机抽取部分学生，调查其最喜欢的图书类别，并根据调查结果绘制成如下不完整的统计表与统计图：图书类别画记人数百分比文学类艺体类正5科普类其他14合计a100%请结合图中的信息解答下列问题：（1）随机抽取的样本容量a为50；（2）在扇形统计图中，“艺体类”所在的扇形圆心角应等于度；（3）补全条形统计图；（4）已知该校有600名学生，估计全校最喜欢文学类图书的学生有人．【解答】解：（1）1428%50a=÷=，故答案为：50；（2）在扇形统计图中，“艺体类”所在的扇形圆心角为：53603650︒⨯=︒，故答案为：36；（3）科普类有5022%11⨯=（人)，文艺类有：505111420---=（人)，补全的条形统计图如右图所示；（4）2060024050⨯=（人)， 答：全校最喜欢文学类图书的学生有240人，故答案为：240．27．（7分）定义：对任意一个两位数a ，如果a 满足个位数字与十位数字互不相同，且都不为零，那么称这个两位数为“迥异数”．将一个“迥异数”个位数字与十位数字对调后得到一个新的两位数，把这个新两位数与原两位数的和与11的商记为f （a ）．例如：12a =，对调个位数字与十位数字得到新两位数21，新两位数与原两位数的和为211233+=，和与11的商为33113÷=，所以(12)3f =．根据以上定义，回答下列问题：（1）填空：①下列两位数：20，21，22中，“迥异数”为 21 ．②计算：(35)f = ，(10)f m n += ．（2）如果一个“迥异数” b 的十位数字是k ，个位数字是2(1)m +，且f （b ）9=；另一个“迥异数” c 的十位数字是4m +，个位数字是21k -，且f （c ）11=，请求出“迥异数” b 和c ．（3）如果一个“迥异数” m 的十位数字是x ，个位数字是3x -，另一个“迥异数” n 的十位数字是4x -，个位数字是2，且满足()()7f m f n -<，请直接写出满足条件的所有x 的值 ．【解答】解：（1）①对任意一个两位数a ，如果a 满足个位数字与十位数字互不相同，且都不为零，那么称这个两位数为“迥异数”．∴ “迥异数”为21；②(35)(3553)118f =+÷=，(10)(1010)11f m n m n n m m n +=+++÷=+；（2）(10)f m n m n +=+，且f （b ）9=，2(1)9k m ∴++=①，f （c ）11=，42111m k ∴++-=②，联立①②解得23m k =⎧⎨=⎩， 故1032(21)36b =⨯+⨯+=，10(24)23165c =⨯++⨯-=；（3）()()7f m f n -<，3(42)7x x x ∴+---+<，解得8x <，30x ->，40x ->，4x ∴>，48x ∴<<，且x 为正整数，5x ∴=，6，7，当5x =时，52m =，12n =当6x =时，63m =，22n =（不合题意舍去）当7x =时，74m =，32n =．综上所述：x 为5或7．故答案为：21；8，m n +；5或7．28．（7分）如图，在直角三角形ABC 中，90ACB ∠=︒，45BAC ∠=︒．点P 是直线AC 上一个动点（点P 不与点A ，C 重合），连接BP ，在线段BC 的延长线上取一点D ，使得BPC DPC ∠=∠．过点B 作BE DP ⊥，交直线DP 于点E ．（1）如图1，当点P 在线段AC 上时，若60BPC ∠=︒，则ABE ∠= 15︒ ；（2）当点P 在线段CA 的延长线上时，在图2中依题意补全图形，并判断ABE ∠与ABP ∠有怎样的数量关系，写出你的结论，并证明；（3）在点P 运动的过程中，直接写出ABE ∠与ABP ∠的数量关系为 ．【解答】解：（1）90ACB ∠=︒，60BPC DPC ∠=∠=︒， 90ACD ∴∠=︒，30D ∠=︒，BE DP ⊥，90E ∴∠=︒，60EBD ∴∠=︒，45BAC ∠=︒，45ABC ∴∠=︒，15ABE EBD ABC ∴∠=∠-∠=︒；故答案为：15︒．（2）如图所示：ABE ABP ∠=∠，证明：BE DP ⊥，90EBD D ∴∠+∠=︒，90ACB ∠=︒，90DPC D ∴∠+∠=︒，EBD DPC ∴∠=∠，BPC DPC ∠=∠，EBD BPC ∴∠=∠，45BAC ∠=︒，45ABP BPC ∴∠=︒-∠，45ABC ∠=︒，45ABE ABC EBD EBD ∴∠=∠-∠=︒-∠，ABE ABP ∴∠=∠；（3）由（1）（2）可知：当点P在线段AC与CA的延长线上时，ABE ABP∠=∠，当点P在AC的延长线上时，如下图所示：设D DBP x∠=∠=，则2∠=，BPE x⊥，BE DP902∴∠=︒-，PBE x∠=︒，BACACB∠=︒，4590∴∠=︒，45ABCABE ABC CBP PBE x x x ∴∠=∠+∠+∠=︒++︒-=︒-，45902135∠=︒+，ABP x45ABE ABP∴∠+∠=︒．180所以当点P在线段AC与CA的延长线上时，ABE ABP∠=∠，当点P在AC延长线上时，180∠+∠=︒．ABE ABP故答案为：ABE ABP∠=∠，180∠+∠=︒．ABE ABP。

2018-2019学年北京市海淀区八年级（下）期末数学试卷一、选择题（本题共30分，每小题3分）在下列各题的四个选项中，只有一个是符合题意的1．（3分）下列实数中，是方程x2﹣4＝0的根的是（）A．1B．2C．3D．42．（3分）如图，在Rt△ABC中，∠C＝90°，BC＝6，AC＝8，则AB的长度为（）A．7B．8C．9D．103．（3分）在下列条件中，能判定四边形为平行四边形的是（）A．两组对边分别平行B．一组对边平行且另一组对边相等C．两组邻边相等D．对角线互相垂直4．（3分）下列各曲线中，不表示y是x的函数的是（）A．B．C．D．5．（3分）数据2，6，4，5，4，3的平均数和众数分别是（）A．5和4B．4和4C．4.5和4D．4和56．（3分）一元二次方程x2﹣8x﹣1＝0配方后可变形为（）A．（x+4）2＝17B．（x+4）2＝15C．（x﹣4）2＝15D．（x﹣4）2＝17 7．（3分）若点A（﹣3，y1），B（1，y2）都在直线y＝x+2上，则y1与y2的大小关系是（）A．y1＜y2B．y1＝y2C．y1＞y2D．无法比较大小8．（3分）如图，正方形ABCD的边长为，对角线AC，BD交于点O，E是AC延长线上一点，且CE＝CO，则BE的长度为（）A．B．C．D．29．（3分）对于一次函数y＝kx+b（k，b为常数），下表中给出5组自变量及其对应的函数值，其中恰好有1个函数值计算有误，则这个错误的函数值是（）X﹣10123Y2581214 A．5B．8C．12D．1410．（3分）博物馆作为征集、典藏、陈列和研究代表自然和人类文化遗产实物的场所，其存在的目的是为众提供知识、教育及欣赏服务．近年来，人们到博物馆学习参观的热情越来越高，2012﹣2018年我国博物馆参观人数统计如下：小明研究了这个统计图，得出四个结论：①2012年到2018年，我国博物馆参观人数持续增②2019年末我国博物馆参观人数估计将达到1082亿人次③2012年到2018年，我国博物馆参观人数年增幅最大的是2017年；④2016年到2018年，我国博物馆参观人数平均年增长率超过10%其中正确的是（）A．①③B．①②③C．①②④D．①②二、填空题（本题共18分，每小题3分）11．（3分）在▱ABCD中，若∠B＝110°，则∠D＝°．12．（3分）八年级（1）班甲、乙两个小组的10名学生进行飞镖训练，某次训练成绩如下甲组成绩（环）87889乙组成绩（环）98797由上表可知，甲、乙两组成绩更稳定的是．13．（3分）若关于x的一元二次方程x2+6x+m＝0有实数根，且所有实数根均为整数，请写出一个符合条件的常数m的值：m＝．14．（3分）如图，某港口P位于南北延伸的海岸线上，东面是大海远洋号，长峰号两艘轮船同时离开港P，各自沿固定方向航行，“远洋”号每小时航行12nmile，“长峰”号每小时航行16nmile，它们离开港口1小时后，分别到达A，B两个位置，且AB＝20nmile，已知“远洋”号沿着北偏东60°方向航行，那么“长峰”号航行的方向是．15．（3分）若一个矩形的长边的平方等于短边与其周长一半的积，则称这样的矩形为“优美矩形”．某公园在绿化时工作人员想利用如图所示的直角墙角（两边足够长）和长为38m的篱笆围成一个“优美矩形”形状的花园ABCD，其中边AB，AD为篱笆且AB大于AD．设AD为xm，依题意可列方程为．16．（3分）在平面直角坐标系xOy中，直线y＝kx+3与x，y轴分别交于点A，B，若将该直线向右平移5单位，线段AB扫过区域的边界恰好为菱形，则k的值为．三、解答题（本题共26分，第17题8分，第18，20题各5分，第19，21题各4分）17．（8分）解下列方程：（1）x2+2x﹣3＝0（用配方法）（2）2x2+5x﹣1＝0（用公式法）18．（5分）在平面直角坐标系xOy中，函数y＝kx+b的图象与直线y＝2x平行，且经过点A（1，6）（1）求一次函数y＝kx+b的解析式；（2）求一次函数y＝kx+b的图象与坐标轴围成的三角形的面积．19．（5分）下面是小丁设计的“利用直角三角形和它的斜边中点作矩形的尺规作图过程：已知：如图，在Rt△ABC中，∠ABC＝90°，O为AC的中点，求作：四边形ABCD，使得四边形ABCD为矩形．作法：①作射线BO，在线段BO的延长线上取点D，使得DO＝BO②连接AD，CD，则四边形ABCD为矩形根据小丁设计的尺规作图过程（1）使用直尺和圆规，在图中补全图形（保留作图痕迹）（2）完成下面的证明证明：∵点O为AC的中点，∴AO＝CO又∵DO＝BO，∴四边形ABCD为平行四边形（）∵∠ABC＝90°，∴▱ABCD为矩形（）20．（4分）方程x 2+2x +k ﹣4＝0有实数根 （1）求k 的取值范围；（2）若k 是该方程的一个根，求2k 2+6k ﹣5的值．21．（4分）小东和小明要测量校园里的一块四边形场地ABCD （如图所示）的周长，其中边CD 上有水池及建筑遮挡，没有办法直接测量其长度小东经测量得知AB ＝AD ＝5m ，∠A ＝60°，BC ＝12m ，∠ABC ＝150°小明说根据小东所得的数据可以求出CD 的长度．你同意小明的说法吗？若同意，请求出CD 的长度；若不同意，请说明理由．四、解答题（本题共13分，第22题7分，第23题6分）22．（7分）三月底，某学校迎来了以“学海通识品墨韵，开卷有益览书山”为主题的学习节活动为了让同学们更好的了解二十四节气的知识，本次学习节在沿袭以往经典项目的基础上，增设了十四节气之旅项目，并开展了相关知识竞赛该学校七、八年级各有400名学生参加了这次竞赛，现从七、八年级各随机抽取20名学生的成绩进行抽样调查 七年级：74 97 96 72 98 99 72 73 76 74 74 69 76 89 78 74 99 97 98 99 八年级：76 88 93 89 78 94 89 94 95 50 89 68 65 88 77 87 89 88 92 91 整理数据如下成绩 人数 年级 50≤x ≤5960≤x ≤6970≤x ≤7980≤x ≤8990≤x ≤100七年级 0 1 10 1 a 八年级 12386分析数据如下年级平均数中位数众数方差七年级84.27774138.56八年级84b89129.7根据以上信息，回答下列问题（1）a＝b＝；（2）你认为哪个年级知识竞赛的总体成绩较好，说明理由（至少从两个不同的角度说明推断的合理性）．（3）学校对知识竞赛成绩不低于80分的学生颁发优胜奖，请你估计学校七、八年级所有学生中获得优胜奖的大约有人．23．（6分）如图，在▱ABCD中，对角线AC，BD交于点O，过点B作BE⊥CD于点E，延长CD到点F，使DF＝CE，连接AF．（1）求证：四边形ABEF是矩形；（2）连接OF，若AB＝6，DE＝2，∠ADF＝45°，求OF的长度．五、解答题（本题共13分，第24题6分，第25题7分）24．（6分）如图，在平面直角坐标系xOy中，直线y＝kx+7与直线y＝x﹣2交于点A（3，m）（1）求k，m的值；（2）已知点P（n，n），过点P作垂直于y轴的直线与直线y＝x﹣2交于点M，过点P 作垂直于x轴的直线与直线y＝kx+7交于点N（P与N不重合）．若PN≤2PM，结合图象，求n的取值范围．25．（7分）在Rt△ABC中，∠BAC＝90°，点O是△ABC所在平面内一点，连接OA，延长OA到点E，使得AE＝OA，连按OC，过点B作BD与OC平行，并使∠DBC＝∠OCB，且BD＝OC，连按DE．（1）如图一，当点O在Rt△ABC内部时，①按题意补全图形；②猜想DE与BC的数量关系，并证明．（2）若AB＝AC（如图二），且∠OCB＝30°，∠OBC＝15°，求∠AED的大小．2018-2019学年北京市海淀区八年级（下）期末数学试卷参考答案与试题解析一、选择题（本题共30分，每小题3分）在下列各题的四个选项中，只有一个是符合题意的1．（3分）下列实数中，是方程x2﹣4＝0的根的是（）A．1B．2C．3D．4【分析】先把方程化为x2＝4，方程两边开平方得到x＝±＝±2，即可得到方程的两根．【解答】解：移项得x2＝4，开方得x＝±2，∴x1＝2，x2＝﹣2．故选：B．【点评】本题考查了解一元二次方程﹣直接开平方法，用直接开方法求一元二次方程的解的类型有：x2＝a（a≥0），ax2＝b（a，b同号且a≠0），（x+a）2＝b（b≥0），a （x+b）2＝c（a，c同号且a≠0）．法则：要把方程化为“左平方，右常数，先把系数化为1，再开平方取正负，分开求得方程解”；2．（3分）如图，在Rt△ABC中，∠C＝90°，BC＝6，AC＝8，则AB的长度为（）A．7B．8C．9D．10【分析】根据勾股定理即可得到结论．【解答】解：在Rt△ABC中，∠C＝90°，BC＝6，AC＝8，∴AB＝＝＝10，故选：D．【点评】本题考查了勾股定理，熟练掌握勾股定理是解题的关键．3．（3分）在下列条件中，能判定四边形为平行四边形的是（）A．两组对边分别平行B．一组对边平行且另一组对边相等C．两组邻边相等D．对角线互相垂直【分析】根据平行四边形的判定定理逐个判断即可．【解答】解：A、两组对边分别平行的四边形是平行四边形，故本选项符合题意；B、一组对边平行且另一组对边相等的四边形是等腰梯形，不是平行四边形，故本选项不符合题意；C、两组邻边相等的四边形不一定是平行四边形，故本选项不符合题意；D、对角线互相平分的四边形才是平行四边形，故本选项不符合题意；故选：A．【点评】本题考查了平行四边形的判定定理，能熟记平行四边形的判定定理的内容是解此题的关键，注意：平行四边形的判定定理有：①两组对边分别平行的四边形是平行四边形，②两组对边分别相等的四边形是平行四边形，③两组对角分别平行的四边形是平行四边形，④一组对边平行且相等的四边形是平行四边形，⑤对角线互相平分的四边形是平行四边形．4．（3分）下列各曲线中，不表示y是x的函数的是（）A．B．C．D．【分析】设在一个变化过程中有两个变量x与y，对于x的每一个确定的值，y都有唯一的值与其对应，那么就说y是x的函数，x是自变量．根据函数的意义即可求出答案．【解答】解：显然A、B、D选项中，对于自变量x的任何值，y都有唯一的值与之相对应，y是x的函数；C选项对于x取值时，y都有2个值与之相对应，则y不是x的函数；故选：C．【点评】本题主要考查了函数的定义，在定义中特别要注意，对于x的每一个值，y都有唯一的值与其对应．5．（3分）数据2，6，4，5，4，3的平均数和众数分别是（）A．5和4B．4和4C．4.5和4D．4和5【分析】根据平均数和众数的概念求解．【解答】解：这组数据的平均数是：（2+6+4+5+4+3）＝4；∵4出现了2次，出现的次数最多，∴这组数据的众数是4；故选：B．【点评】本题考查了众数和平均数的知识，一组数据中出现次数最多的数据叫做众数；平均数是指在一组数据中所有数据之和再除以数据的个数．6．（3分）一元二次方程x2﹣8x﹣1＝0配方后可变形为（）A．（x+4）2＝17B．（x+4）2＝15C．（x﹣4）2＝15D．（x﹣4）2＝17【分析】先把常数项移到方程右边，再把方程两边加上16，然后把方程左边写成完全平方形式即可．【解答】解：x2﹣8x＝1，x2﹣8x+16＝17，（x﹣4）2＝17．故选：D．【点评】本题考查了解一元二次方程﹣配方法：将一元二次方程配成（x+m）2＝n的形式，再利用直接开平方法求解，这种解一元二次方程的方法叫配方法．7．（3分）若点A（﹣3，y1），B（1，y2）都在直线y＝x+2上，则y1与y2的大小关系是（）A．y1＜y2B．y1＝y2C．y1＞y2D．无法比较大小【分析】先根据直线y＝x+2判断出函数图象的增减性，再根据各点横坐标的大小进行判断即可．【解答】解：∵直线y＝x+2，k＝＞0，∴y随x的增大而增大，又∵﹣3＜1，∴y1＜y2．故选：A．【点评】本题考查的是一次函数的增减性，即一次函数y＝kx+b（k≠0）中，当k＞0，y 随x的增大而增大；当k＜0，y随x的增大而减小．8．（3分）如图，正方形ABCD的边长为，对角线AC，BD交于点O，E是AC延长线上一点，且CE＝CO，则BE的长度为（）A．B．C．D．2【分析】利用正方形的性质得到OB＝OC＝BC＝1，OB⊥OC，则OE＝2，然后根据勾股定理计算BE的长．【解答】解：∵正方形ABCD的边长为，∴OB＝OC＝BC＝×＝1，OB⊥OC，∵CE＝OC，∴OE＝2，在Rt△OBE中，BE＝＝．故选：C．【点评】本题考查了正方形的性质：正方形的四条边都相等，四个角都是直角；正方形的两条对角线相等，互相垂直平分，并且每条对角线平分一组对角；正方形具有四边形、平行四边形、矩形、菱形的一切性质．9．（3分）对于一次函数y＝kx+b（k，b为常数），下表中给出5组自变量及其对应的函数值，其中恰好有1个函数值计算有误，则这个错误的函数值是（）X﹣10123Y2581214 A．5B．8C．12D．14【分析】经过观察5组自变量和相应的函数值得（﹣1，2），（0，5），（1，8），（3，14）符合解析式y＝3x+5，（2，12）不符合，即可判定．【解答】解：∵（﹣1，2），（0，5），（1，8），（3，14）符合解析式y＝3x+5，当x＝2时，y＝11≠12∴这个计算有误的函数值是12，故选：C．【点评】本题考查了一次函数图象上点的坐标特征，图象上点的坐标符合解析式是解决本题的关键．10．（3分）博物馆作为征集、典藏、陈列和研究代表自然和人类文化遗产实物的场所，其存在的目的是为众提供知识、教育及欣赏服务．近年来，人们到博物馆学习参观的热情越来越高，2012﹣2018年我国博物馆参观人数统计如下：小明研究了这个统计图，得出四个结论：①2012年到2018年，我国博物馆参观人数持续增②2019年末我国博物馆参观人数估计将达到1082亿人次③2012年到2018年，我国博物馆参观人数年增幅最大的是2017年；④2016年到2018年，我国博物馆参观人数平均年增长率超过10%其中正确的是（）A．①③B．①②③C．①②④D．①②【分析】根据条形统计图中的信息对4个结论矩形判断即可．【解答】解：①2012年到2018年，我国博物馆参观人数持续增，正确；②10.08×（1+）＝10.45，故2019年末我国博物馆参观人数估计将达到10.45亿人次；故错误；③2012年到2018年，我国博物馆参观人数年增幅最大的是2017年；正确；④设平均年增长率为x，则8.50（1+x）2＝10.08，解得：x＝0.0889，故2016年到2018年，我国博物馆参观人数平均年增长率是8.89%，故错误；故选：A．【点评】此题考查了条形统计图，弄清题中图形中的数据是解本题的关键．二、填空题（本题共18分，每小题3分）11．（3分）在▱ABCD中，若∠B＝110°，则∠D＝110°．【分析】直接利用平行四边形的对角相等即可得出答案．【解答】解：∵四边形ABCD是平行四边形，∴∠B＝∠D＝110°．故答案为：110．【点评】此题主要考查了平行四边形的性质，正确得出对角相等是解题关键．12．（3分）八年级（1）班甲、乙两个小组的10名学生进行飞镖训练，某次训练成绩如下甲组成绩（环）87889乙组成绩（环）98797由上表可知，甲、乙两组成绩更稳定的是甲．【分析】根据方差计算公式，进行计算，然后比较方差，小的稳定，在计算方差之前还需先计算平均数．【解答】解：甲＝＝8，乙＝＝8，＝[（8﹣8）2+（7﹣8）2+（8﹣8）2+（8﹣8）2+（9﹣8）2]＝0.4，＝[（9﹣8）2+（8﹣8）2+（7﹣8）2+（9﹣8）2+（7﹣8）2]＝0.8∵＜∴甲组成绩更稳定．故答案为：甲．【点评】考查平均数、方差的计算方法，理解方差是反映一组数据的波动大小的统计量，方差越小，数据越稳定．13．（3分）若关于x的一元二次方程x2+6x+m＝0有实数根，且所有实数根均为整数，请写出一个符合条件的常数m的值：m＝9．【分析】利用判别式的意义得到△＝62﹣4m≥0，解不等式得到m的范围，在此范围内取m＝0即可．【解答】解：△＝62﹣4m≥0，解得m≤9；当m＝0时，方程变形为x2+6x＝0，解得x1＝0，x2＝﹣6，所以m＝9满足条件．故答案为9．【点评】本题考查了根的判别式：一元二次方程ax2+bx+c＝0（a≠0）的根与△＝b2﹣4ac 有如下关系：当△＞0时，方程有两个不相等的实数根；当△＝0时，方程有两个相等的实数根；当△＜0时，方程无实数根．14．（3分）如图，某港口P位于南北延伸的海岸线上，东面是大海远洋号，长峰号两艘轮船同时离开港P，各自沿固定方向航行，“远洋”号每小时航行12nmile，“长峰”号每小时航行16nmile，它们离开港口1小时后，分别到达A，B两个位置，且AB＝20nmile，已知“远洋”号沿着北偏东60°方向航行，那么“长峰”号航行的方向是南偏东30°．【分析】由题意得：P与O重合，得出OA2+OB2＝AB2，由勾股定理的逆定理得出△PAB 是直角三角形，∠AOB＝90°，求出∠COP＝30°，即可得出答案．【解答】解：由题意得：P与O重合，如图所示：OA＝12nmile，OB＝16nmile，AB＝20nmile，∵122+162＝202，∴OA2+OB2＝AB2，∴△PAB是直角三角形，∴∠AOB＝90°，∵∠DOA＝60°，∴∠COP＝180°﹣90°﹣60°＝30°，∴“长峰”号航行的方向是南偏东30°，故答案为：南偏东30°．【点评】此题主要考查了直角三角形的判定、勾股定理的逆定理及方向角的理解及运用．利用勾股定理的逆定理得出△PAB为直角三角形是解题的关键．15．（3分）若一个矩形的长边的平方等于短边与其周长一半的积，则称这样的矩形为“优美矩形”．某公园在绿化时工作人员想利用如图所示的直角墙角（两边足够长）和长为38m的篱笆围成一个“优美矩形”形状的花园ABCD，其中边AB，AD为篱笆且AB大于AD．设AD为xm，依题意可列方程为（38﹣x）2＝38x．【分析】设AD为xm，根据“矩形的长边的平方等于短边与其周长一半的积”列出列出方程即可．【解答】解：设AD的长为x米，则AB的长为（38﹣x）m，根据题意得：（38﹣x）2＝38x，故答案为：（38﹣x）2＝38x．【点评】考查了由实际问题抽象出一元二次方程的知识，解题的关键是表示出另一边的长，难度不大．16．（3分）在平面直角坐标系xOy中，直线y＝kx+3与x，y轴分别交于点A，B，若将该直线向右平移5单位，线段AB扫过区域的边界恰好为菱形，则k的值为±．【分析】根据菱形的性质知AB＝5，由一次函数图象的性质和两点间的距离公式解答．【解答】解：令y＝0，则x＝﹣，即A（﹣，0）．令x＝0，则y＝3，即B（0，3）．∵将该直线向右平移5单位，线段AB扫过区域的边界恰好为菱形，∴AB＝5，则AB2＝25．∴（﹣）2+32＝25．解得k＝±．故答案是：±．【点评】考查了菱形的性质和一次函数图象与几何变换，解题的关键是根据菱形的性质得到AB＝5．三、解答题（本题共26分，第17题8分，第18，20题各5分，第19，21题各4分）17．（8分）解下列方程：（1）x2+2x﹣3＝0（用配方法）（2）2x2+5x﹣1＝0（用公式法）【分析】（1）根据配方法的步骤，可得答案；（2）根据公式法，可得答案．【解答】解：（1）移项，得x2+2x＝3配方，得x2+2x+1＝3+1即（x+1）2＝3开方得x+1＝±2，x1＝1，x2＝﹣3；（2）a＝2，b＝5，c＝﹣1，△＝b2﹣4ac＝25﹣4×2×（﹣1）＝33＞0，x＝＝，x1＝，x2＝．【点评】本题考查了解一元二次方程，配方得出完全平方公式是解题关键．18．（5分）在平面直角坐标系xOy中，函数y＝kx+b的图象与直线y＝2x平行，且经过点A（1，6）（1）求一次函数y＝kx+b的解析式；（2）求一次函数y＝kx+b的图象与坐标轴围成的三角形的面积．【分析】（1）根据函数y＝kx+b的图象与直线y＝2x平行，且经过点A（1，6），即可得出k和b的值，即得出了函数解析式．（2）先求出与x轴及y轴的交点坐标，然后根据三角形面积公式求解即可．【解答】解：（1）∵函数y＝kx+b的图象与直线y＝2x平行，∴k＝2，又∵函数y＝2x+b的图象经过点A（1，6），∴6＝2+b，解得b＝4，∴一次函数的解析式为y＝2x+4；（2）在y＝2x+4中，令x＝0，则y＝4；令y＝0，则x＝﹣2；∴一次函数y＝kx+b的图象与坐标轴交于（0，4）和（﹣2，0），∴一次函数y＝kx+b的图象与坐标轴围成的三角形的面积为×2×4＝4．【点评】本题考查待定系数法求函数解析式及三角形的面积的知识，关键是正确得出函数解析式及坐标与线段长度的转化．19．（5分）下面是小丁设计的“利用直角三角形和它的斜边中点作矩形的尺规作图过程：已知：如图，在Rt△ABC中，∠ABC＝90°，O为AC的中点，求作：四边形ABCD，使得四边形ABCD为矩形．作法：①作射线BO，在线段BO的延长线上取点D，使得DO＝BO②连接AD，CD，则四边形ABCD为矩形根据小丁设计的尺规作图过程（1）使用直尺和圆规，在图中补全图形（保留作图痕迹）（2）完成下面的证明证明：∵点O为AC的中点，∴AO＝CO又∵DO＝BO，∴四边形ABCD为平行四边形（对角线互相平分的四边形是平行四边形）∵∠ABC＝90°，∴▱ABCD为矩形（有一个角是直角的平行四边形是矩形）【分析】（1）根据要求画出图形即可．（2）根据有一个角是直角的平行四边形是矩形即可证明．【解答】解：（1）如图，矩形ABCD即为所求．（2）理由：∵点O为AC的中点，∴AO＝CO又∵DO＝BO，∴四边形ABCD为平行四边形（对角线互相平分的四边形是平行四边形）∵∠ABC＝90°，∴▱ABCD为矩形（有一个角是直角的平行四边形是矩形）．故答案为：对角线互相平分的四边形是平行四边形，有一个角是直角的平行四边形是矩形【点评】本题考查作图﹣复杂作图，矩形的判定等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．20．（4分）方程x2+2x+k﹣4＝0有实数根（1）求k的取值范围；（2）若k是该方程的一个根，求2k2+6k﹣5的值．【分析】（1）根据判别式的意义得到△＝22﹣4（k﹣4）≥0，然后解不等式即可；（2）利用方程解的定义得到k2+3k＝4，再变形得到2k2+6k﹣5＝2（k2+3k）﹣5，然后利用整体代入的方法计算．【解答】解：（1）△＝22﹣4（k﹣4）≥0，解得k≤5；（2）把x＝k代入方程得k2+2k+k﹣4＝0，即k2+3k＝4，所以2k2+6k﹣5＝2（k2+3k）﹣5＝2×4﹣5＝3．【点评】本题考查了根的判别式：一元二次方程ax2+bx+c＝0（a≠0）的根与△＝b2﹣4ac 有如下关系：当△＞0时，方程有两个不相等的实数根；当△＝0时，方程有两个相等的实数根；当△＜0时，方程无实数根．21．（4分）小东和小明要测量校园里的一块四边形场地ABCD（如图所示）的周长，其中边CD上有水池及建筑遮挡，没有办法直接测量其长度小东经测量得知AB＝AD＝5m，∠A＝60°，BC＝12m，∠ABC＝150°小明说根据小东所得的数据可以求出CD的长度．你同意小明的说法吗？若同意，请求出CD的长度；若不同意，请说明理由．【分析】直接利用等边三角形的判定方法得出△ABD是等边三角形，再利用勾股定理得出答案．【解答】解：同意小明的说法．理由：连接BD，∵AB＝AD＝5m，∠A＝60°，∴△ABD是等边三角形，∴BD＝5m，∠ABD＝60°，∵∠ABC＝150°，∴∠DBC＝90°，∵BC＝12m，BD＝5m，∴DC ＝＝13（m ），答：CD 的长度为13m ．【点评】此题主要考查了勾股定理的应用以及等边三角形的判定，正确得出△ABD 是等边三角形是解题关键．四、解答题（本题共13分，第22题7分，第23题6分）22．（7分）三月底，某学校迎来了以“学海通识品墨韵，开卷有益览书山”为主题的学习节活动为了让同学们更好的了解二十四节气的知识，本次学习节在沿袭以往经典项目的基础上，增设了十四节气之旅项目，并开展了相关知识竞赛该学校七、八年级各有400名学生参加了这次竞赛，现从七、八年级各随机抽取20名学生的成绩进行抽样调查 七年级：74 97 96 72 98 99 72 73 76 74 74 69 76 89 78 74 99 97 98 99 八年级：76 88 93 89 78 94 89 94 95 50 89 68 65 88 77 87 89 88 92 91 整理数据如下成绩 人数 年级 50≤x ≤5960≤x ≤6970≤x ≤7980≤x ≤8990≤x ≤100七年级 0 1 10 1 a 八年级 12386分析数据如下年级 平均数 中位数 众数 方差 七年级 84.2 77 74 138.56 八年级84b89129.7根据以上信息，回答下列问题 （1）a ＝8 b ＝ 88.5 ；（2）你认为哪个年级知识竞赛的总体成绩较好，说明理由（至少从两个不同的角度说明推断的合理性）．（3）学校对知识竞赛成绩不低于80分的学生颁发优胜奖，请你估计学校七、八年级所有学生中获得优胜奖的大约有180，280人．【分析】（1）从调查的七年级的人数20减去前几组的人数即可，将八年级的20名学生的成绩排序后找到第10、11个数的平均数即是八年级的中位数，（2）从中位数、众数、方差进行分析，调查结论，（3）用各个年级的总人数乘以样本中优秀人数所占的比即可．【解答】解：（1）a＝20﹣1﹣10﹣1＝8，b＝（88+89）÷2＝88.5故答案为：8，88.5．（2）八年级成绩较好，八年级成绩的众数、中位数比七年级成绩相应的众数、中位数都要大，说明八年级成绩的集中趋势要高，方差八年级较小，说明八年级的成绩比较稳定．（3）七年级优秀人数为：400×＝180人，八年级优秀人数为：400×＝280人，故答案为：180，280．【点评】考查频数分布表、众数、中位数、平均数、方差的意义及计算方法，明确各自的意义和计算方法是解决问题的前提．23．（6分）如图，在▱ABCD中，对角线AC，BD交于点O，过点B作BE⊥CD于点E，延长CD到点F，使DF＝CE，连接AF．（1）求证：四边形ABEF是矩形；（2）连接OF，若AB＝6，DE＝2，∠ADF＝45°，求OF的长度．【分析】（1）根据平行四边形的性质得到AD∥BC且AD＝BC，等量代换得到BC＝EF，推出四边形AEFD是平行四边形，根据矩形的判定定理即可得到结论；（2）根据直角三角形斜边中线可得：OF＝AC，利用勾股定理计算AC的长，可得结论．【解答】（1）证明：∵在▱ABCD中，∴AD∥BC且AD＝BC，∴∠ADF＝∠BCE，在△ADF和△BCE中，∵∴△ADF≌△BCE（SAS），∴AF＝BE，∠AFD＝∠BEC＝90°，∴AF∥BE，∴四边形ABEF是矩形；（2）解：由（1）知：四边形ABEF是矩形，∴EF＝AB＝6，∵DE＝2，∴DF＝CE＝4，∴CF＝4+4+2＝10，Rt△ADF中，∠ADF＝45°，∴AF＝DF＝4，由勾股定理得：AC＝＝＝2，∵四边形ABCD是平行四边形，∴OA＝OC，∴OF＝AC＝．【点评】本题考查了矩形的判定和性质，平行四边形的性质，勾股定理，正确的识别图形是解题的关键．五、解答题（本题共13分，第24题6分，第25题7分）24．（6分）如图，在平面直角坐标系xOy中，直线y＝kx+7与直线y＝x﹣2交于点A（3，m）（1）求k，m的值；（2）已知点P（n，n），过点P作垂直于y轴的直线与直线y＝x﹣2交于点M，过点P 作垂直于x轴的直线与直线y＝kx+7交于点N（P与N不重合）．若PN≤2PM，结合图象，求n的取值范围．【分析】（1）把A点坐标代入y＝x﹣2中，求得m的值，再把求得的A点坐标代入y ＝kx+7中，求得k的值；（2）根据题意，用n的代数式表示出M、N点的坐标，再求得PM、PN的值，根据PN ≤2PM，列出n的不等式，再求得结果．【解答】解：（1）把A（3，m）代入y＝x﹣2中，得m＝3﹣2＝1，∴A（3，1），把A（3，1）代入y＝kx+7中，得1＝3k+7，解得，k＝﹣2；（2）由（1）知，直线y＝kx+7为y＝﹣2x+7，根据题意，作出草图如下：∵点P（n，n），∴M（n+2，n），N（n，﹣2n+7），∴PM＝2，PN＝|3n﹣7|，∵PN≤2PM，∴|3n﹣7|≤2×2，∴1≤n≤，∵P与N不重合，∴n≠﹣2n+7，∴n≠，综上，1≤n≤，且n≠【点评】本题是一次函数图象的相交与平行的问题，主要考查了待定系数法求一次函数的解析式，第（2）小题关键是用n的代数式表示PM与PN的长度．25．（7分）在Rt△ABC中，∠BAC＝90°，点O是△ABC所在平面内一点，连接OA，延长OA到点E，使得AE＝OA，连按OC，过点B作BD与OC平行，并使∠DBC＝∠OCB，且BD＝OC，连按DE．（1）如图一，当点O在Rt△ABC内部时，①按题意补全图形；②猜想DE与BC的数量关系，并证明．（2）若AB＝AC（如图二），且∠OCB＝30°，∠OBC＝15°，求∠AED的大小．【分析】（1）①根据要求画出图形即可解决问题．②结论：DE＝BC．连接OD交BC于F，连接AF．证明AF为Rt△ABC斜边中线，为△ODE的中位线，即可解决问题．（2）分两种情形：如图二中，当点O在△ABC内部时，连接OD交BC于F，连接AF，延长CO交AF于M．连接BM．证明△BMA≌△BMO（AAS），推出AM＝OM，∠BMO＝∠BMA＝120°，推出∠AMO＝120°，即可解决问题．如图三中，当点O在△ABC外部时，当点O在△ABC内部时，连接OD交BC于F，连接AF，延长CO交AF于M．连接BM．分别求解即可．【解答】解：（1）①补全图形如图所示：②结论：DE＝BC．理由：如图一中，连接OD交BC于F，连接AF．∵OC∥BD，∴∠FCO＝∠FBD，∵∠CFO＝∠BFD，OC＝BD，∴△FCO≌△FBD（AAS），∴BF＝CF，∵OA＝AE，∵DE＝2AF，∵∠BAC＝90°，BF＝CF，∴BC＝2AF，∴DE＝BC．（2）如图二中，当点O在△ABC内部时，连接OD交BC于F，连接AF，延长CO交AF于M．连接BM．由（1）可知：AF为Rt△ABC斜边中线，为△ODE的中位线，∵AB＝AC，∴AF垂直平分线段BC，∴MB＝MC，∵∠OCB＝30°，∠OBC＝15°，∴∠MBC＝∠MCB＝30°，∵∠BAC＝90°，AB＝AC，∴∠ABC＝∠ACB＝45°，∠MBO＝∠MBA＝15°，∵∠BAM＝∠BOM＝45°，BM＝BM，∴△BMA≌△BMO（AAS），∴AM＝OM，∠BMO＝∠BMA＝120°，∴∠AMO＝120°，∴∠MAO＝∠MOA＝30°，∴∠AED＝∠MAO＝30°．如图三中，当点O在△ABC外部时，当点O在△ABC内部时，连接OD交BC于F，连接AF，延长CO交AF于M．连接BM．由∠BOM＝∠BAM＝45°，可知A，B，M，O四点共圆，∴∠MAO＝∠MBO＝30°﹣15°＝15°，∵DE∥AM，∴∠AED＝∠MAO＝15°，综上所述，满足条件的∠AED的值为15°或30°．【点评】本题属于三角形综合题，考查了全等三角形的判定和性质，直角三角形斜边中线的性质，三角形中位线定理等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，属于中考压轴题．。

北京市海淀区2019 年八年级学业发展水平评价数学试卷及参考答案一、选择题（本题共30 分，每小题 3 分）在下列各题的四个选项中，只．有．一．个．是符合题意的．1.下列实数中，是方程x2 - 4 = 0 的根的是A. 1B. 2C. 3D. 42019.72.如图，在Rt△ABC 中,A.7B.8C.9D.10∠C = 90 °，BC = 6 ，AC = 8 ，则AB 的长度为3.在下列条件中，能判定四边形为平行四边形的是A. 两组对边分别平行B. 一组对边平行且另一组对边相等C. 两组邻边相等D. 对角线互相垂直4.下列各曲线中，不表示y 是x 的函数的是A B C D5.数据2, 6, 4, 5, 4, 3 的平均数和众数分别是A．5 和4B．4 和4C．4.5 和4D．4 和55 CO 6. 一元二次方程 x 2 - 8x -1 = 0 经过配方后可变形为A. (x + 4)2 = 15B. (x + 4)2 = 17C. (x - 4)2 = 15D. (x - 4)2 = 177.若点 A (-3, y 1 ), B (1, y 2 ) 都在直线 y=x + 2 上，则 y 1 与 y 2 的大小关系是A. y 1＜y 2B. y 1＝y 2C. y 1＞y 2D. 无法比较大小8.如图，正方形 ABCD 的边长为则 BE 的长度为A. B. 102, 对角线 AC , BD 交于点 O , E 是 AC 延长线上一点, 且CE =CO .EDC.D. 2AB9.对于一次函数 y = kx + b （k , b 为常数），下表中给出 5 组自变量及其对应的函数值，其中恰好有一个函数值计算有误，则这个错误的函数值是 A. 5B. 8C. 12D. 1410.博物馆作为征集、典藏、陈列和研究代表自然和人类文化遗产实物的场所，其存在的目的是为公众提供知识、教育及欣赏服务. 近年来，人们到博物馆学习参观的热情越来越高. 2012-2018 年我国博物馆参观人数统计如下：2 35小明研究了这个统计图，得出四个结论：① 2012 年到 2018 年，我国博物馆参观人数持续增长；② 2019 年末我国博物馆参观人数估计将达到 10.82 亿人次；③ 2012 年到 2018 年，我国博物馆参观人数年增幅最大的是 2017 年；④ 2016 年到 2018 年，我国博物馆参观人数平均年增长率超过 10%． 其中正确的是 A ．①③B ．①②③C ．①②④D ．①②③④二、填空题（本题共 18 分，每小题 3 分） 11．如图，在□ABCD 中，∠B =110°，则∠D =°.A12. 八年级（1）班甲、乙两个小组的 10 名学生进行飞镖训练，某次训练成绩如下：由上表可知，甲、乙两组成绩更稳定的是组.13. 若关于 x 的一元二次方程 x26x m 0 有实数根, 且所有实数根均为整数，请写出一个符合条件的常数 m 的值：m =.博物馆参观人数：亿人次2018年2017年2016年2015年2014年2013年2012年425.646 6.387.817.188 8.5010.089.721210 2012-2018年全国博物馆参观人数统计图14. 如图，某港口 P 位于南北延伸的海岸线上，东面是大海.“远洋”号、“长峰”号两艘轮船同时离开港口 P ，各自沿固定方向航行，“远洋”号每小时航行 12 n mile ，“长峰”号每小时航行 16 n mile ，它们离开港口 1 小时后，分别到达 A ，B 两个位置，且 A B =20 n mile ，已知“远洋”号沿着北偏东 60°方向航行，那么“长峰”号航行的方向是.15. 若一个矩形的长边的平方等于短边与其周长一半的积,则称这样的矩形为“优美矩形”.某公园在绿化时,工作人员想利用如图所示的直角墙角（两边足够长）和长为 38 m 的篱笆围成一个“优美矩形”形状的花园 ABCD ,,其中边 AB , AD 为篱笆,且 AB 大于 AD . 设 AD 为 x m, 依题意可列方程为.16. 在平面直角坐标系 xOy 中，直线 y = kx + 3 与 x ，y 轴分别交于点 A ，B ，若将该直线向右平移 5 个单位，线段 A B 扫过区域的边界恰好为菱形，则 k 的值为.三、解答题（本题共 26 分，第 17 题 8 分，第 18，20 题各 5 分，第 19，21 题各 4 分）17. 解方程：（1） x 2 - 2x - 3 = 0 ；（2） 2x 2 + 3x -1 = 0 .18. 在平面直角坐标系 xOy 中，一次函数 y =kx +b 的图象与直线 y ＝2x 平行，且经过点 A (1,6)．（1） 求一次函数 y =kx +b 的解析式；（2） 求一次函数 y =kx +b 的图象与坐标轴围成的三角形的面积．19. 下面是小丁设计的“利用直角三角形和它的斜边中点作矩形”的尺规作图过程． 已知：如图，在 Rt △ABC 中，∠ABC =90°，O 为 AC 的中点． 求作：四边形 ABCD ，使得四边形 ABCD 为矩形．作法：①作射线 BO ，在线段 BO 的延长线上取点 D ，使得 DO =BO ；②连接 AD ，CD ，则四边形 ABCD 为矩形． 根据小丁设计的尺规作图过程.（1）使用直尺和圆规，在图中补全图形（保留作图痕迹）；（2） 完成下面的证明．证明：∵点 O 为AC 的中点，∴ AO =CO ．又∵ DO =BO ，∴四边形 A BCD 为平行四边形（ ）（填推理的依据）．D C∵∠ABC =90°，∴□ABCD 为矩形（）（填推理的依据）．20.关于x 的一元二次方程x2 + 2x +k - 4 = 0 有实数根．（1）求k 的取值范围;（2）若k 是该方程的一个根，求2k 2+ 6k - 5 的值．21.小东和小明要测量校园里的一块四边形场地ABCD（如图所示）的周长，其中边CD 上有水池及建筑遮挡，没有办法直接测量其长度.小东经测量得知AB=AD=5 m，∠A=60°，BC=12 m，∠ABC=150°.小明说根据小东所得的数据可以求出CD 的长度.你同意小明的说法吗？若同意，请求出CD 的长度；若不同意，请说明理由.B CAD四、解答题（本题共13 分，第22 题7 分，第23 题 6 分）22.三月底，某学校迎来了以“学海通识品墨韵，开卷有益览书山”为主题的学习节活动.为了让同学们更好的了解二十四节气的知识, 本次学习节在沿袭以往经典项目的基础上，增设了“二十四节气之旅”项目，并开展了相关知识竞赛. 该学校七、八年级各有400 名学生参加了这次竞赛, 现从七、八年级各随机抽取20 名学生的成绩进行抽样调查.收集数据如下：七年级：74 97 96 72 98 99 72 73 76 7474 69 76 89 78 74 99 97 98 99八年级：76 88 93 89 78 94 89 94 95 5089 68 65 88 77 87 89 88 92 91整理数据如下：人数年级七年级分析数据如下：（1）a= ，b= ；（2）你认为哪个年级知识竞赛的总体成绩较好，说明理由（至少从两个不同的角度说明推断的合；理性）（3）学校对知识竞赛成绩不低于80 分的学生颁发优胜奖，请你估计学校七、八年级所有学生中获得优胜奖的大约有人.23.如图，在□ABCD 中，对角线AC，BD 交于点O，过点B 作BE⊥CD 于点E，延长CD 到点F，使DF=CE，连接AF.（1）求证：四边形ABEF 是矩形；（2）连接OF，若AB=6，DE=2，∠ADF=45°，求OF 的长度.五、解答题（本题共13 分，第24 题 6 分，第25 题7 分）24.如图，在平面直角坐标系xOy 中，直线y =kx + 7 与直线y =x - 2 交于点A(3, m).（1）求k, m 的值；（2）已知点P (n, n)，过点P 作垂直于y 轴的直线与直线y =x - 2 交于点M ，过点P 作垂直于x 轴的直线与直线y =kx + 7 交于点N （P 与N 不重合）. 若PN ≤ 2PM ，结合图象，求n 的取值范围．25. 在 Rt △ABC 中， ∠BAC = 90︒ ，点 O 是△ABC 所在平面内一点，连接 OA ，延长 OA 到点 E ，使得AE =OA ，连接 OC ，过点 B 作 BD 与 OC 平行，并使∠DBC =∠OCB ，且 BD =OC ，连接 DE .（1） 如图一，当点 O 在 Rt △ABC 内部时.① 按题意补全图形；② 猜想 DE 与 BC 的数量关系，并证明.图一（2） 若 A B = AC （如图二）， 且∠OCB = 30︒, ∠OBC = 15︒ ，求∠AED 的大小．图二备用图备用图北京市海淀区2019 年八年级学业发展水平评价数学试卷及参考答案一、选择题二、填空题11．11012．甲13．0（答案不唯一）14．南偏东 30°15．(38 -x)2= 38x （无需写成一般式）16 . ±3（填对一个得 2 分，填对两个得 3 分，含有错误答案得 0 分）4三、解答题17.解：（1）x2 - 2x - 3 = 0 ；解法一：x2 - 2x - 3 = 0x2 - 2x = 3x2 -2x +1 = 4(x -1)2 = 4 x -1 =±2…………………………………………………………………………1分………………………………………………………………………………2分………………………………………………………………………………3分x1 = 3,x2=-1………………………………………………………………………………4 分解法二：x2 -2x -3 =0 (x -3)(x +1) =………………………………………………………………………………2 分x1 = 3,x2=-1………………………………………………………………………………4 分（2）2x2 + 3x -1 = 0 .解：2x2 +3x -1 = 0a =2,b =3,c =-1∴∆=9 -4⨯2⨯(-1) =17> 0……………………………………………………………………1 分x =-3 ± 174………………………………………………………………………………3 分x =-3 + 1 417,x =-3 -172 4……………………………………………………………………4 分注：若（1）中用公式法，请参考（2）中评分细则D（1） 一次函数 y = kx + b 的图象为直线，且与直线 y = 2x 平行，∴k = 2 ................................................................. 1 分又知其过点 A (1,6),∴2 + b = 6 . ∴b = 4 .∴一次函数的解析式为 y = 2x + 4 ........................................ 2 分（2）当 x = 0 时， y = 4 ,可知直线 y = 2x + 4 与 y 轴的交点为(0, 4) ................................... 3 分 当 y = 0 时， x = -2 , 可知直线 y = 2x + 4 与 x 轴交点为(-2, 0) ................................. 4 分可得该直角三角形的两条直角边长度分别为 4 和 2.所以直线 y = 2x + 4 与坐标轴围成的三角形的面积为 1 ⨯ 4 ⨯ 2 = 4 ............ 5 分219. 解：（1） 作图如图所示BA ...............................................................2 分（2） 对角线互相平分的四边形是平行四边形 ...................................... 3 分有一个角是直角的平行四边形是矩形 ......................................... 4 分20. 解：（1）x 2 + 2x + k - 4 = 0 有实数根，∴∆ ≥ 0 ..................................................................... 1 分即22 - 4(k - 4) ≥ 0 .∴ k ≤ 5. .................................................................... 2 分（2） k 是方程 x 2 + 2x + k - 4 = 0 的一个根，∴k 2 + 2k + k - 4 = 0.……………………………………………………………………………3 分∴k 2 + 3k = 4 ............................................................ 4 分 2k 2 + 6k - 5 = 2(k 2 + 3k) - 5= 3. ...................................................................... 5 分同意 ........................................................................ 1 分 连接 BD ，如图.∵AB =AD =5 (m)，∠A =60°，BC∴△ABD 是等边三角形 ....................... 2 分 ∴BD =AB =5 (m)，∠ABD =60°. A∵∠ABC =150°，∴∠CBD =∠ABC －∠ABD =150°－60°=90°. ……3 分 D在 Rt △CBD 中，BD =5 (m)，BC =12 (m)，∴CD = 13 (m) ........................................ 4 分四、解答题22. 解：（1）8，88.5； .................................................................. 2 分 （2）你认为 八 年级知识竞赛的总体成绩较好，理由 1：八年级成绩的中位数较高；理由 2：八年级与七年级成绩的平均数接近且八年级方差较低，成绩更稳定. 或者你认为 七 年级知识竞赛的总体成绩较好， 理由 1：七年级的平均成绩较高；理由 2：低分段人数较少 .…………………………………………………………………………………5 分（答案不唯一，合理即可）（3）460． ...................................................................... 7 分23. （1）证明：∵四边形 ABCD 是平行四边形∴ A B = CD ， A B ∥CD . ∵ DF = CE ,∴ DF + DE = CE + ED , 即: FE = CD .∵点 F 、E 在直线 CD 上, ∴ AB = FE AB ∥ F E .∴四边形 A BEF 是平行四边形 ................................................... 1 分 又∵ BE ⊥ CD ，垂足是 E , ∴ ∠BEF = 90︒ .∴四边形 A BEF 是矩形 ......................................................... 2 分 （2）解：∵四边形 ABEF 是矩形O ,∴ ∠AFC = 90︒ ， A B = FE . ∵AB = 6, DE = 2 , ∴ FD = 4 . ∵ FD = CE , ∴ CE = 4 .29 29 ∴ FC = 10 ....................................................................... 3 分 在Rt △AFD 中， ∠AFD = 90︒ ． ∵ ∠ADF = 45︒ ,∴ AF = FD = 4 ............................................................ 4 分 在Rt △AFC 中， ∠AFC = 90︒ ．∴ AC == 2 ． ............................................... 5 分 ∵点 O 是平行四边形 ABCD 对角线的交点， ∴ O 为 AC 中点.在Rt △AFC 中， ∠AFC = 90︒ ． O 为 AC 中点．∴ O F = 1AC = ． ......................................................... 6 分2五、解答题24. 解：（1） ∵直线 y =kx ＋7 与直线 y =x ﹣2 交于点 A （3，m ），∴m =3k ＋3，m =1 .............................................................. 1 分∴k =﹣2 ..................................................................... 2 分 （2） ∵点 P （n ，n ），过点 P 作垂直于 y 轴的直线与直线 y =x ﹣2 交于点 M ，∴M （n ＋2，n ）.∴PM =2 ...................................................................... 3 分 ∵PN ≤2PM ， ∴PN ≤4.∵过点 P 作垂直于 x 轴的直线与直线 y =kx ＋7 交于点 N ，k =﹣2，∴N (n ,﹣2n +7).∴PN = 3n - 7 ................................... 4 分当 PN =4 时，如图，即 3n - 7 =4，∴n =1 或 n = 11 .3∵P 与 N 不重合, ∴ 3n - 7 ≠ 0 .∴ n ≠ 7.3当 PN ≤4（即 PN ≤2PM ）时，n 的取值范围为：1≤ n < 7 或 7 < n ≤11 .......................................6 分 3 33⎨⎩25. 解：（1） ①补全图形，如图一 .......................... 1 分②猜想 D E =BC .................................. 2 分如图，连接 OD 交 BC 于点 F ，连接 AF. 在△BDF 和△COF 中, ⎧∠DBF = ∠OCF ,⎪∠DFB = ∠OFC , 图 一⎪DB = OC , ∴△BDF ≌△COF.∴DF =OF , BF =CF ................................. 3 分 ∴F 分别为 B C 和 D O 的中点. ∵∠BAC =90°, F 为 BC 的中点,∴ AF = 1BC .2∵OA =AE , F 为 BC 的中点,∴ AF = 1ED .2∴DE =BC ...................................... 4 分（2） 如图二，连接 OD 交 BC 于点 F ，连接 AF ，延长 CO交 AF 于点 M ，连接 BM.由（1）中②可知，点 F 为 BC 的中点，AF 为 Rt △ABC 斜边 BC 边中线，为△OED 的中位线, ∴AF 为 BC 边的垂直平分线. ∴MB =MC.∵∠OCB =30°,∠OBC =15°,DD图二∴∠MBC =∠MCB =30°. ∵∠BAC =90°,AB =AC, ∴∠MBO =∠MBA=15°. 又可证∠BAM =∠BOM=45°. ∴△BMA ≌△BMO.∴AM =OM 且∠BMO =∠BMA=120°. ∴∠OMA=120°. ∴∠MAO=30°. ∵AF 为△OED 的中位线, ∴AF ∥ED. BC∴∠AED=30°.类似的，如备用图可知，∠AED=15°. ………………7 分O备用图(提示：证明△ABO 为等边三角形，得到∠AED=15°.) ∴∠AED=30°或 15°.注：各题中若有其他合理的解法请酌情给分.。

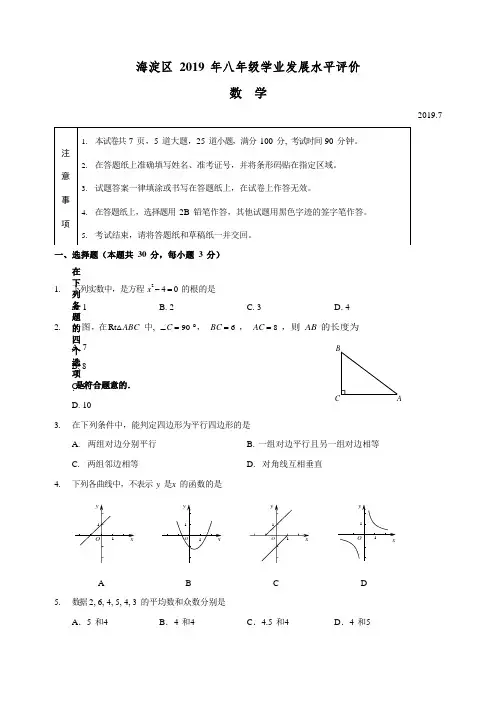
海淀区2019年八年级学业发展水平评价数 学2019.7一、选择题（本题共30分，每小题3分）在下列各题的四个选项中，只有一个．．．．是符合题意的． 1． 下列实数中，是方程240x -=的根的是A. 1B. 2C. 3D. 42． 如图，在Rt △ABC 中, 90C ∠=°，6BC =，8AC =，则AB 的长度为A. 7B. 8C. 9D. 103. 在下列条件中，能判定四边形为平行四边形的是A. 两组对边分别平行B. 一组对边平行且另一组对边相等C. 两组邻边相等D. 对角线互相垂直4. 下列各曲线中，不表示y 是x的函数的是ABCD5． 数据2, 6, 4, 5, 4, 3的平均数和众数分别是A ．5和4B ．4和4C ．4.5和4D ．4和56． 一元二次方程2810xx --=经过配方后可变形为A. 2(4)15x +=B. 2(4)17x +=C. 2(4)15x -=D. 2(4)17x -=7． 若点12(3,),(1,)A y B y -都在直线122y x =+上，则1y 与2y 的大小关系是 A. y 1＜y 2 B. y 1＝y 2C. y 1＞y 2D. 无法比较大小8. 如图，正方形ABCD对角线AC , BD 交于点O , E 是AC 延长线上一点, 且CE =CO .则BE 的长度为A.B.C.D.9. 对于一次函数y kx b =+（k , b 为常数），下表中给出5组自变量及其对应的函数值，其中恰好有一个函数值计算有误，则这个错误的函数值是 A. 5B. 8C. 12D. 1410. 博物馆作为征集、典藏、陈列和研究代表自然和人类文化遗产实物的场所，其存在的目的是为公众提供知识、教育及欣赏服务. 近年来，人们到博物馆学习参观的热情越来越高. 2012-2018年我 国博物馆参观人数统计如下：BCD O EA小明研究了这个统计图，得出四个结论：① 2012年到2018年，我国博物馆参观人数持续增长； ② 2019年末我国博物馆参观人数估计将达到10.82亿人次；③ 2012年到2018年，我国博物馆参观人数年增幅最大的是2017年； ④ 2016年到2018年，我国博物馆参观人数平均年增长率超过10%． 其中正确的是 A ．①③B ．①②③C ．①②④D ．①②③④二、填空题（本题共18分，每小题3分）11． 如图，在□ABCD 中，∠B =110°，则∠D =________°.A BD12．八年级（1）班甲、乙两个小组的10名学生进行飞镖训练，某次训练成绩如下：甲组成绩（环） 8 7 8 8 9 乙组成绩（环）98797由上表可知，甲、乙两组成绩更稳定的是 组. 13．若关于x 的一元二次方程260xx m 有实数根, 且所有实数根均为整数，请写出一个符合条件的常数m 的值：m = .14．如图，某港口P 位于南北延伸的海岸线上，东面是大海.“远洋”号、60°东北PAB“长峰”号两艘轮船同时离开港口P，各自沿固定方向航行，“远洋”号每小时航行12 n mile，“长峰”号每小时航行16 n mile，它们离开港口1小时后，分别到达A，B两个位置，且AB=20 n mile，已知“远洋”号沿着北偏东60°方向航行，那么“长峰”号航行的方向是_______.15．若一个矩形的长边的平方等于短边与其周长一半的积,则称这样的矩Array形为“优美矩形”.某公园在绿化时,工作人员想利用如图所示的直角墙角（两边足够长）和长为38 m的篱笆围成一个“优美矩形”形状的花园ABCD,,其中边AB, AD为篱笆,且AB大于AD. 设AD为x m, 依题意可列方程为.16. 在平面直角坐标系xOy中，直线3=+与x，y轴分别交于点A，B，若将该直线向右平移5个y kx单位，线段AB扫过区域的边界恰好为菱形，则k的值为.三、解答题（本题共26分，第17题8分，第18，20题各5分，第19，21题各4分）17．解方程：（1）2230+-=.x xx x2310--=；（2）218．在平面直角坐标系xOy中，一次函数y=kx+b的图象与直线y＝2x平行，且经过点A(1,6)．（1）求一次函数y=kx+b的解析式；（2）求一次函数y=kx+b的图象与坐标轴围成的三角形的面积．19．下面是小丁设计的“利用直角三角形和它的斜边中点作矩形”的尺规作图过程．已知：如图，在Rt△ABC中，∠ABC =90°，O为AC的中点．求作：四边形ABCD，使得四边形ABCD为矩形．作法：①作射线BO，在线段BO的延长线上取点D，使得DO=BO；②连接AD，CD，则四边形ABCD为矩形．根据小丁设计的尺规作图过程.（1）使用直尺和圆规，在图中补全图形（保留作图痕迹）； （2）完成下面的证明． 证明：∵点O 为AC 的中点，∴ AO =CO ． 又∵ DO =BO ，∴四边形ABCD 为平行四边形（ ）（填推理的依据）． ∵∠ABC =90°，∴□ABCD 为矩形（ ）（填推理的依据）．20. 关于x 的一元二次方程2240x x k ++-=有实数根．（1）求k 的取值范围;（2）若k 是该方程的一个根，求2265k k +-的值．21．小东和小明要测量校园里的一块四边形场地ABCD （如图所示）的周长，其中边CD 上有水池及建筑遮挡，没有办法直接测量其长度.小东经测量得知AB =AD =5 m ，∠A =60°，BC =12 m ，∠ABC =150°. 小明说根据小东所得的数据可以求出CD 的长度.你同意小明的说法吗？若同意，请求出CD 的长度；若不同意，请说明理由.OBACADCB四、解答题（本题共13分，第22题7分，第23题6分）22．三月底，某学校迎来了以“学海通识品墨韵，开卷有益览书山”为主题的学习节活动.为了让同学们更好的了解二十四节气的知识, 本次学习节在沿袭以往经典项目的基础上，增设了“二十四节气之旅”项目，并开展了相关知识竞赛. 该学校七、八年级各有400名学生参加了这次竞赛, 现从七、八年级各随机抽取20名学生的成绩进行抽样调查.收集数据如下：七年级：74 97 96 72 98 99 72 73 76 7474 69 76 89 78 74 99 97 98 99八年级：76 88 93 89 78 94 89 94 95 5089 68 65 88 77 87 89 88 92 91整理数据如下：分析数据如下：（1）a= ，b= ；（2）你认为哪个年级知识竞赛的总体成绩较好，说明理由（至少从两个不同的角度说明推断的合理性）；（3）学校对知识竞赛成绩不低于80分的学生颁发优胜奖，请你估计学校七、八年级所有学生中获得优胜奖的大约有人.23. 如图，在□ABCD中，对角线AC，BD交于点O，过点B作BE⊥CD于点E，延长CD到点F，使DF=CE，连接AF.（1）求证：四边形ABEF是矩形；（2）连接OF，若AB=6，DE=2，∠ADF=45°，求OF的长度.五、解答题（本题共13分，第24题6分，第25题7分）24．如图，在平面直角坐标系xOy 中，直线7y kx =+与直线2y x =-交于点()3,A m .（1）求,k m 的值；（2）已知点(),P n n ，过点P 作垂直于y 轴的直线与直线2y x =-交于点M ，过点P 作垂直于x 轴的直线与直线7y kx =+交于点N （P 与N 不重合）. 若2PN PM ≤，结合图象，求n 的取值范围．25．在Rt △ABC 中，90BAC ∠=︒，点O 是△ABC 所在平面内一点，连接OA ，延长OA 到点E ，使得AE =OA ，连接OC ，过点B 作BD 与OC 平行，并使∠DBC =∠OCB ，且BD =OC ，连接DE . （1）如图一，当点O 在Rt △ABC 内部时.① 按题意补全图形；② 猜想DE 与BC 的数量关系，并证明.（2）若AB = AC （如图二）， 且30,15OCB OBC ∠=︒∠=︒，求AED ∠的大小．图一AB图二AB备用图AB备用图。

海淀区2019年八年级学业发展水平评价数 学2019.7一、选择题（本题共30分，每小题3分）在下列各题的四个选项中，只有一个．．．．是符合题意的． 1． 下列实数中，是方程240x -=的根的是A. 1B. 2C. 3D. 42． 如图，在Rt △ABC 中, 90C ∠=°，6BC =，8AC =，则AB 的长度为A. 7B. 8C. 9D. 103. 在下列条件中，能判定四边形为平行四边形的是A. 两组对边分别平行B. 一组对边平行且另一组对边相等C. 两组邻边相等D. 对角线互相垂直4. 下列各曲线中，不表示y 是x 的函数的是ABCD5． 数据2, 6, 4, 5, 4, 3的平均数和众数分别是A ．5和4B ．4和4C ．4.5和4D ．4和56． 一元二次方程2810x x --=经过配方后可变形为A. 2(4)15x +=B. 2(4)17x +=C. 2(4)15x -=D. 2(4)17x -=7． 若点12(3,),(1,)A y B y -都在直线122y x =+上，则1y 与2y 的大小关系是 A. y 1＜y 2 B. y 1＝y 2C. y 1＞y 2D. 无法比较大小8. 如图，正方形ABCD对角线AC , BD 交于点O , E 是AC 延长线上一点, 且CE =CO .则BE 的长度为A.B.C.D.9. 对于一次函数y kx b =+（k , b 为常数），下表中给出5组自变量及其对应的函数值，其中恰好有一个函数值计算有误，则这个错误的函数值是 A. 5B. 8C. 12D. 1410. 博物馆作为征集、典藏、陈列和研究代表自然和人类文化遗产实物的场所，其存在的目的是为公众提供知识、教育及欣赏服务. 近年来，人们到博物馆学习参观的热情越来越高. 2012-2018年我 国博物馆参观人数统计如下：BCD O EA小明研究了这个统计图，得出四个结论：① 2012年到2018年，我国博物馆参观人数持续增长； ②2019年末我国博物馆参观人数估计将达到10.82亿人次；③ 2012年到2018年，我国博物馆参观人数年增幅最大的是2017年； ④ 2016年到2018年，我国博物馆参观人数平均年增长率超过10%． 其中正确的是 A ．①③B ．①②③C ．①②④D ．①②③④二、填空题（本题共18分，每小题3分）11． 如图，在□ABCD 中，∠B =110°，则∠D =________°.12．八年级（1）班甲、乙两个小组的10名学生进行飞镖训练，某次训练成绩如下：由上表可知，甲、乙两组成绩更稳定的是 组.13．若关于x 的一元二次方程260x x m ++=有实数根, 且所有实数根均为整数，请写出一个符合条件的常数m 的值：m = .A14．如图，某港口P 位于南北延伸的海岸线上，东面是大海.“远洋”号、“长峰”号两艘轮船同时离开港口P ，各自沿固定方向航行，“远洋”号每小时航行12 n mile ，“长峰”号每小时航行16 n mile ，它们离开港 口1小时后，分别到达A ，B 两个位置，且AB =20 n mile ，已知“远 洋”号沿着北偏东60°方向航行，那么“长峰”号航行的方向是_______. 15．若一个矩形的长边的平方等于短边与其周长一半的积,则称这样的矩形为“优美矩形”.某公园在绿化时,工作人员想利用如图所示的直角墙 角（两边足够长）和长为38 m 的篱笆围成一个“优美矩形”形状的花 园ABCD ,,其中边AB , AD 为篱笆,且AB 大于AD . 设AD 为x m, 依题 意可列方程为 .16. 在平面直角坐标系xOy 中，直线3y kx =+与x ，y 轴分别交于点A ，B ，若将该直线向右平移5个单位，线段AB 扫过区域的边界恰好为菱形，则k 的值为 .三、解答题（本题共26分，第17题8分，第18，20题各5分，第19，21题各4分） 17．解方程： （1）2230x x --=；（2）22310x x +-=.18．在平面直角坐标系xOy 中，一次函数y =kx +b 的图象与直线y ＝2x 平行，且经过点A (1,6)．（1）求一次函数y =kx +b 的解析式；（2）求一次函数y =kx +b 的图象与坐标轴围成的三角形的面积．19．下面是小丁设计的“利用直角三角形和它的斜边中点作矩形”的尺规作图过程．已知：如图，在Rt △ABC 中，∠ABC =90°，O 为AC 的中点． 求作：四边形ABCD ，使得四边形ABCD 为矩形．作法：①作射线BO ，在线段BO 的延长线上取点D ，使得DO =BO ；②连接AD ，CD ，则四边形ABCD 为矩形． 根据小丁设计的尺规作图过程.（1）使用直尺和圆规，在图中补全图形（保留作图痕迹）； （2）完成下面的证明． 证明：∵点O 为AC 的中点，∴ AO =CO ． 又∵ DO =BO ，∴四边形ABCD 为平行四边形（ ）（填推理的依据）．∵∠ABC =90°，∴□ABCD 为矩形（ ）（填推理的依据）．20. 关于x 的一元二次方程2240x x k ++-=有实数根．（1）求k 的取值范围;（2）若k 是该方程的一个根，求2265k k +-的值．21．小东和小明要测量校园里的一块四边形场地ABCD （如图所示）的周长，其中边CD 上有水池及建筑遮挡，没有办法直接测量其长度.小东经测量得知AB =AD =5 m ，∠A =60°，BC =12 m ，∠ABC =150°. 小明说根据小东所得的数据可以求出CD 的长度.你同意小明的说法吗？若同意，请求出CD 的长度；若不同意，请说明理由.ADCB四、解答题（本题共13分，第22题7分，第23题6分）22．三月底，某学校迎来了以“学海通识品墨韵，开卷有益览书山”为主题的学习节活动.为了让同学们更好的了解二十四节气的知识, 本次学习节在沿袭以往经典项目的基础上，增设了 “二十四节气之旅”项目，并开展了相关知识竞赛. 该学校七、八年级各有400名学生参加了这 次竞赛, 现从七、八年级各随机抽取20名学生的成绩进行抽样调查. 收集数据如下：七年级：74 97 96 72 98 99 72 73 76 7474 69 76 89 78 74 99 97 98 99八年级：76 88 93 89 78 94 89 94 95 50 89 68 65 88 77 87 89 88 92 91整理数据如下：分析数据如下：年级 平均数 中位数 众数 方差 七年级 84. 2 77 74 138.56 八年级84b89129.7根据以上信息，回答下列问题：（1）a = ，b = ；（2）你认为哪个年级知识竞赛的总体成绩较好，说明理由（至少从两个不同的角度说明推断的合理性）；（3）学校对知识竞赛成绩不低于80分的学生颁发优胜奖，请你估计学校七、八年级所有学生中获得优胜奖的大约有 人.50x ≤≤5960x ≤≤6970x ≤≤7980x ≤≤8990x ≤≤100七年级 0 1 10 1 a 八年级 12386人数 成绩年级23. 如图，在□ABCD 中，对角线AC ，BD 交于点O ，过点B 作BE ⊥CD 于点E ，延长CD 到点F ，使DF =CE ，连接AF . （1）求证：四边形ABEF 是矩形；（2）连接OF ，若AB =6，DE =2，∠ADF =45°，求OF 的长度.五、解答题（本题共13分，第24题6分，第25题7分）24．如图，在平面直角坐标系xOy 中，直线7y kx =+与直线2y x =-交于点()3,A m .（1）求,k m 的值；（2）已知点(),P n n ，过点P 作垂直于y 轴的直线与直线2y x =-交于点M ，过点P 作垂直于x 轴的直线与直线7y kx =+交于点N （P 与N 不重合）. 若2PN PM ≤，结合图象，求n 的取值范围．25．在Rt △ABC 中，90BAC ∠=︒，点O 是△ABC 所在平面内一点，连接OA ，延长OA 到点E ，使得AE =OA ，连接OC ，过点B 作BD 与OC 平行，并使∠DBC =∠OCB ，且BD =OC ，连接DE . （1）如图一，当点O 在Rt △ABC 内部时.① 按题意补全图形；② 猜想DE 与BC 的数量关系，并证明.（2）若AB = AC （如图二）， 且30,15OCB OBC ∠=︒∠=︒，求AED ∠的大小．图一图二备用图海淀区2019年八年级学业发展水平评价数 学参考答案一、选择题二、填空题11． 110 12．甲13．0（答案不唯一） 14．南偏东30°15．2(38)38x x -=（无需写成一般式） 16. 34±（填对一个得2分，填对两个得3分，含有错误答案得0分） 三、解答题 17．解：（1）2230x x --=；解法一： 2230x x --=223x x -=2214x x -+=…………………………………………………………………………1分 2(1)4x -=………………………………………………………………………………2分 12x -=±………………………………………………………………………………3分 123,1x x ==-………………………………………………………………………………4分解法二：2230x x --=(3)(1)0x x -+= ………………………………………………………………………………2分123,1x x ==-………………………………………………………………………………4分备用图（2）22310x x +-=.解：22310x x +-= 2,3,1a b c ===-Q942(1)170∴∆=-⨯⨯-=>……………………………………………………………………1分x = ………………………………………………………………………………3分12x x ……………………………………………………………………4分 注：若（1）中用公式法，请参考（2）中评分细则18．解：（1）Q 一次函数y kx b =+的图象为直线，且与直线2y x =平行，2k ∴=. ……………………………………………………………………………1分 又知其过点A (1,6), 26b ∴+=. 4b ∴=.∴一次函数的解析式为24y x =+. ………………………………………………………2分 （2）当0x =时，4y =,可知直线24y x =+与y 轴的交点为(0,4). ……………………………………………3分当0y =时，2x =-,可知直线24y x =+与x 轴交点为(2,0)-. ……………………………………………4分可得该直角三角形的两条直角边长度分别为4和2.所以直线24y x =+与坐标轴围成的三角形的面积为14242⨯⨯=.…………………5分19．解：（1）作图如图所示…………………………………………………………………2分（2）对角线互相平分的四边形是平行四边形.……………………………………………3分 有一个角是直角的平行四边形是矩形.……………………………………………4分20. 解：（1）2240x x k ++-=Q 有实数根， 0∴∆≥.………………………………………………………………………………………1分即()22440k --≥.5.k ∴≤ …………………………………………………………………………………2分（2）Q k 是方程2240x x k ++-=的一个根，2240.k k k ∴++-= ……………………………………………………………………………3分 234k k ∴+=. …………………………………………………………………………………4分2265k k +-()2235k k =+-3.=…………………………………………………………………………………5分21．解：同意.………………………………………………………………………………………1分连接BD ，如图.∵AB =AD =5 (m)，∠A =60°， ∴△ABD 是等边三角形. ……………………2分 ∴BD =AB =5 (m)，∠ABD =60°. ∵∠ABC =150°，∴∠CBD =∠ABC －∠ABD =150°－60°=90°. ……3分 在Rt △CBD 中，BD =5 (m)，BC =12 (m)， ∴CD13=(m). …………………………………………………4分四、解答题 22．解： （1）8，88.5；…………………………………………………………………………………2分（2）你认为 八 年级知识竞赛的总体成绩较好，理由1：八年级成绩的中位数较高；理由2：八年级与七年级成绩的平均数接近且八年级方差较低，成绩更稳定. 或者你认为 七 年级知识竞赛的总体成绩较好， 理由1：七年级的平均成绩较高； 理由2：低分段人数较少 .…………………………………………………………………………………5分（答案不唯一，合理即可） （3）460． …………………………………………………………………………………7分 23. （1）证明：∵四边形ABCD 是平行四边形∴AB CD =，AB CD ∥.∵DF CE =,∴DF DE CE ED +=+, 即: FE CD =.∵点F 、E 在直线CD 上, ∴AB FE = AB FE ∥. ∴四边形ABEF 是平行四边形. ……………………………………………………………1分又∵BE CD ⊥，垂足是E ,A∴90BEF ∠=︒. ∴四边形ABEF 是矩形.……………………………………………………………2分（2）解：∵四边形ABEF 是矩形O ,∴90AFC ∠=︒，AB FE =. ∵6,2AB DE ==, ∴4FD =.∵FD CE =, ∴4CE =.∴10FC =.…………………………………………………………………………………3分在Rt AFD △中，90AFD ∠=︒． ∵45ADF ∠=︒, ∴4AF FD ==.………………………………………………………………………4分在Rt AFC △中，90AFC ∠=︒．∴AC ==．……………………………………………………………5分∵点O 是平行四边形ABCD 对角线的交点， ∴O 为AC 中点.在Rt AFC △中，90AFC ∠=︒．O 为AC 中点．∴12OF AC == …………………………………………………………………6分五、解答题 24．解：（1）∵直线y =kx ＋7与直线y =x ﹣2交于点A （3，m ），∴m =3k ＋3，m =1. …………………………………………………………………1分∴k =﹣2. …………………………………………………………………2分 （2）∵点P （n ，n ），过点P 作垂直于y 轴的直线与直线y =x ﹣2交于点M ， ∴M （n ＋2，n ）. ∴PM =2. …………………………………………………………………………………3分 ∵PN ≤2PM ， ∴PN ≤4.∵过点P 作垂直于x 轴的直线与直线y =kx ＋∴N (n ,﹣2n +7).∴PN =37n -. 当PN =4时，如图，即37n -=4， ∴n =1或n =113.∵P 与N 不重合,∴370n -≠. ∴73n ≠.当PN ≤4（即PN ≤2PM ）时， n 的取值范围为：713n <≤或71133n <≤.…………………………………………………6分25. 解：（1）①补全图形，如图一.……………………………1分②猜想DE =BC. …………………………………2分如图，连接OD 交BC 于点F ，连接AF . 在△BDF 和△COF 中, ,,,DBF OCF DFB OFC DB OC ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△BDF ≌△COF .∴DF =OF , BF =CF . …………………………………3分 ∴F 分别为BC 和DO 的中点. ∵∠BAC =90°, F 为BC 的中点, ∴12AF BC =. ∵OA =AE , F 为BC 的中点,∴12AF ED =. ∴DE =BC. ………………………………………4分 （2）如图二，连接OD 交BC 于点F ，连接AF ，延长CO交AF 于点M ，连接BM.由（1）中②可知，点F 为BC 的中点，AF 为Rt △ABC 斜边BC 边中线，为△OED 的中位线, ∴AF 为BC 边的垂直平分线. ∴MB =MC.∵∠OCB =30°,∠OBC =15°, ∴∠MBC =∠MCB =30°.图一图二∵∠BAC=90°,AB=AC,∴∠MBO=∠MBA=15°.又可证∠BAM=∠BOM=45°.∴△BMA≌△BMO.∴AM=OM且∠BMO=∠BMA=120°.∴∠OMA=120°.∴∠MAO=30°.∵AF为△OED的中位线,∴AF∥ED.∴∠AED=30°.类似的，如备用图可知，∠AED=15°. ………………7分(提示：证明△ABO为等边三角形，得到∠AED=15°.)∴∠AED=30°或15°.注：各题中若有其他合理的解法请酌情给分.备用图。

七年级第二学期期末调研生物学校班级姓名成绩考生须知1．本试卷共8页，共三道大题，41道小题，满分100分。

考试时间60分钟。

2．在答题纸上认真填写学校名称、姓名和准考证号。

3．试题答案一律填涂或书写在答题纸上，在试卷上作答无效。

4．考试结束，请将本试卷和答题纸一并交回。

一、选择题（在四个选项中，选出最符合题目要求的一项。

每小题1分，共25分）1.下列各项，不能．．作为人类与现代类人猿有共同祖先的证据的是（）A.形态结构相似B.生活环境相似C.生理特征相似D.行为方式相似2.下列器官及生理过程对应错误．．的是（）A.睾丸——产生精子 B.输卵管——精卵结合C.子宫——胎儿发育D.阴茎——分泌性激素3.新个体的第一个细胞是（）A.精子B.卵细胞C.受精卵D.胚泡4.青春期男生、女生会出现遗精或月经现象，以下叙述不正确．．．的是（）A.都受性激素调节 B.是正常的生理现象C.此时需避免运动D.此时更应注意卫生5.下列营养物质中，都能为人体生命活动提供能量的一组是（）①水②无机盐③糖类④脂肪⑤维生素⑥蛋白质A.①③④B．②③④C．③④⑥D．④⑤⑥6.下列4种食品营养成分含量不同，某同学长期以一种食品为主食患了佝偻病，这种食品最可能是（）7.“荤素搭配有营养，饥饱有度利健康”。

下列表示健康成年人膳食中各种食物配置比例最A B C D8.）A.是唾液淀粉酶作用的结果B.是牙齿和舌头作用的结果C.是淀粉溶解在水中的结果D.是蛋白质被分解后的结果9.下列各结构特点，与小肠吸收功能无直接．．．关系的是（）A.小肠长约5～6米，是消化道中最长的一段B.小肠腔中有肠液、胰液和胆汁等多种消化液C.小肠绒毛壁、毛细血管壁由一层上皮细胞组成D.小肠内表面的皱襞和绒毛使其表面积大大增加10.右图为人体消化系统的部分器官，下列叙述不正确．．．的是（）A.①分泌的消化液含有消化酶B.③是消化和吸收的主要场所C.④可短时间内容纳大量食物D.⑤是胰腺，分泌胰液进入③11.医生从病人的消化道中取得少量液体，经化验发现含有蛋白质、蛋白质的初步消化物、维生素、无机盐、水、脂肪和盐酸等。