反比例函数的提高讲义

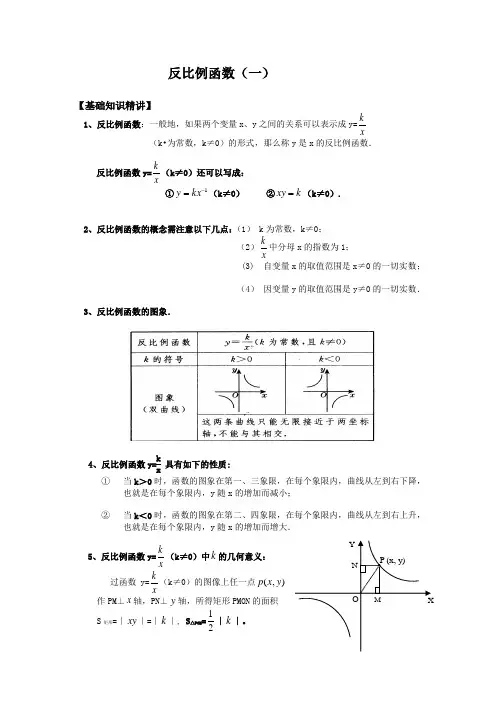
反比例函数（一）【基础知识精讲】1、反比例函数：一般地，如果两个变量x 、y 之间的关系可以表示成y=k x（k•为常数，k ≠0）的形式，那么称y 是x 的反比例函数．反比例函数y=kx（k ≠0）还可以写成： ①1-=kx y （k ≠0） ②k xy =（k ≠0）.2、反比例函数的概念需注意以下几点：（1） k 为常数，k ≠0；（2）kx中分母x 的指数为1； (3) 自变量x 的取值范围是x ≠0的一切实数；（4） 因变量y 的取值范围是y ≠0的一切实数．3、反比例函数的图象．4、反比例函数y=kx具有如下的性质:① 当k ＞0时，函数的图象在第一、三象限，在每个象限内，曲线从左到右下降，也就是在每个象限内，y 随x 的增加而减小；② 当k ＜0时，函数的图象在第二、四象限，在每个象限内，曲线从左到右上升，也就是在每个象限内，y 随x 的增加而增大．5、反比例函数y=kx （k ≠0）中k 的几何意义：过函数 y=kx（k ≠0）的图像上任一点),(y x p作PM ⊥x 轴，PN ⊥y 轴，所得矩形PMON 的面积S 矩形=∣xy ∣=∣k ∣, S △POM =21∣k ∣。

【例题巧解点拨】例1 ①（2012·滨州）下列函数：① y=2x ﹣1； ② y=﹣； ③ y=x 2+8x ﹣2；④ y=； ⑤ y=； ⑥ y=中，y 是x 的反比例函数的有 （填序号）② 若反比列函数1232)12(---=k kx k y 的图像经过二、四象限，则k = _______③（2012•济宁）如图，是反比例函数y=的图象的一个分支，对于给出的下列说法：① 常数k 的取值范围是k ＞2；② 另一个分支在第三象限；③ 在函数图象上取点A （a 1，b 1）和点 B （a 2，b 2），当a 1＞a 2时，则b 1＜b 2； ④ 在函数图象的某一个分支上取点A （a 1，b 1）和点B （a 2，b 2），当a 1＞a 2时，则b 1＜b 2；其中正确的是 （在横线上填出正确的序号）变式训练：1．(2012•天门) 函数 , 的图象如图所示， 则结论： ① 两函数图象的交点A 的坐标为（3 ,3 )② 当时，③ 当 时， BC = 8④ 当逐渐增大时，随着的增大而增大，随着的增大而减小．其中正确结论的序号是 .2. (2012•连云港)如图，直线y ＝k 1x ＋b 与双曲线y ＝xk 2交于A 、B 两点，其横坐标分别为1和5，则不等式 k 1x ＜xk 2＋b 的解集是 ．1(0)y x x =≥xy 92=(0)x >3x >21y y >1x =x 1y x 2y x yy 1＝x y 2＝9xx（第15题图）3. (2012•梅州) 在同一直角坐标系下，直线y=x+1与双曲线 y=1x的交点的个数为（ ）A ．0个B ．1个C ．2个D ．不能确定4．（2012张家界）当在同一坐标系中的图像与函数时，函数ay ax y a =+=≠10 可能是（）6．（2012聊城）如图，在直角坐标系中，正方形的中心在原点O ，且正方形的一组对边与x 轴平行，点P （3a ，a ）是反比例函数y=（k ＞0）的图象上与正方形的一个交点．若图中阴影部分的面积等于9，则这个反比例函数的解析式为 ．7．(2012•德州) 如图，两个反比例函数1y x=和2y x=-的图象分别是1l 和2l ．设点P 在1l 上，PC ⊥x 轴，垂足为C ，交2l 于点A ，PD ⊥y 轴，垂足为D ，交2l 于点B ，则三角形PAB 的面积为（ ） A.3 B.4 C.92D.5例3 某商场出售一批名牌衬衣,衬衣进价为80元，在营销中发现，该衬衣的日销售量y （件）是日销售价x （元）的反比例函数，且当售价定为100元/件时，每日可售出30件。

【本讲教育信息】一、教学内容：反比例函数综合提高 1. 反比例函数的定义．2. 反比例函数的图象和性质．3. 反比例函数与实际问题．二、知识要点： 1. 反比例函数一般地，形如y ＝kx（k 为常数，k ≠0）的函数称为反比例函数，其中x 是自变量，y 是函数．其表达式也可以写成y ＝kx －1，有时利用变形式子xy ＝k ． 2. 反比例函数的图象和性质当k ＞0时，反比例函数的图象的两个分支位于一、三象限．在每个象限内y 值随x 的增大而减小；当k ＜0时，反比例函数的两个分支分别位于第二、四象限，在每个象限内y 值随x 的增大而增大．3. 反比例函数的实际应用（1）利用物理学公式、数学公式和一些实际情境建立函数关系式．（2）很多实际问题中的自变量的取值是有限制的，因此画实际问题的反比例函数图象一定要注意取值范围．三、重点难点：本讲重点是反比例函数图象及其性质，难点是利用反比例函数解决实际问题．四、考点分析：反比例函数是最基本的函数，这部分知识在中考命题中常以选择题形式出现．特别是以判断图象的形式命题．近几年各省、市的中考试卷中出现了不少反比例函数与一次函数、二次函数、几何知识、三角知识等综合编拟的解答题，丰富了压轴题的形式．【典型例题】例 1. 一个圆台物体的上底面积是下底面积的23，如果如图放在桌面上，对桌面的压强是200帕，翻过来放对桌面的压强是多少？分析：由物理知识可知，压力F 、压强P 与受力面积S 之间的关系式是P ＝FS，因为是同一物体，所以，力F 的数值不变，所以，P 与S 成反比例．解：设下底面积为S 0，则上底面积为23S 0．由P ＝FS且S ＝S 0时，p ＝200帕得，F ＝PS ＝200S 0因为是同一物体，所以F ＝200S 0是定值所以当S ＝23S 0时，P ＝200S 023S 0＝300（帕）因此，当翻过来时压强是300帕．评析：近几年来，学科间的综合题目是考查的一个热点问题，做这类题目需要熟练掌握物理学知识，并能找出物理知识与数学知识之间的关系．例2. 如图所示，在直角坐标系中，A 点是双曲线y ＝mx在第一象限内的点，又AB 垂直于x 轴，垂足为B ，且S △AOB ＝1，求m 的值．分析：S △AOB ＝12OB ·BA ，此时因A 点在第一象限，OB 、BA 的长与A 的横、纵坐标分别相等．解：设A （x ，y ）（x ＞0，y ＞0），因点A 在双曲线y ＝mx上，所以xy ＝m ．又S △AOB ＝12OB ·BA ＝12xy ＝1．所以12m ＝1，即m ＝2．评析：对反比例函数y ＝kx（k ≠0）进行变形，可得xy ＝k ，过反比例函数图象上的点，作x 轴的垂线得到的垂足以及原点构成的三角形，所有这类三角形的面积都等于12︱k ︱，这个规律很有用．例3. 有一个容积为60m 3的水池，要在10h 内注满水．（1）写出注水时间T （h ）与每小时注水量H （m 3）之间的函数关系式，并求自变量的取值范围；（2）已知每小时注水量不能超过10m 3，则至少需要多长时间才能注满水池？分析：根据题意，可知容积＝每小时的注水量×注水时间，所以有HT ＝60，H ＝60T．解：（1）因为HT ＝60，所以H ＝60T．因为要在10h 内注满水，所以T ≤10．又因为T ≠0且T 为注水时间，所以0＜T ≤10．（2）将H ＝10代入H ＝60T ，得10＝60T，T ＝6．所以至少需要6小时才能注满水池． 评析：“10h 内注满水”这个条件是最后用来写自变量T 的取值范围的，真正存在关系的是T 、H 与60，弄清了这些，题目就容易解了．例4. 请你在课本所学的函数中选择一个函数，使它的图象经过点A （1，3）和B （3，1）． （1）求出所选函数的解析式，并画出函数的图象； （2）根据图象说出函数的三条性质（或图象的特征）．分析：（1）可以考虑过A 、B 的直线和双曲线两种情形；（2）根据画出的一次函数或反比例函数的图象说出其性质（特征）．解：（1）设函数解析式为y ＝kx．因为y ＝kx 的图象经过A （1，3），所以k ＝3．所以y ＝3x ，且B 也在y ＝3x的图象上，图象如图①所示．或设一次函数的解析式为y ＝kx ＋b ． 因为它的图象过点A （1，3）、B （3，1），所以⎩⎪⎨⎪⎧3＝k ＋b 1＝3k ＋b ，解得⎩⎪⎨⎪⎧k ＝－1b ＝4 ．所以函数的解析式为y ＝－x ＋4，图象如图②所示．（2）以一次函数的图象为例，其性质或特征如下：①y 随x 的增大而减小；②直线不经过第三象限（或直线经过第一、二、四象限）；③直线与两坐标轴围成一个等腰直角三角形；④直线与y 轴的交点为（0，4）等等．评析：如果选择了反比例函数，由A （1，3）确定函数关系式后，必需再对点B （3，1）作出验证．例5. 如图，两个反比例函数y ＝ k 1x 和y ＝ k 2x（其中k 1＞k 2＞0）在第一象限内的图象依次是C 1和C 2，设点P 在C 1上，PC ⊥x 轴于点C ，交C 2于点A ，PD ⊥y 轴于点D ，交C 2于点B ，则四边形PAOB 的面积为（ ）A. k 1＋k 2B. k 1－k 2C. k 1·k 2D. k 1k 2分析：四边形PAOB 的面积＝四边形PCOD 的面积－S △BOD －S △AOC ．由于点P 在C 1（y ＝k 1x ，且k 1＞0）上，所以四边形PCOD 的面积＝︱xy ︱＝︱k 1︱＝k 1；点B 、C 在C 2（y ＝k 2x，且k 2＞0）上，所以S △BOD ＝S △AOC ＝12︱xy ︱＝12︱k 2︱＝12k 2．所以四边形PAOB 的面积＝k 1－12k 2－12k 2＝k 1－k 2．故选B ． 解：B例6. 如图所示，一次函数y ＝kx ＋b 的图象与反比例函数y ＝mx的图象相交于A 、B 两点．（1）根据图象，分别写出A 、B 的坐标； （2）求出两函数解析式；（3）根据图象回答：当x 为何值时，一次函数的函数值大于反比例函数的函数值．4321-2-15-3-4-5-64321-2-1-3y xAB分析：（1）如图，A （－6，－2），B （4，3）（2）一次函数y ＝kx ＋b 过A 、B 两点，所以有⎩⎪⎨⎪⎧－2＝－6k ＋b 3＝4k ＋b ，解得⎩⎪⎨⎪⎧k ＝12b ＝1，所以一次函数的解析式为y ＝12x ＋1；反比例函数y ＝k x 过点B ，所以3＝k 4，得k ＝12，所以反比例函数的解析式为y ＝12x．（3）观察图象发现：x ＜－6时，一次函数图象在反比例函数图象下，一次函数值小于反比例函数值；当－6＜x ＜0时，一次函数值大于反比例函数值；当0＜x ＜4时，一次函数值小于反比例函数值；当x ＞4时，一次函数值大于反比例函数值．所以当－6＜x ＜0或x ＞4时，一次函数值大于反比例函数值．解：（1）A （－6，－2），B （4，3）；（2）一次函数y ＝kx ＋b 过A （－6，－2）、B （4，3）两点，所以有⎩⎪⎨⎪⎧－2＝－6k ＋b3＝4k ＋b ，解得⎩⎪⎨⎪⎧k ＝12b ＝1，所以一次函数的解析式为y ＝12x ＋1；因为反比例函数y ＝kx过点B （4，3），所以3＝k4，得k ＝12，所以反比例函数的解析式为y ＝12x．（3）－6＜x ＜0或x ＞4时，一次函数的函数值大于反比例函数的函数值．【方法总结】1. 理解反比例函数的意义，准确理解“反比例关系”与“反比例函数”的异同；2. 能结合待定系数法在确定反比例函数中的应用，熟悉待定系数法的基本思想；3. 反比例函数的图象是研究反比例函数的性质的重要工具，学习中要把握反比例函数的图象的特点，即反比例函数图象的形状、位置、增减性等，注意反比例函数的增减性是相对于双曲线所在的象限而言的；4. 理解反比例函数的比例系数k 的几何意义，体会数形结合的思想；5. 了解生活中的反比例关系，能够运用反比例函数的模型解决实际问题．【模拟试题】（答题时间：70分钟）一. 选择题1. 如果反比例函数y ＝kx 的图象经点（－2，3），那么k 的值是（ ）A. －6B. －32C. －23D. 62. 若双曲线y ＝－6x经过点A （m ，－2m ），则m 的值为（ ）A. 3B. 3C. ± 3D. ±33. 在一个可以改变容积的密闭容器内，装有一定质量m 的某种气体，当改变容积V 时，气体的密度ρ也随之改变．ρ与V 在一定范围内满足ρ＝mV，它的图象如图所示，则该气体的质量m 为（ ）A. 1.4kgB. 5kgC. 6.4kgD. 7kg3)4. 已知一次函数y ＝kx ＋b 的图象经过第一、二、四象限，则反比例函数y ＝kbx的图象在（ ）A. 第一、二象限B. 第三、四象限C. 第一、三象限D. 第二、四象限**5. 在同一直角坐标系中，函数y ＝kx －k 与y ＝kx（k ≠0）的图象大致是（ ）*6. 已知反比例函数y ＝kx（k ≠0），当x ＜0时，y 随x 的增大而增大，那么一次函数y ＝kx －k 的图象经过（ ）A. 第一、二、三象限B. 第一、二、四象限C. 第一、三、四象限D. 第二、三、四象限7. 已知反比例函数y ＝－1x的图象上有两点A （x 1，y 1）、B （x 2，y 2），且x 1＜x 2，那么下列结论正确的是（ ）A. y 1＜y 2B. y 1＞y 2C. y 1＝y 2D. y 1与y 2之间的大小关系不能确定 8. 已知y ＝（a －1）x a 是反比例函数，则它的图象在（ ）A. 第一、三象限B. 第二、四象限C. 第一、二象限D. 第三、四象限9. 在同一平面直角坐标系中，函数y ＝－1x与函数y ＝x 的图象交点个数是（ ）A. 0个B. 1个C. 2个D. 3个 *10. 已知某反比例函数的图象经过点（m ，n ），则它一定也经过点（ ） A. （m ，－n ） B. （n ，m ） C. （－m ，n ） D. （︱m ︱，︱n ︱）二. 填空题1. 反比例函数y ＝kx 的图象过点P （－1.5，2），则k ＝__________．2. 函数y ＝－2x 的图象，在每一个象限内，y 随x 的增大而________．3. 已知函数y ＝2x，当x ＞0时，函数图象在第____象限．4. 点P （2m －3，1）在反比例函数y ＝1x的图象上，则m ＝__________．5. 已知反比例函数的图象经过点（m ，2）和（－2，3）则m 的值为__________．**6. 如图，一次函数与反比例函数的图象相交于Ａ、B 两点，则图中反比例函数的值小于一次函数的值的x 的取值范围是__________．7. 有x 个小朋友平均分20个苹果，每人分得的苹果y （个/人）与x （个）之间的函数是______函数，其函数关系式是__________．当人数增多时，每人分得的苹果就会减少，这正符合函数y ＝kx（k ＞0），当x ＞0时，y 随x 的增大而__________的性质．*8. 设有反比例函数y ＝k ＋1x，（x 1，y 1）、（x 2，y 2）为其图象上的两点，若x 1＜0＜x 2，y 1＞y 2，则k 的取值范围为____________．**9. 已知n 是正整数，P n （x n ，y n ）是反比例函数y ＝kx图象上的一列点，其中x 1＝1，x 2＝2，…，x n ＝n ，记T 1＝x 1y 2，T 2＝x 2y 3，…，T 9＝x 9y 10；若T 1＝1，则T 1·T 2·…·T 9的值是__________．**10. 如图，在反比例函数y ＝2x（x＞0）的图象上，有点P 1，P 2，P 3，P 4，它们的横坐标依次为1，2，3，4．分别过这些点作x 轴与y 轴的垂线，图中所构成的阴影部分的面积从左到右依次为S 1，S 2，S 3，则S 1＋S 2＋S 3＝__________．4321OxyP 1P 2P 3P 4三. 解答题1. 已知一次函数y ＝kx ＋k 的图象与反比例函数y ＝8x的图象在第一象限交于B （4，n ），求k ，n 的值．*2. 如图所示，一次函数y ＝ax ＋b 的图象与反比例函数y ＝kx 的图象交于A 、B 两点，与x轴交于点C ．已知点A 的坐标为（－2，1），点B 的坐标为（12，m ）．（1）求反比例函数和一次函数的解析式；（2）根据图象写出使一次函数的值小于反比例函数的值的x 的取值范围．O CAB*3. 某蓄水池的排水管每小时排水8m 3，6小时可将满池水全部排空． （1）蓄水池的容积是多少？（2）如果增加排水管，使每小时的排水量达到Q （m 3），那么将满池水排空所需的时间t （h ）将如何变化？（3）写出t 与Q 的关系式．（4）如果准备在5小时内将满池水排空，那么每小时的排水量至少为多少？（5）已知排水管的最大排水量为每小时12m 3，那么最少需多长时间可将满池水全部排空？【试题答案】一. 选择题1. A2. C3. D4. D5. D6. B7. D8. B9. A 10. B二. 填空题1. －32. 增大3. 一4. 25. －36. x ＜－1或0＜x ＜27. 反比例，y ＝20x减小 8. k ＜－1 9. 51.2 10. 32三. 解答题1. k ＝0.4，n ＝22. （1）y ＝－2x ，y ＝－2x －3（2）－2＜x ＜0或x ＞123. （1）蓄水池的容积是6×8＝48（m 3）．（2）增加排水量会使时间缩短，所需的时间t 会减少．（3）因为容积V ＝48m 3，所以所求关系式为t ＝48Q．（4）48Q≤5，Q ≥9.6．（5）设最长用x 小时将满池水排空，根据题意得，12x ≥48，解得x ≥4（h ）．。

《反比例函数》讲义一、反比例函数的定义一般地，如果两个变量 x、y 之间的关系可以表示成 y ＝ k/x（k 为常数，k≠0）的形式，那么称 y 是 x 的反比例函数。

例如，速度 v 一定时，路程 s 与时间 t 的关系为 s ＝ vt，当路程一定时，即 s 为常数时，那么时间 t 与速度 v 的关系就可以表示为 t ＝s/v，此时 t 是 v 的反比例函数。

需要注意的是，反比例函数中，自变量 x 不能等于 0，因为分母不能为 0。

同时，反比例函数的表达式还可以写成 xy ＝ k 或 y ＝ kx^（－1) 的形式。

二、反比例函数的图像反比例函数的图像是双曲线。

当 k＞0 时，双曲线的两支分别位于第一、三象限，在每一象限内 y 随 x 的增大而减小；当 k＜0 时，双曲线的两支分别位于第二、四象限，在每一象限内 y 随 x 的增大而增大。

例如，函数 y ＝ 2/x，因为 k ＝ 2＞0，所以它的图像在第一、三象限，在每个象限内，y 随 x 的增大而减小。

我们可以通过列表、描点、连线的方法来画出反比例函数的图像。

在列表时，要选取一些具有代表性的点，比如 x 取 1、2、－1、－2 等等，然后计算出对应的 y 值，再描点连线。

三、反比例函数的性质1、对称性反比例函数的图像既是轴对称图形，又是中心对称图形。

它的对称轴有两条，分别是直线 y ＝ x 和直线 y ＝ x。

对称中心是坐标原点（0，0）。

2、增减性前面我们提到了，当k＞0 时，在每一象限内y 随x 的增大而减小；当 k＜0 时，在每一象限内 y 随 x 的增大而增大。

需要注意的是，这里说的增减性是在每个象限内，而不是在整个定义域内。

3、渐近线反比例函数的图像无限接近坐标轴，但永远不会与坐标轴相交。

当 x 趋近于正无穷大或负无穷大时，y 趋近于 0；当 y 趋近于正无穷大或负无穷大时，x 趋近于 0。

四、反比例函数中 k 的几何意义设 P（x，y）是反比例函数 y ＝ k/x 图像上的任意一点，过点 P 作x 轴、y 轴的垂线 PM、PN，垂足分别为 M、N，则矩形 PMON 的面积S ＝ PM·PN ＝｜xy| ＝｜k|。

反比例函数全章复习与巩固（提高）【学习目标】1．使学生理解并掌握反比例函数的概念，能根据实际问题中的条件确定反比例函数的解析式()0k y k x=≠，能判断一个给定函数是否为反比例函数；2．能描点画出反比例函数的图象，会用待定系数法求反比例函数的解析式；3．能根据图象数形结合地分析并掌握反比例函数()0k y k x =≠的性质，能利用这些性质分析和解决一些简单的实际问题.【知识网络】【要点梳理】要点一、反比例函数的概念一般地，形如k y x =(k 为常数，0k ≠)的函数称为反比例函数，其中x 是自变量，y 是函数，自变量x 的取值范围是不等于0的一切实数.要点诠释：在k yx =中，自变量x 的取值范围是，k y x =()可以写成()的形式，也可以写成的形式.要点二、反比例函数解析式的确定反比例函数解析式的确定方法是待定系数法.由于反比例函数k y x=中，只有一个待定系数k ，因此只需要知道一对x y 、的对应值或图象上的一个点的坐标，即可求出k 的值，从而确定其解析式.要点三、反比例函数的图象和性质1.反比例函数的图象反比例函数()0k y k x=≠的图象是双曲线，它有两个分支，这两个分支分别位于第一、三象限或第二、四象限．它们关于原点对称，反比例函数的图象与x 轴、y 轴都没有交点，即双曲线的两个分支无限接近坐标轴，但永远不与坐标轴相交．要点诠释：观察反比例函数的图象可得：x 和y 的值都不能为0，并且图象既是轴对称图形，又是中心对称图形，它有两条对称轴，对称中心是坐标原点．①)0(≠=k x k y 的图象是轴对称图形，对称轴为x y x y -==和两条直线；②)0(≠=k x k y 的图象是中心对称图形，对称中心为原点（0，0）；③x k y x k y -==和(k≠0)在同一坐标系中的图象关于x 轴对称，也关于y 轴对称.注：正比例函数x k y 1=与反比例函数xk y 2=，当021<⋅k k 时，两图象没有交点；当021>⋅k k 时，两图象必有两个交点，且这两个交点关于原点成中心对称.2.反比例函数的性质（1）图象位置与反比例函数性质当0k >时，x y 、同号，图象在第一、三象限，且在每个象限内，y 随x 的增大而减小；当0k <时，x y 、异号，图象在第二、四象限，且在每个象限内，y 随x 的增大而增大.（2）若点(a b ，)在反比例函数k y x=的图象上，则点（a b --，）也在此图象上，故反比例函数的图象关于原点对称.（3）正比例函数与反比例函数的性质比较正比例函数反比例函数解析式图像直线有两个分支组成的曲线（双曲线）位置0k >，一、三象限；0k >，一、三象限0k <，二、四象限0k <，二、四象限增减性0k >，y 随x 的增大而增大0k <，y 随x 的增大而减小0k >，在每个象限，y 随x 的增大而减小0k <，在每个象限，y 随x 的增大而增大（4）反比例函数y＝中k 的意义①过双曲线xk y =(k ≠0)上任意一点作x 轴、y 轴的垂线，所得矩形的面积为k .②过双曲线xk y =(k ≠0)上任意一点作一坐标轴的垂线，连接该点和原点，所得三角形的面积为k .要点四、应用反比例函数解决实际问题须注意以下几点1．反比例函数在现实世界中普遍存在，在应用反比例函数知识解决实际问题时，要注意将实际问题转化为数学问题.2．列出函数关系式后，要注意自变量的取值范围.【典型例题】类型一、确定反比例函数的解析式1、（2020•上城区一模）在平面直角坐标系中，反比例函数y=（x ＞0，k ＞0）的图象经过点A （m ，n ），B （2，1），且n ＞1，过点B 作y 轴的垂线，垂足为C ，若△ABC 的面积为2，求点A 的坐标．【思路点拨】根据图象和△ABC 的面积求出n 的值，根据B （2，1），求出反比例函数的解析式，把n 代入解析式求出m 即可．【答案与解析】解：∵B （2，1），∴BC=2，∵△ABC 的面积为2，∴×2×（n ﹣1）=2，解得：n=3，∵B （2，1），∴k=2，反比例函数解析式为：y=，∴n=3时，m=，∴点A 的坐标为（，3）．【总结升华】本题考查的是反比例函数系数k 的几何意义，用待定系数法求出k 、根据三角形的面积求出n 的值是解题的关键，解答时，注意数形结合思想的准确运用．举一反三：【变式】已知反比例函数k y x=与一次函数y ax b =+的图象都经过点P(2，－1)，且当1x =时，这两个函数值互为相反数，求这两个函数的关系式.【答案】因为双曲线k y x=经过点P(2，－1)，所以2(1)2k xy ==⨯-=-．所以反比例函数的关系式为2y x-=，所以当1x =时，2y =-．当1x =时，由题意知2y ax b =+=，所以直线y ax b =+经过点(2，－1)和(1，2)，所以有21,2,a b a b +=-⎧⎨+=⎩解得3,5.a b =-⎧⎨=⎩所以一次函数解析式为35y x =-+．类型二、反比例函数的图象及性质2、已知反比例函数k y x =(k ＜0)的图象上有两点A(11x y ，)，B(22x y ，)，且12x x <，则12y y -的值是()．A．正数B．负数C．非负数D．不能确定【思路点拨】一定要确定了A 点和B 点所在的象限，才能够判定12y y -的值.【答案】D；【解析】分三种情形作图求解．(1)若120x x <<，如图①，有12y y <，12y y -＜0，即12y y -是负数；(2)若120x x <<，如图②，有12y y >，12y y -＞0，即12y y -是正数；(3)若120x x <<，如图③，有12y y <，12y y -＜0，即12y y -是负数．所以12y y -的值不确定，故选D 项．【总结升华】根据反比例函数的性质，比较函数值的大小时，要注意相应点所在的象限，不能一概而论.举一反三：【变式】已知0a b ⋅<，点P（a b ，）在反比例函数xa y =的图象上，则直线b ax y +=不经过的象限是（）A.第一象限B.第二象限C.第三象限D.第四象限【答案】C；提示：由0a b ⋅<，点P（a b ，）在反比例函数xa y =的图象上，知反比例函数经过二、四象限，所以00ab <>，，直线b ax y +=经过一、二、四象限.3、（2020•淄博）反比例函数y=（a ＞0，a 为常数）和y=在第一象限内的图象如图所示，点M 在y=的图象上，MC ⊥x 轴于点C ，交y=的图象于点A ；MD ⊥y 轴于点D ，交y=的图象于点B ，当点M 在y=的图象上运动时，以下结论：①S △ODB =S △OCA ；②四边形OAMB 的面积不变；③当点A 是MC 的中点时，则点B 是MD 的中点．其中正确结论的个数是（）A ．0B ．1C ．2D ．3【思路点拨】①由反比例系数的几何意义可得答案；②由四边形OAMB 的面积=矩形OCMD 面积﹣（三角形ODB 面积+面积三角形OCA ），解答可知；③连接OM ，点A 是MC 的中点可得△OAM 和△OAC 的面积相等，根据△ODM 的面积=△OCM 的面积、△ODB 与△OCA 的面积相等解答可得．【答案】D ．【解析】解：①由于A 、B 在同一反比例函数y=图象上，则△ODB 与△OCA 的面积相等，都为×2=1，正确；②由于矩形OCMD 、三角形ODB 、三角形OCA 为定值，则四边形MAOB 的面积不会发生变化，正确；③连接OM ，点A 是MC 的中点，则△OAM 和△OAC 的面积相等，∵△ODM 的面积=△OCM 的面积=，△ODB 与△OCA 的面积相等，∴△OBM 与△OAM 的面积相等，∴△OBD 和△OBM 面积相等，∴点B 一定是MD 的中点．正确；故选：D ．【总结升华】本题考查了反比例函数y=（k ≠0）中k 的几何意义，即过双曲线上任意一点引x 轴、y 轴垂线，所得矩形面积为|k |，是经常考查的一个知识点；这里体现了数形结合的思想，做此类题一定要正确理解k 的几何意义．4、反比例函数xm y =与一次函数)0(≠-=m m mx y 在同一平面直角坐标系中的图象可能是（）【答案】C；【解析】一次函数()1y mx m m x =-=-是经过定点（1，0）,排除掉B、D 答案；选项A中m 的符号自相矛盾，选项C 符合要求.【总结升华】还可以按照m ＞0，m ＜0分别画出函数图象，看哪一个选项符合要求.举一反三：【变式】已知＞b a ,且,0,0,0≠+≠≠b a b a 则函数b ax y +=与xb a y +=在同一坐标系中的图象不可能是().【答案】B ；提示：因为从B 的图像上分析，对于直线来说是<0,0a b <，则0a b +<，对于反比例函数来说，0a b +>，所以相互之间是矛盾的，不可能存在这样的图形.类型三、反比例函数与一次函数综合5、如图所示，在平面直角坐标系中，一次函数y kx b =+(k ≠0)的图象与反比例函数m y x=(m ≠0)的图象相交于A、B两点．求：(1)根据图象写出A、B 两点的坐标并分别求出反比例函数和一次函数的解析式；(2)根据图象写出：当x 为何值时，一次函数值大于反比例函数值．【答案与解析】解：(1)由图象可知：点A 的坐标为(2，12)，点B 的坐标为(－1，－1)．∵反比例函数(0)m y m x =≠的图象经过点A(2，12)，∴m ＝1．∴反比例函数的解析式为：1y x=．∵一次函数y kx b =+的图象经过点A 12,2⎛⎫ ⎪⎝⎭，点B(－1，－1)，∴12,21,k b k b ⎧+=⎪⎨⎪-+=-⎩解得：1,21.2k b ⎧=⎪⎪⎨⎪=-⎪⎩∴一次函数的解析式为1122y x =-．(2)由图象可知：当x ＞2或－l＜x ＜0时一次函数值大于反比例函数值．【总结升华】一次函数值大于反比例函数值从图象上看就是一次函数的图象在反比例函数的图象上方的部分，这部分图象的横坐标的范围为所求.举一反三：【变式】如图所示，一次函数3y kx =+的图象与反比例函数(0)m y x x=>的图象交于点P，PA⊥x 轴于点A，PB⊥y 轴于点B，一次函数的图象分别交x 轴、y 轴于点C、点D，且27DBP S =△，12OC CA =．(1)求点D 的坐标；(2)求一次函数与反比例函数的表达式；(3)根据图象写出当x 取何值时，一次函数的值小于反比例函数的值？【答案】解：(1)由一次函数3y kx =+可知：D(0，3)(2)设P(a ，b )，则OA＝a ，13OC a =，得1,03C a ⎛⎫ ⎪⎝⎭．由点C 在直线3y kx =+上，得1303ka +=，ka ＝－9，DB＝3－b＝3－(ka ＋3)＝－ka ＝9，BP＝a ．由1192722DBP S DB BP a === △，∴a ＝6，∴32k =-，b ＝－6，m ＝－36．∴一次函数的表达式为332y x =-+，反比例函数的表达式为36y x=-．(3)根据图象可知：当x ＞6时，一次函数的值小于反比例函数的值．类型四、反比例函数的实际应用6、制作一种产品，需先将材料加热达到60℃后，再进行操作，设该材料温度为y (℃)，从加热开始计算的时间为()min x ．据了解，设该材料加热时，温度y 与时间x 成一次函数关系；停止加热进行操作时，温度y 与时间x 成反比例关系(如图)．已知该材料在操作加工前的温度为15℃，加热5min 后温度达到60℃．(1)分别求出将材料加热和停止加热进行操作时，y 与x 的函数关系式；(2)根据工艺要求，当材料的温度低于15℃时，须停止操作，那么从开始加热到停止操作，共经历了多少时间？【思路点拨】（1）首先根据题意，材料加热时，温度y 与时间x 成一次函数关系；停止加热进行操作时，温度y 与时间x 成反比例关系；将题中数据代入用待定系数法可得两个函数的关系式；（2）把y ＝15代入300y x=中，进一步求解可得答案．【答案与解析】解：依题意知两函数图象的交点为(5，60)(1)设材料加热时，函数解析式为y kx b =+．有15956015b k k b b ==⎧⎧⎨⎨+==⎩⎩∴915y x =+(0≤x ≤5)．设进行制作时函数解析式为1k y x=．则1300k =，∴300y x =(x ≥5)．(2)依题意知300x ＝15，x ＝20．∴从开始加热到停止操作共经历了20min．【总结升华】把握住图象的关键点，根据反比例函数与一次函数的定义，用待定系数法求解析式，并利用解析式解决实际问题.。

反比例函数与几何综合讲义及答案一、反比例函数的定义及性质1.反比例函数的定义：如果两个变量的乘积为常数，那么它们之间存在反比例关系，可以表示为y=k/x。

2.反比例函数的性质：函数图像关于坐标轴对称；随着x的增大，y 的值逐渐减小；随着x的减小，y的值逐渐增大。

二、反比例函数的图像与性质1.绘制反比例函数y=k/x的图像。

2.如果k为正数，当x趋近于无穷大时，y趋近于0；当x趋近于0时，y趋近于正无穷大。

3.如果k为负数，当x趋近于无穷大时，y趋近于负无穷大；当x趋近于0时，y趋近于0。

三、反比例函数的解析表达式和图像的关系1.根据解析表达式y=k/x，结合k的正负性质，分析函数图像的大致形状。

2.当k为正数时，函数图像在第一象限逐渐接近于x轴，且没有定义域为x=0的点。

3.当k为负数时，函数图像在第三象限逐渐接近于x轴，且没有定义域为x=0的点。

四、反比例函数的应用1. 反比例函数的例题：如果旅行的时间与旅行的速度成反比例关系，当速度增大时，时间会减少。

求出速度为60 km/h时需要的时间。

答案：假设旅行的时间为t小时，则速度为60 km/h，根据反比例函数的定义可得60 = k/t，解得k = 60t。

根据题意可得t = k/60 = 1小时。

2.反比例函数出题：已知两个变量x和y成反比例关系，在一组数据中，当x=2时，y=5；当x=4时，y=10。

求出该反比例函数的解析表达式。

答案：根据反比例函数的定义可得k = xy，由已知数据可得2k = 5；4k = 10。

解方程可得k = 5/2、将k带入反比例函数中得到y = (5/2)x。

请注意，以上是一些常见的反比例函数综合讲义及试题及答案，实际上反比例函数的应用非常广泛，可以结合实际问题进行更多的应用练习。

初三反比例函数讲义第1节 反比例函数本节内容：反比例函数定义 反比例函数定义的应用（重点）电流I 、电阻R 、电压U 之间满足关系式：U=IR当U=220V 时，可以用含有R 的代数式表示I ：__________________舞台灯光的亮暗就是通过改变电阻来控制电流的变化实现的。

当电流I 较小时，灯光较暗；当电流I 较大时，灯光较亮。

一般地，如果两个变量x 、y 之间的关系可以表示成xky =k (为常数，)0≠k 的形式，那么称y 是x 的反比例函数。

反比例函数的自变量x 不能为零。

小注：（1）x k y =也可以写成1-=kx y 或k xy =的形式； （2）xky =若是反比例函数，则x 、y 、k 均不为零；（3）k xy =)0(>k 通常表示以原点及点()y x ,为对角线顶点的矩形的面积。

下列函数中是反比例关系的有___________________（填序号）。

①3x y -= ②131+=x y ③x y 2-= ④2211x y -= ⑤x y 23-= ⑥21=xy ⑦28xy = ⑧1-=x y ⑨2=x y ⑩x ky =k (为常数，)0≠k确定解析式的方法仍是____________，由于在反比例函数xky =中，只有一个待定系数，因此只需要一对对应值，即可求出k 的值，从而确定其解析式。

由欧姆定律可知，电压不变时，电流强度I 与电阻R 成反比例，已知电压不变，电阻R=12.5欧姆，电流强度I=0.2安培。

（1） 求I 与R 的函数关系式；（2） 当R=5欧姆时，求电流强度。

本节作业：1、小明家离学校1.5km ，小明步行上学需x min ，那么小明的步行速度min)/(m y 可以表示为xy 1500=；水名地面上重1500N 的物体，与地面的接触面积为x 2m ，那么该物体对地面的压强)/(2m N y 可以表示为x y 1500=。

函数表达式xy 1500=还可以表示许多不同情境中变量之间的函数关系，请你再列举一例。

反比例函数提高卷一、例题解析：例1：已知，A、B、C、D、E是反比例函数y = —（x>Q）图象上五个整数点（横、纵坐X标均为整数），分别以这些点向横轴或纵轴作垂线段，由垂线段所在的止方形边长为半径作四分之一圆周的两条弧，组成如图所示的五个橄榄形（阴影部分），求这五个橄榄形的面积总和（用含兀的代数式表示）y 164跟踪练习：已知A. B、C是分比例函数y = _（x〉O）图彖上x的三个整点（即横、纵坐标均为整数的点），分别以这些点向横轴或纵轴作垂线段，由垂线段为边作出三个正方形，再以正方形的边长为直径作两个半圆，组成如图所示的阴影部分，则阴影部分的面积总和是__________________ （用含兀的代数式表示）4 k例2：如图，直线y =—兀与双曲线），=一（兀〉0）,交于点A,3 x4 Q k将直线y = -x向右平移一个单位后，与双曲线y = -（x>0）交于点B,与兀轴交于点C,3 2 xAn若无J求'的值例3：如图，再统一直角坐标系屮，止比例函数的图象可以看作是：将兀轴所在的直线绕着 象限的点B 、D,已知点A （一加，0）、C （加,0）.（1） _________________________________________________________________________ 直接判断并填写：不论Q 取何值，四边形ABCD 的形状一定是 __________________________（2） ①当点B 为（°, 1）时，四边形ABCD 是矩形，试求卩，a 和加的值；②观察猜想：对①中的皿值，能使四边形ABCD 为矩形的点B 共有几个？（3） 试探究：四边形ABCD 能不能是菱形？若能，直接写出B 点的坐标，若不能，说明理 由。

二、练习题：1、如图，已知双曲线y = -（k>0）经过直角三角形OAB 斜边OB 的中 x点D,与直角边AB 相交于点C,若AOBC 的面积为3,则R 二 ____________4一2^函数= x （x > 0）, y 2 = — （x > 0）的图象如图所示，则结论： x ①两函数图象的交点A 的坐标为（2, 2）；②当兀>2时，丁2>戸；③当％=1时，BO3；④当x 逐渐增大时，X 随着x 的增大而增大，力随着兀的增大而减小。

第讲反比例函数1．掌握反比例函数的概念、图象及性质；2．利用相关知识解决实际问题．模块一反比例函数的图形与性质问题11.我们知道，导体的电流I与导体的电阻R、导体两端的电压U之间满足关系式U=IR当U=220V时(1)你能用含有R的代数式表示I吗?(2)利用写出的关系式完成下表：R/Ω20 40 60 80 100I/A(4)变量I是R的函数吗?为什么?亮度可调节的台灯，其灯光亮度的改变，可以通过调节总电阻来控制电流的变化实现。

因为当电流I较小时，灯光较暗；反之，当电流较大时，灯光较亮。

问题2京沪高速铁路全长约1300km ，列车沿京沪高速铁路从上海驶往北京，列车行完全程所需要的时间t(h)与行驶的平均速度v(km/h)之间有怎样的关系?变量t 是v 的函数吗?为什么?1、定义：一般地，形如 y =xk （k 是常数，k ≠0 ）的函数叫做反比 例函数。

注意：（1）常数 k 称为比例系数，k 是非零常数；（2）在y = xk 中，自变量x 是分式xk 的分母，当x ＝０时，分式xk 无意义，所以x 的取值范围是x ≠ 0的一切实数；（3）解析式有三种常见的表达形式：①y =xk （k ≠ 0）；②xy = k （k ≠0）；③y =k 1x （k ≠0）；（4）反比例函数一定存在反比例关系，但存在反比例关系的函数不一定是反比例函数。

1、反比例函数的图象y=2x列表建立直角坐标系描点2、反比例函数的图象反比例函数)0,(≠=k k xk y 是常数的图象是（ ）线，它有两个分支，可用描点法画出反比例函数的图象。

2、反比例函数的性质 如下图：3、k 的符号作用：4、K 值的几何意义：从反比例函数)0,(≠=k k xk y 是常数的图象上任选一点向一坐标轴作垂线，这一点和垂足及坐标原点所构成的三角形面积：S =||21xy =12k 。

5、对称性：①关于原点对称，②关于直线x y ±=对称。