巧求面积---平移旋转

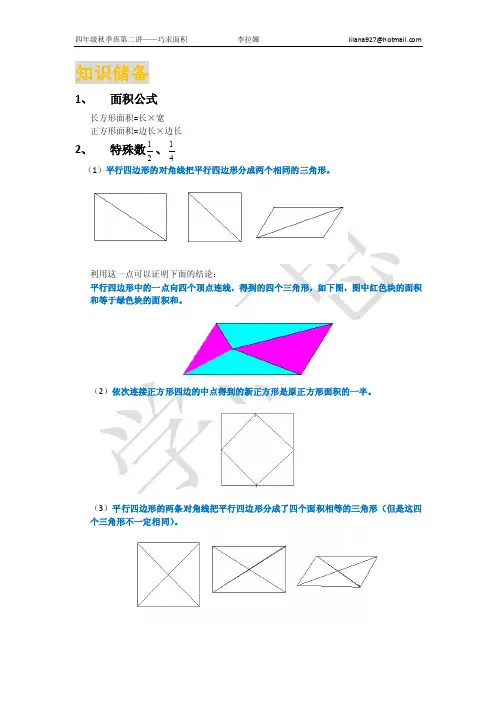
【知识梳理】本讲主要通过求一些不规则图形的面积，体会一种转化思想，重点在于把不规则图形转化为规则图形的方法，包括平移、旋转、割补、差不变原理，通过这些方法的学习，让学生体会求面积的技巧，提高学生的观察能力、动手操作能力、综合运用能力。

1、面积公式：长方形的面积=长⨯宽正方形的面积=边长⨯边长2、把不规则图形转化为规则图形的几种方法。

分割：把不规则图形分割成一些可求面积的规则图形。

添补：添上一个规则图形或者与所求图形有数量关系的图形，使原图形变为可求面积的规则图形。

平移、旋转:主要通过移动的方法把分散的块集中到一个规则的图形中。

【例题讲解】例1、你有什么好的方法计算所给图形的面积呢？(单位：厘米)4993例2、这是一个楼梯的截面图，高280厘米，每级台阶的宽和高都是20 厘米．问，此楼梯截面的面积是多少？例3、有一块菜地长16米，宽8米，菜地中间留了宽2米的路，把菜地平均分成四块，每一块地的面积是多少？例4、下图(单位：厘米)是两个相同的直角梯形重叠在一起，求阴影部分的面积.例5、一块长方形铁板，长15分米，宽12分米，如果长和宽各减少2分米，面积比原来减少多少平方分米？例6、一个边长为20厘米的正方形，依次连接四边中点得到第二个正方形，这样继续下去可得到第三个、第四个、第五个正方形．求第五个正方形的面积？【课堂巩固】1、求图中五边形的面积。

64532、如图是一个楼梯的截面图，每级台阶的宽和高都是20厘米．这楼梯的截面积是多少平方厘米？3、两个相同的直角三角形如下图所示(单位：厘米)重叠在一起，求阴影部分的面积.FBA4、 一个正方形，如果把它的相邻两边都增加6厘米，就可以得到一个新正方形，新正方形 的面积比原正方形大120平方厘米．求原正方形的面积？65、 如图是由5个大小不同的正方形叠放而成的，如果最小的正方形(阴影部分)的周长是8，那么最大的正方形的边长是 ．第6题【课后练习】1、 如图是学校操场一角，请计算它的面积(单位：米)302030402、 如右图所示，图中的ABEFGD 是由一个长方形ABCD 及一个正方形CEFG 拼成的，线段的长度如图所示(单位：厘米)，求ABEFGD 的周长和面积．3、四个完全相同的长方形拼成右图，大正方形的面积是l00平方分米，小正方形的面积是l6平方分米，求每个长方形的面积是多少？长方形的短边是多少分米？164、有一个边长为16厘米的正方形，连接每边的中点构成第二个正方形，再连接每边的中点构成第三个正方形，第四个正方形．求图中阴影部分的面积？。

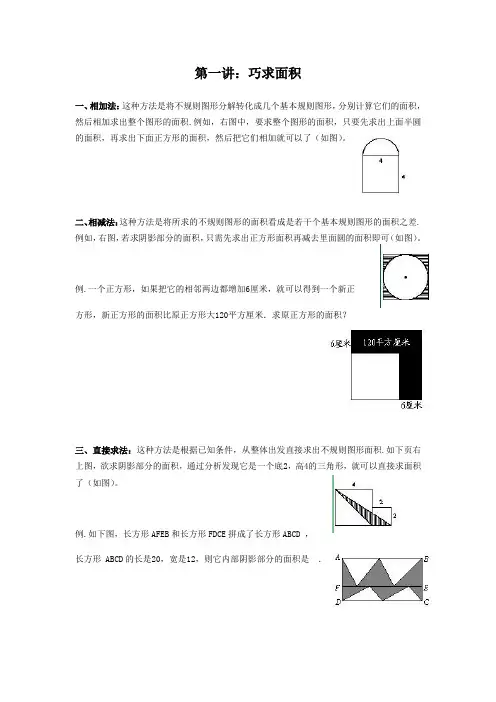
第一讲：巧求面积一、相加法：这种方法是将不规则图形分解转化成几个基本规则图形，分别计算它们的面积，然后相加求出整个图形的面积.例如，右图中，要求整个图形的面积，只要先求出上面半圆的面积，再求出下面正方形的面积，然后把它们相加就可以了（如图）。

二、相减法：这种方法是将所求的不规则图形的面积看成是若干个基本规则图形的面积之差.例如，右图，若求阴影部分的面积，只需先求出正方形面积再减去里面圆的面积即可（如图）。

例.一个正方形，如果把它的相邻两边都增加6厘米，就可以得到一个新正方形，新正方形的面积比原正方形大120平方厘米．求原正方形的面积？三、直接求法：这种方法是根据已知条件，从整体出发直接求出不规则图形面积.如下页右上图，欲求阴影部分的面积，通过分析发现它是一个底2，高4的三角形，就可以直接求面积了（如图）。

例.如下图，长方形AFEB和长方形FDCE拼成了长方形ABCD ，长方形 ABCD的长是20，宽是12，则它内部阴影部分的面积是．四、重新组合法：这种方法是将不规则图形拆开，根据具体情况和计算上的需要，重新组合成一个新的图形，设法求出这个新图形面积即可.例如，欲求右图中阴影部分面积，可以把它拆开使阴影部分分布在正方形的4个角处，这时采用相减法就可求出其面积了（如图）。

例.已知大正方形边长是7厘米，小正方形边长5厘米，求阴影部分的面积。

五、辅助线法：这种方法是根据具体情况在图形中添一条或若干条辅助线，使不规则图形转化成若干个基本规则图形，然后再采用相加、相减法解决即可.如右图，求两个正方形中阴影部分的面积.此题虽然可以用相减法解决，但不如添加一条辅助线后用直接法作更简便（如图）。

六、割补法：这种方法是把原图形的一部分切割下来补在图形中的另一部分使之成为基本规则图形，从而使问题得到解决.例如，如右图，欲求阴影部分的面积，只需把右边弓形切割下来补在左边，这样整个阴影部分面积恰是正方形面积的一半（如图）.例.求阴影部分的面积。

第十三讲巧求面积知识点睛：长方形的面积＝长×宽，正方形的面积＝边长×边长。

但是，在平时的学习过程中，我们常常会遇到一些已知条件比较隐蔽、图形比较复杂、不能简单地用公式直接求出所求面积的题目，这就需要我们切实掌握有关概念，利用“割补”“平移”“旋转”等方法，使复杂的问题转化为普通的长方形、正方形面积的问题，从而正确解答。

例1:下图是一个养禽专业户用一段16米的篱笆围成的一个长方形养鸡场，求它的占地面积。

练习1：1、右图是某个养禽专业户用一段长13米的篱笆围成的一个长方形养鸡场，求养鸡场的占地面积。

2、用56米长的木栏围成长或宽是20米的长方形，其中一边利用围墙，怎样才能使围成的面积最大？例2:下图是一块水稻田，请计算它的面积（单位：米）练习2：1、求下图的面积。

（单位：分米）2、求下面图形的面积（单位：米）8471040302020151020155020例3：一个长方形，如果宽不变，长增加6米，那么它的面积增加54平方米；如果长不变，宽减少3米，那么它的面积减少36平方米。

这个长方形原来的面积是多少平方米？练习3：1、一个长方形，如果宽不变，长减少3米，那么它的面积减少24平方米；如果长不变，宽增加4米，那么它的面积增加60平方米。

这个长方形原来的面积是多少平方米？2、一个长方形，如果宽不变，长增加5米，那么它的面积增加30平方米；如果长不变，宽增加3米，那么它的面积增加48平方米。

这个长方形原来的面积是多少平方米？例4：如图所示，一块长方形草地。

长方形长16米，宽10米，中间有两条宽2米的道路，一条是长方形，另一条是平行四边形。

求有草部分（阴影部分）的周长。

练习4：1、求下图阴影部分的面积（单位：厘米）。

2、如图所示，公园里有一个长方形湖泊，湖上有一座景观桥（桥墩忽略不计）。

已知湖泊长30米，宽20米，桥面的宽度为2米，这座桥的面积是多少？210例5：街心花园有一个正方形花坛，四周有一条宽1米的通道（如图），如果通道的面积是12平方米，那么中间花坛的面积是多少平方米？练习5：1、有一个正方形水池，在它的周围修一条宽4米的路，这条路的面积是240平方米，这个水池的面积是多少？2、下图中阴影部分是边长为5厘米的正方形，四块完全一样的长方形的宽是8厘米，求这个图形的面积。

师：这确实是一种方法，老师刚刚在下面还看到有同学有不同做法，请你来说下你的思路。

生2：我是用大长方形的面积减去蓝色正方形的面积，再减去绿色正方形的面积，剩下的就是红色长方形的面积。

师：非常好，这也是一种很好的方法，你能具体说说具体的算法吗？生2: 大长方形的面积是6×10=60（平方厘米），蓝色正方形的面积是6×6=36 （平方厘米），绿色正方形的面积是4×4=16（平方厘米）师：那红色长方形的面积是多少呢？生2：60-36-16=8（平方厘米）。

师：这样求出来的答案也是8平方厘米。

这样做的同学举手示意一下。

师：看来也有很多同学是这么想的。

其实两种方法都是可以的。

同学们的思维真是活跃啊。

我们一起看下答案算对了吗。

板书：方法一：（10-6）×（6-4）=8（平方厘米）方法二：6×10-6×6-4×4=8（平方厘米）答：红色部分面积是8平方厘米。

师：刚刚我们解决了例题3，两种方法大家都会了吗？生：会了。

师：很好，很多题目我们可以从不同角度去思考。

我相信下面的练习3肯定也难不倒同学们。

大家自己动手做一做吧。

练习3：（5分）由两个完全相同的图形组成的图形（如图），计算下列图的面积。

分析：将图形进行平移、剪拼后可以发现这个图形的面积是一个边长为6厘米的大正方形减去一个边长为2厘米的小正方形的面积。

板书：6×6-2×2=32（平方厘米）答：这个图的面积是32平方厘米。

（二）例题4：（12分）一块长方形草地，长是38米，宽是28米，中间有两条宽2米的小路可以通过，这块草地的绿化面积是多少平方米？讲解重点：这个题目有2中方法，一个是用平移法，将两条小路移到一边，求空白小长方形的面积，就是绿化面积；或者可以求出两条小路的面积之和，要注意的是中间有一块2×2的地被重复计算了一次，要减掉。

再用草地面积减去小路面积，师：题目中要我们求这块草地的绿化面积是多少平方米，你们会怎么思考？生1：像上一个题目一样，我们可以用平移法把两条小路移到一边，中间就是绿化面积。

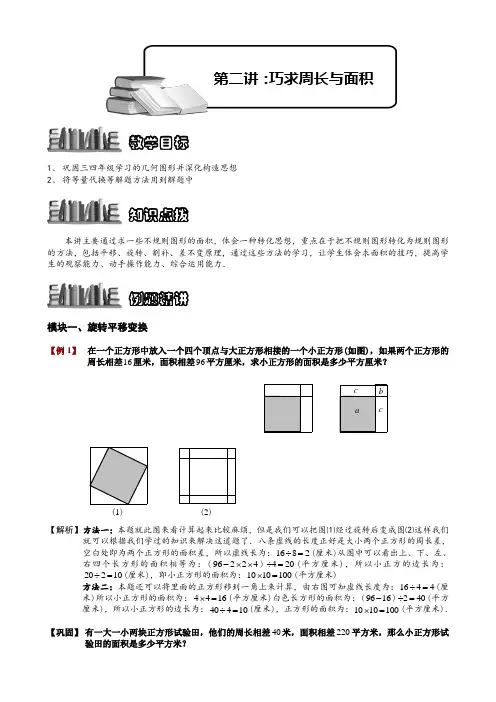
1、 巩固三四年级学习的几何图形并深化构造思想2、 将等量代换等解题方法用到解题中本讲主要通过求一些不规则图形的面积，体会一种转化思想，重点在于把不规则图形转化为规则图形的方法，包括平移、旋转、割补、差不变原理，通过这些方法的学习，让学生体会求面积的技巧，提高学生的观察能力、动手操作能力、综合运用能力．模块一、旋转平移变换【例 1】 在一个正方形中放入一个四个顶点与大正方形相接的一个小正方形(如图)，如果两个正方形的周长相差16厘米，面积相差96平方厘米，求小正方形的面积是多少平方厘米？(1) (2)【解析】 方法一：本题就此图来看计算起来比较麻烦，但是我们可以把图⑴经过旋转后变成图⑵这样我们就可以根据我们学过的知识来解决这道题了．八条虚线的长度正好是大小两个正方形的周长差，空白处即为两个正方形的面积差，所以虚线长为：1682÷=(厘米)从图中可以看出上、下、左、右四个长方形的面积相等为：(96224-⨯⨯)420÷=(平方厘米)，所以小正方的边长为：20210÷=(厘米)，即小正方形的面积为：1010100⨯=(平方厘米)方法二：本题还可以将里面的正方形移到一角上来计算，由右图可知虚线长度为：1644÷=(厘米)所以小正方形的面积为：4416⨯=(平方厘米)白色长方形的面积为：(9616-)240÷=(平方厘米)，所以小正方形的边长为：40410÷=(厘米)，正方形的面积为：1010100⨯=(平方厘米)．【巩固】 有一大一小两块正方形试验田，他们的周长相差40米，面积相差220平方米，那么小正方形试验田的面积是多少平方米？知识点拨教学目标例题精讲第二讲：巧求周长与面积c b ca图a图b【解析】 根据已知条件，我们将两个正方形试验田的一个顶点对齐，画出示意图(如图a )，将大正方形在小正方形外的部分分割成两个直角梯形，再拼成一个长方形(如图b )．由于两个正方形的周长相差40米，从而它们的每边相差40410÷=米，即图b 中的长方形的宽是10米．又因为长方形的面积是两个正方形的面积之差，即为220平方米，从而长方形的长为：2201022÷=(米)．由图可知，长方形的长是大正方形与小正方形的边长之和，长方形的宽为大正方形与小正方形的边长之差，从而小正方形的边长为：(2210)26-÷=(米)．所以小正方形的面积为：6636⨯=(平方米)．【例 2】 长方形ABCD 的周长是30厘米，以这个长方形的每一条边为边长向外画正方形．已知这四个正方形的面积之和为290平方厘米，那么长方形ABCD 的面积是多少平方厘米？C 1D 1E 1A 1EBC DA【解析】 从图形我们可以看出，1A B 的长度恰好为长方形的长与宽之和，即为长方形ABCD 周长的一半，可以看出若以1A B 和1BC 为边能构成大正方形111A BC E (如右下图所示)，其中包含两个长方形和两个正方形，而且两个长方形的面积是相等的，两个正方形的面积刚好是290平方厘米的一半．这样我们容易求出：大正方形111A BC E 的边长为30215÷=厘米，面积为：1515225⨯=平方厘米，正方形11CDD C 与正方形1ADEA 的面积之和为：2902145÷=(平方厘米)．长方形ABCD 与长方形11EDD E 的面积相等．所以，长方形ABCD 的面积为：(225145)240-÷=(平方厘米)．【例 3】 一条白色的正方形手帕，它的边长是18厘米，手帕上横竖各有二道黑条，黑条宽都是2厘米，这条手帕白色部分的面积是多少？【解析】 方法一：由于手帕边长是18厘米，所以手帕的面积是1818324⨯=(平方厘米)．要求白色部分的面积，只需减去红色部分的面积就可以了．红色部分是四个长为18厘米，宽为2厘米的红色长条，所以这四个红色长条面积是：4182144⨯⨯=(平方厘米)，但每个横红条与每个竖红条在交叉处重叠一个边长为2厘米的正方形，即多计算了224⨯=(平方厘米)，因此两个横红条与两个竖红条共重叠4416⨯=(平方厘米)，所以两个横红条与两个竖红条覆盖的面积为14416128-=(平方厘米)，所以这块白手帕白色部分的面积是324128196-=(平方厘米)方法二：换个方式思考：把竖的两个红条平行移动一下，使它们紧贴在一起，再移到紧贴正方形的左端边上，把横的两个红条也做同样的位置平移，使它们紧贴在正方形下端的边上，如图所示．这样通过平移横、竖红条后使原来分散的白色部分集中起来了，而且所得图形的白色部分的面积不变．这时白色部分面积一目了然，它等于变成为14厘米的正方形面积，即1414196⨯=(平方厘米)【例 4】 7个完全相同的长方形拼成了图中阴影部分，图中空白部分的面积是多少平方厘米？【解析】 由图可知，长方形的长是宽的4倍，宽的6倍是24厘米，则长方形的宽是4厘米，故图中空白部分的面积是44232⨯⨯=(平方厘米)．【巩固】 (第五届”祖冲之杯”数学邀请赛)如右图所示，在长方形ABCD 中，放入六个形状大小相同的长方形(尺寸如图)，图中阴影部分的面积是__________．B【解析】 由图中可以看出小长方形的长3+⨯小长方形的宽14=，小长方形的长-小长方形的宽6=． 第二式乘以3再与第一式相加得 4⨯小长方形的长146332=+⨯=．所以小长方形的长8=，小长方形的宽2=，小长方形的面积8216⨯=，大长方形的面积14(622)140=⨯+⨯=， 阴影面积14061644=-⨯=．模块二、完美长方形【例 5】 （第十二届“迎春杯”刊赛试题）如图，边长是整数的四边形AFED 的面积是48平方厘米，FB为8厘米．那么，正方形ABCD 的面积是 平方厘米．A BCDE F 488【解析】 根据题意，有48AD AF ⨯=且8AF AD +=，又AD 、AF 都是整数，于是根据尝试可得，12AD =厘米，4AF =厘米．所以1212144ABCDS=⨯=（平方厘米）．【例 6】 如图，一个正方形被分成4个小长方形，它们的面积分别是110平方米、15平方米、310平方米和25平方米．已知图中的阴影部分是正方形，那么它的面积是多少平方米？【解析】 为了方便叙述，将某些点标上字母，如右上图。

六年级数学思维：组合图形的面积计算，例题解析！主要题型：一、求不规则图形面积（阴影部分面积）；二、求不能直接利用公式计算的图形面积；三、求规则图形的面积，但条件比较隐蔽，用常规思路无法解答。

基本解题思路：解题的基本思路是，先通过分割、切拼、旋转、平移、翻折、缩放、等积替换等方法，把不规则图形转化为规则图形（或规则图形面积的和差），让隐蔽条件明朗化，再合理运用面积公式，巧求不规则图形面积。

解题技巧：这一块分六讲，以后会陆续更新，每一块各有侧重地介绍了六种求面积的计算方法，但每一种解题方法并不是孤立存在的，在实际解题时一道题常常需要综合运用多种方法，才能巧妙解题。

例如加减法求面积常需要对图形进行割补，而用割补法求面积常需要添加辅助线、平移、旋转、进行加减运算等。

在解答图形面积问题时，关键就是要注意寻找不同图形或同一个图形的各个部分之间的内在联系，可以变换角度或适当添加辅助线帮助观察，特别要注意观察图形边角的形状、长度和角度，及是否隐藏有等底等高之类的条件。

从而根据图形的形状特征，合理地进行分割重组，化不规则为规则，巧妙地运用题目给出的各种条件。

小学阶段常见的面积公式：长方形的面积＝长×宽S＝ab正方形的面积＝边长×边长S＝a.a＝a2三角形的面积＝底×高÷2S＝ah÷2平行四边形的面积＝底×高S＝ah梯形的面积＝（上底+下底）×高÷2S＝（a＋b）h÷2圆的面积＝圆周率×半径×半径S＝πr2今天我们讲第一块内容：加减法求面积方法介绍：根据组合图形的形状特征，从整体上观察，将不规则图形分解转化成几个基本规则图形，分别计算它们的面积。

再变化角度思考，通过相加或相减求出所求图形的面积。

例题1：求下图中阴影部分的面积（最后结果保留一位小数）。

（单位：厘米）【解析】：上图阴影部分可以分割成3个完全相同的弓形，先求出其中一个弓形的面积，再求出3个弓形的总面积就是所求阴影部分的面积。

利用几何变换巧求图形面积作者：洪倩来源：《启迪与智慧·教育版》2018年第06期几何变换包括旋转变换、平移变换、轴对称变换等变换形式，通过几何变化巧求图形面积，往往能达到化难为易的效果。

一、旋转变换在平面内，一个图形绕着一个定点旋转一定的角度得到另一个图形的变化叫做旋转。

在利用几何变换求面积的几种变换中，旋转变换最常用。

求几何面积的诸多问题中，如果用常规解法往往过程繁琐，甚至会出现学生现有知识无法解答的情况。

这个时候我们就需要另辟蹊径，借助旋转变换进行解答。

例1 如图1，△ABC是直角三角形，四边形ACDE、FGBA都是正方形，AB=3cm，BC=4cm，求△AEF的面积。

解析：在这里，很多人在一开始看到此类题目，首先会利用勾股定理算出AC的长度，然后无从下手，或者构造三角形，利用三角形全等来解决。

如果我们利用旋转变换的思想，就可以化简为易。

将△ABC逆时针旋转90°，使AC和AE重合，得到△AME（因为∠EAC=∠FAB=90°，所以∠EAF+∠BAC=180°，F、A、M在同一条直线上）S△EFA=S△EAM=3×4÷2=6cm2例2 如图3，在直角三角形中有一个正方形，已知BD=10cm，DC=7cm，求阴影部分面积。

解析：将三角形CED绕D点逆时针旋转90°。

（如图4）使得E与F重合，则C点落到线段AB与G点，阴影部分面积转化为Rt△BGD的面积所以阴影部分面积为：10×7÷2=35cm2二、平移变换在平面内，将一个图形上的所有点都按照某个直线方向做相同距离的移动，这样的图形运动叫做图形的平移运动。

平移是几何变换的一种，利用平移对图形中有关部分进行变换，将其余部分保持不变，为题目所求变换，化不利条件为有利条件，巧求图形面积。

例3 如图5，六边行ABCDEF中，AB=ED， AF=CD， BC=EF，且有AB//ED，AF//CD， BC//EF，对角线FD垂直于BD，已知FD=24cm，BD=18cm，求六边行ABCDEF的面积是多少平方厘米？例题解析：将△BCD平移，使得CD与AF重合，将△DEF平移，使得ED与AB重合，这样EF、BC都重合到图中的AG上，组成了一个长方形BGFD（如图6），它的面积与原六边形的面积相等，即为：24×18=432cm2三、对称变换如果一个图形沿着一条线对折后两部分完全重合，这样的图形叫做轴对称图形。

第十六章巧求面积知识导航同学们都知道，物体的表面或封闭图形的大小，叫作物体的面积。

我们已经学会运用公式求长方形和正方形的面积了。

但是，在平时的学习过程中，我们常常会遇到一些已知条件比较隐蔽、图形比较复杂、不能简单地用公式直接求出面积的题目。

这就需要我们切实掌握有关概念，利用“割补”“平移”“旋转”“分解”“合并”等转化方法，化难为易，化繁为简，从而正确解决问题。

图解思维训练题例1　一个长方形，如果宽不变，长增加6米，那么它的面积就增加54平方米；如果长不变，宽减少4米，那么它的面积就减少48平方米。

这个长方形的面积是多少平方米？图解思路如下图所示，这个长方形的宽用“增加的面积÷增加的长”可以求出，长用“减少的面积÷减少的宽”可以求出，然后用“长×宽”求出面积。

规范解答宽：54÷6＝9（米）长：48÷4＝12（米）面积：9×12＝108（平方米）答：这个长方形的面积是108平方米。

例2　下图中大正方形的边长比小正方形的边长多4厘米，大正方形的面积比小正方形的面积多96平方厘米。

大正方形和小正方形的面积各是多少平方厘米？图解思路如下图所示，把大正方形比小正方形多出的96平方厘米分成了三部分。

这三部分中一部分是带阴影的小正方形，另外两个部分是没有阴影的长方形。

可以先求出带阴影的小正方形的面积，再用多出的96平方厘米减去带阴影的小正方形的面积，得到两个长方形的面积，再除以2就是一个长方形的面积。

长方形的面积知道了，再除以宽就是长。

这个长等于小正方形的边长，边长求出来了，面积就迎刃而解了。

规范解答带阴影的小正方形的面积：4×4＝16（平方厘米）一个长方形的面积：（96-16）÷2＝40（平方厘米）长方形的长（也就是小正方形的边长）：40÷4＝10（厘米）小正方形的面积：10×10＝100（平方厘米）大正方形的面积：100＋96＝196（平方厘米）答：大正方形的面积是196平方厘米，小正方形的面积是100平方厘米。

⼩学数学常见⼏何模型典型例题解题思路⼩学数学常见⼏何模型典型例题及解题思路（1）巧求⾯积常⽤⽅法：直接求；整体减空⽩；不规则转规则（平移、旋转等）；模型（鸟头、蝴蝶、漏⽃等模型）；差不变1、ABCG 是边长为12厘⽶的正⽅形，右上⾓是⼀个边长为6厘⽶的正⽅形FGDE ，求阴影部分的⾯积。

答案：72A H FE C B I D G思路：1）直接求，但是阴影部分的三⾓形和四边形⾯积都⽆法直接求；2）整体减空⽩。

关键在于如何找到整体，发现梯形BCEF 可求，且空⽩分别两个矩形⾯积的⼀半。

2、在长⽅形ABCD 中，BE=5，EC=4，CF=4，FD=1。

△AEF 的⾯积是多少？答案：20A DB FC E思路：1）直接求，⽆法直接求；2）由于知道了各个边的数据，因此空⽩部分的⾯积都可求3、如图所⽰的长⽅形中，E 、F 分别是AD 和DC 的中点。

（1）如果已知AB=10厘⽶，BC=6厘⽶，那么阴影部分⾯积是多少平⽅厘⽶？答案：22.5（2）如果已知长⽅形ABCD 的⾯积是64平⽅厘⽶，那么阴影部分的⾯积是多少平⽅厘⽶？答案：24B CDF E思路（1）直接求，⽆法直接求；2）已经知道了各个边的数据，因此可以求出空⽩的位置；3）也可以利⽤鸟头模型4、正⽅形ABCD 边长是6厘⽶，△AFD （甲）是正⽅形的⼀部分，△CEF （⼄）的⾯积⽐△AFD （甲）⼤6平⽅厘⽶。

请问CE 的长是多少厘⽶。

答案：8A B DC F思路：差不变5、把长为15厘⽶，宽为12厘⽶的长⽅形，分割成4个三⾓形，其⾯积分别为S 1、S 2、S 3、S 4，且S 1=S 2=S 3+S 4。

求S 4。

答案：10DC E F S 1S 2S 3S 4思路：求S4需要知道FC 和EC 的长度；FC 不能直接求，但是DF 可求，DF 可以由三分之⼀矩形⾯积S1÷AD ×2得到，同理EC 也求。

最后⼀句三⾓形⾯积公式得到结果。

巧算面积知识导航我们会算规则的长方形、正方形、平行四边形、梯形、三角形平面图形的面积，但我们也会常遇到已知条件比较隐蔽，图形比较复杂，不能简单地用面积计算公式直接求出面积的图形，需要我们认真掌握有关概念，利用“割补”、“平移”、“旋转”等方法，使复杂的问题转化为普通的规则的平面图形的面积问题，从而正确解答。

举一反三经典例题1下图中，长方形的长为21厘米，宽为8厘米，把长分3等份，宽分为2等份，长方形内任一点与分点及顶点接起来，阴影部分的面积和是多少平方厘米？[分析]每个阴影部分的底可算出，但高是多少，不知道，我们发现，宽边上两个三角形的高的和是长，长边上两个三角形的高的和是宽。

解：)(7042282212828321平方厘米=+=÷⨯÷+÷⨯÷答：阴影部分面积的和是70平方厘米。

名师一点通：对于单个三角形的面积求解过程如果缺少条件，需转变思路，把等底等高的三角形合起来算巩固练习：（1）平行四边形的面积为60平方厘米， P 为其中任一点，求阴影部分面积。

（2）图中正方形边长为4厘米和3厘米，求阴影部分面积。

（3）将正方形每边分成四等份（如图），正方形边长是16厘米，P为正方形内任一点，阴影部分的面积是多少？经典例题2四边形ABCD是一个长为10厘米，宽为6厘米的长方形，△ADE的面积比△CEF的面积大10平方厘米，求CF的长。

[分析]从图上可以看出，△ADE与△CEF没有直接联系，我们发现，如果它们再添上梯形ECBA，就分别得到长方形和△AFB，它们的面积差不变。

解：将△ADE和△CEF分别加上梯形ECBA，得到长方形和△AFB，它们的面积差不变，) (46102506102)10610(厘米=-÷⨯=-÷⨯-⨯答：CF长为4厘米。

巩固练习：（1）已知长方形ABCD长为20厘米，宽为10厘米，四边形EOFH的面积为25平方厘米，求阴影部分面积。

第14讲巧求图形的面积和周长第一部分：知识介绍巧求图形的面积和周长的方法：1、平移法2、差不变3、旋转法4、图形的切割拼第二部分：例题精讲【例 1】下图中标出的数表示每边长，单位是厘米．它的周长是多少厘米?【考点】巧求图形的周长。

【解析】长方形的长5+6=11(厘米)，宽1+3=4(厘米)，周长(11+4)×2=30(厘米)。

【答案】30厘米【例 2】有9个小长方形，它们的长和宽分别相等，用这9个小长方形拼成的大长方形(如图)的面积是45平方厘米，求这个大长方形的周长。

【考点】巧求图形的周长【解析】从图上可以知道，小长方形的长的4倍等于宽的5倍，所以长是宽的54 1.25÷=倍。

每个小长方形的面积为4595÷=平方厘米，所以1.25⨯宽⨯宽5=，所以宽为2厘米，长为2.5厘米。

大长方形的周长为(2.542 2.5)229⨯++⨯=厘米。

【答案】29厘米【例 3】如右图，计算这个格点三角形的面积。

【考点】巧求图形的面积【解析】这个三角形是处在长是6、宽是4的矩形内，除此之外还有其他三个直角三角形，如下右图（b），这三个直角三角形面积很容易求出，再用矩形面积减去这三个直角三角形面积,就是所要求的三角形面积。

矩形面积是6×4=24 ；直角三角形Ｉ的面积是：6×2÷2＝6 ；直角三角形Ⅱ的面积是：4×2÷2=4 ；直角三角形Ⅲ的面积是：4×2÷2=4 ；所求三角形的面积是：24-（6＋4＋4）=10（面积单位）。

【答案】10【例 4】如右图，ABFE和CDEF都是矩形，AB的长是4厘米，BC的长是3厘米，那么图中阴影部分的面积是平方厘米．【考点】巧求图形的面积、一半模型EC【解析】图中阴影部分的面积等于长方形ABCD面积的一半，即4326⨯÷=(平方厘米)。

【答案】10【例 5】(2005年口试真题)右图中甲的面积比乙的面积大 __________ 平方厘米。

课题：微专题：巧用平移变换求图形的周长、面积课时：1课时执教：林冰玲时间：2016年6月14日一、教材分析在初中数学以及日常生活中有着大量的平移变换的知识，这是中考数学的必考内容。

本节课是平移在求图形周长、面积中的应用。

教学中常遇见平移情形下求图形周长或者阴影部分的面积类问题，其中所求的部分或成一个整体或是零散分布，其形状或是规则图形或是不规则图形，其状态往往是动态的．解决此类问题的关键是以静制动，化不规则图形为规则图形，再用相应规则图形的周长、面积公式求解．二、学情分析本课之前学生已经能理解掌握平移的概念、性质及能利用平移作图，学生还须具有一定的观察、归纳、探索能力。

但学生的抽象概括、探索能力稍微弱一些，而且虽然学生对动手操作活动较为感兴趣，探索精神和学习毅力却又不足.三、教学目标1、知识与技能目标：使学生能够利用平移变换解决简单的计算问题，如求图形的周长、图形的面积。

2、过程与方法目标：在研究问题的过程中培养学生的直观感知能力和归纳能力。

3、情感、态度与价值观：体验数学知识是通过观察猜想和验证的过程，欣赏数学图形之美；体验数学的学习是一个观察、猜想、归纳、验证的过程。

四、教学重点：平移变换的正确使用五、教学难点：能对复杂图形进行恰当的平移变换六、教学准备：学生准备剪刀、作图工具。

利用电脑多媒体优化课堂教学。

七、教学过程：环节教学活动过程设计设计意图时间分配教学内容及教师活动学生活动环节一一、以题点知。

1、将如图所示的图案通过平移后可以得到的图案是（）A．B．C．D．2、如图，△ABC平移之后成为△DCE，则平移的距离为.3、如图，多边形的相邻两边互相垂直，则这个多边形的周长为（）.（A）21 （B）26 （C）37（D）42独立完成复习回顾平移的概念、性质。

3分钟二、操作探究1、如图，某公园有一块长42米、宽20米的长方形草地。

现公园要在草坪中铺设一条纵向的小路(小路任何地方的水平宽度都要求是2米）。