利用平移计算面积

第4课时利用平移求不规则图形的周长和面积
教学目标：
1.让学生在学习平移的基础上，采取用平移方法把图转变成学过的图形，然后求出图形的周长和面积。

2.学会灵活平移变换的方法。

难点重点：
平移变换的方法。

教学过程：
一、情景导入
1. 平移后的图形与原图比较有什么特点？
2.求长方形和正方形的面积。

二、探究新知
出示课本例4图
下面这个图形的面积是多少？
师：请同学们认真观察，看用什么方法计算这个图形的面积？
这是一个不规则图形，不能像我们之前学过的长方形、正方形那样直接求出面积。

那么能不能把它变换成我们学过的图形，求出它的面积呢？
让学生说说如何进行变换图形，学生回答后教师集体反馈学生的想法。

师：我们先把左侧的半圆剪下来，再向右平移6格。

变成了一个长方形，它的面积怎样计算？
用长乘宽计算出长方形的面积。

小结：不规则图形可以通过平移的方式转化成规则图形，从而求得图形的周长或面积，转化前后面积不变。

三、巩固练习
1.做一做，画一画，量一量，算出下面这个火箭的面积。

2.涂色部分占整个图形的几分之几？
3. 计算这个风车的面积。

（小方格边长为1m）
4. 想一想，怎样才能算出下面图形的周长。

四、全课小结
通过这节课的学习，你学到了什么？
有些不规则的图案，我们可以运用平移的方法，将图形转化成已学过的规则图形，从而求得图形的周长或面积。

五、课后作业
完成学习之友课时练习。

板书设计：
第4课时利用平移求不规则图形的周长和面积。

三年级面积平移练习题一、题目：三年级面积平移练习题问题1：将一个边长为5个单位的正方形向右平移3个单位，向上平移2个单位后，它的面积是多少？解答1：首先计算正方形的面积。

正方形的面积等于边长的平方。

这个正方形的边长为5个单位，所以面积为5^2=25平方单位。

接下来，我们将正方形向右平移3个单位，向上平移2个单位。

平移操作并不改变正方形的形状和面积，只是改变了它所处的位置。

所以无论怎么平移，正方形的面积仍然是25平方单位。

所以，经过平移后，这个正方形的面积仍然是25平方单位。

问题2：一个矩形的长为6个单位，宽为4个单位。

将它向左平移2个单位，向下平移1个单位后，它的面积是多少？解答2：首先计算矩形的面积。

矩形的面积等于长乘以宽。

这个矩形的长为6个单位，宽为4个单位，所以面积为6*4=24平方单位。

接下来，我们将矩形向左平移2个单位，向下平移1个单位。

平移操作并不改变矩形的形状和面积，只是改变了它所处的位置。

所以无论怎么平移，矩形的面积仍然是24平方单位。

所以，经过平移后，这个矩形的面积仍然是24平方单位。

问题3：一个边长为7个单位的正方形，将它向右平移5个单位，向下平移3个单位后，它的面积是多少？解答3：首先计算正方形的面积。

正方形的面积等于边长的平方。

这个正方形的边长为7个单位，所以面积为7^2=49平方单位。

接下来，我们将正方形向右平移5个单位，向下平移3个单位。

平移操作并不改变正方形的形状和面积，只是改变了它所处的位置。

所以无论怎么平移，正方形的面积仍然是49平方单位。

所以，经过平移后，这个正方形的面积仍然是49平方单位。

问题4：一个矩形的长为8个单位，宽为3个单位。

将它向左平移4个单位，向上平移2个单位后，它的面积是多少？解答4：首先计算矩形的面积。

矩形的面积等于长乘以宽。

这个矩形的长为8个单位，宽为3个单位，所以面积为8*3=24平方单位。

接下来，我们将矩形向左平移4个单位，向上平移2个单位。

将直角梯形ABCD平移，得到梯形EFGH，其中HG=10，MC=2，MG=4，求图中阴影部分的面积。

这道题，是七年级下册，图形平移这个内容里一道经典考试题型。

把图形上所有的点，都按同一方向上移动相同的距离，图形这的这种位置变换，叫做平移。

图形平移的三个注意点：⑴平移的方向和距离是平移的两个要素。

⑵图形的平移是整体平移，不是局部平移。

⑶图形平移中所有的点平移方向一致。

图形平移后，主要有以下4个性质特征：⑴不改变图形的形状和大小。

⑵新图形与原图形中，两组对应点的连线平行（或者在同一条直线上）且相等。

⑶平移前后的两个图形的对应线段平行（或在同一条直线上）且相等。

⑷平移后前后的两个图形的对应角相等。

也就是平移后，两个图形全等。

这道题，就是图形平移后，梯形EFGH的面积，和梯形ABCD的面积相等。

所以，阴影部分的面积，等于梯形ABCD面积减去梯形EFMD面积，就是等于梯形DM GH的面积。

巧用平移妙求面积 Document number：NOCG-YUNOO-BUYTT-UU986-1986UT巧用平移妙求面积求解与长方形有关的面积是日常生活、生产中常见的问题之一，解决这类问题有一种巧妙的方法那就是采用平移.通过平移，使分散、零碎的图形得以集中，从而方便运用整体思想进行求解.例1如图1－1是小明家一个长方形花坛，空白部分准备用于种花，种草部分分别是一大一小的正方形.已知大正方形的面积为49平方米，小正方形的面积为9平方米.问种花的面积是多少平方米析解：采用平移，将小正方形向上平移到边缘，如图1－2所以.由已知易得种花部分是长方形，长为大正方形的边长减去小长方形的边长，即7-3=4（米），宽恰好是小正方形的边长3米.因此，种花的面积为3×4=12（平方米）.想一想：如果图形不加处理，解题思路又是怎样的呢例2如图2－1，某小区规划在一个长为AD=40米，宽为AB=26米的长方形场地ABCD上，修建三条宽都是2米的小路，其中两条与AB平行，另一条与AD 平行，其余部分种草.问种草区域的面积是多少析解：将图2－1的小路分别沿BA，BC平移到如图2－2所示的位置，则易知种草的长方形的长为40-2×2=36（米），宽为26-2=24（米），所以，种草区域的面积为36×24=864（平方米）.想一想：如果图形不加处理，分别求出三条小路的面积，然后用场地的总面积减去三条小路的面积，求得种草区域的面积.与运用平移来解，感觉怎样例3 如图3－1所示，在一块长为24米，宽为16米的草坪上有一条宽为2米的曲折小路，你能运用你所学的知识求出这块草坪的绿地面积吗析解：小路的面积只与小路的宽度和长度有关，与其位置没有关系.可以将路分解成向下和向右分别平移的两部分，平移后如图3－2所示.这时，绿地转化为长22 米，宽18 米的长方形，可求得绿地的面积为：22×18=396 （平方米）.想一想：直接求小路的面积是无法求解的， 那么，本题中将曲折的小路进行平移，意义何在坐标系中求图形的面积图形的面积可以利用相应的面积公式求得，但是在平面直角坐标系内的求面积问题，往往不直接给出边或高之类的条件，而是给出一些点的坐标.现对这类题目的解法举例说明如下.一、计算三角形的面积例1 如图1所示，三角形ABC 的三个顶点的坐标分别是A （-4，-3），B （0，-3），C （-2，1）.求三角形ABC 的面积.分析：观察图形，在坐标系中读取三角形ABC 的一边的长度，和该边上的高的长度.因为AB ∥x 轴，所以AB 可以作为底边.图3-（1）图3-（2）yB CA O 11 图1解：因为AB=0-（-4）=4，AB 边上的高为h=1-（-3）=4，所以三角形ABC 的面积是：21AB ·h=21×4×4=8. 评注：当两点在平行于x 轴的直线上时，两点之间的距离是两点的横坐标的差的绝对值；当两点在平行于y 轴的直线上时，两点之间的距离是两点的纵坐标的差的绝对值.如果三角形中有一边在坐标轴上或与坐标轴平行时，可以直接利用三角形的面积公式求解.例2 如图2所示，在三角形AOB 中，A ，B ，C 三点的坐标分别为（-1，2），（-3，1），（0，-1），求三角形AOB 的面积.分析：三角形的三边都不与坐标轴平行，根据平面直角系的特点，可以将三角形的面积转化为正方形EFCD 的面积减去多余的直角三角形的面积，即可求出此三角形的面积.解：如图2，作正方形EFCD ，则该正方形的面积为EF ·FC=3×3=9.因为三角形AEB 的面积是：21×AE ·EB=21×2×1=1，三角形BFC 的面积是：21BF ·FC=21×2×3=3，三角形ACD 的面积是：21×AC ·AD=21×3×1=23，所以三角形ABC 的面积是：9-1-3-23=27.点评：如果三角形的三边中没有任何一边在坐标轴上或与坐标轴平行时，则应将其进行转化为几个规则图形的面积和或差.二、计算四边形的面积E FD图2例3 如图3，四边形ABCD 的四个顶点的坐标分别为A（-2，2），B （-3，-3），C （3，3），D （2，1），求四边形ABCD 的面积.分析：四边形ABCD 不是规则的四边形，要求其面积，可将该四边形的面积转化为两个直角三角形和一个梯形的面积的和来计算.解：作AE ⊥BC 于E ，DF ⊥BC 于F ，则四边形ABCD 的面积=三角形ABE 的面积+梯形AEFD 的面积+三角形DFC 的面积，因为三角形ABE 的面积为：21BE ·AE=21×1×5=25，梯形AEFD 的面积为：21（DF+AE ）·EF=21×（4+5）×4=18，三角形DFC 的面积为：21FC ·DF=21×1×4=2，所以四边形ABCD 的面积为：25+18+2=2221. 点评：解决平面直角坐标系中的四边形的面积问题，一般思路是将不规则的图形转化为规则的图形，再利用相关的图形的面积公式求解.。

米，宽为15米，所修小路的宽度均为2米，请问：剩余草坪的面积 是多少？下列为修小路的几种方案，剩余草坪的面积相同吗？
二、知识讲解
例题 如图（1），在一个矩形的草坪中修一条小路，若草坪的长 为40米，宽为15米，所修小路的宽度均为2米，请问：剩余草坪的 面积是多少？
40米
15米
解：剩余草坪的面积=（40-2）×15 =38×15 =570（平方米）
答：草坪的实有面积是864平方米。
有志登山顶，无志站山脚。 才自清明志自高。 丈夫志不大，何以佐乾坤。
36米
四、知识演变 街心公园里有一块草坪，长37米，宽26米，草坪中间修有1
米宽的小路，将草坪分成两块（如图）。草坪的实有面积是多少？
37米
解：草坪的实有面积=（37-1）×（26-1）
26 米
25
难点名称：利用平移将不规则图形转化为规 人这教个版 图数形学的七面级积下是册多少5c.m²？
2、某宾馆再重新装修后，准备在大厅的主楼梯上铺设某种红色地毯，已知这种地毯每平米售价30元，主楼梯道宽2米，其侧面如图所示，则购买地毯至少需要_____元.
则图形求面积 一解个：人 剩如余果草胸坪无的大面志积，=（既4使0-再2）有×壮15丽的举动也称不上是伟人。
=36×25
米
=900（平方米）
36米
答：草坪的实有面积是900平方米。
五、课堂练习
1、如图，是一块长方形草地，长方形的长是16米， 宽是10米。中间有两条道路，一条是长方形，一条是
平行四边形。草地部分的面积有 112平方米。
五、课堂练习 2、某宾馆再重新装修后，准备在大厅的主楼梯上铺设某 种红色地毯，已知这种地毯每平米售价30元，主楼梯道 宽2米，其侧面如图所示，则购买地毯至少需要_5_0_4__元.

旋转的几何意义
旋转是指图形绕某一固定点转动一定 的角度，旋转过程中图形的每一点都 绕该固定点做圆周运动。
02 图形平移与旋转后的面积 变化
图形平移后的面积变化
图形平移不改变面积
图形在平面内沿某一方向进行 平移时，其形状和大小不会发 生变化，因此面积也不会改变
。
平行四边形平移
平行四边形沿其一边进行平移 时，面积保持不变。
巧求面积-平移旋转
contents
目录
• 平移与旋转的基本概念 • 图形平移与旋转后的面积变化 • 利用平移与旋转求面积的策略 • 经典例题解析 • 练习题与答案
01 平移与旋转的基本概念
平移的定义与性质
定义
平移是将图形沿某一方向移动一 定的距离，而不改变其形状和大 小。
性质
平移不改变图形的形状、大小和 方向，只改变图形的位置。平移 后，图形与原图形是全等的。
02
例如：求圆心角为90度的扇形所 夹的弓形面积。可以将扇形旋转 90度，将弓形变为等腰直角三角 形，再利用三角形面积公式计算 。
平移与旋转结合例题解析
平移与旋转结合法求面积的原理是通过将图形进行平移和旋 转，使其成为规则图形，从而利用公式计算面积。
例如：求一个正方形内部被切去一个角后所形成的图形的面 积。可以将切去的角向下平移并旋转90度，将不规则图形变 为等腰梯形，再利用梯形面积公式计算。
05 练习题与答案
平移练习题与答案
题目：一个平行四边形经 过平移后，它的一个顶点A 移动到点A'，其对应点之 间的距离是2cm，那么原 平行四边形的一个边长增 加了多少cm。
答案：2cm
题目：一个三角形经过平 移后，它的一个顶点P移动 到点P'，其对应点之间的 距离是3cm，那么原三角 形的一个边长增加了多少 cm。

50×5+（40-5）×5 =250+35×5 由图可知，这条小路=的2面50积+可17分5 为两部分来计算：横着的3段与竖 着的4段，横着的3段=接42起5来（是m一2）个长为50米，宽为5米的长方形， 竖着的4段接起来是一个长为（40-5）米，宽为5米的长方形，因 此，计算出这两个长方形的面积，进而解决问题．
图形的运动（二）
利用平移解决面积问 题（例4）
绿色圃中学资源网 绿色圃中学资源网
1cm ︷
2×2=4（cm²） 4×1=4（cm²）
从前有个老地主，他有两块地，分 别分给了他的大儿子和小儿子，可 大儿子说父亲偏心，说分给自己的 地没有弟弟的大。
1cm︷
1cm︷
大儿子
小儿子
1cm︷ 6×4=24（cm²）
小组合作要求： 一、画一画、剪一剪、移一移、拼一拼， 想办法求出大儿子的土地面积。 二、在操作中注意用剪刀的安全， 剪的废纸不要乱扔。 三、比一比哪个小组合作得又快又好。
数方格
平移
平移
1cm︷
1cm︷
面积不变！
原图形面积 = 拼成的长方形面积 = 6 ×4 = 24（ cm²）
2.求这个图形的面积（每个小正方形的边长是1cm）。
..
..
.
.
.
（5＋2）×2＝14（cm²） 答：这个图形的面积是14cm²。
课堂小结
如图是一块长方形草坪，长是16米，宽是10米，中间有两条小路， 一条是长方形，一条是平行四边形，那么有草部分（阴影部分） 的面积有多大？
如图所示，为了绿化校园，学校决定修 一块长方形草坪，草坪长30m，宽20m， 并在草坪上修建如图所示的十字路 如图所示，为了绿化校园，学校决定修 一块长方形草坪，草坪长30m，宽20m， 并在草坪上修建如图所示的十字路，其 余面积种草，小路宽为a m，用代数式 表示：（1）小路的面积是多少？（2） 种草部分的面积是多少？

弯曲小路面积平移法弯曲小路面积平移法，这是一个有趣而有挑战性的数学概念。

它涉及到曲线的面积计算问题，以及如何通过平移曲线来得到更大范围的面积。

在本文中，我将以简单、清晰的方式介绍这个概念，帮助你更好地理解。

1. 弯曲小路面积的计算弯曲小路面积平移法是一种通过平移曲线来计算曲线所围成的面积的方法。

我们需要理解弯曲小路的定义。

弯曲小路是指一条曲线，它由两个垂直于 x 轴的函数所确定。

这两个函数分别是上方曲线函数 f(x) 和下方曲线函数 g(x)。

如果我们将这条弯曲小路在 x 轴上平移一个单位，然后计算新的曲线所围成的面积，这个面积将比原先的面积大。

这是因为，平移后的曲线将覆盖原先曲线所围成的面积，并且在 x 轴上面积变大的地方，会增加面积。

通过不断平移曲线并计算面积增量，我们可以得到整条弯曲小路所围成的面积。

2. 示例为了更好地理解弯曲小路面积平移法，我们来看一个简单的示例。

假设我们有一个弯曲小路，上方曲线函数为 f(x) = x^2，下方曲线函数为 g(x) = 0。

现在，我们将这条小路在 x 轴上平移一个单位，并计算新的曲线所围成的面积增量。

- 当 x = 0 时，原曲线的面积为 0。

- 当 x = 1 时，新曲线的面积增量为 (1^2 - 0) = 1。

- 当 x = 2 时，新曲线的面积增量为 (2^2 - 0) = 4。

- 当 x = 3 时，新曲线的面积增量为 (3^2 - 0) = 9。

如此继续下去，我们可以得到整条弯曲小路所围成的面积为 1 + 4+ 9 + ...3. 总结与回顾弯曲小路面积平移法是一种通过平移曲线并计算面积增量来求解弯曲小路面积的方法。

通过不断平移曲线，并计算每次平移后的面积增量，我们最终可以得到整条弯曲小路所围成的面积。

这个方法的精髓在于通过平移曲线来增加面积，并利用数学计算方法将面积增量相加得到最终结果。

它不仅能够帮助我们解决曲线面积计算的问题，还能锻炼我们的数学思维和计算能力。

平移法解决有关面积问题黑龙江 王国仁一元二次方程的实际应用是教材的重点，也是中考的热点，它的应用十分广泛，设计到面积问题、经济问题、行程问题、增长率问题等等，在面积问题中有一些计算题，如采用平移的方法适当改变图形的形状，可以给解决问题带来意想不到的美妙的效果．现举例说明如下．例1． 一块矩形耕地大小尺寸如图1所示，要在这块地上沿东西和南北方向分别挖2条和4条小渠，如果小渠的宽相等，而且要保证余下的耕地面积为9600米2，那么水渠应挖多宽？图1分析：这类问题的特点是，挖掘渠道所占用土地面积只与挖渠的条数，渠道的宽度有关，而与渠道的位置无关，为了研究问题方便可分别把东西和南北方向的渠道移动到一起（最好靠一边）．如图2所示，那么剩余的长方形土地的长为（162－2x ）米，宽为（64－4x ）米．图2解：设水渠的长应挖x 米，则根据题意，得()()16226449600--=x x ．整理，得 x x 297960-+=解得：，舍去x x 12196==()答：水渠应挖1米宽．例2． 如图3，从一块长80厘米、宽60厘米的铁片中间截去一个小长方形，使剩下的长方框四周的宽度一样，并且小长方形的面积是原来铁片面积的一半，求这个宽度．图3 图4分析：如果将剩下的铁片平移到一角如图４，可以看出剪掉的边长为（80-2x ）厘米与（60-2x ）厘米，这样问题就容易多了！解：设宽度x cm依题意，得1(802)(602)80602x x --=⨯⨯， 整理，得2706000x x -+=，解得121060x x ==，（不合题意，舍去）．答：剩下长方框四周的宽度为10厘米．例3．一块矩形耕地大小尺寸如图5，如果修筑同样宽的两条“之”字形的道路，如图5所示，余下的部分作为耕地．要使耕地的面积为5402m ，道路的宽应是多少?分析：此题如不采用“平移法”，很难人手．若把“之”字道路平移一下位置，变为图6，则此题即可迎刃而解．图5 图6解：设道路的宽应是x 米，依题意得 (20)(32)540x x --=整理得 2521000x x -+=解得：12250x x ==，（不符合题意，舍去）答：道路的宽应是2米．。

由抛物线平移形成的面积的求法
解：
由抛物线平移形成的面积可以用分段函数法求解，将抛物线分段后，根据每个小段的面积公式（长方形面积除以2、三角形面积）将所有段的面积相加即可求出总面积。

例如，如果抛物线由x轴正半轴和负半轴所组成，抛物线的函数为y=ax2，则面积
公式为：
Area = 1/3ax3 + b/2ax2 + cx。

其中a, b, c分别是抛物线在x轴正半轴，x轴负半轴以及抛物线相交处的x坐标。

因此，可以通过求出抛物线在x轴正半轴，x轴负半轴以及抛物线相交处的x坐标，来求出抛物线的总面积。

另外，可以使用整合法来计算抛物线的总面积，即求出抛物线函数的积分值，然后将积分结果减去抛物线上每个点的面积，即可得到抛物线的总面积。

积分中也可以添加抛物线的阶跃，以更准确的计算抛物线的总面积。

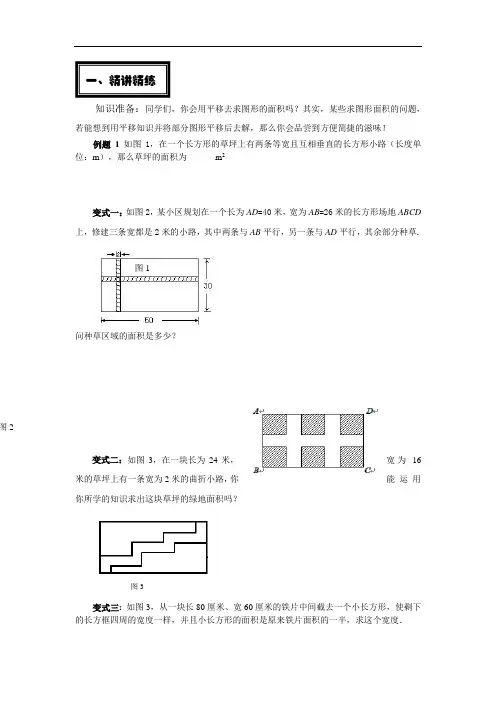
一、精讲精练知识准备：同学们，你会用平移去求图形的面积吗？其实，某些求图形面积的问题，若能想到用平移知识并将部分图形平移后去解，那么你会品尝到方便简捷的滋味！例题1 如图1，在一个长方形的草坪上有两条等宽且互相垂直的长方形小路（长度单位：m），那么草坪的面积为______ m2变式一：如图2，某小区规划在一个长为AD=40米，宽为AB=26米的长方形场地ABCD 上，修建三条宽都是2米的小路，其中两条与AB平行，另一条与AD平行，其余部分种草.图1问种草区域的面积是多少？图2变式二：如图3，在一块长为24米，宽为16米的草坪上有一条宽为2米的曲折小路，你能运用你所学的知识求出这块草坪的绿地面积吗？图3变式三: 如图3，从一块长80厘米、宽60厘米的铁片中间截去一个小长方形，使剩下的长方框四周的宽度一样，并且小长方形的面积是原来铁片面积的一半，求这个宽度．图4图4变式四:如图5是重叠的两个直角三角形．将其中一个直角三角形沿BC方向平移得到△DEF的位置．若AB=8cm，BE=4cm，DG=3cm，则图中阴影部分的面积为_____cm．图5二、勇攀高峰如图6所示是一块待开发的土地，规划人员把它分割成①号区（空白部分）、②号区（阴影部分）、③号区（图下方的空白部分）三块，拟在①号区种花、②号区建房、③号区植树，已知图中四边形ABCD与四边形EFGH是两个完全相同的直角梯形（一腰和底相交成直角的梯形叫做直角梯形，这里∠C和∠G都是直角），求种花部分的面积．图6三、参考答案例题1将两条小路分别作如图平移，则草坪的面积就是图3中空白部分（长方形）的面积，即（50－2）×（30－2）＝1344 m ．变式一：将小路分别沿BA ，BC 平移到如图位置，则易知种草的长方形的长为40-2×2=36（米），宽为26-2=24（米），所以，种草区域的面积为36×24=864（平方米）变式二：小路的面积只与小路的宽度和长度有关，与其位置没有关系.可以将路分解成向下和向右分别平移的两部分，平移后如图所示.这时，绿地转化为长22 米，宽18 米的长方形，可求得绿地的面积为：22×18=396（平方米）.变式三: 如果将剩下的铁片平移到一角，可以看出剪掉的边长为（80-2x ）厘米与（60-2x ）厘米，这样问题就容易多了！解：设宽度x cm依题意，得1(802)(602)80602x x --=⨯⨯， 整理，得2706000x x -+=，解得121060x x ==，（不合题意，舍去）．变式四:显然，因①号区是不规则的图形，不易直接求其面积，考虑到四边形ABCD 与四边形EFGH 是两个完全相同的直角梯形，故可将四边形EFGH 看成是四边形ABCD 沿AB方向平移得到的，所以①号区面积等于③号区面积，而③号区面积等于×（EM +AD）×MD＝×（200－1＋200）×2＝399（m），所以种花部分的面积为399（m）．四、回顾小结在初中数学学习中，图形的面积是日常生活、生产中常见的问题之一，解决这类问题有一种巧妙的方法那就是采用平移.通过平移，使分散、零碎的图形得以集中，从而方便运用整体思想进行求解.。

四年级下册数学教案-1.1 平移和运用平移解决面积问题
教学目标
1.了解平移的定义；
2.掌握平移的基本方法和规则；
3.运用平移解决面积问题。

教学重点
1.平移的定义和基本方法；
2.运用平移解决面积问题。

教学难点
1.运用平移解决面积问题。

教学过程
教学内容1：平移的定义与规则
教学目标
1.了解平移的定义；
2.掌握平移的基本方法和规则。

教学步骤
1.引入：老师向学生展示图形，问：“如果我们要把它移到另一个地方，应该怎么做呢？”
2.介绍平移的概念：告诉学生平移是指把一幅图形整体沿着某个方向移动一段距离的操作。

3.讨论平移的规则：对于任何一个图形，平移有以下规则：
–平移是整体移动，每一个点都沿着同一个方向移动相同的距离；
–平移前后的图形形状大小都不变，只是位置改变；
–平移可以向上下左右四个方向进行；
–平移可以是正方向也可以是反方向；
–平移中间的空白部分可以忽略不计。

教学内容2：运用平移解决面积问题
教学目标
1.掌握平移运用解决面积问题的方法。

教学步骤
1.回顾上一节课的知识，介绍运用平移解决面积问题的方法：将图形平移后，再用已知面积的图形去填补所求图形，从而得出所求图形的面积。

2.通过实例让学生了解平移解决面积问题的方法。

3.带领学生完成练习。

课后作业
1.完成课堂练习；
2.自选一个待解决的面积问题，用平移的方法求解。

总结
通过这节课的学习，学生了解了平移的定义和基本规则，并掌握了运用平移解决面积问题的方法。

这些知识将为后续的学习提供基础。