画图法巧解鸡兔同笼问题(优.选)
- 格式:doc
- 大小:44.50 KB
- 文档页数:3

“鸡兔同笼”讲解方法(13种)『方法一:人见人爱的列表法』如果二年级小朋友做这道题,可以用列表法!直观、易理解,还不容易出错~好啦,我们来看一下!根据上面的表格,我们可以看出,鸡为9只,兔子为5只。
我们在列表的时候不要按顺序列,否则做题的速度会很慢,比如说列完鸡为0只,兔子为14只,发现腿的数量56条,和实际38条相差较大,那么下一个你可以跳过鸡的数量为2只这种情况,直接列鸡的数量为3只,这样做速度会快一些哦!『方法二:最快乐的画图法』画图可以让数学变得形象化,而且经常画图还有助于创造力的培养!假设14只全部是鸡,先把鸡给画好。
14×2=28条,差38-28=10条,而每一只鸡补2条腿就变成兔子,需要把5只鸡每只补2条腿,所以有5只兔子,14-5=9只鸡。
『方法三:最酷的金鸡独立法』分析:让每只鸡都一只脚站立着,每只兔都用两只后脚站立着,那么地上的总脚数只是原来的一半,即19只脚。
鸡的脚数与头数相同,而兔的脚数是兔的头数的2倍,因此从19里减去头数14,剩下来的就是兔的头数19-14=5只,鸡有14-5=9只。
『方法四:最逗的吹哨法』分析:假设鸡和兔接受过特种部队训练,吹一声哨,它们抬起一只脚,还有38-14=24只腿在站着,再吹一声哨,它们又抬起一只脚,这时鸡都一屁股坐地上了,兔子还有两只脚立着。
这时还有24-14=10只腿在站着,而这10只腿全部是兔子的,所以兔子有10÷2=5只,鸡有14-5=9只。
(惊现跑男中包贝尔的抬脚法有木有!)『方法五:最常用的假设法』分析:假设全部是鸡,则有14×2=28条腿,比实际少38-28=10只,一只鸡变成一只兔子腿增加2条,10÷2=5只,所以需要5只鸡变成兔子,即兔子为5只,鸡为14-5=9只。
『方法六:最常用的假设法』分析:假设全部是兔子,则有14×4=56条腿,比实际多56-38=18只,一只兔子变成一只鸡腿减少2条,18÷2=9只,所以需要9只兔子变成鸡,即鸡为9只,兔子为14 - 9=5只。

鸡兔同笼13种解题方法鸡兔同笼问题是一类经典的数学问题,常见于初中数学题目中。
这个问题的基本思路是通过解方程组来求解鸡和兔子的数量。
在本文中,将介绍13种不同的解题方法,包括逆向思维、代数法、图形法等多种方法,帮助读者更好地理解和掌握这一问题。
一、逆向思维法逆向思维法是一种比较简单易懂的方法,其基本思路是先确定总数量,再确定其中一个物品的数量,最后计算出另一个物品的数量。
1. 假设笼子里有13只动物,则鸡和兔子的总数量为13。
2. 假设有x只鸡,则有13-x只兔子。
3. 根据题目所给条件“总腿数为32”,得到方程式2x+4(13-x)=32。
4. 解方程得到x=6,则笼子里有6只鸡和7只兔子。
二、代数法代数法是一种常用的解题方法,其基本思路是通过设定未知量来建立方程组,并通过求解方程组来得到答案。
1. 设鸡和兔子的数量分别为x和y,则有方程组:x+y=132x+4y=322. 通过求解方程组得到x=6,y=7,则笼子里有6只鸡和7只兔子。
三、图形法图形法是一种直观易懂的方法,其基本思路是通过画图来解决问题。
1. 在平面直角坐标系中,设鸡和兔子的数量分别为x和y,则可以用一条直线表示鸡和兔子的总数量为13。
2. 根据题目所给条件“总腿数为32”,可以得到另一条直线表示鸡和兔子的总腿数为32。
3. 通过求解两条直线的交点,即可得到笼子里有6只鸡和7只兔子。
四、枚举法枚举法是一种简单易行的方法,其基本思路是通过列举所有可能情况来找到符合条件的答案。
1. 从1到12枚举鸡的数量x。
2. 根据题目所给条件“总腿数为32”,计算出相应的兔子数量y。
3. 如果x+y=13,则找到符合条件的答案。
五、分段函数法分段函数法是一种利用函数性质解题的方法,其基本思路是将问题拆分成多个部分,并建立相应的函数关系式来求解问题。
1. 假设笼子里有x只鸡,则有13-x只兔子。
2. 根据题目所给条件“总腿数为32”,可以得到下列函数关系式: f(x)=2x+4(13-x)3. 通过求解f(x)=32的解,即可得到笼子里有6只鸡和7只兔子。

“鸡兔同笼”例题13种讲解方法题目:现有一笼子,里面有鸡和兔子若干只,数一数,共有头14个,腿38条,球鸡和兔子各有多少只?(请用尽量多的方法解答)『方法一:人见人爱的列表法』如果二年级小朋友做这道题,可以用列表法!直观、易理解,还不容易出错~好啦,我们来看一下!9 ... 鸡0 3 5 7兔14 11 9 7 5 ...腿56 50 46 42 38 ...根据上面的表格,我们可以看出,鸡为9只,兔子为5只。
我们在列表的时候不要按顺序列,否则做题的速度会很慢,比如说列完鸡为0只,兔子为14只,发现腿的数量56条,和实际38条相差较大,那么下一个你可以跳过鸡的数量为2只这种情况,直接列鸡的数量为3只,这样做速度会快一些哦!『方法二:最快乐的画图法』画图可以让数学变得形象化,而且经常画图还有助于创造力的培养!假设14只全部是鸡,先把鸡给画好。
14×2=28条,差38-28=10条,而每一只鸡补2条腿就变成兔子,需要把5只鸡每只补2条腿,所以有5只兔子,14-5=9只鸡。
『方法三:最酷的金鸡独立法』分析:让每只鸡都一只脚站立着,每只兔都用两只后脚站立着,那么地上的总脚数只是原来的一半,即19只脚。
鸡的脚数与头数相同,而兔的脚数是兔的头数的2倍,因此从19里减去头数14,剩下来的就是兔的头数19-14=5只,鸡有14-5=9只。
『方法四:最逗的吹哨法』分析:假设鸡和兔接受过特种部队训练,吹一声哨,它们抬起一只脚,还有38-14=24只腿在站着,再吹一声哨,它们又抬起一只脚,这时鸡都一屁股坐地上了,兔子还有两只脚立着。
这时还有24-14=10只腿在站着,而这10只腿全部是兔子的,所以兔子有10÷2=5只,鸡有14-5=9只。
(惊现跑男中包贝尔的抬脚法有木有!)『方法五:最常用的假设法』分析:假设全部是鸡,则有14×2=28条腿,比实际少38-28=10只,一只鸡变成一只兔子腿增加2条,10÷2=5只,所以需要5只鸡变成兔子,即兔子为5只,鸡为14-5=9只。
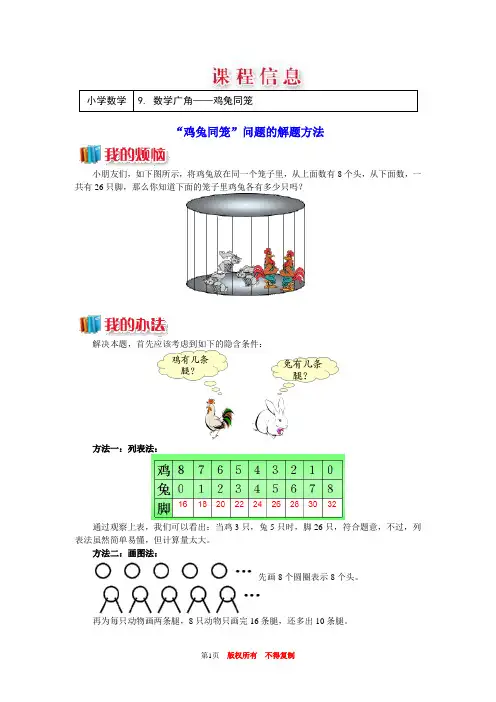
小学数学9. 数学广角——鸡兔同笼“鸡兔同笼”问题的解题方法小朋友们,如下图所示,将鸡兔放在同一个笼子里,从上面数有8个头,从下面数,一共有26只脚,那么你知道下面的笼子里鸡兔各有多少只吗?解决本题,首先应该考虑到如下的隐含条件:方法一:列表法:通过观察上表,我们可以看出:当鸡3只,兔5只时,脚26只,符合题意,不过,列表法虽然简单易懂,但计算量太大。
方法二:画图法:先画8个圆圈表示8个头。
再为每只动物画两条腿,8只动物只画完16条腿,还多出10条腿。
把剩下的10条腿画完,要给其中的5只动物各添2条腿,这5只就是兔子,另外的3只就是鸡。
小朋友快看,一休哥哥也来帮忙了。
方法三:假设法假设8只全是鸡,有几条腿?8×2=16(条)与条件26条相比还剩下几条腿?26-16=10(条)这里的10条腿,如果再添的话就只能添给兔子了。
下面开始给兔子添腿,每只还需要添几条腿就是兔子了?4-2=2(条)剩下的10条腿,能添出几只兔子?10÷2=5(只)鸡有几只?8-5=3(只)1. 假如让鸡抬起一只脚,兔子抬起两只脚,还有26÷2=13只脚。
2. 这时每只鸡一只脚,每只兔子两只脚。
笼子里只要有一只兔子,则脚的总数就比头的总数多1。
3. 这时脚的总数与头的总数之差13-8=5,就是兔子的只数。
解答“鸡兔同笼”问题一般用假设法,可以先假设都是鸡,也可以假设都是兔,如果先假设都是鸡,然后以兔换鸡;如果先假设都是兔,然后以鸡换兔,这类问题也叫置换问题,通过先假设,再置换,使问题得到解决。
具体可以归纳为:已知总头数和总脚数,求鸡、兔各多少:(总脚数-每只鸡的脚数×总头数)÷(每只兔的脚数-每只鸡的脚数)=兔数;总头数-兔数=鸡数。
或者是(每只兔的脚数×总头数-总脚数)÷(每只兔的脚数-每只鸡的脚数)=鸡数;总头数-鸡数=兔数。
例题1在一个停车场上共停了汽车和三轮摩托车共24辆,其中汽车有4个轮子,摩托车有3个轮子,这些车共有86个轮子,那么三轮摩托有()辆。

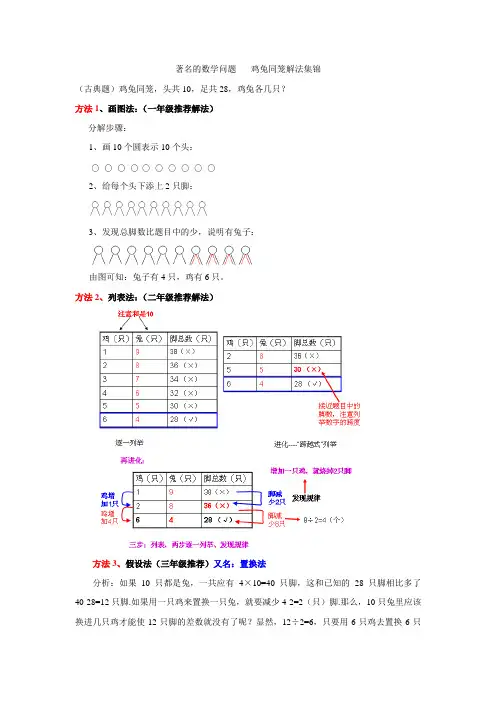
著名的数学问题-----鸡兔同笼解法集锦(古典题)鸡兔同笼,头共10,足共28,鸡兔各几只?方法1、画图法:(一年级推荐解法)分解步骤:1、画10个圆表示10个头:2、给每个头下添上2只脚:3、发现总脚数比题目中的少,说明有兔子:由图可知:兔子有4只,鸡有6只。
方法2、列表法:(二年级推荐解法)方法3、假设法(三年级推荐)又名:置换法分析:如果10只都是兔,一共应有4×10=40只脚,这和已知的28只脚相比多了40-28=12只脚.如果用一只鸡来置换一只兔,就要减少4-2=2(只)脚.那么,10只兔里应该换进几只鸡才能使12只脚的差数就没有了呢?显然,12÷2=6,只要用6只鸡去置换6只兔就行了.所以,鸡的只数就是6,兔的只数是10-6=4。
解:假设全部是兔:4×10=40(只)比实际的脚多:40-28=12(只)鸡的只数:12÷2=6(只)兔子的只数:10-6=4(只)友情提示:同学们,有发现吗?假设对象和你先求出的对象是相反的,你还会为搞不清求的是谁而烦恼吗?我们来总结一下这道题的解题思路:先假设它们全是兔.于是根据鸡兔的总只数就可以算出在假设下共有几只脚,把这样得到的脚数与题中给出的脚数相比较,看相差多少.每差2只脚就说明有一只鸡;将所差的脚数除以2,就可以算出共有多少只鸡.我们称这种解题方法为假设法.概括起来,解鸡兔同笼问题的基本关系式是:鸡数=(每只兔脚数×兔总数- 实际脚数)÷(每只兔子脚数-每只鸡的脚数)兔数=鸡兔总数-鸡数当然,也可以先假设全是鸡。
方法4、方程法(四五年级推荐)解:设鸡有x只,兔子有(10-x)只:2x+4(10-x)=28解之得:x=6兔子:10-6=4(只)5、另有一法(有局限,有能力的学生推荐)鸡兔腿都是偶数,各去掉一半,这样鸡变成1只脚,兔子是2只脚,总脚数就是28÷2=14只,兔子:14-10=4(只),鸡:10-4=6(只)。



第二十讲画图解鸡兔同笼前续知识点:二年级第一讲;XX模块第X讲后续知识点:X年级第X讲;XX模块第X讲把里面的人物换成相应红字标明的人物.卡莉娅萱萱小高卡莉娅卡莉娅小高小高这一讲我们学习经典的鸡兔同笼问题,并且学会用画图法感受“头数”和“腿数”的变化规律.在解决鸡兔同笼问题时,往往会分为这样几个步骤:首先,假设笼中全都是鸡或者兔子,根据头数(即动物的个数)求出假设时的腿数,再把假设时的腿数与实际情况相比较,找到差距和造成差距的原因(例如:把兔子假设成鸡造成的腿数差距),最后经过调整找到正确结果.例题1在一个笼子里养着鸡和兔,从上面数共有5个头,从下面数共有14条腿.鸡和兔各有多少只?【提示】假设笼子里只有一种动物,算出总腿数与实际的腿数进行比较,再调整.练习1笼子里有鸡和兔,数数头有8个,数数腿有22条,笼子里分别有多少只鸡和兔?鸡兔同笼问题不仅仅是指这些以“鸡”和“兔”为内容的题,而是指可以用这类思想方法去解决的问题.例题2阿呆很喜欢吃草莓,而且他有很奇怪的吃法,每次吃两个草莓或者三个草莓.阿呆的妈妈给他洗了25个草莓,阿呆吃了9次,全部吃完.请问:他有几次一下吃三个,有几次一下吃两个?【提示】用“假设法”的三个步骤做一做.练习234名学生去划船,共租了7条船.已知每条大船坐6人,每条小船坐4人.问大船、小船各租了多少条?例题3张奶奶买5角和2角的邮票共10张,花去3元8角.那么这两种邮票各买了多少张?【提示】3元8角=()角.练习3妈妈到花卉市场买玫瑰花和月季花共9枝,每枝玫瑰花3元,每枝月季花2元,共付款22元.妈妈买玫瑰花和月季花各几枝?除了基本的鸡兔同笼问题之外,有些题目中会把“头和”隐藏起来,这个时候,就需要同学们把这些隐藏的条件挖掘出来.例题4唐老鸭带着家人来羊村度假,已知鸭和羊只数一样多,共54条腿.鸭和羊各多少只?【提示】把1只鸭和1只羊作为一组,有几条腿?共有多少组?练习4三脚猫和四脚蛇一样多,总共有77条腿.求三脚猫和四脚蛇各有多少只?例题5一个养殖园内,乌龟比白鹤多2只,共有44条腿,那么乌龟和白鹤分别有多少只?【提示】多出的2只乌龟有几条腿?例题6100个和尚吃100个馒头,大和尚1人吃3个,小和尚3人吃1个.求大、小和尚各多少人?【提示】把1个大和尚和3个馒头与3个小和尚和1个馒头作为一组,这样每一组的和尚数和馒头数相等.课堂内外孙子算经《孙子算经》卷下第31题,可谓是后世“鸡兔同笼”题的始祖,后来传到日本,变成“鹤龟算”.书中是这样叙述的:“今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几何?”这四句话的意思是:有若干只鸡、兔同在一个笼子里,从上面数有35个头,从下面数有94只脚,求笼中各有几只鸡和兔?美国杰出数学教育家G•波利亚对这种解法创设了教学情景:意外地看见笼中的禽畜正在作一种古怪的姿式,每一只鸡都用一条腿站着,而每一只兔子都用其(两条)后腿站着跳舞,在这个不寻常的情况下,只用了半数的腿,即47条腿.在47这个数目中,鸡的头只计算了一次,而兔子的头则计算了两次,从47这个数减去所有头数35,就剩下兔子的头数了.当然,鸡的只数可立刻求出.这种解法虽然巧妙,但它需要清晰的掌握题中的数量关系.作业1.笼子里有鸡和兔,从上面数共有4个头,从下面数共有10条腿,鸡和兔各有多少只?2.李老师把31名同学分到7间宿舍里,已知每间大宿舍住5人,每间小宿舍住3人.大宿舍和小宿舍各有多少间?3.淘淘在面包房买大面包和小面包共8个,每个大面包6元,每个小面包4元,共付款38元.淘淘分别买了多少个大面包和小面包?4.鸭子和大象是好朋友,现在有一样多的鸭子和大象,总共有30条腿.鸭子和大象各有多少只?5.独角兽和山羊(两个角)在山坡上玩耍,独角兽比山羊多1只,共有16个角.山羊和独角兽各有多少只?第二十讲画图解鸡兔同笼1.例题1答案:鸡有3只,兔有2只详解:如图所示:第1步:假设全是鸡,总腿数是5210⨯=(条);第2步:比较,假设的总腿数与实际的相差14104-=(条);第3步:把一些鸡调整成兔子,一只鸡“变成”一只兔,需要加2条腿,共需要调整422÷=(只),所以兔子有2只,523-=(只),鸡有3只.2.例题2答案2个详解:第1步:假设阿呆每次都吃2个草莓,共吃9218⨯=(个);第2步:比较,25187-=(个);第3步:调整,一次2个“变成”一次3个,需要加1个,共需要调整717÷=(次),所以阿呆有7次一下吃3个草莓,972-=(次),有2次一下吃2个草莓.3.例题3答案:5角的邮票有6张,2角的邮票有4张详解:3元8角=38角.第1步:假设全是2角的邮票,总钱数是21020⨯=(角);第2步:比较,382018-=(角);第3步:调整,一张2角的邮票“变成”一张5角的邮票,需要加3角钱,共需要调整1836÷=(张),所以5角的邮票有6张,1064-=(张),2角的邮票有4张.4.例题4答案:鸭和羊各有9只详解:如图所示,把1只鸭和1只羊作为一组,426+=(条),有6条腿;5469÷=(组),所以鸭和羊各有9只.5.例题5答案:白鹤有6只,乌龟有8只详解:如图所示,先画多出的2只乌龟,有248⨯=(条)腿,44836-=(条),再把1只乌龟和1只白鹤作为一组,246+=(条),有6条腿;3666÷=(组),所以白鹤有6只,628+=(只),乌龟有8只.6条6条6条……6. 例题6 答案:大和尚有25人,小和尚有75人详解:如图所示,把1个大和尚和3个馒头与3个小和尚和1个馒头作为一组,这样每一组的和尚数和馒头数相等,分别是4个,共8个;100100200+=(个),和尚和馒头的总数是200个,200825÷=(组),每组有1个大和尚,所以大和尚有25人,每组有3个小和尚,25375⨯=(人),所以小和尚有75人.7. 练习1答案:鸡有5只,兔有3只 简答:第1步:假设全是鸡,总腿数是8216⨯=(条);第2步:比较,22166-=(条);第3步:调整,一只鸡“变成”一只兔,需要加2条腿,共需要调整623÷=(只),所以兔子有3只,835-=(只),鸡有5只.8. 练习2答案:大船有3条,小船有4条简答:第1步:假设全是小船,总人数是7428⨯=(人);第2步:比较,34286-=(人);第3步:调整,一条小船“变成”一条大船,需要加2个人,共需要调整623÷=(条),所以大船有3条,734-=(条),小船有4条.9. 练习3答案:玫瑰花有4支,月季花有5支简答:第1步:假设全是月季花,总钱数是9218⨯=(元);第2步:比较,22184-=(元);第3步:调整,一支月季花“变成”一支玫瑰花,需要加1元钱,共需要调整414÷=(支),所以玫瑰花有4支,945-=(支),月季花有5支.10. 练习48个……6条 6条6条 ……8条答案:三脚猫和四脚蛇各有11只简答:把1只三脚猫和1只四脚蛇作为一组,347+=(条),有7条腿;77711÷=(组),所以三脚猫和四脚蛇各有11只.11. 作业1答案:鸡有3只,兔有1只简答:第1步:假设全是鸡,总腿数是428⨯=(条);第2步:比较,1082-=(条);第3步:调整,一只鸡“变成”一只兔,需要加2条腿,共需要调整221÷=(只),所以兔子有1只,413-=(只),鸡有3只.12. 作业2答案:大宿舍有5间,小宿舍有2间简答:第1步:假设全是小宿舍,总人数是7321⨯=(人);第2步:比较,312110-=(人);第3步:调整,一间小宿舍“变成”一间大宿舍,需要加2人,共需要调整1025÷=(间),所以大宿舍有5间,752-=(间),小宿舍有2间.13. 作业3答案:大面包有3个,小面包有5个简答:第1步:假设全是小面包,总钱数是8432⨯=(元);第2步:比较,38326-=(元);第3步:调整,一个小面包“变成”一个大面包,需要加2元钱,共需要调整623÷=(个),所以大面包有3个,835-=(只),小面包有5个.14. 作业4答案:鸭子有5只,大象有5头简答:把1只鸭子和1头大象作为一组,246+=(条),有6条腿;3065÷=(组),所以共有5只鸭子和5头大象.15. 作业5答案:山羊有5只,独角兽有6只简答:先去掉多出的一只独角兽的角数:16115-=(个);再把1只独角兽和1只山羊作为一组,123+=(个),有3个角;1535÷=(组),所以共有5只山羊和516+=(只)独角兽.。

鸡兔同笼的五种方法
鸡兔同笼问题是一个经典的数学逻辑问题,通常涉及到两种动物的数量及其腿数,需要通过解方程组来求解。
以下是五种解决鸡兔同笼问题的方法:
1. 列方程法:设鸡和兔的数量分别为x和y,根据题目所给出的条件列方程组,例如2x+4y=20和x+y=8,然后解方程求出x和y 的值。
2. 矩阵法:将方程组转化成矩阵形式,然后使用矩阵运算求解,这种方法适用于多元线性方程组的求解。
3. 图像法:在平面直角坐标系中画出鸡和兔的数量的图像,然后根据题目所给的条件确定交点的位置,从而求出鸡和兔的数量。
4. 枚举法:根据题目所给的总数量和总腿数,枚举不同的鸡和兔的组合方式,判断哪一种组合方式符合条件。
5. 巧用因式分解法:根据题目所给的总数量和总腿数,可以巧妙地利用因式分解的方法推导出鸡和兔的数量,这种方法适用于特定情况下的问题。
以上是解决鸡兔同笼问题的五种方法,不同的方法适用于不同的情况和水平的考生,可以选择最适合自己的方法进行求解。
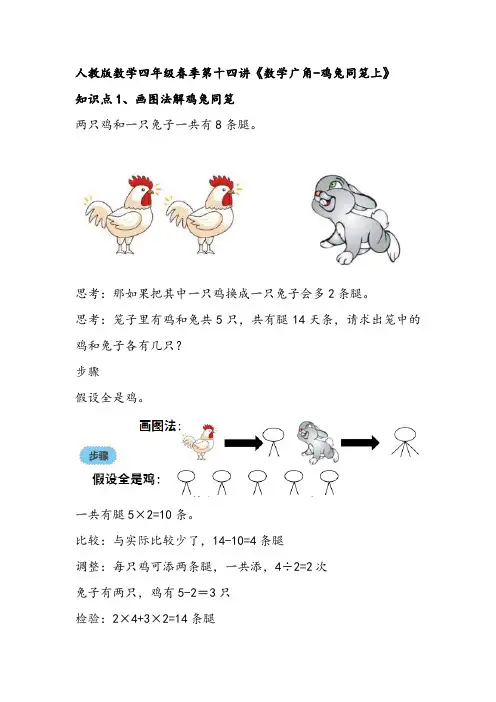
人教版数学四年级春季第十四讲《数学广角-鸡兔同笼上》知识点1、画图法解鸡兔同笼两只鸡和一只兔子一共有8条腿。
思考:那如果把其中一只鸡换成一只兔子会多2条腿。
思考:笼子里有鸡和兔共5只,共有腿14天条,请求出笼中的鸡和兔子各有几只?步骤假设全是鸡。
一共有腿5×2=10条。
比较:与实际比较少了,14-10=4条腿调整:每只鸡可添两条腿,一共添,4÷2=2次兔子有两只,鸡有5-2=3只检验:2×4+3×2=14条腿总结:把一只鸡变成一只兔子,会多两条腿。
小练习:鸡、兔共有6只,共有16条腿,鸡和兔各有几只?答案:鸡4只,兔2只2.鸡,兔共7只,共有20条腿,鸡和兔各有几只?答案:鸡4只,兔3只3.鸡兔共有10只,共有28条腿,鸡和兔各有几只?答案:鸡6只,兔4只笔记部分:画图解鸡兔同笼用简易图表示鸡和兔子,假设全是鸡多出的腿数,再进行调整。
例题1、笼子里有一些鸡和兔,数一数鸡腿和兔腿一共有50条,请问。
1.如果从笼子里拿走三只鸡,这是腿和是多少?2.如果从笼子里拿走5只鸡,再放进去5只兔,这时腿和是多少?答案:44条,60条练习1、笼子里有一些鸡和兔,数一数鸡腿和兔腿一共有80条,现在卡莉亚用魔法把笼子里的10只鸡变成了10只兔子,请问这是笼子里的腿和是多少?答案:100条4-2=2条。
10×2=20条。
80+20=100条。
例题2、笼子里有鸡和兔共8只,共有腿24条,那么下图中应该把几只鸡换成兔子?答案:8×2=16条(24-16)÷2=4次把4只鸡。
换成了兔子,这是鸡有4只,兔子也有4只,腿和正好是:4×2+4×4=24条练习2、笼子里鸡和兔有10只共有腿32条,那么下图中应该把几只鸡换成兔子?答案:10×2=20条(32-20)÷2=6(次)也就是把6只鸡换成了兔子,这是鸡有4只,兔子有6只。
鸡兔同笼的五种解法鸡兔同笼问题是一个经典的数学问题。
在这个问题里,给定了笼子里的动物的总数和腿的总数,需要求出鸡和兔的数量。
这个问题可以用多种方法解决。
在这里,我们将介绍五种解题方法。
方法一:列方程假设鸡的数量是x,兔的数量是y,根据题意,我们可以得到以下方程组:x + y = 总数2x + 4y = 腿的总数根据这个方程组,我们可以解出x和y的值,从而得到鸡和兔的数量。
方法二:画图法我们可以画出一张鸡和兔的图,用数字表示每只鸡和兔的数量和腿的数量,然后用这张图来解题。
这种方法比较直观,适合孩子或初学者使用。
方法三:数学归纳法我们可以观察鸡兔同笼问题的特征,发现每增加一只动物,会增加两条腿。
因此,我们可以将问题转化为:有n 个动物,它们共有m条腿,求鸡和兔的数量。
然后使用数学归纳法来解决这个问题。
方法四:递归算法我们可以将问题分解为小问题,再利用递归算法来解决。
具体地,假设有n只动物,其中m只是鸡,n-m只是兔。
如果这些动物共有k条腿,我们可以先考虑只有一只动物的情况,然后逐步增加动物的数量,直到n只为止。
方法五:运用数学知识我们可以运用一些数学知识,如组合数学和二元一次方程等,来解决这个问题。
具体地,我们可以用组合数学的方法计算出在给定腿的数量下,鸡的数量和兔的数量的所有可能组合,然后用二元一次方程来验证哪种组合符合题意。
以上五种方法各有特点。
对于初学者来说,列方程和画图法比较易懂;对于高中学生或数学专业学生来说,数学归纳法和递归算法可能更加适合;而对于数学专业研究生或数学爱好者来说,运用数学知识的方法可能更为有趣和有挑战性。
不管采用哪种方法,解决鸡兔同笼问题都可以让人在玩乐中学习,锻炼数学思维能力。
画图巧解鸡兔同笼问题
例1(古典题)鸡兔同笼,头共15个,足共40条,鸡兔各几只?
这类应用题有两个未知数,如果用方程或假设的方法,低年级同学理解算理都有困难,可是
用画图理解比较直观。
第一步先画15)
第二步每个头画2条腿(||),
第三步剩下的10条腿可以分给5个头,每个头画2条腿
由此可见:有4条腿的是兔子2条腿的是鸡。
答案5条兔子10只鸡。
说明:这类应用题有两个未知数,如果用方程或假设的方法,低年级同学理解算理都有困难,可是用画图理解比较直观。
同学们你学会了吗?请画一画,
刘老师带了41名同学去北海公园划船,共租了8条船.每条大船坐6人,每条小船坐4人,问大船、小船各租几条?
一个算术题竟能辗转传抄,世代相授,历经千年而不衰,其内容之有趣,解法之奇巧,不能不说是一个很重要的原因。
鸡兔同笼问题是一个有趣的算术题,对初学初学算术四则应用题的学生的逻辑推理能力和运算技巧很有帮助。
因而历代算书中多有引录。
但在题目及解题方法上却各有不同。
“鸡兔同笼”问题在民间也广为流传,甚至编入了小说。
在我国著名的古典小说《镜花缘》里就有这样一段故事:宗伯府的女主人卞宝云邀请女才子们到府中的小鳌山观灯。
当众才女在一片音乐声中来到小整山时,只见楼上楼下俱挂灯球,五彩缤纷,宛如列星,高低错藩,竟难分辨其多少。
18、100个馒头100个和尚吃,大和尚每人吃3个,小和尚3人吃一个,则大和尚有( )个,小和尚有( )个。
解鸡兔同笼的方法鸡兔同笼是一个经典的智力游戏,也是数学中的一道著名问题。
这个问题是这样的:有一只笼子里面有若干只鸡和兔,它们的脚加起来共有若干只。
问笼子里面有多少只鸡和兔?这个问题看似简单,实际上却有一定的难度。
但是,如果我们掌握了一些解题方法和技巧,就能够轻松地解决这个问题。
下面,我将介绍几种解鸡兔同笼问题的方法。
方法一:列方程法这是最常见的解决鸡兔同笼问题的方法。
我们假设笼子里有x只鸡和y只兔,它们的脚加起来共有f只。
由于一只鸡有两只脚,一只兔有四只脚,因此得到以下方程组:2x + 4y = fx + y = 总数其中,总数是鸡和兔的总数。
通过解这个方程组,我们就能够得到笼子里面鸡和兔的数量了。
方法二:画图法这个方法比较直观,适合于小学生和初中生。
我们可以画一个矩形,表示笼子里面的动物数量,然后用圆圈表示鸡的数量,用三角形表示兔的数量。
根据鸡和兔的脚数,我们就能够得到以下关系:2×圆圈 + 4×三角形 = 脚的总数通过观察这个关系,我们就能够得到笼子里面鸡和兔的数量了。
方法三:解题思路法这个方法比较巧妙,需要一定的数学思维。
我们可以通过观察题目的特点,找到一些规律和性质,从而解决问题。
首先,我们可以发现,如果笼子里面只有鸡或者只有兔,那么它们的脚数都是偶数。
因此,如果脚数是奇数,那么鸡和兔一定都有。
其次,我们可以发现,如果鸡和兔的数量相等,那么它们的脚数一定是偶数。
因此,如果脚数是奇数,那么鸡和兔的数量一定不相等。
最后,我们可以通过试错的方法,逐步逼近正确答案。
假设笼子里面有x只鸡和y只兔,我们可以从x+y=总数这个方程入手,逐步试探x和y的值,直到符合2x+4y=脚数这个方程为止。
总结以上三种方法都是解决鸡兔同笼问题的有效方法。
不同的方法适合不同的人群,我们可以根据自己的情况选择合适的方法。
当然,掌握多种方法会更有益于我们的数学学习和思维训练。
小学数学奥数:“鸡兔同笼”13种解题方法题目:现有一笼子,里面有鸡和兔子若干只,数一数,共有头14个,腿38条,球鸡和兔子各有多少只?(请用尽量多的方法解答)『方法一:人见人爱的列表法』如果二年级小朋友做这道题,可以用列表法!直观、易理解,还不容易出错~好啦,我们来看一下!鸡:0、3、5、7、9兔:14、11、9、7、5腿:56、50、46、42、38根据上面的表格数据,我们可以看出,鸡为9只,兔子为5只。
我们在列表的时候不要按顺序列,否则做题的速度会很慢,比如说列完鸡为0只,兔子为14只,发现腿的数量56条,和实际38条相差较大,那么下一个你可以跳过鸡的数量为2只这种情况,直接列鸡的数量为3只,这样做速度会快一些哦!『方法二:最快乐的画图法』画图可以让数学变得形象化,而且经常画图还有助于创造力的培养!假设14只全部是鸡,先把鸡给画好。
14×2=28条,差38-28=10条,而每一只鸡补2条腿就变成兔子,需要把5只鸡每只补2条腿,所以有5只兔子,14-5=9只鸡。
『方法三:最酷的金鸡独立法』分析:让每只鸡都一只脚站立着,每只兔都用两只后脚站立着,那么地上的总脚数只是原来的一半,即19只脚。
鸡的脚数与头数相同,而兔的脚数是兔的头数的2倍,因此从19里减去头数14,剩下来的就是兔的头数19-14=5只,鸡有14-5=9只。
『方法四:最逗的吹哨法』分析:假设鸡和兔接受过特种部队训练,吹一声哨,它们抬起一只脚,还有38-14=24只腿在站着,再吹一声哨,它们又抬起一只脚,这时鸡都一屁股坐地上了,兔子还有两只脚立着。
这时还有24-14=10只腿在站着,而这10只腿全部是兔子的,所以兔子有10÷2=5只,鸡有14-5=9只。
(惊现跑男中包贝尔的抬脚法有木有!)『方法五:最常用的假设法』分析:假设全部是鸡,则有14×2=28条腿,比实际少38-28=10只,一只鸡变成一只兔子腿增加2条,10÷2=5只,所以需要5只鸡变成兔子,即兔子为5只,鸡为14-5=9只。
画图法巧解鸡兔同笼问题
【专题解析】小朋友们在解题时,会遇到一些较难的题目,这时可用画图的方法把题目中的条件画出来再思考,往往会容易得多,你不妨试一试。
在有些数学题中,数量之间的关系不容易看出来。
而画图却能比较清楚地显示出来,小朋友们一定要学会这种帮助解题的好方法——画图示意法,这样能提高大家的动手能力和分析能力。
二、综合讲解:
【例题1】鸡、兔关在同一笼子里,共有10个头,28条腿,笼里有几只鸡?几只兔?
【思路导航】我们用“○”表示头,画10个“○”;用“|”表示腿,鸡有两条腿,兔子有四条腿,鸡的腿数比兔子的少。
先全画成鸡:
从图中可以看出,10只鸡只有20条腿,而条件说“共有28条腿”,显然少了28﹣20﹦8(条)腿,这样,在鸡图上一只加两条腿,把它变成兔子,8条腿添改4次即可。
答:笼里有4只兔,有6只鸡。
举一反三
1、鸡兔同笼,共有10个头,30条腿,有几只鸡?几只兔?
2、鸡兔同笼,共有14个头,38条腿,有几只鸡?几只兔?
【例题3】一只蛐蛐6条腿,一只蜘蛛8条腿。
有蛐蛐和蜘蛛共10只,共68
蛐蛐和蜘蛛各有多少只?
【思路导航】可以用图来帮助分析。
用“○”表示头,但由于蛐蛐和蜘蛛的腿比较多,画“|”不方便,我们就用数字表示,写在头的下面。
先把它们看成是腿较少的动物——蛐蛐。
6 6 6 6 6 6 6 6 6 6
从图中可以看出,10只蛐蛐共有60条腿,比已知条件少了68-60=8(条)腿。
而一只蜘蛛比一只蛐蛐多2条腿,8条腿只需改4只蛐蛐就可以了。
6 6 6 6 6 6 6 6 6 6
2 2 2 2
答:有6只蛐蛐,4只蜘蛛。
举一反三
1、蛐蛐和蜘蛛共10只,74条腿,蛐蛐和蜘蛛各有几只?
2、蛐蛐和蜘蛛共12只,82条腿,蛐蛐和蜘蛛各有几只?
【例题3】一辆自行车有2个轮子,一辆三轮车有3个轮子。
车棚里放着自行车和三轮车共8辆,共20个轮子。
自行车和三轮车各有多少辆?
【思路导航】根据以上方法,这题同样可画图示意。
先画成自行车,如图
从图中可以看出,8辆自行车有16个轮子,20-16=4(个)轮子,这样,应该在4辆自行车上各添上1个轮子即可。
1.一辆自行车有2个轮子,一辆三轮车有3个轮子。
车棚里放着自行车和三轮
车共10辆,共26个轮子。
自行车和三轮车各有多少辆?
2.停车场停着大汽车和小汽车共14辆,大汽车有6个轮子,小汽车有4个轮
子,现在14辆车子一共有72个轮子,问有辆大汽车?几辆小汽车?
最新文件---------------- 仅供参考--------------------已改成word文本--------------------- 方便更改。