实验三 无失真信源编码
- 格式:doc
- 大小:48.50 KB
- 文档页数:4






信息论与编码实验报告一、实验目的信息论与编码是一门涉及信息的度量、传输和处理的学科,通过实验,旨在深入理解信息论的基本概念和编码原理,掌握常见的编码方法及其性能评估,提高对信息处理和通信系统的分析与设计能力。
二、实验原理(一)信息论基础信息熵是信息论中用于度量信息量的重要概念。
对于一个离散随机变量 X,其概率分布为 P(X) ={p(x1), p(x2),, p(xn)},则信息熵H(X) 的定义为:H(X) =∑p(xi)log2(p(xi))。
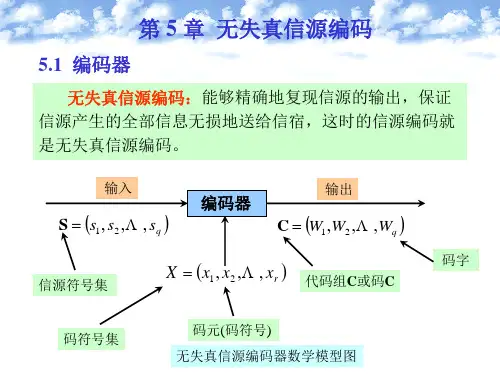
(二)编码原理1、无失真信源编码:通过去除信源中的冗余信息,实现用尽可能少的比特数来表示信源符号,常见的方法有香农编码、哈夫曼编码等。
2、有噪信道编码:为了提高信息在有噪声信道中传输的可靠性,通过添加冗余信息进行纠错编码,如线性分组码、卷积码等。
三、实验内容及步骤(一)信息熵的计算1、生成一个离散信源,例如信源符号集为{A, B, C, D},对应的概率分布为{02, 03, 01, 04}。
2、根据信息熵的定义,使用编程语言计算该信源的信息熵。
(二)香农编码1、按照香农编码的步骤,首先计算信源符号的概率,并根据概率计算每个符号的编码长度。
2、确定编码值,生成香农编码表。
(三)哈夫曼编码1、构建哈夫曼树,根据信源符号的概率确定树的结构。
2、为每个信源符号分配编码,生成哈夫曼编码表。
(四)线性分组码1、选择一种线性分组码,如(7, 4)汉明码。
2、生成编码矩阵,对输入信息进行编码。
3、在接收端进行纠错译码。
四、实验结果与分析(一)信息熵计算结果对于上述生成的离散信源,计算得到的信息熵约为 184 比特/符号。
这表明该信源存在一定的不确定性,需要一定的信息量来准确描述。
(二)香农编码结果香农编码表如下:|信源符号|概率|编码长度|编码值|||||||A|02|232|00||B|03|174|10||C|01|332|110||D|04|132|111|香农编码的平均码长较长,编码效率相对较低。


实验三 无失真信源编码
一、[实验目的]
1、理解香农第一定理指出平均码长与信源之间的关系;
2、加深理解香农编码具有的重要的理论意义。
3、掌握霍夫曼编码的原理;
4、掌握霍夫曼编码的方法和步骤;
二、[实验环境]
windows XP,MATLAB 7
三、[实验原理]
香农第一定理:
设离散无记忆信源为
12 (1)
(2)....()S s s sq P p s p s p sq ⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦
熵为H(S),其N 次扩展信源为 12 (1)
(2)....()N q S p p p q P αααααα⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦ 熵为H(S N )。
码符号集X=(x1,x2,…,xr )。
先对信源N S 进行编码,总可以找
到一种编码方法,构成惟一可以码,使S 中每个信源符号所需的平均码长满足: 1N L H S H S N N +>≥()()logr logr
当N →∞时 lim
()N r N L H S N
→∞= N L 是平均码长 1
()N q N i i i L p αλ==∑ i λ是i α对应的码字长度
四、[实验内容]
1、在给定离散无记忆信源
S
P s1 s2 s3 s4 1/8 5/16 7/16 1/8
=
条件下,实现二进制霍夫曼编码,求最后得到的码字并算出编码效率。
五、[实验过程]
每个实验项目包括:1)设计思路2)实验中出现的问题及解决方法;
某一离散信源概率分布:p=[1/2,1/4,1/8,1/16,1/16] 求信源的熵,并对该信源进行二元哈夫曼编码,得到码字和平均码长以及编码效率。
Matlab程序:
function [h,l]=huffman(p)
p=[1/2 1/4 1/8 1/16 1/16];
if length(find(p<0))~=0,
error('Not a prob.vector,there is negative component')
end
if abs (sum(p)-1)>10e-10
error('Input is not a prob.vector,the sun of the components is not equal to 1')
end
n=length(p);
q=p;
m=zeros(n-1,n);
for i=1:n-1
[q,l]=sort(q);
m(i,:)=[l(1:n-i+1),zeros(1,i-1)];
q=[q(1)+q(2),q(3:n),1];
end
for i=1:n-1
c(i,:)=blanks(n*n);
end
c(n-1,n)='0';
c(n-1,2*n)='1';
for i=2:n-1
c(n-i,1:n-1)=c(n-i+1,n*(find(m(n-i+1,:)==1))...
-(n-2):n*(find(m(n-i+1,:)==1)));
c(n-i,n)='0';
c(n-i,n+1:2*n-1)=c(n-i,1:n-1);
c(n-i,2*n)='1';
for j=1:i-1
c(n-i,(j+1)*n+1:(j+2)*n)=c(n-i+1,... n*(find(m(n-i+1,:)==j+1)-1)+1:n*find(m(n-i+1,:)==j+1));
end;
end
for i=1:n
h(i,1:n)=c(1,n*(find(m(1,:)==i)-1)+1:find(m(1,:)==i)*n);
l1(i)=length(find(abs(h(i,:))~=32));
end
l=sum(p.*l1)
运行结果为:l =
1.8750
ans =
1
01
001
0000
0001
六、[实验总结]。