2018年湖北省武汉市高考数学模拟试卷(理科)(4月份)

武汉市2018届高中毕业生四月调研测试理科数学参考答案一、选择题1-5: BDABC 6-10: BDABD 11、12：CC二、填空题13. 25 14. 13- 15. (0,)2π三、解答题17.（1）由已知212132a a a a +=+-，而12a =，∴2222232(2)a a -=+-，即222230a a --=.而20a >，则23a =.又由323252a a a a +=+-，23a =，∴233952(3)a a -=+-，即233280a a --=.而30a >，则34a =.∴23a =，34a =.（2）由已知条件可知：22112()21n n n n a a a a n ---=-+-，∴22221(1)(1)(1)n n a a n n ----=--，则22221(1)(1)(1)n n a n a n ---=---223(1)2a =⋅⋅⋅=--222(1)1a =--0=，而22(1)n n b a n =--，∴0n b =，数列{}n b 为等差数列.∴22(1)n a n -=.而0n a >，故1n a n =+.18.解：（1）过M 作1MT AA ⊥于点T ，连1B T ，则11AT =.易证：111AA E A BT ∆≅∆，于是111AA E A BT ∠=∠.由111190A BT ATB ∠+∠=，知11190AA E ATB ∠+∠=，∴11A E BT ⊥.显然MT ⊥面11AA B B ，而1A E ⊂面11AA B B ，∴1M T A E ⊥，又1B T M T T =，∴1A E ⊥面MTB ，∴11A E MB ⊥.连11B D ，则1111B D AC ⊥. 又111D M AC ⊥，1111BD D M D =，∴11AC ⊥面11MD B ，∴111ACMB ⊥.由11A E MB ⊥，111AC MB ⊥，1111A E AC A =，∴1B M ⊥面11A EC .（2）在11D C 上取一点N ，使11ND =，连接EF . 易知1//A E FN .∴1111A EFC N EFC E NFC V V V ---==11113(23)33332NFC S ∆=⋅⨯=⨯⨯⨯=. 对于11A EC ∆，11AC =，1A E =1EC =11cos EAC∠==.∴11A EC ∆的面积11111sin 2S A C A E EA C =⋅∠12=⨯=.由等体积法可知F 到平面11A EC 之距离h 满足111113A EC A EFC S h V ∆-⋅=，则133h =，∴h =，又1FC =1FC 与平面1AEC 所成角为θ，∴sin θ===.19.解：（1）设直线AB 的斜率为tan k α=，方程为1(1)y k x -=-，代入2224x y +=中，∴222[(1)]40x kx k +---=.∴222(12)4(1)2(1)40k x k k x k +--+--=.判别式222[4(1)]4(21)[2(1)4]k k k k ∆=--+--28(321)k k =++.设11(,)A x y ，22(,)B x y ，则12221224(1)212(1)421k k x x k k x x k -⎧+=⎪⎪+⎨--⎪=⎪+⎩.∵AB 中点为(1,1)，∴12212(1)()1221k k x x k -+==+，则12k =.∴直线的AB 方程为11(1)2y x -=-，即210x y -+=. （2）由（1）知12AB x =-==.设直线的CD 方程为1(1)(0)y k x k -=--≠.同理可得CD =∴0)AB k CD λ==≠. ∴2241312kk kλ=++-41132k k=++-.令13t k k =+，则4()12g t t =+-，(,[23,)t ∈-∞-+∞.()g t 在(,-∞-，)+∞分别单调递减，∴2()1gt ≤<或1()2g t <≤故221λ<或212λ<≤.即6(1,λ+∈. 20.解：（1）由题意知：∴450.1550.15650.2750.3x =⨯+⨯+⨯+⨯850.15950.170.5+⨯+⨯=，∴4000名考生的竞赛平均成绩x 为70.5分.（2）依题意z 服从正态分布2(,)N μσ，其中70.5x μ==，2204.75D σξ==，14.31σ=，∴z 服从正态分布22(,)(70.5,14.31)N N μσ=，而()(56.1984.81)0.6826P z P z μσμσ-<<+=<<=，∴10.6826(84.81)0.15872P z -≥==.∴竞赛成绩超过84.81分的人数估计为0.158********.8⨯=人634≈人.（3）全市竞赛考生成绩不超过84.81分的概率10.15870.8413-=.而(4,0.8413)B ξ，∴444(3)1(4)10.8413P P C ξξ≤=-==-⋅10.5010.499=-=.21.解：（1）定义域为：(0,)+∞，当a e =时，(1)()'()x x xe e f x x+-=.∴()f x 在(0,1)时为减函数；在(1,)+∞时为增函数.（2）记ln t x x =+，则ln t x x =+在(0,)+∞上单增，且t R ∈.∴()(ln )x f x xe a x x =-+()t e at g t =-=.∴()f x 在0x >上有两个零点等价于()t g t e at =-在t R ∈上有两个零点.①在0a =时，()t g t e =在R 上单增，且()0g t >，故()g t 无零点；②在0a <时，'()tg t e a =-在R 上单增，又(0)10g =>，11()10a g e a=-<，故()g t 在R 上只有一个零点；③在0a >时，由'()0t g t e a =-=可知()g t 在ln t a =时有唯一的一个极小值(ln )(1ln )g a a a =-.若0a e <<，(1ln )0g a a =->最小，()g t 无零点；若a e =，0g =最小，()g t 只有一个零点；若a e >时，(1ln )0g a a =-<最小，而(0)10g =>，由于ln ()xf x x=在x e >时为减函数，可知：a e >时，2a e e a a >>.从而2()0a g a e a =->，∴()g x 在(0,ln )a 和(ln ,)a +∞上各有一个零点.综上讨论可知：a e >时()f x 有两个零点，即所求a 的取值范围是(,)e +∞.22.解：（1）由l ：cos sin 100ρθρϕ+-=，及cos x ρθ=，sin y ρθ=.∴l 的方程为2100x y +-=.由3cos x θ=，2sin y θ=，消去θ得22194x y +=. （2）在C 上取点(3cos ,2sin )M ϕϕ，则d=05cos()10ϕϕ=--.其中003cos 54sin 5ϕϕ⎧=⎪⎪⎨⎪=⎪⎩，当0ϕϕ=时，d此时093sin 3cos 5ϕϕ==，0082sin 2cos 5ϕϕ==，98(,)55M .。

2018年湖北省高考数学模拟试卷（理科）（4月份）一、选择题：本大题共12个小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1. 已知集合A={x|log2x≤1}，集合B={y|y=2x+1}，则A∩B=()A.[1, 2]B.(1, 2]C.[12,2] D.(12,2]【答案】B【考点】交集及其运算【解析】先求出集合A，B，然后进行交集的运算即可．【解答】解：A={x|0<x≤2}，B={y|y>1}；∴A∩B=(1, 2]．故选B.2. 欧拉公式e ix=cosx+isinx（i为虚数单位）是由著名数学家欧拉发明的，她将指数函数定义域扩大到复数，建立了三角函数和指数函数的关系，它在复变函数论里占有非常重要的地位，被誉为“数学中的天桥”．根据欧拉公式，若将eπ2i表示的复数记为z，则z⋅(1+2i)的值为()A.−2+iB.−2−iC.2+iD.2−i【答案】A【考点】欧拉公式复数代数形式的乘除运算【解析】由已知求得z，再由复数代数形式的乘除运算化简得答案．【解答】解：∵z=e π2i=cosπ2+isinπ2=i，∴z⋅(1+2i)=i(1+2i)=−2+i．故选A.3. 记不等式组{2x+y−2≥0x≤1y≤2的解集为D，若∀x，y∈D，y≤a(x+1)，则实数a的最小值是（）A.0B.1C.2D.4【答案】C【考点】简单线性规划【解析】由约束条件作出可行域D ，结合直线y =a(x +1)过定点(−1, 0)，求出过点(−1, 0)，(0, 2)的直线的斜率得答案． 【解答】解：由约束条件{2x +y −2≥0x ≤1y ≤2 作出可行域如图，直线y =a(x +1)过定点(−1, 0)，而经过(−1, 0)，(0, 2)两点的直线的斜率为2，∴ 要使∀x ，y ∈D ，y ≤a(x +1)成立，则a ≥2． ∴ 实数a 的最小值是2． 故选C ．4. 已知α∈(0, π2)，cos(π6+α)=13，则sinα的值等于（ ） A.2√2−√36B.2√2+√36C.2√6−16D.−2√6−16【答案】 C【考点】三角函数的恒等变换及化简求值 【解析】由已知求得sin(π6+α)，结合sinα=sin[(π6+α)−π6]，展开两角差的正弦求解． 【解答】∵ α∈(0, π2)，∴ π6+α∈(π6, 2π3)，由cos(π6+α)=13，得sin(π6+α)=√1−cos 2(π6+α)=2√23， 则sinα=sin[(π6+α)−π6]=sin(π6+α)cos π6−cos(π6+α)sin π6 =2√23×√32−13×12=2√6−16．5. 函数f(x)=xe x 2x+lnx的图象大致为（ ）A.B.C.D.【答案】 C【考点】函数的图象变化 【解析】根据题意，对于函数f(x)，分析有2x +lnx ≠0，即lnx ≠−2x ，据此分析函数的定义域，可以排除A 、D ，进而利用特殊值分析f(x)的值，排除B ，即可得答案． 【解答】根据题意，函数f(x)=xe x2x+lnx，有2x +lnx ≠0，即lnx ≠−2x ，设当0<m <1时，lnm =−2m ，则函数的定义域为(0, m)∪(m, +∞)，排除A ，D 当0<x <m 时，2x +lnx <0，xe x >0，则f(x)<0，排除B ；6. 已知双曲线C:x 2a 2−y 2=1(a >0)的一条渐近线方程为x +2y =0，F 1，F 2分别是双曲线C 的左、右焦点，点P 在双曲线C 上，且|PF 1|=5，则|PF 2|=（ ） A.1 B.3 C.1或9 D.3或7 【答案】 C【考点】 双曲线的特性 【解析】 此题暂无解析 【解答】解：由双曲线的方程和一条渐近线方程可得1a=12⇒a =2，因为c 2=a 2+b 2=4+1=5， 所以c =√5，所以c −a =√5−2<1．由双曲线的定义可得||PF 2|−5|=4， 所以|PF 2|=1或9． 故选C ．7. 执行如图所示的程序框图，若输出k 的值为6，且判断框内填入的条件是s >t ，则t 的取值范围是（ ）A.[35,45) B.(35,45brackC.[710,45) D.(710,45brack【答案】C【考点】程序框图【解析】模拟程序的运行，可得判断框内s的范围，结合条件s>t，可得t的范围．【解答】模拟程序的运行，可得当s=910×89=45时，满足判断框内的条件，可得：s=910×89×78=710，k=6时，此时，不满足判断框内的条件，退出循环，输出k的值为6．可得判断框内的s的范围为：710<s≤45，由于判断框内填入的条件是s>t，则t的取值范围是[710, 45 )．8. 党的十九打报告指出，建设教育强国是中华民族伟大复兴的基础工程，必须把教育事业放在优先位置，深化教育资源的均衡发展．现有4名男生和2名女生主动申请毕业后到两所偏远山区小学任教．将这6名毕业生全部进行安排，每所学校至少安排2名毕业生，则每所学校男女毕业至少安排一名的概率为（）A.4 25B.25C.1425D.45【答案】B【考点】古典概型及其概率计算公式【解析】基本事件总数n=(C62C44+C63C33A22)×A22=50，每所学校男女毕业至少安排一名包含的基本事件m=C21C11A22×(C41C33+C42C22A22)×A22=20，由此能求出每所学校男女毕业至少安排一名的概率．【解答】现有4名男生和2名女生主动申请毕业后到两所偏远山区小学任教．将这6名毕业生全部进行安排，每所学校至少安排2名毕业生，基本事件总数n=(C62C44+C63C33A22)×A22=50，每所学校男女毕业至少安排一名包含的基本事件m=C21C11A22×(C41C33+C42C22A22)×A22=20，∴每所学校男女毕业至少安排一名的概率为p=mn =2050=25．9. 已知a=2.12.2，b=2.22.1，c=log2.22.1，则（）A.c<b<aB.c<a<bC.a<b<cD.a<c<b 【答案】B【考点】对数值大小的比较【解析】设f(x)=lnxx (x>0)．f′(x)=1−lnxx2，利用导数研究其单调性可得a，b的大小关系，又c=log2.22.1<1，即可得出结论．【解答】设f(x)=lnxx(x>0)．f′(x)=1−lnxx2，可得函数f(x)在(0, e)内单调递增，∴f(2.1)<f(2.2)，即ln2.12.1<ln2.22.2，化为：2.12.2<2.22.1．∴1<a<b．c=log2.22.1<1，∴c<a<b．10. 锐角△ABC中，角A所对的边为a，△ABC的面积S=a24，给出以下结论：①sinA=2sinB⋅sinC；②tanB+tanC=2tanB⋅tanC；③tanA+tanB+tanC=tanA⋅tanB⋅tanC；④tanA⋅tanB⋅tanC有最小值8．其中正确结论的个数为（）A.1B.2C.3D.4【答案】D【考点】两角和与差的三角函数【解析】由三角形面积公式可得a=2bsinC，结合正弦定理说明①正确；把①中的A用B、C表示，化弦为切说明②正确；由tan(A+B)=−tanC，展开两角和的正切说明③正确；由tanA=−tan(B+C)=tanB+tanCtanBtanC−1，结合②转化为关于tanBtanC的代数式，令m= tanBtanC−1换元求最值．【解答】由S=a24=12absinC，得a=2bsinC，又asinA =bsinB，得sinA=2sinB⋅sinC，故①正确；由sinA=2sinB⋅sinC，得sin(B+C)=sinBcosC+cosBsinC=2sinB⋅sinC，两边同时除以cosBcosC，可得tanB+tanC=2tanB⋅tanC，故②正确；由tan(A+B)=tanA+tanB1−tanAtanB，且tan(A+B)=tan(π−C)=−tanC，∴tanA+tanB1−tanAtanB=−tanC，整理移项即得tanA+tanB+tanC=tanA⋅tanB⋅tanC，故③正确；由tanB+tanC=2tanBtanC，tanA=−tan(B+C)=tanB+tanCtanBtanC−1，且tanA，tanB，tanC都是正数．得tanAtanBtanC=tanB+tanCtanBtanC−1⋅tanBtanC=2tanBtanCtanBtanC−1⋅tanBtanC=2(tanBtanC)2tanBtanC−1．设m=tanBtanC−1，则m>0，tanAtanBtanC=2(m+1)2m =2(m+1m)+4≥4+2⋅2√m∗1m=8．当且仅当m=tanBtanC−1=1即tanBtanC=2时取“=”，此时tanBtanC=2，tanB+ tanC=4，tanA=4，∴tanAtanBtanC的最小值是8，故④正确．∴正确结论的个数有4个．11. 已知正三棱锥S−ABC的顶点均在球O的球面上，过侧棱SA及球心O的平面截三棱锥及球面所得截面如图所示，已知三棱锥的体积为2√3，则球O的表面积为（）A.16πB.18πC.24πD.32π【答案】A【考点】球的体积和表面积【解析】此题暂无解析【解答】解：如图，设正三棱锥的底面边长为a，外接球的半径为R.因为正三棱锥的底面为正三角形，边长为a ，所以AD =√32a ，则AO =23AD =√33a ，所以√33a =R ，即a =√3R ．又因为三棱锥的体积为2√3，所以13×√34a 2R =13×√34×(√3R)2×R =2√3，解得R =2，所以球的表面积为S =4πR 2=16π． 故选A .12. 设D =√(x −a)2+(e x −2√a)2+a +2．其中e ≈2.71828，则D 的最小值为（ ）A.√2B.√3C.√2+1D.√3+1【答案】 C【考点】函数的最值及其几何意义 【解析】 此题暂无解析 【解答】解：由题意可得a ≥0．因为√(x −a)2+(e x −2√a)2表示点C (x,e x )与点A(a,2√a)的距离，而点A(a,2√a)在抛物线y 2=4x 上，抛物线的焦点为F(1,0)，准线为x =−1，点C 在指数函数y =e 2的图象上，则D 表示点A 与C 的距离加上点A 与准线的距离再加上1．由抛物线的定义可得D 表示A 与C 的距离加上点A 与F 的距离再加上1．作出函数图象，如图所示．由图象可知，当F,A,C 三点共线，且CF 与曲线y =e x 在点C 的切线垂直时，D 取得最小值，设C (m,e m )，由e m −0m−1⋅e m =−1，可得m +e 2m =1．设g(m)=m +e 2m ，则g(m)单调递增，且g(0)=1，∴ C(0,1)，即有|FC|=√1+1=√2，则D 的最小值为√2+1. 故选C .二、填空题（每题5分，满分20分，将答案填在答题纸上）在(2x −√x 3)8的展开式中，常数项等于________（用数字作答）【答案】 112【考点】二项式定理的应用 【解析】根据题意，可得其二项展开式的通项为T r+1，进而分析可得，8−4r 3=0时，有r =6，将r =6代入可得答案． 【解答】根据题意，可得其二项展开式的通项为T r+1=C 8r ⋅(2x)8−r ⋅x3)r =C 8r ⋅(−1)r ⋅(2)8−r⋅x8−4r 3，分析可得，8−4r 3=0时，有r =6，此时，T 7=112，已知向量a →与b →的夹角为30∘，|a →−b →|=2，则|a →+b →|的最大值为________．【答案】 2+3√3 【考点】平面向量数量积的性质及其运算律 【解析】由向量a →与b →的夹角为30∘，|a →−b →|=2，得a →2+b →2−√3|a →|∗|b →|=4，由a →2+b →2≥2|a →|⋅|b →|，得到a →2+b →2−√3|a →|∗|b →|≥(2−√3)|a →|⋅|b →|=4，当且仅当|a →|=|b →|=(2−√3)12=2√2+√3时取等号，由此能求出|a →+b →|的最大值．【解答】∵ 向量a →与b →的夹角为30∘，|a →−b →|=2，∴ |a →−b →|=√(a →−b →)2=√a →2−2a →∗b →+b →2=√a →2+b →2−√3|a →|∗|b →|=2， ∴ a →2+b →2−√3|a →|∗|b →|=4， ∵ a →2+b →2≥2|a →|⋅|b →|，∴ a →2+b →2−√3|a →|∗|b →|≥(2−√3)|a →|⋅|b →|=4，当且仅当|a →|=|b →|=(2−√3)12=2√2+√3时取等号，∴ |a →+b →|=√(a →+b →)2=√a →2+b →2+√3|a →|∗|b →|≤√a →2+b →2+√3×a →2+b →2 =√4+√34√a →2+b →2，当且仅当|a →|=|b →|=(2−√3)12=2√2+√3时取等号，∴|a→+b→|的最大值为：√4+√34×√2(8+4√3)=2+3√3．已知函数f(x)=cos(ωx−π3)−12(ω>0)在区间[0, π]上恰有三个零点，则ω的取值范围是________．【答案】[2,8 3 )【考点】函数的零点【解析】函数f(x)=cos(ωx−π3)−12(ω>0)在区间[0, π]上恰有三个零点，转化为cos(ωx−π3)与函数y=12在区间[0, π]上恰有三个交点问题，利用余弦函数的图象即可求解．【解答】解：由题意：转化为y=cos(ωx−π3)与函数y=12在区间[0, π]上恰有三个交点问题，∵x∈[0, π]上，∴−π3≤ωx−π3≤ωπ−π3．当x=0，可得y=12．根据余弦函数的图象：可得5π3≤ωπ−π3<7π3，解得：2≤ω<83，∴ω的取值范围是[2, 83).故答案为：[2,83).点P(x, y)是直线2x+y+4=0上的动点，PA，PB是圆C:x2+(y−1)2=1的两条切线，A，B是切点，则三角形PAB面积的最小值为________．【答案】85【考点】直线与圆的位置关系【解析】当PC与直线2x+y+4=0垂直时，PA最小，设PC=d，则d≥√5，求出PA=PB的值，再求出AB，进一步得到AD的值，因而可求得三角形PAB面积的最小值．【解答】圆C的半径为r=1，圆心C(0, 1)到直线2x+y+4=0的距离为√22+1=√5，设PC =d ，则d ≥√5，PA =PB =√d 2−1， AB =2⋅PA∗AC PC=2⋅√d 2−1d=2√1−1d 2，∴ 当d 取得最小值√5时，PA 取得最小值为√5−1=2， AB 取得最小值为4√55，AD 取得最小值为2√55， CD =√AC 2−AD 2=√1−(2√55)2=√55， PD =PC −CD =√5−√55=4√55， ∴ 三角形PAB 面积的最小值为12AB ∗PD =12×4√55×4√55=85．三、解答题（本大题共5小题，共70分.解答应写出文字说明、证明过程或演算步骤.）已知数列{a n }，{b n }，其中a 1=3，b 1=−1，且满足a n =12(3a n−1−b n−1)，b n =−12(a n−1−3b n−1),n ∈N ∗，n ≥2． （1）求证：数列{a n −b n }为等比数列；（2）求数列{2na n ∗a n+1}的前n 项和S n ．【答案】证明：n ≥2时，a n −b n =12(3a n−1−b n−1)−(−12)(a n−1−3b n−1)=2(a n−1−b n−1)． 又a 1−b 1=3−(−1)=4，∴ {a n −b n }是首项为4，公比为2的等比数列． 由（1）知，a n −b n =2n+1①又a n +b n =12(3a n−1−b n−1)+(−12)(a n−1−3b n−1)=a n−1+b n−1． 又a 1+b 1=3+(−1)=2，所以{a n +b n }为常数数列，a n +b n =2 ② 联立①②得：a n =2n +1，∴ 2nan a n+1=2n(2n +1)(2n+1+1)=12n +1−12n+1+1，∴ T n =(121+1−122+1)+(122+1−123+1)+⋯(12n +1−12n+1+1) =12+1−12+1=13−12+1．【考点】 数列递推式 【解析】（1）a n −b n =12(3a n−1−b n−1)−(−12)(a n−1−3b n−1)=2(a n−1−b n−1)．即可证明． （2）由（1）知，a n −b n =2n+1，又a n +b n =12(3a n−1−b n−1)+(−12)(a n−1−3b n−1)=a n−1+b n−1．可得{a n +b n }为常数数列，a n +b n =2．联立得：a n =2n+1，可得：2nan a n+1=2n(2n +1)(2n+1+1)=12n +1−12n+1+1，利用裂项求和方法即可得出． 【解答】证明：n ≥2时，a n −b n =12(3a n−1−b n−1)−(−12)(a n−1−3b n−1)=2(a n−1−b n−1)． 又a 1−b 1=3−(−1)=4，∴ {a n −b n }是首项为4，公比为2的等比数列． 由（1）知，a n −b n =2n+1①又a n +b n =12(3a n−1−b n−1)+(−12)(a n−1−3b n−1)=a n−1+b n−1． 又a 1+b 1=3+(−1)=2，所以{a n +b n }为常数数列，a n +b n =2 ② 联立①②得：a n =2n +1，∴ 2nan a n+1=2n(2n +1)(2n+1+1)=12n +1−12n+1+1，∴ T n =(121+1−122+1)+(122+1−123+1)+⋯(12n +1−12n+1+1) =121+1−12n+1+1=13−12n+1+1．如图，在平行四边形ABCD 中，AB =1，AD =2，∠BAD =120∘，四边形EBDF 是矩形，BE =a ，平面EBDF ⊥平面ABCD ．(1)若a =1，求证：AE ⊥CF ；（2）二面角A −EF −C 的正弦值为√215，求a 的值．【答案】(1)证明：连结AC ，在△ABC 中， 由AB =1,BC =2,∠ABC =60∘， 结合余弦定理易得AC =√3， 又AB 2+AC 2=BC 2,∴ AB ⊥AC . 同理，BD =√7，由四边形EBDF 是矩形，得BE ⊥BD ，又平面EBDF ⊥平面ABCD ，平面EBDF ∩平面ABCD =BD ， 所以BE ⊥平面ABCD ，所以BE ⊥BC ， 同理FD ⊥DC ，由勾股定理易求得EC =√5,CF =√2. 又∵ EF =BD =√7，∴ EF 2=CE 2+CF 2，故CE ⊥CF . ∵ AC ⊥CD,AC ⊥DF,CD ∩DF =D ，所以AC ⊥面CDF ，所以AC ⊥CF ，又AC ∩CE =C ，所以CF ⊥面ACE ，所以CF ⊥AE .(2)解：以A 点为原点，AB,AC 所在的直线分别为x 轴，y 轴， 过点A 与平面ABC 垂直的直线为z 轴建立空间直角坐标系， 则A(0,0,0),B(1,0,0),C(0,√3,0),F(−1,√3,a),E(1,0,a)， 则AE →=(1,0,a),EF →=(−2,√3,0),CF →=(−1,0,a). 设平面AEF 的法向量为n 1=(x,y,z)， 则{n 1⋅AE →=0,n 1⋅EF →=0,即{x +az =0,−2x +√3y =0. 取x =3，则y =2√3,z =−3a ，即n 1→=(3,2√3,−3a )， 同理可求得平面CEF 的一个法向量为n 2→=(3,2√3,3a )， 设二面角的平面角为θ，则sinθ=√215，则|cos⟨n 1→,n 2→⟩|=25，即|9+12−9a 29+12+9a2|=25，解得a =±1或±37，又a >0，所以a =1或37.【考点】二面角的平面角及求法 【解析】 此题暂无解析 【解答】(1)证明：连结AC ，在△ABC 中， 由AB =1,BC =2,∠ABC =60∘， 结合余弦定理易得AC =√3， 又AB 2+AC 2=BC 2,∴ AB ⊥AC . 同理，BD =√7，由四边形EBDF 是矩形，得BE ⊥BD ，又平面EBDF ⊥平面ABCD ，平面EBDF ∩平面ABCD =BD ， 所以BE ⊥平面ABCD ，所以BE ⊥BC ， 同理FD ⊥DC ，由勾股定理易求得EC =√5,CF =√2. 又∵ EF =BD =√7，∴ EF 2=CE 2+CF 2，故CE ⊥CF . ∵ AC ⊥CD,AC ⊥DF,CD ∩DF =D ， 所以AC ⊥面CDF ，所以AC ⊥CF ，又AC ∩CE =C ，所以CF ⊥面ACE ，所以CF ⊥AE .(2)解：以A 点为原点，AB,AC 所在的直线分别为x 轴，y 轴， 过点A 与平面ABC 垂直的直线为z 轴建立空间直角坐标系， 则A(0,0,0),B(1,0,0),C(0,√3,0),F(−1,√3,a),E(1,0,a)， 则AE →=(1,0,a),EF →=(−2,√3,0),CF →=(−1,0,a). 设平面AEF 的法向量为n 1=(x,y,z)，则{n 1⋅AE →=0,n 1⋅EF →=0,即{x +az =0,−2x +√3y =0. 取x =3，则y =2√3,z =−3a ，即n 1→=(3,2√3,−3a )， 同理可求得平面CEF 的一个法向量为n 2→=(3,2√3,3a )， 设二面角的平面角为θ，则sinθ=√215，则|cos⟨n 1→,n 2→⟩|=25，即|9+12−9a 29+12+9a2|=25，解得a =±1或±37，又a >0，所以a =1或37.随着网络的飞速发展，人们的生活发生了很大变化，其中无现金支付是一个显著特征，某评估机构对无现金支付的人群进行网络问卷调查，并从参与调查的数万名受访者中随机选取了300人，把这300人分为三类，即使用支付宝用户、使用微信用户、使用银行卡用户，各类用户的人数如图所示，同时把这300人按年龄分为青年人组与中年人组，制成如图所示的列联表：（1）完成列联表，并判断是否有99%的把握认为使用支付宝用户与年龄有关系？（2）把频率作为概率，从所有无现金支付用户中（人数很多）随机抽取3人，用X 表示所选3人中使用支付宝用户的人数，求X 的分布列与数学期望． 附：K 2=n(ad−bc)2(a+b)(c+d)(a+c)(b+d)，其中n =a +b +c +d ． 【答案】列联表补充如下K2=300(60×30−120×90)2150×150×180×120=50>6.635，故有99%的把握认为支付宝用户与年龄有关系．把频率作为概率，从所有无现金支付用户（人数最多）中抽取3人，可以近似看作3次独立重复实验，所以X的取值依次为0，1，2，3，且X服从二项分布B(3,35)P(X=0)=C30(1−35)3=8125;P(X=1)=C31⋅35(1−35)2=36125P(X=2)=C32⋅(35)2(1−35)1=54125;P(X=3)=C33(35)3=27125所以X的分布列为EX=0×8125+1×36125+2×54125+3×27125=95【考点】独立性检验【解析】（1）根据题意，由已知可得2×2列联表，由独立性检验计算公式计算K2的值，结合独立性检验的意义可得答案；（2）把频率作为概率，从所有无现金支付用户（人数最多）中抽取3人，可以近似看作3次独立重复实验，所以X的取值依次为0，1，2，3，且X服从二项分布，进而得到X的分布列与数学期望【解答】列联表补充如下K2=300(60×30−120×90)2150×150×180×120=50>6.635，故有99%的把握认为支付宝用户与年龄有关系．把频率作为概率，从所有无现金支付用户（人数最多）中抽取3人，可以近似看作3次独立重复实验，所以X的取值依次为0，1，2，3，且X服从二项分布B(3,35)P(X=0)=C30(1−35)3=8125;P(X=1)=C31⋅35(1−35)2=36125P(X=2)=C32⋅(35)2(1−35)1=54125;P(X=3)=C33(35)3=27125所以X的分布列为EX=0×8125+1×36125+2×54125+3×27125=95已知椭圆C:x2a2+y2b2=1(a>b>0)的离心率为√32,F1F2分别为椭圆的左、右焦点，点P在椭圆上，当PF1⊥PF2时，△PF1F2内切圆的半径为2−√3．（1）求椭圆C的方程；（2）已知直线l:y=kx+m与椭圆C相关于A，B两点，且P(0, 1)．当直线PA，PB的斜率之和为2时，问：点P到直线l的距离是否存在最大值？若存在，求出最大值；若不存在，说明理由．【答案】解：（1）易知|PE1|+|PF2|+|F1F2|22−√3，故|PE1|+|PF2|−|F1F2|=4−2√3，即2a−2c=4−2√3，又ca =√32，∴a=2,c=√3，故b=1，所以椭圆的方程为x24+y2=1．（2）设A(x1y1)B(x2,y2)，联立直线和椭圆的方程得，(4k2+1)x2+8kmx+4(m2−1)=0，∴Δ=16(4k2+1−m2)>0,x1+x2=−8km4k2+1,x1x2=4(m2−1)4k2+1，由k AP+k BP=2得y1−1x1+y2−1x2=2，即kx1+m−1x1+kx2+m−1x2=2，整理得(2k−2)x1x2+(m−1)(x1+x2)=0，所以(2k−2)⋅4(m2−1)4k2+1+(m−1)⋅−8mk4k2+1=0，化简整理得k=m+1，又∵16(4k2+1−m2)>0，∴4k2−(k−1)2+1>0，解得k>0或k<−23，显然点P不在直线l上，∴m≠1,∴ k≠2.点P到直线l的距离d=2=2=√1+3−4kk2+1，设t=3−4k，易得t<3或t>173，且t≠−5.则d=√1+16tt2−6t+25，当t =0时，d =1；当t ≠0时，d =√1+16t+25t−6，若t <0，且t ≠−5，则d ∈(0,1)；若0<t <3，则 d ∈(1,2)， 若t >173，则d ∈(1,8√1313). 综上所述d ∈(0,8√1313)，故点P 到l 的距离没有最大值．【考点】椭圆的定义 【解析】 此题暂无解析 【解答】 解：（1）易知|PE 1|+|PF 2|+|F 1F 2|22−√3，故|PE 1|+|PF 2|−|F 1F 2|=4−2√3，即2a −2c =4−2√3， 又ca =√32， ∴ a =2,c =√3，故b =1， 所以椭圆的方程为x 24+y 2=1．（2）设A (x 1y 1)B (x 2,y 2)，联立直线和椭圆的方程得，(4k 2+1)x 2+8kmx +4(m 2−1)=0， ∴ Δ=16(4k 2+1−m 2)>0,x 1+x 2=−8km 4k 2+1,x 1x 2=4(m 2−1)4k 2+1，由k AP +k BP =2得y 1−1x 1+y 2−1x 2=2，即kx 1+m−1x 1+kx 2+m−1x 2=2，整理得(2k −2)x 1x 2+(m −1)(x 1+x 2)=0， 所以(2k −2)⋅4(m 2−1)4k 2+1+(m −1)⋅−8mk4k 2+1=0，化简整理得k =m +1，又∵ 16(4k 2+1−m 2)>0， ∴ 4k 2−(k −1)2+1>0， 解得k >0或k <−23，显然点P 不在直线l 上，∴ m ≠1,∴ k ≠2.点P 到直线l 的距离d =√k 2+1=√k 2+1=√1+3−4kk 2+1，设t =3−4k ，易得t <3或t >173，且t ≠−5.则d =√1+16tt 2−6t+25，当t =0时，d =1；当t ≠0时，d =√1+16t+25t−6，若t <0，且t ≠−5，则d ∈(0,1)；若0<t <3，则 d ∈(1,2)， 若t >173，则d ∈(1,8√1313).综上所述d ∈(0,8√1313)，故点P 到l 的距离没有最大值．已知函数f(x)=ae x x +lnx −x ．（1）当a =1e 时，讨论函数f(x)的单调性；（2）求函数f(x)的极值． 【答案】解：(1)函数f(x)的定义域为(0,+∞)， 其导数f ′(x)=a ⋅e x (x−1)x 2−x−1x=(x−1)(ae x −x)x 2.当a =1e 时，f ′(x)=(x−1)(e x−1−x)x 2.设u(x)=xe x ，则u ′(x)=1−x e x，显然x ∈(0,1)时u ′(x)>0,u(x)递增； x ∈(1,+∞)时，u ′(x)<0,u(x)递减， 故u(x)≤u(1)=1e ，于是1e −xe x ≥0， 所以x ∈(0,1)时，f ′(x)<0,f(x)递减； x ∈(1,+∞)时，f ′(x)>0,f(x)递增. (2)由（1）知，f ′(x)=(aex −x)(x−1)x 2=e x (a−xe x )(x−1)x 2(x >0)函数u(x)=xe x 在(0, 1)递增，在(1, +∞)上递减， 且u(x)≤u(1)=1e .又当x >0时，e x >1,0<u(x)≤1e ， ①当a ≤0时，a −xe x <0，此时，若x ∈(0, 1)时，则f′(x)>0，f(x)递增；若x ∈(1, +∞)，则f′(x)<0，f(x)递减， 所以f(x)极大值=f(1)=ae −1，无极小值； ②当a ≥1e 时，a −xe x ≥0，此时，若x ∈(0, 1)，则f′(x)<0，f(x)递减；若x ∈(1, +∞)，则f′(x)>0，f(x)递增， 所以f(x)极小值=f(1)=ae −1，无极大值.③当0<a <1e 时，u(a)=a e a <a e 0=a,u(1)=1e >a ，又u(x)在(a, 1)递增，所以u(x)在(a, 1)上有唯一零点x 1，且x1e x 1=a ，易证：x >e 时，2lnx <x ，所以2ln 1a <1a ，所以u (ln 1a 2)=ln1a 2e ln 1a=ln1a 21a 2=a2ln1a1a<a,u(1)=1e >a ，又u(x)在(1, +∞)上递减，所以u(x)在(1,ln 1a 2)上有唯一零点x 2，且x2e x 2=a ，故当x ∈(0, x 1)时，f′(x)<0，f(x)递减； 当x ∈(x 1, 1)，f′(x)>0，f(x)递增； 当x ∈(1, x 2)时，f′(x)<0，f(x)递减； 当x ∈(x 2, +∞)，f′(x)>0，f(x)递增； 所以，f(x)极大值=f(1)=ae −1， ∵ ,f(x 1)=ae x 1x 1+lnx 1−x 1=1+lna,f(x 2)=ae x 2x 2+lnx 2−x 2=1+lna ，f(x)极小值=1+lna .【考点】利用导数研究函数的极值 【解析】 此题暂无解析 【解答】解：(1)函数f(x)的定义域为(0,+∞)， 其导数f ′(x)=a ⋅e x (x−1)x 2−x−1x=(x−1)(ae x −x)x 2.当a =1e 时，f ′(x)=(x−1)(e x−1−x)x 2.设u(x)=xe ，则u ′(x)=1−x e x，显然x ∈(0,1)时u ′(x)>0,u(x)递增； x ∈(1,+∞)时，u ′(x)<0,u(x)递减， 故u(x)≤u(1)=1e ，于是1e −xe x ≥0， 所以x ∈(0,1)时，f ′(x)<0,f(x)递减； x ∈(1,+∞)时，f ′(x)>0,f(x)递增. (2)由（1）知，f ′(x)=(ae x −x)(x−1)x 2=e x (a−xe x )(x−1)x 2(x >0)函数u(x)=xe x 在(0, 1)递增，在(1, +∞)上递减， 且u(x)≤u(1)=1e .又当x >0时，e x >1,0<u(x)≤1e ， ①当a ≤0时，a −xe x <0，此时，若x ∈(0, 1)时，则f′(x)>0，f(x)递增；若x ∈(1, +∞)，则f′(x)<0，f(x)递减， 所以f(x)极大值=f(1)=ae −1，无极小值； ②当a ≥1e 时，a −x e x ≥0，此时，若x ∈(0, 1)，则f′(x)<0，f(x)递减；若x ∈(1, +∞)，则f′(x)>0，f(x)递增， 所以f(x)极小值=f(1)=ae −1，无极大值.③当0<a <1e 时，u(a)=a e a <a e 0=a,u(1)=1e >a ，又u(x)在(a, 1)递增，所以u(x)在(a, 1)上有唯一零点x 1，且x1e x 1=a ，易证：x >e 时，2lnx <x ，所以2ln 1a <1a ， 所以u (ln 1a 2)=ln1a 2e ln 1a=ln1a 21a 2=a2ln1a1a<a,u(1)=1e >a ，又u(x)在(1, +∞)上递减，所以u(x)在(1,ln 1a 2)上有唯一零点x 2，且x2e x 2=a ，故当x ∈(0, x 1)时，f′(x)<0，f(x)递减； 当x ∈(x 1, 1)，f′(x)>0，f(x)递增； 当x ∈(1, x 2)时，f′(x)<0，f(x)递减； 当x ∈(x 2, +∞)，f′(x)>0，f(x)递增； 所以，f(x)极大值=f(1)=ae −1， ∵ ,f(x 1)=ae x 1x 1+lnx 1−x 1=1+lna,f(x 2)=ae x 2x 2+lnx 2−x 2=1+lna ，f(x)极小值=1+lna .请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分.[选修4-4：坐标系与参数方程]在直角坐标系xOy 中，曲线C 1:x 22+y 2=1，曲线C 2:{x =cosφy =1+sinφ （φ为参数），以坐标原点O 为极点，以x 轴正半轴为极轴，建立极坐标系．（1）求曲线C 1，C 2的极坐标方程；（2）已知射线l:θ=α(ρ≥0)与曲线C 1，C 2分别交于点A ，B （异于原点O ），当0<α<π4时，求|OA|2+|OB|2的取值范围．【答案】因为C 2:{x =cosϕy =1+sinϕ， 所以曲线C 2的普通方程为：x 2+(y −1)2=1， 由{x =ρcosθy =ρsinθ ，得曲线C 2的极坐标方程ρ=2sinθ， 对于曲线C 1:x 22+y 2=1，{x =ρcosθy =ρsinθ ，则曲线C 1的极坐标方程为ρ2=21+sin 2θ．由（1）得|OA|2=ρ2=21+sin 2α，|OB|2=ρ2=4sin 2α， |OA|2+|OB|2=21+sin 2α+4sin 2α=21+sin 2α+4(sinα2+1)−4，因为0<α<π4,1<1+sin 2α<32， 则|OA|2+|OB|2∈(2,103)，故|OA|2+|OB|2的取值范围是(2, 103)．【考点】参数方程与普通方程的互化 【解析】（1）由曲线C 2的参数方程能求出曲线C 2的普通方程，从而能求出曲线C 2的极坐标方程；由曲线C 1:x 22+y 2=1，{x =ρcosθy =ρsinθ ，能求出曲线C 1的极坐标方程．（2）由|OA|2=ρ2=21+sin 2α，|OB|2=ρ2=4sin 2α，能求出|OA|2+|OB|2的取值范围． 【解答】因为C 2:{x =cosϕy =1+sinϕ， 所以曲线C 2的普通方程为：x 2+(y −1)2=1， 由{x =ρcosθy =ρsinθ ，得曲线C 2的极坐标方程ρ=2sinθ， 对于曲线C 1:x 22+y 2=1，{x =ρcosθy =ρsinθ， 则曲线C 1的极坐标方程为ρ2=21+sin 2θ．由（1）得|OA|2=ρ2=21+sin 2α，|OB|2=ρ2=4sin 2α， |OA|2+|OB|2=21+sin 2α+4sin 2α=21+sin 2α+4(sinα2+1)−4， 因为0<α<π4,1<1+sin 2α<32， 则|OA|2+|OB|2∈(2,103)，故|OA|2+|OB|2的取值范围是(2, 103)． [选修4-5：不等式选讲]已知函数f(x)=|2x +a|+|2x −b|+2的最小值为3． （1）求a +b 的值；（2）若a >0，b >0，求证：a +b ≥3−log 3(4a +1b )．【答案】f(x)=|2x +a|+|2x −b|+2≥|(2x +a)−(2x −b)|+2=|a +b|+2， 所以|a +b|+2=3，即a +b =±1；证明：由a +b =1，则原式等价为：log 3(4a +1b )≥2，即4a +1b ≥9， 而4a +1b =(4a +1b)(a +b)=5+4b a+a b ≥5+2√4b a ×ab =9，故原不等式成立．【考点】绝对值不等式的解法与证明【解析】（1）根据绝对值不等式的性质求出a+b的值即可；（2）求出a+b=1，根据基本不等式的性质证明即可．【解答】f(x)=|2x+a|+|2x−b|+2≥|(2x+a)−(2x−b)|+2=|a+b|+2，所以|a+b|+2=3，即a+b=±1；证明：由a+b=1，则原式等价为：log3(4a +1b)≥2，即4a+1b≥9，而4a +1b=(4a+1b)(a+b)=5+4ba+ab≥5+2√4ba×ab=9，故原不等式成立．试卷第21页，总21页。

2018年湖北省新联考高考理科数学四模试卷（带答案和解
释）
5 5不等式选讲]
23．已知函数f（x）=|x﹣2a|+|x+ |
（1）当a=1时，求不等式f（x）＞4的解集；
（2）若不等式f（x）≥2﹣+2 对任意实数x及a恒成立，求实数的取值范围．
5不等式选讲]
23．（2018湖北四模）已知函数f（x）=|x﹣2a|+|x+ |
（1）当a=1时，求不等式f（x）＞4的解集；
（2）若不等式f（x）≥2﹣+2 对任意实数x及a恒成立，求实数的取值范围．
【考点】绝对值三角不等式；绝对值不等式的解法．
【分析】（1）当a=1时，分类讨论，求不等式f（x）＞4的解集；
（2）f（x）=|x﹣2a|+|x+ |≥|2a+ |=|2a|+| | ，利用不等式f（x）≥2﹣+2 对任意实数x及a恒成立，求实数的取值范围．【解答】解（1）当a=1时，不等式f（x）＞4为|x﹣2|+|x+1|＞4．
x＜﹣1时，不等式可化为﹣（x﹣2）﹣（x+1）＞4，解得x＜﹣，∴x＜﹣；
﹣1≤x≤2时，不等式可化为﹣（x﹣2）+（x+1）＞4，不成立；
x＞2时，不等式可化为（x﹣2）+（x+1）＞4，解得x＞，∴x ＞；
综上所述，不等式的解集为{x|x＜﹣或x＞ }；
（2）f（x）=|x﹣2a|+|x+ |≥|2a+ |=|2a|+| | ，
不等式f（x）≥2﹣+2 对任意实数x及a恒成立，∴2 2﹣+2 ，。

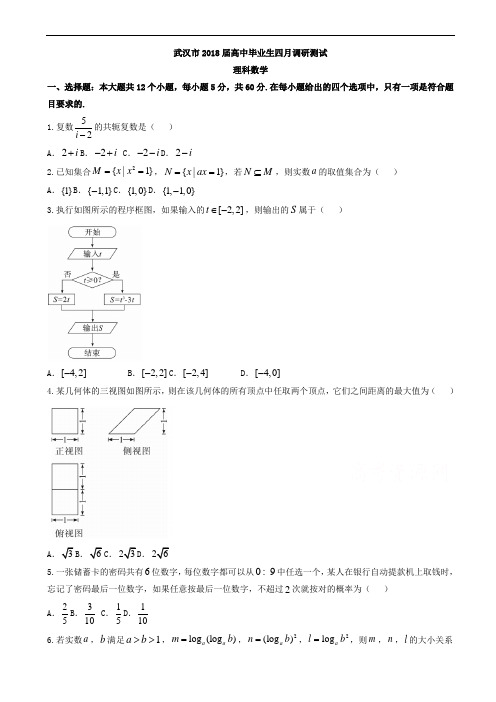
武汉市2018届高中毕业生四月调研测试理科数学一、选择题：本大题共12个小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的. 1.复数52i -的共轭复数是（ ） A ．2i +B ．2i -+ C ．2i --D ．2i -2.已知集合2{|1}M x x ==，{|1}N x ax ==，若N M ⊆，则实数a 的取值集合为（ ） A ．{1}B ．{1,1}-C ．{1,0}D ．{1,1,0}-3.执行如图所示的程序框图，如果输入的[2,2]t ∈-，则输出的S 属于（ ）A ．[4,2]-B ．[2,2]-C ．[2,4]-D ．[4,0]-4.某几何体的三视图如图所示，则在该几何体的所有顶点中任取两个顶点，它们之间距离的最大值为（ ）A ．．5.一张储蓄卡的密码共有6位数字，每位数字都可以从09中任选一个，某人在银行自动提款机上取钱时，忘记了密码最后一位数字，如果任意按最后一位数字，不超过2次就按对的概率为（ ） A ．25B ．310 C ．15D ．1106.若实数a ，b 满足1a b >>，log (log )a a m b =，2(log )a n b =，2log a l b =，则m ，n ，l 的大小关系为（ ）A ．m l n >>B ．l n m >>C ．n l m >>D ．l m n >>7.已知直线1y kx =-与双曲线224x y -=的右支有两个交点，则k 的取值范围为（ ） A． B． C．( D． 8.在ABC ∆中，角A 、B 、C 的对应边分别为a ，b ，c ，条件p ：2b c a +≤，条件q ：2B CA +≤，那么条件p 是条件q 成立的（ ）A ．充分而不必要条件B ．必要而不充分条件C ．充要条件D ．既不充分也不必要条件 9.在61(1)x x+-的展开式中，含5x 项的系数为（ ） A ．6B ．6- C ．24D ．24-10.若x ，y 满足1212x y -++≤，则2222M x y x =+-的最小值为（ ） A ．2-B ．211 C ．4D ．49- 11.函数()2sin()(0)3f x x πωω=+>的图象在[0,1]上恰有两个最大值点，则ω的取值范围为（ ）A ．[2,4]ππB ．9[2,)2ππ C ．1325[,)66ππ D ．25[2,)6ππ 12.过点(2,1)P -作抛物线24x y =的两条切线，切点分别为A ，B ，PA ，PB 分别交x 轴于E ，F 两点，O 为坐标原点，则PEF ∆与OAB ∆的面积之比为（ ）A．12 D ．34二、填空题：本大题共4小题，每小题5分，共20分. 13.已知sin 2cos αα=，则sin cos αα=．14.已知向量a ，b ，c 满足20a b c ++=，且1a =，3b =，2c =，则22a b a c b c ⋅+⋅+⋅=． 15.已知(,)22x ππ∈-，()1y f x =-为奇函数，'()()tan 0f x f x x +>，则不等式()cos f x x >的解集为． 16.在四面体ABCD 中，1AD DB AC CB ====，则四面体体积最大时，它的外接球半径R =． 三、解答题：共70分.解答应写出文字说明、证明过程或演算步骤.第17题～第21题为必考题，每个试题考生都必须作答.第22题～第23题为选考题，考生根据要求作答. （一）必考题：共60分.17.已知正数数列{}n a 满足：12a =，11212n n n n n a a a a ---+=+-(2)n ≥.（1）求2a ，3a ；（2）设数列{}n b 满足22(1)n n b a n =--，证明：数列{}n b 是等差数列，并求数列{}n a 的通项n a .18.如图，在棱长为3的正方体1111ABCD A BC D -中，E ，F 分别在棱AB ，CD 上，且1AE CF ==.（1）已知M 为棱1DD 上一点，且11D M =，求证：1B M ⊥平面11A EC . （2）求直线1FC 与平面11A EC 所成角的正弦值.19.已知椭圆Γ：22142x y +=，过点(1,1)P 作倾斜角互补的两条不同直线1l ，2l ，设1l 与椭圆Γ交于A 、B 两点，2l 与椭圆Γ交于C ，D 两点.（1）若(1,1)P 为线段AB 的中点，求直线AB 的方程； （2）记AB CDλ=，求λ的取值范围.20.在某市高中某学科竞赛中，某一个区4000名考生的参赛成绩统计如图所示.（1）求这4000名考生的竞赛平均成绩x （同一组中数据用该组区间中点作代表）；（2）由直方图可认为考生竞赛成绩z 服正态分布2(,)N μσ，其中μ，2σ分别取考生的平均成绩x 和考生成绩的方差2s ，那么该区4000名考生成绩超过84.41分（含84.81分）的人数估计有多少人？（3）如果用该区参赛考生成绩的情况来估计全市的参赛考生的成绩情况，现从全市参赛考生中随机抽取4名考生，记成绩不超过．．．84.81分的考生人数为ξ，求(3)P ξ≤.（精确到0.001）附：①2204.75s =14.31=；②2(,)zN μσ，则()0.6826P z μσμσ-<<+=，(22)0.9544P z μσμσ-<<+=；③40.84130.501=.21.已知函数()(ln )x f x xe a x x =-+，a R ∈. （1）当a e =时，求()f x 的单调区间； （2）若()f x 有两个零点，求实数a 的取值范围.（二）选考题：共10分.请考生在22、23题中任选一题作答，如果多做，则按所做的第一题记分.作答时请写清题号.22.[选修4-4：坐标系与参数方程]在平面直角坐标系xOy 中，以坐标原点O 为极点，x 轴正半轴为极轴建立极坐标系，l 的极坐标方程为(cos 2sin )10ρθθ+=，C 的参数方程为3cos 2sin x y θθ=⎧⎨=⎩（θ为参数，R θ∈）. （1）写出l 和C 的普通方程；（2）在C 上求点M ，使点M 到l 的距离最小，并求出最小值. 23.[选修4-5：不等式选讲] 已知()22f x ax x =--+.（1）在2a =时，解不等式()1f x ≤；（2）若关于x 的不等式4()4f x -≤≤对x R ∈恒成立，求实数a 的取值范围.武汉市2018届高中毕业生四月调研测试理科数学参考答案一、选择题1-5: BDABC 6-10: BDABD 11、12：CC 二、填空题 13.25 14. 13- 15. (0,)2π三、解答题17.（1）由已知212132a a a a +=+-，而12a =，∴2222232(2)a a -=+-，即222230a a --=. 而20a >，则23a =. 又由323252a a a a +=+-，23a =，∴233952(3)a a -=+-，即233280a a --=. 而30a >，则34a =. ∴23a =，34a =.（2）由已知条件可知：22112()21n n n n a a a a n ---=-+-，∴22221(1)(1)(1)n n a a n n ----=--， 则22221(1)(1)(1)n n a n a n ---=---223(1)2a =⋅⋅⋅=-- 222(1)1a =--0=，而22(1)n n b a n =--，∴0n b =，数列{}n b 为等差数列. ∴22(1)n a n -=.而0n a >， 故1n a n =+.18.解：（1）过M 作1MT AA ⊥于点T ，连1B T ，则11AT =. 易证：111AA E A BT ∆≅∆，于是111AA E A BT ∠=∠. 由111190A BT ATB ∠+∠=，知11190AA E ATB ∠+∠=， ∴11A E BT ⊥.显然MT ⊥面11AA B B ，而1A E ⊂面11AA B B ， ∴1MT A E ⊥，又1BT MT T =，∴1A E ⊥面MTB ，∴11A E MB ⊥. 连11B D ，则1111B D AC ⊥. 又111D M AC ⊥，1111B D D M D =，∴11AC ⊥面11MD B ， ∴111AC MB ⊥.由11A E MB ⊥，111AC MB ⊥，1111A E AC A =，∴1B M ⊥面11A EC .（2）在11D C 上取一点N ，使11ND =，连接EF . 易知1//A E FN .∴1111A EFC N EFC E NFC V V V ---==11113(23)33332NFC S ∆=⋅⨯=⨯⨯⨯=.对于11A EC ∆，11AC =，1A E =而1EC ，由余弦定理可知11cos EAC ∠==∴11A EC ∆的面积11111sin 2S A C A E EA C =⋅∠12=⨯=由等体积法可知F 到平面11A EC 之距离h 满足111113A EC A EFC S h V ∆-⋅=，则133h =，∴h =，又1FC =1FC 与平面1AEC 所成角为θ，∴sinθ===. 19.解：（1）设直线AB 的斜率为tan k α=，方程为1(1)y k x -=-，代入2224x y +=中，∴222[(1)]40x kx k +---=.∴222(12)4(1)2(1)40k x k k x k +--+--=.判别式222[4(1)]4(21)[2(1)4]k k k k ∆=--+--28(321)k k =++. 设11(,)A x y ，22(,)B x y ，则12221224(1)212(1)421k k x x k k x x k -⎧+=⎪⎪+⎨--⎪=⎪+⎩. ∵AB 中点为(1,1)， ∴12212(1)()1221k k x x k -+==+，则12k =. ∴直线的AB 方程为11(1)2y x -=-，即210x y -+=. （2）由（1）知12AB x =-==. 设直线的CD 方程为1(1)(0)y k x k -=--≠.同理可得CD =∴0)ABk CD λ==≠. ∴2241312kk k λ=++-41132k k=++-. 令13t k k=+， 则4()12g t t =+-，(,[23,)t ∈-∞-+∞. ()g t 在(,-∞-，)+∞分别单调递减，∴2()1gt ≤<或1()2g t <≤故221λ≤<或212λ<≤.即6(1,λ+∈. 20.解：（1）由题意知：∴4000名考生的竞赛平均成绩x 为70.5分.（2）依题意z 服从正态分布2(,)N μσ，其中70.5x μ==，2204.75D σξ==，14.31σ=，∴z 服从正态分布22(,)(70.5,14.31)N N μσ=，而()(56.1984.81)0.6826P z P z μσμσ-<<+=<<=， ∴10.6826(84.81)0.15872P z -≥==. ∴竞赛成绩超过84.81分的人数估计为0.158********.8⨯=人634≈人. （3）全市竞赛考生成绩不超过84.81分的概率10.15870.8413-=. 而(4,0.8413)B ξ，∴444(3)1(4)10.8413P P C ξξ≤=-==-⋅10.5010.499=-=.21.解：（1）定义域为：(0,)+∞，当a e =时，(1)()'()x x xe e f x x+-=.∴()f x 在(0,1)时为减函数；在(1,)+∞时为增函数.（2）记ln t x x =+，则ln t x x =+在(0,)+∞上单增，且t R ∈. ∴()(ln )x f x xe a x x =-+()t e at g t =-=.∴()f x 在0x >上有两个零点等价于()t g t e at =-在t R ∈上有两个零点. ①在0a =时，()t g t e =在R 上单增，且()0g t >，故()g t 无零点； ②在0a <时，'()tg t e a =-在R 上单增，又(0)10g =>，11()10a g e a=-<，故()g t 在R 上只有一个零点； ③在0a >时，由'()0t g t e a =-=可知()g t 在ln t a =时有唯一的一个极小值(ln )(1ln )g a a a =-. 若0a e <<，(1ln )0g a a =->最小，()g t 无零点； 若a e =，0g =最小，()g t 只有一个零点；若a e >时，(1ln )0g a a =-<最小，而(0)10g =>， 由于ln ()x f x x=在x e >时为减函数，可知：a e >时，2a e e a a >>. 从而2()0ag a e a =->，∴()g x 在(0,ln )a 和(ln ,)a +∞上各有一个零点.综上讨论可知：a e >时()f x 有两个零点，即所求a 的取值范围是(,)e +∞. 22.解：（1）由l ：cos sin 100ρθρϕ+-=，及cos x ρθ=，sin y ρθ=. ∴l 的方程为2100x y +-=.由3cos x θ=，2sin y θ=，消去θ得22194x y +=. （2）在C 上取点(3cos ,2sin )M ϕϕ，则d=05cos()10ϕϕ=--. 其中003cos 54sin 5ϕϕ⎧=⎪⎪⎨⎪=⎪⎩，当0ϕϕ=时，d此时093sin 3cos 5ϕϕ==，0082sin 2cos 5ϕϕ==，98(,)55M . 23.解：（1）在2a =时，2221x x --+≤. 在1x ≥时，(22)(2)1x x --+≤，∴15x ≤≤； 在2x ≤-时，(22)(2)1x x --++≤，3x ≥，∴x 无解； 在21x -≤≤时，(22)(2)1x x ---+≤，13x ≥-，∴113x -≤≤. 综上可知：不等式()1f x ≤的解集为1{|5}3x x -≤≤. （2）∵224x ax +--≤恒成立， 而22(1)x ax a x +--≤+， 或22(1)4x ax a x +--≤-+，故只需(1)4a x +≤恒成立，或(1)44a x -+≤恒成立， ∴1a =-或1a =. ∴a 的取值为1或1-.。

2018年普通高等学校招生全国统一考试理科数学（模拟一）一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的。

(1) 已知集合},421|{},034|{2N x x B x x x A x∈≤<=<+-=，则A B =I（A ）∅（B ）(]1,2（C ）{}2（D ）{}1,2(2) 欧拉公式cos sin ix e x i x =+(i 为虚数单位)是由瑞士著名数学家欧拉发现的，它将指数函数的定义域扩大到复数，建立了三角函数和指数函数的关系，它在复变函数论里非常重要，被誉为“数学中的天桥”。

根据欧拉公式可知，i e π32018表示的复数位于复平面中的（A ）第一象限（B ）第二象限（C ）第三象限（D ）第四象限(3) 要得到函数()sin 2f x x =的图象，只需将函数()cos 2g x x =的图象（A ）向左平移12个周期 （B ）向右平移12个周期 （C ）向左平移14个周期 （D ）向右平移14个周期 (4) 某地区空气质量监测表明，一天的空气质量为优良的概率是75.0，连续两天为优良的概率是6.0，已知某天的空气质量为优良，则随后一天空气质量为优良的概率是（A ）8.0 （B ）75.0 （C ）6.0 （D ）45.0(5) 如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则此几何体各面中直角三角形的个数是（A ）2 （B ）3 （C ）4 （D ）5 (6) 等比数列}{n a 的前n 项和为n S ，下列结论一定成立的是（A ）若05>a ，则02017<a（B ）若06>a ，则02018<a （C ）若05>a ，则02017>S（D ）若06>a ，则02018>S(7) 我们可以用随机模拟的方法估计π的值，如下程序框图表示其基本步骤（函数RAND 是产生随机数的函数，它能随机产生)1,0(内的任何一个实数），若输出的结果为527，则由此可估计π的近似值 （A ）126 （B ） 3.132 （C ）3.151 （D ） 3.162(8) 函数2(1)cos π()=||x xf x x -的部分图像为（A （B ） （C ）（D ）(9) 已知三棱锥ABC D -的所有顶点都在球O 的球面上，2==BC AB ，22=AC ，若三棱锥D ABC -体积的最大值为2，则球O 的表面积为 （A ）8π（B ） 9π （C ）25π3 （D ） 9121π(10) 已知双曲线2222:1x y E a b-=（0,0a b >>）的左、右焦点分别为12,F F ，126F F =，P 是E右支上的一点，1PF 与y 轴交于点A ，2PAF △的内切圆在边2AF 上的切点为Q．若AQ =E 的离心率是 （A ）3（B（C ）32（D(11) 向量≠，1||=，对R t ∈∀，||||t -≤+，则（A ）e a ⊥（B ）)(e a a +⊥ （C ）)(e a e +⊥（D ）)()(e a e a +⊥-(12) 函数)1(ln )1()(--+=x a x x x f 有三个零点，则实数a 的取值范围是 （A ）)2,0(（B ）),2(e（C ）),(+∞e（D ）),2(+∞二、填空题：本大题共4小题，每小题5分。

武汉市2018届高中毕业生四月调研测试理科数学一、选择题：本大题共12个小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.复数52i -的共轭复数是（ ）A ．2i +B ．2i -+C ．2i --D ．2i -2.已知集合2{|1}M x x ==，{|1}N x ax ==，若N M ⊆，则实数a 的取值集合为（ ）A ．{1}B ．{1,1}-C ．{1,0}D ．{1,1,0}-3.执行如图所示的程序框图，如果输入的[2,2]t ∈-，则输出的S 属于（ ）A ．[4,2]-B ．[2,2]-C ．[2,4]-D ．[4,0]-4.某几何体的三视图如图所示，则在该几何体的所有顶点中任取两个顶点，它们之间距离的最大值为（ ）A C ．． 5.一张储蓄卡的密码共有6位数字，每位数字都可以从09中任选一个，某人在银行自动提款机上取钱时，忘记了密码最后一位数字，如果任意按最后一位数字，不超过2次就按对的概率为（ ） A ．25 B ．310 C ．15 D ．1106.若实数a ，b 满足1a b >>，log (log )a a m b =，2(log )a n b =，2log a l b =，则m ，n ，l 的大小关系为（ ）A ．m l n >>B ．l n m >>C ．n l m >>D ．l m n >> 7.已知直线1y kx =-与双曲线224x y -=的右支有两个交点，则k 的取值范围为（ ）A ．(0,2 B ．[1,]2C ．(22-D ．(1,2 8.在ABC ∆中，角A 、B 、C 的对应边分别为a ，b ，c ，条件p ：2b c a +≤，条件q ：2B CA +≤，那么条件p 是条件q 成立的（ ）A ．充分而不必要条件B ．必要而不充分条件C ．充要条件D ．既不充分也不必要条件 9.在61(1)x x+-的展开式中，含5x 项的系数为（ ）A ．6B ．6-C ．24D ．24- 10.若x ，y 满足1212x y -++≤，则2222M x y x =+-的最小值为（ ）A ．2-B ．211 C ．4 D ．49- 11.函数()2sin()(0)3f x x πωω=+>的图象在[0,1]上恰有两个最大值点，则ω的取值范围为（ ）A ．[2,4]ππB ．9[2,)2ππ C ．1325[,)66ππ D ．25[2,)6ππ 12.过点(2,1)P -作抛物线24x y =的两条切线，切点分别为A ，B ，PA ，PB 分别交x 轴于E ，F 两点，O 为坐标原点，则PEF ∆与OAB ∆的面积之比为（ ）AC ．12D ．34二、填空题：本大题共4小题，每小题5分，共20分.13.已知sin 2cos αα=，则sin cos αα= ．14.已知向量a ，b ，c 满足20a b c ++=，且1a =，3b =，2c =，则22a b a c b c ⋅+⋅+⋅= ．15.已知(,)22x ππ∈-，()1y f x =-为奇函数，'()()tan 0f x f x x +>，则不等式()cos f x x >的解集为 ．16.在四面体ABCD 中，1AD DB AC CB ====，则四面体体积最大时，它的外接球半径R = ．三、解答题：共70分.解答应写出文字说明、证明过程或演算步骤.第17题～第21题为必考题，每个试题考生都必须作答.第22题～第23题为选考题，考生根据要求作答. （一）必考题：共60分.17.已知正数数列{}n a 满足：12a =，11212n n n n n a a a a ---+=+-(2)n ≥.（1）求2a ，3a ；（2）设数列{}n b 满足22(1)n n b a n =--，证明：数列{}n b 是等差数列，并求数列{}n a 的通项n a .18.如图，在棱长为3的正方体1111ABCD A B C D -中，E ，F 分别在棱AB ，CD 上，且1AE CF ==.（1）已知M 为棱1DD 上一点，且11D M =，求证：1B M ⊥平面11A EC .（2）求直线1FC 与平面11A EC 所成角的正弦值.19.已知椭圆Γ：22142x y +=，过点(1,1)P 作倾斜角互补的两条不同直线1l ，2l ，设1l 与椭圆Γ交于A 、B 两点，2l 与椭圆Γ交于C ，D 两点.（1）若(1,1)P 为线段AB 的中点，求直线AB 的方程；（2）记ABCDλ=，求λ的取值范围.20.在某市高中某学科竞赛中，某一个区4000名考生的参赛成绩统计如图所示.（1）求这4000名考生的竞赛平均成绩x （同一组中数据用该组区间中点作代表）；（2）由直方图可认为考生竞赛成绩z 服正态分布2(,)N μσ，其中μ，2σ分别取考生的平均成绩x 和考生成绩的方差2s ，那么该区4000名考生成绩超过84.41分（含84.81分）的人数估计有多少人？（3）如果用该区参赛考生成绩的情况来估计全市的参赛考生的成绩情况，现从全市参赛考生中随机抽取4名考生，记成绩不超过．．．84.81分的考生人数为ξ，求(3)P ξ≤.（精确到0.001）附：①2204.75s =14.31=；②2(,)zN μσ，则()0.6826P z μσμσ-<<+=，(22)0.9544P z μσμσ-<<+=；③40.84130.501=.21.已知函数()(ln )xf x xe a x x =-+，a R ∈.（1）当a e =时，求()f x 的单调区间；（2）若()f x 有两个零点，求实数a 的取值范围.（二）选考题：共10分.请考生在22、23题中任选一题作答，如果多做，则按所做的第一题记分.作答时请写清题号.22.[选修4-4：坐标系与参数方程]在平面直角坐标系xOy 中，以坐标原点O 为极点，x 轴正半轴为极轴建立极坐标系，l 的极坐标方程为(cos 2sin )10ρθθ+=，C 的参数方程为3cos 2sin x y θθ=⎧⎨=⎩（θ为参数，R θ∈）. （1）写出l 和C 的普通方程；（2）在C 上求点M ，使点M 到l 的距离最小，并求出最小值.23.[选修4-5：不等式选讲] 已知()22f x ax x =--+.（1）在2a =时，解不等式()1f x ≤；（2）若关于x 的不等式4()4f x -≤≤对x R ∈恒成立，求实数a 的取值范围.武汉市2018届高中毕业生四月调研测试理科数学参考答案一、选择题1-5: BDABC 6-10: BDABD 11、12：CC二、填空题13.25 14. 13- 15. (0,)2π三、解答题17.（1）由已知212132a a a a +=+-，而12a =，∴2222232(2)a a -=+-，即222230a a --=.而20a >，则23a =.又由323252a a a a +=+-，23a =，∴233952(3)a a -=+-，即233280a a --=.而30a >，则34a =.∴23a =，34a =.（2）由已知条件可知：22112()21n n n n a a a a n ---=-+-，∴22221(1)(1)(1)n n a a n n ----=--，则22221(1)(1)(1)n n a n a n ---=---223(1)2a =⋅⋅⋅=--222(1)1a =--0=，而22(1)n n b a n =--，∴0n b =，数列{}n b 为等差数列.∴22(1)n a n -=.而0n a >，故1n a n =+.18.解：（1）过M 作1MT AA ⊥于点T ，连1B T ，则11AT =.易证：111AA E A B T ∆≅∆，于是111AA E A B T ∠=∠.由111190A B T ATB ∠+∠=，知11190AAE ATB ∠+∠=，∴11A E B T ⊥.显然MT ⊥面11AA B B ，而1AE ⊂面11AA B B ，∴1M T A E ⊥，又1B T MT T =，∴1A E ⊥面MTB ，∴11A E MB ⊥.连11B D ，则1111B D AC ⊥.又111D M A C ⊥，1111B D D M D =，∴11A C ⊥面11MD B ，∴111AC MB ⊥.由11A E MB ⊥，111AC MB ⊥，1111A E A C A =，∴1B M ⊥面11A EC .（2）在11D C 上取一点N ，使11ND =，连接EF .易知1//A E FN .∴1111A EFC N EFC E NFC V V V ---==11113(23)33332NFC S ∆=⋅⨯=⨯⨯⨯=.对于11A EC ∆，11AC =，1A E =1EC =，由余弦定理可知11cos EAC ∠==.∴11A EC ∆的面积11111sin 2S AC A E EAC =⋅∠12=⨯=.由等体积法可知F 到平面11A EC 之距离h 满足111113A EC A EFC S h V ∆-⋅=，则133h =，∴h =，又1FC =，设1FC 与平面1AEC 所成角为θ，∴sin 95θ===. 19.解：（1）设直线AB 的斜率为tan k α=，方程为1(1)y k x -=-，代入2224x y +=中，∴222[(1)]40x kx k +---=.∴222(12)4(1)2(1)40k x k k x k +--+--=.判别式222[4(1)]4(21)[2(1)4]k k k k ∆=--+--28(321)k k =++.设11(,)A x y ，22(,)B x y ，则12221224(1)212(1)421k k x x k k x x k -⎧+=⎪⎪+⎨--⎪=⎪+⎩.∵AB 中点为(1,1)，∴12212(1)()1221k k x x k -+==+，则12k =. ∴直线的AB 方程为11(1)2y x -=-，即210x y -+=. （2）由（1）知12AB x =-==. 设直线的CD 方程为1(1)(0)y k x k -=--≠.同理可得CD =.∴0)ABk CD λ==≠.∴2241312k k k λ=++-41132k k=++-.令13t k k =+，则4()12g t t =+-，(,[23,)t ∈-∞-+∞.()g t 在(,-∞-，)+∞分别单调递减，∴2()1gt ≤<或1()2g t<≤+故221λ≤<或212λ<≤.即6(1,λ+∈. 20.解：（1）由题意知：∴450.1550.15650.2750.3x =⨯+⨯+⨯+⨯850.15950.170.5+⨯+⨯=，∴4000名考生的竞赛平均成绩x 为70.5分.（2）依题意z 服从正态分布2(,)N μσ，其中70.5x μ==，2204.75D σξ==，14.31σ=，∴z 服从正态分布22(,)(70.5,14.31)N N μσ=，而()(56.1984.81)0.6826P z P z μσμσ-<<+=<<=，∴10.6826(84.81)0.15872P z -≥==.∴竞赛成绩超过84.81分的人数估计为0.158********.8⨯=人634≈人.（3）全市竞赛考生成绩不超过84.81分的概率10.15870.8413-=.而(4,0.8413)B ξ，∴444(3)1(4)10.8413P P C ξξ≤=-==-⋅10.5010.499=-=.21.解：（1）定义域为：(0,)+∞，当a e =时，(1)()'()x x xe e f x x+-=.∴()f x 在(0,1)时为减函数；在(1,)+∞时为增函数.（2）记ln t x x =+，则ln t x x =+在(0,)+∞上单增，且t R ∈.∴()(ln )x f x xe a x x =-+()t e at g t =-=.∴()f x 在0x >上有两个零点等价于()t g t e at =-在t R ∈上有两个零点.①在0a =时，()t g t e =在R 上单增，且()0g t >，故()g t 无零点；②在0a <时，'()tg t e a =-在R 上单增，又(0)10g =>，11()10a g e a =-<，故()g t 在R 上只有一个零点； ③在0a >时，由'()0tg t e a =-=可知()g t 在ln t a =时有唯一的一个极小值(ln )(1ln )g a a a =-. 若0a e <<，(1ln )0g a a =->最小，()g t 无零点；若a e =，0g =最小，()g t 只有一个零点；若a e >时，(1ln )0g a a =-<最小，而(0)10g =>，由于ln ()x f x x =在x e >时为减函数，可知：a e >时，2a e e a a >>.从而2()0a g a e a =->，∴()g x 在(0,ln )a 和(ln ,)a +∞上各有一个零点.综上讨论可知：a e >时()f x 有两个零点，即所求a 的取值范围是(,)e +∞.22.解：（1）由l ：cos sin 100ρθρϕ+-=，及cos x ρθ=，sin y ρθ=.∴l 的方程为2100x y +-=.由3cos x θ=，2sin y θ=，消去θ得22194x y +=. （2）在C 上取点(3cos ,2sin )M ϕϕ，则d=05cos()10ϕϕ=--. 其中003cos 54sin 5ϕϕ⎧=⎪⎪⎨⎪=⎪⎩，当0ϕϕ=时，d此时093sin 3cos 5ϕϕ==，0082sin 2cos 5ϕϕ==，98(,)55M . 23.解：（1）在2a =时，2221x x --+≤.在1x ≥时，(22)(2)1x x --+≤，∴15x ≤≤；在2x ≤-时，(22)(2)1x x --++≤，3x ≥，∴x 无解；在21x -≤≤时，(22)(2)1x x ---+≤，13x ≥-，∴113x -≤≤.综上可知：不等式()1f x ≤的解集为1{|5}3x x -≤≤.（2）∵224x ax +--≤恒成立，而22(1)x ax a x +--≤+，或22(1)4x ax a x +--≤-+， 故只需(1)4a x +≤恒成立，或(1)44a x -+≤恒成立，∴1a =-或1a =.∴a 的取值为1或1-.。

武汉市２０１８届高中毕业生四月调研测试理　科　数　学武汉市教育科学研究院命制２０１８．４．１９本试卷共６页，２３题（含选考题）。

全卷满分１５０分。

考试用时１２０分钟。

★祝考试顺利★注意事项：１ 答题前，先将自己的姓名、准考证号填写在试卷和答题卡上，并将准考证号条形码粘贴在答题卡上的指定位置。

２ 选择题的作答：每小题选出答案后，用２Ｂ铅笔把答题卡上对应题目的答案标号涂黑。

写在试卷、草稿纸和答题卡上的非答题区域均无效。

３ 非选择题的作答：用黑色签字笔直接答在答题卡上对应的答题区域内。

写在试卷、草稿纸和答题卡上的非答题区域均无效。

４ 选考题的作答：先把所选题目的题号在答题卡上指定的位置用２Ｂ铅笔涂黑。

答案写在答题卡上对应的答题区域内，写在试卷、草稿纸和答题卡上的非答题区域均无效。

５ 考试结束后，请将本试卷和答题卡一并上交。

一、选择题：本题共１２小题，每小题５分，共６０分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

１ 复数５ｉ－２的共轭复数是Ａ ２＋ｉＢ －２＋ｉＣ －２－ｉＤ ２－ｉ２ 已知集合Ｍ＝｛ｘ｜ｘ２＝１｝，Ｎ＝｛ｘ｜ａｘ＝１｝，若Ｎ Ｍ，则实数ａ的取值集合为Ａ ｛１｝Ｂ ｛－１，１｝Ｃ ｛１，０｝Ｄ ｛１，－１，０｝３ 执行如图所示的程序框图，如果输入的ｔ∈［－２，２］，则输出的Ｓ属于Ａ ［－４，２］Ｂ ［－２，２］Ｃ ［－２，４］Ｄ ［－４，０］４ 某几何体的三视图如图所示，则在该几何体的所有顶点中任取两个顶点，它们之间距离的最大值为槡Ａ ３槡Ｂ ６槡Ｃ ２３槡Ｄ ２６５ 一张储蓄卡的密码共有６位数字，每位数字都可以从０～９中任选一个，某人在银行自动提款机上取钱时，忘记了密码最后一位数字，如果任意按最后一位数字，不超过２次就按对的概率为Ａ ２５Ｂ ３１０Ｃ １５Ｄ １１０６ 若实数ａ，ｂ满足ａ＞ｂ＞１，ｍ＝ｌｏｇａ（ｌｏｇａｂ），ｎ＝（ｌｏｇａｂ）２，ｌ＝ｌｏｇａｂ２，则ｍ，ｎ，ｌ的大小关系为Ａ ｍ＞ｌ＞ｎＢ ｌ＞ｎ＞ｍＣ ｎ＞ｌ＞ｍＤ ｌ＞ｍ＞ｎ７ 已知直线ｙ＝ｋｘ－１与双曲线ｘ２－ｙ２＝４的右支有两个交点，则ｋ的取值范围为Ａ （０，槡５２）Ｂ ［１，槡５２］Ｃ （－槡５２，槡５２）Ｄ （１，槡５２）８ 在△ＡＢＣ中，角Ａ、Ｂ、Ｃ的对应边分别为ａ，ｂ，ｃ，条件ｐ：ａ≤ｂ＋ｃ２，条件ｑ：Ａ≤Ｂ＋Ｃ２，那么条件ｐ是条件ｑ成立的Ａ 充分而不必要条件Ｂ 必要而不充分条件Ｃ 充要条件Ｄ 既不充分又不必要条件９ 在（ｘ＋１ｘ－１）６的展开式中，含ｘ５项的系数为Ａ ６Ｂ －６Ｃ ２４Ｄ －２４１０ 若ｘ，ｙ满足｜ｘ－１｜＋２｜ｙ＋１｜≤２，则Ｍ＝２ｘ２＋ｙ２－２ｘ的最小值为Ａ －２Ｂ ２１１Ｃ ４Ｄ －４９１１ 函数ｆ（ｘ）＝２ｓｉｎ（ｗｘ＋π３）（ｗ＞０）的图象在［０，１］上恰有两个最大值点，则ｗ的取值范围为Ａ ［２π，４π］Ｂ ［２π，９π２）Ｃ ［１３π６，２５π６）Ｄ ［２π，２５π６）１２ 过点Ｐ（２，－１）作抛物线ｘ２＝４ｙ的两条切线，切点分别为Ａ，Ｂ，ＰＡ，ＰＢ分别交ｘ轴于Ｅ，Ｆ两点，Ｏ为坐标原点，则△ＰＥＦ与△ＯＡＢ的面积之比为Ａ 槡３２Ｂ 槡３３Ｃ １２Ｄ ３４二、填空题：本大题共４小题，每小题５分，共２０分。