数学建模校内选拔
- 格式:doc
- 大小:567.00 KB
- 文档页数:16


第十三届“中国电机工程学会杯”全国大学生电工数学建模竞赛
校内选拔赛报名细则及参赛规范
1.报名时间:截止2021年4月25日12:00。
2.报名方式:加入竞赛QQ群,在线填写腾讯文档竞赛报名表报名,报名样表见附件2。
3.竞赛时间:2021-4-27 0:00至2021-4-30 24:00。
4.参赛方式:参赛队根据选择的竞赛题目,给出解决问题的方案和结果,并撰写论文
作为参赛作品提交。
5.竞赛论文内容:涉及模型的假设、建立和求解,算法的设计和计算机实现,结果的
分析和检验,模型的改进等方面。
6.每个参赛队应严格按照要求独立完成竞赛论文,如有雷同,取消参赛资格。
7.竞赛题目可从竞赛QQ群758156250自行下载(时间2021.4.27 0:00可开始下载)。
8.参赛作品提交方式:每个参赛队将完成的论文纸制版于2021年5月1日17:00前
交至郑州轻工业大学东风校区西二楼110室。
9.竞赛QQ群:758756250。
10.竞赛评奖公布:2021年5月初。
11.竞赛其他事宜:注意参看竞赛群公告。
本规范的最终解释权属于郑州轻工业大学第十三届“中国电机工程学会杯”全国大学生电工数学建模竞赛校内选拔赛组委会。
第十三届“中国电机工程学会杯”全国大学生
电工数学建模竞赛校内选拔赛组委会
2021年4月。
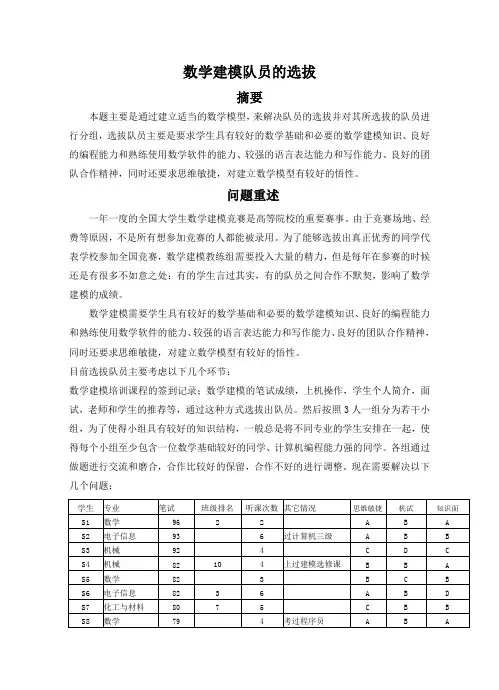
数学建模队员的选拔摘要本题主要是通过建立适当的数学模型,来解决队员的选拔并对其所选拔的队员进行分组,选拔队员主要是要求学生具有较好的数学基础和必要的数学建模知识、良好的编程能力和熟练使用数学软件的能力、较强的语言表达能力和写作能力、良好的团队合作精神,同时还要求思维敏捷,对建立数学模型有较好的悟性。
问题重述一年一度的全国大学生数学建模竞赛是高等院校的重要赛事。
由于竞赛场地、经费等原因,不是所有想参加竞赛的人都能被录用。
为了能够选拔出真正优秀的同学代表学校参加全国竞赛,数学建模教练组需要投入大量的精力,但是每年在参赛的时候还是有很多不如意之处:有的学生言过其实,有的队员之间合作不默契,影响了数学建模的成绩。
数学建模需要学生具有较好的数学基础和必要的数学建模知识、良好的编程能力和熟练使用数学软件的能力、较强的语言表达能力和写作能力、良好的团队合作精神,同时还要求思维敏捷,对建立数学模型有较好的悟性。
目前选拔队员主要考虑以下几个环节:数学建模培训课程的签到记录;数学建模的笔试成绩,上机操作,学生个人简介,面试,老师和学生的推荐等,通过这种方式选拔出队员。
然后按照3人一组分为若干小组,为了使得小组具有较好的知识结构,一般总是将不同专业的学生安排在一起,使得每个小组至少包含一位数学基础较好的同学、计算机编程能力强的同学。
各组通过做题进行交流和磨合,合作比较好的保留,合作不好的进行调整。
现在需要解决以下几个问题:学生专业笔试班级排名听课次数其它情况思维敏捷机试知识面S1数学96 22 A B A S2电子信息93 6过计算机三级 A B B S3机械92 4 C D C S4机械82 104上过建模选修课 B B A S5数学82 3 B C B S6电子信息82 36 A B D S7化工与材料80 75 C B B S8数学79 4考过程序员 A B AS, , 9电子信息78 124学过MATLAB A C C S10电子信息77 5学过MATLAB A B B S11化工与材料76 6 C A B S12化工与材料74 2 A C A S13计算机78 2 B A D S14计算机76 5 A B A S15计算机66 6 C B B1.根据你们所了解的数学建模知识,选拔数学建模队员要考察学生的哪些情况?哪些素质是数学建模的关键素质,如何进行考察?2.根据上表中信息,建立建模队员选拔的数学模型,从中选出9位同学,并组成3个队,使得这三个队具有良好的知识机构。

成功组织并指导学生参加全国数学建模竞赛全国数学建模竞赛是中国最具影响力和参与度高的数学竞赛之一。
它旨在提高学生在数学、统计和计算科学领域的综合能力。
成功组织并指导学生参加全国数学建模竞赛对于学生的学习成果、个人发展和学校声誉都有着重要的意义。
本文将探讨如何成功组织并指导学生参加全国数学建模竞赛。
一、了解竞赛规则和要求在组织学生参加全国数学建模竞赛之前,我们首先要了解竞赛的规则和要求。
该竞赛通常由主办方发布竞赛题目,要求参赛学生在一定时间内完成,并提交解题报告和相关材料。
我们需要仔细研读竞赛题目,了解解题要求、评分标准和提交截止日期,以便顺利组织学生参赛。
二、选拔合适的参赛学生成功组织并指导学生参加全国数学建模竞赛,需要我们有明确的选拔机制,以确保选派的学生具备相应的数学基础和竞赛能力。
我们可以通过举办校内预选赛、组织数学建模培训班等方式来选拔合适的学生。
参赛学生应该具备较强的数学思维能力、解决实际问题的能力和团队合作精神。
三、制定合理的备赛计划在学生选拔完成后,我们需要制定合理的备赛计划,确保学生能够充分准备竞赛。
备赛计划可以包括以下内容:1. 深入学习数学建模相关知识:我们可以组织针对竞赛题型的培训,让学生系统学习数学建模的基础知识和方法,提高解题能力。
2. 队内合作与分工:数学建模竞赛通常是以小组形式参赛,我们需要指导学生合理分工,明确每个队员的职责和任务,培养团队合作意识。
3. 解题技巧与经验分享:我们可以邀请曾经获奖或有丰富竞赛经验的学生来分享解题技巧和经验,启发其他队员的思维,提高整个团队的竞赛水平。
四、提供良好的竞赛环境和支持为了提高学生参赛的效果和体验,我们需要为他们提供良好的竞赛环境和全面的支持:1. 提供必要的学习资源:为学生提供各类适合竞赛题目的数学教材和学习资料,帮助他们在备赛过程中有更好的准备。
2. 配备必要的设备和软件:为了便于学生进行模拟训练和实际解题过程,我们需要配备必要的计算机、软件和相关设备。

2014年河南科技大学模拟训练一承诺书我们仔细阅读了数学建模选拔赛的规则.我们完全明白,在做题期间不能以任何方式(包括电话、电子邮件、网上咨询等)与队外的任何人研究、讨论与选拔题有关的问题。
我们知道,抄袭别人的成果是违反选拔规则的, 如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺,严格遵守选拔规则,以保证选拔的公正、公平性。
如有违反选拔规则的行为,我们将受到严肃处理。
我们选择的题号是(从A/B/C中选择一项填写): A 队员签名:1.2.3.日期: 2014 年月日2014年河南科技大学数学建模竞赛选拔编号专用页评阅编号(评阅前进行编号):我校数学建模竞赛参赛队员选拔与组队摘要一年一度的全国大学生数学建模竞赛是高等院校的重要赛事。
但在对参赛队员进行选拔时,往往会遇到很多难题,以至有时并不能选出真正优秀的队员代表学校参加全国竞赛。
本文通过建立数学模型研究了数学建模竞赛参赛队员选拔与组队问题。
我们针对本题所要解决的实际问题,提出了不同的模型或算法,过程如下:问题一:假设问题给出的数据均为可供分析的可靠数据,不存在错误数据,利用SPSS对已给数据进行标准化处理;EXCEL分析数据;主成分分析法对影响综合成绩的五个因素:校内竞赛答题稿成绩、校内竞赛答题稿答辩成绩、数学模型公选课测试成绩、软件比赛成绩、三次模拟点评成绩,做无关性处理;从而作出五个环节的成绩汇总表(表1);问题二:根据成绩汇总表(表1)用SPSS作单个样本统计量表(表2);对统计量作T检验得单个样本检验表(表3);由表2和表3得出第一组评委比较严格,第四组和第五组评委比较松;问题三:利用席位分配(Q值法)从参加竞赛的120个队中选出相对优秀的36个队公费参加全国竞赛;根据评奖标准各个高校最多推荐10个国家奖,最后我们首先利用层次分析法计算出准则层(P)对目标层(O)的权重再利用动态规化法对选出的10个队进行重新组队,用MATLAB求解,选出整体实力最强的组队法,以及最佳组合阵容,使得我校获得全国奖最大化。

2014年宁夏师范学院大学生数学建模校内选拔赛承诺书我们仔细阅读了《全国大学生数学建模竞赛章程》和《全国大学生数学建模竞赛参赛规则》(以下简称为“竞赛章程和参赛规则”,可从全国大学生数学建模竞赛网站下载)。
我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与队外的任何人(包括指导教师)研究、讨论与赛题有关的问题。
我们知道,抄袭别人的成果是违反竞赛章程和参赛规则的,如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺,严格遵守竞赛章程和参赛规则,以保证竞赛的公正、公平性。
如有违反竞赛章程和参赛规则的行为,我们将受到严肃处理。
我们授权全国大学生数学建模竞赛组委会,可将我们的论文以任何形式进行公开展示(包括进行网上公示,在书籍、期刊和其他媒体进行正式或非正式发表等)。
我们参赛选择的题号是(从A/B/C/D中选择一项填写): C我们的参赛报名组号为:第4 组所属学校(请填写完整的全名):宁夏师范学院参赛队员(打印并签名) :1. 赵倩2. 高瑞宁3. 杨金仓指导教师或指导教师组负责人(打印并签名):杨纪华(论文纸质版与电子版中的以上信息必须一致,只是电子版中无需签名。
以上内容请仔细核对,提交后将不再允许做任何修改。
如填写错误,论文可能被取消评奖资格。
)日期:2013 年12月22日关于饮料罐的制罐用料问题的分析[摘要]本文对饮料罐的最优设计主要从节省用料的角度研究。
建立模型时,在满足体积以及其它设计要求的限制下,以用料最少为目标建立最优化模型。
求解模型的主要方法包括:lagrange 乘子法、条件极值法以及数学软件(matlab)求解等。
在对饮料罐形状及尺寸设计进行研究时,需要选择适当的工具,运用多次测量求平均值的方法确定出必要的数据。
实际中饮料罐的设计考虑到多方面的因素,如美观、实用、生产、运输以及其自身各部分的抗压能力等。


对高校数学竞赛和数学建模竞赛的思考和建议摘要:分析高校数学竞赛和数学建模竞赛的异同。
对高校数学竞赛和数学建模竞赛提出若干建议。
关键词:数学竞赛;数学建模;建议中图分类号:g642.0 文献标志码:a 文章编号:1674-9324(2013)09-0116-02数学是一门科学,也是一门艺术,更是一种文化。
在大学生中开展数学竞赛和数学建模竞赛活动可以视为数学文化在高校中的一种普及。
一、高校数学竞赛和数学建模竞赛的比较在高校数学教育中,高校数学竞赛和数学建模竞赛属于竞赛数学的范畴,竞赛数学更多的体现素质的培养和能力的发展。
二者之间既有差异,也有联系。
1.高校数学竞赛和数学建模竞赛的侧重点不同。
高校数学竞赛是一种基础型数学竞赛,侧重于学生对基础知识的掌握。
以全国大学生数学竞赛为例,它的赛题主要集中在微积分课程范围内,少部分涉及到高等代数课程。
数学建模竞赛是一种应用型数学竞赛。
数学建模竞赛的问题来自于工程技术、经济、生物、交通运输等领域。
解决这些问题需要从问题对象中提取信息,将这些信息转化为数学语言,建立模型,应用所学的数学知识(主要是分析、代数、概率、运筹学方面的知识)解决数学模型,并对原始问题进行解释验证或预测。
数学建模的并无确定答案。
从对学生素质的培养这个角度看,数学竞赛促进学生的纵向发展。
要在数学竞赛中取得成绩,学生学好基础知识是必要条件,此外还需要掌握较深的内容。
而数学建模竞赛较好地体现了对学生横向思维和发散思维能力的促进。
因为数学建模的问题一般来自其他领域,学生必须把掌握的数学知识进行整合,对问题进行综合整理。
一篇好的数学建模答卷就是一篇优秀的数学论文。
2.高校数学竞赛和数学建模竞赛在本质上是一种基础教育,也是一种素质教育。
数学教育逐渐从传统的灌输式教育向开放式教育过渡。
高校数学竞赛和数学建模竞赛所体现出的数学教育,是开放式教育的一种表现形式。
学生的数学知识一般是在课堂上获得的,但要培养学生的数学兴趣,必须将学生引入到种种数学活动中,数学竞赛和数学建模竞赛正是这样的一个较好的平台,是一种培养学生的兴趣的好的活动,为学有余力的学生提供了表现数学才能和天赋的机会。
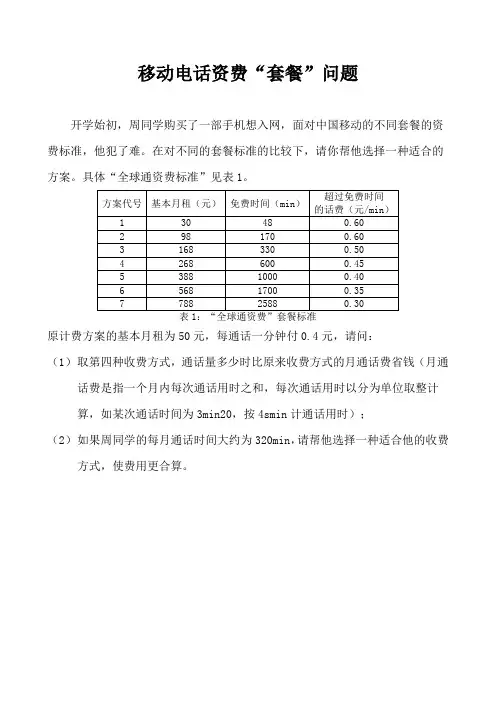
移动电话资费“套餐”问题开学始初,周同学购买了一部手机想入网,面对中国移动的不同套餐的资费标准,他犯了难。
在对不同的套餐标准的比较下,请你帮他选择一种适合的方案。
具体“全球通资费标准”见表1。
原计费方案的基本月租为50元,每通话一分钟付0.4元,请问:(1)取第四种收费方式,通话量多少时比原来收费方式的月通话费省钱(月通话费是指一个月内每次通话用时之和,每次通话用时以分为单位取整计算,如某次通话时间为3min20,按4smin计通话用时);(2)如果周同学的每月通话时间大约为320min,请帮他选择一种适合他的收费方式,使费用更合算。
内容摘要现在的生活中,到处都用手机了,可是很多人,不知道怎样省话费,怎样充分的利用话费,今天我们就一起来讨论这个问题,让每一个人都利用好自己的手机话费,充分的选择正确的话费套餐。
关键词套餐,省钱,数学模型一:问题重述购买手机入网,套餐有如表1的标准,请选同人,不同需求合适的套餐。
套餐表1原计费方案的基本月租为50元,每通话一分钟付0.4元,请问:(3)取第四种收费方式,通话量多少时比原来收费方式的月通话费省钱(月通话费是指一个月内每次通话用时之和,每次通话用时以分为单位取整计算,如某次通话时间为3min20,按4smin计通话用时);(4)如果周同学的每月通话时间大约为320min,请帮他选择一种适合他的收费方式,使费用更合算。
二:基本假设假设1:用户一个月都用这个套餐假设2:用户一个月客服都不增加其他的套餐 三:符号说明X 为总话费,y 总通话时间,z 为免费时间内通话的时间。
四:分析建模求解 1:在二基本假设的范围内,可得出: X=z*0.4 则由matlab 可得的如图:附录1 按照第4种收费的方式可得:X=268<50+0.45*600 所以有:X=268+0.45*(z-600)>50+0.4*z 0.85z>52 解得z>61.1764704 则由matlab 可得的如图:附录2 两个图组合图如:附录3第二小问:根据题目和第二步的假设可得一下三种方案可公选⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧--++=-+=-+=)17048(*60.0983006.0*)170(9860.0*)48(30z x z x z x 如附录3解这三个二元一次方程,当z=320时第二个方案最合适。


数学建模混合泳接力队选拔摘要本文研究的是体育赛事中混合泳队员的选拔问题。
结合运筹学中的指派问题及应用线性规划理论,我们建立0-1整数规划数学模型,运用MATLAB软件对模型进行求解,得出了较为科学的选拔方案。
为了从5名候选人中选出4名队员组成接力队,参加4×100米混合泳比赛,我们以5位候选人的平时游泳成绩的数据为基础,运用0-1整数规划建立相关的数学模型,求解出乙进行蝶泳→丙进行仰泳→丁进行蛙泳→甲进行自由泳的比赛方案。
此比赛方案下的比赛最佳总得分为z=251.4s。
混合泳的比赛成绩除了和团队的配合及一些外部因素相关外,更与队员在不同时期内的比赛发挥相关。
因此,当候选人的在成绩发生变化时,我们应依据具体情况,优化游泳队的选拔方案。
当然我们的模型也存在不足之处,在模型的改进中提出了改进方法。
关键字:混合泳队员选拔指派问题线性规划理论 0-1规划模型一、问题重述现拟从5名候选人中选出4名队员组成接力队,参加4100 米混合泳比赛。
5名队员的4种泳姿的百米平均成绩如下表:5名队员的4种泳姿的米平均成绩(表一)1.如何选择队员进行接力队才能获得最佳成绩?2.若队员丁的蛙泳成绩退步到1’15”2,戊的自由泳成绩进步到57”5,组成接力队的方案又当如何?二、问题分析混合泳队员的选拔问题中,主要有以下几个难点:①每个队员比赛成绩数据的分析;②每个队员进行哪个项目才能使团队混合泳成绩最佳;③当有队员的一些项目比赛成绩发生变化时,接力队方案如何选择。
因此,在怎样的选拔机制下,如何处理搜集的数据,建立何种数学模型,是我们首先要解决的问题。
对于问题一,如何选择队员进行接力赛才能使团队获得最佳成绩。
根据5名队员4种泳姿的百米平均成绩,由穷举法我们可以计算出最多有120种选拔方案。
假设队员在比赛现场发挥的成绩与其平均成绩一致。
我们结合0-1规划的思想,以混合泳 甲 乙 丙 丁 戊 蝶泳 1’06”8 57”2 1’18’ 1’10” 1’07”6 仰泳 1’15”6 1’06” 1’07”8 1’14”2 1’11” 蛙泳 1’27” 1’06”4 1’24”6 1’09”6 1’23”8 自由泳 58”6 53” 59”4 57”2 1’02”4总成绩最佳为目标函数,依据其各泳姿的百米平均成绩,建立合理的数学模型,由MATLAB 迅速求解选拔方案。
数学建模比赛策划一、引言数学建模比赛是一种培养学生探索、分析和解决实际问题能力的重要途径。
本文将详细介绍如何策划一场具有挑战性和教育意义的数学建模比赛。
二、比赛主题选择1. 确定比赛的领域和范围:数学建模涵盖广泛的领域,如经济学、物理学、生物学等。
根据参赛学生的年级和经验,选择适合的比赛领域。
2. 确定比赛的主题:主题应该是一个实际的问题,能够激发参赛学生的兴趣和热情。
同时,主题应该有一定的挑战性,有助于培养学生的分析和解决问题能力。
三、参赛队伍报名1. 宣传比赛信息:通过学校官网、校内电子公告栏、班级群等渠道宣传比赛信息,引起学生的关注。
2. 报名方式:提供在线报名通道,确保学生能够便捷地完成报名手续。
同时,鼓励学生组队参赛,以促进合作和团队精神的培养。
四、比赛安排1. 比赛时间:选择一个合适的时间段,避免与其他重要考试或活动冲突,以确保学生能够全身心地投入到比赛中。
2. 比赛形式:考虑到每位参赛学生的时间和能力限制,可以将比赛分为若干阶段。
初赛可以采用在线编程或书面答题形式,决赛可以组织现场答辩或报告展示。
3. 比赛规则:制定清晰的比赛规则和评分标准,确保比赛的公平性和公正性。
规则包括时间限制、作答格式要求等。
五、比赛题目设计1. 题目数量与类型:根据比赛的时间安排和参赛人数,确定合适的题目数量。
同时,题目类型应该多样化,包括理论分析、建模求解和实际应用等。
2. 题目难度:根据参赛学生的年级和水平,设置不同难度的题目,以促进学生的思维发展和能力提升。
六、评委选拔与培训1. 评委选拔:从学校的教师团队中选拔具有丰富数学建模经验和专业知识的老师作为评委,确保评分的准确性和公正性。
2. 评委培训:组织评委培训,介绍比赛的规则和评分标准,并进行案例分析和讨论,以提高评委的评判水平。
七、奖项设置1. 奖项等级:根据参赛队伍的表现,设置一、二、三等奖等奖项,以及优秀组织奖、最佳创意奖等特别奖项。
2. 奖项设置:奖品可以是实物奖品、证书或者奖学金等形式,以激励学生的学习热情和参赛动力。
2013数学建模组别:第四组题目:评阅问题数学建模论文校内选拔赛的评阅问题摘要自1985年全国数学建模大赛开始举办,越来越受各大高校和广大学生的关注。
竞赛后的评阅试卷过程往往需要很大的人力物力,如何评阅最少的试卷与最小的评分误差就能将优胜者选出是本文解决的关键问题。
对于问题一,为了实现兼顾公平,效率优先,我们制定如下两个指标:一是公平度,即必须保证评阅过程以及评阅结果公平、合理,必须避免因为评阅者的偏好不同或其它因素而对参赛论文造成误判;二是高效率,即面对大量答卷,既要在尽量短时间内完成阅卷,又要减少每位评阅者的阅卷数量,即使每位评阅者的工作量越少越好。
对于问题二,我们根据上述指标对题中所给方案进行合理性和缺点评价。
相对于理想情况,每个评阅者评阅所有答卷的方法,题中所述评阅方案评阅时间、评阅人数相对减少,评阅效率相对提高,但相对公平度较低。
对于问题三,题目中用到四个变量P 、M 、S 、N ,我们通过查阅大量权威资料,对其之间存在的意义关系进行深入分析,试图建立其相关量间的规划模型。
在此过程中,引入阅卷循环次数变量n ,利用等比求和公式得到剩余论文量N 与淘汰率S 之间的关系;并以P M 为约束条件,以淘汰率S 相对较小来求解每位评阅者评阅答卷总份数记为y ,建立y 与M 、S 、N 和n 的目标函数。
假设每位评阅者阅卷量相同,采用计算机模拟,通过具体数据得到每位阅卷者所评阅的答卷总份数。
对于问题四,根据现实生活中的评卷情况,我们构建系统偏差模型。
通过对整个评卷过程系统偏差值1W 和2W 进行累加求和,计算出阅卷人最小的阅卷份数。
采用列举法将一些方案列出,根据计算机不断模拟打分,取各方案中此两个值均较小的方案作为最佳评卷策略。
根据模拟出的结果,进行分析之后得出分组方案还与试卷分数的方差有关,分数离散度越大评卷的次数越小,分数越集中评卷的次数越大。
关键词:公平度 高效率 淘汰率 规划模型 计算机模拟 系统偏差 离散度一、问题重述自1985年全国数学建模大赛开始举办,参赛学校不断增多,参赛人数不断增加,给越来越多的学生提供了一个展示才华,丰富自我的平台,因此越来越受各大高校和广大学生的关注。
数学建模竞赛参赛队员的选拔与组队摘要如何选拔最优秀的队员并科学合理的组队,是一个非常具有实际意义的数学模型问题。
本篇文章根据实际数据,综合考虑各方面因素的影响,给出了可以判断队员组队情况好坏的一般规律,并联系实际,运用所得规律进行科学的预测。
为了给出可以判断队员组队情况好坏的一般规律,本文综合考虑队员的性别、所属学院类型、在校期间的成绩。
为了分析前两者的影响,本文对三类(获国家奖、获省奖、没获奖)队伍的性别分布及所属学院类型分布进行了对比。
发现:规律1:队员不同的性别组合对数学建模成绩没有显著影响。
规律2:三个队员中至少有两个来自理工类学院时,组队效果好。
三个队员都来自文科类学院,组队效果不好。
在分析成绩的影响时,首先,联合使用计算机筛选(以课程开设学院为筛选依据,仅筛选出统计与数学学院、计算机与信息工程学院、人文学院、马克思学院开设的课程)与人工筛选,选出每个人学过的能反映数学建模能力的所有课程。
根据实际经验,数学建模是数学能力、计算机能力和写作能力的综合运用,利用筛选出的成绩可以对每个人的各项能力进行量化。
而后,为了得到衡量数学建模综合能力的指标,本文利用层次分析法求解出数学能力、计算机能力、写作能力对数学建模综合能力的权重分别为0.5396、0.2969、0.1634。
文中使用了两种方法确定了两个综合能力指标,其一为队伍能发挥的最大综合能力,该指标下每个队伍的单项能力为三个队员该项能力的最大值;其二为平均综合能力,该指标下每个队伍的单项能力为三个队员该项能力的平均值。
经过对比,得到如下规律:规律3:队伍能发挥的最大综合能力越高,组队效果越好。
队伍能发挥的最大综合能力低于80.6时,组队效果不好,高于90.69时,组队效果非常好。
规律4:队伍能发挥的平均综合能力越高,组队效果越好。
队伍能发挥的平均综合能力低于75.32时,组队效果不好,高于88.48时,组队效果非常好。
根据以上规律对问题二的5支队伍进行预测,发现:这5支队伍都有很大的几率获奖(国家奖或省奖),X1很有可能获得国家奖,X5最好成绩应该为省奖。
云南大学旅游文化学院第一届大学生数学建模竞赛组织的通知全国大学生数学建模竞赛是全国高校规模最大的课外科技活动之一,于每年9月举行。
为培训和选拔我校优秀学生参加2014年全国大学生数学建模竞赛,特举办此次预选赛。
一、竞赛目的:激发学生学习数学的积极性,开拓知识面,提高学生独立分析问题、建立数学模型、运用计算机技术模拟解决实际问题、论文写作等的综合能力,鼓励广大青年学生在基础及应用学科研究中推陈出新,提升对数学科学理论及其应用的价值认识;加强数学与经济金融、计算机等学科之间的联系,促进数学教育改革;培养学生的创造精神及合作意识,塑造同学们的科创意识与团队精神,为同学们将来能更好地走上社会、服务社会打下更为坚实的基础。
二、参赛对象及报名方式:1、参赛对象:信科系、会计系、经管系学生。
2、报名方式:参赛者以个人为单位报名,每队1人三、竞赛内容及相关要求:1、竞赛内容:本次预赛提供A、B两个竞赛题目,题目有较大的灵活性供参赛者发挥其创造能力,参赛者自选其中一个题目,根据题目要求,完成一篇包括模型的假设、建立和求解、计算方法的设计和计算机实现、结果的分析和检验、模型的改进等方面的论文(即答卷)。
2、竞赛时间:6月10日——6月20日3、竞赛要求:竞赛采取开放形式,参赛学生可到信科系吕小俊、李睿、靳巧花老师处复制或到所在系部复制参赛试题,完成作品。
各参赛队于6月20日下午6点前完成论文,并将电子稿(WORD 或PDF版本)与打印稿交到信科系办公室2-204。
电子稿统一命名格式为“专业_姓名_学号”,如“国贸_张三_088”。
论文(包括电子稿与打印稿)需要制作论文封面,论文封面参见附件三。
论文不得抄袭,如发现论文抄袭,直接取消参赛资格!四、奖项设置根据参赛情况评选出一等奖5%,二等奖10%,三等奖20%及优胜奖若干。
获奖者可获得由学院颁发的证书,并参加2014年全国大学生数学建模大赛校内集训。
联系人及电话:杨七九 086(办公室)附件:1、预赛试题A题2、预赛试题B题3、数学建模论文格式4、数学建模论文范文5、数学建模论文封面云南大学信息科学与技术系二〇一四年六月十日附件1云南大学旅游文化学院数学建模竞赛选拔说明:竞赛试题共有A、B试题两种,参赛学生任选一种试题,写成数学建模论文的形式,论文参照格式见附件3,参照论文见附件4。
美国大学留学申请问题的数学模型摘要本文将申请美国大学研究生录取的问题和根据自身经济条件选择学校数问题分别转化成层次分析问题和线性规划中的 0-1 规划问题,从而帮助申请人做结果的定性和定量评估。
首先利用层次分析法考虑影响录取因素对申请留学的学生进行分析,得出一个申请人被录取的可能性;再考虑申请人是否曾经发表过相关专业的论文,或是参加了一些竞赛并获奖等优势条件对模型进行改善。
在资金有限的条件下,对于申请学校数问题,我们利用0-1规划方法,在极大可能性被录取的条件下,用Matlab软件计算被录取的学校和最少的费用支出。
在以上模型的条件下,本文给出了合理选择学校的分析报告,帮助申请人能取得好的申请结果,多拿“offer”。
本文的最终模型可扩展性好,算法复杂度低,较好的解决了本文提出的所有问题。
关键词:集对分析法层次分析法 0-1规划比例系数一问题重述现在,越来越多的学生选择去海外留学,尤其是美国。
校园中随处可见考托、考G者的身影。
申请的程序很繁杂,录取的时候影响因素也很多。
为了这些同学都能取得好的申请结果,多拿“offer”。
现在我们建立一个模型,来帮助他们做结果的定性和定量评估。
本次模型主要考虑的对象是申请美国研究生的同学,包括硕士研究生(master)和博士研究生(Ph.D.)。
不考虑申请其它国家和申请本科、博后的情况。
问题一:一个申请人是否能够被录取,需要考虑很多因素,比如申请的专业、他/她的平均成绩(GPA)、托福分数、GRE分数、班级/专业排名等等。
现在,我们假设一个申请人只能申请一个学校。
请根据以上列举的影响因素建立模型,来计算一个申请者录取的可能性。
如果一个申请人曾经发表过相关专业的论文,或是参加了一些竞赛并获奖(例如全国大学生数学建模竞赛、美国大学生数学建模竞赛、电子设计竞赛等),这样他/她就会比其他人更有优势,从而拿到“offer”。
请考虑以上两个因素,进而改善你们的模型。
问题二:大多数情况下,一个申请人会同时申请多个学校。
申请的学校越多,获得录取的可能性也就越大。
但是,每一次申请都需要缴纳不菲的申请费和材料寄送费。
如果一个申请人认为只要能拿到一个录取就算是成功的,在资金有限的情况下,他/她应该申请几个学校呢?请建立模型,帮助你的同学做分析。
问题三:几乎所有的申请人都想拿到美国顶尖学校的录取通知,比如麻省理工学院、哈佛大学、斯坦福大学等。
可是,学校的排名越高,获得录取的可能性就越小。
根据你的模型,写一份分析报告,帮助申请人合理的选择学校。
二模型的假设模型假设1.学校择优录取,成绩好的被录取的可能大,即不考虑人际关系等等因素;2.各年GRE成绩变化是一平缓的过程;3.各年申请者的GDP变化是一平缓过程;4.各年被申请学校的录取标准基本不变。
三符号说明四模型的建立与分析美国大学研究生录取问题和公司人力资源配置问题非常类似,都是通过双向选择更好地优化组织的人员结构,提高组织的整体效能。
由于在实际操作中尚缺乏科学,可行的方法,往往达不到理想的效果。
我们知道,组织是一个多因素,多层次的人造系统,是由许多相互作用相互依存的要素组成的有机整体,要使它形成一个合理、有效的结构,必须将人员配置的方法建立在对构成组织的相关要素进行综合、系统分析和客观评价的基础上。
考虑到组织的人员结构是不同素质、不同能力的人在组织内各岗位上的分布状态。
我们建模的思路是,以使申请人拿到更多的“offer”为目标,通过对申请人、学校进行定量测评和综合分析,建立一个系统优化模型,以此寻求申请人申请合理的学校及学校数,实现申请的优化。
以下就方法和模型的建立分步阐述:(一)、用层次分析法对申请人进行分析(1)层次分析法介绍:层次分析法是一种定性与定量相结合的、系统化、层次化的分析方法,它用来帮助我们处理决策问题。
特别是考虑的因素较多的决策问题,而且各个因素的重要性、影响力、或者优先程度难以量化的时候,层次分析法为我们提供了一种科学的决策方法。
层次分析法的基本思路与人对一个复杂的决策问题的思维、判断过程大体上是一致的。
现在便用层次分析法模型来对10名申请人做排序。
设最上层为目标层,即某个美国大学;中间层为准则层,申请的专业、他/她的平均成绩(GPA)、托福分数、GRE分数、班级/专业排名语等 5个准则;最下层为方案层,有 10 名学生供选择。
各层联系用相连的直线表示。
(如下图)目标层 准则层 方案层图 1:申请人录取的层次结构通过相互比较确定各准则对于目标的权重,及各方案对于每一准则的权重。
这些权重在各所美国大学的录取过程中通常是定性的,而在层次分析法中则要给出得到权重 的定量方法。
考虑到待选学生 5 个评测因素中,申请的专业、他/她的平均成绩(GPA )、托福分数、GRE 分数、班级/专业排名语等 5个准则等相比并不太重要,因此我们现在主要对这 5 个因素分配合理的权重,而权重的计算一般用 Saaty 提出的 AHP 法。
(2)具体计算权重的 AHP 法:AHP 法是将各要素配对比较,根据各要素的相对重要程度进行判断,再根据计算成对比较矩阵的特征值获得权重向量W k 。
被所报学校录取GPA 分 数 GRE 分 数专 业 排 名专 业 热 门 成 度托 福学生Step1. 构造成对比较矩阵比较第二层5个因素C1,C2,C3,C4,C5。
对一层因素Z的影响,每次两个因素Ci,Cj,用Cij表示Ci和Cj对Z的影响之比,全部比较结果构成成对比较矩阵,也叫正互反矩阵。
Step2.计算该矩阵的权重通过解正反矩阵的特征值,可求得相应的特征向量,经归一化后即为权重向量Step3. 一致性检验为了度量判断的可靠程度,可计算此时的一致性度量指标CIλ-n)/(n-1)CI= (m axλ表示矩阵C的最大特征值,CI越小说明权重的可靠性越高。
当CR = 其中m axCI/< 0.1 时,(CR称为一致性比率,RI是通过大量数据测出来的随机一致RI性指标,可查表找到(详见附录1))可认为判断是满意的,此时的正互反矩阵称之为一致性矩阵。
进入 Step4. 否则说明矛盾,应重新修正该正互反矩阵。
转入 Step2.Step4. 得到最终权值向量将该一致性矩阵任一列或任一行向量归一化就得到所需的权重向量。
(3)按权重大小进行申请人录取将计算出来的方案层对准则层的权重及准则层对目标层的权重进行综合,最终确定方案层对目标层的权重,也即不同申请人在多因素考虑下的最终权重。
这样一来,我们就可以按权重大小进行申请人录取工作了。
假设第一层(目标层)只有一个元素,第二层(规则层)有 5 个元素,第三层(方案层)有10个元素。
假设通过第二层对第一层的正互反矩阵计算得到第二层对第一层的权向量为W2∈5R,同样方法构造第三层对第二层的每一项的正互反矩阵,将得到5个10 * 10 的矩阵,求解得到5个权向量W r3∈5R , r =1,2,...,5,将这p个向量排成一个矩阵Q∈5*10R,则Q *W2为一个 10维的列向量,其中的第i个元素就代表方案i对目标的权重,三层以上的情况可以类似得到。
五模型的实现及求解1.问题一建立一个模型,计算一个申请者是否能被录取为了讨论该模型合理性,需要计算一组数据。
因为每年申请大学的学生的成绩完全是随机的,即成绩的分布没有固定的比例,故可以用计算机模拟出少数样本来进行测试,从结果中进行分析。
随机模拟了10组GPA、GRE的成绩,各人的系内排名,及其专业的热门指数、托福分数具体情况如下(假设所有学生都来自同一所学校):模型分析结合层次分析法和集对分析法进行学生录取在只考虑申请的专业、他/她的平均成绩(GPA)、托福分数、GRE分数、班级/专业排名语等 5个因素情况下,可以确定研究生的录取名额。
成绩影响因素相同,因此直接利用层次分析法中的 AHP 法效果会比较随机,因此我们选择采用集对分析法得到初始权值和相应的正互反矩阵,再用 AHP 法对其进行修正,按照最终的权值计算申请人每个指标的成绩。
模型建立以下构造判断矩阵步骤:(1)自上而下,先求判断矩阵A的最大特征根与特征向量。
由上表可知:m axλ=5.6698对应于m axλ的正规化的特征向量为:)2(W =()T1203.0,1493.0,3647.0,1249.0,2407.0(2)计算与准则层各准则相关的判断矩阵最大特征跟及权向量: C1-P 矩阵1B由上表可得:m axλ=11.0624,对应于m axλ的正规化的特征向量为:)3(1W =()T 1056.0,0840.0,1269.0,0800.0,0904.0,0820.0,1338.0,0808.0,1155.0,1008.0(3)用matlab 软件算出2B ,5,43,B B B 的最大特征值(详见附录2)分别为)2m ax(λ=()11.2029,)3m ax(λ=10.8054,)4m ax(λ=10.7436,)5m ax(λ=10.9244 所对应的特征向量分别为:)3(2W =()T ,0.14679250.0851,0.0, ,0.0893 ,0.1317 ,0.0816 ,0.1072 ,0.0792 0.0975 , 0.0893)3(3W =()T0.1144 0.0925 0.1116 0.0961 0.0879 0.1179 0.0838 0.1103 0.0848 0.1007)3(4W =()T0.0931 0.0931, 467,0.0840,0.1 3,0884,0.101,0.1143,0.214,0.07610.0817,0.1)3(5W ()T0.136 0.1145 0.0812 0.0915 0.0837 0.1060 0.1359 0.0789 0.0895 0.0915 =以 )3(K w 为列向量构成矩阵:),,,,()3(5)3(4)3(3)3(2)3(1)3(W W W W W W =(4)一致性检验:由以上表格可得检验矩阵A 一致性:CR<0.1同理,对于第二层次的GPA 分数B1、GRE 分数B2、专业排名B3、专业热门度B4、托福分数的B5五个判断矩阵的一致性检验均通过。
(5)层次总排序各个方案优先程度的排序向量为:==)2()3(*W W W ()T0.1157 0.0932 0.1131 0.0890 0.0955 0.0989 0.1096 0.0904 0.0998 0.0953若录取权重比重应大于0.1,则录取结果是 第4、8、10位申请者 。
2.问题一优化 发表了一些论文,或者曾经在竞赛中获奖(例如MCM ),被录取的可能性也将增加。
所以模型应该改进。
符号说明 t1——获得奖项的影响力;t2——申请专业与获奖类别的相关性;模型建立 竞赛取得成绩(或者论文的发表)的作用反映到申请上就在于提高了申请者获得offer 的概率,但并非所有竞赛(或论文发表)都能使一个GPA,GRE 成绩平平的申请者获得offer ,类似省内或者国内的大多数竞赛只能锦上添花,真正使申请者脱颖而出的是国际性的比赛获奖记录(或在国际性刊物上发表论文)。