高考数学(文)一轮总复习检测：第三章 第四节 函数y=Asin(ωx+φ)的图象及三角

2009~2013年高考真题备选题库 第3章 三角函数、解三角形第4节 函数y ＝Asin(ωx ＋φ)的图像及三角函数模型的简单应用考点 函数y ＝Asin(ωx ＋φ)的图像 1．（2013山东，5分）函数y ＝xcos x ＋sin x 的图象大致为( )解析：本题考查函数的性质在分析判断函数图象中的综合运用，考查一般与特殊的数学思想方法，考查运算求解能力，考查综合运用知识分析问题和解决问题的能力．函数是奇函数，图象关于坐标原点对称，当0<x<π2时，显然y>0，而当x ＝π时，y ＝－π<0，据此排除选项A 、B 、C ，正确选项为D. 答案：D2．(2013福建，5分)将函数f(x)＝sin (2x ＋θ)⎝ ⎛⎭⎪⎫－π2<θ<π2的图像向右平移φ(φ>0)个单位长度后得到函数g(x)的图像，若f(x)，g(x)的图像都经过点P ⎝ ⎛⎭⎪⎫0，32，则φ的值可以是( ) A.5π3 B.5π6 C.π2D.π6解析：本题主要考查三角函数图像的变换及三角函数值求角等基础知识，意在考查考生的数形结合能力、转化和化归能力、运算求解能力．因为函数f(x)的图像过点P ，所以θ＝π3，所以f(x)＝sin ⎝ ⎛⎭⎪⎫2x ＋π3；又函数f(x)的图像向右平移φ个单位长度后，得到函数g(x)＝sin ⎣⎢⎡⎦⎥⎤－φ＋π3，所以sin ⎝ ⎛⎭⎪⎫π3－2φ＝32，所以φ可以为5π6. 答案：B3．（2013新课标全国Ⅱ，5分）函数y ＝cos(2x ＋φ)(－π≤φ<π)的图像向右平移π2个单位后，与函数y ＝sin ⎝⎛⎭⎪⎫2x ＋π3的图像重合，则φ＝________. 解析：本题主要考查三角函数图像的平移、三角函数的性质、三角运算等知识，意在考查考生的运算求解能力及转化与化归思想的应用．将y ＝cos(2x ＋φ)的图像向右平移π2个单位后得到y ＝cos ⎣⎢⎡⎦⎥⎤2⎝ ⎛⎭⎪⎫x －π2＋φ的图像，化简得y ＝－cos(2x ＋φ)，又可变形为y ＝sin ⎝ ⎛⎭⎪⎫2x ＋φ－π2.由题意可知φ－π2＝π3＋2k π(k ∈Z)，所以φ＝5π6＋2k π(k ∈Z)，结合－π≤φ<π知φ＝5π6.答案：5π64．（2013山东，12分）设函数f(x)＝32－3sin2ωx －sin ωxcos ωx(ω＞0)，且y ＝f(x)图像的一个对称中心到最近的对称轴的距离为π4.(1)求ω的值；(2)求f(x)在区间⎣⎢⎡⎦⎥⎤π，3π2上的最大值和最小值． 解：本题主要考查三角函数的图像和性质，考查转化思想和运算能力． (1)f(x)＝32－3sin2ωx －sin ωxcos ωx ＝32－3·1－cos 2ωx 2－12sin 2ωx ＝32cos 2ωx －12sin 2ωx ＝－sin ⎝⎛⎭⎪⎫2ωx －π3.因为图像的一个对称中心到最近的对称轴的距离为π4，又ω>0， 所以2π2ω＝4×π4，因此ω＝1.(2)由(1)知f(x)＝－sin ⎝ ⎛⎭⎪⎫2x －π3.当π≤x≤3π2时，5π3≤2x－π3≤8π3.所以－32≤sin ⎝⎛⎭⎪⎫2x －π3≤1.因此－1≤f(x)≤32. 故f(x)在区间π，3π2上的最大值和最小值分别为32，－1.5．(2012浙江，5分)把函数y ＝cos 2x ＋1的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变)，然后向左平移1个单位长度，再向下平移1个单位长度，得到的图象是( )解析：变换后的三角函数为y ＝cos(x ＋1)，结合四个选项可得A 选项正确． 答案：A6．（2010福建，5分）将函数f(x)＝sin(ωx ＋φ)的图象向左平移π2个单位．若所得图象与原图象重合，则ω的值不可能等于( ) A ．4 B ．6 C ．8 D ．12解析：由题意得：sin[ω(x ＋φω＋π2)]＝sin(ωx ＋φ)，则π2ω＝2k π，k ∈Z ，∴ω＝4k ，k ∈Z ，而6不是4的整数倍，故应选B.答案：B7．（2009天津，5分）设f(x)＝asin2x ＋bcos2x ，其中a ，b ∈R ，ab≠0，若f(x)≤|f(π6)|对一切x ∈R 恒成立，则 ①f(11π12)＝0②|f(7π10)|<|f(π5)|③f(x)即不是奇函数也不是偶函数④f(x)的单调递增区间是[k π＋π6，k π＋2π3](k ∈Z)⑤存在经过点(a ，b)的直线与函数f(x)的图像不相交以上结论正确的是________(写出所有正确结论的编号)．解析：f(x)＝asin2x ＋bcos2x ＝a2＋b2sin(2x ＋φ)(tan φ＝b a ，因为对一切x ∈R ，f(x)≤|f(π6)|恒成立，所以sin(π3＋φ)＝±1，可得φ＝2k π＋π6或φ＝2k π－5π6，故f(x)＝a2＋b2sin(2x ＋π6)或f(x)＝－a2＋b2sin(2x ＋π6)．而f(11π12)＝±a2＋b2sin(2×11π12＋π6)＝0，所以①正确；|f(7π10)|＝|a2＋b2sin 4730π|＝|a2＋b2sin 1730π|，|f(π5)|＝|a2＋b2sin 1730π|，所以|f(7π10)|＝|f(π5)|，故②错误；③明显正确；④错误；由函数f(x)＝a2＋b2sin(2x ＋π6)和f(x)＝－a2＋b2sin(2x ＋π6)图像可知，不存在经过点(a ，b)的直线与函数f(x)的图像不相交，故⑤错． 答案：①③8．(2009江苏，5分)函数y ＝Asin(ωx ＋φ)(A ，ω，φ为常数，A>0，ω>0)在闭区间[－π，0]上的图象如图所示，则ω＝________.解析：由图中可以看出： 32T ＝π，∴T ＝23π＝2πω， ∴ω＝3. 答案：39．（2012福建，14分）已知函数f(x)＝axsin x －32(a ∈R)，且在[0，π2]上的最大值为π－32.(1)求函数f(x)的解析式；(2)判断函数f(x)在(0，π)内的零点个数，并加以证明． 解：(1)由已知得f′(x)＝a(sin x ＋xcos x)， 对于任意x ∈(0，π2)，有sin x ＋xcos x>0.当a ＝0时，f(x)＝－32，不合题意；当a<0时，x ∈(0，π2)时，f′(x)<0，从而f(x)在(0，π2)内单调递减，又f(x)在[0，π2]上的图象是连续不断的，故f(x)在[0，π2]上的最大值为f(0)＝－32，不合题意；当a>0，x ∈(0，π2)时，f′(x)>0，从而f(x)在(0，π2)内单调递增，又f(x)在[0，π2]上的图象是连续不断的，故f(x)在[0，π2]上的最大值为f(π2)，即π2a －32＝π－32，解得a ＝1.综上所述，得f(x)＝xsin x －32.(2)f(x)在(0，π)内有且只有两个零点．证明如下：由(1)知，f(x)＝xsin x －32，从而有f(0)＝－32<0，f(π2)＝π－32>0，又f(x)在[0，π2]上的图象是连续不断的，所以f(x)在(0，π2)内至少存在一个零点．又由(1)知f(x)在[0，π2]上单调递增，故f(x)在(0，π2)内有且只有一个零点．当x ∈[π2，π]时，令g(x)＝f′(x)＝sin x ＋xcos x.由g(π2)＝1>0，g(π)＝－π<0，且g(x)在[π2，π]上的图象是连续不断的，故存在m ∈(π2，π)，使得g(m)＝0.由g′(x)＝2cos x －xsin x ，知x ∈(π2，π)时，有g′(x)<0，从而g(x)在(π2，π)内单调递减．当x ∈(π2，m)时，g(x)>g(m)＝0，即f′(x)>0，从而f(x)在(π2，m)内单调递增，故当x ∈[π2，m]时，f(x)≥f(π2)＝π－32>0，故f(x)在[π2，m]上无零点；当x ∈(m ，π)时，有g(x)<g(m)＝0，即f′(x)<0，从而f(x)在(m ，π)内单调递减．又f(m)>0，f(π)<0，且f(x)在[m ，π]上的图象是连续不断的，从而f(x)在(m ，π)内有且仅有一个零点．综上所述，f(x)在(0，π)内有且只有两个零点．10．（2012湖南，12分）已知函数f(x)＝Asin(ωx ＋φ)(x ∈R ，ω>0,0<φ<π2)的部分图象如图所示．(1)求函数f(x)的解析式；(2)求函数g(x)＝f(x －π12)－f(x ＋π12)的单调递增区间．解：(1)由题设图象知，周期T ＝2(11π12－5π12)＝π，所以ω＝2πT ＝2，因为点(5π12，0)在函数图象上，所以Asin(2×5π12＋φ)＝0，即sin(5π6＋φ)＝0.又因为0<φ<π2，所以5π6<5π6＋φ<4π3.从而5π6＋φ＝π，即φ＝π6.又点(0,1)在函数图象上，所以Asin π6＝1，得A ＝2.故函数f(x)的解析式为f(x)＝2sin(2x ＋π6)．(2)g(x)＝2sin[2(x －π12)＋π6]－2sin[2(x ＋π12)＋π6]＝2sin 2x －2sin(2x ＋π3)＝2sin 2x －2(12sin 2x ＋32cos 2x)＝sin 2x －3cos 2x ＝2sin(2x －π3)．由2k π－π2≤2x－π3≤2k π＋π2，得k π－π12≤x≤k π＋5π12，k ∈Z.所以函数g(x)的单调递增区间是[k π－π12，k π＋5π12]，k ∈Z.。

第4讲函数y＝A sin(ωx＋φ)的图象及应用1.“五点法”作函数y＝A sin(ωx＋φ)(A>0，ω>0)的简图“五点法”作图的五点是在一个周期内的最高点、最低点及与x轴相交的三个点，作图时的一般步骤为：(1)定点：如下表所示．(2)作图：在坐标系中描出这五个关键点，用平滑的曲线顺次连接得到y＝A sin(ωx＋φ)在一个周期内的图象．(3)扩展：将所得图象，按周期向两侧扩展可得y＝A sin(ωx＋φ)在R上的图象．2．函数y＝sin x的图象经变换得到y＝A sin(ωx＋φ)(A>0，ω>0)的图象的步骤1．概念辨析(1)将函数y ＝3sin2x 的图象左移π4个单位长度后所得图象的解析式是y ＝3sin ⎝⎛⎭⎪⎫2x ＋π4.( ) (2)利用图象变换作图时，“先平移，后伸缩”与“先伸缩，后平移”中平移的长度一致．( )(3)将函数y ＝2sin x 的图象上所有点的横坐标缩短为原来的12，纵坐标不变，得函数y＝2sin x2的图象．( )(4)由图象求解析式时，振幅A 的大小是由一个周期内图象中最高点的值与最低点的值确定的．( )答案 (1)× (2)× (3)× (4)√ 2．小题热身(1)函数y ＝2sin ⎝ ⎛⎭⎪⎫2x ＋π4的振幅、频率和初相分别为( ) A ．2，1π，π4B ．2，12π，π4 C ．2，1π，π8D ．2，12π，－π8答案 A解析 函数y ＝2sin ⎝⎛⎭⎪⎫2x ＋π4的振幅是2，周期T ＝2π2＝π，频率f ＝1T ＝1π，初相是π4，故选A.(2)用五点法作函数y ＝sin ⎝⎛⎭⎪⎫x －π6在一个周期内的图象时，主要确定的五个点是________、________、__________、________、________.答案 ⎝⎛⎭⎪⎫π6，0⎝ ⎛⎭⎪⎫2π3，1⎝ ⎛⎭⎪⎫7π6，0⎝ ⎛⎭⎪⎫5π3，－1⎝ ⎛⎭⎪⎫13π6，0解析 列表：五个点依次是⎝ ⎛⎭⎪⎫π6，0、⎝ ⎛⎭⎪⎫2π3，1、⎝ ⎛⎭⎪⎫7π6，0、⎝ ⎛⎭⎪⎫5π3，－1、⎝ ⎛⎭⎪⎫13π6，0.(3)将函数f (x )＝－12cos2x 的图象向右平移π6个单位长度后，再将图象上各点的纵坐标伸长到原来的2倍，得到函数y ＝g (x )的图象，则g ⎝⎛⎭⎪⎫3π4＝________.答案32解析 函数f (x )＝－12cos2x 的图象向右平移π6个单位长度后得函数y ＝－12cos2⎝ ⎛⎭⎪⎫x －π6＝－12cos ⎝ ⎛⎭⎪⎫2x －π3，再将图象上各点的纵坐标伸长到原来的2倍，得到函数g (x )＝－cos ⎝ ⎛⎭⎪⎫2x －π3，所以g ⎝ ⎛⎭⎪⎫3π4＝－cos ⎝ ⎛⎭⎪⎫3π2－π3＝sin π3＝32.(4)(2018·长春模拟)函数f (x )＝A sin(ωx ＋φ)(A >0，ω>0，|φ|<π)的部分图象如图所示，则函数f (x )的解析式为________．答案 f (x )＝2sin ⎝⎛⎭⎪⎫2x ＋π3 解析 由图象可知A ＝2，T 4＝7π12－π3＝π4，所以2πω＝π，ω＝2，所以f (x )＝2sin(2x＋φ)，又f ⎝⎛⎭⎪⎫7π12＝－2，所以2×7π12＋φ＝2k π＋3π2，k ∈Z ，φ＝2k π＋π3，k ∈Z ，又|φ|<π，所以φ＝π3，所以f (x )＝2sin ⎝⎛⎭⎪⎫2x ＋π3.题型 一 函数y ＝A sin(ωx ＋φ)的图象及变换1．(2017·全国卷Ⅰ)已知曲线C 1：y ＝cos x ，C 2：y ＝sin ⎝ ⎛⎭⎪⎫2x ＋2π3，则下面结论正确的是( )A ．把C 1上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向右平移π6个单位长度，得到曲线C 2B ．把C 1上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向左平移π12个单位长度，得到曲线C 2C ．把C 1上各点的横坐标缩短到原来的12，纵坐标不变，再把得到的曲线向右平移π6个单位长度，得到曲线C 2D ．把C 1上各点的横坐标缩短到原来的12，纵坐标不变，再把得到的曲线向左平移π12个单位长度，得到曲线C 2答案 D解析 由C 2：y ＝sin ⎝ ⎛⎭⎪⎫2x ＋2π3＝sin ⎝ ⎛⎭⎪⎫2x ＋π6＋π2＝cos ( 2x ＋π6 )＝cos ⎣⎢⎡⎦⎥⎤2⎝ ⎛⎭⎪⎫x ＋π12. 根据三角函数图象变换的规律，可得D 正确．2．(2018·蚌埠一模)已知ω>0，顺次连接函数y ＝sin ωx 与y ＝cos ωx 的任意三个相邻的交点都构成一个等边三角形，则ω＝( )A ．π B.6π2 C.4π3D.3π 答案 B解析 当正弦值等于余弦值时，函数值为±22，故等边三角形的高为2，由此得到边长为2×33×2＝263，边长即为函数的周期，故2πω＝263，ω＝6π2.3．已知函数f (x )＝2sin ωx (ω>0)在区间⎣⎢⎡⎦⎥⎤－π3，π4上单调递增，求ω的最大值．解 函数f (x )＝2sin ωx (ω>0)在⎣⎢⎡⎦⎥⎤－π2ω，π2ω上单调递增，所以⎣⎢⎡⎦⎥⎤－π3，π4⊆⎣⎢⎡⎦⎥⎤－π2ω，π2ω，所以⎩⎪⎨⎪⎧－π2ω≤－π3，π2ω≥π4.解得0<ω≤32，所以ω的最大值为32.4．已知函数y ＝cos ⎝ ⎛⎭⎪⎫2x －π3.(1)求它的振幅、周期、初相；(2)用“五点法”作出它在区间[0，π]内的图象；(3)说明y ＝cos ⎝⎛⎭⎪⎫2x －π3的图象可由y ＝cos x 的图象经过怎样的变换而得到．解 (1)函数y ＝cos ⎝ ⎛⎭⎪⎫2x －π3的振幅为1，周期T ＝2π2＝π，初相是－π3. (2)列表：描点，连线．(3)解法一：把y ＝cos x 的图象上所有的点向右平移π3个单位长度，得到y ＝cos ⎝ ⎛⎭⎪⎫x －π3的图象；再把y ＝cos ⎝ ⎛⎭⎪⎫x －π3的图象上所有点的横坐标缩短到原来的12(纵坐标不变)，得到y ＝cos ⎝⎛⎭⎪⎫2x －π3的图象．解法二：将y ＝cos x 的图象上所有点的横坐标缩短为原来的12(纵坐标不变)，得到y ＝cos2x 的图象；再将y ＝cos2x 的图象向右平移π6个单位长度，得到y ＝cos ⎣⎢⎡⎦⎥⎤2⎝ ⎛⎭⎪⎫x －π6＝cos ⎝ ⎛⎭⎪⎫2x －π3的图象．作函数y ＝A sin(ωx ＋φ)(A >0，ω>0)的图象常用的两种方法(1)五点法作图：用“五点法”作y ＝A sin(ωx ＋φ)的简图，主要是通过变量代换，设z ＝ωx ＋φ，由z 取0，π2，π，3π2，2π来求出相应的x ，通过列表，计算得出五点坐标，描点后得出图象．(2)图象的变换：由函数y ＝sin x 的图象通过变换得到y ＝A sin(ωx ＋φ)的图象有两种途径：“先平移后伸缩”与“先伸缩后平移”.1.要想得到函数y ＝sin2x ＋1的图象，只需将函数y ＝cos2x 的图象( ) A.向左平移π4个单位长度，再向上平移1个单位长度B.向右平移π4个单位长度，再向上平移1个单位长度C.向左平移π2个单位长度，再向下平移1个单位长度D.向右平移π2个单位长度，再向下平移1个单位长度答案 B解析 先将函数y ＝cos2x 的图象向右平移π4个单位长度，得到y ＝sin2x 的图象，再向上平移1个单位长度，即得y ＝sin2x ＋1的图象，故选B.2.(2018·青岛模拟)将函数f (x )＝2sin ⎝ ⎛⎭⎪⎫2x ＋π3图象上的每个点的横坐标缩短为原来的一半，纵坐标不变，再将所得图象向左平移π12个单位得到函数g (x )的图象，在g (x )图象的所有对称轴中，离原点最近的对称轴方程为( )A.x ＝－π24B ．x ＝π4C.x ＝5π24D ．x ＝π12答案 A解析 当函数f (x )＝2sin ⎝ ⎛⎭⎪⎫2x ＋π3图象上的每个点的横坐标缩短为原来的一半，纵坐标不变时，此时函数解析式可表示为f 1(x )＝2sin ⎝ ⎛⎭⎪⎫4x ＋π3，再将所得图象向左平移π12个单位得到函数g (x )的图象，则g (x )可以表示为g (x )＝2sin ⎣⎢⎡⎦⎥⎤4⎝ ⎛⎭⎪⎫x ＋π12＋π3＝2sin ⎝ ⎛⎭⎪⎫4x ＋2π3.则函数g (x )的图象的对称轴可表示为4x ＋2π3＝π2＋k π，k ∈Z ，即x ＝－π24＋k π4，k∈Z .则g (x )的图象离原点最近的对称轴，即g (x )的图象离y 轴最近的对称轴为x ＝－π24.题型 二 由图象确定y ＝A sin(ωx ＋φ)的解析式1.已知函数f (x )＝A sin(ωx ＋φ)(A >0，ω>0,0<φ<π)，其导函数f ′(x )的图象如图所示，则f ⎝ ⎛⎭⎪⎫π2的值为( )A ．2 2 B. 2 C ．－22 D ．－24答案 D解析 依题意得f ′(x )＝Aωcos(ωx ＋φ)，结合函数y ＝f ′(x )的图象，则T ＝2πω＝4⎝⎛⎭⎪⎫3π8－π8＝π，ω＝2.又Aω＝1，因此A ＝12.因为0<φ<π，3π4<3π4＋φ<7π4，且f ′⎝ ⎛⎭⎪⎫3π8＝cos ⎝ ⎛⎭⎪⎫3π4＋φ＝－1，所以3π4＋φ＝π，即φ＝π4，所以f (x )＝12sin ⎝ ⎛⎭⎪⎫2x ＋π4，f ⎝ ⎛⎭⎪⎫π2＝12sin ⎝⎛⎭⎪⎫π＋π4＝－12×22＝－24. 2.设f (x )＝A sin(ωx ＋φ)(A >0，ω>0，|φ|<π)，其图象上最高点M 的坐标是(2，2)，曲线上的点P 由点M 运动到相邻的最低点N 时，在点Q (6,0)处越过x 轴．(1)求A ，ω，φ的值；(2)函数f (x )的图象能否通过平移变换得到一个奇函数的图象？若能，写出变换方法；若不能，说明理由．解 (1)由题意知A ＝2，T ＝(6－2)×4＝16，所以ω＝2πT ＝π8.又因为Q (6,0)是零值点，且|φ|<π，所以π8×6＋φ＝π，所以φ＝π4，经验证，符合题意．所以A ＝2，ω＝π8，φ＝π4.(2)f (x )的图象经过平移变换能得到一个奇函数的图象．由(1)知f (x )＝2sin ⎝ ⎛⎭⎪⎫π8x ＋π4，当f (x )的图象向右平移2个单位长度后，所得图象的函数解析式为g (x )＝2sin π8x ，是奇函数.确定y ＝A sin(ωx ＋φ)＋b (A >0，ω>0)中参数的方法(1)求A ，b ：确定函数的最大值M 和最小值m ，则A ＝M －m2，b ＝M ＋m2；(2)求ω：确定函数的周期T ，则可得ω＝2πT；(3)求φ：常用的方法有：①代入法：把图象上的一个已知点代入(此时A ，ω，b 已知)或代入图象与直线y ＝b 的交点求解(此时要注意交点在上升区间上还是在下降区间上)．②五点法：确定φ值时，往往以寻找“五点法”中的某一个点为突破口．具体如下：1．(2018·四川绵阳诊断)如图是函数f (x )＝cos(πx ＋φ)⎝⎛⎭⎪⎫0<φ<π2的部分图象，则f (3x 0)＝( )A.12 B ．－12C.32D ．－32答案 D解析 ∵f (x )＝cos(πx ＋φ)的图象过点⎝ ⎛⎭⎪⎫0，32， ∴32＝cos φ，结合0<φ<π2，可得φ＝π6.∴由图象可得cos ⎝⎛⎭⎪⎫πx 0＋π6＝32，πx 0＋π6＝2π－π6，解得x 0＝53. ∴f (3x 0)＝f (5)＝cos ⎝⎛⎭⎪⎫5π＋π6＝－32.2.已知函数f (x )＝A tan(ωx ＋φ)⎝⎛⎭⎪⎫ω>0，|φ|＜π2，y ＝f (x )的部分图象如图所示，则f ⎝ ⎛⎭⎪⎫π24等于________．答案3解析 观察图象可知T 2＝3π8－π8，所以π2ω＝π4，ω＝2，所以f (x )＝A tan(2x ＋φ)．又因为函数图象过点⎝⎛⎭⎪⎫3π8，0，所以0＝A tan ⎝ ⎛⎭⎪⎫2×3π8＋φ，所以3π4＋φ＝k π(k ∈Z )，所以φ＝k π－3π4(k ∈Z )．又因为|φ|<π2，所以φ＝π4.又图象过点(0,1)，所以A ＝1.综上知，f (x )＝tan ⎝⎛⎭⎪⎫2x ＋π4，故f ⎝ ⎛⎭⎪⎫π24＝tan ⎝ ⎛⎭⎪⎫2×π24＋π4＝ 3.题型 三 三角函数图象性质的应用角度1 三角函数模型的应用1．如图，某港口一天6时到18时的水深变化曲线近似满足函数y ＝3sin ⎝ ⎛⎭⎪⎫π6x ＋φ＋k ，据此函数可知，这段时间水深(单位：m)的最大值为( )A.5 B ．6 C ．8 D ．10答案 C解析 由图象可知，y min ＝2，因为y min ＝－3＋k ，所以－3＋k ＝2，解得k ＝5，所以这段时间水深的最大值是y max ＝3＋k ＝3＋5＝8.角度2 函数零点(方程根)问题2.已知关于x 的方程2sin ⎝ ⎛⎭⎪⎫x ＋π6＋1－a ＝0在区间⎣⎢⎡⎦⎥⎤0，2π3上存在两个根，则实数a的取值范围是________．答案 [2,3)解析 2sin ⎝ ⎛⎭⎪⎫x ＋π6＋1－a ＝0化为sin ⎝ ⎛⎭⎪⎫x ＋π6＝a －12，令t ＝x ＋π6，由x ∈⎣⎢⎡⎦⎥⎤0，2π3得，t ＝x ＋π6∈⎣⎢⎡⎦⎥⎤π6，5π6，画出函数y ＝sin t ，t ∈⎣⎢⎡⎦⎥⎤π6，5π6的图象和直线y ＝a －12，当12≤a －12<1，即2≤a <3时，函数y ＝sin t ，t ∈⎣⎢⎡⎦⎥⎤π6，5π6的图象和直线y ＝a －12有两个公共点，原方程有两个根.角度3 三角函数图象性质的综合3.函数f (x )＝A sin(ωx ＋φ)⎝⎛⎭⎪⎫ω>0，|φ|<π2的部分图象如图，则( )A ．函数f (x )的对称轴方程为x ＝4k π＋π4(k ∈Z )B.函数f (x )的递减区间为⎣⎢⎡⎦⎥⎤8k π＋π4，8k π＋5π4(k ∈Z )C.函数f (x )的递增区间为[8k ＋1,8k ＋5](k ∈Z )D.f (x )≥1的解集为⎣⎢⎡⎦⎥⎤8k －13，8k ＋73(k ∈Z )答案 D解析 由题图知，A ＝2，函数f (x )的最小正周期T ＝4×(3－1)＝8，故ω＝2π8＝π4，所以f (x )＝2sin ⎝ ⎛⎭⎪⎫π4x ＋φ，因为点(1,2)在图象上，所以2sin ⎝ ⎛⎭⎪⎫π4＋φ＝2，因为|φ|<π2，所以φ＝π4，即f (x )＝2sin ⎝ ⎛⎭⎪⎫π4x ＋π4，由π4x ＋π4＝k π＋π2(k ∈Z )得x ＝4k ＋1，即函数f (x )的对称轴方程为x ＝4k ＋1(k ∈Z )，所以A 项错误；由2k π＋π2≤π4x ＋π4≤2k π＋3π2(k ∈Z )得8k ＋1≤x ≤8k ＋5，即函数f (x )的单调减区间为[8k ＋1,8k ＋5](k ∈Z )，所以B ，C两项错误；由2sin ⎝ ⎛⎭⎪⎫π4x ＋π4≥1，得sin ⎝ ⎛⎭⎪⎫π4x ＋π4≥12，所以2k π＋π6≤π4x ＋π4≤2k π＋5π6(k ∈Z )，解得8k －13≤x ≤8k ＋73(k ∈Z )，即不等式f (x )≥1的解集为⎣⎢⎡⎦⎥⎤8k －13，8k ＋73(k ∈Z )，故选D.(1)三角函数模型在实际应用中体现的两个方面①已知三角函数模型，利用三角函数的有关性质解决问题，其关键是准确理解自变量的意义及自变量与函数之间的对应法则；②把实际问题抽象转化成数学问题，建立三角函数模型，再利用三角函数的有关知识解决问题，其关键是建模．(2)三角函数的零点、不等式问题的求解思路①把函数表达式转化为正弦型函数形式y ＝A sin(ωx ＋φ)＋B (A >0，ω>0)； ②画出一个周期上的函数图象；③利用图象解决有关三角函数的方程、不等式问题．(3)研究y ＝A sin(ωx ＋φ)的性质时可将ωx ＋φ视为一个整体，利用换元法和数形结合思想解题.1.设函数f (x )＝⎪⎪⎪⎪⎪⎪sin ⎝⎛⎭⎪⎫x ＋π3(x ∈R )，则f (x )( )A.在区间⎣⎢⎡⎦⎥⎤2π3，7π6上是增函数B.在区间⎣⎢⎡⎦⎥⎤－π，－π2上是减函数 C.在区间⎣⎢⎡⎦⎥⎤－π3，π4上是增函数D.在区间⎣⎢⎡⎦⎥⎤π3，5π6上是减函数答案 A解析 函数f (x )＝⎪⎪⎪⎪⎪⎪sin ⎝ ⎛⎭⎪⎫x ＋π3(x ∈R )的图象如图所示，由图象可知函数f (x )＝⎪⎪⎪⎪⎪⎪sin ⎝ ⎛⎭⎪⎫x ＋π3(x ∈R )在区间⎣⎢⎡⎦⎥⎤2π3，7π6上是增函数．故选A.2.一个大风车的半径为8 m,12 min 旋转一周，它的最低点P 0离地面2 m ，风车翼片的一个端点P 从P 0开始按逆时针方向旋转，则点P 离地面距离h (m)与时间t (min)之间的函数关系式是( )A ．h (t )＝－8sin π6t ＋10B.h (t )＝－cos π6t ＋10C.h (t )＝－8sin π6t ＋8D.h (t )＝－8cos π6t ＋10答案 D解析 设h (t )＝A cos ωt ＋B ，因为12 min 旋转一周， 所以2πω＝12，所以ω＝π6，由于最大值与最小值分别为18,2.所以⎩⎪⎨⎪⎧－A ＋B ＝18，A ＋B ＝2，解得A ＝－8，B ＝10.所以h (t )＝－8cos π6t ＋10.3.若函数f (x )＝sin ⎝ ⎛⎭⎪⎫ωx ＋π6(ω>0)满足f (0)＝f ⎝ ⎛⎭⎪⎫π3，且函数在⎣⎢⎡⎦⎥⎤0，π2上有且只有一个零点，则f (x )的最小正周期为( )A.π2 B ．π C.3π2D ．2π 答案 B解析 依题意，函数f (x )图象的一条对称轴为x ＝0＋π32＝π6，又因为函数f (x )在⎣⎢⎡⎦⎥⎤0，π2上有且只有一个零点，所以π6－0≤T 4≤π2－π6，所以2π3≤T ≤4π3.根据选项可得，f (x )的最小正周期为π.。

考向20 函数y=Asin(ωx +φ)的图象及其应用【2022·浙江·高考真题】为了得到函数2sin3y x =的图象，只要把函数π2sin 35y x ⎛⎫=+ ⎪⎝⎭图象上所有的点（ ） A ．向左平移π5个单位长度B ．向右平移π5个单位长度C ．向左平移π15个单位长度 D ．向右平移π15个单位长度【2022·全国·高考真题（文）】将函数π()sin (0)3f x x ωω⎛⎫=+> ⎪⎝⎭的图像向左平移π2个单位长度后得到曲线C ，若C 关于y 轴对称，则ω的最小值是（ ） A ．16B ．14C ．13D ．121．已知()()sin (0,0)f x A x A ωφω=+>>的部分图象求A 的方法： （1）利用极值点的纵坐标求A ；（2）把某点的坐标代入求A ． 2．已知()()sin (0,0)f x A x A ωφω=+>>的部分图象求ω的方法： 由2Tπω=，即可求出ω．常用结论：（1）相邻两个极大（小）值点之间的距离为T ；（2）相邻两个零点之间的距离为;2T （3）极值点到相邻的零点，自变量取值区间长度为4T．3．已知()()sin (0,0)f x A x A ωφω=+>>的部分图象求φ的方法： 求φ的值时最好选用最值点求． 峰点：22x k πωφπ+=+；谷点：22x k πωφπ+=-+．也可用零点求，但要区分该零点是升零点，还是降零点． 升零点（图象上升时与x 轴的交点）：2x k ωφπ+=；降零点（图象下降时与x 轴的交点）：2x k ωφππ+=+（以上k z ∈）．此外也可以把图象上的一个已知点代入（此时要注意该点在上升区间上还是在下降区间上）．函数sin()(0,0)y A x A ωϕω=+>>的物理意义简谐运动的图象所对应的函数解析式sin(),[0,)y A x x ωϕ=+∈+∞，其中0,0A ω>>．在物理中，描述简谐运动的物理量，如振幅、周期和频率等都与这个解析式中的常数有关：A 就是这个简谐运动的振幅，它是做简谐运动的物体离开平衡位置的最大距离；这个简谐运动的周期是2T πω=，这是做简谐运动的物体往复运动一次所需要的时间；这个简谐运动的频率由公式1f T=给出，它是做简谐运动的物体在单位时间内往复运动的次数；x ωϕ+称为相位；0x =时的相位ϕ称为初相．1．平移与伸缩由函数sin y x =的图像变换为函数2sin(2)33y x π=++的图像的步骤；方法一：(2)23x x x ππ→+→+．先相位变换，后周期变换，再振幅变换，不妨采用谐音记忆：我们“想欺负”（相一期一幅）三角函数图像，使之变形．3sin y x π=−−−−−−→向左平移个单位的图像sin()3y x π=+的图像12−−−−−−−−−→所有点的横坐标变为原来的纵坐标不变sin(2)3y x π=+的图像2−−−−−−−−−→所有点的纵坐标变为原来的倍横坐标不变2sin(2)3y x π=+的图像 3−−−−−−→向上平移个单位2sin(2)33y x π=++方法二：(2)23x x x ππ→+→+．先周期变换，后相位变换，再振幅变换． sin y x =的图像12−−−−−−−−−→所有点的横坐标变为原来的纵坐标不变6sin 2y x π=−−−−−−→向左平移个单位的图像sin 2()sin(2)62y x x ππ=+=+的图像2−−−−−−−−−→所有点的纵坐标变为原来的倍横坐标不变32sin(2)3y x π=+−−−−−−→向上平移各单位的图像2sin(2)33y x π=++注：在进行图像变换时，提倡先平移后伸缩（先相位后周期，即“想欺负”），但先伸缩后平移（先周期后相位）在题目中也经常出现，所以必须熟练掌握，无论哪种变化，切记每一个变换总是对变量x 而言的，即图像变换要看“变量x ”发生多大变化，而不是“角wx φ+”变化多少．1．（2022·全国·模拟预测（理））函数()f x 的图象按以下次序变换：①横坐标变为原来的12；②向左平移23π个单位长度；③向上平移一个单位长度；④纵坐标变为原来的2倍，得到sin y x =的图象，则()f x 的解析式为（ ）A ．()112sin 1223f x x π⎛⎫=-- ⎪⎝⎭ B ．()11sin 1223f x x π⎛⎫=-- ⎪⎝⎭C ．()12sin 2123f x x π⎛⎫=-- ⎪⎝⎭D ．()1sin 2123f x x π⎛⎫=-- ⎪⎝⎭2．（2022·河南省杞县高中模拟预测（文））已知点π,06⎛⎫ ⎪⎝⎭是函数()π2sin 3f x x ω⎛⎫=+ ⎪⎝⎭图象的一个对称中心，其中()0,6ω∈，将函数()f x 的图象向右平移5π24个单位长度得到函数()g x 的图象，则()g x =（ ） A ．π2sin 28x ⎛⎫+ ⎪⎝⎭B ．2sin 4x -C ．2cos2x -D ．2cos4x -3．（2022·河南·平顶山市第一高级中学模拟预测（文））已知直线8x π=是函数()2sin(2)||2πϕϕ⎛⎫=+< ⎪⎝⎭f x x 的图像的一条对称轴，为了得到函数()y f x =的图像，可把函数2cos 26y x π⎛⎫=- ⎪⎝⎭的图像（ ）A ．向左平移24π个单位长度 B ．向右平移24π个单位长度 C ．向左平移12π个单位长度 D ．向右平移12π个单位长度4．（2022·全国·高三专题练习（文））将函数π()sin (0)3f x x ωω⎛⎫=+> ⎪⎝⎭的图像向左平移π2个单位长度后得到曲线C ，若C 关于y 轴对称，则ω的最小值是（ ） A ．16B ．14C ．13D ．125．（2022·青海·海东市第一中学模拟预测（文））将函数()πsin(2)6f x x =+的图象向右平移6π个单位长度，然后将所得图象上所有点的横坐标缩小到原来的12（纵坐标不变），得到函数()y g x =的图象，则下列说法正确的是（ ）A ．π()sin 46g x x ⎛⎫=+ ⎪⎝⎭B ．()g x 在ππ,123⎡⎤⎢⎥⎣⎦上单调C ．()g x 的图象关于直线π2x =对称D ．当π0,4x ⎡⎤∈⎢⎥⎣⎦时，函数()g x 的值域为1,12⎡⎤-⎢⎥⎣⎦1．（2022·上海浦东新·二模）将函数()sin2f x x =的图像向左平移4π个单位后，得到函数()g x 的图像，设,,A B C 为以上两个函数图像不共线的三个交点，则ABC 的面积不可能为（ ） A ．22πB 2πC 2D 2 2．（2022·青海·海东市第一中学模拟预测（理））将函数()sin(2)6f x x π=+的图象向右平移6π个单位长度，然后将所得图象上所有点的横坐标缩小到原来的12 （纵坐标不变），得到函数()y g x =的图象，则当0,4x π⎡⎤∈⎢⎥⎣⎦时，函数()g x 的值域为（ ）A ．11,22⎡⎤-⎢⎥⎣⎦B ．11,2⎡⎤-⎢⎥⎣⎦C ．[]1,1-D ．1,12⎡⎤-⎢⎥⎣⎦3．（2022·青海·海东市第一中学模拟预测（文））已知函数()2sin cos f x x x =+的图象向左平移()0ϕϕ>个单位长度后得到函数()sin 2cos g x x x =+的图象，则()g ϕ=（ ） A ．65B ．115C ．15D ．854．（2022·广东茂名·二模）已知函数π()3sin(2)(||)2f x x ϕϕ=+< 的部分图象如图所示．将函数()f x 的图象向左平移π12个单位得到()g x 的图象，则（ ）A ．()3sin(2)6g x x π+） B ．()3sin(2)12g x x 5π=+C ．()32g x x =D ．()32g x x =5．（2022·安徽省舒城中学三模（理））将函数π()2sin()(0)3f x x ωω=->的图象向左平移3ωπ个单位，得到函数()y g x =的图象，若()y g x =在π[0,]4上为增函数，则ω最大值为（ ） A ．2B ．3C ．4D ．526．（2022·黑龙江·哈九中三模（文））已知函数()()()sin 0,0,0πf x A x A ωϕωϕ=+>><<的部分图象如图所示，且13π23f ⎛⎫= ⎪⎝⎭．将()f x 图象上所有点的横坐标缩小为原来的14，再向上平移一个单位长度，得到()g x 的图象．若()()129g x g x =，1x，[]20,4πx ∈，则21x x -的最大值为（ ）A ．πB ．2πC ．3πD ．4π7．（多选题）（2022·全国·模拟预测）将函数()()sin 3cos 0f x x x ωωω=>的图象向右平移π3个单位，得到的图象关于y 轴对称，则下列说法正确的是（ ） A ．()f x 最小正周期的最大值为4π5 B ．()f x 最小正周期的最大值为4π11C ．当()f x 的最小正周期取最大值时，平移后的函数在π0,5⎡⎤⎢⎥⎣⎦上单调递增D ．当()f x 的最小正周期取最大值时，平移后的函数在π0,11⎡⎤⎢⎥⎣⎦上单调递减8．（多选题）（2022·山东·德州市教育科学研究院三模）已知函数π()sin (0)6f x x ωω⎛⎫=-> ⎪⎝⎭图像的一条对称轴和一个对称中心的最小距离为34π，则（ ） A ．函数()f x 的最小正周期为3πB ．将函数()f x 的图像向左平移π4个单位长度后所得图像关于原点对称 C ．函数()f x 在5π,π2⎡⎤⎢⎥⎣⎦上为增函数D ．设||3π()e 24x g x f x ⎛⎫=+ ⎪⎝⎭，则()g x 在(10π,10π)-内有20个极值点9．（多选题）（2022·全国·模拟预测）已知函数()()sin cos sin f x x x x =-，则下列说法正确的是（ ）A ．函数()f x 的最小正周期为2πB ．()f x 21-C ．()f x 的图像关于直线8x π=-对称 D ．将()f x 的图像向右平移8π个单位长度，再向上平移12个单位长度后所得图像对应的函数为奇函数10．（多选题）（2022·全国·模拟预测）函数()()()cos 02f x x ωϕϕπ=+≤<的部分图像如图所示，则（ ）A ．3ω=B ．65ϕπ=C ．函数()f x 在314,55ππ⎡⎤⎢⎥⎣⎦上单调递增D ．函数()f x 图像的对称轴方程为()315k x k ππ=-∈Z 11．（2022·上海闵行·二模）若函数3sin cos y x x =+的图像向右平移ϕ个单位后是一个奇函数的图像，则正数ϕ的最小值为___________；12．（2022·河北衡水·高三阶段练习）把函数()22cos cos 23f x x x π⎛⎫=++ ⎪⎝⎭的图像向右平移ϕ个单位长度，得到的图像所对应的函数()g x 为偶函数，则ϕ的最小正值为__________．13．（2022·山东潍坊·三模）已知函数()cos 2f x x =向右平移12π个单位长度后得到()g x ．若对于任意的1,36x ππ⎡⎤∈-⎢⎥⎣⎦，总存在[]2,x m n ∈，使得()()12f x g x =，则m n -的最小值为______．14．（2022·江苏扬州·模拟预测）已知函数()π2sin 3f x x ⎛⎫=- ⎪⎝⎭，将()y f x =的图象上所有点横坐标变为原来的12倍（纵坐标不变），再将所得函数图象向左平移π4个单位长度，得到()y g x =图象，若()32gx =在[]0,2π有n 个不同的解12,,,n x x x ，则1tan n i i x =⎛⎫= ⎪⎝⎭∑__________.15．（2022·重庆八中模拟预测）已知函数()sin()0,0,||2f x A x B A πωϕωϕ⎛⎫=++>>< ⎪⎝⎭的部分图象如图所示．(1)求函数()f x 的解析式；(2)将函数()y f x =的图象上所有的点向右平移12π个单位，再将所得图象上每一个点的横坐标变为原来的2倍（纵坐标不变），得到函数()y g x =的图象．当130,6x π⎡⎤∈⎢⎥⎣⎦时，方程()0g x a -=恰有三个不相等的实数根()123123,,x x x x x x <<，求实数a 的取值范围和1232x x x ++的值．16．（2022·全国·模拟预测）条件①：()()()f x g x h x =⋅；条件②：()()()2f x g x h x =．已知()3sin cos g x x x =-，()cos sin 44h x x x ππ⎛⎫⎛⎫=--- ⎪ ⎪⎝⎭⎝⎭，再从条件①、条件②这两个条件中选择一个作为条件，求： (1)求()f x 的解析式；(2)将()y f x =的图象上的各点的横坐标变为原来的12倍（纵坐标不变），再将得到的图象向左平移12π个单位长度，得到()y t x =的图象，求函数()y t x =在0,2π⎛⎫ ⎪⎝⎭上的单调递减区间和最大值．17．（2022·湖北·襄阳五中模拟预测）已知数2()32sin 1(0)6212x f x x πωπωω⎛⎫⎛⎫=+++-> ⎪ ⎪⎝⎭⎝⎭的相邻两对称轴间的距离为2π.(1)求()f x 的解析式；(2)将函数()f x 的图象向右平移6π个单位长度，再把各点的横坐标缩小为原来的12（纵坐标不变），得到函数()y g x =的图象，当,126x ππ⎡⎤∈-⎢⎥⎣⎦时，求函数()g x 的值域；(3)对于第（2）问中的函数()g x ，记方程4()3g x =在4,63x ππ⎡⎤∈⎢⎥⎣⎦上的根从小到大依次为12,,n x x x ，若m =1231222n n x x x x x -+++++，试求n 与m 的值.18．（2022·()3cos 22sin 0011cos A A x A x A x>按第一列展开11213132M M M ++，记函数()1121f x M M =+，且()f x 的最大值是4． (1)求A ；(2)将函数()y f x =的图像向左平移12π个单位，再将所得图像上各点的横坐标扩大为原来的2倍，纵坐标不变，得到函数()y g x =的图像，求()g x 在11,1212ππ⎛⎫- ⎪⎝⎭上的值域．19．（2022·陕西·武功县普集高级中学高三阶段练习（理））已知函数()()*sin ,2f x x N πωϕωϕ⎛⎫=+∈< ⎪⎝⎭的图像关于直线512x π=-对称，且在区间5,012π⎛⎫- ⎪⎝⎭上单调递增；(1)求()f x 解析式．(2)若02f π⎛⎫< ⎪⎝⎭，将函数()f x 的图象所有的点向右平移12π个单位长度，再把所得图像上各点横坐标缩短到原来的12（纵坐标不变），得到()g x 的图象；若()g x m =在,64x ππ⎡⎤∈-⎢⎥⎣⎦上恰有两个零点，求m 的取值范围．1．（2022·浙江·高考真题）为了得到函数2sin3y x =的图象，只要把函数π2sin 35y x ⎛⎫=+ ⎪⎝⎭图象上所有的点（ ） A ．向左平移π5个单位长度B ．向右平移π5个单位长度C ．向左平移π15个单位长度 D ．向右平移π15个单位长度 2．（2022·全国·高考真题（文））将函数π()sin (0)3f x x ωω⎛⎫=+> ⎪⎝⎭的图像向左平移π2个单位长度后得到曲线C ，若C 关于y 轴对称，则ω的最小值是（ ） A ．16B ．14C ．13D ．123．（2021·全国·高考真题（理））把函数()y f x =图像上所有点的横坐标缩短到原来的12倍，纵坐标不变，再把所得曲线向右平移3π个单位长度，得到函数sin 4y x π⎛⎫=- ⎪⎝⎭的图像，则()f x =（ ）A ．7sin 212x π⎛⎫-⎪⎝⎭B ．sin 212x π⎛⎫+ ⎪⎝⎭C ．7sin 212x π⎛⎫- ⎪⎝⎭D ．sin 212x π⎛⎫+ ⎪⎝⎭4．（2020·天津·高考真题）已知函数()sin 3f x x π⎛⎫=+ ⎪⎝⎭．给出下列结论：①()f x 的最小正周期为2π； ②2f π⎛⎫⎪⎝⎭是()f x 的最大值；③把函数sin y x =的图象上所有点向左平移3π个单位长度，可得到函数()y f x =的图象． 其中所有正确结论的序号是（ ） A ．①B ．①③C ．②③D ．①②③5．（2019·天津·高考真题（文））已知函数()sin()(0,0,||)f x A x A ωϕωϕπ=+>><是奇函数，将()y f x =的图像上所有点的横坐标伸长到原来的2倍（纵坐标不变），所得图像对应的函数为()g x .若()g x 的最小正周期为2π，且24g π⎛⎫= ⎪⎝⎭，则38f π⎛⎫= ⎪⎝⎭A ．2-B ．2-C ．2D ．26．（2014·辽宁·高考真题（文））将函数3sin(2)3y x π=+的图象向右平移2π个单位长度，所得图象对应的函数A ．在区间7[,]1212ππ上单调递减B ．在区间7[,]1212ππ上单调递增C ．在区间[,]63ππ-上单调递减 D ．在区间[,]63ππ-上单调递增 7．（2015·湖南·高考真题（理））将函数()sin 2f x x =的图像向右平移(0)2πϕϕ<<个单位后得到函数()g x 的图像，若对满足12()()2f x g x -=的，，有，则ϕ=A ．512πB ．3π C ．4π D ．6π 8．（2012·天津·高考真题（文））将函数()sin f x x ω=（其中ω>0）的图像向右平移4π个单位长度，所得图像经过点3,04π⎛⎫⎪⎝⎭，则ω的最小值是A ．13B ．1C ．53D ．29．（2018·天津·高考真题（理））将函数sin(2)5y x π=+的图象向右平移10π个单位长度，所得图象对应的函数 A ．在区间35[,]44ππ上单调递增 B ．在区间3[,]4ππ上单调递减 C ．在区间53[,]42ππ上单调递增 D ．在区间3[,2]2ππ上单调递减 10．（2018·天津·高考真题（文））将函数sin 25y x π⎛⎫=+ ⎪⎝⎭的图象向右平移10π个单位长度，所得图象对应的函数A ．在区间,44ππ⎡⎤-⎢⎥⎣⎦上单调递增B ．在区间,04π⎡⎤-⎢⎥⎣⎦ 上单调递减C ．在区间,42ππ⎡⎤⎢⎥⎣⎦上单调递增D ．在区间,2ππ⎡⎤⎢⎥⎣⎦上单调递减11．（2017·全国·高考真题（理））已知曲线C 1：y =cos x ，C 2：y =sin (2x +2π3)，则下面结论正确的是A ．把C 1上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向右平移π6个单位长度，得到曲线C 2B ．把C 1上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向左平移π12个单位长度，得到曲线C 2C ．把C 1上各点的横坐标缩短到原来的12倍，纵坐标不变，再把得到的曲线向右平移π6个单位长度，得到曲线C 2D ．把C 1上各点的横坐标缩短到原来的12倍，纵坐标不变，再把得到的曲线向左平移π12个单位长度，得到曲线C 2。

第四节 函数y =A sin ()x ωϕ+的图象强化训练1.将函数y =sin2x 的图象向左平移4π个单位长度,再向上平移1个单位长度,所得图象的函数解析式是( )A.y =2cos 2xB.y =2sin 2xC.y =1+sin (2)4x π+D.y =cos2x答案:A解析:将函数y =sin2x 的图象向左平移4π个单位长度,得到函数y =sin 2()4x π+,即y =sin (2)2x π+=cos2x 的图象,再向上平移1个单位长度,所得图象的函数解析式为y =1+cos2x =2cos 2x ,故选A.2.已知函数f (x )=sin ()(4x x ωπ+∈R 0)ω,>的最小正周期为π,将y =f (x )的图象向左平移(0)ϕϕ>个单位长度,所得图象关于y 轴对称,则ϕ的一个值是( )A.2πB.38π C.4π D.8π答案:D解析:由已知,周期为π22ωωπ=,=,则结合平移公式和诱导公式可知平移后是偶函数,sin [2()]4x ϕπ++=±cos2x ,故选D.3.(2011山东高考,文6)若函数f (x )=sin (0)x ωω>在区间[0]3π,上单调递增,在区间[]32ππ,上单调递减,则ω等于( ) A.23B.32C.2D.3答案:B解析:由题意知,函数在3x π=处取得最大值1,所以1=sin 3ωπ,故选B.4.要得到函数y =sin x 的图象,只需将函数y =cos(x -)3π的图象 . 答案:向右平移6π个单位长度解析:y =sin x =cos ()2x π-=cos ()2x π- =cos [()]36x ππ--.∴y =cos ()3x π-的图象向右平移6π个单位长度得到y =sin x 的图象.5.已知函数y =A sin ()(x ωϕ+A >00(0))2ωϕπ,>,∈,在一个周期内的图象如图所示,求其解析式.解:由图象知A =2,272()21212T ωωπππ==-⇒=.∴y =2sin (2)x ϕ+.又图象过点(2)12π,,所以2=2sin (2)12ϕπ⨯+⇒sin ()16ϕπ+=623ϕϕπππ⇒+=⇒=.故所求解析式为y =2sin (2)3x π+.见课后作业A题组一 函数y =A sin ()x ωϕ+图象的作法和变换1.函数y =cos (x x ∈R )的图象向左平移2π个单位长度后,得到函数y =g (x )的图象,则g (x )的解析式为( ) A.g (x )=-sin x B.g (x )=sin x C.g (x )=-cos x D.g (x )=cos x答案:A解析:y =cos ()2x π+=-sin x .2.设函数f (x )=cos (0)x ωω>,将y =f (x )的图象向右平移3π个单位长度后,所得的图象与原图象重合,则ω的最小值等于( ) A.13B.3C.6D.9答案:C解析:将y =f (x )的图象向右平移3π个单位长度后,所得的图象与原图象重合,说明了3π是此函数周期的整数倍.由题知2(3k k ωππ=⋅∈Z ),解得6k ω=.令k =1,即得min 6ω=.3.已知函数f (x )=sin ()(4x x ωπ+∈R 0)ω,>的最小正周期为π,为了得到函数g (x )=cos x ω的图象,只要将y =f (x )的图象( )A.向左平移8π个单位长度B.向右平移8π个单位长度C.向左平移4π个单位长度D.向右平移4π个单位长度答案:A解析:由题知2ω=, 所以f (x )=sin (2)4x π+=cos [(2)]42x ππ-+=cos (2)4x π-=cos 2()8x π-,故选择A.4.把函数y =sin (x x ∈R )的图象上所有的点向左平行移动3π个单位长度,再把所得图象上所有点的横坐标缩短到原来的12倍(纵坐标不变),得到的图象所表示的函数是( )A.y =sin (2)3x x π-,∈RB.y =sin ()26x x π+,∈RC.y =sin (2)3x x π+,∈RD.y =sin 2(2)3x x π+,∈R答案:C5.函数y =sin (2)3x π-在区间[2π-,π]上的简图是( )答案:A6.已知函数y =f (x )的图象上的每一点的纵坐标扩大到原来的4倍,横坐标扩大到原来的2倍,然后把所得的图象沿x 轴向左平移2π个单位长度,这样得到的曲线和y =2sin x 的图象相同,则已知函数y =f (x )的解析式为 . 答案:12y =-cos2x解析:y =2sin x 右移2π个单位长度y =2sin ()2x π-横坐标缩小到原来的12倍纵坐标不变y =2sin (2)2x π-纵坐标缩小到原来的14倍横坐标不变y =12sin (2)2x π-12=-cos2x .7.已知函数12y =sin (2)6x x π+,∈R .(1)求它的振幅、周期、初相; (2)用五点法作出它的简图;(3)该函数的图象可由y =sin (x x ∈R )的图象经过怎样的平移和伸缩变换得到? 解:(1)函数12y =sin (2)6x π+的振幅为12,周期为π,初相为6π.(2)列表:画简图如下图所示:(3)方法一:函数y =sin x 的图象向左平移6π个单位长度函数y =sin ()6x π+的图象各点的横坐标缩短到原来的12倍(纵坐标不变)函数y =sin(2x +)6π的图象各点的纵坐标缩短到原来的12倍(横坐标不变)函数y =12sin(2x +)6π的图象.方法二:函数y =sin x 的图象各点的横坐标缩短到原来的12倍(纵坐标不变)函数y =sin2x 的图象向左平移12π个单位长度函数y =sin (2)6x π+的图象各点的纵坐标缩短到原来的12倍(横坐标不变)函数y =12sin(2x +)6π的图象.题组二 求函数y =A sin ()x b ωϕ++的解析式8.已知简谐运动f (x )=2sin ()(3x ϕπ+|ϕ|)2π<的图象经过点(0,1),则该简谐运动的最小正周期T 和初相ϕ分别为( ) A.66T ϕπ=,= B.63T ϕπ=,= C.T =6π6ϕπ,=D.T =6π3ϕπ,=答案:A解析:263T π==,π又∵f (0)=2sin 1ϕ=,∴sin 12ϕ=.∵|ϕ|2π<,∴6ϕπ=.9.函数f (x )=A sin ()(x ωϕ+其中00A ω>,>,|ϕ|)2π<的图象如图所示,则f (0)等于( )A.1B.12答案:D解析:由图可知A =1,22274()123Tωππ===,ππ⨯-∴f (x )=sin (2)x ϕ+,()3f π=sin (2)03ϕπ⨯+=. ∵A >0,|ϕ|2π<,∴3ϕπ=.∴f (0)=sin (0)3π+=sin3π=10.已知函数y =sin ()x ωϕ+(0ω>,-πϕ≤<π)的图象如图所示,则ϕ= .答案:910π解析:由图可知,T =2(2π35)42ππ-=,∴45ω=,把(2π,1)代入y =sin 4()5x ϕ+,有1=sin 8()5ϕπ+,∴910ϕπ=.11.已知函数f (x )=2sin ()(0x ωϕω+>,π0)ϕ<<的图象如图所示,则7()12f π= .答案:0解析:由图象知最小正周期5222()3443T ωππππ=-==,故3ω=.又4x π=时,f (x )=0,即2sin (3)04ϕπ⨯+=,可得34ϕπ=-,所以7()212f π=sin 73(3)0124ππ⨯-=.12.已知函数f (x )=A sin ()(00x A ωϕω+>,>,|ϕ|)2π<的部分图象如图所示.(1)求函数f (x )的解析式;(2)如何由函数y =2sin x 的图象通过适当的变换得到函数f (x )的图象,写出变换过程. 解:(1)由图象知A =2,f (x )的最小正周期54()126T ππ=⨯-=π,故22Tωπ==.将点(2)6π,代入f (x )的解析式得sin ()13ϕπ+=,又|ϕ|2π<,∴6ϕπ=.故函数f (x )的解析式为f (x )=2sin (2)6x π+.(2)变换过程如下:y =2sin x 图象向左平移6π个单位长度y =2sin(x +)6π所有点的横坐标缩短为原来的12倍纵坐标不变y =2sin (2)6x π+;另解:y =2sin x 所有点的横坐标缩短为原来的12倍纵坐标不变y =2sin2x 图象向左平移12π个单位长度y =2sin (2)6x π+.高考学习网－中国最大高考学习网站 | 我们负责传递知识！。

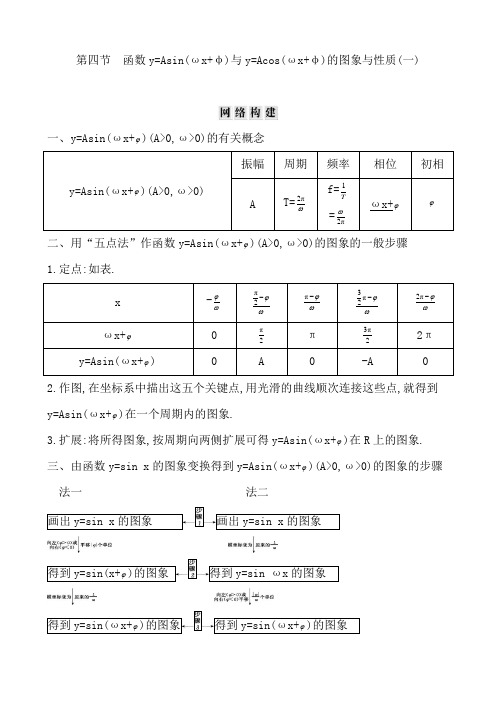
第四节 函数y=Asin(ωx+φ)与y=Acos(ωx+φ)的图象与性质(一)一、y=Asin(ωx+ϕ)(A>0,ω>0)的有关概念二、用“五点法”作函数y=Asin(ωx+ϕ)(A>0,ω>0)的图象的一般步骤 1.定点:如表.2.作图,在坐标系中描出这五个关键点,用光滑的曲线顺次连接这些点,就得到y=Asin(ωx+ϕ)在一个周期内的图象.3.扩展:将所得图象,按周期向两侧扩展可得y=Asin(ωx+ϕ)在R 上的图象. 三、由函数y=sin x 的图象变换得到y=Asin(ωx+ϕ)(A>0,ω>0)的图象的步骤 法一法二1.法则理解(1)无论哪种变换,每一个变换总是针对“自变量x ”而言的. 即图象变换要看“自变量x ”发生什么变化,而不是看角“ωx+ϕ”的变化.(2)在图象变换时运用“先平移后伸缩”与“先伸缩后平移”两种途径,左右平移的单位长度个数是不一样的.前者平移|ϕ|个单位长度,后者平移|ϕω|个单位长度,原因在于相位变换和周期变换都是针对变量x 而言的,因此在用这样的变换法作图象时一定要注意平移与伸缩的先后顺序,否则会出现错误. (3)平移的法则是“左+右-,上+下-”.2.与确定解析式y=Asin(ωx+ϕ)+b 中参数相关的结论 (1)求ϕ①代入法.把图象上的一个已知点代入(此时A,ω,b 已知)或代入图象与直线y=b 的交点求解(此时要注意交点在上升区间上还是在下降区间上).②五点法.确定ϕ值时,往往寻找“五点法”中的第一个点为突破口,具体如下: 选“第一点”(即图象上升时与x 轴的交点)时,令ωx+ϕ=0; 选“第二点”(即图象的“峰点”)时,令ωx+ϕ=π2; 选“第三点”(即图象下降时与x 轴的交点)时,令ωx+ϕ=π; 选“第四点”(即图象的“谷点”)时,令ωx+ϕ=3π2; 选“第五点”时,令ωx+ϕ=2π. (2)求ω:因为T=2πω,所以求ω即求T.①图象上相邻的两个最高点(或最低点)之间的距离为T,相邻的一个最高点与最低点之间的距离是2T.②图象的相邻的对称轴(中心)之间的距离为2T,相邻的一个对称中心与对称轴之间的距离为2T.1.设函数f(x)=cos ωx(ω>0),将y=f(x)的图象向右平移π3个单位长度后,所得的图象与原图象重合,则ω的最小值等于( C )(A)13(B)3 (C)6 (D)9解析:由题意可知,nT=π3(n∈N*),所以n·2πω=π3(n∈N*),所以ω=6n(n∈N*),所以当n=1时,ω取得最小值6.故选C.2.为了得到函数y=sin(2x-π3)的图象,只需把函数y=sin(2x+π6)的图象( B )(A)向左平移π4个单位长度(B)向右平移π4个单位长度(C)向左平移π2个单位长度(D)向右平移π2个单位长度解析:y=sin(2x+π6)=sin[2(x+π12)],y=sin(2x-π3)=sin[2(x-π6)]=sin[2(x-π4+π12)],所以将y=sin(2x+π6)的图象向右平移π4个单位长度得到y=sin(2x-π3)的图象.故选B.3.如图是函数y=Asin(ωx+ϕ)+2(A>0,ω>0)的图象的一部分,它的振幅、周期、初相各是( C )(A)A=3,T=4π3,ϕ=-π6(B)A=1,T=4π3,ϕ=3π4(C)A=1,T=4π3,ϕ=-3π4(D)A=1,T=4π3,ϕ=-π6解析:由图象知,A=312-=1,2T = 5π6-π6=2π3,则T=4π3,ω=32,由5π6×32+ϕ=π2+2k π,k ∈Z,得ϕ=-3π4+2k π,k ∈Z,令k=0,得ϕ=-3π4.故选C.4.函数f(x)=Asin(ωx+ϕ)(A>0,ω>0,|ϕ|<π)的部分图象如图所示,则函数f(x)的解析式为 .解析:由图可知4T=7π12-π3=π4,所以T=π,故ω=2, 因此ϕ).又函数图象过点(π3,0) 因此2×π3+ϕ=π+2k π,k ∈Z, 又根据|ϕ|<π,所以ϕ=π3,故π3).答案π3)5.将函数∈R)的图象向左平移m(m>0)个单位长度后,所得到的图象关于y 轴对称,则m 的最小值是 .解析12sin x)=2sin(x+π3)的图象向左平移m 个单位长度后,得到y=2sin(x+m+π3)的图象,此图象关于y 轴对称,则x=0时,y=±2,即2sin(m+π3)=±2,所以m+π3=π2+k π,k ∈Z,即m=π6+k π,k ∈Z,由于m>0,所以m min =π6. 答案:π6(对应学生用书第66～68页)考点一 五点法作图【例1】 设x ∈R,函数y=f(x)=cos(ωx+ϕ)(ω>0,- π2<ϕ<0)的最小正周期为π,且f(π4.(1)求ω和ϕ的值;(2)在给定坐标系中作出函数f(x)在[0,π]上的图象;(3)若,求x 的取值范围.解:(1)因为函数f(x)的最小正周期T=2πω=π, 所以ω=2,因为f(π4)=cos(2×π4+ϕ)=cos(π2+ϕ)=-sin ϕ且-π2<ϕ<0, 所以ϕ=-π3. (2)由(1)知f(x)=cos(2x-π3),列表如下:图象如图:(3)因为,即cos(2x-π3,所以2k π-π4<2x-π3<2k π+π4,k ∈Z, 则2k π+π12<2x<2k π+7π12,k ∈Z,即k π+π24<x<k π+7π24,k ∈Z. 所以x 的取值范围是{x|k π+π24<x<k π+7π24,k ∈Z}.用“五点法”作y=Asin(ωx+ϕ)或y=Acos(ωx+ϕ)的简图,主要是通过列表,计算得出五点的坐标,描点后得到,由于表中“五点”相邻两点的横向距离均为4T ,因此可以通过“定两端,分中间”的方法快速写出“五点”的坐标.某同学用“五点法”画函数f(x)=Asin(ωx+ϕ),ω>0,|ϕ|<π2在某一个周期内的图象时,列表并填入了部分数据,如下表:(1)请将上表数据补充完整,并直接写出函数f(x)的解析式;(2)将y=f(x)图象上所有点向左平行移动θ(θ>0)个单位长度,得到y=g(x)的图象.若y=g(x)图象的一个对称中心为(5π12,0),求θ的最小值;(3)说明函数f(x)的图象可由y=sin x 的图象经过怎样的变换而得到. 解:(1)根据表中已知数据,解得A=5,ω=2,ϕ=- π6,数据补全如下表:且函数解析式为f(x)=5sin(2x-π6). (2)由(1)知f(x)=5sin(2x-π6), 则g(x)=5sin(2x+2θ-π6). 因为函数y=sin x 图象的对称中心为(k π,0),k ∈Z,令2x+2θ-π6=k π,k ∈Z,解得x=π2k +π12-θ,k ∈Z. 由于函数y=g(x)的图象关于点(5π12,0)成中心对称,所以令π2k +π12-θ=5π12,解得θ=π2k -π3,k ∈Z. 由θ>0可知,当k=1时,θ取得最小值π6. (3)把y=sin x 的图象上所有的点向右平移π6个单位长度,得到y=sin(x-π6)的图象,再把y=sin(x-π6)的图象上的点的横坐标缩短到原来的12(纵坐标不变),得到y=sin(2x-π6)的图象,最后把y=sin(2x-π6)上所有点的纵坐标伸长到原来的5倍(横坐标不变),即可得到f(x)=5sin(2x-π6)的图象. 考点二 函数y=Asin(ωx+ϕ)(A>0,ω>0)的图象变换【例2】 (1)将函数f(x)=2sin(2x+π4)的图象向右平移ϕ(ϕ>0)个单位,再将图象上每一点的横坐标缩短到原来的12(纵坐标不变),所得图象关于直线x=π4对称,则ϕ的最小值为( )(A)18π (B)12π (C)34π (D)38π(2)将函数y=cos(2x+ϕ)的图象沿x 轴向右平移π6后,得到的图象关于原点对称,则ϕ的一个可能取值为( )(A)-π3 (B)π6 (C)π3 (D)5π6解析:(1)将函数f(x)=2sin(2x+π4)的图象向右平移ϕ(ϕ>0)个单位,可得函数y=2sin[2(x-ϕ)+π4]=2sin(2x+π4-2ϕ)的图象,再将图象上每一点的横坐标缩短到原来的12(纵坐标不变),可得函数y=2sin(4x+π4-2ϕ)的图象;再根据所得图象关于直线x=π4对称,可得π+π4-2ϕ=k π+π2(k ∈Z),即ϕ=3π8-π2k ,k ∈Z,所以ϕ的最小值为3π8,故选D.(2)将函数y=cos(2x+ϕ)的图象沿x 轴向右平移π6后,得到的图象对应的解析式为y=cos[2(x-π6)+ϕ]=cos(2x-π3+ϕ).再根据得到的图象关于原点对称,则-π3+ϕ=k π+π2,k ∈Z,即ϕ=k π+5π6,k ∈Z.结合所给的选项,故选D.(1)解决三角函数图象变换问题,应先把变换前后两个函数化为同名函数,然后找出它们的不同,指出实施的变换.(2)平移变换要注意平移量和平移方向,其实质是点的坐标的变换,横坐标的变换对应着图象的左右平移,纵坐标的平移变换对应着图象的上下平移.将函数f(x)=sin(2x+θ)(-π2<θ<π2)的图象向右平移ϕ(ϕ>0)个单位长度后得到函数g(x)的图象,若f(x),g(x)的图象都经过点),则ϕ的值可以是( B )(A)5π3 (B)5π6 (C)π2 (D)π6解析:因为函数f(x)的图象过点P,所以θ=π3,所以f(x)=sin(2x+π3).又函数f(x)的图象向右平移ϕ个单位长度后,得到函数g(x)=sin[2(x-ϕ)+π3]的图象,所以sin(π3-2ϕ所以ϕ可以为5π6.故选B.考点三求函数y=Asin(ωx+ϕ)+b的解析式【例3】 (1)函数f(x)=Asin(ωx+θ)(A>0,ω>0)的部分图象如图所示,则f(x)等于( )π6)π3)π3)π6)(2)已知函数f(x)=Asin(ωx+ϕ),x∈R(其中A>0,ω>0,0<ϕ<π2)的图象与x轴的交点中,相邻两个交点之间的距离为π2,且图象上一个最低点为M(2π3,-2),则f(x)的解析式为.解析:(1)由题图知f(x)在x=512π且最小正周期T满足34T=512π+π3.故34×2πω=3π4,ω×5π12+θ5π6+θ)=1,5π6+θ=2kπ+π2,k∈Z,θ=2kπ-π3,k∈Z.所以f(x)的解析式可为π3).故选B.(2)由最低点为M(2π3,-2)得A=2.由题意得2T=π2,即T=π,ω=2πT=2ππ=2, 由点M(2π3,-2)在图象上得2sin(2×2π3+ϕ)=-2, 即sin(4π3+ϕ)=-1,故4π3+ϕ=2k π-π2,k ∈Z, 所以ϕ=2k π-11π6,k ∈Z,又ϕ∈(0,π2), 所以ϕ=π6, 故f(x)=2sin(2x+π6). 答案:(1)B (2)f(x)=2sin(2x+π6)确定y=Asin(ωx+ϕ)+b(A>0,ω>0)的解析式的步骤(1)求A,b,确定函数的最大值M 和最小值m,则A=2M m -,b=2M m+.(2)求ω,确定函数的周期T,则ω=2πT. (3)求ϕ,常用方法有:①代入法:把图象上的一个已知点代入(此时要注意该点在上升区间上还是在下降区间上)或把图象的最高点或最低点代入.②五点法:确定ϕ值时,往往寻找“五点法”中的特殊点作为突破口.已知函数f(x)=Atan(ωx+ϕ)(ω>0,|ϕ|<π2),y=f(x)的部分图象如图,则f(π24)等于( B )解析:由图象可知T=2(3π8-π8)=π2,所以ω=2,所以2×π8+ϕ=k π+π2,k ∈Z,得ϕ=π4+k π,k ∈Z, 又|ϕ|<π2, 所以ϕ=π4. 又f(0)=1,所以Atan π4=1,得A=1, 所以f(x)=tan(2x+π4), 所以f(π24)=tan(π12+π4)=tan π3.考点四 易错辨析【例4】 (2018·浙江金华十校模拟)已知函数f(x)=sin(ωx+π3)(x ∈R,ω>0)与g(x)=cos(2x+ϕ)的对称轴完全相同,为了得到h(x)=cos(ωx+π3)的图象,只需将y=f(x)的图象( ) (A)向左平移π4个单位长度 (B)向右平移π4个单位长度 (C)向左平移π2个单位长度 (D)向右平移π2个单位长度 解析:因为对称轴一样,所以两个三角函数的周期必定一样,即ω=2,所以f(x)=sin(2x+π3),h(x)=cos(2x+π3)=sin[2(x+π4)+π3],故得到h(x)的图象仅需将y=f(x)的图象向左平移π4个单位长度,故选A.(1)忽略函数名称的不同,误以为同名三角函数之间的变换;(2)忽略系数ω的存在,误将x 的变换认为是ωx 的变换.已知函数f(x)=sin(ωx+ϕ)(ω>0,|ϕ|< π2)的最小正周期是π,若将f(x)的图象向右平移π3个单位后得到的图象关于原点对称,则函数f(x)的图象( B )(A)关于直线x=π12对称(B)关于直线x=5π12对称(C)关于点(π12,0)对称(D)关于点(5π12,0)对称解析:因为f(x)的最小正周期为π, 所以2πω=π,ω=2,所以f(x)的图象向右平移π3个单位后得到g(x)=sin[2(x-π3)+ϕ]=sin(2x-2π3+ϕ)的图象,又g(x)的图象关于原点对称, 所以-2π3+ϕ=kπ,k∈Z,所以ϕ=2π3+kπ,k∈Z,又|ϕ|<π2,所以ϕ=-π3,所以f(x)=sin(2x-π3).当x=π12时,2x-π3=-π6,所以A,C错误;当x=5π12时,2x-π3=π2,所以B正确,D错误.故选B.(对应学生用书第68～69页)三角函数图象【例题】已知函数f(x)的图象是由函数g(x)=cos x的图象经如下变换得到:先将g(x)图象上所有点的纵坐标伸长到原来的2倍(横坐标不变),再将所得到的图象向右平移π2个单位长度.(1)求函数f(x)的解析式,并求其图象的对称轴方程;(2)已知关于x的方程f(x)+g(x)=m在[0,2π)内有两个不同的解α,β.a.求实数m 的取值范围;b.证明:cos(α-β)=225m -1. (1)解:将g(x)=cos x 的图象上所有点的纵坐标伸长到原来的2倍(横坐标不变)得到y=2cos x 的图象,再将y=2cos x 的图象向右平移π2个单位长度后得到y=2cos(x-π2)的图象,故f(x)=2sin x. 从而函数f(x)=2sin x 图象的对称轴方程为x=k π+π2(k ∈Z). (2)a.解:f(x)+g(x)=2sin x+cossin cos ϕ)(其中sinϕϕ依题意知,sin(x+ϕ[0,2π)内有两个不同的解α,β,当且仅当故m 的取值范围是b.证明:因为α,βϕ)=m 在[0,2π)内的两个不同的解,所以sin(α+ϕβ+ϕ当1≤,α+β=2(π2-ϕ), 即α+ϕ=π-(β+ϕ); 当时,α+β=2(3π2-ϕ),即α+ϕ=3π-(β+ϕ). 所以cos(α+ϕ)=-cos(β+ϕ). 于是cos(α-β)=cos[(α+ϕ)-(β+ϕ)] =cos(α+ϕ)cos(β+ϕ)+sin(α+ϕ)sin(β+ϕ) =-cos 2(β+ϕ)+sin(α+ϕ)sin(β+ϕ)22=225m -1.规范要求:(1)根据图象变换规律求出函数解析式,再根据对称轴的特点求对称轴方程.(2)通过三角变换将f(x)+g(x)化为一个角的一种三角函数形式.(3)分离参数法转化为求函数的值域,从而解绝对值不等式求得参数范围.(4)利用三角函数相等,求得α,β的关系,从而判定cos(α+ϕ)与cos(β+ϕ)的关系,进而利用两角和与差公式求值.(5)解决给值求值问题的关键是找出未知角与已知角关系,从而选择对应公式求解.【规范训练1】如图为y=Asin(ωx+ϕ)(A>0,ω>0)的图象的一段.(1)求其解析式;(2)若将y=Asin(ωx+ϕ)的图象向左平移π6个单位长度后得y=f(x),求f(x)的对称轴方程.解:(1)由图象知由“五点法”列方程组π0,35ππ,6ωϕωϕ⎧⋅+=⎪⎪⎨⎪⋅+=⎪⎩解之2,2π,3ωϕ=⎧⎪⎨=-⎪⎩得所以所求解析式为2π3 ).π6)-2π3sin(2x-π3),令2x-π3=π2+kπ(k∈Z),则x=512π+π2k(k∈Z),所以f(x)的对称轴方程为x=512π+π2k (k ∈Z).【规范训练2】 设关于x在区间(0,2π)内有相异的两个实根α,β. (1)求实数a 的取值范围; (2)求α+β的值.解:(1)原方程可化为sin(x+π3)=-2a ,作出函数y=sin(x+π3)(x ∈(0,2π))的图象.由图知,方程在(0,2π)内有相异实根α,β的充要条件是11,2a a ⎧-<-<⎪⎪⎨⎪-⎪⎩ 即(2)由图知,当即-2a∈)时,直线 y=-2a 与三角函数y=sin(x+π3)的图象交于C,D 两点,它们中点的横坐标为76π, 所以2αβ+=7π6, 所以α+β=7π3. 当即-2a∈,1)时,直线y=-2a 与三角函数y=sin(x+π3)的图象有两交点A,B,由对称性知,2αβ+=π6, 所以α+β=π3. 综上所述,α+β=π3或73π.(对应学生用书第69页)类型一 三角函数图象变换1.把函数y=cos 2x+1的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),然后向左平移1个单位长度,再向下平移1个单位长度,得到的图象是( A )解析:把函数y=cos 2x+1的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),得到函数y=cos x+1的图象,然后把所得函数图象向左平移1个单位长度,再向下平移1个单位长度,得到函数y=cos(x+1)的图象.故选A.2.(2018·浙江镇海中学期中)将函数f(x)=3sin(4x+π6)图象上所有点的横坐标伸长到原来的2倍,再向右平移π6个单位长度,得到函数y=g(x)的图象,则y=g(x)图象的一条对称轴是( C )(A)x=π12 (B)x=π6 (C)x=π3 (D)x=2π3解析:将函数f(x)=3sin(4x+π6)图象上所有点的横坐标伸长到原来的2倍,得到函数y=3sin(2x+π6)的图象,再向右平移π6个单位长度,得g(x)=3sin[2(x-π6)+π6]=3sin(2x-π6)的图象,令2x-π6=k π+π2,k ∈Z,则y=g(x)图象的对称轴是x=π2k +π3,k ∈Z,故选C. 类型二 求函数y=Asin(ωx+ϕ)+b 的解析式3.如图是函数y=Asin(ωx+ϕ)(A>0,ω>0)在一个周期内的图象,此函数的解析式可为( B ) (A)y=2sin(2x+π3) (B)y=2sin(2x+2π3)(C)y=2sin(2x -π3)(D)y=2sin(2x-π3)解析:由题图可知A=2,2T =5π12-(-π12)=π2, 所以T=π,ω=2, 所以f(x)=2sin(2x+ϕ),又f(-π12)=2sin(-π6+ϕ)=2, 即-π6+ϕ=π2+2k π,k ∈Z, 所以ϕ=2π3+2k π(k ∈Z),结合选项知选B.4.已知函数f(x)=Asin(ωx+ϕ)(A>0,ω>0,|ϕ|<π)图象的最高点的纵坐标是4,相邻的两对称中心距离为π2,图象经过点(π6,0),则函数f(x)的解析式为 .解析:由题意知A=4,T=2×π2=π, 所以2πω=π,则ω=2, 所以f(x)=4sin(2x+ϕ). 又函数图象经过点(π6,0), 所以4sin(2×π6+ϕ)=0, 所以ϕ+π3=k π(k ∈Z), 所以ϕ=k π-π3(k ∈Z),又|ϕ|<π, 所以ϕ=-π3或ϕ=2π3. 所以f(x)=4sin(2x-π3)或f(x)=4sin(2x+2π3). 答案:f(x)=4sin(2x-π3)或f(x)=4sin(2x+2π3)5.如图所示,为了研究钟表与三角函数的关系,建立如图所示的坐标系,设秒针尖位置P(x,y).若初始位置为P 012),当秒针从P 0(注:此时t=0)正常开始走时,那么点P 的纵坐标y 与时间t 的函数关系为 .解析:由题意可得,函数的初相位是π6,又函数周期是60秒且秒针按顺时针旋转,即T=2πω=60,所以|ω|=π30,即ω=-π30,故y=sin(-π30t+π6). 答案:y=sin(-π30t+π6) 类型三 函数y=Asin(ωx+ϕ)与y=Acos(ωx+ϕ)图象的应用6.函数y=f(x)=Asin(ωx+ϕ)(A>0,ω>0,|ϕ|< π2)的部分图象如图所示,若x 1,x 2∈(-π6,π3),且f(x 1)=f(x 2),则f(x 1+x 2)等于( D )(A)1 (B)12解析:观察图象可知,A=1,T=π, 所以ω=2,f(x)=sin(2x+ϕ).将(-π6,0)代入上式得sin(-π3+ϕ)=0, 由|ϕ|<π2,得ϕ=π3, 则f(x)=sin(2x+π3). 函数图象的一条对称轴为x=ππ632-+=π12.又x 1,x 2∈(-π6,π3),且f(x 1)=f(x 2),所以122xx +=π12,所以x 1+x 2=π6,所以f(x 1+x 2)=sin(2×π6+π3.故选D.7.已知直线y=b(b<0)与曲线y=f(x)=sin(2x+π2)在y 轴右侧依次的三个交点的横坐标成等比数列,则b 的值是 . 解析:设三个横坐标依次为x 1,x 2,x 3,由图及题意有12232213π,2π,,x x x x x x x ⎧+=⎪+=⎨⎪=⎩解得x 2=2π3,所以b=f(2π3)=-12. 答案:-12。

（浙江专版）2019年高考数学一轮复习专题4.5 函数y＝Asin（ωx＋φ）的图象及三角函数模型的简单应用（讲）编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（（浙江专版）2019年高考数学一轮复习专题4.5 函数y＝Asin（ωx＋φ）的图象及三角函数模型的简单应用（讲））的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为（浙江专版）2019年高考数学一轮复习专题4.5 函数y＝Asin（ωx＋φ）的图象及三角函数模型的简单应用（讲）的全部内容。

第05节 函数y ＝Asin （ωx ＋φ)的图象及三角函数模型的简单应用【考纲解读】考 点考纲内容5年统计分析预测函数y ＝Asin(ωx ＋φ)的图象及三角函数模型的简单应用了解函数 y ＝A sin （ωx ＋φ） 的物理意义，掌握 y ＝A sin （ωx ＋φ) 的图象，了解参数 A ，ω，φ 对函数图象变化的影响。

2013浙江文6理4；2014浙江文4，理4;2016浙江文11，理10。

1.“五点法”作图; 2。

函数图象的变换；3。

三角函数模型的应用问题.4。

往往将恒等变换与图象和性质结合考查 5。

备考重点：（1）掌握函数图象的变换；(2） 掌握三角函数模型的应用。

【知识清单】1.求三角函数解析式（1）()sin y A x ωϕ=+的有关概念()sin y A x ωϕ=+()0,0A ω>>， [)0,x ∈+∞表示一个振动量时振幅 周期 频率相位 初相A2T πω=12f T ωπ==x ωϕ+ ϕ (2)()sin y A x =+用五点法画()sin y A x ωϕ=+一个周期内的简图时,要找五个关键点,如下表所示：xϕω-2ϕπωω-+πϕω- 32ϕπωω-+2πϕω-x ωϕ+2π π 32π 2π ()sin y A x ωϕ=+ 0A－A（3)由()sin y A x ωϕ=+的图象求其函数式：已知函数()sin y A x ωϕ=+的图象求解析式时，常采用待定系数法,由图中的最高点、最低点或特殊点求A ；由函数的周期确定ω；确定ϕ常根据“五点法”中的五个点求解,其中一般把第一个零点,0ϕω⎛⎫-⎪⎝⎭作为突破口，可以从图象的升降找准第一个零点的位置． （4)利用图象变换求解析式：由sin y x =的图象向左()0ϕ>或向右()0ϕ<平移ϕ个单位，，得到函数()sin y x ϕ=+，将图象上各点的横坐标变为原来的1ω倍(0ω>)，便得()sin y x ωϕ=+，将图象上各点的纵坐标变为原来的A 倍（0A >)，便得()sin y A x ωϕ=+。