下载文档原格式
热学基础热传导与热平衡的分析与计算热学是物理学的一个重要分支，它研究热量传递和热平衡等热现象。
本文将对热传导和热平衡进行详细的分析和计算。
一、热传导热传导是指热量通过物质的传递，常见的方式有导热、导热和辐射等。
导热是最常见的传热方式，它依赖于物质内部的分子热运动。
导热可以通过热传导方程来描述：q = -kA∆T/∆x其中，q表示单位时间内通过物体的热量，k是热导率，A是传热面积，∆T是温度差，∆x是传热距离。
根据热传导方程，我们可以计算物体的热传导率和传热功率。
二、热平衡热平衡是指两个物体之间的温度差为0，不再存在热量传递。
当两个物体之间达到热平衡时，它们的温度相等。
热平衡的条件可以通过热平衡方程来表达：q1 = q2其中，q1和q2分别代表两个物体的热量。
热平衡方程告诉我们，当两个物体之间的热量相等时，它们达到热平衡状态。
三、热传导与热平衡的计算在实际问题中，我们常常需要计算热传导和热平衡的相关参数。
下面以一个具体的例子来说明如何进行计算。
考虑一个铜棒，长度为L，横截面积为A，温度分布随传热方向x变化。
假设铜棒的热导率为k，铜棒上端温度为T1，下端温度为T2，我们希望计算出铜棒内各点的温度分布。
首先，根据热传导方程，我们可以得到铜棒内各点的温度分布：∆T/∆x = -q/kA其中，∆T是铜棒内两个相邻点的温度差，∆x是相邻点之间的距离。
假设我们已知铜棒上下端的温度，即T1和T2，我们可以利用以上方程进行计算。
首先，选择适当的步长∆x，将铜棒分为N个小段，假设第i段的温度为Ti。
根据以上方程，我们可以得到：(Ti+1 - Ti)/∆x = -q/(kA)其中，i取值从1到N-1。
根据热平衡方程，我们有：q = -kA(T2 - T1)/L将其带入上述方程，可以得到：Ti+1 - Ti = kA(T2 - T1)/(L∆x)根据以上方程，我们可以利用迭代的方法，从上端到下端，求解各段的温度。
四、总结通过上述分析和计算，我们可以详细了解热传导和热平衡的概念、原理和计算方法。
第五章能量衡算第一节概述第二节热量衡算第三节过程的热效应第四节热量衡算举例第五节加热剂、冷却剂及其其他能量消耗的计算5.1 概述5.1.1 能量衡算的目的和意义计算过程能耗指标进行方案比较，选定先进生产工艺。
能量衡算数据是设备选型和计算的依据；是组织、管理、生产、经济核算和最优化的基础5.1.2 能量衡算的的依据及必要条件依据为能量守恒定律条件：物料衡算的数据，相关热力学物性数据。
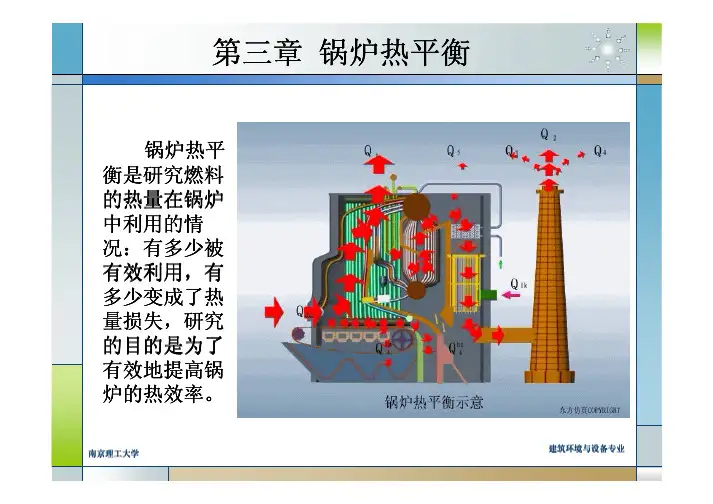
5.1.3 能量守恒的基本方程输出能量+消耗能量+积累能量=输入能量+生成能量5.1.4 能量衡算的分类单元设备的能量衡算和系统的能量衡算5.2 热量衡算5.2.1 热量平衡方程式Q —物料带入设备的热量，kJ ;Q2—加热剂或冷却剂传给设备及所处理物料的热量，kJ ;Q3 —过程的热效应，kJ;（注意符号规定）Q4—物料带出设备的热量，kJ ；Q5—加热或冷却设备所消耗的热量或冷量，kJ ；Q6 —设备向环境散失的热量，kJ。
注意各Q勺符号规定Q为设备的热负荷。
若Q为正值，需要向设备及所处理的物料提供热量; 反之，表明需要从设备及所处理的物料移走热量。
对间歇操作，按不同的时间段分别计算Q的值，并取其最大值作为设备热负荷的设计依据。
522 各项热量的计算1、计算基准一般情况下，可以0C和1.013 105Pa为计算基准有反应的过程，也常以25C和1.013 105Pa为计算基准。
2、Q或Q的计算无相变时物料的恒压热容与温度的函数关系常用多项式来表示：若知物料在所涉及温度范围内的平均恒压热容，贝心3、Q的计算过程的热效应由物理变化热Q和化学变化热Q两部分组成物理变化热是指物料的浓度或状态发生改变时所产生的热效应。
若过程为纯物理过程，无化学反应发生，如固体的溶解、硝化混酸的配制、液体混合物的精馏等，则Q C= 0 。
化学变化热是指组分之间发生化学反应时所产生的热效应，可根据物质的反应量和化学反应热计算。
4、Q的计算稳态操作过程Q 5= 0非稳态操作过程由下式求QQ=' GC (T2-T1)G-设备各部件的质量，kg;G—设备各部件材料的平均恒压热容，kJ kg-1「C-1;T1—设备各部件的初始温度，C；T2—设备各部件的最终温度，C。
