大气扩散浓度估算模式

第四章大气扩散浓度估算模式第一节湍流扩散的基本理论一、湍流概念简介大气的无规则运动称为大气湍流。

风速的脉动（或涨落）和风向的摆动就是湍流作用的结果。

按照湍流形成原因可分为两种湍流：一是由于垂直方向温度分布不均匀引起的热力湍流，其强度主要取决于大气稳定度；二是由于垂直方向风速分布不均匀及地面粗糙度引起的机械湍流，其强度主要取决于风速梯度和地面粗糙度。

实际的湍流是上述两种湍流叠加的结果。

湍流有极强的扩散能力，比分子扩散快105～106倍。

但在风场运动的主风方向上，由于平均风速比脉动风速大的多，所以在主风方向上风的平流输送作用是主要的。

归结起来，风速越大，湍流越强，大气污染物的扩散速度越快，污染物的浓度就越低。

风和湍流是决定污染物在大气中扩散稀释的最直接最本质的因素，其他一切气象因素都是通过风和湍流的作用来影响扩散稀释的。

二、湍流扩散理论简介大气扩散的基本问题，是研究湍流与烟流传播和物质浓度衰减的关系问题。

目前处理这类问题有三种广泛应用的理论：梯度输送理论、湍流统计理论和相似理论。

1.梯度输送理论梯度输送理论是通过与菲克扩散理论的类比而建立起来的。

菲克认为分子扩散的规律与傅立叶提出的固体中的热传导的规律类似，皆可用相同的数学方程式描述。

湍流梯度输送理论进一步假定，由大气湍流引起的某物质的扩散，类似于分子扩散，并可用同样的分子扩散方程描述。

为了求得各种条件下某污染物的时、空分布，必须对分子扩散方程在进行扩散的大气湍流场的边界条件下求解。

然而由于边界条件往往很复杂，不能求出严格的分析解，只能是在持定的条件下求出近似解，再根据实际情况进行修正。

2．湍流统计理论泰勒首先应用统计学方法研究湍流扩散问题，并于1921年提出了著名的泰勒公式。

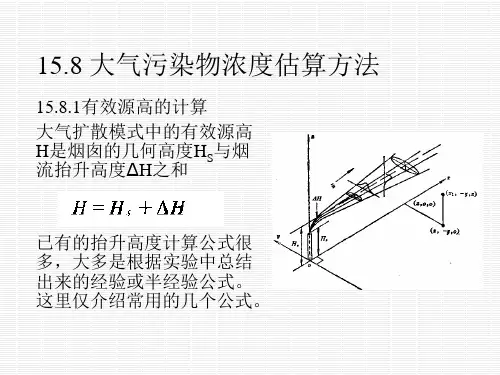
图4-1是从污染源放心的粒子，在风沿着x方向吹的湍流大气中的扩散情况。

假定大气湍流场是均匀、稳定的。

从原点放出的一个粒子的位置用y表示，则y随时间而变化，但其平均值为零。

如果从原点放出很多粒子，则在x轴上粒子的浓度最高，浓度分布以x轴为对称轴，并符合正态分布。

大气污染扩散及浓度估算模式概述大气污染是指空气中某些物质或能量的浓度超过了一定的标准，对人类健康、生态系统和环境产生一定危害的现象。

而大气污染扩散及浓度估算模式则是一种基于数学、物理学原理的模拟工具，用来描述和预测大气污染物在大气中的扩散传播过程及其浓度分布情况。

扩散模式的基本原理大气污染物的扩散传播是受到气象条件、地形地貌、大气污染物排放源等多种因素的影响。

因此，扩散模式一般包括了以下几个基本原理：1.对流扩散：大气中的对流运动是造成大气污染物扩散的主要因素之一。

通过对流运动，大气中的污染物会随着空气的流动在近地层逐渐扩散。

2.湍流扩散：湍流是大气中涡动和乱流的运动形式，对大气污染物的扩散传播起着重要作用。

湍流扩散模式一般基于大气边界层内的湍流动力学理论建立。

3.稳定度影响：大气的稳定度会影响大气污染物的扩散情况。

在稳定的大气层中，扩散较小，而不稳定的大气层则容易形成污染物下沉和较大范围的扩散。

4.地形地貌影响：地形地貌会对大气污染物的扩散产生重要的影响，如山脉、山谷等地形特征会对污染物传播产生局部影响。

浓度估算模式的发展随着大气环境科学的发展和计算机技术的进步，大气污染扩散及浓度估算模式得到了长足的发展。

目前，常用的大气污染扩散及浓度估算模式主要包括了以下几种：1.高斯模型：高斯模型是最简单的扩散模型之一，假设大气污染物的传播呈现高斯分布。

其适用于平坦地形、均匀排放源的情况。

2.拉格朗日模型：拉格朗日模型是一种基于粒子运动轨迹的扩散模式，可以更准确地描述污染物的扩散传播路径。

3.欧拉模型：欧拉模型是一种基于流体动力学方程的扩散模型，适用于描述大气边界层内的湍流扩散过程。

4.数值模拟模型：数值模拟模型是最常用的大气污染扩散及浓度估算模式之一，利用数值计算方法对复杂的大气扩散传播过程进行模拟。

应用及展望大气污染扩散及浓度估算模式在环境保护、城市规划、应急响应等领域具有重要的应用意义。

通过对大气污染物的扩散传播过程进行模拟和预测，可以帮助政府及相关部门制定合理的环境政策和控制措施。

大气扩散浓度估算模式第一节 湍流扩散的基本理论一 湍流1．定义：大气的无规则运动风速的脉动 风向的摆动2．类型：按形成原因 热力湍流：温度垂直分布不均（不稳定）引起，取决于大气稳定度机械湍流：垂直方向风速分布不均匀及地面粗糙度引起3．扩散的要素风：平流输送为主，风大则湍流大 湍流：扩散比分子扩散快105～106倍二 湍流扩散理论（主要阐述湍流与烟流传播及湍流与物质浓度衰减的关系）1.梯度输送理论通过与菲克扩散理论类比建立起来的（菲克定律：单位时间内通过单位断面上的物质的数量与浓度梯度呈正比）类比于分子扩散，污染物的扩散速率与负浓度梯度成正比xCkF ∂∂-= 式中，F — 污染物的输送通量k — 湍流扩散系数 C — 污染物的浓度X — 与扩散截面垂直的空间坐标（扩散过程的长度）xC∂∂— 浓度梯度 要求得各种条件下某污染物的时、空分布，由于边界条件往往很复杂，不能求出严格的分析解，只能是在特定的条件下求出近似解，再根据实际情况进行修正。

2.湍流统计理论泰勒首先将统计理论应用在湍流扩散上图4-1显示：从原点O 放出的粒子，在风沿着x 方向吹的湍流大气中扩散。

粒子的位置用y 表示，则结论为：①y 随时间变化，但其变化的平均值为零②若从原点放出很多粒子，则在x 轴上粒子的浓度最高，浓席分布以x 轴为对称轴，并符合正态分布。

萨顿实用模式：解决污染物在大气中扩散的实用模式高斯模式：应用湍流统计理论得出正态分布假设下的扩散模式 3.相似理论第二节 高斯扩散模式一 坐标系的建立—右手坐标系1．原点O ：无界点源或地面源，O 为污染物的排放点高架源，O 为污染物的排放点在地面上的投影点补充：点源 高架源 连续源 固定源线源 地面源 间歇源 流动源 面源2．x 轴：正向为平均风向，烟流中心线与x 轴重合 3．y 轴：垂直于x 轴 4．z 轴：垂直于xoy 平面二 高斯模式的有关假定1．污染物浓度在y 、z 轴上的分布为正态分布；)2exp(21)(22y yy y f σπσ-=)2exp(21)(22z zz z f σπσ-=y σ，z σ— 分别为污染物在y 和z 方向上分布的标准差，m2．全部高度风速均匀稳定，即风速u 为常数；3．源强是连续均匀稳定的，源强Q 为定值；4．扩散中污染物是守恒的，不考虑转化，即烟云在扩散过程中没有沉降、化合、分解及地面吸收、吸附作用发生；0=∂∂tC5．在x 方向上，输送作用远远大于扩散作用，即 )(xCk x x C u x ∂∂∂∂>>∂∂； 6．地面足够平坦。