第三章受弯构件_
- 格式:ppt
- 大小:599.00 KB
- 文档页数:25




第3章 作业答案1 已知单筋矩形截面梁b ×h = 250mm ×500mm ,承受弯矩设计值M= 260kN.m ,混凝土强度为C30及HRB400级钢筋,环境类别为一类,计算梁的纵向受拉钢筋As ? 解: (1)查表确定个参数2/3.14mm N f c =,2/43.1mm N f t =,2/360mm N f y =,0.11=amm a h h s 460405000=-=-=,518.0=b ξ (2)计算s A344.04602503.1411026026201=⨯⨯⨯⨯==bh f a M a c sb s a ξξ<=--=441.0211 不超筋78.02211=-+=ss a γ260201446036078.010260mm h f M A y s s =⨯⨯⨯==γ实配钢筋:)1964(2542mm A s =φ(3)验算配筋率 %2.0)%178.045,2.0max (%71.14602501964min 0===>=⨯==yt s f f bh A ρρ 故满足要求。
2 已知单筋矩形截面简支梁,b ×h = 200mm ×450mm ,承受弯矩设计值M= 145kN.m ,混凝土强度为C40及HRB400级钢筋,环境类别为二类a ,计算梁的纵向受拉钢筋As ? 解: (1)查表确定个参数2/1.19mm N f c =,2/71.1mm N f t =,2/360mm N f y =,0.11=amm a h h s 405454500=-=-=,518.0=b ξ (2)计算s A231.04052001.1911014526201=⨯⨯⨯⨯==bh f a M a c sb s a ξξ<=--=267.0211 不超筋866.02211=-+=ss a γ2608.1147405360866.010145mm h f M A y s s =⨯⨯⨯==γ实配钢筋:)1140(2232mm A s =φ(3)验算配筋率 %213.0)%213.045,2.0max (%41.14052001140min 0===>=⨯==yt s f f bh A ρρ 故满足要求。

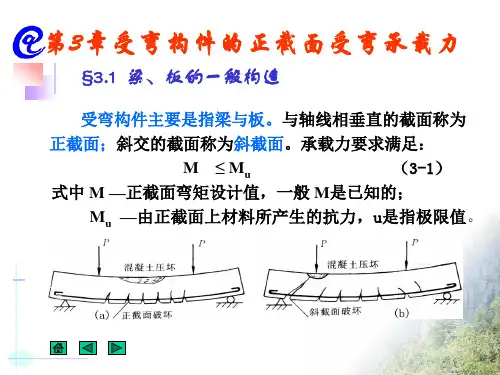




第三章 受弯构件正截面承载力一、填空题一、受弯构件正截面计算假定的受压区混凝土压应力散布图形中,0ε= ,cu ε= 。
二、梁截面设计时,可取截面有效高度:一排钢筋时,0h h =- ;两排钢筋时,0h h =- 。
3、梁下部钢筋的最小净距为 mm 及≥d 上部钢筋的最小净距为 mm 及≥。
4、适筋梁从加载到破坏可分为3个时期,试选择填空:A 、I ;B 、I a ;C 、II ;D 、II a ;E 、III ;F 、III a 。
①抗裂度计算以 时期为依据;②利历时期裂痕宽度和挠度计算以 时期为依据;③承载能力计算以 时期为依据。
五、受弯构件min ρρ≥是为了 ;max ρρ≤是为了 。
六、第一种T 形截面梁的适用条件及第二种T 形截面梁的适用条件中,没必要验算的条件别离是 及 。
7、T 形截面持续梁,跨中按 截面,而支座边按 截面计算。
八、界限相对受压区高度b ζ需要依照 等假定求出。
九、单筋矩形截面梁所能经受的最大弯矩为 ,不然应 。
10、在理论上,T 形截面梁,在M 作用下,f b '越大那么受压区高度χ 。
内力臂 ,因此可 受拉钢筋截面面积。
11、受弯构件正截面破坏形态有 、 、 3种。
12、板内散布筋的作用是:(1) ;(2) ;(3) 。
13、避免少筋破坏的条件是 ,避免超筋破坏的条件是 。
14、受弯构件的最小配筋率是 构件与 构件的界限配筋率,是依照 确信的。
15、双筋矩形截面梁正截面承载力计算公式的适用条件是:(1) 保证;(2) 保证 。
当<2s a χ'时,求s A 的公式为 ,还应与不考虑s A '而按单筋梁计算的s A 相较,取 (大、小)值。
16、双筋梁截面设计时,s A 、s A '均未知,应假设一个条件为 ,缘故是 ;承载力校核时如显现0>b h χξ时,说明 ,现在u M = ,如u M M ≤外,那么此构件 。
二、判定题一、在梁的设计中,幸免显现超筋破坏是通过构造方法来实现的。