随机过程第四章3

1.定义：设有随机过程{},n X n T ∈若对任意的整数n T ∈和任意的121,,...,n i i i I +∈,条件概率满足()()111111,...,n n n n n n n n p x i x i x i p x i x i ++++======则称其为马尔科夫链。

2.马尔科夫链的统计特性完全有条件概率()11n n n n p x i x i ++==决定。

3.一步转移概率称条件概率()()1p xjx i n ij n n p ==+=为马尔科夫链{},n X n T ∈在时刻n 的一步转移概率。

,i j I ∈,若()ij p n 与n 无关，则称马尔科夫链为齐次的。

();0;1;,ij ij ij ij j Ip n p p p j i I ∈=>==∈∑4.n 步转移概率称()()n p x j x i m m n ijp ==+=,i j I ∈0,1m n >=>=为马尔科夫链{},n X n T ∈的n步转移概率。

()()0;1;,n n ijijj Ip p j i I ∈>==∈∑5.n 步转移矩阵。

()()()n n ijP p =；()()()1011;0;;;ij ijij i p p P P j p i j=⎧=⎨≠==⎩6.()n p ij具有如下性质：设{},n X n T ∈为马尔科夫链，则对任意整数n>=0,1=<l<n ；,i j I ∈()()()11112........n n i k Ik Il n l n p p p p p p ijikkjik k k I k k j--∈∈-=∑∈=∑∑； ()()1n n n PP PP-==7初始概率：()0i p p X i == 8.初始概率向量：()()120,....TPp p =9.初始分布：{},i p i I ∈10绝对概率：()()j n p n p X j == 11绝对概率向量：()()()()12,....TPn p n p n =12绝对分布：(){},j p n j I ∈13性质如下：()()()()10;n TT T Pn P n P P P =-=()()()1;nj i ij i ij i Ii Ip n p p p n p ∈∈==-∑∑14马氏链的有限维分布：设{},n X n T ∈为马氏链，则对任意的12,,...,;1n i i i I n ∈≤有{}11....11,....,n n i Ip p p i ii i i n n p X i X i ∈-===∑完全有初始概率和一步转移概率决定。

1第四章 马尔可夫过程内容提要1. 马尔可夫过程的概念 （1）马尔可夫过程给定随机过程{}(),X t t T ∈，如果对122,∀≥∀<<<∈n n t t t T ，有11221111{()|(),(),,()}{()|()}n n n n n n n n P X t x X t x X t x X t x P X t x X t x ----<====<=则称{}(),X t t T ∈为马尔可夫过程。

称(){}:,==∈E x X t x t T 为状态空间。

参数集和状态空间都是离散的马尔可夫过程称为离散参数马氏链. 参数连续、状态空间离散的马尔可夫过程称为连续参数马氏链. （2）k 步转移概率设{}(),0,1,2,=X n n 为离散参数马氏链，称()(),(,){|},0,1=+==≥≥i j p n k P X n k j X n i n k为{}(),0,1,2,=X n n 在时刻n 的k 步转移概率，称(),(,)((,)),P =∈i j n k p n k i j E为{}(),0,1,2,=X n n 在时刻n 的k 步转移概率矩阵. 特别地，当1k =时，在时刻n 的一步转移概率和一步转移概率矩阵分别简记为()ij p n 和()n P . （3）初始分布、绝对分布称((0)),,==∈i p P X i i E 为离散参数马氏链{}(),0,1,2,=X n n 的初始分布，记为0P ，称()(){},,==∈j p n P X n j j E 为马尔可夫链{}0n X n ≥的绝对分布，记为P n . （4）离散参数齐次马氏链设{}(),0,1,2,=X n n 是一离散参数马氏链，如果其一步转移概率()ij p n 恒与起始时刻n 无关，记为ij p ，则称{}(),0,1,2,=X n n 为离散参数齐次马氏链。

若{}(),0,1,2,=X n n2是离散参数齐次马氏链，则其k 步转移概率记为(),i j p k ，一步转移概率矩阵和k 转移概率矩阵分别记为P 和().P k(5) 离散参数齐次马氏链的遍历性离散参数齐次马氏链{X (n ) ,n=0,1,2… }，若对一切状态i ，j ，存在与i 无关的极限()()lim 0,ij j n p n i j E →+∞=π>∈则称此马氏链具有遍历性.0,1j j j Ej E ππ∈>∈=∑若且则称{},j j E π∈为离散参数齐次马氏链{X (n ) ,n=0,1,2… }的极限分布，或称为最终分布，记为{},j j E ∏=∈π（6）离散参数齐次马氏链的平稳分布离散参数齐次马氏链{X (n ) ,n=0,1,2… }，若存在{v j , j ∈E } 满足条件：1)0,2)13)j jj Ej i iji Ev j E vv v p ∈∈≥∈==∑∑则称此马氏链是平稳的，称 { v j , j ∈E } 为此马氏链的平稳分布。

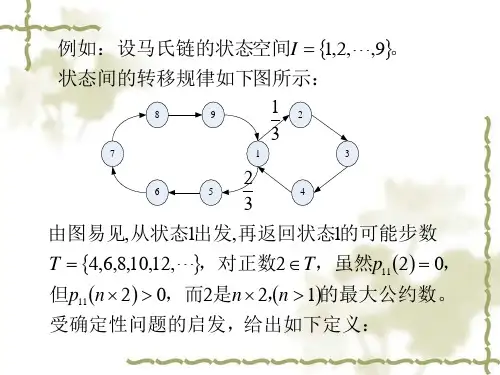
第四章 Markov 过程本章我们先讨论一类特殊的参数离散状态空间离散的随机过程，参数为0{0,1,2,}T N ==L ，状态空间为可列{1,2,}I =L 或有限{1,2,,}I n =L 的情况，即讨论的过程为Markov 链。

Markov 链最初由Markov 于1906年引入，至今它在自然科学、工程技术、生命科学及管理科学等诸多领域中都有广泛的应用。

之后我们将讨论另一类参数连续状态空间离散的随机过程，即纯不连续Markov 过程。

§4.1 Markov 链的定义与性质一、Markov 链的定义定义 4.1设随机序列{;0}n X n ≥的状态空间为I ，如果对0n N ∀∈，及0110011,,,,,{,,,}0n n n n i i i i I P X i X i X i +∈===>L L ，有：11001111{,,,}{}n n n n n n n n P X i X i X i X i P X i X i ++++=======L （4.1.0)则称{;0}n X n ≥为Markov 链。

注1：等式（4.1.0）刻画了Markov 链的特性，称此特性为Markov 性或无后效性，简称为马氏性。

Markov 链也称为马氏链。

定义4.2 设{;0}n X n ≥为马氏链，状态空间为I ，对于,i j I ∀∈，称1{}()ˆn n i j P X j X i p n +===为马氏链{;0}n X n ≥在n 时刻的一步转移概率。

注2：一步转移概率满足：()0,,()1,i j i jj Ip n i j Ipn i I ∈≥∈=∈∑若对于,i j I ∀∈，有1{}()ˆn n i j i j P X j X i p n p +===≡即上面式子的右边与时刻n 无关，则称此马氏链为齐次（或时齐的）马氏链。

设{}0()(0),p i P X i i I ==∈，如果对一切i I ∈都有00()0,()1i Ip i p i ∈≥=∑，称0()p i 为马氏链的初始分布。

随机过程_课件---第四章第四章 Poisson 过程4.1 齐次Poisson 过程到达时间间隔与等待时间的分布1、定理4-1强度为λ的齐次Poisson 过程{,0}t N t≥的到达时间间隔序列{},1,2,n X n = 是独立同分布的随机变量序列，且是具有相同均值1λ的指数分布。

证：事件{}1X t >发生当且仅当Poisson 过程在区间[]0,t 内没有事件发生，即事件{}1X t >等价于{0}tN =，所以有()(0)t t t P X t P N e λ->===因此，1X 具有均值为1λ的指数分布，再求已知1X 的条件下，2X 的分布。

(](](]211(|)(|)((0tP X t X s P X s P P e λ->====在s,s+t 内没有事件发生（由独立增量性）在s,s+t 内没有事件发生)（由平稳增量性）在,t 内没有事件发生)上式表明2X 与1X 相互独立，而且2X 也是一个具有均值为1λ的指数分布的随机变量，重复同样的推导可以证明定理4-1的结论。

2、定理4-2等待时间n S 服从参数为n ，λ的Γ分布，即分布密度为1()(),(1)!n tt f t e n λλλ--=- 0t ≥证：因为第n 个事件在时刻t 或之前发生当且仅当到时间t 已发生的事件数目至少是n ，即事件{}{}t n N n S t ≥?≤是等价的，因此()()()!j tn t j nt P S t P N n ej λλ∞-=≤=≥=∑上式两边对t 求导得n S 的分布密度为11()()()!(1)!(),0(1)!j j tt j nj nn tt t f t e e j j t et n λλλλλλλλλ-∞∞--==--=-+-=≥-∑∑注：定理4-2又给出了定义Poisson 过程的另一种方法。

从一列均值为1/λ的独立同分布的指数随机变量序列{},1n X n ≥出发，定义第n 个事件发生的时刻为n S ，则12n n S X X X =+++这样就定义了一个计数过程，且所得计数过程{},0t N t ≥就是参数为λ的Poisson 过程。

（已经编辑到115页2008-3-20）第四章随机过程（电子版：盛艳霞OCR，编辑张学文2007.12 -2008.01）1. 随机过程的概念及其分布律原书91-132页90第四章随机过程为了从统计角度研究气象要素随时间和空间的变化,最好是利用近数十年发展起来的一个统计数学分支----随机过程和随机场理论。

为研究气象信息随时间和空间的分布也要对随机过程有所了解。

针对如上情况我们在这一章对随机过程的有关概念、性质和在气象上的个别应用作简要介绍。

1、随机过程的概念及其分布律孤立的研究各点的气压、温度或风等气象要素时，我们把它看成随机变量（矢量）。

这时可以分析它的期望值、方差、概率分布等等。

然而当把不同时刻的同一点的气压、温度或风连贯起来看时，这就是一连串的随机变量（矢量）。

它们以时间为参数而有所变化。

随机变量随某一参数（这里指时间）的变化给人们以过程的概念。

所以就把随机变量随参数值的变化而变化的过程这一总体称为随机过程。

当掷骰子时，骰子出现的点数是随机变量。

某次“3”点向上，就说这一次随机变量取值为3。

而我们所谓的随机变量远不仅只有一个“3”，而应理解为很多次点子数的集合。

同样地，随机过程一词也是指一个总体集合，而不是仅指某一时段的变量取值。

例如说“春季北京的气温是一个随机过程”，则是指很多很多年的每年春季北京的气温的变化过程这个总体而言的。

如1978年北京春季气温的变程仅是总体中的一个个例。

它在随机过程中的地位和骰子为“3”点在随机变量中原书91-132页91的地位是相当的。

我们把这一条春季气温曲线称为这个随机过程的一个“现实”这样一个随机过程实际上是由无数具有同一的统计属性的现实组成的。

图4.1是乌鲁木齐冬季1月份的四年的气温曲线。

它们就代表了1月气温这个随机过程的四个现实。

而这一随机过程应为无数条这种曲线组成。

如以T示表气温，y代表年代，d 代表日期，则一个随机过程可以表示为T=T(y,d) （4．1）图4.1 乌鲁木齐1月份气温曲线、式中y有固定值时，例如y=1963年，则得到随机过程的一个现实。