随机过程 第四章4

1第四章 马尔可夫过程内容提要1. 马尔可夫过程的概念 （1）马尔可夫过程给定随机过程{}(),X t t T ∈，如果对122,∀≥∀<<<∈n n t t t T ，有11221111{()|(),(),,()}{()|()}n n n n n n n n P X t x X t x X t x X t x P X t x X t x ----<====<=则称{}(),X t t T ∈为马尔可夫过程。

称(){}:,==∈E x X t x t T 为状态空间。

参数集和状态空间都是离散的马尔可夫过程称为离散参数马氏链. 参数连续、状态空间离散的马尔可夫过程称为连续参数马氏链. （2）k 步转移概率设{}(),0,1,2,=X n n 为离散参数马氏链，称()(),(,){|},0,1=+==≥≥i j p n k P X n k j X n i n k为{}(),0,1,2,=X n n 在时刻n 的k 步转移概率，称(),(,)((,)),P =∈i j n k p n k i j E为{}(),0,1,2,=X n n 在时刻n 的k 步转移概率矩阵. 特别地，当1k =时，在时刻n 的一步转移概率和一步转移概率矩阵分别简记为()ij p n 和()n P . （3）初始分布、绝对分布称((0)),,==∈i p P X i i E 为离散参数马氏链{}(),0,1,2,=X n n 的初始分布，记为0P ，称()(){},,==∈j p n P X n j j E 为马尔可夫链{}0n X n ≥的绝对分布，记为P n . （4）离散参数齐次马氏链设{}(),0,1,2,=X n n 是一离散参数马氏链，如果其一步转移概率()ij p n 恒与起始时刻n 无关，记为ij p ，则称{}(),0,1,2,=X n n 为离散参数齐次马氏链。

若{}(),0,1,2,=X n n2是离散参数齐次马氏链，则其k 步转移概率记为(),i j p k ，一步转移概率矩阵和k 转移概率矩阵分别记为P 和().P k(5) 离散参数齐次马氏链的遍历性离散参数齐次马氏链{X (n ) ,n=0,1,2… }，若对一切状态i ，j ，存在与i 无关的极限()()lim 0,ij j n p n i j E →+∞=π>∈则称此马氏链具有遍历性.0,1j j j Ej E ππ∈>∈=∑若且则称{},j j E π∈为离散参数齐次马氏链{X (n ) ,n=0,1,2… }的极限分布，或称为最终分布，记为{},j j E ∏=∈π（6）离散参数齐次马氏链的平稳分布离散参数齐次马氏链{X (n ) ,n=0,1,2… }，若存在{v j , j ∈E } 满足条件：1)0,2)13)j jj Ej i iji Ev j E vv v p ∈∈≥∈==∑∑则称此马氏链是平稳的，称 { v j , j ∈E } 为此马氏链的平稳分布。

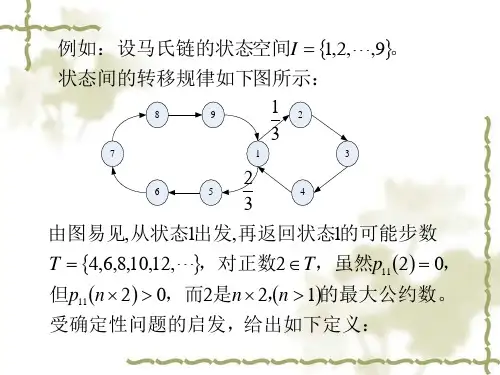
第四章 习题41、对泊松过程{},0t N t ≥（1）证明：当s t <时，{}1,0,1,,kn ks t n s s P N k N n k n k t t -⎛⎫⎛⎫⎛⎫===-= ⎪⎪⎪⎝⎭⎝⎭⎝⎭（2）当2λ=时，试求：()()()112112;1,3;21P N P N N P N N ≤==≥≥（3）设顾客到达某商店是泊松事件，平均每小时以30人的速度到达。

求下列事件的概率：相继到达的两顾客的时间间隔为大于2分钟、小于2分钟、在1分钟到3分钟之间。

答：（1）证明：{}()()()()()()()()()()()()()()()()()()(),,!!!!!!!1!!s t s t s s t s s t t t t n kkt s sk n kn k nk n ktn kk n kk nP N k N n P N k N n k P N k P N n k P N k N n P N n P N n P N n t s s e ek n k s t s n k n k t t t e n n s t s n s s k t k n k t t λλλλλλλλλλ------------====-==-========-⎡⎤⎣⎦--==--⎛⎫⎛⎫⎛⎫==- ⎪⎪ ⎪-⎝⎭⎝⎭⎝⎭（2）()()()()()()()()11110121112222201211120!1!2!225P N P N N N e e e e e e e λλλλλλλ-------≤==+=+==++-=++=()()()()12121224111,31,3112224P N N P N N P N P N ee e----=====-=====()()()()()()()()()()111111121112112,122111121011311101P N N P N P N N P N P N P N P N P N e P N P N e --≥≥≥≥≥==≥≥-<-=-=-===-<-=-（3） 解法一：顾客到达事件间隔服从参数为λ的指数分布：()()()30,03030,0x x Z Z f t e x f t e x λλλ--=≥=⇒=≥①()30301111303023030106030x x P Z e dx e e e ∞∞----⎧⎫>===--=⎨⎬-⎩⎭⎰②()11303011303000230301116030x x P Z e dx e e e ----⎧⎫<===--=-⎨⎬-⎩⎭⎰ ③1131133030202022221160601330301606030x x P Z e dx e e e e e ------⎛⎫⎧⎫<<===--=-⎨⎬ ⎪-⎩⎭⎝⎭⎰解法二：()3030==0.560λ∴平均每小时有人到达人/分钟根据齐次Poisson 过程的到达时间间隔{},1,2,n X n =是独立同分布于均值为1λ的指数分布的，故可有： 相继到达的顾客的时间间隔大于2分钟的概率为：()12t n P X e e λ-->== 相继到达的顾客的时间间隔小于2分钟的概率为：()1211t n P X e e λ--<=-=-相继到达的顾客的时间间隔在1分钟到3分钟之间的概率为：()()()()1.50.50.5 1.5133111n n n P X P X P X e e e e ----<<=<-<=---=-2、{},0t N t ≥是强度为λ的泊松过程。

随机过程-课件-第四章第四章Poion过程4.1齐次Poion过程到达时间间隔与等待时间的分布1、定理4-1强度为的齐次Poion过程{Nt,t0}的到达时间间隔序列某n,n1,2,是独立1同分布的随机变量序列，且是具有相同均值证：事件的指数分布。

即事件某1t等某1t发生当且仅当Poion过程在区间0,t内没有事件发生，价于{Nt0}，所以有P(某tt)P(Nt0)et因此，某1具有均值为1的指数分布，再求已知某1的条件下，某2的分布。

P(某2t|某1)P(在,+t内没有事件发生|某1)（由独立增量性）（由平稳增量性）et上式表明P(在,+t内没有事件发生)P(在0,t内没有事件发生)某2与某1相互独立，而且某2也是一个具有均值为1的指数分布的随机变量，重复同样的推导可以证明定理4-1的结论。

2、定理4-2等待时间Sn服从参数为n，的分布，即分布密度为f(t)et证：(t)n1,t0(n1)!因为第n个事件在时刻t或之前发生当且仅当到时间t已发生的事件数目至少是n，即事件NtnSnt是等价的，因此P(Snt)P(Ntn)ejnt(t)jj!上式两边对t求导得Sn的分布密度为f(t)etjnj1(t)j(t)etj!(j1)!jnet(t),t0(n1)!n1注：定理4-2又给出了定义Poion过程的另一种方法。

从一列均值为1/的独立同分布的指数随机变量序列某n,n1出发，定义第n个事件发生的时刻为Sn，则Sn某1某2某n这样就定义了一个计数过程，且所得计数过程Nt,t0就是参数为的Poion过程。

3、定理4-3条件随机变量(某1证：对|Nt1)U(0,t)，即在区间0,t内为均匀分布。

t,(某1|Nt1)的分布函数为P(某1,Nt1)P(某1|Nt1)P(Nt1)P(在0,内有一个事件发生，在，t内没有事件发生)P(Nt1)P(在0,内有一个事件发生)P(在，t内没有事件发生)P(Nt1)P(N1)P(Nt0)P(N1)ee(t)tett这说明(某14、顺序统计量|Nt1)在0,t上服从均匀分布。

第四章 二阶矩过程、平稳过程和随机分析 习题完整答案，请搜淘宝1、 设∑=-=N k k k k n U n X 1)cos(2ασ，其中k σ和k α为正常数，)2,0(~πU U k ，且相互独立，N k ,,2,1 =，试计算},1,0,{ ±=n X n 的均值函数和相关函数，并说明其是否是平稳过程。

2、 设有随机过程))(cos()(t t A t X πηω+=，其中0>ω为常数，}0),({≥t t η是泊松过程，A 是与)(t η独立的随机变量，且2/1}1{}1{===-=A P A P 。

（1） 试画出此过程的样本函数，并问样本函数是否连续？（2） 试求此过程的相关函数，并问该过程是否均方连续？3、 设}0),({≥t t X 是一实的零初值正交增量过程，且),(~)(2t N t X σμ。

令1)(2)(-=t X t Y ，0≥t 。

试求过程}0),({≥t t Y 的相关函数),(t s R Y 。

4、 设有随机过程)sin(2)(Θ+=t Z t X ，+∞<<∞-t ，其中Z 、Θ是相互独立的随机变量，)1,0(~N Z ，2/1)4/()4/(=-=Θ==ΘππP P 。

问过程)(t X 是否均方可积过程？说明理由。

5、 设随机过程t Y t X t 2sin 2cos )(+=ξ，+∞<<∞-t ，其中随机变量X 和Y 独立同分布。

（1） 如果)1,0(~U X ，问过程)(t ξ是否平稳过程？说明理由；（2） 如果)1,0(~N X ，问过程)(t ξ是否均方可微？说明理由。

6、 设随机过程});({+∞<<∞-t t X 是一实正交增量过程，并且0)}({=t X E ，及满足：{}+∞<<∞--=-t s s t s X t X E ,,)]()([2；令：+∞<<∞---=t t X t X t Y ),1()()(，试证明)(t Y 是平稳过程。

（已经编辑到115页2008-3-20）第四章随机过程（电子版：盛艳霞OCR，编辑张学文2007.12 -2008.01）1. 随机过程的概念及其分布律原书91-132页90第四章随机过程为了从统计角度研究气象要素随时间和空间的变化,最好是利用近数十年发展起来的一个统计数学分支----随机过程和随机场理论。

为研究气象信息随时间和空间的分布也要对随机过程有所了解。

针对如上情况我们在这一章对随机过程的有关概念、性质和在气象上的个别应用作简要介绍。

1、随机过程的概念及其分布律孤立的研究各点的气压、温度或风等气象要素时，我们把它看成随机变量（矢量）。

这时可以分析它的期望值、方差、概率分布等等。

然而当把不同时刻的同一点的气压、温度或风连贯起来看时，这就是一连串的随机变量（矢量）。

它们以时间为参数而有所变化。

随机变量随某一参数（这里指时间）的变化给人们以过程的概念。

所以就把随机变量随参数值的变化而变化的过程这一总体称为随机过程。

当掷骰子时，骰子出现的点数是随机变量。

某次“3”点向上，就说这一次随机变量取值为3。

而我们所谓的随机变量远不仅只有一个“3”，而应理解为很多次点子数的集合。

同样地，随机过程一词也是指一个总体集合，而不是仅指某一时段的变量取值。

例如说“春季北京的气温是一个随机过程”，则是指很多很多年的每年春季北京的气温的变化过程这个总体而言的。

如1978年北京春季气温的变程仅是总体中的一个个例。

它在随机过程中的地位和骰子为“3”点在随机变量中原书91-132页91的地位是相当的。

我们把这一条春季气温曲线称为这个随机过程的一个“现实”这样一个随机过程实际上是由无数具有同一的统计属性的现实组成的。

图4.1是乌鲁木齐冬季1月份的四年的气温曲线。

它们就代表了1月气温这个随机过程的四个现实。

而这一随机过程应为无数条这种曲线组成。

如以T示表气温，y代表年代，d 代表日期，则一个随机过程可以表示为T=T(y,d) （4．1）图4.1 乌鲁木齐1月份气温曲线、式中y有固定值时，例如y=1963年，则得到随机过程的一个现实。

第四章习题解答4.1Y1,Y2,···是来自总体Y的随机变量，与X0独立，h(x,y)是实函数.对于n 1，取X n=h(X n−1,Y n).设{X n}的状态空间为I，验证{X n}是马氏链，给出转移概率p ij.解：由题知，Y k与X1,···,X k−1独立,k 1,∀n,i,j,i1,...,i n−1∈I有，P(X n+1=j|X n=i,X n−1=i n−1, (X0)i0)=P(h(i,Y n+1)=j|X n=i,X n−1=i n−1,···,X0=i0)=P(h(i,Y n+1)=j|X n=i)=P(h(i,Y)=j)=P(h(i,Y1)=j|X0=i)=P(X1=j|X0=i).∴X n是马氏链，P ij=P(h(i,Y)=j).4.2设{X i,i 0}是取非负整数值的独立同分布的随机变量序列，V ar(X0)>0.验证以下随机序列是马氏链：(a){X n,n 0};(b){S n,n 0}，其中S n=∑ni=0X i;(c){ξn,n 0}，其中ξn=∑ni=0(1+X i).解：∀n,i,j,i0,···,i n−1∈N+,(a).P(X n+1=j|X n=i,X n−1=i n−1,···,X0=i0)=P(X n+1=j)= P(X n+1=j|X n=i)=P(X1=j)=P(X1=j|X0=i).1第四章离散时间马尔可夫链第四章离散时间马尔可夫链(b).P(S n+1=j|S n=i,S n−1=i n−1,···,X0=i0)=P(X n+1=j−i|X n=i−i n−1,···,X0=i0)=P(X n+1=j−i)=P(X n+1=j−i,S n=i|S n=i)=P(S n+1=j|S n=i)=P(X1=j−i)=P(X1=j−i|X0=i)=P(S1=j|S0=i).(c).P(ξn+1=j|ξn=i,ξn−1=i n−1,···,ξ0=i0)=P(X n+1=ji −1)=P(X n+1=ji−1|ξn=i)=P(ξn+1=j|ξn=i)=P(X1=ji −1)=P(X1=ji−1|X0=i)=P(ξ1=j|ξ0=i).4.3马氏链的状态空间是I=(1,2,3,4,5)，转移概率矩阵P=0.20.80000.50.5000000.50.500.20.3000.500001界定马氏链的状态。