基函数神经网络及应用_第五章Hermite神经网络
- 格式:pdf
- 大小:329.26 KB
- 文档页数:13


神经网络基本知识一、内容简述神经网络是机器学习的一个重要分支,是一种模拟生物神经网络结构和功能的计算模型。
它以其强大的学习能力和自适应能力广泛应用于多个领域,如图像识别、语音识别、自然语言处理等。
《神经网络基本知识》这篇文章将带领读者了解神经网络的基本概念、原理和应用。
1. 神经网络概述神经网络是一种模拟生物神经系统结构和功能的计算模型。
它由大量神经元相互连接构成,通过学习和调整神经元之间的连接权重来进行数据处理和模式识别。
神经网络的概念自上世纪五十年代提出以来,经历了漫长的发展历程,逐渐从简单的线性模型演变为复杂的多层非线性结构。
神经网络在人工智能领域发挥着核心作用,广泛应用于计算机视觉、语音识别、自然语言处理等领域。
神经网络的基本构成单元是神经元,每个神经元接收来自其他神经元的输入信号,通过特定的计算方式产生输出信号,并传递给其他神经元。
不同神经元之间的连接强度称为权重,通过训练过程不断调整和优化。
神经网络的训练过程主要是通过反向传播算法来实现的,通过计算输出层误差并反向传播到输入层,不断调整权重以减小误差。
神经网络具有强大的自适应能力和学习能力,能够处理复杂的模式识别和预测任务。
与传统的计算机程序相比,神经网络通过学习大量数据中的规律和特征,自动提取高级特征表示,避免了手动设计和选择特征的繁琐过程。
随着深度学习和大数据技术的不断发展,神经网络的应用前景将更加广阔。
神经网络是一种模拟生物神经系统功能的计算模型,通过学习和调整神经元之间的连接权重来进行数据处理和模式识别。
它在人工智能领域的应用已经取得了巨大的成功,并将在未来继续发挥重要作用。
2. 神经网络的历史背景与发展神经网络的历史可以追溯到上个世纪。
最初的神经网络概念起源于仿生学,模拟生物神经网络的结构和功能。
早期的神经网络研究主要集中在模式识别和机器学习的应用上。
随着计算机科学的快速发展,神经网络逐渐成为一个独立的研究领域。
在20世纪80年代和90年代,随着反向传播算法和卷积神经网络的提出,神经网络的性能得到了显著提升。



神经⽹络(NeuralNetwork)⼀、激活函数激活函数也称为响应函数,⽤于处理神经元的输出,理想的激活函数如阶跃函数,Sigmoid函数也常常作为激活函数使⽤。
在阶跃函数中,1表⽰神经元处于兴奋状态,0表⽰神经元处于抑制状态。
⼆、感知机感知机是两层神经元组成的神经⽹络,感知机的权重调整⽅式如下所⽰:按照正常思路w i+△w i是正常y的取值,w i是y'的取值,所以两者做差,增减性应当同(y-y')x i⼀致。
参数η是⼀个取值区间在(0,1)的任意数,称为学习率。
如果预测正确,感知机不发⽣变化,否则会根据错误的程度进⾏调整。
不妨这样假设⼀下,预测值不准确,说明Δw有偏差,⽆理x正负与否,w的变化应当和(y-y')x i⼀致,分情况讨论⼀下即可,x为负数,当预测值增加的时候,权值应当也增加,⽤来降低预测值,当预测值减少的时候,权值应当也减少,⽤来提⾼预测值;x为正数,当预测值增加的时候,权值应当减少,⽤来降低预测值,反之亦然。
(y-y')是出现的误差,负数对应下调,正数对应上调,乘上基数就是调整情况,因为基数的正负不影响调整情况,毕竟负数上调需要减少w的值。
感知机只有输出层神经元进⾏激活函数处理,即只拥有⼀层功能的神经元,其学习能⼒可以说是⾮常有限了。
如果对于两参数据,他们是线性可分的,那么感知机的学习过程会逐步收敛,但是对于线性不可分的问题,学习过程将会产⽣震荡,不断地左右进⾏摇摆,⽽⽆法恒定在⼀个可靠地线性准则中。
三、多层⽹络使⽤多层感知机就能够解决线性不可分的问题,输出层和输⼊层之间的成为隐层/隐含层,它和输出层⼀样都是拥有激活函数的功能神经元。
神经元之间不存在同层连接,也不存在跨层连接,这种神经⽹络结构称为多层前馈神经⽹络。
换⾔之,神经⽹络的训练重点就是链接权值和阈值当中。
四、误差逆传播算法误差逆传播算法换⾔之BP(BackPropagation)算法,BP算法不仅可以⽤于多层前馈神经⽹络,还可以⽤于其他⽅⾯,但是单单提起BP算法,训练的⾃然是多层前馈神经⽹络。
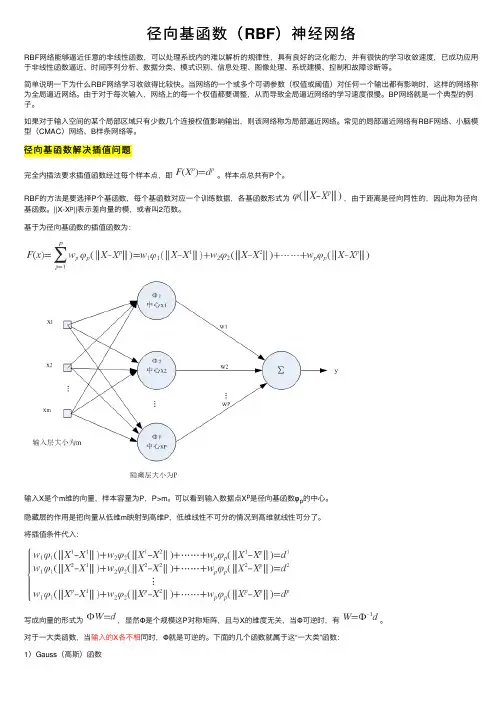
径向基函数(RBF)神经⽹络RBF⽹络能够逼近任意的⾮线性函数,可以处理系统内的难以解析的规律性,具有良好的泛化能⼒,并有很快的学习收敛速度,已成功应⽤于⾮线性函数逼近、时间序列分析、数据分类、模式识别、信息处理、图像处理、系统建模、控制和故障诊断等。
简单说明⼀下为什么RBF⽹络学习收敛得⽐较快。
当⽹络的⼀个或多个可调参数(权值或阈值)对任何⼀个输出都有影响时,这样的⽹络称为全局逼近⽹络。
由于对于每次输⼊,⽹络上的每⼀个权值都要调整,从⽽导致全局逼近⽹络的学习速度很慢。
BP⽹络就是⼀个典型的例⼦。
如果对于输⼊空间的某个局部区域只有少数⼏个连接权值影响输出,则该⽹络称为局部逼近⽹络。
常见的局部逼近⽹络有RBF⽹络、⼩脑模型(CMAC)⽹络、B样条⽹络等。
径向基函数解决插值问题完全内插法要求插值函数经过每个样本点,即。
样本点总共有P个。
RBF的⽅法是要选择P个基函数,每个基函数对应⼀个训练数据,各基函数形式为,由于距离是径向同性的,因此称为径向基函数。
||X-X p||表⽰差向量的模,或者叫2范数。
基于为径向基函数的插值函数为:输⼊X是个m维的向量,样本容量为P,P>m。
可以看到输⼊数据点X p是径向基函数φp的中⼼。
隐藏层的作⽤是把向量从低维m映射到⾼维P,低维线性不可分的情况到⾼维就线性可分了。
将插值条件代⼊:写成向量的形式为,显然Φ是个规模这P对称矩阵,且与X的维度⽆关,当Φ可逆时,有。
对于⼀⼤类函数,当输⼊的X各不相同时,Φ就是可逆的。
下⾯的⼏个函数就属于这“⼀⼤类”函数:1)Gauss(⾼斯)函数2)Reflected Sigmoidal(反常S型)函数3)Inverse multiquadrics(拟多⼆次)函数σ称为径向基函数的扩展常数,它反应了函数图像的宽度,σ越⼩,宽度越窄,函数越具有选择性。
完全内插存在⼀些问题:1)插值曲⾯必须经过所有样本点,当样本中包含噪声时,神经⽹络将拟合出⼀个错误的曲⾯,从⽽使泛化能⼒下降。





神经网络及深度学习(包含matlab代码).pdf
神经网络可以使用中间层构建出多层抽象,正如在布尔电路中所做的那样。
如果进行视觉模式识别,那么第1 层的神经元可能学会识别边;第2 层的神经元可以在此基础上学会识别更加复杂的形状,例如三角形或矩形;第3 层将能够识别更加复杂的形状,以此类推。
有了这些多层抽象,深度神经网络似乎可以学习解决复杂的模式识别问题。
正如电路示例所体现的那样,理论研究表明深度神经网络本质上比浅层神经网络更强大。
《深入浅出神经网络与深度学习》PDF+代码分析
《深入浅出神经网络与深度学习》PDF中文,249页;PDF英文,292页;配套代码。
提取码: 6sgh
以技术原理为导向,辅以MNIST 手写数字识别项目示例,介绍神经网络架构、反向传播算法、过拟合解决方案、卷积神经网络等内容,以及如何利用这些知识改进深度学习项目。
学完后,将能够通过编写Python 代码来解决复杂的模式识别问题。
径向基神经网络1985年,Powell提出了多变量插值的径向基函数(Radical Basis Function,RBF)方法。
1988年,Moody和Darken提出了一种神经网络结构,即RBF神经网络,属于前向神经网络类型,它能够以任意精度逼近任意连续函数,特别适合于解决分类问题。
RBF网络的结构与多层前向网络类似,它是一种三层前向网络。
输入层由信号源节点组成;第二层为隐含层,隐单元数视所描述问题的需要而定,隐单元的变换函数RBF是对中心点径向对称且衰减的非负非线性函数;第三层为输出层,它对输入模式的作用做出响应。
从输入空间到隐含层空间的变换是非线性的,而从隐含层空间的输出层空间变换是线性的。
RBF网络的基本思想是:用RBF作为隐单元的“基”构成隐含层空间,这样就可以将输入向量直接映射到隐空间。
当RBF的中心点确定以后,这种映射关系也就确定了。
而隐含层空间到输出空间的映射是线性的,即网络的输出是隐单元输出的线性加权和。
此处的权即为网络可调参数。
由此可见,从总体上看,网络由输入到输出的映射是非线性的,而网络的输出对可调参数而言却是线性的。
这烟大哥网络的权就可由线性方程直接解出,从而大大加快学习速度并避免局部极小问题。
一、RBF神经元模型径向基函数神经元的传递函数有各种各样的形式,但常用的形式是高斯函数(radbas)。
与前面介绍的神经元不同,神经元radbas的输入为输入向量p和权值向量ω之间的距离乘以阈值b。
径向基传递函数可以表示为如下形式:二、RBF网络模型径向基神经网络的激活函数采用径向基函数,通常定义为空间任一点到某一中心之间欧氏距离的单调函数。
径向基神经网络的激活函数是以输入向量和权值向量之间的距dist为自变量的。
径向神经网络的激活函数一般表达式为随着权值和输入向量之间距离的减少,网络输出是递增的,当输入向量和权值向量一致时,神经元输出1。
b为阈值,用于调整神经元的灵敏度。
利用径向基神经元和线性神经元可以建立广义回归神经网络,该种神经网络适用于函数逼近方面的应用;径向基神经元和竞争神经元可以组件概率神经网络,此种神经网络适用于解决分类问题。