verygood带电粒子在磁场中做匀速圆周运动题型归类
- 格式:doc
- 大小:1.07 MB
- 文档页数:20

带电粒子在磁场中做匀速圆周运动题型归类一、运动电荷在磁场中的运动一、洛仑兹力的方向、大小及回旋角、弦切角等的关系1、在不计带电粒子(如电子、质子、α粒子等基本粒子)的重力的条件下,带电粒子在匀强磁场有三种典型的运动,它们决定于粒子的速度(v )方向与磁场的磁感应强度(B )方向的夹角(θ)。
(1)若带电粒子的速度方向与磁场方向平行时,粒子不受洛仑兹力作用而作匀速直线运动。
(2)若粒子的速度方向与磁场方向垂直,则带电粒子在垂直于磁感线的平面内以入射速度v 作匀速圆周运动,其运动所需的向心力全部由洛仑兹力提供。
(3)若带电粒子的速度方向与磁场方向成一夹角θ(θ≠0°,θ≠90°),则粒子的运动轨迹是一螺旋线(其轨迹如图):粒子垂直磁场方向作匀速圆周运动,平行磁场方向作匀速运动,螺距S=v ∥T 。
2、带电粒子在匀强磁场中做匀速圆周运动的方向及几个基本公式向心力公式:安培力是洛伦兹力的宏观表现,因而洛伦兹力的方向仍由左手定则判定,只是注意:四指的指向为正电荷运动方向或负电荷运动的反方向。
由于洛伦兹力与带电粒子的运动方向垂直,故洛伦兹力不做功。
当带电粒子的运动方向与磁场方向垂直时,洛伦兹力为带电粒子做匀速圆周运动提供向心力。
B q V m V R=2轨道半径公式:BqmV R = 周期、频率和角频率公式:T R V m B q==22ππ mBq T f π21==m Bq f T ===ππω22动能公式:()E m V P m B q R m K ===1222222T 、f 和ω的两个特点第一、T 、 f 的ω的大小与轨道半径(R )和运行速率(V )无关,而只与磁场的磁感应强度(B )和粒子的荷质比(q/m )有关。
第二、荷质比(q/m )相同的带电粒子,在同样的匀强磁场中,T 、f 和ω相同。
3.注意圆周运动的对称性与特殊性(1)从一直线边界射入的粒子从同一直线边界射出时,速度与边界的夹角相等;(2)在圆形磁场区域内,粒子射入时的速度方向过圆心,射出时的速度方向也过圆心;(3)圆形磁场区域的半径与粒子轨道半径相等时,出射方向一定垂直入射点与磁场圆心的连线。

高考物理带电粒子在磁场中的运动常见题型及答题技巧及练习题(含答案)含解析一、带电粒子在磁场中的运动专项训练1.如图所示,在一直角坐标系xoy平面内有圆形区域,圆心在x轴负半轴上,P、Q是圆上的两点,坐标分别为P(-8L,0),Q(-3L,0)。
y轴的左侧空间,在圆形区域外,有一匀强磁场,磁场方向垂直于xoy平面向外,磁感应强度的大小为B,y轴的右侧空间有一磁感应强度大小为2B的匀强磁场,方向垂直于xoy平面向外。
现从P点沿与x轴正方向成37°角射出一质量为m、电荷量为q的带正电粒子,带电粒子沿水平方向进入第一象限,不计粒子的重力。
求:(1)带电粒子的初速度;(2)粒子从P点射出到再次回到P点所用的时间。
【答案】(1)8qBLvm=;(2)41(1)45mtqBπ=+【解析】【详解】(1)带电粒子以初速度v沿与x轴正向成37o角方向射出,经过圆周C点进入磁场,做匀速圆周运动,经过y轴左侧磁场后,从y轴上D点垂直于y轴射入右侧磁场,如图所示,由几何关系得:5sin37oQC L=15 sin37O OQO Q L==在y轴左侧磁场中做匀速圆周运动,半径为1R,11R O Q QC =+21v qvB m R=解得:8qBLv m=; (2)由公式22v qvB m R =得:2mv R qB =,解得:24R L =由24R L =可知带电粒子经过y 轴右侧磁场后从图中1O 占垂直于y 轴射放左侧磁场,由对称性,在y 圆周点左侧磁场中做匀速圆周运动,经过圆周上的E 点,沿直线打到P 点,设带电粒子从P 点运动到C 点的时间为1t5cos37o PC L =1PCt v=带电粒子从C 点到D 点做匀速圆周运动,周期为1T ,时间为2t12mT qBπ=2137360oot T =带电粒子从D 做匀速圆周运动到1O 点的周期为2T ,所用时间为3t22·2m mT q B qBππ== 3212t T =从P 点到再次回到P 点所用的时间为t12222t t t t =++联立解得:41145mt qB π⎛⎫=+⎪⎝⎭。
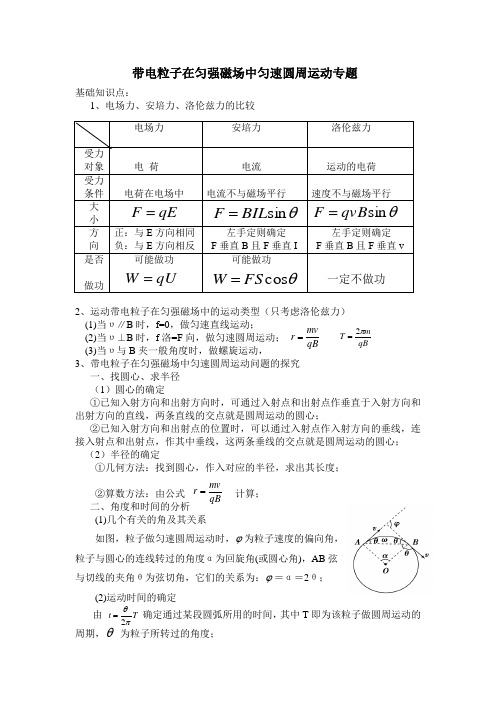
基础知识点:1、电场力、安培力、洛伦兹力的比较2、运动带电粒子在匀强磁场中的运动类型(只考虑洛伦兹力) (1)当υ∥B 时,f=0,做匀速直线运动;(2)当υ⊥B 时,f 洛=F 向,做匀速圆周运动; (3)当υ与B 夹一般角度时,做螺旋运动,3、带电粒子在匀强磁场中匀速圆周运动问题的探究 一、找圆心、求半径 (1)圆心的确定①已知入射方向和出射方向时,可通过入射点和出射点作垂直于入射方向和出射方向的直线,两条直线的交点就是圆周运动的圆心;②已知入射方向和出射点的位置时,可以通过入射点作入射方向的垂线,连接入射点和出射点,作其中垂线,这两条垂线的交点就是圆周运动的圆心; (2)半径的确定①几何方法:找到圆心,作入对应的半径,求出其长度; ②算数方法:由公式 计算;二、角度和时间的分析 (1)几个有关的角及其关系如图,粒子做匀速圆周运动时,ϕ为粒子速度的偏向角, 粒子与圆心的连线转过的角度α为回旋角(或圆心角),AB 弦 与切线的夹角θ为弦切角,它们的关系为:ϕ=α=2θ; (2)运动时间的确定由 确定通过某段圆弧所用的时间,其中T 即为该粒子做圆周运动的周期, 为粒子所转过的角度;电场力 安培力 洛伦兹力 受力 对象电 荷电流运动的电荷 受力 条件电荷在电场中电流不与磁场平行速度不与磁场平行大 小qE F =θsin BIL F = θsin qvB F =方 向 正:与E 方向相同 负:与E 方向相反 左手定则确定 F 垂直B 且F 垂直I 左手定则确定F 垂直B 且F 垂直v 是否 做功可能做功qUW = 可能做功θcos FS W =一定不做功qBmv r =qB mT π2=qB mvr =T t πθ2=θ例题1、已知氢核与氦核的质量之比m1∶m2=1∶4,电荷量之比q1∶q2=1∶2,当氢核与氦核以v1∶v2=4∶1的速度,垂直于磁场方向射入磁场后,分别做匀速圆周运动,则氢核与氦核半径之比r1∶r2=________,周期之比T1∶T2=________.例题2、如图所示,一束电子(电荷量为e)以速度v 垂直射入磁感应强度为B ,宽度为d 的匀强磁场中,穿透磁场时速度方向与电子原来入射方向的夹角是30°,则电子的质量是________,穿透磁场的时间是________.例题3、如图所示,一带电量为q =+2×10-9C 、质量为m =1.8×10-16kg 的粒子,在直线上一点O 处沿与直线成30°角的方向垂直进入磁感应强度为B 的匀强磁场中,经历t =1.5×10-6s 后到达直线上另一点P.求: (1)粒子做圆周运动的周期T ; (2)磁感应强度B 的大小;(3)若OP 的距离为0.1 m ,则粒子的运动速度v 多大?evdvB。



高考物理带电粒子在磁场中的运动常见题型及答题技巧及练习题(含答案)含解析一、带电粒子在磁场中的运动专项训练1.如图所示,一质量为m 、电荷量为+q 的粒子从竖直虚线上的P 点以初速度v 0水平向左射出,在下列不同情形下,粒子经过一段时间后均恰好经过虚线右侧的A 点.巳知P 、A 两点连线长度为l ,连线与虚线的夹角为α=37°,不计粒子的重力,(sin 37°=0.6,cos 37°=0.8).(1)若在虚线左侧存在垂直纸面向外的匀强磁场,求磁感应强度的大小B 1;(2)若在虚线上某点固定一个负点电荷,粒子恰能绕该负点电荷做圆周运动,求该负点电荷的电荷量Q (已知静电力常量为是);(3)若虚线的左侧空间存在垂直纸面向外的匀强磁场,右侧空间存在竖直向上的匀强电场,粒子从P 点到A 点的过程中在磁场、电场中的运动时间恰好相等,求磁场的磁感应强度的大小B 2和匀强电场的电场强度大小E .【答案】(1)0152mv B ql = (2)2058mv lQ kq= (3)0253mv B ql π= 220(23)9mv E qlππ-=【解析】 【分析】 【详解】(1)粒子从P 到A 的轨迹如图所示:粒子在磁场中做匀速圆周运动,设半径为r 1 由几何关系得112cos 25r l l α==由洛伦兹力提供向心力可得2011v qv Bm r =解得:0152mv B ql=(2)粒子从P 到A 的轨迹如图所示:粒子绕负点电荷Q 做匀速圆周运动,设半径为r 2 由几何关系得252cos 8l r l α==由库仑力提供向心力得20222v Qqk mr r = 解得:2058mv lQ kq=(3)粒子从P 到A 的轨迹如图所示:粒子在磁场中做匀速圆周运动,在电场中做类平抛运动 粒子在电场中的运动时间00sin 35l lt v v α== 根据题意得,粒子在磁场中运动时间也为t ,则2Tt = 又22mT qB π=解得0253mv B qlπ=设粒子在磁场中做圆周运动的半径为r ,则0v t r π= 解得:35l r π=粒子在电场中沿虚线方向做匀变速直线运动,21cos 22qE l r t mα-=⋅ 解得:220(23)9mv E qlππ-=2.欧洲大型强子对撞机是现在世界上最大、能量最高的粒子加速器,是一种将质子加速对撞的高能物理设备,其原理可简化如下:两束横截面积极小,长度为l -0质子束以初速度v 0同时从左、右两侧入口射入加速电场,出来后经过相同的一段距离射入垂直纸面的圆形匀强磁场区域并被偏转,最后两质子束发生相碰。
带电粒子在磁场中做匀速圆周运动题型归类一、运动电荷在磁场中的运动一、洛仑兹力的方向、大小及回旋角、弦切角等的关系1、在不计带电粒子(如电子、质子、α粒子等基本粒子)的重力的条件下,带电粒子在匀强磁场有三种典型的运动,它们决定于粒子的速度(v )方向与磁场的磁感应强度(B )方向的夹角(θ)。
(1)若带电粒子的速度方向与磁场方向平行时,粒子不受洛仑兹力作用而作匀速直线运动。
(2)若粒子的速度方向与磁场方向垂直,则带电粒子在垂直于磁感线的平面内以入射速度v 作匀速圆周运动,其运动所需的向心力全部由洛仑兹力提供。
(3)若带电粒子的速度方向与磁场方向成一夹角θ(θ≠0°,θ≠90°),则粒子的运动轨迹是一螺旋线(其轨迹如图):粒子垂直磁场方向作匀速圆周运动,平行磁场方向作匀速运动,螺距S=v ∥T 。
2、带电粒子在匀强磁场中做匀速圆周运动的方向及几个基本公式向心力公式:安培力是洛伦兹力的宏观表现,因而洛伦兹力的方向仍由左手定则判定,只是注意:四指的指向为正电荷运动方向或负电荷运动的反方向。
由于洛伦兹力与带电粒子的运动方向垂直,故洛伦兹力不做功。
当带电粒子的运动方向与磁场方向垂直时,洛伦兹力为带电粒子做匀速圆周运动提供向心力。
B q V m V R=2轨道半径公式:BqmV R = 周期、频率和角频率公式:T R V m B q==22ππ mBq T f π21==m Bq f T ===ππω22动能公式:()E m V P m B q R m K ===1222222T 、f 和ω的两个特点第一、T 、 f 的ω的大小与轨道半径(R )和运行速率(V )无关,而只与磁场的磁感应强度(B )和粒子的荷质比(q/m )有关。
第二、荷质比(q/m )相同的带电粒子,在同样的匀强磁场中,T 、f 和ω相同。
3.注意圆周运动的对称性与特殊性(1)从一直线边界射入的粒子从同一直线边界射出时,速度与边界的夹角相等;(2)在圆形磁场区域内,粒子射入时的速度方向过圆心,射出时的速度方向也过圆心;(3)圆形磁场区域的半径与粒子轨道半径相等时,出射方向一定垂直入射点与磁场圆心的连线。
(此结论解题很难想到,也较难证明,利用几何知识。
)二、“电偏转”与“磁偏转”的比较1、概念:带电粒子垂直电场方向进入匀强电场后,在电场力作用下的偏转叫“电偏转”。
带电粒子垂直磁场进入匀强磁场后,在洛伦兹力作用下的偏转叫“磁偏转”。
2、“电偏转”和“磁偏转”的比较。
(1)带电粒子运动规律不同。
电偏转中:粒子做类平抛运动,轨迹为抛物线,研究方法为运动分解和合成,加速度a =Eq/m ,(粒子的重力不计)侧移量(偏转量)y =at 2/2=qEt 2/2m ;磁偏转中:带电粒子做匀速圆周运动,从时间看T=2πm/qB ,从空间看:R=mv/qB 。
x x(2)带电粒子偏转程度的比较。
电偏转:偏转角(偏向角)θE =tan -1(V Y /V X )=tan -1(Eqt/mv 0),由式中可知:当偏转区域足够大,偏转时间t 充分长时,偏转角θE 接近π/2,但不可能等于π/2。
磁偏转的偏转角θB =ωt =Vt/r =qBt/m ,容易实现0—π角的偏转 O 0带电粒子在有界磁场中运动的分析方法:确定带电粒子在磁场中做匀速圆周运动的圆心、半径和运动时间的方法解决在洛伦兹力作用下带电粒子在磁场中的匀速圆周运动问题时,要注意以下三点:1.圆心的确定因为洛伦兹力F 指向圆心,根据F ⊥v ,画出粒子运动轨迹中任意两点(一般是射入和射出磁场两点),先作出切线找出v 的方向再确定F 的方向,沿两个洛伦兹力F 的方向画其延长线,两延长线的交点即为圆心,或利用圆心位置必定在圆中一根弦的中垂线上,作出圆心位置,如图1所示。
2.半径的计算一般是利用几何知识解直角三角形求出.3.粒子在磁场中运动时间的确定若要计算转过任一段圆弧所用的时间,则必须确定粒子转过的圆弧所对的圆心角,利用圆心角α与弦切角的关系,或者利用四边形内角和等于360°计算出圆心角α的大小,并由表达式,即Bq m t α=,确定通过该段圆弧所用的时间,其中T 即为该粒子做圆周运动的周期,转过的圆心角越大,所用时间t 越长,注意t 与运动轨迹的长短无关。
有界磁场的典型模型: (1)单直线边界磁场(如图1所示)。
O 1O 2O V 1V 2V V V 1V 2θ1θ2θ1θ2图(1)带电粒子垂直磁场进入磁场时。
①如果垂直磁场边界进入,粒子作半圆运动后垂直原边界飞出;②如果与磁场边界成夹角θ进入,仍以与磁场边界夹角θ飞出(有两种轨迹,图1中若两轨迹共弦,则θ1=θ2)【例1】一个负离子,质量为m ,电量大小为q ,以速率v 垂直于屏S 经过小孔O 射入存在着匀强磁场的真空室中,如图所示。
磁感应强度B 的方向与离子的运动方向垂直,并垂直于图1中纸面向里.(1)求离子进入磁场后到达屏S 上时的位置与O 点的距离.(2)如果离子进入磁场后经过时间t 到达位置P ,证明:直线OP 与离子入射方向之间的夹角θ跟t 的关系是tm qB 2=θ。
解析:(1)离子的初速度与匀强磁场的方向垂直,在洛仑兹力作用下,做匀速圆周运动.设圆半径为r ,则据牛顿第二定律可得:r v m Bqv 2= ,解得Bq mvr =如图所示,离了回到屏S 上的位置A 与O 点的距离为:AO=2rO BSvθ P所以Bq mv AO 2= (2)当离子到位置P 时,圆心角:t m Bq r vt ==α 因为θα2=,所以t mqB 2=θ. 【例2】 如图直线MN 上方有磁感应强度为B 的匀强磁场。
正、负电子同时从同一点O 以与MN 成30°角的同样速度v 射入磁场(电子质量为m ,电荷为e ),它们从磁场中射出时相距多远?射出的时间差是多少?解:由公式知,它们的半径和周期是相同的。
只是偏转方向相反。
先确定圆心,画出半径,由对称性知:射入、射出点和圆心恰好组成正三角形。
所以两个射出点相距2r ,由图还可看出,经历时间相差2T /3。
答案为射出点相距Be mv s 2=,时间差为Bqm t 34π=∆。
关键是找圆心、找半径和用对称。
【例3】如图所示,x 轴上方有垂直纸面向里的匀强磁场.有两个质量相同,电荷量也相同的带正、负电的离子(不计重力),以相同速度从O点射入磁场中,射入方向与x 轴均夹θ角.则正、负离子在磁场中A.运动时间相同B.运动轨道半径相同C.重新回到x 轴时速度大小和方向均相同D.重新回到x 轴时距O 点的距离相同答案:BCD【例4】 一个质量为m 电荷量为q 的带电粒子从x 轴上的P (a ,0)点以速度v ,沿与x 正方向成60°的方向射入第一象限内的匀强磁场中,并恰好垂直于y 轴射出第一象限。
求匀强磁场的磁感应强度B 和射出点的坐标。
解:由射入、射出点的半径可找到圆心O /,并得出半径为aq mv B Bqmv a r 23,32===得;射出点坐标为(0,a 3)。
5.如图所示,在y <0的区域内存在匀强磁场,磁场方向垂直于xy 平面并指向纸里,磁感应强度为B .一带负电的粒子(质量为m 、电荷量为q )以速度v 0从O 点射入磁场,入射方向在xy 平面内,与x 轴正向的夹角为θ.求:(1)该粒子射出磁场的位置;(2)该粒子在磁场中运动的时间.(粒子所受重力不计)M NBO v y xo B v v a O /解:(1)带负电粒子射入磁场后,由于受到洛伦兹力的作用,粒子将沿图示的轨迹运动,从A 点射出磁场,设O 、A 间的距离为L ,射出时速度的大小仍为v ,射出方向与x 轴的夹角仍为θ,由洛伦兹力公式和牛顿定律可得:qv 0B =m Rv 20 式中R 为圆轨道半径,解得:R =qB mv 0 ①圆轨道的圆心位于OA 的中垂线上,由几何关系可得:2L =R sin θ ②联解①②两式,得:L =qBmv θsin 20 所以粒子离开磁场的位置坐标为(-qB mv θsin 20,0) (2)因为T =02v R π=qB m π2 所以粒子在磁场中运动的时间,t =qB m T )(2222θππθπ-=•-(2)平行直线边界磁场(如图2所示)。
V 1V2V 3O 1O 2O 3图(2)q带电粒子垂直磁场边界并垂直磁场进入磁场时,①速度较小时,作半圆运动后从原边界飞出;②速度增加为某临界值时,粒子作部分圆周运动其轨迹与另一边界相切;③速度较大时粒子作部分圆周运动后从另一边界飞出。
1.穿过矩形磁场区:如图3所示,一定要先画好辅助线(半径、速度及延长线)。
(1)带电粒子在穿过磁场时的偏向角由sin θ=L /R 求出;(θ、L 和R 见图标)(2)带电粒子的侧移由R 2=L 2-(R-y )2解出;(y 见所图标) (3)带电粒子在磁场中经历的时间由得出。
注意,这里射出速度的反向延长线与初速度延长线的交点不再是宽度线段的中点,这点与带电粒子在匀强电场中的偏转结论不同!【例1】如图所示,一束电子(电量为e )以速度v 垂直射入磁感强度为B ,宽度为d 的匀强磁场中,穿透磁场时速度方向与电子原来入射方向的夹角是30°,则电子的质量是 ,穿透磁场的时间是 。
解析:电子在磁场中运动,只受洛仑兹力作用,故其轨迹是圆弧的一部分,又因为f ⊥v ,故圆心在电子穿入和穿出磁场时受到洛仑兹力指向交点上,如图中的O 点,由几何知识知,AB 间圆心角θ=30°,OB 为半径。
∴r =d /sin30°=2d ,又由r =mv /Be 得m =2dBe/v又∵AB 圆心角是30°,∴穿透时间t =T /12,故t =πd /3v 。
带电粒子在长足够大的长方形磁场中的运动时要注意临界条件的分析。
如已知带电粒子的质量m 和电量e ,若要带电粒子能从磁场的右边界射出,粒子的速度v 必须满足什么条件?这时必须满足r =mv/Be >d ,即v>Bed/m .【例2】如图7所示,矩形匀强磁场区域的长为L ,宽为L /2。
磁感应强度为B ,质量为m ,电荷量为e 的电子沿着矩形磁场的上方边界射入磁场,欲使该电子由下方边界穿出磁场,求:电子速率v 的取值范围?解析:(1)带电粒子射入磁场后,由于速率大小的变化,导致粒子轨迹半径的改变,如图所示。
当速率最小时,粒子恰好从d 点射出,由图可知其半径R 1=L/4,再由R 1=mv 1/eB ,得:当速率最大时,粒子恰好从c 点射出,由图可知其半径R 2满足,即R 2=5L/4,再由R 2=mv 2/eB ,得:电子速率v 的取值范围为:。
在处理这类问题时重点是画出临界状态粒子运动的轨迹图,再根据几何关系确定对应的轨迹半径,最后求解临界状态的速率。