幂函数图像

幂函数的图像与性质一、相关内容1、形如αx y =的函数叫做幂函数，其中x 是自变量，α是常数。

2、幂函数的图像0<α10<<α1>α第一象限图像其他象限图像根据定义域和奇偶性判断性质总结1、幂函数的图像一定在第一象限，不在第四象限2、图像过定点（1，1）3、当0=α时，表示与X 轴平行，过（1，1），不过（0，1）的两条射线二、基础练习1、判断下列哪些是幂函数（1）xy 2.0= （2）21x y = （3）x y -=3 （4）1-=x y （5）x y 4= （6）5x y =2、画出下列函数的图像（1）43x y = （2）34x y =（3）76-=x y （4）31x y =（5）x y = （6）98x y =3、若幂函数y =()x f 的图象经过点（9,13）, 则f(25)的值是_________4、若函数()x f 既是幂函数又是反比例函数,则这个函数是()x f =5、幂函数()f x 的图象过点43,27)（，则()f x 的解析式是____________6、函数2223()(1)m m f x m m x --=--是幂函数，且在(0,)x ∈+∞上是减函数，则实数m =______7、已知－1<a <0，则三个数331,,3a a a由小到大的顺序是___________8、在32521,2,,y y x y x x y x x===+=四个函数中，幂函数有 （ ） A 、1个 B 、2个 C 、3个 D 、4个9、已知幂函数()y f x =的图象过点2(2,)2，则(4)f 的值为（ ）A ．1B ． 2C ．12D ．8 10、幂函数y ＝xm 2－3m －4(m ∈Z)的图象如下图所示，则m 的值为( )A ．－1<m <4B ．0或2C ．1或3D ．0,1,2或311、若)1(,,)1(,1,4,)21(,2522>==-=+====a a y x y x y x y x y y x y xx上述函数是幂函数的个数是（ ）A ．0个B ．1个C ．2个D ．3个12、幂函数y ＝x α(α是常数)的图象( )A 、一定经过点(0，0)B ．一定经过点(1，1)C ．一定经过点(－1，1)D ．一定经过点(1，－1) 13、对于幂函数54)(x x f =，若210x x <<，则)2(21x x f +，2)()(21x f x f +大小关系是（ ） A ．)2(21x x f +>2)()(21x f x f + B ． )2(21x x f +<2)()(21x f x f + C ． )2(21x x f +=2)()(21x f x f + D ． 无法确定。

幂函数图像及性质什么是幂函数？幂函数是指在极坐标或复平面上将某一点按某一规则移动，使其形成一种函数。

这种函数是关于某一点的未知函数，这一点可以表示为一个复数，且该复数可以表示某一点的坐标。

幂函数也可以用复数表示，其中一个具体的形式为：z =r^n*cos(θ+2πm) + ir^n*sin(θ+2πm)，其中r 为极径，θ为极角，m为整数，n为实常数。

幂函数的图像是一条曲线，所以它也被称为曲线函数，它的图像可以根据x，y轴的定义方法来确定。

在极坐标系中，幂函数的形状一般是环状曲线，并且其形状受n值的影响很大，比如当n=1时，图像的形状为单个圆；当n=2时，图像的形状为集中的双圆；当n=3时，图像的形状为三角形；当n=4时，图像的形状为集中的四方形；当n=5时，图像的形状为五角星状等。

幂函数的性质可以用幂函数的微积分形式来说明，即dz/dr=n*r^(n-1)，其中n 为实常数，r 为极径，z为极坐标系的一点的坐标，推导出dz/dr的值，可以用于表示幂函数的形状及特性。

此外，还可以用基本物理运算来说明，所谓幂函数是指坐标变换时r和θ之间存在一定的关系，此关系可以表示为r=f(θ)，其中f(θ)是幂函数，这里的幂函数可以通过幂函数的大小因子或者指数来表示，而指数n就是幂函数的性质，只有当n>0或者n<0时，才能使幂函数表达出不同的性质。

幂函数在物理学中也被广泛使用，例如，在声学领域，幂函数可以用来描述声波的传播规律，这就是为什么音量大小是一个幂函数的原因。

此外，在光学领域，幂函数可以用来描述光的传播规律，例如，可以用来计算光的反射系数或者折射系数。

而在数学中，幂函数不仅表示曲线的性质，还可以用来研究复数的性质，以及形成更复杂的曲线。

以上就是我们关于幂函数图像及性质的简单介绍，幂函数是一种非常有趣的曲线函数，它在物理学，数学及光学领域有着重要的应用。

虽然它看起来很复杂，但它所提供的知识却是非常有价值的，只要我们多多使用幂函数，就能够获得丰富的经验和数学知识。

幂函数的一般形式为y = x^n，其中n 是一个实数，x 是自变量，y 是因变量。

以下是幂函数的主要性质：
1.当n > 0 时，幂函数是增函数；当n < 0 时，幂函数是减函数。

2.当n 是偶数时，幂函数的图像关于y 轴对称；当n 是奇数时，幂函
数的图像关于原点对称。

3.当n > 1 时，幂函数的图像在第一象限和第三象限上都是上升的；当0
< n < 1 时，幂函数的图像在第一象限和第三象限上都是下降的。

4.当n > 1 时，幂函数的图像在x 轴正半轴上有一个水平渐近线，而在
x 轴负半轴上没有水平渐近线；当0 < n < 1 时，幂函数的图像在x 轴正半轴上没有水平渐近线，而在x 轴负半轴上有一个水平渐近线。

5.幂函数的导数为y' = nx^(n-1)，因此在n > 0 时，幂函数在定义域内处
处可导。

以下是一些常见幂函数的图像：。

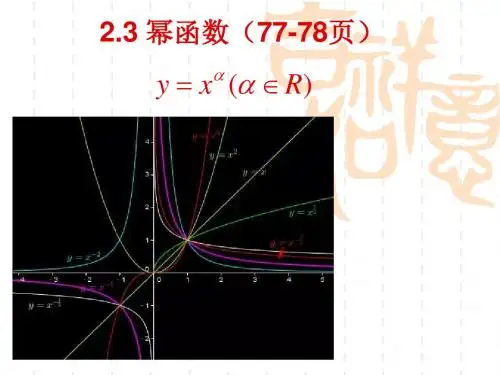
学习幂函数，图像是关键。

y=xa（a≠0、1）在第一象限的图像可以分为三类：
只要掌握了这三种情况，然后根据幂函数的奇偶性，就可作出y=xa（a≠0、1）在其定义域内的完整图像，这时它的一切属性将是直观、显然的。

幂函数的图像一定经过第一象限，且一定不经过第四象限。

幂函数y=xa。

α只能从（±3，±2，±1，±1/2，±1/3）中取值。

幂函数y=x的图像表（见右表）：
在记忆这个表时要记住两点：
其一，图像的形态：
当n/m<1时，y=x在第一象限的图像下凹，呈上升趋势。

当0<n/m时，y=x在第一象限的图像下凸，呈上升趋势。

当n/m<0时，y=x在第一象限的图像下凹，呈下降趋势。

其二，图像所在的象限。

用一句话可以简单概括为：奇偶图在第一象限，偶奇图在第一、二象限，奇奇图在第一、三象限。

幂函数图像及性质一、什么是幂函数在数学中，幂函数是一种形式为 f(x) = x^a 的函数，其中 a 是实数。

当 a = 1 时，幂函数就是我们熟悉的一次函数，而当a > 1 时，幂函数的图像呈现出特定的形状。

二、幂函数的图像特点1. 当 a > 1 时•当 a > 1 时，幂函数的图像呈现出向上凹曲的形状。

•随着 x 的增大，函数值快速增加，增长迅猛。

•函数图像在第一象限，并在原点围绕原点对称。

2. 当 a = 1 时•当 a = 1 时，幂函数就是一次函数，函数图像为一条过原点的直线。

3. 当 0 < a < 1 时•当 0 < a < 1 时，函数的增长趋于缓慢，图像在第一象限被压缩，所占的范围变小。

三、幂函数的性质1. 定义域和值域•对于幂函数 f(x) = x^a，当 a 为奇数时，定义域为实数集，值域也为实数集；当 a 为偶数时，定义域为非负实数集，值域也为非负实数集。

2. 奇偶性•当 a 为奇数时，幂函数是奇函数，关于原点对称；•当 a 为偶数时，幂函数是偶函数，关于 y 轴对称。

3. 单调性•当 a > 1 时，幂函数是增函数；•当 0 < a < 1 时，幂函数是减函数。

4. 特殊情况•当 a < 0 时，幂函数的图像为反比例函数的图像。

四、实例分析示例 1考虑函数 f(x) = x^2，这是一个以原点为中心向上开口的抛物线图像。

随着 x 的增大，函数值快速增加，形成一个向上凸起的形状。

示例 2当考虑函数 f(x) = x^0.5 时，函数的图像呈现出一个缓慢上升的曲线，范围也变小了，整体呈现出一种被压缩的状态。

五、总结幂函数是数学中非常重要的一类函数，通过本文的讨论，我们了解了幂函数的图像特点和性质。

无论是在理论研究还是实际应用中，对于幂函数的理解都具有重要的意义。

希望本文内容能够帮助读者更深入地理解幂函数及其性质。