幂函数图像与性质

幂函数•冥函数的定义：一般地，函数y=xα叫做幂函数，其中x是自变量，α是常数。

幂函数的解析式：y=xα幂函数的图像：•幂函数图像的性质：所有幂函数在(0，+∞)上都有定义．①α＞0，图像都过定点（0，0）和（1，1）；在区间（0，+∞）上单调递增；②α＜0，图像都过定点（1，1）；在区间（0，+∞）上单调递减;③当O<a<l时，曲线上凸，当a>l时，曲线下凸．④当a=l时，图象为过点(0，0)和(1，1)的直线．⑤当a=0时，表示过点(1，1)且平行于x轴的直线(除去点(0，1)) 。

幂函数图象的其他性质：(1)图象的对称性：把幂函数的幂指数a（只讨论a是有理数的情况）表示成既约分数的形式（整数看作是分母1的分数），则不论a>0还是a<0，幂函数的图象的对称性用口诀记为：“子奇母偶孤单单；母奇子偶分两边；分子分母均为奇，原点对称莫忘记”，(2)图象的形状：①若a>0，则幂函数的图象为抛物线形，当a>l时，图象在[0，+∞）上是向下凸的（称为凸函数）；当O<a<l时，图象在[o，+∞）上是向上凸的（称为凹函数）．②若a<0，则幂函数y=x“的图象是双曲线形，图象与x轴、y轴无限接近，在(0，+∞)上图象都是向下凸的。

幂函数的单调性和奇偶性：对于幂函数（a∈R)．(1)单调性当a>0时，函数在第一象限内是增函数；当a<0时，函数在第一象限内是减函数．(2)奇偶性①当a为整数时，若a为偶数，则是偶函数；若a为奇数，则是奇函数。

②当n为分数，即（p，q互素，p，q∈Z）时，若分母q为奇数，则分子p为奇数时，为奇函数；分子p为偶数时，为偶函数，若分母q为偶数，则为非奇非偶函数．。

一知识梳理1、幂函数（1）定义：一般地，形如_________的函数称为幂函数，其中为常数。

几种常见幂函数的图像：①②③④⑤（2）幂函数的性质①所有幂函数在_________都有定义，并且图像都过点________；②时，幂函数的图像通过_________，并且在区间上是_________，特别的，当时，幂函数的图像________，当时，幂函数的图像________。

③时，幂函数的图像在区间上是_________，在第一象限内，当x从右边趋向原点时，图像在y轴右方无限地逼近y轴正半轴，当x趋向时，图像在x轴上方无限地逼近x轴正半轴。

（4）幂函数的图象，在第一象限内，直线的右侧，图象由下至上，指数. 轴和直线之间，图象由上至下，指数.二.常见幂函数的性质：定义域值域奇偶性单调性定点三、例题解析例1.已知函数若关于x的方程有两个不同的实根，则k的取值范围是___________例2.若曲线处的切线与两个坐标轴围城的三角形的面积为18，a=____例3 已知函数为何值时，：（1）是正比例函数，（2）是反比例函数，（3）是二次函数，（4）是幂函数例4 若点在幂函数的图像上，点在幂函数的图像上，定义，试求函数的最大值以及单调区间。

四：巩固练习1.已知幂函数(p,q∈N+且p与q互质)的图象如图所示,则A.p、q均为奇数且<0B.p为奇数,q为偶数且<0C.p为奇数,q为偶数且>0D.p为偶数,q为奇数且<02.给定一组函数解析式:如图所示一组函数图象.图象对应的解析式号码顺序正确的是()A.⑥③④②⑦①⑤B.⑥④②③⑦①⑤C.⑥④③②⑦①⑤D.⑥④③②⑦⑤①3、已知，则（）ＡＢＣＤ4、幂函数的图像过点，则它的单调递增区间是（）ＡＢＣＤ5.（2011·山东高考）若点（a,9）在函数的图象上，则tan=的值为：（A）0 （B）（C）1 （D）6.设，则使函数的定义域为R且为奇函数的所有值为_________。

幂函数的图像和性质幂函数的图像和性质是指关于某一变量x的多项式形式为y=ax^n（a≠0）的函数，其中a是实数，n∈Z，称为幂函数。

由于幂函数有着独特的形式，它的图像和性质也有许多独特之处。

一、图像1. 对于任意实常数a>0，n>0，y=ax^n的图像是一条以原点为极坐标的曲线；2. 对于任意实常数a>0,n<0,y=ax^n的图像是一条以x轴上的无穷远点为极坐标的曲线；3. 对于任意实常数a<0,n>0,y=ax^n的图像是一条以y轴上的无穷远点为极坐标的曲线；4. 对于任意实常数a<0,n<0,y=ax^n的图像是一条以原点为极坐标的曲线。

二、性质（1）当n>0时，y=ax^n的图像在x轴上的对称轴是x=0，且函数值y随x的增加而不断增大，直至无穷大；（2）当n<0时，y=ax^n的图像在x轴上的对称轴是x=0，且函数值y随x的增加而不断减小，直至无穷小；（3）当n=0时，y=ax^n即为常数函数y=a，其图像是一条水平线；（4）当n>0时，y=ax^n在x轴上的渐近线是y=0，其图像开口向上；（5）当n<0时，y=ax^n在x轴上的渐近线是y=0，其图像开口向下；（6）对于任意实数m，y=ax^n的图像关于y=m的对称轴是x=(m/a)^(1/n)；（7）当n>0时，在y轴上截取y=ax^n的图像时，可以得到一段区间[0, +∞]，在这段区间内，函数值y 随x的增加而增大；（8）当n<0时，在y轴上截取y=ax^n的图像时，可以得到一段区间(-∞, 0]，在这段区间内，函数值y 随x的增加而减小；三、总结幂函数的图像和性质是指函数形式为y=ax^n（a≠0）的函数的图像和性质，其中a是实数，n∈Z。

幂函数的性质有：对称轴、渐近线、函数值随x的变化而变化等，此外，图像表明幂函数的变化趋势，可以直观地看出函数值y 随x的变化趋势，从而有助于理解函数的特点。

幂函数的性质与图像 幂函数及其性质 1、幂函数的定义一般地，形如y x α=（x ∈R ）的函数称为幂孙函数，其中x是自变量，α是常数.如11234,,y x y x y x-===等都是幂函数，幂函数与指数函数，对数函数一样，都是基本初等函数. 2、函数的图像（1）y x = （2）12y x= （3）2y x= （4）1y x-= （5）3yx=用描点法在同一坐标系内画出以上五个函数图像，通过观察图像，可以看出幂函数的性质。

3．幂函数性质（1）所有的幂函数在（0，+∞）都有定义，并且图象都过点（1，1）；（2）x ＞0时，幂函数的图象都通过原点，并且在[0，+∞]上，是增函数（3）α＜0时，幂函数的图象在区间（0，+∞）上是减函数.（4）在第一象限内，图象向上及向右都与坐标轴无限趋近.3. 幂函数y x α=的图象，在第一象限内，直线1x =的右侧，图象由下至上，指数 . y 轴和直线1x =之间，图象由上至下，指数α .：4. 规律总结1．在研究幂函数的性质时，通常将分式指数幂化为根式形式，负整指数幂化为分式形式再去进行讨论；2．对于幂函数y ＝αx ，我们首先应该分析函数的定义域、值域和奇偶性，由此确定图象的位置，即所在象限，其次确定曲线的类型，即α＜0，0＜α＜1和α＞1三种情况下曲线的基本形状，还要注意α＝0，±1三个曲线的形状；对于幂函数在第一象限的图象的大致情况可以用口诀来记忆：“正抛负双，大竖小横”，即α＞0（α≠1）时图象是抛物线型；α＜0时图象是双曲线型；α＞1时图象是竖直抛物线型；0＜α＜1时图象是横卧抛物线型． 在[0，+∞]上，y x =、2y x=、3y x=、12y x=是增函数， 在（0，+∞）上，1y x -=是减函数。

例1．已知函数()()2531m f x m m x --=--，当 m 为何值时，()f x ：（1）是幂函数；（2）是幂函数，且是()0,+∞上的增函数；（3）是正比例函数；（4）是反比例函数；（5）是二次函数；简解：（1）2m =或1m =-（2）1m =-（3）45m =-（4）25m =-（5）1m =-变式训练： 已知函数()()2223m m f x m m x--=+，当 m 为何值时，()f x 在第一象限内它的图像是上升曲线。

幂函数知识点1. 幂函数定义幂函数是形如 \(y = x^n\) 的函数，其中 \(n\) 是实数。

当 \(n\) 为正整数时，幂函数的图像是一系列经过原点的点，且随着 \(n\) 的增加，曲线逐渐趋于平坦。

2. 幂函数的图像特征- 当 \(n > 1\) 时，幂函数在 \(x > 0\) 区域内单调递增。

- 当 \(0 < n < 1\) 时，幂函数在 \(x > 0\) 区域内单调递减。

- 当 \(n\) 为负整数时，幂函数在 \(x > 0\) 区域内表现为周期函数，周期为 \(4\pi\)。

- 当 \(n = 0\) 时，函数退化为常数函数 \(y = 1\)。

3. 幂函数的性质- 奇次幂函数是奇函数，即 \(y(-x) = -y(x)\)。

- 偶次幂函数是偶函数，即 \(y(-x) = y(x)\)。

- 幂函数的导数是 \(y' = n \cdot x^{n-1}\)。

- 幂函数的积分是 \(\int x^n dx = \frac{x^{n+1}}{n+1} + C\)，其中 \(C\) 是积分常数。

4. 幂函数的应用- 在物理学中，幂函数常用于描述物体的速度与加速度的关系。

- 在经济学中，幂函数可以用来模拟市场需求与价格的关系。

- 在工程学中，幂函数用于描述材料的强度与应力的关系。

5. 特殊幂函数- 指数函数 \(y = a^x\) 是幂函数的一种特殊形式，其中 \(a\) 是正实数且 \(a \neq 1\)。

- 对数函数 \(y = \log_a x\) 也是幂函数的一种特殊形式，其中\(a\) 是正实数且 \(a \neq 1\)。

6. 幂函数的运算法则- 幂的乘法：\(x^m \cdot x^n = x^{m+n}\)- 幂的除法：\(x^m / x^n = x^{m-n}\)- 幂的幂：\((x^m)^n = x^{m \cdot n}\)7. 幂函数的极限- 当 \(x \to 0\) 时，\(x^n\) 的极限取决于 \(n\) 的值。

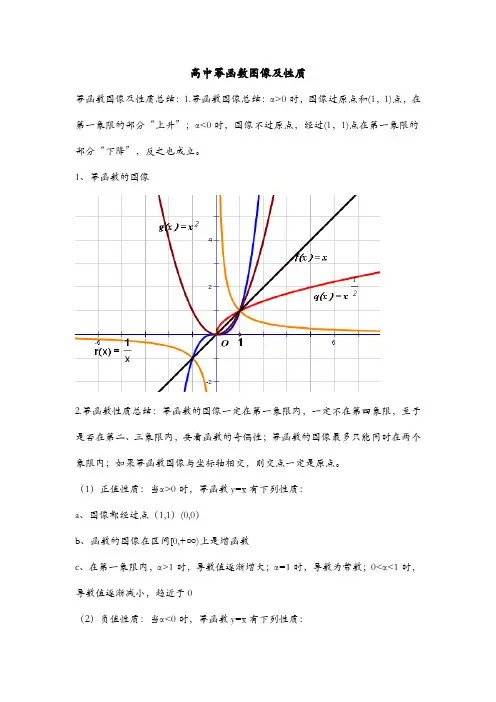
高中幂函数图像及性质
幂函数图像及性质总结：1.幂函数图像总结：α>0时，图像过原点和(1，1)点，在第一象限的部分“上升”；α<0时，图像不过原点，经过(1，1)点在第一象限的部分“下降”，反之也成立。

1、幂函数的图像
2.幂函数性质总结：幂函数的图像一定在第一象限内，一定不在第四象限，至于是否在第二、三象限内，要看函数的奇偶性；幂函数的图像最多只能同时在两个象限内；如果幂函数图像与坐标轴相交，则交点一定是原点。

（1）正值性质：当α>0时，幂函数y=x有下列性质：
a、图像都经过点（1,1）(0,0）
b、函数的图像在区间[0,+∞)上是增函数
c、在第一象限内，α>1时，导数值逐渐增大；α=1时，导数为常数；0<α<1时，导数值逐渐减小，趋近于0
（2）负值性质：当α<0时，幂函数y=x有下列性质：
a、图像都通过点（1,1）
b、图像在区间（0，+∞）上是减函数；（内容补充：若为X易得到其为偶函数。

利用对称性，对称轴是y轴，可得其图像在区间（-∞，0）上单调递增。

其余偶函数亦是如此）
c、在第一象限内，有两条渐近线（即坐标轴），自变量趋近0，函数值趋近+∞，自变量趋近+∞，函数值趋近0。

幂函数图像及性质总结幂函数是一种常见的函数形式，表示为 $ f(x) = ax^b $，其中a和b是实数常数，且b不等于零。

在本文中，我们将探讨幂函数的图像和性质，帮助读者更好地理解幂函数在数学中的应用和意义。

幂函数的图像特征幂函数的图像一般呈现为一条曲线，其形状取决于幂函数中的指数b的正负性和大小。

当b>0时，幂函数的图像在第一象限中从左向右递增；当b<0时，幂函数的图像在第一象限中从左向右递减。

若b为偶数，则幂函数的图像在第一和第三象限中均为非负，且在原点处取得最小值；若b为奇数，则幂函数的图像在第一、第三象限中一正一负，且在原点处有切线。

幂函数的性质总结1.定义域和值域：幂函数的定义域为全体实数集 $ \mathbb{R} $，值域取决于指数b的正负性。

2.奇偶性：当指数 $ b $ 为偶数时，幂函数是偶函数；当指数 $ b $ 为奇数时，幂函数是奇函数。

3.对称性：如果 $ b $ 为偶数，则幂函数关于y轴对称；如果 $ b $ 为奇数，则幂函数关于原点对称。

4.增减性：当 $ b > 0 $ 时，幂函数在定义域上递增；当 $ b < 0 $ 时，幂函数在定义域上递减。

5.极值点和拐点：幂函数的极值点和拐点通常出现在指数b为偶数的情况下。

6.与常函数的比较：当幂函数的指数b大于1时，其增长速度快于常函数；当指数b在 0 到 1 之间时，其增长速度为常函数；当指数b为负时，其绝对值小于 1 时，其增长速度慢于常函数。

结语通过以上对幂函数图像及性质的总结，我们可以更深入地理解幂函数在数学中的重要性和应用。

幂函数在数学建模、物理学等领域有着广泛的应用，希望本文能够帮助读者更好地理解幂函数的概念和特性。

授课主题：幂函数教学目标1．通过具体实例了解幂函数的图象和性质.2．类比研究指数函数、对数函数的过程与方法，研究幂函数的图象和性质.3．体会幂函数图象的变化规律及蕴含其中的对称性，并能进行简单的应用.教学内容1．幂函数的定义：一般地，形如()Ry xαα=∈的函数称为幂函数，其中α是常数．2．幂函数的图象：函数y x=2y x=3y x=12y x=1y x-=的图象-1-111y=xy=x3y=x2y=xy=1xyxOy x=2y x=3y x=12y x=1y x-=定义域R R R[0,)+∞(0)(0)-∞+∞，，值域R[0,)+∞R[0,)+∞(0)(0)-∞+∞，，奇偶性奇函数偶函数奇函数非奇非偶函数奇函数单调性单调递增在(0]-∞，上减在[0)+∞，上增单调递增单调递增在(0)-∞，和(0)+∞，上单调递减公共点(11)，(11)，(11)，(11)，(11)，图象所在象限一、三一、二一、三一一、三3．幂函数的性质：（1）所有的幂函数在(0)+∞，都有定义，并且图象都通过点(11)，； （2）0a >时，幂函数的图象通过原点，并且在[0)+∞，上是增函数； （3）0a <时，①幂函数在(0,)+∞上是减函数；②在第一象限内，图象向上与y 轴无限地接近，向右与x 轴无限地接近．（4）任何幂函数图象都不经过第四象限； （5）任何两个幂函数的图象最多有三个交点． （6）任何幂函数的图象与坐标轴至多只有一个交点； （7）幂函数nm y x =奇偶性①当n 为偶数时，nm y x =为偶函数；②当n 为奇数，m 为奇数时，nm y x =为奇函数； ③当n 为奇数，m 为偶数时，n m y x =为非奇非偶函数．特别地，幂函数n y x =（Z n ∈），当n 为偶数时，n y x =为偶函数；当n 为奇数时，n y x =为奇函数．题型一 幂函数概念的理解应用例1 函数223()(1)mm f x m m x +-=--是幂函数，且当()0,x ∈+∞时，()f x 是增函数，求()f x 的解析式.点评：幂函数y ＝x α(α∈R)其中α为常数，其本质特征是以幂的底x 为自变量，指数α为常数(也可以为0)．这是判断一个函数是否为幂函数的重要依据和唯一标准．对例1来说，还要根据单调性验根，以免增根．巩 固 函数221()(2)mm f x m m x +-=+是幂函数且是奇函数，则实数m 的值是___________.答案：-1题型二 利用幂函数的性质比较大小例2 比较下列各组中两个数的大小：点评：比较两个幂的大小的关键是搞清楚底数与指数是否相同，若底数相同，利用指数函数的性质比较大小；若指数相同，利用幂函数的性质比较大小；若底数指数均不同，考虑利用中间值来比较大小．巩固比较下列各组数的大小：题型三求幂函数的解析式例3巩固幂函数f(x)的图象过点(4,2)，则f(9)＝________.答案：3A组2．下列四类函数中，具有性质“对任意的x>0，y>0，函数f(x)满足f(x＋y)＝f(x)f(y)”的是() A．幂函数B．对数函数C．指数函数D．二次函数解析：本题考查幂的运算性质f(x)f(y)＝a x a y＝a x＋y＝f(x＋y).答案：C3．函数f(x)＝(m2－3m＋3)x m＋2是幂函数且函数f(x)为偶函数，求m的值．解析：∵f(x)＝(m2－3m＋3)x m＋2是幂函数，∴m2－3m＋3＝1，即m2－3m＋2＝0，∴m＝1或m＝2.当m＝1，f(x)＝x3为奇函数，不符合题意；当m＝2时，f(x)＝x4为偶函数，符合题意，∴m＝2.B组1．下列所给出的函数中，属于幂函数的是()A．y＝－x3B．y＝x－3C．y＝2x3D．y＝x3－1答案：B答案：B 3．函数y ＝x－2在区间⎣⎡⎦⎤12，2上的最大值是( )A.14 B ．－14 C ．4 D ．－4答案：①＜ ②＜ ③＞ ④＜答案：AC 组1．给出两个结论：(1)当α＝0时，幂函数y ＝x α的图象是一条直线；(2)幂函数y ＝x α的图象都经过(0,0)和(1,1)点，则正确的判断是( )A ．(1)对(2)错B ．(1)错(2)对C ．(1)(2)都错D ．(1)(2)都对 答案:C2．上图所示的曲线是幂函数y ＝x α在第一象限内的图象，已知α分别取－1,1，12，2四个值，则相应图象依次为：______.答案:C 4，C 2，C 3，C 1 3．设f (x )＝(a －3)x (a＋1)(a －2)，当a 为何值时，(1)f (x )为常数函数？ (2)f (x )为幂函数？(3)f (x )为正比例函数？ 答案:1．下列函数中，其定义域和值域不同的函数是( )A ．y ＝x 13 B ．y ＝x －12 C ．y ＝x 53D ．y ＝x 23解析：选D.y ＝x 23＝3x 2，其定义域为R ，值域为[0，＋∞)，故定义域与值域不同．2．如图，图中曲线是幂函数y ＝x α在第一象限的大致图象．已知α取－2，－12，12，2四个值，则相应于曲线C 1，C 2，C 3，C 4的α的值依次为( )A ．－2，－12，12，2B ．2，12，－12，－2C ．－12，－2,2，12D ．2，12，－2，－12解析：选B.当x ＝2时，22＞212＞2－12＞2－2， 即C 1：y ＝x 2，C 2：y ＝x 12，C 3：y ＝x －12，C 4：y ＝x －2. 3．以下关于函数y ＝x α当α＝0时的图象的说法正确的是( )A ．一条直线B ．一条射线C ．除点(0,1)以外的一条直线D ．以上皆错 解析：选C.∵y ＝x 0，可知x ≠0， ∴y ＝x 0的图象是直线y ＝1挖去(0,1)点． 4．函数f (x )＝(1－x )0＋(1－x )12的定义域为________．解析：⎩⎪⎨⎪⎧1－x ≠01－x ≥0，∴x <1.答案：(－∞，1)5．已知幂函数f (x )的图象经过点(2，22)，则f (4)的值为( ) A ．16 B.116 C.12D ．2解析：选C.设f (x )＝x n ，则有2n ＝22，解得n ＝－12，即f (x )＝x －12，所以f (4)＝4－12＝12. 6．下列幂函数中，定义域为{x |x ＞0}的是( )A ．y ＝x 23 B ．y ＝x 32 C ．y ＝x －13D ．y ＝x －34解析：选D.A.y ＝x 23＝3x 2，x ∈R ；B.y ＝x 32＝x 3，x ≥0；C.y ＝x －13＝13x ，x ≠0；D.y ＝x －34＝14x3，x ＞0.7．已知幂函数的图象y ＝xm 2－2m －3(m ∈Z ，x ≠0)与x ，y 轴都无交点，且关于y 轴对称，则m 为( )A ．－1或1B ．－1,1或3C ．1或3D ．3解析：选B.因为图象与x 轴、y 轴均无交点，所以m 2－2m －3≤0，即－1≤m ≤3.又图象关于y 轴对称，且m ∈Z ，所以m 2－2m －3是偶数，∴m ＝－1,1,3.故选B. 8．下列结论中，正确的是( )①幂函数的图象不可能在第四象限②α＝0时，幂函数y ＝x α的图象过点(1,1)和(0,0) ③幂函数y ＝x α，当α≥0时是增函数④幂函数y ＝x α，当α<0时，在第一象限内，随x 的增大而减小 A ．①② B ．③④ C ．②③D ．①④解析：选D.y ＝x α，当α＝0时，x ≠0；③中“增函数”相对某个区间，如y ＝x 2在(－∞，0)上为减函数，①④正确． 9．在函数y ＝2x 3，y ＝x 2，y ＝x 2＋x ，y ＝x 0中，幂函数有( )A ．1个B ．2个C ．3个D ．4个解析：选B.y ＝x 2与y ＝x 0是幂函数．10．幂函数f (x )＝x α满足x ＞1时f (x )＞1，则α满足条件( )A ．α＞1B ．0＜α＜1C ．α＞0D ．α＞0且α≠1解析：选A.当x ＞1时f (x )＞1，即f (x )＞f (1)，f (x )＝x α为增函数，且α＞1. 11．幂函数f (x )的图象过点(3，3)，则f (x )的解析式是________．解析：设f (x )＝x α，则有3α＝3＝312⇒α＝12.答案：f (x )＝x 1212．设x ∈(0,1)时，y ＝x p (p ∈R )的图象在直线y ＝x 的上方，则p 的取值范围是________．解析：结合幂函数的图象性质可知p <1. 答案：p <113．如图所示的函数F (x )的图象，由指数函数f (x )＝a x 与幂函数g (x )＝x α“拼接”而成，则a a 、a α、αa 、αα按由小到大的顺序排列为________．解析：依题意得⎩⎨⎧ a 14＝1214α＝12⇒⎩⎨⎧a ＝116，α＝12.所以a a＝(116)116＝[(12)4]116，a α＝(116)12＝[(12)32]116，αa ＝(12)116，αα＝(12)12＝[(12)8]116，由幂函数单调递增知a α＜αα＜a a ＜αa . 答案：a α＜αα＜a a ＜αa11 14．函数f (x )＝(m 2－m －5)x m －1是幂函数，且当x ∈(0，＋∞)时，f (x )是增函数，试确定m 的值．解：根据幂函数的定义得：m 2－m －5＝1，解得m ＝3或m ＝－2，当m ＝3时，f (x )＝x 2在(0，＋∞)上是增函数；当m ＝－2时，f (x )＝x －3在(0，＋∞)上是减函数，不符合要求．故m ＝3.15．已知函数f (x )＝(m 2＋2m )·x m 2＋m －1，m 为何值时，f (x )是：(1)正比例函数；(2)反比例函数；(3)二次函数；(4)幂函数？解：(1)若f (x )为正比例函数，则⎩⎪⎨⎪⎧ m 2＋m －1＝1m 2＋2m ≠0⇒m ＝1. (2)若f (x )为反比例函数，则⎩⎪⎨⎪⎧ m 2＋m －1＝－1m 2＋2m ≠0⇒m ＝－1. (3)若f (x )为二次函数，则⎩⎪⎨⎪⎧m 2＋m －1＝2m 2＋2m ≠0⇒m ＝－1±132. (4)若f (x )为幂函数，则m 2＋2m ＝1，∴m ＝－1±2.16．已知幂函数y ＝x m 2－2m －3(m ∈Z )的图象与x 、y 轴都无公共点，且关于y 轴对称，求m 的值，并画出它的图象．解：由已知，得m 2－2m －3≤0，∴－1≤m ≤3.又∵m ∈Z ，∴m ＝－1,0,1,2,3.当m ＝0或m ＝2时，y ＝x －3为奇函数，其图象不关于y 轴对称，不适合题意．∴m ＝±1或m ＝3.当m ＝－1或m ＝3时，有y ＝x 0，其图象如图(1)．当m ＝1时，y ＝x －4，其图象如图(2)．。

幂函数的性质与图像1、幂函数的定义一般地，形如y x α=（x ∈R ）的函数称为幂函数，其中x 是自变量，α是常数.如11234,,y x y x y x -===等都是幂函数，幂函数与指数函数，对数函数一样，都是基本初等函数. 2、函数的图像（1）y x = （2）12y x = （3）2y x = （4）1y x -= （5）3y x =用描点法在同一坐标系内画出以上五个函数图像，通过观察图像，可以看出幂函数的性质。

3．幂函数性质（1）所有的幂函数在（0，+∞）都有定义，并且图象都过点（1，1）；（2）x ＞0时，幂函数的图象都通过原点，并且在[0， +∞]上，是增函数（3）α＜0时，幂函数的图象在区间（0，+∞）上是减函数. （4）在第一象限内，图象向上及向右都与坐标轴无限趋近.3. 幂函数y x α=的图象，在第一象限内，直线1x =的右侧，图象由下至上，指数 . y 轴和直线1x =之间，图象由上至下，指数α .：4. 规律总结1．在研究幂函数的性质时，通常将分式指数幂化为根式形式，负整指数幂化为分式形式再去进行讨论；2．对于幂函数y ＝αx ，我们首先应该分析函数的定义域、值域和奇偶性，由此确定图象的位置，即所在象限，其次确定曲线的类型，即α＜0，0＜α＜1和α＞1三种情况下曲线的基本形状，还要注意α＝0，±1三个曲线的形状；对于幂函数在第一象限的图象的大致情况可以用口诀来记忆：“正抛负双，大竖小横”，即α＞0（α≠1）时图象是抛物线型；α＜0时图象是双曲线型；α＞1时图象是竖直抛物线型；0＜α＜1时图象是横卧抛物线型． 在[0，+∞]上，y x =、2y x =、3y x =、12y x =是增函数， 在（0，+∞）上， 1y x -=是减函数。

例1．已知函数()()2531m f x m m x --=--，当 m 为何值时，()f x ：（1）是幂函数；（2）是幂函数，且是()0,+∞上的增函数；（3）是正比例函数；（4）是反比例函数；（5）是二次函数； 简解：（1）2m =或1m =-（2）1m =-（3）45m =-（4）25m =-（5）1m =- 变式训练：已知函数()()2223m m f x m m x --=+，当 m 为何值时，()f x 在第一象限内它的图像是上升曲线。