金属材料形变硬化指数的测定
- 格式:doc
- 大小:187.50 KB
- 文档页数:5

AZ31镁合金拉伸应变硬化指数的测试王宝;池成忠;梁伟;李黎忱;聂慧慧;黄莉莉【摘要】针对镁合金板材在拉伸时呈现微型锯齿屈服效应曲线时应如何计算拉伸应变硬化指数n值的问题,采用差分平均法、两点分析法、解析拟合法以及国标线性回归法对AZ31镁合金板材拉伸曲线进行计算,以国标线性回归法所得结果nline 为参考基准,将另外三种方法得出的ndiff、ntwo-point、npoty同nline进行比较.结果表明:用差分平均法、两点分析法和解析拟合法计算的n值非常吻合.解析拟合法得到的结果同线性回归法的结果相符程度最高,误差仅为0.27%,差分平均法次之,为-0.53%,两点法计算误差在1%左右.验证了金属材料拉伸呈现微型锯齿屈服效应曲线时,其n值仍然可用这四种方法计算.当金属材料拉伸均匀塑性变形阶段曲线变化较平稳时,建议优先采用解析拟合法,此时用该方法计算n值既方便又可信度高.【期刊名称】《轻合金加工技术》【年(卷),期】2013(041)002【总页数】5页(P53-56,61)【关键词】AZ31镁合金;拉伸应变硬化指数;差分平均法;两点分析法;解析拟合法【作者】王宝;池成忠;梁伟;李黎忱;聂慧慧;黄莉莉【作者单位】太原理工大学材料科学与工程学院,山西太原030024;太原理工大学材料科学与工程学院,山西太原030024;太原理工大学材料科学与工程学院,山西太原030024;太原理工大学材料科学与工程学院,山西太原030024;太原理工大学材料科学与工程学院,山西太原030024;太原理工大学材料科学与工程学院,山西太原030024【正文语种】中文【中图分类】TG146.22镁合金是密度最小的结构金属材料,它不仅具有高的比刚度和比强度,而且有着优良的散热性能、电磁屏蔽性能和减震性能[1],因而其在航空航天业、汽车工业以及3C行业也得到了广泛的应用,被称为21世纪的“绿色”工程材料[2-4]。
AZ31镁合金是目前应用最广泛的变形镁合金[5],因而对AZ31镁合金板材的研究逐渐成为研究热点。

加工硬化指数n值加工硬化指数英文名即hardening index。
该指数由真应力应变关系定义,指金属薄板成形时真应力S一真应变ε关系式中的幂指数n,关系式如下:S = Kεn,式中K为强度系数。
亦即双对数坐标系lgS-lgε中,真应力-真应变关系式lgS=lgK+nlgε直线的斜率n是无量纲值,又称加工硬化指数。
(见真应力一真应变曲线)从数值上看,硬化指数n值等于(或近似等于)单向拉伸时材料最大均匀伸长应变的大小,即所谓细颈点应变。
也就是说,n表征了颈缩点位置。
应变分布不均是板材成形中的一个重要特点,n值的大小实际上反映了板材的应变均化能力,主要说明:(1)成形件的应变峰值不同。
n值小的材料产生的应变峰值高,n值大的材料产生的应变峰值低;(2)成形件上的应变分布不同。
n值小的材料应变分布不均匀,n值大的材料应变分布均匀。
硬化指数n值对板材成形极限曲线具有明显的影响,n值大材料的成形极限曲线高,n值小材料的成形极限曲线低。
板材的拉胀性能在很大程度上取决于材料的n值,n值高时,拉胀性能也好。
因此,硬化指数n值是评价板材成形性能的重要指标之一。
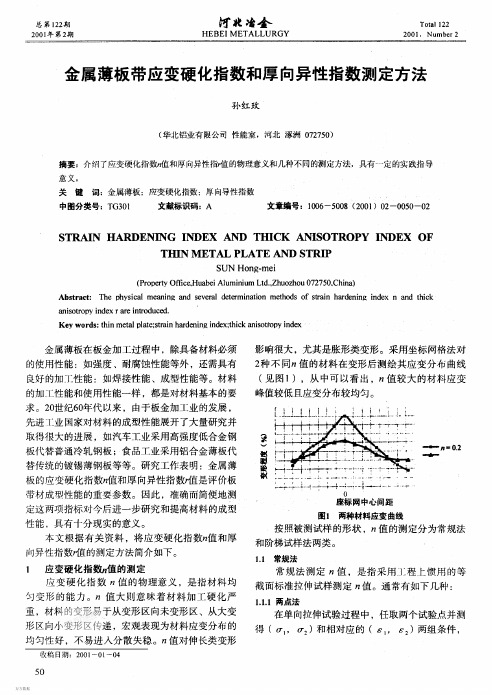
-可编辑修改-在双对数的坐标中真应力和真应变成线性关系,直线的斜率即为n,而K相当于ε=1.0时的真应力,见图1-5。
理想的弹性体和理想的塑性体限定了一般材料加工硬化指数n的变化范围,-可编辑修改-1.计算工程应力σ,工程应变ε。
2.计算真应力、真应变。
真应力=σ(1+ε)真应变=ln(1+ε)3.分别对真应力、真应变求Ln对数。
4.Ludwik-Hollomon方程式为:σ=K1+K2εn (σ、ε分别为真应力和真应变)公式变化可以得到:Lnσ= Ln K1+n Ln K2ε再把第3步求得的数据代进去进行Y=B+AX的拟合,斜率即为要求的n。
加工硬化和真应力-真应变曲线-可编辑修改-工程应力工程应变曲线的形状是不变的,并且对试样卸载和重新加载时,应力也没有区别(必须保证卸载和重新加载之间的时间足够短).然而,如果用真应力和真应变来绘制曲线的话就会有区别,例如真应变的定义是长度的增量除以标距瞬时长度,然而工程应变是长度的增量除以原始标距的长度.比较这两种绘制曲线的方法,会发现随着应变的增加,应力应变的数据会发生越来越显著的差.一会儿会给出一些例子.加工硬化率总是从真应力真应变数据中测量得到的.绝大多数应力应变曲线都遵循一个简单的能量表达式,称之为Holloman方程,如下:σt=Kεt n当n 为硬化比率或者硬化系数的时候,这个方程对中断的测试同样适用(但仅适用于立刻重新加载的测试,在室温下被延迟了几个小时后再加载就不适用了).由少量塑性应变,比如1%,引起的应力增加会很显著,在拉伸试验中可以测量出来,从而估计少量塑性应变后屈服强度的增加.对于给定应变,应力增量越大,冷加工屈服强度越大.这个有用的参数被称做加工硬化指数,可以通过绘制如下曲线得到:lnσ=ln K+n.lnε当塑性应变增加时,真应变和工程应变之间的差别也越来越大.一个可以选择的能精确测量 n 值的方法是在给定的应变处,测出真应力应变曲线的斜率:-可编辑修改-dσ/dε=n KεT n−1为了取代εn我们有:-dσ/dε=nσT/εT或者n=dσ/dε.εT/σT这里σT和εT是测量的 dσ/dε处的真应力和真应变.加工硬化指数n的实际意义-可编辑修改--可编辑修改-加工硬化指数n 反应了材料开始屈服以后,继续变形时材料的应变硬化情况,它决定了材料开始发生颈缩时的最大应力。

拉伸曲线及形变硬化指数在塑性加工中的应用与探讨引言在机械加工中,塑性加工是常见的一种加工方式,常常需要对金属材料进行塑性变形,从而达到所需的形状和尺寸。
然而,在塑性加工中,金属材料可能会在加工过程中发生形变硬化而导致加工难度增加,因此需要对形变过程加以研究和控制。
本文将就拉伸曲线及形变硬化指数在塑性加工中的应用进行探讨和讲解。
一、拉伸曲线的基本理论和意义拉伸曲线是描述材料在拉伸时所表现出的力与位移之间的关系,通常情况下它是一种先递增后递减的曲线。
在材料学中,拉伸曲线是非常重要的一个概念,它可以用来描述材料的拉伸特性和应力应变关系,在塑性加工中,它可以帮助掌握材料的变形规律,从而更好地控制加工质量。
在拉伸曲线中,有一些特征点是需要重点关注的,比如说屈服点、极限点、破断点等。
屈服点是材料开始发生塑性变形的点,通常用屈服强度来表示。
极限点是材料发生断裂的点,通常用抗拉强度来表示。
破断点是材料彻底断裂的点,通常用断面收缩率和断口形貌来描述。
这些特征点在材料的力学性能研究中都具有重要的意义。
二、形变硬化指数的含义和计算方法形变硬化指数是材料学中的一个比较重要的概念,它描述了材料随着塑性变形程度的增加而呈现出的硬化现象。
通常来说,形变硬化指数越大,说明材料的变形难度越大,材料的加工性能也越差。
形变硬化指数的计算方法通常有几种,其中比较常用的是Hill泰勒公式和Voce公式。
Hill泰勒公式表达式如下:$$ \frac{\Delta\sigma}{\sigma_0} = K\cdot\left(\frac{\varepsilon}{\varepsilon_0}\right)^n $$其中,$K$和$n$是材料的可靠性系数,$\sigma_0$是初始应力,$\varepsilon_0$是初始应变,$\Delta\sigma$是应力增量,$\varepsilon$是应变增量。
该公式适用于高应变区域。
Voce公式表达式如下:$$ \frac{\Delta\sigma}{\sigma_0} = C\cdot \left(1-e^{-m\cdot\varepsilon}\right) $$其中,$C$和$m$是Voce硬化系数,$e$是自然对数的底数,其他符号与Hill泰勒公式中的一致。


金属材料薄板和薄带拉伸应变硬化指数(n值)的测定1范围本文件规定了金属薄板和薄带拉伸应变硬化指数(n值)的测定方法。
本方法仅适用于塑性变形范围内应力-应变曲线呈单调连续上升的部分(见8.4)。
如果材料在加工硬化阶段的应力-应变曲线呈锯齿状(如某些AlMg合金呈现出的Portevin-Le Chatelier锯齿屈服效应),为使所给出的结果具有一定的重复性,应采用自动测量方法(对真实应力-真实塑性应变的对数进行线性回归,见8.7)。
2规范性引用文件下列文件中的内容通过文中的规范性引用而构成本文件必不可少的条款。
其中,注日期的引用文件,仅该日期对应的版本适用于本文件;不注日期的引用文件,其最新版本(包括所有的修改单)适用于本文件。
GB/T228.1金属材料室温拉伸试验方法(GB/T228.1—2021,ISO6892-1:2019,MOD)GB/T16825.1静力单轴试验机的检验第一部分:拉力和(或)压力试验机测力系统的检验与校准(GB/T16825.1—2022,ISO7500-1:2018,IDT)GB/T12160 GB/T5027GB/T8170单轴试验用引伸计的标定(GB/T12160—2019,ISO9513:2012,IDT)金属材料薄板和薄带塑性应变比(r值)的测定(GB/T5027—2024,ISO10113:2020,MOD)数值修约规则与极限数值的表示和判定3术语和定义本文件未列出术语和定义。
4符号和说明4.1本文件使用的符号及说明见表1。
1表1符号和说明符号说明单位L e引伸计标距mm ΔL引伸计标距部分的瞬时延伸mm L引伸计标距部分的瞬时长度L=L e+ΔL mme p测定拉伸应变硬化指数的约定(工程)塑性应变水平(用于单应变量测算方法)%e pα-e pβ测定拉伸应变硬化指数的约定(工程)塑性应变范围(线性回归方式,e pα:塑性应变下%限,e pβ:塑性应变上限)S o试样平行长度部分的原始横截面积mm2 S真实横截面积mm2 F施加于试样上的瞬时力N R应力MPa σ真实应力MPa εp真实塑性应变-m E应力-应变曲线弹性部分的斜率MPa n拉伸应变硬化指数-C强度系数MPa N测定拉伸应变硬化指数时的测量点数目-r塑性应变比-R m抗拉强度MPaA e屈服点延伸率%A g最大力塑性延伸率% A,B,x,y采用人工方式测定n值的几个变量注:1MPa=1N/mm2。
金属材料的硬度测试一、实验目的123二、实验原理金属材料的硬度可以认为是金属材料表面局部区域在接触应力作用下抵抗塑性变形或破裂度值可以综合反映压痕附近局部体积内金属的弹性、微量塑变抗力、塑变强化能力以及大量材料产生塑性变形就越困难。
硬度测量能够定量地给出金属材料软硬程度的相对数量概念。
1、2、实验3、金属的硬度与强бb=K*HB式中:бb —K—HB—布氏硬度。
表一系数K取值表材料及状态退火碳钢合金调质钢有色金属合金K 0.34~0.36 0.33~0.35 0 .33~0.53 4、5、加工质量。
(一)布氏硬度实验是对试样施加一定大小的载荷P D如图1FHB表示。
计算公式如下HB=P/F凹HB—P—N F凹—mm2。
根据压痕面积和球面之比等于压痕深度h和钢球直径DF凹=πDhD—mm h—mm。
由于测量压痕直径d要比测定压痕深度h h的改换成dd直接查表得到HB值。
HBS450HBW450~650的金属材料。
,所测工件有厚有薄,,,而对,会发生整个压头陷入试样中或将试样压透的现象。
所以,P和不同的直径D的钢球。
D和P以保证所得到的压痕形状的几何相似关系。
经数学推导可知,P/D2=常数,得到的HB值就是一样的,P和压头直径D所得到的HB可以进行相互比较。
国标GB231-88对此进行了规定,试验规范。
表一布氏硬度试验规范试样厚度不应小于压痕深度的10倍。
压痕中心距试样边缘的距离不应小于压痕直径的2.5,而距相邻压痕中心距离不小于压痕直径的4倍。
2%。
实验后压痕直径大小应在0.25D d0.6D(二)洛氏硬度试验常用的压头为圆锥角1200、顶部曲率半径0.2MM的金刚石锥体或直径D=1.588mm的淬火钢球。
试验时先对试样施加初试验力F0h0F1h1。
金属在F1作用下产生的总变形h1F1作用下的残余压痕深度h痕深度h表示成e0.002e则表明硬度越高。
为了k减去e以符号HRHR=k—ek定为100k定位130。