初三数学反函数练习

反函数练习一、选择题1．定义在R 上的函数y=f(x)有反函数，下列命题中假命题为（ ）A ．y=f(x)与)(1y f x -=的图象不一定关于y=x 对称B ．)(1x f y -=与)(1x f y --=的图象关于x 轴对称 C ．y=f(x)与)(1x f y -=的图象不可能有交点 D ．y=f(x)与)(1x f y -=的图象可能有交点，有时交点个数有无穷多个2．下列说法中正确的是（ ）①一函数图象上的任意两点的连线都不平行于x 轴，则此函数在定义域上一定是单调的 ②图象关于直线y=x 对称的函数一定有反函数，且其反函数是它自己③一函数是奇函数，且有反函数，则它的反函数也是奇函数④定义域是一个闭区间并且图象连续的函数，一定有最大值与最小值。

A ．②③④B ．②④C ．③④D ．①②③④二、填空题3．如果点（1，2）既在函数b ax x f +=)(的图象上，又在函数f(x)的反函数)(1x f -的图象上，那么a=__________b=__________。

4．函数196)(--+==x x x f y 的反函数为___________。

三、解答题5．已知实数a ≠0 ，a ≠1，函数)1,(11a x R x ax x y ≠∈--=且。

求证：函数)1,(11a x R x ax x y ≠∈--=且的图象关于直线y=x 成轴对称图形。

6．已知函数)2(12-≤-=x x y ，求)4(1-f 。

7．已知x x x f 32)3(+=，求)3(x f -。

8．已知x x x f 324)(++=，求)]([1x f f -及)]([1x f f -的解析式，并判定它们是否为同一函数。

9．已知y=f(x)的定义域为]0,(-∞，且x x x f 2)1(2+=+，求)2(1-f 。

10．设y=f(x)是单调递增函数，求证)(1x f y -=也是单调递增函数。

11．函数⎩⎨⎧-∞∈-+∞∈-=]0,( 1],0[ 22x x x x y 是否存在反函数，若存在，请求出来；若不存在，请说明理由。

反函数基础练习(一)选择题1．函数y ＝－x 2(x ≤0)的反函数是[ ]A y (x 0)B y (x 0)C y (x 0)D y |x|．＝－≥．＝≤．＝－≤．＝－x x x --2．函数y ＝－x(2＋x)(x ≥0)的反函数的定义域是 [ ]A ．[0，＋∞)B ．[－∞，1]C ．(0，1]D ．(－∞，0]3y 1(x 2)．函数＝＋≥的反函数是x -2[ ]A ．y ＝2－(x －1)2(x ≥2)B ．y ＝2＋(x －1)2(x ≥2)C ．y ＝2－(x －1)2(x ≥1)D ．y ＝2＋(x －1)2(x ≥1)4．下列各组函数中互为反函数的是[ ]A y y xB y y 2．＝和＝．＝和＝x x x11C y y (x 1)D y x (x 1)y (x 0)2．＝和＝≠．＝≥和＝≥3131311x x x x x +-+-5．如果y ＝f(x)的反函数是y ＝f -1(x)，则下列命题中一定正确的是[ ]A ．若y ＝f(x)在[1，2]上是增函数，则y ＝f -1(x)在[1，2]上也是增函数B．若y＝f(x)是奇函数，则y＝f-1(x)也是奇函数C．若y＝f(x)是偶函数，则y＝f-1(x)也是偶函数D．若f(x)的图像与y轴有交点，则f-1(x)的图像与y轴也有交点6．如果两个函数的图像关于直线y＝x对称，而其中一个函数是x 1y＝－，那么另一个函数是[ ] A．y＝x2＋1(x≤0)B．y＝x2＋1(x≥1)C．y＝x2－1(x≤0)D．y＝x2－1(x≥1)7．设点(a，b)在函数y＝f(x)的图像上，那么y＝f-1(x)的图像上一定有点[ ] A．(a，f-1(a))B．(f-1(b)，b)C．(f-1(a)，a) D．(b，f-1(b))8．设函数y＝f(x)的反函数是y＝g(x)，则函数y＝f(－x)的反函数是[ ] A．y＝g(－x) B．y＝－g(x)C．y＝－g(－x) D．y＝－g-1(x)9．若f(x－1)＝x2－2x＋3(x≤1)，则函数f-1(x)的草图是[ ]10y g(x)．函数＝的反函数是，则13x[ ]A ．g(2)＞g(－1)＞g(－3)B ．g(2)＞g(－3)＞g(－1)C ．g(－1)＞g(－3)＞g(2)D ．g(－3)＞g(－1)＞g(2) (二)填空题1y 32y (x 0)y f(x)y x ．函数＝＋的反函数是．．函数＝＞与函数＝的图像关于直线＝对称，x x ++2121 解f(x)＝________．3．如果一次函数y ＝ax ＋3与y ＝4x －b 的图像关于直线y ＝x 对称，那a ＝________，b ＝________．4y (1x 0)．函数＝－＜＜的反函数是，反函数的定92-x义域是________．5．已知函数y ＝f(x)存在反函数，a 是它的定义域内的任意一个值，则f -1(f(a))＝________．6y 7y (x 1)(x 1)8f(x)(x 1)f ()1．函数＝的反函数的值域是．．函数＝≥－＜的反函数是：．．函数＝＜－，则－＝．121121232x x x x ---⎧⎨⎪⎩⎪-- (三)解答题1y 12f(x)．求函数＝＋的反函数，并作出反函数的图像．．已知函数＝．x ax x +++252(1)求函数y ＝f(x)的反函数y ＝f -1(x)的值域；(2)若点P(1，2)是y ＝f -1(x)的图像上一点，求函数y ＝f(x)的值域．3．已知函数y ＝f(x)在其定义域内是增函数，且存在反函数，求证y ＝f(x)的反函数y ＝f -1(x)在它的定义域内也是增函数．4f(x)y g(x)y f (x 1)．设函数＝，函数＝的图像是＝＋的图像2311x x +-- 关于y ＝x 对称，求g(2)的值．参考答案(一)选择题1．(C)．解：函数y=－x 2(x ≤0)的值域是y ≤0，由y=－x 2得x=－－，∴反函数－－≤．y x f (x)=(x 0)1-2．(D)．解：∵y=－x 2－2x=－(x ＋1)2，x ≥0，∴函数值域y ≤0，即其反函数的定义域为x ≤0．3(D)y =x 21x 2y 1y =x 2．．解：∵－＋，≥，∴函数值域≥，由－＋1，得反函数f －1(x)=(x －1)2＋1，(x ≥1)．4．(B)．解：(A)错．∵y=x 2没有反函数．(B)中如两个函数互为反函数．中函数＋－≠的反函数是＋－≠而不是＋－．中函数≥的值域为≥．应是其反函数的定义域≥．但中的定义域≥，故中两函数不是互为反函数．(C)y =3x 1x (x 1)y =x 1x 3(x 3)y =3x 13x 1(D)y =x (x 1)y 1x 1y =x x 0(D)21 5．(B)．解：(A)中．∵y=f(x)在[1，2]上是增函数．∴其反函数y=f -1(x)在[f(1)，f(2)]上是增函数，∴(A)错．(B)对．(C)中如y=f(x)=x 2是偶函数但没有反函数．∴(C)错．(D)中如函数f(x)=x 2＋1(x ≥0)的图像与y 轴有交点，但其反函数－≥的图像与轴没有交点．∴错．f -(x)=x 1(x 1)y (D)1 6(A)y =y 0f (x)=x 12．．解：∵函数－－的值域≤；其反函数＋x 1-＋1(x ≤0)．选(A)．7．(D)．解：∵点(a ，b)在函数y=f(x)的图像上，∴点(b ，a)必在其反函数y=f -1(x)的图像上，而a=f -1(b)，故点(b ，f －1(b))在y=f -1(x)的图像上．选(D)．8．(B)．解：∵y=f(x)的反函数是y=f -1(x)即g(x)=f -1(x)，而y=f(－x)的反函数是y=－f -1(x)=－g(x)，∴选(B)．9．(C)．解：令t=x －1．∵x ≤1，∴t ≤0，f(t)=t 2＋2(t ≤0)，即f(x)=x 2＋2(x ≤0)，值域为f(x)≥2，∴反函数f -1(x)的定义域是x ≥2，值域y ≤0，故选(C)．10(B)g(x)=1x (0)33．．解：∵在－∞，上是减函数，又－＜－＜1 00g(3)g(1)g(2)=120g(2)g(3)g(1)3，∴＞－＞－而＞，∴＞－＞－．故选 (B)．(二)填空题1y =3y 3y =x 6x 2．解：∵函数＋＋的值域≥，其反函数－＋x 27(x ≥3)2y =12x 1(x 0)y 1f(x)=1x2x(x 1)．解：＋＞的值域＜，其反函数－＜． 3y =4x b y =14x x =ax ．解：函数－的反函数是＋，则＋＋，b b41443 比较两边对应项系数得，．a =14b =12 4y =9x (1x 0)y (223)2．解：函数－－＜＜的值域∈，，反函数f -1 (x)=(223)－－．反函数的定义为，．92x5．a6．[0，2)∪(2，＋∞)7f (x)=x 1(x 1)1x (x 0)122．＋≥－＜-⎧⎨⎪⎩⎪8．－2(三)解答题1x 2y 1y =x 21=．解：∵≥－，得值域为≥．由＋＋得反函数f x -1()(x －1)2－2，(x ≥1)，其图像如右图．2．解(1)：∵y=f(x)的定义域是{x|x ≠1，x ∈R ，∴y=f -1(x)的值域是{y|y ≠1，y ∈R}．解(2)：∵点P(1，2)在，y=f -1(x)的图像上，点P(1，2)关于直线y=x的对称点为′，一定在的图像上，即由＋＋得－，∴－＋，其反函数－＋．∵的定义域为≠－，∈，∴的值域为≠－，∈．P (21)y =f(x)=1a =f(x)=10x 2x 4f -(x)=104x 2x 1f -(x){x|x x R}y =f(x){y|y y R}112522121212a3．证明略．4f(x)=2x 3x 1f -(x)=x 3f (x 1)=11．略解；＋－的反函数是＋－，∴＋x 2x 4x 1x 4x 1=2x =6g(2)=6＋－，由＋－得即．（注：可编辑下载，若有不当之处，请指正，谢谢!）。

反函数练习题一、 选择题1、 已知函数)1(156≠∈-+=x R x x x y 且，那么它的反函数为( ) A 、()1156≠∈-+=x R x x x y 且 B 、()665≠∈-+=x R x x x y 且 C 、⎪⎭⎫ ⎝⎛-≠∈+-=65561x R x x x y 且 D 、()556-≠∈+-=x R x x x y 且 2、 函数⎪⎩⎪⎨⎧≥-=)0(21)0(2x x x x y 的反函数是( ) A 、()⎩⎨⎧≤-=0)0(2 x x x x y B 、()⎩⎨⎧-≤-=0)0(2 x x x x y C 、()()⎪⎩⎪⎨⎧≤-=0021 x x x x y D 、()()⎪⎩⎪⎨⎧-≤-=0021 x x x x y 3、 已知点(a,b)在y=f(x)的图像上，则下列各点中位于其反函数图像上的点是（ ）A 、))(,(1a f a -B 、()()b b f ,1-C 、()()a a f ,1-D 、()()b f b 1,-4、 若函数)1(1)(2-≤-=x x x f ，则)4(1-f 的值为（ ）A 、5B 、5-C 、15D 、3二、 填空题5、 函数f(x)2916x -=是否有反函数？ ；当⎥⎦⎤⎢⎣⎡∈34,0x 时，反函数为 ，定义域为 ；当⎥⎦⎤⎢⎣⎡-∈0,34x 时，反函数为 ，定义域为 。

6、 设f(x)的反函数为)(1x f -，23)(1+=-x x f ，则=-)3(1f ，f(3)=7、 若点(1,2)既在函数b ax x f +=)(的图象上，又在函数f(x)的反函数)(1x f -的图象上，则a= ,b=8、 f(x)在()+∞,0上为递增函数，则)1(1-f 与)3(1-f 的大小关系是三、 解答题9、 函数y=f(x)的图象是过点(2,1)的直线，其反函数的图象经过点(-2,-1)，求函数f(x)10、函数)(c x R x c x b ax y -≠∈++=且的反函数为213+-=x x y ，求a,b,c 的值 11、已知132)(1≥-=-x x x f ，，求f(x)12、函数f(x)=x 2-2tx+1(t ∈R)，定义域为[][]8,71,0 ∈x ，（1）f(x)在定义域内是否一定有反函数？（2）若f(x)有反函数，求t 的范围。

反函数练习题反函数是数学中的一个重要概念，它与函数之间的关系密切相关。

在本文中，我们将通过一些练习题来加深对反函数的理解和运用。

题目一：求反函数已知函数f(x) = 2x - 3，求其反函数f^{-1}(x)。

解析：为求反函数f^{-1}(x)，我们先将f(x)写成关于x的等式y = 2x - 3。

接下来，我们将x和y交换位置，得到x = 2y - 3。

接下来，解出y，即可得到反函数f^{-1}(x)。

将x = 2y - 3两边加3，得到x + 3 = 2y。

再将等式两边同时除以2，得到(y = (x + 3)/2)。

所以，反函数f^{-1}(x) = (x + 3)/2。

题目二：验证反函数已知函数f(x) = 4x - 5，求其反函数f^{-1}(x)并验证是否为反函数。

解析：首先，我们仍然将f(x)写成关于x的等式y = 4x - 5。

然后，将x和y交换位置，得到x = 4y - 5。

再次解出y，即可得到反函数f^{-1}(x)。

将x = 4y - 5两边加5，得到x + 5 = 4y。

再将等式两边同时除以4，得到((x + 5)/4 = y)。

所以，反函数f^{-1}(x) = (x + 5)/4。

为了验证f^{-1}(x)是否为f(x)的反函数，我们需要计算复合函数f(f^{-1}(x))和f^{-1}(f(x))，并判断它们是否等于x。

首先，计算f(f^{-1}(x)) = f((x + 5)/4)。

将(x + 5)/4代入f(x)的表达式中，得到f(f^{-1}(x)) = 4((x + 5)/4) - 5 = x - 1。

我们可以看到，f(f^{-1}(x))得到了x。

接下来，计算f^{-1}(f(x)) = f^{-1}(4x - 5)。

将4x - 5代入f^{-1}(x)的表达式中，得到f^{-1}(f(x)) = ((4x - 5) + 5)/4 = x。

我们可以看到，f^{-1}(f(x))也得到了x。

初三数学下册反函数练习题反函数是数学中一个重要的概念，在初三数学下册中也有一些关于反函数的练习题。

下面将通过一些例题，帮助大家更好地理解和掌握相关知识。

1.已知函数f(x) = 2x + 3，求其反函数f^{-1}(x)。

解答：首先，我们将f(x)表示为y = 2x + 3。

然后，交换x和y的位置，得到x = 2y + 3。

接下来，将此方程关于y解出，得到y = \frac{{x -3}}{2}。

最后，将y替换为f^{-1}(x)，得到反函数f^{-1}(x) = \frac{{x - 3}}{2}。

2.已知函数g(x) = \sqrt{x}，求其反函数g^{-1}(x)。

解答：类似地，我们将g(x)表示为y = \sqrt{x}，然后将x和y的位置交换，得到x = \sqrt{y}。

为了解出y，我们两边平方，得到x^2 = y。

最后，将y替换为g^{-1}(x)，得到反函数g^{-1}(x) = x^2。

3.已知函数h(x) = \frac{1}{x + 2}，求其反函数h^{-1}(x)。

解答：将h(x)表示为y = \frac{1}{x + 2}，交换x和y的位置，得到x =\frac{1}{y + 2}。

我们可以通过一系列的步骤将y解出来。

首先，将x的分母移至等号右侧，得到xy + 2x = 1。

然后，将y的系数提取出来，得到xy = 1 - 2x。

最后，将y替换为h^{-1}(x)，得到反函数h^{-1}(x) = \frac{1 - 2x}{x}。

通过上面几个例题，我们可以看到，求一个函数的反函数主要是通过将函数的自变量和因变量进行交换，并解出关于自变量的方程来得到反函数的表达式。

反函数在数学中有着广泛的应用。

它可以用于解决方程、求解逆运算以及构建函数的复合和函数图像的翻转等问题。

因此，掌握反函数的概念和求解方法对于学习数学和解题都是非常重要的。

当然，反函数也有着一些限制条件。

在求反函数时，要确保原函数是一一对应的，并且反函数在定义域和值域上是有定义的。

反函数经典例题t 反函数是指： f(x)=ax(y)-yf(x)dx，而实际上它可表示为：f(x)=(a-x)f(y)，这样的函数就叫做反函数。

１．，这种函数图象称为y轴上的反函数。

2．若反函数y=f(x)，则该函数称为原函数的反函数。

3．， f'(y)=(y-1)f(x)，称为x轴上的反函数。

4．若反函数y=f'(x)，则该函数称为原函数的反函数。

5．函数是有两个自变量的，则称该函数为二次函数。

6．函数是有两个未知量的，则称该函数为三次函数。

7．函数是有三个自变量的，则称该函数为三次函数。

8．含有两个未知量和一个常数的二次函数图象的顶点为原点，若顶点在坐标轴上，则称为顶点在坐标轴上的函数。

9．若函数y=f(x)与x轴交于两点a、 b，则该函数图象关于直线y=x=a+b对称，记作： y=a+bx。

10．函数的图象关于坐标轴对称，记作： y=ax(a+bx)-bx，其中a、 b为常数。

可见，反函数其实并不神秘，只是我们平时没有去注意它，只要我们能多加练习，熟悉他，我相信，任何一个函数我们都可以把它变成一个反函数。

以下是两道经典的反函数例题：下面我们继续利用反函数解决函数问题。

1．f(x) = x。

2． f(x) = -(-3)^x + 2。

3．当x=-1时， f(x)的值为2， f(0)的值为-3。

4．，当f(0)等于0时， f(x) = -5，当f(0)不等于0时， f(x)等于5。

以上两道例题都给出了利用f(x)=a(y)dx求函数解析式。

为什么前一道题f(x)=0，而后一道题f(x)=-5，是不是f(x)=-5比f(x)=0小呢？答案是否定的，因为： a是正整数，即使它是0，但它还是个整数，而f(x)是-3的反函数，而-3是一个负整数，它等于-5，也就是说，当a是正整数时， f(x)将比f(x)小，而当a是负整数时， f(x)比f(x)大。

《中国著名数学家的学习故事》中有一篇文章《如何获得成功》，主人公海伦·凯勒曾说过：“我们不得不惊奇地发现，我们已经很久没有以严肃的态度开始新的一天了。

提能拔高限时训练7 反函数一、选择题1.若y ＝f(x)有反函数,则方程f(x)＝a(a 为常数)的实根的个数为( )A.无实数根B.只有一个实数根C.至多有一个实数根D.至少有一个实数根解析:y ＝f(x)存在反函数,则x 与y 是“一对一”的.但a 可能不在值域内,因此至多有一个实根. 答案:C2.设函数y ＝f(x)的反函数y ＝f -1(x),若f(x)＝2x ,则f -1(21)的值为( ) A.2 B.1 C.21 D.-1 解析:令f(x)＝2x ＝21,则x ＝-1,故f -1(21)＝-1,故选D. 答案:D3.若函数y ＝f(x-1)的图象与函数1ln +=x y 的图象关于直线y ＝x 对称,则f(x)等于…( )A.e 2x-1B.e 2xC.e 2x+1D.e 2x+2 解析:由函数y ＝f(x-1)的图象与函数1ln+=x y 的图象关于直线y ＝x 对称,可知y ＝f(x-1)与1ln +=x y 互为反函数,有1ln +=x y ⇒1ln -=y x ⇒1-=y e x ⇒x ＝e 2y-2,所以y ＝e 2x-2⇒y ＝f(x-1)＝e 2x-2.故f(x)＝e 2x .答案:B4.已知函数f(x)＝2x+3,f -1(x)是f(x)的反函数,若mn ＝16(m,n ∈R +),则f -1(m)+f -1(n)的值为( )A.-2B.1C.4D.10 解析:设y ＝2x+3,则有x+3＝log 2y,可得f -1(x)＝log 2x-3.于是f -1(m)+f -1(n)＝log 2m+log 2n-6＝log 2mn-6＝-2.答案:A5.设函数x x f -=11)((0≤x ＜1)的反函数为f -1(x),则( )A.f -1(x)在其定义域上是增函数且最大值为1B.f -1(x)在其定义域上是减函数且最小值为0C.f -1(x)在其定义域上是减函数且最大值为1D.f -1(x)在其定义域上是增函数且最小值为0解析:由x x f -=11)((0≤x ＜1),得该函数是增函数,且值域是［1,+∞),因此其反函数f -1(x)在其定义域上是增函数,且最小值是0.答案:D6.函数⎩⎨⎧<-≥=0,,0,22x x x x y 的反函数是( )A.⎪⎩⎪⎨⎧<-≥=0,0,2x x x x y B.⎩⎨⎧<-≥=0,0,2x x x x y C.⎪⎩⎪⎨⎧<--≥=0,0,2x x x x y D.⎩⎨⎧<--≥=0,0,2x x x x y解析:当x ≥0时,y ＝2x,且y ≥0, ∴2)(1x x f =-(x ≥0). 当x ＜0时,y ＝-x 2且y ＜0, ∴x x f --=-)(1(x ＜0).∴函数⎩⎨⎧<-≥=0,,0,22x x x x y 的反函数是⎪⎩⎪⎨⎧<--≥=.0,,0,2x x x x y 答案:C7.(2009北京东城期末检测,7)已知函数24)(x x f --=在区间M 上的反函数是其本身,则M 可以是( )A.［-2,-1］B.［-2,0］C.［0,2］D.［-1,0］ 解析:画出函数24)(x x f --=; 由24x y --=得y 2＝4-x 2且y ≤0,即x 2+y 2＝4,y ≤0,所以图象是以(0,0)为圆心,以2为半径的圆在x 轴下方的部分(包括点(±2,0));又y ＝f(x)在区间M 上反函数是其本身,故y ＝f(x)图象自身关于y ＝x 对称,故区间M 可以是［-2,0］.答案:B8.设0＜a ＜1,函数)2(log log )(1x x x f aa -+=,则函数f -1(x)＜1的x 的取值范围是( )A.(0,2)B.(2,+∞)C.(0,+∞)D.(log a (2-a),+∞) 解析:f(x)在(0,2)上是减函数,所以x ＞f(1)＝0.故选C.答案:C9.设函数为y ＝f(x)的反函数为y ＝f -1(x),将y ＝f(2x-3)的图象向左平移2个单位,再作关于x 轴的对称图形所对应的函数的反函数是( ) A.21)(1--=-x f y B.2)(11x f y --=- C.2)(1x f y -= D.21)(-=x f y解析:由题意知,最后得到的图形对应的函数可以表示为y ＝-f ［2(x+2)-3］＝-f(2x+1),即-y ＝f(2x+1),2x+1＝f -1(-y),21)(1--=-y f x ,故所求函数的反函数是21)(1--=-x f y . 答案:A 10.已知函数⎪⎩⎪⎨⎧>-+≤-=,1,13,1,12)(x x x x x x f 若函数y ＝g(x)的图象与函数y ＝f -1(x-1)的图象关于直线y ＝x 对称,则g(11)的值是( ) A.512 B.913 C.513 D.1115 解析:∵函数y ＝g(x)的图象与函数y ＝f -1(x-1)的图象关于直线y ＝x 对称,∴函数y ＝g(x)与函数y ＝f -1(x-1)互为反函数.由g(11)得f -1(x-1)＝11,∴x-1＝f(11),即x ＝f(11)+1.∵57)11(=f ,∴512)11(=g . 答案:A二、填空题11.设f(x)＝x 5-5x 4+10x 3-10x 2+5x+1,则f(x)的反函数为f -1(x)＝_____________.解析:∵f(x)＝(x-1)5+2, ∴12)(51+-=-x x f .答案:125+-x12.若函数)54(541≠++=a x ax y 的图象关于直线y ＝x 对称,则a ＝_________. 解析:∵54≠a , ∴541++=x ax y 不是常函数,且存在反函数. 在f(x)的图象上取一点(0,51),它关于y ＝x 的对称点(51,0)也在函数f(x)的图象上,可解得a ＝-5.答案:-513.已知函数f(x)的定义域为［-1,1］,值域为［-3,3］,其反函数为f -1(x),则f -1(3x-2)的定义域为___________,值域为____________.解析:由于函数f(x)的定义域为［-1,1］,值域为［-3,3］,所以其反函数f -1(x)的定义域为［-3,3］,值域为［-1,1］.所以由-3≤3x-2≤3,解得31-≤x ≤35.故函数f -1(3x-2)的定义域为［31-,35］,值域为［-1,1］.答案:［31-,35］ ［-1,1］ 14.(2009河南南阳期末质检,14)定义在R 上的函数y ＝f(x)有反函数,则函数y ＝f(x+1)+2与y ＝f -1(x+1)+2的图象关于直线__________对称.解析:函数y ＝f(x)沿向量(-1,2)平移得到函数y ＝f(x+1)+2,函数y ＝f -1(x)沿向量(-1,2)平移得到函数y ＝f -1(x+1)+2,又y ＝f(x)与y ＝f -1(x)关于y ＝x 对称,y ＝x 沿向量(-1,2)平移得到y ＝x+3,∴y ＝f(x+1)+2与y ＝f -1(x+1)+2关于y ＝x+3对称.答案:y ＝x+3三、解答题15.已知函数11)(-+=x x x f ,g(x)＝f -1(-x),求g(x). 解: 由11-+=x x y ,得xy-y ＝x+1, ∴11-+=y y x ,即11)(1-+=-x x x f . ∴g(x)＝f -1(-x)＝11+-x x . 16.已知函数f(x)＝2(1121+-x a )(a ＞0且a≠1). (1)求函数y ＝f(x)的反函数y ＝f -1(x);(2)判定f -1(x)的奇偶性；(3)解不等式f -1(x)＞1.解:(1)化简，得11)(+-=x x a a x f . 设11+-=x x a a y ,则y y a x -+=11. ∴yy x a -+=11log . ∴所求反函数为xx x f y a-+==-11log )(1(-1＜x ＜1). (2)∵)(11log )11(log 11log )(111x f x x x x x x x f a a a ----=-+-=-+=+-=-, ∴f -1(x)是奇函数. (3)111log >-+xx a . 当a ＞1时， 原不等式⇒a x x >-+11⇒011)1(<--++x a x a . ∴11+-a a ＜x ＜1.当0＜a ＜1时，原不等式⇒⎪⎪⎩⎪⎪⎨⎧>-+<-+,011,11xx a x x 解得⎪⎩⎪⎨⎧<<->+-<.11,111x x a a x 或 ∴-1＜x ＜aa +-11. 综上，当a ＞1时，所求不等式的解集为(11+-a a ,1); 当0＜a ＜1时，所求不等式的解集为(-1，11+-a a ). 教学参考例题 志鸿优化系列丛书【例1】 设函数⎪⎩⎪⎨⎧<-=>=,0,1,0,0,0,1)(x x x x f 若g(x)＝(x-1)2f(x-1),y ＝g(x)的反函数为y ＝g -1(x),则g(-1)·g -1(-4)＝___________.解析:由题意得⎪⎩⎪⎨⎧<-=>=-.1,1,1,0,1,1)1(x x x x f∴g(x)＝(x-1)2f(x-1)＝⎪⎩⎪⎨⎧<--=>-.1,)1(,1,0,1,)1(22x x x x x设g(x)＝-4,可得-(x-1)2＝-4且x ＜1,解得x ＝-1.∴g(-1)＝-4.∴g -1(-4)＝-1.∴g(-1)·g -1(-4)＝-4×(-1)＝4.答案:4【例2】 已知f(x)是定义在R 上的函数,它的反函数为f -1(x).若f -1(x+a)与f(x+a)互为反函数且f(a)＝a(a 为非零常数),则f(2a)＝____________.解析:设y ＝f -1(x+a),则x ＝f(y)-a,即y ＝f -1(x+a)的反函数为y ＝f(x)-a,∴f(x+a)＝f(x)-a. 令x ＝a,得f(2a)＝f(a)-a ＝a-a ＝0.答案:0。

初三数学上册综合算式专项练习题求函数的反函数函数的反函数是指将原函数的输出作为输入时，能够得到原函数的输入值。

在数学中，求函数的反函数是一项重要的技巧和方法，它可以帮助我们解决一些实际问题。

下面我们将通过综合算式专项练习题来探索如何求函数的反函数。

1. 题目一已知函数 f(x) = 2x + 5，求函数 f(x) 的反函数 f^(-1)(x)。

解析：设 f^(-1)(x) = y，根据反函数的定义，我们需要找到一个 y 值，使得f(y) = x。

将 f(x) = 2x + 5 代入等式，得到 2y + 5 = x。

将 x 移到等式左边，整理得到 2y = x - 5。

再将 y 从等式中解出，得到 y = (x - 5) / 2。

因此，函数 f(x) 的反函数为 f^(-1)(x) = (x - 5) / 2。

2. 题目二已知函数 g(x) = 3x^2，求函数 g(x) 的反函数 g^(-1)(x)。

解析：设 g^(-1)(x) = y，根据反函数的定义，我们需要找到一个 y 值，使得 g(y) = x。

将 g(x) = 3x^2 代入等式，得到 3y^2 = x。

将 x 移到等式左边，整理得到 y^2 = x / 3。

再将 y 从等式中解出，得到y = √(x / 3)。

因此，函数 g(x) 的反函数为 g^(-1)(x) = √(x / 3)。

3. 题目三已知函数 h(x) = (2x + 1) / (x - 3)，求函数 h(x) 的反函数 h^(-1)(x)。

解析：设 h^(-1)(x) = y，根据反函数的定义，我们需要找到一个 y 值，使得 h(y) = x。

将 h(x) = (2x + 1) / (x - 3) 代入等式，得到 (2y + 1) / (y - 3) = x。

将 x 移到等式左边，整理得到 (2y + 1) / (y - 3) - x = 0。

将分数形式转化为分子与分母相乘的形式，得到 (2y + 1) - x(y - 3) = 0。

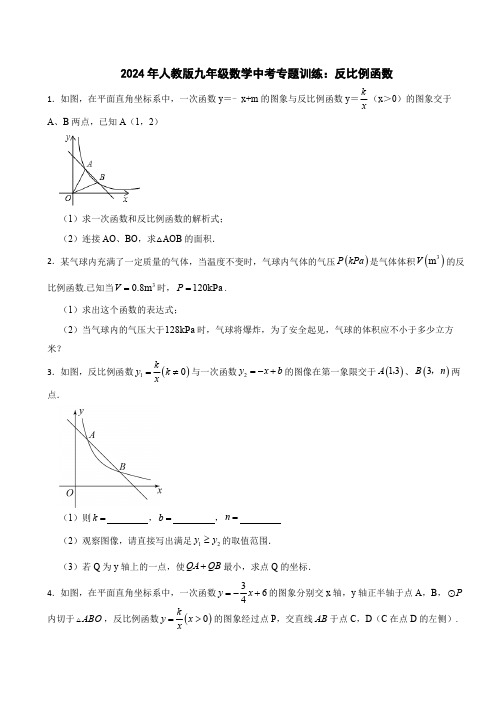
2024年人教版九年级数学中考专题训练：反比例函数1．如图，在平面直角坐标系中，一次函数y ＝﹣x+m 的图象与反比例函数y＝（x ＞0）的图象交于A 、B 两点，已知A （1，2）（1）求一次函数和反比例函数的解析式；（2）连接AO 、BO ，求△AOB 的面积．2．某气球内充满了一定质量的气体，当温度不变时，气球内气体的气压是气体体积的反比例函数.已知当时，.（1）求出这个函数的表达式；（2）当气球内的气压大于时，气球将爆炸，为了安全起见，气球的体积应不小于多少立方米？3．如图，反比例函数与一次函数的图像在第一象限交于、两点．（1）则 ，　　，　（2）观察图像，请直接写出满足的取值范围．（3）若Q 为y 轴上的一点，使最小，求点Q 的坐标．4．如图，在平面直角坐标系中，一次函数的图象分别交x 轴，y 轴正半轴于点A ，B ，内切于，反比例函数的图象经过点P ，交直线于点C ，D （C 在点D 的左侧）.kx()P kPa ()3mV 30.8m V =120kPa P =128kPa ()10ky k x=≠2y x b =-+()13A ，()3B n ，k =b =n =12y y ≥QA QB +364y x =-+P ABO ()0ky x x=>AB（1）求反比例函数的解析式；（2）过点C ，D 分别作x 轴，y 轴的平行线交于点E ，求的面积.5．如图1，点A （1，0），B （0，m ）都在直线y ＝﹣2x+b 上，四边形ABCD 为平行四边形，点D 在x轴上，AD=3，反比例函数（x>0）的图象经过点C ．（1）求k 的值；（2）将图1的线段CD 向右平移n 个单位长度（n≥0），得到对应线段EF ，线段EF 和反比例函数（x>0）的图象交于点M ．①在平移过程中，如图2，若点M 为EF 的中点，求△ACM 的面积；②在平移过程中，如图3，若AM ⊥EF ，求n 的值．6．如图，点A 是反比例函数图象上的点，AB 平行于y 轴，且交x 轴于点，点C 的坐标为，AC 交y 轴于点D ，连接BD ，（1）求反比例函数的表达式；（2）设点P 是反比例函数图象上一点，点Q 是直线AC 上一点，若以点O ，P ，D ，Q CDE ky x=ky x=()0ky k x=>()10B ，()10-，AD =()0ky x x=>为顶点的四边形是平行四边形，求点Q 的坐标； （3）若点是该反比例函数图象上的点，且满足∠MDB>∠BDC ，请直接写a 的取值范围.7．某种商品上市之初采用了大量的广告宣传，其销售量与上市的天数之间成正比，当广告停止后，销售量与上市的天数之间成反比（如图），现已知上市30天时，当日销售量为120万件．（1）写出该商品上市以后销售量y （万件）与时间x （天数）之间的表达式；（2）求上市至第100天（含第100天），日销售量在36万件以下（不含36万件）的天数；（3）广告合同约定，当销售量不低于100万件，并且持续天数不少于12天时，广告设计师就可以拿到“特殊贡献奖”，那么本次广告策划，设计师能否拿到“特殊贡献奖”？8．在学习反比例函数后，小华在同一个平面直角坐标系中画出了（x>0）和的图象，两个函数图象交于A （x 1，y 2），B （x 2，y 2）两点，在线段AB 上选取一点P ，过点P 作y 轴的平行线交反比例函数图象于点 O （如图1）.在点P 移动的过程中，发现PO 的长度随着点P 的运动而变化.为了进一步研究 PO 的长度与点P 的横坐标之间的关系，小华提出了下列问题∶（1）设点P 的横坐标为x ，PQ 的长度为y ，则y 与x 之间的函数关系式为 （x 1<x<x 2）；（2）为了进一步的研究（1）中的函数关系，决定运用列表，描点，连线的方法绘制函数的图象；①列表∶()M a b ，ky x=1y x=5y x =-+x 1234ym3n表中 m ＝ ，n ＝；②描点∶根据上表中的数据，在图2中描出各点；③连线∶请在图2中画出该函数的图象.观察函数图象，当x ＝时，y 的最大值为；（3）应用∶已知某矩形的一组邻边长分别为m ，n ，且该矩形的周长 W 与n 存在函数关系，求 m 取最大值时矩形的对角线长.9．如图，点P 为函数与函数图象的交点，点P 的纵坐标为4，轴，垂足为点B ．（1）求m 的值；（2）点M 是函数图象上一动点，过点M 作于点D ，若，求点M 的坐标．10．若关于x 的函数y ，当时，函数y 的最大值为M ，最小值为N ，令函数，我们不妨把函数h 称之为函数y 的“共同体函数”.（1）①若函数，当时，求函数y 的“共同体函数”h 的值；②若函数（，k ，b 为常数），求函数y 的“共同体函数”h 的解析式；（2）若函数，求函数y 的“共同体函数”h 的最大值；（3）若函数，是否存在实数k ，使得函数y 的最大值等于函数y 的“共同体函数”h 的最小值.若存在，求出k 的值；若不存在，请说明理由.11．已知一块矩形草坪的两边长分别是2米与3米，现在要把这个矩形按照如图1的方式扩大到面积为1x 13122x 535234220W n=-+1y x =+()0my x x=>PB x ⊥()0m y x x =>MD BP ⊥12tan PMD ∠=1122t x t -≤≤+2M Nh -=4044y x =1t =y kx b =+0k ≠21y x x=≥（）24y x x k =-++原来的2倍，设原矩形的一边加长a 米，另一边长加长b 米，可得a 与b 之间的函数关系式b＝﹣2．某班“数学兴趣小组”对此函数进一步推广，得到更一般的函数y ＝﹣2，现对这个函数的图象和性质进行了探究，研究过程如下，请补充完整：（1）类比反比例函数可知，函数y ＝﹣2的自变量x 的取值范围是 ，这个函数值y 的取值范围是　　．（2）“数学兴趣小组”进一步思考函数y ＝|﹣2|的图象和性质，请根据函数y ＝﹣2的图象，画出函数y ＝|﹣2|的图象；（3）结合函数y ＝|﹣2|的图象解答下列问题：①求出方程|﹣2|＝0的根；②如果方程|﹣2|＝a 有2个实数根，请直接写出a 的取值范围．12．如图，抛物线与x 轴交于两点（在的左边），与y 轴交于C ，；双曲线经过抛物线的顶点，点的横坐标为1．123a +123x +123x +123x +123x +123x +123x +123x +123x +23y ax bx =++A B 、A B 3tan CAB ∠=(0)ky k x=≠23y ax bx =++D D（1）求抛物线和双曲线的解析式．（2）点P 为抛物线上一动点，且在第一象限，连接，求当四边形取得最大值时，点P 的坐标，并求出这个最大值．（3）若在此抛物线和双曲线上存在点Q ，使得，请求出点Q 的坐标．13．如图，在平面直角坐标系中，一次函数的图象与反比例函数的图象相交于，两点．（1）分别求一次函数及反比例函数的表达式；（2）在第三象限内的B 点右侧的反比例函数图象上取一点P ，连接且满足．i ）求点P 的坐标；ii ）过点A 作直线，在直线l 上取一点Q ，且点Q 位于点A 的左侧，连接，试问：能否与相似？若能，求出此时点Q 的坐标；若不能，请说明理由．14．定义：函数图象上到两坐标轴的距离都不大于的点叫做这个函数图象的“n 阶方点”．例如，点是函数图像的“阶方点”；点是函数图像的“2阶方点”．（1）在①；②；③三点中，是反比例函数图像的“1阶方点”的有 （填序号）；（2）若y 关于x 的一次函数图像的“2阶方点”有且只有一个，求a 的值；（3）若y 关于x 的二次函数图像的“n 阶方点”一定存在，请直接写出n 的取值范围．15．如图1，已知反比例函数的图象与一次函数的图象相交于A （2，a ），B 两点.BP CP 、ABPC QB QC =xOy y kx b =+my x=(14)A ，(4)B n -，PA PB ，15PAB S = l PB BQ QAB ABP (0)n n ≥1133⎛⎫⎪⎝⎭，y x =12(21)，2y x =122⎛⎫-- ⎪⎝⎭，(11)--，(11)，1y x=31y ax a =-+2()21y x n n =---+(0)ky k x=≠1y x =-（1）求反比例函数的表达式及A ，B 两点的坐标；（2）M 是x 轴上一点，N 是y 轴上一点，若以A ，B ，M ，N 为顶点的四边形是以为边的平行四边形，求点M 的坐标；（3）如图2，反比例函数的图象上有P ，Q 两点，点P 的横坐标为，点Q 的横坐标与点P 的横坐标互为相反数，连接，，，.若的面积是的面积的3倍，求m 的值.16．如图，直线AC 与双曲线交于A （m ，6），B （3，n ）两点，与x 轴交于点C ，直线AD 与x 轴交于点D （－11，0），（1）请直接写出m ，n 的值；（2）若点E 在x 轴上，若点F 在y 轴上，求的最小值；（3）P 是直线AD 上一点，Q 是双曲线上一点，是否存在点P ，Q ，使得四边形ACQP 是正方形？若存在，求出点P ，Q 的坐标；若不存在，请说明理由．17．在平面直角坐标系中，将一点（横坐标与纵坐标不相等）横坐标与纵坐标互换后得到的点叫这一点的“H 点”，如（2，-3）与（-3，2）是一对“H 点”.（1）点 和它的“H 点”均在直线 上，求k 的值；AB ky x=(2)m m >AP AQ BP BQ ABQ ABP ()60y k x=≠AF EF BE ++()m n ，y kx a =+（2）若直线 经过的A ，B 两点恰好是一对“H 点”，其中点A 还在反比例函数 的图象上，一条抛物线 也经过A ，B 两点，求该抛物线的解析式；（3）已知 ，B 为抛物线 上的一对“H 点”，且满足：， ，点P 为抛物线上一动点，若该抛物线上有且仅存在3个点P 满足△PAB 的面积为16，求 的值.18．已知：如图，一次函数y ＝-2x+10的图象与反比例函数y＝的图象相交于A 、B 两点（A 在B 的右侧），点A 横坐标为4.（1）求反比例函数解析式及点B 的坐标；（2）观察图象，直接写出关于x 的不等式-2x+10-＞0的解集；（3）反比例函数图象的另一支上是否存在一点P ，使△PAB 是以AB 为直角边的直角三角形？若存在，求出所有符合条件的点P 的坐标；若不存在，请说明理由.19．如图，反比例函数与一次函数相交于点A （1，4）和点B （4，1），直线 的图象与y 轴和x 轴分别相交于点C 和点D ；（1）请直接写出当时自变量x 的取值范围；（2）将一次函数向下平移8个单位长度得到直线EF ，直线EF 与x 和y 轴分别交于点E 和点F ，抛物线过点A 、D 、E 三点，求该抛物线的函数解析式（也称函数表达式）；3y kx =+2y x=2y x bx c =++()()A m n m n <，()20y ax bx c a =++≠2m n +=3mn =-a b c ++kxkx()110k y x x=>22y k x n =+2y 12y y ≥22y k x n =+2y ax bx c =++（3）在（2）抛物线的对称轴上是否存在一点P ，使得△PBF 是以BF 为斜边的直角三角形，若存在，请用尺规作图（圆规和无刻度直尺）画出点P 所在位置，保留作图痕迹，并直接写出点P 的坐标；若不存在，请说明理由．20．如图1，平面直角坐标系中，，反比例函数的图象分别交矩形的两边、于E 、F （E 、F 不与A 重合），沿着将矩形折叠使A 、D 重合．（1）当点E 为中点时，求点F 的坐标，并直接写出与对角线的关系；（2）如图2，连接．①的周长是否有最小值，若有，请求出最小值；若没有，请说明理由；②当平分时，直接写出k 的值．21．如图1，四边形为正方形，点A 在y 轴上，点B 在x 轴上，且，，反比例函数在第一象限的图象经过正方形的顶点C ．（1）求点C 的坐标和反比例函数的关系式；（2）如图，将正方形沿x 轴向右平移m 个单位长度得到正方形A ′B ′C ′D ′，点A ′恰好落在反比例函数的图象上，求n 值．（3）在（2）的条件下，坐标系内是否存在点P ，使以点O ，A ′，B ′，P 为顶点的四边形为平行四边形，若存在，请直接写出点P的坐标，若不存在，请说明理由．xOy (43)A -，(0)ky k x=<ABOC AC AB EF ABOC AC EF BC CD CDE CD ACO ∠ABCD 4OA =2OB =()0ky k x=≠2ABCD22．如图，在平面直角坐标系中，A （8，0）、B （0，6）是矩形OACB 的两个顶点，双曲线y＝（k≠0，x ＞0）经过AC 的中点D ，点E 是矩形OACB 与双曲线y ＝的另一个交点．（1）点D 的坐标为 ，点E 的坐标为 ；（2）动点P 在第一象限内，且满足S △PBO ＝S △ODE ．①若点P 在这个反比例函数的图象上，求点P 的坐标；②若点Q 是平面内一点，使得以A 、C 、P 、Q 为顶点的四边形是菱形，请你直接写出满足条件的所有点Q 的坐标．23．如图，一次函数的图像与反比例函数的图像交于，两点．（，，为常数）（1）求一次函数和反比例函数的解析式；（2）将一次函数向下平移个单位后与反比例函数的图像有且只有一个公共点，求的值；（3）为轴上一点，若的面积为，求点的坐标．24．如图，一次函数的图象与反比例函数（k 为常数且）的图象交于A ，B 两点，其中，直线与y 轴、x 轴分别交于C ，D 两点．kxkx561y k x b =+2k y x=()41A -，()4B m ，1k 2k b 1y k x b =+m 2k y x=m P y PAB 3P 4y x =+ky x=0k ≠()13A -，4y x =+（1）求反比例函数的表达式；（2）在x 轴上找一点P ，使的值最小，并求满足条件的点P 的坐标；（3）在坐标平面中是否存在点Q ，使得以Q ，A ，B 为顶点的三角形与相似？如果存在，请直接写出所有满足条件的点Q的坐标．PA PB COD答案解析部分1．【答案】（1）解：把点A （1，2）代入y ＝-x+m ，得-1+m ＝2，∴m ＝3，∴一次函数解析式为y ＝﹣x+3；把点A （1，2）代入y ＝，∴k ＝1×2＝2，∴反比例函数解析式为y ＝；（2）解：联立方程组{y ＝−x +3y ＝2x ， 解得或，∴B （2，1），设直线y ＝﹣x+3与y 轴的交点为C ，∴C （0，3），∴S △AOB =S △COB -S △COA =×3×2-×3×1=1.5.【解析】【分析】（1）利用待定系数法求出一次函数的解析式和反比例函数的解析式即可；（2）先求出点B 的坐标，再求出直线与y 轴的交点C 的坐标，再利用S △AOB =S △COB -S △COA ，根据三角形的面积公式进行计算即可.2．【答案】（1）解：设P 与V 之间的函数表达式为，当时，，所以，∴，∴P 与V 之间的函数表达式为；（2）解：当时，，∴，∴为确保气球不爆炸，气球的体积应不小于.【解析】【分析】（1）由题意可设，把V=0.8，P=120代入解析式计算可求得F 的值，则解析式可k x 2x12x y =⎧⎨=⎩21x y =⎧⎨=⎩1212F P V=0.8V =120P =1200.8F =96F =96P V =128P ≤96128V ≤0.75V ≥30.75m F P V=求解；（2）由题意可得关于V 的不等式，解这个不等式可求解.3．【答案】（1）3；4；1（2）解：0＜x≤1或x≥3（3）解：作A 关于y 轴的对称点，连接，如图，∵，∴A 关于y 轴的对称点A ′(−1，3)．设直线的解析式为，将A ′(−1，3)，代入可得：∴，解得：．∴直线的解析式为，令，则，∴．【解析】【解答】（1）解：∵反比例函数与一次函数的图像在第一象限交于、两点，∴，，∴，，∴反比例函数和一次函数的表达式分别为：，；将点代入得；故答案为：3，4，1（2）解：由图像可得：满足的取值范围是或；A 'A B '()13A ，A B 'y ax c =+()31B ，331a c a c -+=⎧⎨+=⎩1252a c ⎧=-⎪⎪⎨⎪=⎪⎩A B '1522y x =-+0x =52y =502Q ⎛⎫ ⎪⎝⎭，()10k y k x=≠2y x b =-+()13A ，()3B n ，3k =31b =-+3k =4b =13y x =24y x =-+()3B n ，13y x=1n =12y y ≥01x <≤3x ≥【分析】（1）将点A 、B 的坐标代入求出k 、n 的值，再将点A 的坐标代入求出b 的值即可； （2）结合函数图象，利用函数值大的图象在上方的原则求解即可；（3）作A 关于y 轴的对称点，连接，利用待定系数法求出直线的解析式，再将代入解析式求出y 的值，可得点Q 的坐标。

反函数练习（含详细解析）反函数练习一．填空题1．若f（x）=（x﹣1）2（x≤1），则其反函数f﹣1（x）=．2．定义在R上的函数f（x）=2x﹣1的反函数为y=f﹣1（x），则f﹣1（3）=3．若函数f（x）=x a的反函数的图象经过点（，），则a=．4．已知函数f（x）=2x﹣1的反函数是f﹣1（x），则f﹣1（5）=．5．函数y=x2+2（﹣1≤x≤0）的反函数是f﹣1（x）=．6．已知函数f（x）=2x+m，其反函数y=f﹣1（x）图象经过点（3，1），则实数m 的值为．7．设f﹣1（x）为的反函数，则f﹣1（1）=．8．函数f（x）=x2，（x＜﹣2）的反函数是．9．函数的反函数是．10．函数y=x2+3（x≤0）的反函数是．11．设函数f（x）=3x，若g（x）为函数f（x）的反函数，则g （1）=．12．设函数y=f（x）存在反函数y=f﹣1（x），且函数y=x ﹣f（x）的图象经过点（2，5），则函数y=f﹣1（x）+3的图象一定过点．13．函数（x≤0）的反函数是．14．已知函数，则=．15．函数的反函数为f﹣1（x）=．16．函数的反函数的值域是．17．函数f（x）=x2﹣2（x＜0）的反函数f﹣1（x）=．18．设f（x）=4x﹣2x+1（x≥0），则f﹣1（0）=．19．若函数y=ax+8与y=﹣x+b的图象关于直线y=x对称，则a+b=．20．已知函数f（x）=log2（x2+1）（x≤0），则f﹣1（2）=．参考答案一．填空题（共20小题）1．1﹣（x≥0）；2．2；3．；4．3；5．，x∈[2，3]；6．1；7．1；8．；9．f﹣1（x）=（x﹣1）2（x≥1）；10．y=﹣（x ≥3）；11．0；12．（﹣3，5）；13．（x≥﹣1）；14．﹣2；15．，（x∈（0，1））；16．；17．（x＞﹣2）；18．1；19．2；20．﹣；。

反函数基础练习含标准答案.doc反函数基础练习含标准答案一、选择题1.设函数f(x) = 2x + 3，那么它的反函数是： A. f(x) = 2x + 3 B. f(x)= (x - 3) / 2 C. f(x) = (x + 3) / 2 D. f(x) = (x - 3) / 2 + 3答案：C2.设函数f(x) = x^2，那么它的反函数是： A. f(x) = x^2 B. f(x) = √xC. f(x) = x^(1/2)D. f(x) = x^2 - 1答案：B3.设函数f(x) = e^x，其中e为自然对数的底数，那么它的反函数是： A.f(x) = e^x B. f(x) = ln(x) C. f(x) = e^(1/x) D. f(x) = ln(e^x)答案：B4.设函数f(x) = |x|，那么它的反函数是： A. f(x) = |x| B. f(x) = x C.f(x) = -x D. f(x) = x^2答案：B5.设函数f(x) = x^3，那么它的反函数是： A. f(x) = x^3 B. f(x) = ∛x C.f(x) = x^(1/3) D. f(x) = x^2 - 1答案：C二、填空题1.设函数f(x) = 2x + 1，那么它的反函数是________。

答案：f(x) = (x -1) / 22.设函数f(x) = x^2，那么它的反函数是________。

答案：f(x) = √x3.设函数f(x) = e^x，其中e为自然对数的底数，那么它的反函数是________。

答案：f(x) = ln(x)4.设函数f(x) = |x|，那么它的反函数是________。

答案：f(x) = x5.设函数f(x) = x^3，那么它的反函数是________。

答案：f(x) = ∛x三、计算题1.设函数f(x) = 2x + 1，求它的反函数f^(-1)(x)。

1．如图，点A、B在反比例函数y＝－ 4 x 的图象上，且点A、B的横坐标分别为a、2a（a＜0）．（1）求△AOB的面积；（2）若点C在x轴上，点D在y轴上，且四边形ABCD为正方形，求a的值．2．如图，点P是反比例函数y＝－ 2 x （x＜0）图象上一动点，点A、B分别在x轴，y轴上，且OA＝OB ＝2，PM⊥x轴于M，交AB于E，PN⊥y轴于N，交AB于F．（1）当动点P的纵坐标为 5 3 时，连接OE、OF，求△EOF的面积；（2）设动点P的坐标为P（a，b）（－2＜a＜0，0＜b＜2且| a |≠| b |），其他条件不变，探索：以AE、EF、BF为边的三角形是怎样的三角形？并证明你的结论．3．如图，在△OAB中，OA＝OB，点A坐标为（－33，3），点B在x轴负半轴上．（1）将△OAB沿x轴向右平移a个单位后，点A恰好落在反比例函数y＝ 63 x 的图象上，求a的值；（2）将△OAB绕点O按逆时针方向旋转α角（0°＜α＜90°）．①当α＝30°时，点B恰好落在反比例函数y＝ k x 的图象上，求k的值；②点A、B能否同时落在①中的反比例函数的图象上，若能，求α角的大小；若不能，请说明理由．4．如图，△AOB为等腰直角三角形，斜边OB在x轴上，一次函数y＝3x－4的图象经过点A，交y轴于点C，反比例函数y＝ k x （x＞0）的图象也经过点A．（1）求反比例函数的解析式；（2）过O点作OD⊥AC于D点，求CD 2－AD 2的值；（3）若点P是x轴上的动点，在反比例函数的图象上是否存在点Q，使得△PAQ为等腰直角三角形？若存在，求点Q的坐标，若不存在，请说明理由．5．如图，已知一次函数y＝kx＋b的图象交反比例函数y＝ 4－2m x （x＞0）图象于点A、B，交x轴于点C．（1）求的m的取值范围；（2）若点A的坐标是（2，－4），且 BC AB ＝ 1 3 ，求m的值和一次函数的解析式；（3）在（2）的条件下，设点P是一次函数图象上的第一、四象限内的动点，点Q是反比例函数图象上的动点，过点P作PP1⊥x轴于P1，PP2⊥y轴于P2；过点Q作QQ1⊥x轴于Q1，QQ2⊥y轴于Q2．设点P 的横坐标为x，请直接写出使四边形PP1OP2的面积小于四边形QQ1OQ2的面积的x的取值范围．6．在平面直角坐标系xOy中，直线l1过A（1，0）且与y轴平行，直线l2过点B（0，2）且与x轴平行，直线l1与l2相交于点P．点E为直线l2上一点，反比例函数y＝ k x （k＞0）的图象过点E且与直线l1相交于点F．（1）若点E与点P重合，求k的值；（2）连接OE、OF、EF．若k＞2，且△OEF的面积为△PEF的面积的2倍，求点E的坐标；（3）是否存在点E及y轴上的点M，使得以点M、E、F为顶点的三角形与△PEF全等？若存在，求点E 的坐标，若不存在，请说明理由．7．如图，已知直线l经过点A（1，0），且与曲线y＝ m x （x＞0）交于点B（2，1）．过点P（p，p－1)（p＞1）作x轴的平行线分别交曲线y＝ m x （x＞0）和y＝－ m x （x＜0）于M、N两点．（1）求m的值及直线l的解析式；（2）若点P在直线y＝2上，求证：△PMB∽△PNA；（3）是否存在实数p，使得S△AMN ＝4S△APM？若存在，请求出所有满足条件的p的值；若不存在，请说明理由．8．如图，在平面直角坐标系中，O为坐标原点，P是反比例函数y＝ 6 x （x＞0）图象上的任意一点，以P 为圆心，PO为半径的圆与x、y轴分别交于点A、B．（1）判断P是否在线段AB上，并说明理由；（2）求△AOB的面积；（3）Q是反比例函数y＝ 6 x （x＞0）图象上异于点P的另一点，请以Q为圆心，QO半径画圆与x、y轴分别交于点M、N，连接AN、MB．求证：AN∥MB．9．如图，将—矩形OABC放在直角坐标系中，O为坐标原点，点A在y轴正半轴上，点E是边AB上的—个动点（不与点A、B重合），过点E的反比例函数y＝ k x （x＞0）的图象与边BC交于点F．（1）若△OAE、△OCF的面积分别为S1、S2，且S1＋S2＝2，求k的值；（2）若OA＝2，OC＝4，问当点E运动到什么位置时，四边形OAEF的面积最大，其最大值为多少？10．如图，已知抛物线y＝( 3－m )x 2＋2( m－3 )x＋4m－m 2的顶点A在双曲线y＝ 3 x 上，直线y＝mx ＋b经过点A，与y轴交于点B，与x轴交于点C．（1）求直线AB的解析式；（2）将直线AB绕点O顺时针旋转90°，与x轴交于点D，与y轴交与点E，求sin∠BDE的值；（3）过点B作x轴的平行线与双曲线交于点F，点M在直线BF上，且到抛物线的对称轴的距离为6．若点N在直线BF上，直接写出使得∠AMB＋∠ANB＝45°的点N的坐标．11．如图，在平面直角坐标系中，直线y＝mx（m＞0）与双曲线y＝ k x 交于A、B两点，过点A作AC ∥x轴，过点B作BC∥y轴，AC与BC交于点C，AC与y轴交于点M，BC与x轴交于点N，若∠BAC ＝60°，AB＝4．（1）求m、k的值；（2）将一把三角尺的直角顶点放在原点O处，绕着点O旋转三角尺，三角尺的两直角边分别交射线CA、射线BC于点P、Q，设点P的横坐标为x，PQ的长为L，当点P在边AC上运动时，求L与x的函数关系式；（3）当△PQC的面积为 3 2 时，求点P的坐标．12．如图，在平面直角坐标系中，直线y＝ax＋1（a≠0）与x轴交于点A，与y轴交于点B，与双曲线y＝ k x 在第三象限的交点为C（－2 3，m），且△AOB的面积为 3 2 ．（1）求a、m、k的值；（2）以BC为一边作等边三角形BCD，求D点的坐标．13．已知一次函数y＝2 x＋8 与反比例函数y＝ k x 的图象相交于A、B两点，点A的横坐标为x1，点B 的横坐标为x2，且x1－x2＝2．（1）求k的值；（2）求△AOB的面积；（3）若一条开口向下的抛物线经过A、B两点，并在过点A且与OB平行的直线上截得的线段长为 13，求抛物线的解析式．14．如图，已知A、B两点的坐标分别为A（0，2 3），B（2，0）直线AB与反比例函数y＝ m x 的图象交与点C和点D（－1，a）．（1）求直线AB和反比例函数的解析式；（2）求∠ACO的度数；（3）将△OBC绕点O逆时针方向旋转α角（α为锐角），得到△OB′C′，当α为多少度时OC′⊥AB，并求此时线段AB′的长．15．在矩形AOBC中，OA＝4，OB＝6．分别以OB、OA所在直线为x轴和y轴，建立如图所示的平面直角坐标系．F是边BC上的一个动点（不与B、C重合），过F点的反比例函数y＝ k x （k＞0）的图象与AC边交于点E．（1）若点E的坐标为（2，4），求经过O、E、F三点的抛物线的解析式；（2）设点P是（1）中所求抛物线上一点，且△PEF的面积等于△OEF的面积，求点P的坐标；（3）是否存在这样的点F，使得将△CEF沿EF对折后，C点恰好落在OB上？若存在，求出此时OF的长；若不存在，请说明理由．16．如图，矩形ABCD的顶点A在坐标原点，顶点B坐标为（－2，1），顶点C在y轴上．（1）求顶点D的坐标；（2）将矩形ABCD绕点O顺时针旋转，使点D落在x轴的点G处，得到矩形AEFG，EF与AD交于点M，过点M的反比例函数图象交FG于点N，求△AMN的面积；（3）求证：△AMN是直角三角形．17．如图，已知反比例函数y＝ m x （m是常数，m≠0），一次函数y＝ax＋b（a、b为常数，a≠0），其中一次函数与x轴，y轴的交点分别是A（－4，0），B（0，2）．（1）求一次函数的关系式；（2）反比例函数图象上有一点P满足：①PA⊥x轴；②PO＝ 17（O为坐标原点），求反比例函数的关系式；（3）求点P关于原点的对称点Q的坐标，判断点Q是否在该反比例函数的图象上．18．如图，已知反比例函数y＝ m x （m＞0）的图象与一次函数y＝－x＋b的图象分别交于A（1，3）、B 两点．（1）求m、b的值；（2）若点M是反比例函数图象上的一动点，直线MC⊥x轴于C，交直线AB于点N，MD⊥y轴于D，NE⊥y轴于E．设四边形MDOC、NEOC的面积分别为S1、S2，S＝S2－S1，求S的最大值．19．如图，已知函数y＝ 6 x （x＞0）的图象与一次函数y＝kx＋b的图象交于点A（1，m），B（n，2）两点．（1）求一次函数的解析式；（2）将一次函数y＝kx＋b的图象沿x轴负方向平移a（a＞0）个单位长度得到新图象，求这个新图象与函数y＝ 6 x （x＞0）的图象只有一个交点M时a的值及交点M的坐标．20．如图，一次函数的图象与反比例函数y1＝－ 3 x （x＜0）的图象相交于A点，与y轴、x轴分别相交于B、C两点，且C（2，0）．当x＜－1时，一次函数值大于反比例函数值，当x＞－1时，一次函数值小于反比例函数值．（1）求一次函数的解析式；（2）设函数y2＝ a x （x＞0）的图象与y1＝－ 3 x （x＜0）的图象关于y轴对称，在y2＝ a x （x＞0）的图象上取一点P（P点的横坐标大于2），过P作PQ⊥x轴，垂足为Q，若四边形BCQP的面积等于2，求P点的坐标．21．如图，已知二次函数y＝ax 2＋2x＋c（a＞0）图象的顶点M在反比例函数y＝ 3 x 的图象上，且与x 轴相交于A、B两点．（1）若二次函数图象的对称轴为x＝－ 1 2 ，试求a、c的值；（2）在（1）的条件下，求线段AB的长；（3）若二次函数图象的对称轴与x轴的交点为N，当NO＋MN取最小值时，试求二次函数的解析式．22．如图，一次函数y＝k x＋4的图象与反比例函数y＝ m x （x＞0，m＞0）的图象交于A、B两点，与x 轴、y轴分别交于C、D两点．（1）求证：AC＝BD；（2）若△COD的面积是△AOB的面积的 2 倍，求k与m之间的函数关系式；（3）在（2）的条件下，是否存在实数k和m，使得以AB为直径的圆经过点P（2，0）？若存在，求出k 和m的值；若不存在，请说明理由．23．已知一次函数y＝－ 1 2 x＋b的图象与反比例函数y＝ 6 x （x＞0）的图象交于A、B两点，与x轴、y轴分别交于C、D两点．（1）如图1，若AB＝2AC，求b的值；（2）在（1）的条件下，将一块直角三角板的直角顶点P放在反比例函数y＝ 6 x （x＞0）图象的AB段上滑动，两直角边始终与坐标轴平行，且与线段AB分别交于Q、R两点．设点P的横坐标为x，QR的长为L，求L关于x的函数关系式，并求L的最大值；（3）如图2，过点A作直线AE∥x轴，交y轴于点E；过点B作直线BF∥y轴交x轴于点F，交直线AE 于点G．当四边形OAGB的面积为8时，请判断线段AE与AG的大小关系，并说明理由．24．如图，已知反比例函数y＝ k x 的图象经过A（－1，a）、B（2，a＋33）两点，点C的坐标为（－1，0）．（1）求反比例函数的解析式；（2）在反比例函数y＝ k x 的图象上求点D，使得以A、B、C、D为顶点的四边形是梯形．25．如图，在平面直角坐标系中，双曲线y＝ k x 过点A（－4，1），点P是双曲线上一动点（不与A重合），过点A和P分别向两坐标轴作垂线，垂足分别为B、C和D、E．（1）求k、S△ADC及S△PDC的值；（2）判断AP和DC的位置关系，并说明理由；（3）若点P在双曲线上运动时，探索以A、P、C、D四点为顶点的四边形能否成为菱形和等腰梯形？若能，请直接写出所有满足条件的点P的坐标；若不能，请说明理由．26．已知关于x的一元二次方程( a－1 )x 2＋( 2－3a )x＋3＝0．（1）求证：当a取不等于1的实数时，此方程总有两个实数根；（2）若m，n（m＜n）是此方程的两根，且1 m ＋ 1 n ＝ 4 3 ，直线l：y＝mx＋n交x轴于点A，交y 轴于点B，坐标原点O关于直线l的对称点O′在反比例函数y＝ k x 的图象上，求反比例函数的解析式；（3）在（2）的条件下，将直线l绕点A逆时针旋转θ角（0°＜θ＜90°），得到直线l′，l′交y轴于点P，过点P作x轴的平行线，与（2）中的反比例函数图象交于点Q，当四边形APQO′的面积为9－ 33 2 时，求θ角的大小．27．在平面直角坐标系中，一次函数y＝－ 1 2 x＋5的图象交x轴于点A，交y轴于点B，交直线y＝x－1于点C，过点A作y轴的平行线交直线y＝x－1于点D，点E为线段AD上一点，且tan∠DCE＝ 1 2 ．动点P从原点O出发沿OA边向点A匀速运动，同时，动点Q从B点出发沿BO边向原点O匀速运动，点P与点Q同时到达A点和O点，设BQ＝m．（1）求点E的坐标；（2）在整个运动过程中，是否存在这样的实数m，使得△PQD为直角三角形．若存在，求m的值；若不存在，请说明理由；（3）反比例函数y＝ k x 的图象经过点C，R为y＝ k x 图象上一点，在整个运动过程中，若以P、Q、E、R为顶点的四边形是平行四边形，求R点的坐标．。

反函数练习题一、选择题1. 下列函数中，有反函数的是：A. f(x) = x^2B. f(x) = |x|C. f(x) = 2x + 1D. f(x) = 1/x2. 设函数f(x) = 3x 5，则其反函数f^(1)(x) 的表达式为：A. f^(1)(x) = (x + 5)/3B. f^(1)(x) = (x 5)/3C. f^(1)(x) = 3x + 5D. f^(1)(x) = 3x 53. 若函数f(x) = 2x + 3（x∈R）的反函数为f^(1)(x)，则f^(1)(4) 的值为：A. 1B. 1C. 2D. 2二、填空题1. 已知函数f(x) = 5 2x，则f^(1)(x) = _______。

2. 若函数f(x) = (1/2)^x 的反函数为f^(1)(x)，则f^(1)(1/8) = _______。

3. 设函数f(x) = log2(x + 1)，则f^(1)(2) = _______。

三、解答题1. 求函数f(x) = 4x^3 + 2的反函数。

2. 已知函数f(x) = e^x，求f^(1)(3) 的值。

3. 设函数f(x) = (x 1)^2（x ≥ 1），求其反函数，并求出反函数的定义域。

4. 已知函数f(x) = 2sin(x)（x∈[π/2, π/2]），求其反函数。

5. 设函数f(x) = 1/(x 2)（x ≠ 2），求f^(1)(1/3) 的值。

四、综合题1. 已知函数f(x) = 3x 4，求f(f^(1)(x)) 的表达式。

2. 设函数f(x) = (1/2)^x + 1，求f^(1)(3) 的值。

3. 已知函数f(x) = 2x + 3，g(x) = 4x 5，求f(g^(1)(x)) 的表达式。

4. 设函数f(x) = log3(x + 2)，求f^(1)(f(x)) 的表达式。

5. 已知函数f(x) = 2x 1（x > 0），求f^(1)(f^(1)(x)) 的表达式。

人教版九年级数学下反函数经典拔高题型汇总50题（后附答案详解）一、单选题（共15题；共30分）1.如图，直线y=kx+b与双曲线y=m2+1x(x>0)交于A(x1,y1)，B(x2,y2)(x1<x2)，直线AB交x轴于C(x0,0)，下列命题：① x1y2=x2y1；②当x1<x<x2时，kx+b>m2+1x；③若M(t,s)为线段AB的中点，则t=12x0，其中正确的命题有（）A. ①②B. ②③C. ①③D. ①②③2.如图，点A、M是第一象限内双曲线y=kx（k为常数，k≠0，x>0）上的点（点M在点A的左侧），若M点的纵坐标为1，且△OAM为等边三角形，则k的值为（）A. √3B. 2+√3C. 2−√3D. 2±√33.如图，△OA1B1，△A1A2B2，△A2A3B3，…是分别以A1，A2，A3，…为直角顶点，一条直角边在x轴正半轴上的等腰直角三角形，其斜边的中点C1（x1，y1），C2（x2，y2），C3（x3，y3），…均在反比例函数y=4x(x>0)的图象上，则y1+y2+......+y100的值为（）A. 6B. 4√2C. 20D. 2√104.如图，在平面直角坐标系中，正方形OABC的顶点O与坐标原点重合，顶点A、C分别在x轴、y轴上，反比例函数y=kx(k≠0,x>0)的图象与正方形OABC的两边AB、BC分别交于点M、N，ND⊥x轴，垂足为D，连接OM、ON、MN，下列结论错误的是① △OCN≌△OAM；②四边形DAMN与△OMN面积相等；③ ON=MN；④若∠MON=45%，MN=2，则点C的坐标为(0,√2+1).其中正确的结论有（）A. ①②B. ①②④C. ②③④D. ①②③④5.如图，在平面直角坐标系中，直线y=−x与双曲线y=kx交于A、B两点，P是以点C(2,2)为圆心，半径长1的圆上一动点，连结AP，Q为AP的中点.若线段OQ长度的最大值为2，则k 的值为（）A. −12B. −32C. -2D. −146.如图，函数y=−1x(x<0)的图象经过Rt△ABO斜边OB的中点D，与直角边AB相交于C，连结AD.若AD=3，则△ABO的周长为（）A. 12B. 6+√38C. 6+2√10D. 6+2√117.如图，在以 O 为原点的平面直角坐标系中，矩形 OABC 的两边 OC 、 OA 分别在 x 轴、 y 轴的正半轴上，反比例函数 y =kx (x >0) 的图象与 AB 相交于点 D ，与 BC 相交于点 E ，若 BD =3AD ，且 △ODE 的面积是 6 ，则 k 的值为（ ）.A. 85B. 8C. 6D. 1658.如图，正比例函数 y =x 的图象与反比例函数 y =k x (k ≠0) 的图象交于 A ， B 两点， ∠CAD =90° ，两边分别交 x 轴， y 轴于点 D ， C ，四边形 OCAD 的面积为 1 ， AE ⊥x 轴于点 E .有下列结论：① OA =OB ；②三角形 OAE 的面积为 12 ；③线段 AB 的长为 √6 ；④不等式 x >k x 的解集是 x >1 或 x <−1 .其中正确结论的个数是（ ）.A. 1B. 2C. 3D. 49.函数y ＝kx ﹣3与y ＝ （k≠0）在同一坐标系内的图象可能是（ ）A. B. C. D.10.如图在平面直角坐标系中，直线 y =−x +6 分别与x 轴、y 轴交于点A 、B ， 与 y =kx (x >0) 的图象交于点C 、D ． 若CD = 13 AB ， 则k 的值为（ ）A. 4．B. 6．C. 8．D. 10．11.如图，已知ΔOAB的一边AB平行于x轴，且反比例函数y=k经过ΔOAB顶点B和OA上的x，则k的值为（）一点C，若OC=2AC且ΔOBC的面积为103A. 4B. 6C. 8D. 912.如图，在平面直角坐标系中，Rt△ABC的斜边AB的中点与坐标原点重合，点D是x轴上一(k<0,x<0)的图象经过CD上的两点，连接CD、AD.若CB平分∠OCD，反比例函数y=kx点C、E，且CE=DE，△ACD的面积为12，则k的值为（）A. －4B. －8C. －12D. －16x+3与x轴、y轴分别交于点A和点B,C是线段AB上13.如图，在平面直角坐标系中，直线y=−32一点，过点C作CD⊥x轴，垂足为D，CE⊥y轴，垂足为E，S△BEC:S△CDA=4:1．若双曲(x>0)经过点C，则k的值为（）线y=kxA. 43B. 34C. 25D. 5214.如图，在平面直角坐标系中，矩形ABCD 的顶点A ，C 分别在x 轴，y 轴的正半轴上，点D （﹣2，3），AD ＝5，若反比例函数y ＝ k x （k ＞0，x ＞0）的图象经过点B ，则k 的值为（ ）A. 163B. 8C. 10D. 32315.如图，在平面直角坐标系中，矩形ABCD 的对角线AC 的中点与坐标原点重合，点E 是x 轴上一点，连接AE.若AD 平分∠OAE ，反比例函数y ＝ k x （k ＞0，x ＞0）的图象经过AE 上的两点A ，F ，且AF ＝EF ，△ABE 的面积为18，则k 的值为（ ）A. 6B. 12C. 18D. 24二、填空题（共16题；共20分）16.如图，反比例函数 y =kx(x >0) 的图象经过矩形 OABC 对角线的交点 M ，分别交 AB ， BC 于点 D 、 E .若四边形 ODBE 的面积为12，则 k 的值为________.17.如图，▱ABCD的顶点A在反比例函数y=−2x的图象上，顶点B在x轴的正半轴上，顶点C和D在反比例函数y=8x的图象上，且对角线AC//x轴，则▱ABCD的面积等于________．18.如图，在平面直角坐标系中，点A，B的坐标分别为(−1,0)，(0,2)，点C是反比例函数y=k x (x>0)图象上一点，∠ABC=135°，AC交y轴于点D，ADDC=23，则k的值为________．19.如图，直线y= 12x+4与x轴、y轴交于4、B两点，AC⊥AB，交双曲线y= kx(x<0)于C点，且BC交x轴于M点，BM=2CM，则k=________。

反函数练习题（打印版）### 反函数练习题#### 一、选择题1. 若函数 \( f(x) = 2x + 3 \) 的反函数是 \( f^{-1}(x) \)，求\( f^{-1}(-1) \) 的值。

- A. -5- B. -3- C. 0- D. 12. 已知 \( g(x) = x^2 \) 的反函数是 \( g^{-1}(x) \)，求\( g^{-1}(4) \) 的值。

- A. 2- B. -2- C. 4- D. ±23. 函数 \( h(x) = \log_{10} x \) 的反函数是 \( h^{-1}(x) \)，求 \( h^{-1}(100) \) 的值。

- A. 2- B. 3- C. 4- D. 5#### 二、填空题4. 函数 \( f(x) = \sqrt{x + 1} \) 的反函数是 \( f^{-1}(x) \)，当 \( x = 4 \) 时，求 \( f^{-1}(x) \) 的值。

5. 若 \( y = 3^x \)，求 \( x \) 关于 \( y \) 的反函数表达式。

6. 函数 \( s(x) = \frac{1}{x} \) 的反函数是 \( s^{-1}(x) \)，当 \( x = 0.5 \) 时，求 \( s^{-1}(x) \) 的值。

#### 三、解答题7. 已知函数 \( p(x) = 4x - 1 \)，求其反函数，并计算 \( p^{-1}(5) \)。

8. 函数 \( q(x) = 2^x \) 有反函数吗？如果有，请写出其反函数，并计算 \( q^{-1}(8) \)。

9. 函数 \( r(x) = 5x + 7 \) 的反函数是 \( r^{-1}(x) \)，求\( r^{-1}(12) \)。

#### 四、应用题10. 某工厂生产的产品数量与价格之间的关系由函数 \( v(x) = 100 - 0.5x \) 表示，其中 \( x \) 表示产品数量，\( v \) 表示价格。

反函数基础练习(一)选择题1．函数y ＝－x 2(x ≤0)的反函数是[ ]A y (x 0)B y (x 0)C y (x 0)D y |x|．＝－≥．＝≤．＝－≤．＝－x x x --2．函数y ＝－x(2＋x)(x ≥0)的反函数的定义域是 [ ]A ．[0，＋∞)B ．[－∞，1]C ．(0，1]D ．(－∞，0]3y 1(x 2)．函数＝＋≥的反函数是x -2[ ]A ．y ＝2－(x －1)2(x ≥2)B ．y ＝2＋(x －1)2(x ≥2)C ．y ＝2－(x －1)2(x ≥1)D ．y ＝2＋(x －1)2(x ≥1)4．下列各组函数中互为反函数的是[ ]A y y xB y y 2．＝和＝．＝和＝x x x11C y y (x 1)D y x (x 1)y (x 0)2．＝和＝≠．＝≥和＝≥3131311x x x x x +-+-5．如果y ＝f(x)的反函数是y ＝f -1(x)，则下列命题中一定正确的是[ ]A ．若y ＝f(x)在[1，2]上是增函数，则y ＝f -1(x)在[1，2]上也是增函数B ．若y ＝f(x)是奇函数，则y ＝f -1(x)也是奇函数C．若y＝f(x)是偶函数，则y＝f-1(x)也是偶函数D．若f(x)的图像与y轴有交点，则f-1(x)的图像与y轴也有交点6．如果两个函数的图像关于直线y＝x对称，而其中一个函数是x 1y＝－，那么另一个函数是[ ] A．y＝x2＋1(x≤0)B．y＝x2＋1(x≥1)C．y＝x2－1(x≤0)D．y＝x2－1(x≥1)7．设点(a，b)在函数y＝f(x)的图像上，那么y＝f-1(x)的图像上一定有点[ ] A．(a，f-1(a))B．(f-1(b)，b)C．(f-1(a)，a) D．(b，f-1(b))8．设函数y＝f(x)的反函数是y＝g(x)，则函数y＝f(－x)的反函数是[ ] A．y＝g(－x) B．y＝－g(x)C．y＝－g(－x) D．y＝－g-1(x)9．若f(x－1)＝x2－2x＋3(x≤1)，则函数f-1(x)的草图是[ ]10y g(x)．函数＝的反函数是，则13x[ ]A ．g(2)＞g(－1)＞g(－3)B ．g(2)＞g(－3)＞g(－1)C ．g(－1)＞g(－3)＞g(2)D ．g(－3)＞g(－1)＞g(2) (二)填空题1y 32y (x 0)y f(x)y x ．函数＝＋的反函数是．．函数＝＞与函数＝的图像关于直线＝对称，x x ++2121 解f(x)＝________．3．如果一次函数y ＝ax ＋3与y ＝4x －b 的图像关于直线y ＝x 对称，那a ＝________，b ＝________．4y (1x 0)．函数＝－＜＜的反函数是，反函数的定92-x义域是________．5．已知函数y ＝f(x)存在反函数，a 是它的定义域内的任意一个值，则f -1(f(a))＝________．6y 7y (x 1)(x 1)8f(x)(x 1)f ()1．函数＝的反函数的值域是．．函数＝≥－＜的反函数是：．．函数＝＜－，则－＝．121121232x x x x ---⎧⎨⎪⎩⎪--(三)解答题1y 12f(x)．求函数＝＋的反函数，并作出反函数的图像．．已知函数＝．x ax x +++252(1)求函数y ＝f(x)的反函数y ＝f -1(x)的值域；(2)若点P(1，2)是y ＝f -1(x)的图像上一点，求函数y ＝f(x)的值域．3．已知函数y ＝f(x)在其定义域内是增函数，且存在反函数，求证y ＝f(x)的反函数y ＝f -1(x)在它的定义域内也是增函数．4f(x)y g(x)y f (x 1)．设函数＝，函数＝的图像是＝＋的图像2311x x +-- 关于y ＝x 对称，求g(2)的值．参考答案(一)选择题1．(C)．解：函数y=－x 2(x ≤0)的值域是y ≤0，由y=－x 2得x=－－，∴反函数－－≤．y x f (x)=(x 0)1-2．(D)．解：∵y=－x 2－2x=－(x ＋1)2，x ≥0，∴函数值域y ≤0，即其反函数的定义域为x ≤0．3(D)y =x 21x 2y 1y =x 2．．解：∵－＋，≥，∴函数值域≥，由－＋1，得反函数f －1(x)=(x －1)2＋1，(x ≥1)．4．(B)．解：(A)错．∵y=x 2没有反函数．(B)中如两个函数互为反函数．中函数＋－≠的反函数是＋－≠而不是＋－．中函数≥的值域为≥．应是其反函数的定义域≥．但中的定义域≥，故中两函数不是互为反函数．(C)y =3x 1x (x 1)y =x 1x 3(x 3)y =3x 13x 1(D)y =x (x 1)y 1x 1y =x x 0(D)21 5．(B)．解：(A)中．∵y=f(x)在[1，2]上是增函数．∴其反函数y=f -1(x)在[f(1)，f(2)]上是增函数，∴(A)错．(B)对．(C)中如y=f(x)=x 2是偶函数但没有反函数．∴(C)错．(D)中如函数f(x)=x 2＋1(x ≥0)的图像与y 轴有交点，但其反函数－≥的图像与轴没有交点．∴错．f -(x)=x 1(x 1)y (D)1 6(A)y =y 0f (x)=x 12．．解：∵函数－－的值域≤；其反函数＋x 1-＋1(x ≤0)．选(A)．7．(D)．解：∵点(a ，b)在函数y=f(x)的图像上，∴点(b ，a)必在其反函数y=f -1(x)的图像上，而a=f -1(b)，故点(b ，f －1(b))在y=f -1(x)的图像上．选(D)．8．(B)．解：∵y=f(x)的反函数是y=f -1(x)即g(x)=f -1(x)，而y=f(－x)的反函数是y=－f -1(x)=－g(x)，∴选(B)．9．(C)．解：令t=x －1．∵x ≤1，∴t ≤0，f(t)=t 2＋2(t ≤0)，即f(x)=x 2＋2(x ≤0)，值域为f(x)≥2，∴反函数f -1(x)的定义域是x ≥2，值域y ≤0，故选(C)．10(B)g(x)=1x (0)33．．解：∵在－∞，上是减函数，又－＜－＜100g(3)g(1)g(2)=120g(2)g(3)g(1)3，∴＞－＞－而＞，∴＞－＞－．故选 (B)．(二)填空题1y =3y 3y =x 6x 2．解：∵函数＋＋的值域≥，其反函数－＋x 27(x ≥3)2y =12x 1(x 0)y 1f(x)=1x2x(x 1)．解：＋＞的值域＜，其反函数－＜． 3y =4x b y =14x x =ax ．解：函数－的反函数是＋，则＋＋，b b41443比较两边对应项系数得，．a =14b =12 4y =9x (1x 0)y (223)2．解：函数－－＜＜的值域∈，，反函数f -1 (x)=(223)－－．反函数的定义为，．92x5．a6．[0，2)∪(2，＋∞)7f (x)=x 1(x 1)1x(x 0)122．＋≥－＜-⎧⎨⎪⎩⎪8．－2(三)解答题1x 2y 1y =x 21=．解：∵≥－，得值域为≥．由＋＋得反函数f x -1()(x －1)2－2，(x ≥1)，其图像如右图．2．解(1)：∵y=f(x)的定义域是{x|x ≠1，x ∈R ，∴y=f -1(x)的值域是{y|y ≠1，y ∈R}．解(2)：∵点P(1，2)在，y=f -1(x)的图像上，点P(1，2)关于直线y=x的对称点为′，一定在的图像上，即由＋＋得－，∴－＋，其反函数－＋．∵的定义域为≠－，∈，∴的值域为≠－，∈．P (21)y =f(x)=1a =f(x)=10x 2x 4f -(x)=104x 2x 1f -(x){x|x x R}y =f(x){y|y y R}112522121212a3．证明略．4f(x)=2x 3x 1f -(x)=x 3f (x 1)=11．略解；＋－的反函数是＋－，∴＋x 2x 4x 1x 4x 1=2x =6g(2)=6＋－，由＋－得即．。

习题优选一、选择题1．在同一坐标系中 , 图象表示同一曲线的是 ().A．与 B ．与C．与 D ．与2．若函数存在反函数 , 则的方程为常数 )().A．起码有一实根 B ．有且仅有一实根C．至多有一实根D．没有实根3．点在函数的图象上 , 则以下各点中必在其反函数图象上的是 ().A．B．C．D．4．（）的反函数是（）A．（） B ．（）C．（） D．（）5．设函数，，则的定义域是（）A． B ．C． D ．6．已知，则的表达式为（）A．B．C．D．7．将的图象向右平移一个单位，向上平移 2 个单位再作对于的对称图象，所得图象的函数的分析式为（）A． B ． C ．D．8．定义在上的函数有反函数，下例命题中假命题为（）A．与的图象不必定对于对称；B．与的图角对于轴对称；C．与的图象不行能有交点；D．与的图象可能有交点，有时交点个数有无量多个9．若有反函数，以下命题为真命题的是（）A．若在上是增函数，则在上也是增函数；B．若在上是增函数，则在上是减函数；C．若在上是增函数，则在上是增函数；D．若在上是增函数，则在上是减函数10．设函数（），则函数的图象是（）11．函数（）的反函数= （）A．（）B．（）C．（）D．（）二、填空题1．求以下函数的反函数 :（1）;（2）;（3）;（4）.2．函数的反函数是_____________________．3．函数（）的反函数是_________．4．函数的值域为__________．5．, 则的值为_________.6．要使函数在上存在反函数,则的取值范围是_____________．7．若函数有反函数,则实数的取值范围是_____________．8．已知函数（），则为__________．9．已知的反函数为，若的图像经过点，则=________．三、解答题1．求函数的反函数．2．若点（1，2）既在函数的图象上，又在它的反函数的图象上，求，的值．3．已知，求及的分析式，并判断它们能否为同一函数．4．给定实数，且，设函数（且）证明：这个函数的图象对于直线成轴对称图形．5．若点在函数的反响函数的图象上，求．6．已知函数的定义域是，，求．7．求以下函数的值域；（1）；（2）．8．已知函数与的图象对于直线对称，求、的值．9．已知函数的图象对于直线对称,求的值．10．函数与的图象对于直线对称,求常数的值．11．求与函数的图象对于直线对称的图象所对应的函数．12．函数能否存在反函数，若存在，恳求出来；若不存在，请说明原因．13．设是上的增函数，而且对随意，有建立，证明．参照答案：一、1．C2．C3．D4 ．C5．D6．B7．A8．C9 ．C10． B11 ．B二、 1．（ 1）; （2）;（3）; （4）;2．3．解：由，可得，即，函数（）的反函数为（）4． 5 ． 6 ．或7．且.8 ．9．b=1三、 1．解：当时，则反函数为（）；当时，则反函数为（），原函数的反函数为2．解：利用条件可知，（ 1，2），（ 2，1）两点都在函数的图象上，则，解之得3．解：由求出反函数（），则（）（）固然与两函数有同样的表达式，但它们的定义域不一样，故它们不是同一函数．说明：判断两个函数为同一个函数应具备两个条件：一是表达式同样；二是定义域同样．4．解：先求所给函数的反函数，由（），可得（* ）若，则，又由（*）得，故，即与已知矛盾，，于是由（ * ）得（）进而函数（且）的反函数为（且），二者完整同样，为同一个函数．因为的图象与的图象对于直线对称，故函数（且）的图象对于直线成轴对称图形．说明：证明函数对于直线成轴对称图形，分为两步：第一步，证明原函数与反函数为同一函数；第二步，利用轴对称的定义证明．5．解：由反函数的观点及题设条件可得在函数的图象上，即，解得．6．解：设，则，将其代入故（），则（）说明：此题在求解过程中要注意两点：一点是注意运算次序，先求，再求；另一点是在求反函数时，两边开方，注意符号．7．解：（ 1）先由可得，，故原函数的值域（2）先由可得，，故原函数的值域为说明：经过求反函数的定义域来求原函数值域的方法，常常合用于函数的分析式为一次分式的状况．8．解：，的图象对于直线对称，的反函数就是又的反函数为，故和应为同一函数，则9．10．11．解：由可得，即，即所求函数12．解：不存在反函数，原因为：已知函数不是单一函数，如取时，对应的值有两个值为，．13．解：若存在矛盾，同理可证也不行能有，有，不如设对全部，则，即有．。

关于反函数的练习题反函数是数学中一个常见且重要的概念，它指的是对于给定函数f(x)，存在一个函数 g(x) 使得对于所有的 x 在定义域中成立 g(f(x)) = x。

反函数可以帮助我们求出原函数的逆变换，从而解决一系列实际问题。

为了更好地理解和掌握反函数的性质，下面将给出一些有关反函数的练习题，希望能够帮助读者更好地理解和应用反函数。

题目一：设函数 f(x) = 2x + 3，求反函数 g(x) 的表达式。

首先，我们先假设 g(x) = y，根据反函数的定义，我们有 f(g(x)) = x。

将 f(x) 的表达式代入得到：2g(x) + 3 = x接下来，解方程可以得到g(x) = (x - 3) / 2因此，反函数为 g(x) = (x - 3) / 2。

题目二：已知函数 f(x) = x^2 + 1，求反函数 g(x) 的表达式。

同样地，我们假设 g(x) = y，根据反函数的定义，有 f(g(x)) = x。

代入 f(x) 的表达式得到：(g(x))^2 + 1 = x接下来，解这个二次方程可以得到：g(x) = √(x - 1)题目三：已知函数 f(x) = 3x，求反函数 g(x) 的表达式。

假设 g(x) = y，根据反函数的定义，有 f(g(x)) = x。

代入 f(x) 的表达式得到：3g(x) = x解这个一次方程可以得到：g(x) = x/3通过这些练习题，我们可以发现一些反函数的性质和规律。

首先，对于线性函数 f(x) = a*x + b，其反函数的表达式为 g(x) = (x - b) / a。

这表明了线性函数与其反函数之间存在着一种简单的关系。

其次，平方函数 f(x) = x^2 的反函数是开方函数g(x) = √x。

这一结果说明了平方和开方之间存在着一种互逆的关系，通过平方操作可以获得一个数的平方，通过开方操作可以得到平方根。

最后，我们观察到常数函数 f(x) = c 的反函数也是一个常数函数 g(x) = c'，其中 c 可以是任意实数，c' 是 c 的逆元。

（完整版）有理函数求反函数专题练习题一、选择题1. 设函数 $f(x) = \frac{3x+1}{2}$，则函数 $f^{-1}(x)$ 等于（）A. $\frac{x}{3} + \frac{1}{2}$B. $\frac{x-1}{3}$C. $\frac{x-1}{2}$D. $\frac{x}{2} + \frac{1}{3}$2. 已知函数 $y = f(x)$ 与 $y = f^{-1}(x)$ 的图象关于直线 $y =x$ 对称，则函数 $f(x)$ 的图象关于直线 $y = x$ 的对称图象为（）A. 左右翻折B. 上下翻折C. 经过 $y$ 轴平移得到D. 经过 $x$ 轴平移得到3. 设 $y = \frac{ax+b}{cx+d}$，其中 $ad-bc \neq 0$，若 $y =f(x)$ 是其反函数，则 $f(x)$ 的解析式为（）A. $f(x) = \frac{dx-b}{-cx+a}$B. $f(x) = \frac{bx+a}{-cx+d}$C. $f(x) = \frac{dx-b}{cx-a}$D. $f(x) = \frac{x-d}{cx-a}$4. 设函数 $y = f(x)$ 和 $y = f^{-1}(x)$ 的图象关于点 $P(1,1)$ 对称，且 $f(1) = 3$，则函数 $f^{-1}(x)$ 的解析式为（）A. $f^{-1}(x) = 3x + 2$B. $f^{-1}(x) = 3x - 2$C. $f^{-1}(x) = 2x + 3$D. $f^{-1}(x) = -2x + 3$二、填空题1. 设函数 $y = f(x)$ 的图象关于直线 $y = x$ 对称，则函数$f^{-1}(x)$ 的图象关于直线 \_\_\_\_\_\_\_\_\_\_ 对称。

2. 设函数 $y = f(x)$ 和 $y = f^{-1}(x)$ 的图象关于直线 $y = x$ 对称，且 $f(x) = \frac{1}{3}$，则 $f^{-1}(x) = $\_\_\_\_\_\_\_。