原函数与反函数训练题20201027
- 格式:docx
- 大小:1.03 MB
- 文档页数:27

反函数基础练习含答案-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN反函数基础练习(一)选择题1.函数y =-x 2(x ≤0)的反函数是[ ]A y (x 0)B y (x 0)C y (x 0)D y |x|.=-≥.=≤.=-≤.=-x x x --2.函数y =-x(2+x)(x ≥0)的反函数的定义域是[ ]A .[0,+∞)B .[-∞,1]C .(0,1]D .(-∞,0]3y 1(x 2).函数=+≥的反函数是x -2[ ]A .y =2-(x -1)2(x ≥2)B .y =2+(x -1)2(x ≥2)C .y =2-(x -1)2(x ≥1)D .y =2+(x -1)2(x ≥1)4.下列各组函数中互为反函数的是[ ]A y y xB y y 2.=和=.=和=x x x11C y y (x 1)D y x (x 1)y (x 0)2.=和=≠.=≥和=≥3131311x x x x x +-+-5.如果y =f(x)的反函数是y =f -1(x),则下列命题中一定正确的是[ ]A .若y =f(x)在[1,2]上是增函数,则y =f -1(x)在[1,2]上也是增函数B .若y =f(x)是奇函数,则y =f -1(x)也是奇函数C .若y =f(x)是偶函数,则y =f -1(x)也是偶函数D .若f(x)的图像与y 轴有交点,则f -1(x)的图像与y 轴也有交点 6.如果两个函数的图像关于直线y =x 对称,而其中一个函数是y =-,那么另一个函数是x -1[ ]A .y =x 2+1(x ≤0)B .y =x 2+1(x ≥1)C .y =x 2-1(x ≤0)D .y =x 2-1(x ≥1)7.设点(a,b)在函数y=f(x)的图像上,那么y=f-1(x)的图像上一定有点[ ] A.(a,f-1(a))B.(f-1(b),b)C.(f-1(a),a)D.(b,f-1(b))8.设函数y=f(x)的反函数是y=g(x),则函数y=f(-x)的反函数是[ ] A.y=g(-x)B.y=-g(x)C.y=-g(-x) D.y =-g-1(x)9.若f(x-1)=x2-2x+3(x≤1),则函数f-1(x)的草图是[ ]10y g(x).函数=的反函数是,则13x[ ]A .g(2)>g(-1)>g(-3)B .g(2)>g(-3)>g(-1)C .g(-1)>g(-3)>g(2)D .g(-3)>g(-1)>g(2) (二)填空题1y 32y (x 0)y f(x)y x .函数=+的反函数是..函数=>与函数=的图像关于直线=对称,x x ++2121 解f(x)=________.3.如果一次函数y =ax +3与y =4x -b 的图像关于直线y =x 对称,那a =________,b =________.4y (1x 0).函数=-<<的反函数是,反函数的定92-x义域是________.5.已知函数y =f(x)存在反函数,a 是它的定义域内的任意一个值,则f -1(f(a))=________.6y 7y (x 1)(x 1)8f(x)(x 1)f ()1.函数=的反函数的值域是..函数=≥-<的反函数是:..函数=<-,则-=.121121232x x x x ---⎧⎨⎪⎩⎪-- (三)解答题1y 12f(x).求函数=+的反函数,并作出反函数的图像..已知函数=.x ax x +++252 (1)求函数y =f(x)的反函数y =f -1(x)的值域;(2)若点P(1,2)是y =f -1(x)的图像上一点,求函数y =f(x)的值域.3.已知函数y =f(x)在其定义域内是增函数,且存在反函数,求证y =f(x)的反函数y =f -1(x)在它的定义域内也是增函数.4f(x)y g(x)y f (x 1).设函数=,函数=的图像是=+的图像2311x x +-- 关于y =x 对称,求g(2)的值.参考答案(一)选择题1.(C).解:函数y=-x 2(x ≤0)的值域是y ≤0,由y=-x 2得x=--,∴反函数--≤.y x f (x)=(x 0)1-2.(D).解:∵y=-x 2-2x=-(x +1)2,x ≥0,∴函数值域y ≤0,即其反函数的定义域为x ≤0.3(D)y =x 21x 2y 1y =x 2..解:∵-+,≥,∴函数值域≥,由- +1,得反函数f -1(x)=(x -1)2+1,(x ≥1).4.(B).解:(A)错.∵y=x 2没有反函数.(B)中如两个函数互为反函数.中函数+-≠的反函数是+-≠而不是+-.中函数≥的值域为≥.应是其反函数的定义域≥.但中的定义域≥,故中两函数不是互为反函数.(C)y =3x 1x (x 1)y =x 1x 3(x 3)y =3x 13x 1(D)y =x (x 1)y 1x 1y =x x 0(D)21 5.(B).解:(A)中.∵y=f(x)在[1,2]上是增函数.∴其反函数y=f -1(x)在[f(1),f(2)]上是增函数,∴(A)错.(B)对.(C)中如y=f(x)=x 2是偶函数但没有反函数.∴(C)错.(D)中如函数f(x)=x 2+1(x ≥0)的图像与y 轴有交点,但其反函数-≥的图像与轴没有交点.∴错.f -(x)=x 1(x 1)y (D)16(A)y =y 0f (x)=x 12..解:∵函数--的值域≤;其反函数+x 1- +1(x ≤0).选(A).7.(D).解:∵点(a ,b)在函数y=f(x)的图像上,∴点(b ,a)必在其反函数y=f -1(x)的图像上,而a=f -1(b),故点(b ,f -1(b))在y=f -1(x)的图像上.选(D).8.(B).解:∵y=f(x)的反函数是y=f -1(x)即g(x)=f -1(x),而y=f(-x)的反函数是y=-f -1(x)=-g(x),∴选(B).9.(C).解:令t=x -1.∵x ≤1,∴t ≤0,f(t)=t 2+2(t ≤0),即f(x)=x 2+2(x ≤0),值域为f(x)≥2,∴反函数f -1(x)的定义域是x ≥2,值域y ≤0,故选(C).10(B)g(x)=1x (0)33..解:∵在-∞,上是减函数,又-<-<100g(3)g(1)g(2)=120g(2)g(3)g(1)3,∴>->-而>,∴>->-.故选 (B). (二)填空题1y =3y 3y =x 6x 2.解:∵函数++的值域≥,其反函数-+x 27( x ≥3)2y =12x 1(x 0)y 1f(x)=1x2x(x 1).解:+>的值域<,其反函数-<. 3y =4x b y =14x x =ax .解:函数-的反函数是+,则++,b b41443 比较两边对应项系数得,.a =14b =12 4y =9x (1x 0)y (223)2.解:函数--<<的值域∈,,反函数f 1 (x)=(223)--.反函数的定义为,.92x5.a6.[0,2)∪(2,+∞)7f (x)=x 1(x 1)1x(x 0)122.+≥-<-⎧⎨⎪⎩⎪8.-2 (三)解答题1x 2y 1y=x 21=.解:∵≥-,得值域为≥.由++得反函数f x -1() (x -1)2-2,(x ≥1),其图像如右图.2.解(1):∵y=f(x)的定义域是{x|x ≠1,x ∈R ,∴y=f -1(x)的值域是{y|y ≠1,y ∈R}.解(2):∵点P(1,2)在,y=f -1(x)的图像上,点P(1,2)关于直线y=x的对称点为′,一定在的图像上,即由++得-,∴-+,其反函数-+.∵的定义域为≠-,∈,∴的值域为≠-,∈.P (21)y =f(x)=1a =f(x)=10x 2x 4f -(x)=104x2x 1f -(x){x|x x R}y =f(x){y|y y R}112522121212a3.证明略.4f(x)=2x 3x 1f -(x)=x 3f (x 1)=11.略解;+-的反函数是+-,∴+x 2-x4 x1x4x1=2x=6g(2)=6+-,由+-得即.。



反函数练习题反函数是数学中的一个重要概念,它与函数之间的关系密切相关。
在本文中,我们将通过一些练习题来加深对反函数的理解和运用。
题目一:求反函数已知函数f(x) = 2x - 3,求其反函数f^{-1}(x)。
解析:为求反函数f^{-1}(x),我们先将f(x)写成关于x的等式y = 2x - 3。
接下来,我们将x和y交换位置,得到x = 2y - 3。
接下来,解出y,即可得到反函数f^{-1}(x)。
将x = 2y - 3两边加3,得到x + 3 = 2y。
再将等式两边同时除以2,得到(y = (x + 3)/2)。
所以,反函数f^{-1}(x) = (x + 3)/2。
题目二:验证反函数已知函数f(x) = 4x - 5,求其反函数f^{-1}(x)并验证是否为反函数。
解析:首先,我们仍然将f(x)写成关于x的等式y = 4x - 5。
然后,将x和y交换位置,得到x = 4y - 5。
再次解出y,即可得到反函数f^{-1}(x)。
将x = 4y - 5两边加5,得到x + 5 = 4y。
再将等式两边同时除以4,得到((x + 5)/4 = y)。
所以,反函数f^{-1}(x) = (x + 5)/4。
为了验证f^{-1}(x)是否为f(x)的反函数,我们需要计算复合函数f(f^{-1}(x))和f^{-1}(f(x)),并判断它们是否等于x。
首先,计算f(f^{-1}(x)) = f((x + 5)/4)。
将(x + 5)/4代入f(x)的表达式中,得到f(f^{-1}(x)) = 4((x + 5)/4) - 5 = x - 1。
我们可以看到,f(f^{-1}(x))得到了x。
接下来,计算f^{-1}(f(x)) = f^{-1}(4x - 5)。
将4x - 5代入f^{-1}(x)的表达式中,得到f^{-1}(f(x)) = ((4x - 5) + 5)/4 = x。
我们可以看到,f^{-1}(f(x))也得到了x。

初三数学下册反函数练习题反函数是数学中一个重要的概念,在初三数学下册中也有一些关于反函数的练习题。
下面将通过一些例题,帮助大家更好地理解和掌握相关知识。
1.已知函数f(x) = 2x + 3,求其反函数f^{-1}(x)。
解答:首先,我们将f(x)表示为y = 2x + 3。
然后,交换x和y的位置,得到x = 2y + 3。
接下来,将此方程关于y解出,得到y = \frac{{x -3}}{2}。
最后,将y替换为f^{-1}(x),得到反函数f^{-1}(x) = \frac{{x - 3}}{2}。
2.已知函数g(x) = \sqrt{x},求其反函数g^{-1}(x)。
解答:类似地,我们将g(x)表示为y = \sqrt{x},然后将x和y的位置交换,得到x = \sqrt{y}。
为了解出y,我们两边平方,得到x^2 = y。
最后,将y替换为g^{-1}(x),得到反函数g^{-1}(x) = x^2。
3.已知函数h(x) = \frac{1}{x + 2},求其反函数h^{-1}(x)。
解答:将h(x)表示为y = \frac{1}{x + 2},交换x和y的位置,得到x =\frac{1}{y + 2}。
我们可以通过一系列的步骤将y解出来。
首先,将x的分母移至等号右侧,得到xy + 2x = 1。
然后,将y的系数提取出来,得到xy = 1 - 2x。
最后,将y替换为h^{-1}(x),得到反函数h^{-1}(x) = \frac{1 - 2x}{x}。
通过上面几个例题,我们可以看到,求一个函数的反函数主要是通过将函数的自变量和因变量进行交换,并解出关于自变量的方程来得到反函数的表达式。
反函数在数学中有着广泛的应用。
它可以用于解决方程、求解逆运算以及构建函数的复合和函数图像的翻转等问题。
因此,掌握反函数的概念和求解方法对于学习数学和解题都是非常重要的。
当然,反函数也有着一些限制条件。
在求反函数时,要确保原函数是一一对应的,并且反函数在定义域和值域上是有定义的。

利用反函数求值练习题反函数是指原函数经过变换得到的新函数,它的定义域和值域与原函数相反。
利用反函数求值是一种常见的数学问题,通过给定函数的反函数,可以通过给定的函数值来求得相应的自变量值。
本文将介绍一些反函数求值练习题,以帮助读者更好地理解和应用反函数的概念。
在介绍具体的练习题之前,我们先回顾一下反函数的定义和性质。
对于函数f(x)和它的反函数f^{-1}(x),满足以下条件:1. f(f^{-1}(x)) = x,即函数f和它的反函数f^{-1}互为反函数;2. f^{-1}(f(x)) = x,即函数f和它的反函数f^{-1}互为反函数。
基于上述性质,我们可以利用反函数求解一些特定的数值问题。
下面是几个具体实例,希望能对读者有所帮助:例题一:已知函数y = f(x) = 2x - 3,求f^{-1}(5)的值。
解析:根据反函数的定义和性质,求解f^{-1}(5)即为求解f(x) = 5的解。
我们可以使用方程2x - 3 = 5,得到x = 4。
因此,f^{-1}(5)的值为4。
例题二:已知函数y = g(x) = \frac{1}{x-2},求g^{-1}(3)的值。
解析:同样地,根据反函数的性质,我们要求解g^{-1}(3)即为求解g(x) = 3的解。
将3代入函数g(x),我们得到\frac{1}{x-2} = 3,通过变换可得x - 2 = \frac{1}{3},解得x = \frac{7}{3}。
因此,g^{-1}(3)的值为\frac{7}{3}。
例题三:已知函数y = h(x) = \sqrt{x+4},求h^{-1}(9)的值。
解析:类似地,我们要求解h^{-1}(9)即为求解h(x) = 9的解。
将9代入函数h(x),我们得到\sqrt{x+4} = 9,通过变换可得x + 4 = 81,解得x = 77。
因此,h^{-1}(9)的值为77。
通过以上例题,我们可以看到反函数求值的基本思路,即将给定的函数值代入函数表达式,通过变换和求解方程得到相应的自变量值。

反函数练习(含详细解析)反函数练习一.填空题1.若f(x)=(x﹣1)2(x≤1),则其反函数f﹣1(x)=.2.定义在R上的函数f(x)=2x﹣1的反函数为y=f﹣1(x),则f﹣1(3)=3.若函数f(x)=x a的反函数的图象经过点(,),则a=.4.已知函数f(x)=2x﹣1的反函数是f﹣1(x),则f﹣1(5)=.5.函数y=x2+2(﹣1≤x≤0)的反函数是f﹣1(x)=.6.已知函数f(x)=2x+m,其反函数y=f﹣1(x)图象经过点(3,1),则实数m 的值为.7.设f﹣1(x)为的反函数,则f﹣1(1)=.8.函数f(x)=x2,(x<﹣2)的反函数是.9.函数的反函数是.10.函数y=x2+3(x≤0)的反函数是.11.设函数f(x)=3x,若g(x)为函数f(x)的反函数,则g (1)=.12.设函数y=f(x)存在反函数y=f﹣1(x),且函数y=x ﹣f(x)的图象经过点(2,5),则函数y=f﹣1(x)+3的图象一定过点.13.函数(x≤0)的反函数是.14.已知函数,则=.15.函数的反函数为f﹣1(x)=.16.函数的反函数的值域是.17.函数f(x)=x2﹣2(x<0)的反函数f﹣1(x)=.18.设f(x)=4x﹣2x+1(x≥0),则f﹣1(0)=.19.若函数y=ax+8与y=﹣x+b的图象关于直线y=x对称,则a+b=.20.已知函数f(x)=log2(x2+1)(x≤0),则f﹣1(2)=.参考答案一.填空题(共20小题)1.1﹣(x≥0);2.2;3.;4.3;5.,x∈[2,3];6.1;7.1;8.;9.f﹣1(x)=(x﹣1)2(x≥1);10.y=﹣(x ≥3);11.0;12.(﹣3,5);13.(x≥﹣1);14.﹣2;15.,(x∈(0,1));16.;17.(x>﹣2);18.1;19.2;20.﹣;。

反函数基础练习含标准答案.doc反函数基础练习含标准答案一、选择题1.设函数f(x) = 2x + 3,那么它的反函数是: A. f(x) = 2x + 3 B. f(x)= (x - 3) / 2 C. f(x) = (x + 3) / 2 D. f(x) = (x - 3) / 2 + 3答案:C2.设函数f(x) = x^2,那么它的反函数是: A. f(x) = x^2 B. f(x) = √xC. f(x) = x^(1/2)D. f(x) = x^2 - 1答案:B3.设函数f(x) = e^x,其中e为自然对数的底数,那么它的反函数是: A.f(x) = e^x B. f(x) = ln(x) C. f(x) = e^(1/x) D. f(x) = ln(e^x)答案:B4.设函数f(x) = |x|,那么它的反函数是: A. f(x) = |x| B. f(x) = x C.f(x) = -x D. f(x) = x^2答案:B5.设函数f(x) = x^3,那么它的反函数是: A. f(x) = x^3 B. f(x) = ∛x C.f(x) = x^(1/3) D. f(x) = x^2 - 1答案:C二、填空题1.设函数f(x) = 2x + 1,那么它的反函数是________。
答案:f(x) = (x -1) / 22.设函数f(x) = x^2,那么它的反函数是________。
答案:f(x) = √x3.设函数f(x) = e^x,其中e为自然对数的底数,那么它的反函数是________。
答案:f(x) = ln(x)4.设函数f(x) = |x|,那么它的反函数是________。
答案:f(x) = x5.设函数f(x) = x^3,那么它的反函数是________。
答案:f(x) = ∛x三、计算题1.设函数f(x) = 2x + 1,求它的反函数f^(-1)(x)。

反函数的练习题反函数是数学中一个重要的概念,用于描述两个函数之间的逆关系。
在这篇文章中,我们将探讨一些关于反函数的练习题,帮助读者更好地理解和应用这一概念。
1. 将函数f(x) = 2x + 3表示为反函数的形式。
解法:首先,我们将f(x)表示为y = 2x + 3的形式。
然后,我们将x和y互换,得到x = 2y + 3。
接下来,解出y,得到y = (x - 3) / 2。
因此,将函数f(x)表示为反函数的形式为f^(-1)(x) = (x - 3) / 2。
2. 判断函数f(x) = x^2是否有反函数,并给出理由。
解析:要判断函数是否有反函数,我们需要检查函数是否是一对一函数。
一对一函数是指每个自变量对应一个唯一的因变量,即函数图像没有重复的点。
对于函数f(x) = x^2,我们可以看到它的图像是一个开口向上的抛物线。
由于抛物线的每个y值可以由两个x值得到(正负根),所以函数f(x) = x^2并没有反函数。
3. 确定函数f(x) = e^x的反函数。
解法:为了确定函数f(x) = e^x的反函数,我们将f(x)表示为y = e^x的形式。
然后,我们将x和y互换,得到x = e^y。
接下来,解出y,得到y = ln(x)。
因此,函数f(x) = e^x的反函数为f^(-1)(x) = ln(x)。
4. 给定函数f(x) = 3x - 5,求f(x)和其反函数f^(-1)(x)在x = 2处的值。
解法:首先,我们计算f(x)在x = 2处的值。
将x = 2代入函数f(x) = 3x - 5,得到f(2) = 3(2) - 5 = 1。
其次,我们计算反函数f^(-1)(x)在x = 2处的值。
将x = 2代入反函数f^(-1)(x) = (x + 5) / 3,得到f^(-1)(2) = (2 + 5) / 3 = 7/3。
因此,函数f(x)在x = 2处的值为1,其反函数f^(-1)(x)在x = 2处的值为7/3。
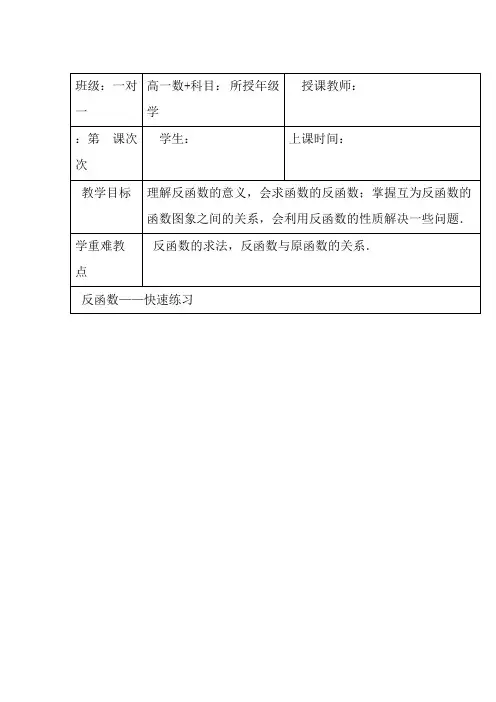

反函数练习题(打印版)### 反函数练习题#### 一、选择题1. 若函数 \( f(x) = 2x + 3 \) 的反函数是 \( f^{-1}(x) \),求\( f^{-1}(-1) \) 的值。
- A. -5- B. -3- C. 0- D. 12. 已知 \( g(x) = x^2 \) 的反函数是 \( g^{-1}(x) \),求\( g^{-1}(4) \) 的值。
- A. 2- B. -2- C. 4- D. ±23. 函数 \( h(x) = \log_{10} x \) 的反函数是 \( h^{-1}(x) \),求 \( h^{-1}(100) \) 的值。
- A. 2- B. 3- C. 4- D. 5#### 二、填空题4. 函数 \( f(x) = \sqrt{x + 1} \) 的反函数是 \( f^{-1}(x) \),当 \( x = 4 \) 时,求 \( f^{-1}(x) \) 的值。
5. 若 \( y = 3^x \),求 \( x \) 关于 \( y \) 的反函数表达式。
6. 函数 \( s(x) = \frac{1}{x} \) 的反函数是 \( s^{-1}(x) \),当 \( x = 0.5 \) 时,求 \( s^{-1}(x) \) 的值。
#### 三、解答题7. 已知函数 \( p(x) = 4x - 1 \),求其反函数,并计算 \( p^{-1}(5) \)。
8. 函数 \( q(x) = 2^x \) 有反函数吗?如果有,请写出其反函数,并计算 \( q^{-1}(8) \)。
9. 函数 \( r(x) = 5x + 7 \) 的反函数是 \( r^{-1}(x) \),求\( r^{-1}(12) \)。
#### 四、应用题10. 某工厂生产的产品数量与价格之间的关系由函数 \( v(x) = 100 - 0.5x \) 表示,其中 \( x \) 表示产品数量,\( v \) 表示价格。
高三数学反函数试题1.函数的反函数为_______.【答案】【解析】由题意得,,所以反函数为.【考点】反函数.2.已知函数,则.【答案】1【解析】因为,所以因此【考点】反函数3.设点在曲线上,点Q在曲线上,则最小值为()A.B.C.D.【答案】B【解析】函数与函数互为反函数,图象关于对称函数上的点到直线的距离为.设函数,由图象关于对称得:最小值为.4.已知,设函数的零点为,的零点为,则的最大值为( )A.B.C.D.【答案】B【解析】由得,函数的零点为,即的图象相交于点;由得,函数的零点为,即的图象相交于点因为互为反函数,所以,即且,由基本不等式得,当且仅当时“=”成立,所以的最大值为.故选.【考点】函数的零点,反函数的图象和性质,基本不等式.5.已知函数的反函数满足,则的最小值为()A.B.C.D.【答案】C【解析】函数的反函数为又,所以且 , .【考点】反函数,对数运算,均值不等式6..设的反函数的解析式是,【答案】【解析】解:因为,那么配凑变形可知的反函数的解析式是7.如果函数的图象与函数的图象关于直线对称,则的单调递减区间是A.B.C.D.【答案】D【解析】函数f(x)与g(x)互为反函数,所以,所以由,所以函数的单调递减区间为8.函数,则函数()A.B.C.D.【答案】C【解析】此题考查函数解析式和反函数的求法、考查反函数性质;【解法一】利用反函数性质:即;设,所以选C【解法二】因为,选C9.函数的图像与图像关于直线对称,则函数的单调增区间是__________【答案】【解析】略10.已知函数,则的反函数是A.B.C.D.【答案】A【解析】本题考查反函数概念,能根据原函数求出反函数.由得:则的反函数为.故选A11.函数的反函数为A.B.C.D.【答案】B【解析】由得:则反函数为故选B12.(本小题满分12分) 设a > 1,函数.(1)求的反函数;(2)若在[0,1]上的最大值与最小值互为相反数,求a的值;(3)若的图象不经过第二象限,求a的取值范围.【答案】解:(1) 由∴∴··································································· 4分(2) ∵ a > 1 ∴在[0,1]上递增∴,∴即∴······························································································· 8分(3) 在y轴上的截距为要使的图象不过第二象限,只需∴∴因此,a的取值范围为····································································· 12分【解析】略13.已知的图象关于点对称且存在反函数,若,则()A.B.C.D.【答案】A【解析】本题考查函数图像的对称性,反函数的概念,互为反函数的关系.若的反函数为则因为函数的图像关于点对称,所以则即则故选A14.(13分)已知的反函数为.(1)若函数在区间上单增,求实数的取值范围;(2)若关于的方程在内有两个不相等的实数根,求实数的取值范围.【答案】解:(1),因为,故题意在上单增且恒正,故必有于是且,解得;(2)方程,令,因为,故当时题意等价于方程即有两个不相等的正数根,故【解析】略15.已知函数的图象与函数的图象关于直线对称,则()A.B.C.D.【答案】A【解析】本题考查反函数的概念及互为反函数的图像性质及基本运算.因为指数函数与对数函数是互为反函数,互为反函数的函数图像关于直线对称;所以则故选A16.已知函数的反函数为(),则函数的图象必过定点()A.(1,0)B.(0,1)C.(-1,0)D.(0,-1)【答案】A【解析】略17.已知函数f(x)=()x,函数y=f-1(x)是函数y=f(x)的反函数.(1)若函数y=f-1(mx2+mx+1)的定义域为R,求实数m的取值范围;(2)当x∈[-1,1]时,求函数y=[f(x)]2-2af(x)+3的最小值g(a);(3)是否存在实数m>n>3,使得g(x)的定义域为[n,m],值域为[n2,m2]?若存在,求出m、n 的值;若不存在,请说明理由【答案】(1)∵f-1(x)=logx(x>0),∴f-1(mx2+mx+1)=log(mx2+mx+1),由题知,mx2+mx+1>0恒成立,∴①当m=0时,1>0满足题意;②当m≠0时,应有⇒0<m<4,∴实数m的取值范围为0≤m<4.(2)∵x∈[-1,1],∴()x∈[,3],y=[f(x)]2-2af(x)+3=[()x]2-2a()x+3=[()x-a]2+3-a2,当a<时,=g(a)=-;ymin当≤a≤3时,=g(a)=3-a2;ymin当a>3时,y=g(a)min=12-6a.∴g(a)=(3)∵m>n>3,且g(x)=12-6x在(3,+∞)上是减函数.又g(x)的定义域为[n,m],值域为[n2,m2].∴②-①得:6(m-n)=(m+n)(m-n)∵m>n>3,∴m+n=6.但这与“m>n>3”矛盾.∴满足题意的m、n不存在.【解析】略18.已知函数的反函数是,则函数的图像必过定点()A.B.C.D.【答案】D【解析】略19.函数的反函数是_______ ___.【答案】【解析】略20.若函数存在反函数,且函数的图像过点,则函数的图象一定过点()A.B.C.D.【答案】D【解析】略21.已知函数的定义域为R,它的反函数为,如果与互为反函数,且,则的值为()A.B.0C.D.【答案】B【解析】略22.【答案】f -1(x) = e2x(x∈R)【解析】略23.已知在区间上的反函数是其本身,则可以是()A.B.C.D.【答案】B【解析】略24.函数的反函数是()A.B.C.D.【答案】D【解析】略25.函数f(x)=的反函数是()A.B.C.D.【答案】B【解析】略26.已知函数的反函数的对称中心为(-1,3),则实数a的值为。
反函数基础练习(一)选择题1.函数y =-x 2(x ≤0)的反函数是[ ]A y (x 0)B y (x 0)C y (x 0)D y |x|.=-≥.=≤.=-≤.=-x x x --2.函数y =-x(2+x)(x ≥0)的反函数的定义域是 [ ]A .[0,+∞)B .[-∞,1]C .(0,1]D .(-∞,0]3y 1(x 2).函数=+≥的反函数是x -2[ ]A .y =2-(x -1)2(x ≥2)B .y =2+(x -1)2(x ≥2)C .y =2-(x -1)2(x ≥1)D .y =2+(x -1)2(x ≥1)4.下列各组函数中互为反函数的是[ ]A y y xB y y 2.=和=.=和=x x x11C y y (x 1)D y x (x 1)y (x 0)2.=和=≠.=≥和=≥3131311x x x x x +-+-5.如果y =f(x)的反函数是y =f -1(x),则下列命题中一定正确的是[ ]A .若y =f(x)在[1,2]上是增函数,则y =f -1(x)在[1,2]上也是增函数B .若y =f(x)是奇函数,则y =f -1(x)也是奇函数C.若y=f(x)是偶函数,则y=f-1(x)也是偶函数D.若f(x)的图像与y轴有交点,则f-1(x)的图像与y轴也有交点6.如果两个函数的图像关于直线y=x对称,而其中一个函数是x 1y=-,那么另一个函数是[ ] A.y=x2+1(x≤0)B.y=x2+1(x≥1)C.y=x2-1(x≤0)D.y=x2-1(x≥1)7.设点(a,b)在函数y=f(x)的图像上,那么y=f-1(x)的图像上一定有点[ ] A.(a,f-1(a))B.(f-1(b),b)C.(f-1(a),a) D.(b,f-1(b))8.设函数y=f(x)的反函数是y=g(x),则函数y=f(-x)的反函数是[ ] A.y=g(-x) B.y=-g(x)C.y=-g(-x) D.y=-g-1(x)9.若f(x-1)=x2-2x+3(x≤1),则函数f-1(x)的草图是[ ]10y g(x).函数=的反函数是,则13x[ ]A .g(2)>g(-1)>g(-3)B .g(2)>g(-3)>g(-1)C .g(-1)>g(-3)>g(2)D .g(-3)>g(-1)>g(2) (二)填空题1y 32y (x 0)y f(x)y x .函数=+的反函数是..函数=>与函数=的图像关于直线=对称,x x ++2121 解f(x)=________.3.如果一次函数y =ax +3与y =4x -b 的图像关于直线y =x 对称,那a =________,b =________.4y (1x 0).函数=-<<的反函数是,反函数的定92-x义域是________.5.已知函数y =f(x)存在反函数,a 是它的定义域内的任意一个值,则f -1(f(a))=________.6y 7y (x 1)(x 1)8f(x)(x 1)f ()1.函数=的反函数的值域是..函数=≥-<的反函数是:..函数=<-,则-=.121121232x x x x ---⎧⎨⎪⎩⎪--(三)解答题1y 12f(x).求函数=+的反函数,并作出反函数的图像..已知函数=.x ax x +++252(1)求函数y =f(x)的反函数y =f -1(x)的值域;(2)若点P(1,2)是y =f -1(x)的图像上一点,求函数y =f(x)的值域.3.已知函数y =f(x)在其定义域内是增函数,且存在反函数,求证y =f(x)的反函数y =f -1(x)在它的定义域内也是增函数.4f(x)y g(x)y f (x 1).设函数=,函数=的图像是=+的图像2311x x +-- 关于y =x 对称,求g(2)的值.参考答案(一)选择题1.(C).解:函数y=-x 2(x ≤0)的值域是y ≤0,由y=-x 2得x=--,∴反函数--≤.y x f (x)=(x 0)1-2.(D).解:∵y=-x 2-2x=-(x +1)2,x ≥0,∴函数值域y ≤0,即其反函数的定义域为x ≤0.3(D)y =x 21x 2y 1y =x 2..解:∵-+,≥,∴函数值域≥,由-+1,得反函数f -1(x)=(x -1)2+1,(x ≥1).4.(B).解:(A)错.∵y=x 2没有反函数.(B)中如两个函数互为反函数.中函数+-≠的反函数是+-≠而不是+-.中函数≥的值域为≥.应是其反函数的定义域≥.但中的定义域≥,故中两函数不是互为反函数.(C)y =3x 1x (x 1)y =x 1x 3(x 3)y =3x 13x 1(D)y =x (x 1)y 1x 1y =x x 0(D)21 5.(B).解:(A)中.∵y=f(x)在[1,2]上是增函数.∴其反函数y=f -1(x)在[f(1),f(2)]上是增函数,∴(A)错.(B)对.(C)中如y=f(x)=x 2是偶函数但没有反函数.∴(C)错.(D)中如函数f(x)=x 2+1(x ≥0)的图像与y 轴有交点,但其反函数-≥的图像与轴没有交点.∴错.f -(x)=x 1(x 1)y (D)1 6(A)y =y 0f (x)=x 12..解:∵函数--的值域≤;其反函数+x 1-+1(x ≤0).选(A).7.(D).解:∵点(a ,b)在函数y=f(x)的图像上,∴点(b ,a)必在其反函数y=f -1(x)的图像上,而a=f -1(b),故点(b ,f -1(b))在y=f -1(x)的图像上.选(D).8.(B).解:∵y=f(x)的反函数是y=f -1(x)即g(x)=f -1(x),而y=f(-x)的反函数是y=-f -1(x)=-g(x),∴选(B).9.(C).解:令t=x -1.∵x ≤1,∴t ≤0,f(t)=t 2+2(t ≤0),即f(x)=x 2+2(x ≤0),值域为f(x)≥2,∴反函数f -1(x)的定义域是x ≥2,值域y ≤0,故选(C).10(B)g(x)=1x (0)33..解:∵在-∞,上是减函数,又-<-<100g(3)g(1)g(2)=120g(2)g(3)g(1)3,∴>->-而>,∴>->-.故选 (B).(二)填空题1y =3y 3y =x 6x 2.解:∵函数++的值域≥,其反函数-+x 27(x ≥3)2y =12x 1(x 0)y 1f(x)=1x2x(x 1).解:+>的值域<,其反函数-<. 3y =4x b y =14x x =ax .解:函数-的反函数是+,则++,b b41443比较两边对应项系数得,.a =14b =12 4y =9x (1x 0)y (223)2.解:函数--<<的值域∈,,反函数f -1 (x)=(223)--.反函数的定义为,.92x5.a6.[0,2)∪(2,+∞)7f (x)=x 1(x 1)1x(x 0)122.+≥-<-⎧⎨⎪⎩⎪8.-2(三)解答题1x 2y 1y =x 21=.解:∵≥-,得值域为≥.由++得反函数f x -1()(x -1)2-2,(x ≥1),其图像如右图.2.解(1):∵y=f(x)的定义域是{x|x ≠1,x ∈R ,∴y=f -1(x)的值域是{y|y ≠1,y ∈R}.解(2):∵点P(1,2)在,y=f -1(x)的图像上,点P(1,2)关于直线y=x的对称点为′,一定在的图像上,即由++得-,∴-+,其反函数-+.∵的定义域为≠-,∈,∴的值域为≠-,∈.P (21)y =f(x)=1a =f(x)=10x 2x 4f -(x)=104x 2x 1f -(x){x|x x R}y =f(x){y|y y R}112522121212a3.证明略.4f(x)=2x 3x 1f -(x)=x 3f (x 1)=11.略解;+-的反函数是+-,∴+x 2x 4x 1x 4x 1=2x =6g(2)=6+-,由+-得即.。
关于反函数的练习题反函数是数学中一个常见且重要的概念,它指的是对于给定函数f(x),存在一个函数 g(x) 使得对于所有的 x 在定义域中成立 g(f(x)) = x。
反函数可以帮助我们求出原函数的逆变换,从而解决一系列实际问题。
为了更好地理解和掌握反函数的性质,下面将给出一些有关反函数的练习题,希望能够帮助读者更好地理解和应用反函数。
题目一:设函数 f(x) = 2x + 3,求反函数 g(x) 的表达式。
首先,我们先假设 g(x) = y,根据反函数的定义,我们有 f(g(x)) = x。
将 f(x) 的表达式代入得到:2g(x) + 3 = x接下来,解方程可以得到g(x) = (x - 3) / 2因此,反函数为 g(x) = (x - 3) / 2。
题目二:已知函数 f(x) = x^2 + 1,求反函数 g(x) 的表达式。
同样地,我们假设 g(x) = y,根据反函数的定义,有 f(g(x)) = x。
代入 f(x) 的表达式得到:(g(x))^2 + 1 = x接下来,解这个二次方程可以得到:g(x) = √(x - 1)题目三:已知函数 f(x) = 3x,求反函数 g(x) 的表达式。
假设 g(x) = y,根据反函数的定义,有 f(g(x)) = x。
代入 f(x) 的表达式得到:3g(x) = x解这个一次方程可以得到:g(x) = x/3通过这些练习题,我们可以发现一些反函数的性质和规律。
首先,对于线性函数 f(x) = a*x + b,其反函数的表达式为 g(x) = (x - b) / a。
这表明了线性函数与其反函数之间存在着一种简单的关系。
其次,平方函数 f(x) = x^2 的反函数是开方函数g(x) = √x。
这一结果说明了平方和开方之间存在着一种互逆的关系,通过平方操作可以获得一个数的平方,通过开方操作可以得到平方根。
最后,我们观察到常数函数 f(x) = c 的反函数也是一个常数函数 g(x) = c',其中 c 可以是任意实数,c' 是 c 的逆元。
反函数练习题反函数是高中数学中的一个重要概念,它与函数的定义域和值域有着密切的关系。
在学习反函数的过程中,练习题是非常重要的一环,通过练习题的解答,可以帮助我们更好地理解和掌握反函数的性质和应用。
本文将通过一些典型的反函数练习题,帮助读者加深对反函数的理解。
1. 练习题一:已知函数f(x) = 2x + 5,求其反函数f^(-1)(x)。
解答:要求函数f(x)的反函数,即求出一个函数f^(-1)(x),使得f^(-1)(f(x)) = x。
根据题目给出的函数f(x) = 2x + 5,我们可以将其表示为y = 2x + 5。
接下来,将x和y互换位置,得到x = 2y + 5。
然后,解方程x = 2y + 5,得到y = (x - 5)/2。
因此,函数f^(-1)(x) = (x - 5)/2。
2. 练习题二:已知函数g(x) = 3x^2 + 1,求其反函数g^(-1)(x)。
解答:同样地,要求函数g(x)的反函数,即求出一个函数g^(-1)(x),使得g^(-1)(g(x)) = x。
根据题目给出的函数g(x) = 3x^2 + 1,我们可以将其表示为y =3x^2 + 1。
接下来,将x和y互换位置,得到x = 3y^2 + 1。
然后,解方程x =3y^2 + 1,得到y = √((x - 1)/3)。
因此,函数g^(-1)(x) = √((x - 1)/3)。
3. 练习题三:已知函数h(x) = e^x,求其反函数h^(-1)(x)。
解答:函数h(x) = e^x是一个指数函数,指数函数的反函数是对数函数。
因此,我们可以得到函数h^(-1)(x) = ln(x),其中ln表示自然对数。
4. 练习题四:已知函数k(x) = sin(x),求其反函数k^(-1)(x)。
解答:函数k(x) = sin(x)是一个三角函数,三角函数的反函数称为反三角函数。
对于函数k(x) = sin(x),其反函数为k^(-1)(x) = arcsin(x),其中arcsin表示反正弦函数。
反函数练习题
大新中学
选择题
已知函数,那么它的反函数为( )
A、B、
C、D、
函数的反函数是( )
A、B、
C、D、
已知点(a,b)在y=f(x)的图像上,则下列各点中位于其反函数图像上的点是()
A、B、C、D、
若函数,则的值为()
A、B、C、15 D、
填空题
函数f(x)是否有反函数?;当时,反函数为,定义域为;当时,反函数为,定义域为。
设f(x)的反函数为,,则,f(3)=
若点(1,2)既在函数的图象上,又在函数f(x)的反函数的图象上,则a= ,b=
f(x)在上为递增函数,则与的大小关系是
解答题
函数y=f(x)的图象是过点(2,1)的直线,其反函数的图象经过点(-2,-1),求函数f(x)
10、函数的反函数为,求a,b,c的值
11、已知,求f(x)
12、函数f(x)=x2-2tx+1(t∈R),定义域为,
(1)f(x)在定义域内是否一定有反函数?
(2)若f(x)有反函数,求t的范围。