人教版八年级数学上河南省虞城县第一初级中学三角形单元测试题.docx

人教版八年级上册《三角形》单元测试卷满分：100分时间：90分钟[典例分析]1．一个三角形的三边长是m 、3 、5，那么m的取值范围是（）A ．3<m<5B ．0<m<5C ．2<m<8D ．0<m<82．下列图形中不具有稳定性的有( )A ．2个B ．3个C ．4个D ．5个3．三角形按边可分为()A ．等腰三角形、直角三角形、锐角三角形B ．直角三角形、不等边三角形C ．等腰三角形、不等边三角形D ．等腰三角形、等边三角形知识点二与三角形有关的线段⏹三角形的高概念：从三角形一个顶点向它的对边做垂线，顶点和垂足之间的线段叫做三角形的高线（简称三角形的高）.⏹三角形的中线概念：在三角形中，连接一个顶点和它对边的中点的线段叫做三角形的中线.性质：三角形三条中线的交于一点，这一点叫做“三角形的重心”.三角形的中线可以将三角形分为面积相等的两个小三角形.⏹三角形的角平分线概念：三角形的一个角的平分线与这个角的对边相交，这个角的顶点和交点间的线段叫做三角形的角平分线. [典例分析]4．下列说法不正确的是（）A ．三角形的三条角平分线相交于三角形内一点.B ．三角形的一条中线把三角形分成面积相等的两个三角形.C ．正多边形的每一个外角都相等.D ．三角形的三条高都在三角形内部.5．三角形的高线是（）A ．直线B ．线段C ．射线D ．三种情况都可能6．如图所示,A D 是△A B C 的角平分线,A E是△A B D 的角平分线.若∠B A C =80°,则∠EA D 的度数是( )A ．20°B ．30°C ．45°D ．60°知识点三与三角形有关的角⏹三角形的内角和定理三角形三个内角和等于180°.推论：①直角三角形的两个锐角互余.②三角形的一个外角等于和它不相邻的来两个内角的和.③三角形的一个外角大于任何一个和它不相邻的内角.备注：在同一个三角形中：等角对等边；等边对等角；大角对大边；大边对大角.等角的补角相等，等角的余角相等.⏹三角形的外角和定理三角形的一边与另一边的延长线组成的角叫做三角形的外角⏹三角形的外角和性质三角形的一个外角等于与它不相邻的两个内角之和. 三角形的一个外角大于与它不相邻的任何一个内角.[典例分析]7．将一块直尺与一块三角板如图放置，若∠1=45°，则∠2的度数为（）A ．145°B ．135°C ．120°D ．115°8．如果三角形的一个外角和与它不相邻的两个内角的和为180°,那么与这个外角相邻的内角的度数为( )A ．30°B ．60°C ．90°D ．120°9．如图，A B ∥EF，C D ⊥EF，∠B A C =50°，则∠A C D =（）A ．120°B ．130°C ．140°D ．150°知识点四多边形及其多边形内角和⏹多边形的概念➢在平面中，由一些线段首尾顺次相接组成的图形叫做多边形，多边形中相邻两边组成的角叫做它的内角.多边形的边与它邻边的延长线组成的角叫做外角.➢连接多边形不相邻的两个顶点的线段叫做多边形的对角线.➢一个n边形从一个顶点出发的对角线的条数为（n－3）条，其所有的对角线条数为2)3(nn⏹凸多边形画出多边形的任何一条边所在的直线，如果多边形的其它边都在这条直线的同侧，那么这个多边形就是凸多边形.⏹正多边形各角相等，各边相等的多边形叫做正多边形.（两个条件缺一不可，除了三角形以外，因为若三角形的三内角相等，则必有三边相等，反过来也成立）⏹多边形的内角和➢n边形的内角和定理：n边形的内角和为(n−2)∙180°➢n边形的外角和定理：多边形的外角和等于360°，与多边形的形状和边数无关.[典例分析]10．下列图形中，不能镶嵌成平面图案的（）A ．正三角形B ．正四边形C ．正五边形D ．正六边形11．当一个多边形的边数增加时，其外角和（）A ．增加B ．减少C ．不变D ．不能确定12．九边形的对角线有（）A ．25条B ．31条C ．27条D ．30条参考答案[典例分析]1．一个三角形的三边长是m 、3 、5，那么m的取值范围是（）A ．3<m<5B ．0<m<5C ．2<m<8D ．0<m<8[答案]C[解析]根据三角形的三边关系即可求出第三边的取值.[详解]∵一个三角形的三边长是m 、3 、5，∴5-3＜x＜5+3即2＜x＜8故选C .点睛：此题主要考查三角形的三边关系，解题的关键是熟知三角形两边的和大于第三边，三角形两边的差小于第三边.2．下列图形中不具有稳定性的有( )A ．2个B ．3个C ．4个D ．5个[答案]B[解析]根据三角形具有稳定性，只要图形分割成了三角形，则具有稳定性．[详解]解：根据三角形具有稳定性，只要图形分割成了三角形，则具有稳定性．显然（2）、（4）、（5）三个．故选B ．点睛：本题主要考查了三角形的稳定性原理，熟练掌握三角形的稳定性原理是解题的关键．3．三角形按边可分为()A ．等腰三角形、直角三角形、锐角三角形B ．直角三角形、不等边三角形C ．等腰三角形、不等边三角形D ．等腰三角形、等边三角形[答案]C[解析]由于三角形按边分类可以分为：等腰三角形和不等边三角形两大类.故选C .知识点二与三角形有关的线段⏹三角形的高概念：从三角形一个顶点向它的对边做垂线，顶点和垂足之间的线段叫做三角形的高线（简称三角形的高）.⏹三角形的中线概念：在三角形中，连接一个顶点和它对边的中点的线段叫做三角形的中线.性质：三角形三条中线的交于一点，这一点叫做“三角形的重心”.三角形的中线可以将三角形分为面积相等的两个小三角形.⏹三角形的角平分线概念：三角形的一个角的平分线与这个角的对边相交，这个角的顶点和交点间的线段叫做三角形的角平分线. [典例分析]4．下列说法不正确的是（）A ．三角形的三条角平分线相交于三角形内一点.B ．三角形的一条中线把三角形分成面积相等的两个三角形.C ．正多边形的每一个外角都相等.D ．三角形的三条高都在三角形内部.[答案]D[解析]利用三角形的中线、角平分线及高的性质和正多边形的外角关系逐一判断后即可确定正确的选项．[详解]A . 三角形的三条角平分线相交于三角形内一点.正确；B . 三角形的一条中线把三角形分成面积相等的两个三角形.正确；C . 正多边形的每一个外角都相等.正确；D . 三角形的三条高不一定在三角形内部，钝角三角形的高在三角形的外部. 此选项错误；故选：D ．点睛：本题考查了三角形的角平分线、中线和高的性质及正多边形的外角，熟练掌握相关性质是解题关键. 5．三角形的高线是（）A ．直线B ．线段C ．射线D ．三种情况都可能[答案]B[解析]由三角形高的定义：“过三角形的一个顶点向对边或对边所在的直线引垂线，顶点到垂足之间的线段叫三角形的高线”可知：三角形的高线是线段.故选B .6．如图所示,A D 是△A B C 的角平分线,A E 是△A B D 的角平分线.若∠B A C =80°,则∠EA D 的度数是( )A ．20°B ．30°C ．45°D ．60°[答案]A[解析]∵A D △A B C 的角平分线，∠B A C =80°，∴∠B A D =∠B A C =40°. 又∵A E 是△A B D 的角平分线，∴∠EA D =∠B A D =20°. 故选A .知识点三 与三角形有关的角⏹ 三角形的内角和定理三角形三个内角和等于180°.推论：①直角三角形的两个锐角互余.②三角形的一个外角等于和它不相邻的来两个内角的和.③三角形的一个外角大于任何一个和它不相邻的内角.备注：在同一个三角形中：等角对等边；等边对等角；大角对大边；大边对大角.等角的补角相等，等角的余角相等.⏹ 三角形的外角和定理三角形的一边与另一边的延长线组成的角叫做三角形的外角⏹ 三角形的外角和性质三角形的一个外角等于与它不相邻的两个内角之和. 三角形的一个外角大于与它不相邻的任何一个内角.[典例分析]7．将一块直尺与一块三角板如图放置，若∠1=45°，则∠2的度数为（ ）1212A ．145°B ．135°C ．120°D ．115°[答案]C[解析]如图：由三角形的外角性质得，∠3=90°+∠1=90°+45°=135°，∵直尺的两边互相平行，∴∠2=∠3=135°．故选：B ．8．如果三角形的一个外角和与它不相邻的两个内角的和为180°,那么与这个外角相邻的内角的度数为( ) A ．30° B ．60° C ．90° D ．120°[答案]C[解析]如图，∠1+∠B +∠A =180°，∵∠1是△A B C 的一个外角，∴∠1=∠A +∠B ，∴2∠1=180°，∴∠1=90°．故选C ．9．如图，A B ∥EF，C D ⊥EF，∠B A C =50°，则∠A C D =（）A ．120°B ．130°C ．140°D ．150°[答案]C [解析]试题分析：如图，延长A C 交EF 于点G ；∵A B ∥EF ，∴∠D GC =∠B A C =50°；∵C D ⊥EF ，∴∠C D G=90°，∴∠A C D =90°+50°=140°，故选C ．考点：垂线的定义；平行线的性质；三角形的外角性质知识点四 多边形及其多边形内角和⏹ 多边形的概念➢ 在平面中，由一些线段首尾顺次相接组成的图形叫做多边形，多边形中相邻两边组成的角叫做它的内角.多边形的边与它邻边的延长线组成的角叫做外角.➢ 连接多边形不相邻的两个顶点的线段叫做多边形的对角线.➢ 一个n 边形从一个顶点出发的对角线的条数为（n －3）条，其所有的对角线条数为⏹ 凸多边形画出多边形的任何一条边所在的直线，如果多边形的其它边都在这条直线的同侧，那么这个多边形就是凸多边形.⏹ 正多边形各角相等，各边相等的多边形叫做正多边形.（两个条件缺一不可，除了三角形以外，因为若三角形的三内角相等，则必有三边相等，反过来也成立）⏹ 多边形的内角和➢ n 边形的内角和定理：n 边形的内角和为(n −2)∙180°➢ n 边形的外角和定理：多边形的外角和等于360°，与多边形的形状和边数无关.[典例分析]10．下列图形中，不能镶嵌成平面图案的（ ）A ．正三角形B ．正四边形C ．正五边形D ．正六边形 [答案]C[解析]几何图形镶嵌成平面的关键是：围绕一点拼在一起的多边形的内角加在一起恰好组成一个周角．[详解]解：A 、正三角形的每一个内角等于60°，6×60°=360°，即能密铺，不合题意；2)3( n nB 、正四边形的每一个内角等于90°，4×90°=360°，即能密铺，不合题意；C 、正五边形每个内角是180°﹣360°÷5=108°，不能整除360°，不能密铺，符合题意；D 、正六边形每个内角是120°，能整除360°，故能密铺，不合题意．故选：C ．点睛：本题考查的知识点是：一种正多边形的镶嵌应符合一个内角度数能整除360°.任意多边形能进行镶嵌,说明它的内角和应能整除360°．11．当一个多边形的边数增加时，其外角和（）A ．增加B ．减少C ．不变D ．不能确定[答案]C[解析]任何多边形的外角和都为360°，则多边形的边数增加时，其外角和是不变的.故选C .12．九边形的对角线有（）A ．25条B ．31条C ．27条D ．30条[答案]C[解析]试题解析：从n边形的一个顶点可以引(n−3)条对角线，n边形一共有n(n−3)2条对角线.当n=9时，n(n−3)2=9×62=27.故选C .点睛：n边形一共有n(n−3)2条对角线.。

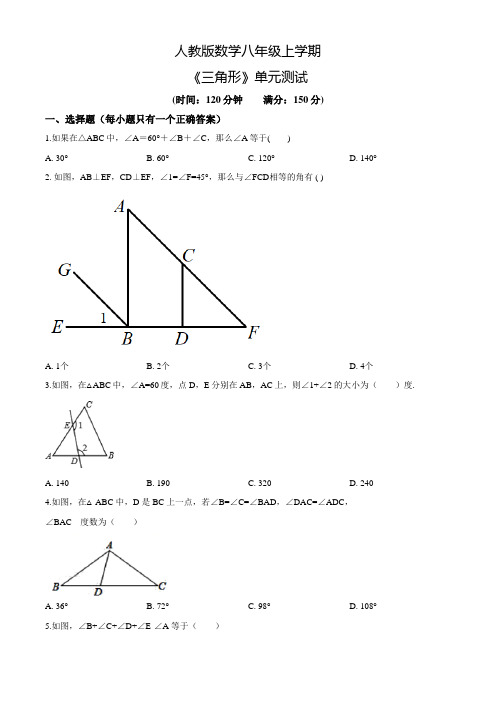
新人教版八年级数学上册《三角形》单元测试卷及答案考试时间：100分钟；命题人：七年级数学备课组题号一二三总分得分评卷人得分一、选择题1、以下列各组线段为边，能构成三角形的是（）A．2，3，6 B．3，4，5 C．2，7，9 D．，3，2、已知等腰三角形的其中二边长分别为4，9，则这个等腰三角形的周长为（）A．17 B．22 C．17或22 D．无法确定3、五边形的对角线共有（）条。

A．2 B．4 C．5 D．64、若△ABC的边长都是整数，周长为12，且有一边长为4，则这个三角形的最大边长为（）。

A．7 B．6 C．5 D．85、如图，把一副含30°角和45°角的直角三角板拼在一起，那么图中∠ADE是（）A．100°B．120° C．135° D．150°6、等腰三角形的边长是3和8，则它的周长是( )A．11 B．14 C．19 D．14或197、一个三角形三个内角的度数之比为2：3：5，这个三角形一定是（）A．等腰三角形B．直角三角形 C．锐角三角形D．钝角三角形8、如图所示，三角形纸片中，有一个角为60°，剪去这个角后，得到一个四边形，则的度数为（）A．120°B．180°C．240°D．300°9、如图，∠BDC=98°，∠C=38°，∠A=37°，∠B的度数是（）A．33°B．27°C．37°D．23°10、比较下图长方形内阴影部分面积的大小，甲（）乙。

A.＞ B. ＜ C. ＝评卷人得分二、填空题11、如图，梯形的上底是6.5厘米，下底是16厘米。

三角形甲的面积与三角形乙面积的最简比是（_______）。

12、已知△ABC 的两条边长分别为 5 和 8，那么第三边长 x 的取值范围____________-.13、如图，AO⊥CO，直线BD经过O点，且∠1＝20°，则∠COD的度数为_________.14、如图，△ABC的角平分线BO、CO相交于点O，且∠BOC=132°，则∠A=__________．15、已知三角形的三边长分别为3，5，x，则化简式子|x－2|＋|x－9|＝___．16、直线l1∥l2，一块含45°角的直角三角板如图放置，∠1=85°，则∠2=_____．17、如图,DAE是一条直线,DE∥BC，则∠BAC=___度.18、如图，一扇窗户打开后，用窗钩BC可将其固定，这里所运用的几何原理是__________．19、如图，直线a∥b，一块含60°角的直角三角板ABC（∠A=60°）按如图所示放置．若∠1=45°，则∠2的度数为__________20、等腰三角形的一条边长为6，另一边长为13，则它的周长为_______．21、在△ABC中，∠A：∠B：∠C=2：3：4，则∠A=______________度评卷人得分三、解答题22、如图，在⊿ABC中，∠B = 50º，∠C = 70º，AD是高，AE是角平分线，（1）∠BAC=__________,∠DAC=__________。

人教版八年级上册《三角形》单元测试卷满分：100分时间：90分钟一．选择题(共12小题)1．三角形按边可分为()A ．等腰三角形,直角三角形,锐角三角形B ．直角三角形,不等边三角形C ．等腰三角形,不等边三角形D ．等腰三角形,等边三角形2．若三角形两边长分别是4、5,则第三边C 的范围是()A ．1＜C ＜9B ．9＜C ＜14 C ．10＜C ＜18D ．无法确定3．如图在△A B C 中,∠A C B ＞90°,A D ⊥B D ,B E⊥A E,C F⊥A B ,垂足分别是点D 、E、F,则下列说法错误的是()A ．A D 是△AB D 的高 B ．C F是△A B C 的高C ．B E是△A B C 的高D ．B C 是△B C F的高4．已知：如图,A D 是△A B C 的角平分线,A E是△A B C 的外角平分线,若∠D A C ＝20°,问∠EA C ＝()A ．60°B ．70°C ．80°D ．90°5．可以把三角形分成两个面积相等的三角形的是()A ．三角形的中线B ．三角形的高线第4题C ．三角形的角平分线D ．三角形一边的垂线6．在现实的生产、生活中有以下四种情况：①用“人”字梁建筑屋顶；②自行车车梁是三角形结构；③用窗钩来固定窗扇；④商店的推拉防盗铁门．其中用到三角形稳定性的是()A ．①②B ．②③C ．①②③D ．②③④7．在△A B C 中,O为∠C A B 和∠C B A 的角平分线的交点,若∠A OB ＝120°,则∠C 的度数为()A ．120°B ．60°C ．50°D ．308．如图,对任意的五角星,结论正确的是()A ．∠A +∠B +∠C +∠D +∠E＝90° B ．∠A +∠B +∠C +∠D +∠E＝180°C ．∠A +∠B +∠C +∠D +∠E＝270° D ．∠A +∠B +∠C +∠D +∠E＝360°9．直角三角形中有一锐角为15°,则另一锐角为()A ．85°B ．75°C ．15°D ．90°第8题10．角度是多边形的内角和的是()A ．1900°B ．1800°C ．560°D ．270°11．若正多边形的一个外角等于45°,那么这个正多边形的内角和等于()A ．1 080°B ．720°C ．540°D ．360°12．已知△A B C 的三边长分别是A 、B 、C ,化简|A +B ﹣C |﹣|B ﹣A ﹣C |的结果是()A ．2AB ．﹣2BC ．2(A +B )D ．2(B ﹣C )二．填空题(共4小题)13．如图所示,其中∠1＝°．14．如图所示,求∠D +∠E+∠F+∠G+∠M+∠N＝．第13题第14题第15题15．如图,在△A B C 中,A D ⊥B C 于D ,A E为∠B A C 的平分线,且∠D A E＝15°,∠B ＝35°,则∠C ＝°．16．如图,在△A B C 中,∠A ＝m°,∠A B C 和∠A C D 的平分线交于点A 1,得∠A 1,∠A 1B C 和∠A 1C D 的平分线交于点A 2,得∠A 1…；求∠A 2014＝．三．解答题(共8小题)17．已知：在△A B C 中,∠A +∠B ＝2∠C ,∠A ﹣∠B ＝20°,求三角形三个内角的度数．18．已知等腰三角形A B C 中,一腰A C 上的中线B D 将三角形的周长分成9C m和15C m两部分,求这个三角形的腰长和底边的长．19．已知：△A B C 中,B C ＝2C m,A B ＝8C m,A C 的长度是奇数,求△A BC 的周长．20．如图,△A B C 中,∠1＝∠2,∠3＝∠4,∠5＝∠6．∠A ＝60°．求∠EC F、∠FEC 的度数．21．如图,在△A B C C 中,∠A C B ＝90°,C D ⊥A B ,A F 是角平分线,交C D 于点E ．求证：∠1＝∠2．22．如图所示,△A B C 中,∠B ：∠C ＝3：4,FD ⊥B C ,D E ⊥A B ,且∠A FD＝146°,求∠ED F 的度数．23．如图,A D 、A E 分别为△A B C 的高和角平分线,∠B ＝35°,∠C ＝45°,求∠D A E 的度数． 24．(1)如图1,点P 为△A B C 的内角平分线B P 与C P 的交点,求证：∠B PC ＝90°+21∠A ； (2)如图2,点P 为△A B C 内角平分线B P 与外角平分线C P 的交点,请直接写出∠B PC 与∠A 的关系；(3)如图3,点P 是△A B C 的外角平分线B P 与C P 的交点,请直接∠B PC 与∠A 的关系．参考答案一．选择题(共12小题)1．三角形按边可分为()A ．等腰三角形,直角三角形,锐角三角形B ．直角三角形,不等边三角形C ．等腰三角形,不等边三角形D ．等腰三角形,等边三角形[分析]三角形按边分类即有三条边都不相等和有两条边相等,所以分为了不等边三角形和等腰三角形．等边三角形是特殊的等腰三角形．[解答]解：三角形按边分类分为不等边三角形和等腰三角形．故选C ．2．若三角形两边长分别是4、5,则第三边C 的范围是()A ．1＜C ＜9B ．9＜C ＜14 C ．10＜C ＜18D ．无法确定[分析]直接利用三角形的三边关系进而得出答案．[解答]解：∵三角形两边长分别是4、5,∴第三边C 的范围是：5﹣4＜C ＜4+5,则1＜C ＜9．故选：A ．3．如图在△A B C 中,∠A C B ＞90°,A D ⊥B D ,B E⊥A E,C F⊥A B ,垂足分别是点D 、E、F,则下列说法错误的是()A ．A D 是△AB D 的高 B ．C F是△A B C 的高C ．B E是△A B C 的高D ．B C 是△B C F的高[分析]根据三角形的一个顶点到对边的垂线段叫做三角形的高对各选项分析判断后利用排除法求解．[解答]解：A 、A D 是△A B D 的高正确,故本选项错误；B 、C F 是△A B C 的高正确,故本选项错误；C 、B E 是△A B C 的高正确,故本选项错误；D 、B C 是△B C F 的高错误,故本选项正确．故选：D ．4．已知：如图,A D 是△A B C 的角平分线,A E 是△A B C 的外角平分线,若∠D A C ＝20°,问∠EA C ＝( )A ．60°B ．70°C ．80°D ．90°[分析]根据三角形的外角性质得到∠EA C ＝∠B +∠A C D ,求出∠EA C 的度数,根据角平分线的定义求出即可．[解答]解：∵A D 是△A B C 的角平分线,∠D A C ＝20°,∴∠B A C ＝2∠D A C ＝40°,∴∠B +∠A C D ＝140°,∴． 故选：B ．5．可以把三角形分成两个面积相等的三角形的是( )A ．三角形的中线B ．三角形的高线C ．三角形的角平分线D ．三角形一边的垂线 [分析]三角形的中线把三角形分成面积相等的两个三角形．[解答]解：能够把一个三角形分成面积相等的两部分的线段是三角形的中线．()︒=∠+∠=∠=∠702121ACD B FAC EAC故选：A ．6．在现实的生产、生活中有以下四种情况：①用“人”字梁建筑屋顶；②自行车车梁是三角形结构；③用窗钩来固定窗扇；④商店的推拉防盗铁门．其中用到三角形稳定性的是()A ．①②B ．②③C ．①②③D ．②③④[分析]根据生活常识对各小题进行判断即可得解．[解答]解：①用“人”字梁建筑屋顶,是利用三角形具有稳定性；②自行车车梁是三角形结构,是利用三角形具有稳定性；③用窗钩来固定窗扇,是利用三角形具有稳定性；④商店的推拉防盗铁门,不是利用三角形具有稳定性；综上所述,用到三角形稳定性的是①②③．故选：C ．7．在△A B C 中,O为∠C A B 和∠C B A 的角平分线的交点,若∠A OB ＝120°,则∠C 的度数为()A ．120°B ．60°C ．50°D ．30[分析]根据三角形的内角和求得∠OA B +∠OB A ,利用角平分线的定义求得∠C A B +∠C B A ,利用三角形的内角和定理列式计算求得答案即可．[解答]解：∵∠C A B 与∠C B A 的平分线相交于O点,∴∠OA B +∠OB A ＝(∠A B C +∠B A C )＝180°﹣120°＝60°, ∴∠A B C +∠B A C ＝120°,∴∠C ＝180°﹣(∠A B C +∠B A C )＝60°．故选：B ．8．如图,对任意的五角星,结论正确的是( )A ．∠A +∠B +∠C +∠D +∠E ＝90°B ．∠A +∠B +∠C +∠D +∠E ＝180° C ．∠A +∠B +∠C +∠D +∠E ＝270° D ．∠A +∠B +∠C +∠D +∠E ＝360°[分析]根据三角形的一个外角等于和它不相邻的两个内角的和得到∠1＝∠2+∠D ,∠2＝∠A +∠C ,根据三角形内角和定理得到答案．[解答]解：∵∠1＝∠2+∠D ,∠2＝∠A +∠C ,∴∠1＝∠A +∠C +∠D ,∵∠1+∠B +∠E ＝180°,∴∠A +∠B +∠C +∠D +∠E ＝180°,故选：B ．9．直角三角形中有一锐角为15°,则另一锐角为( )A ．85°B ．75°C ．15°D ．90°[分析]根据直角三角形中两个锐角互余即可得出答案．[解答]解：∵直角三角形中有一锐角为15°,根据直角三角形中两个锐角互余,∴另一锐角＝90°﹣15°＝75°,21故选：B ．10．角度是多边形的内角和的是()A ．1900°B ．1800°C ．560°D ．270°[分析]根据多边形的内角和公式(n﹣2)•180°可知多边形的内角和是180°的倍数,然后找出各选项中180°的倍数的选项即可．[解答]解：多边形的内角和公式(n﹣2)•180°可知,多边形的内角和是180°的倍数,纵观各选项,只有1800°是180°的倍数,所以,角度是多边形的内角和的是1800°．故选：B ．11．若正多边形的一个外角等于45°,那么这个正多边形的内角和等于()A ．1 080°B ．720°C ．540°D ．360°[分析]先根据多边形的外角和定理求出多边形的边数,再根据多边形的内角和公式求出这个正多边形的内角和．[解答]解：正多边形的边数为：360°÷45°＝8,则这个多边形是正八边形,所以该多边形的内角和为(8﹣2)×180°＝1080°．故选：A ．12．已知△A B C 的三边长分别是A 、B 、C ,化简|A +B ﹣C |﹣|B ﹣A ﹣C |的结果是()A ．2AB ．﹣2BC ．2(A +B )D ．2(B ﹣C )[分析]先根据三角形三边关系判断出A +B ﹣C 与B ﹣A ﹣C 的符号,再把要求的式子进行化简,即可得出答案．[解答]解：∵△A B C 的三边长分别是A 、B 、C ,∴A +B ＞C ,B ﹣A ＜C ,∴A +B ﹣C ＞0,B ﹣A ﹣C ＜0,∴|A +B ﹣C |﹣|B ﹣A ﹣C |＝A +B ﹣C ﹣(﹣B +A +C )＝A +B ﹣C +B ﹣A ﹣C ＝2(B ﹣C )；故选：D ．二．填空题(共4小题)13．如图所示,其中∠1＝145°．[分析]首先求得∠2,然后根据三角形的外角的性质即可求解．[解答]解：∠2＝180°﹣100°＝80°,∴∠1＝65°+∠2＝65°+80°＝145°．故答案是：145°．14．如图所示,求∠D +∠E+∠F+∠G+∠M+∠N＝360°．[分析]根据三角形的一个外角等于与它不相邻的两个内角的和可得∠D +∠E＝∠1,∠F+∠G＝∠2,∠M+∠N＝∠3,再根据三角形的外角和等于360°解答．[解答]解：如图,由三角形的外角性质得,∠D +∠E＝∠1,∠F+∠G＝∠2,∠M+∠N＝∠3,∵△A B C 的外角和等于360°,即∠1+∠2+∠3＝360°,∴∠D +∠E+∠F+∠G+∠M+∠N＝360°．故答案为：360°．15．如图,在△A B C 中,A D ⊥B C 于D ,A E为∠B A C 的平分线,且∠D A E＝15°,∠B ＝35°,则∠C ＝65°．[分析]利用三角形内角和定理求得∠A ED ＝75°；然后根据已知条件和三角形外角定理可以求得∠B A E 的度数；最后结合三角形角平分线的定义和三角形内角和定理进行解答．[解答]解：如图,∵A D ⊥B C ,∴∠A D E ＝90°．又∵∠D A E ＝15°,∴∠A ED ＝75°．∵∠B ＝35°,∴∠B A E ＝∠A ED ﹣∠B ＝40°．又∵A E 为∠B A C 的平分线,∴∠B A C ＝2∠B A E ＝80°,∴∠C ＝180°﹣∠B ﹣∠B A C ＝65°．故答案是：65．16．如图,在△A B C 中,∠A ＝m °,∠A B C 和∠A C D 的平分线交于点A 1,得∠A 1,∠A 1B C 和∠A 1C D 的平分线交于点A 2,得∠A 1…；求∠A 2014＝ ()° ．[分析]利用角平分线的性质、三角形外角性质,易证∠A 1＝∠A ,进而可求∠A 1,由于∠A 1＝∠A ,∠A 2＝∠A 1＝∠A ,…,以此类推可知∠A 2014∠A ．[解答]解：∵A 1B 平分∠A B C ,A 1C 平分∠A C D ,∴∠A 1B C ＝∠A B C ,∠A 1C A ＝∠A C D , ∵∠A 1C D ＝∠A 1+∠A 1B C ,即∠A C D ＝∠A 1+∠A B C , 20142m21212121212121∴∠A 1＝(∠A C D ﹣∠A B C ), ∵∠A +∠A B C ＝∠A C D ,∴∠A ＝∠A C D ﹣∠A B C ,∴∠A 1＝∠A , ∠A 2＝∠A 1∠A ,…, 以此类推可知∠ A 2014＝∠A ＝°．故答案为：°．三．解答题(共8小题)17．已知：在△A B C 中,∠A +∠B ＝2∠C ,∠A ﹣∠B ＝20°,求三角形三个内角的度数．[分析]设∠B ＝x °,则∠A ＝x °+20,∠C ＝x °+10°,根据∠A +∠B +∠C ＝180°得出方程x +20+x +x +10＝180,求出方程的解即可．[解答]解：∵在△A B C 中,∠A +∠B ＝2∠C ,∠A ﹣∠B ＝20°,∴设∠B ＝x °,∠A ＝x °+20,∴∠A +∠B ＝2x °+20°,∴∠C ＝x °+10°,∵∠A +∠B +∠C ＝180°,∴x +20+x +x +10＝180解得：x ＝50212121则∠A ＝70°,∠B ＝50°,∠C ＝60°．18．已知等腰三角形A B C 中,一腰A C 上的中线B D 将三角形的周长分成9C m 和15C m 两部分,求这个三角形的腰长和底边的长．[分析]分腰长与腰长的一半是9C m 和15C m 两种情况,求出腰长,再求出底边,然后利用三角形的任意两边之和大于第三边进行判断即可．[解答]解：设腰长为xC m ,①腰长与腰长的一半是9C m 时,x +x ＝9, 解得x ＝6,所以,底边＝15﹣×6＝12, ∵6+6＝12,∴6C m 、6C m 、12C m 不能组成三角形；②腰长与腰长的一半是15C m 时,x +x ＝15, 解得x ＝10, 所以,底边＝9﹣×10＝4, 所以,三角形的三边为10C m 、10C m 、4C m ,能组成三角形,综上所述,三角形的腰长为10C m ,底边为4C m ．19．已知：△A B C 中,B C ＝2C m ,A B ＝8C m ,A C 的长度是奇数,求△A B C 的周长．[分析]根据三角形的三边关系,第三边的长一定大于已知的两边的差,而小于两边的和,求得相应范围后,根据A C 的长度是奇数,求出周长即可．[解答]解：设第三边A C 是x ,∵B C ＝2C m ,A B ＝8C m21212121∴6＜x ＜10．∴x ＝7、8或9．∵A C 的长度是奇数,∴A C ＝7C m 或9C m ,∴△A B C 的周长为：2+8+7＝17(C m )；2+8+9＝19(C m )．20．如图,△A B C 中,∠1＝∠2,∠3＝∠4,∠5＝∠6．∠A ＝60°．求∠EC F 、∠FEC 的度数．[分析]先根据三角形内角和定理及角平分线的性质求出∠2+∠3的度数,再由三角形外角的性质求出∠FEC 的度数；根据B 、C 、D 共线,∠3＝∠4,∠5＝∠6,可得出∠4+∠5＝90°,故可求出∠EC F 的度数．[解答]解：∵∠A ＝60°,且∠1＝∠2,∠3＝∠4,∴∠2+∠3＝(180°﹣∠A )＝(180°﹣60°)＝60°, ∵∠FEC 是△B C E 的外角,∴∠FEC ＝∠2+∠3＝60°,又∵B 、C 、D 共线,∠3＝∠4,∠5＝∠6,∴∠4+∠5＝90°；∴∠FC E ＝∠4+∠5＝90°．21．如图,在△A B C C 中,∠A C B ＝90°,C D ⊥A B ,A F 是角平分线,交C D 于点E ．求证：∠1＝∠2．[分析]根据角平分线的定义可得∠C A F ＝∠B A F ,再根据直角三角形两锐互余列式证明即可．[解答]证明：∵A F 是角平分线,∴∠C A F ＝∠B A F ,∵∠A C B ＝90°,C D ⊥A B ,∴∠C A F +∠2＝90°,∠B A F +∠A ED ＝90°,2121∴∠2＝∠A ED ,∵∠1＝∠A ED ,∴∠1＝∠2．22．如图所示,△A B C 中,∠B ：∠C ＝3：4,FD ⊥B C ,D E ⊥A B ,且∠A FD ＝146°,求∠ED F 的度数．[分析]根据三角形的一个外角等于与它不相邻的两个内角的和列式求出∠C 的度数,然后求出∠B 的度数,再根据直角三角形两锐角互余求出∠B D E ,然后根据垂直的定义列式计算即可得解．[解答]解：∵∠A FD ＝146°,FD ⊥B C ,∴∠C ＝∠A FD ﹣∠FD C ＝146°﹣90°＝56°,∵∠B ：∠C ＝3：4,∴∠B ＝56＝42°,∵D E ⊥A B ,∴∠B ED ＝90°,∴∠B D E ＝90°﹣42°＝48°,∵∠B D E +∠ED F ＝90°,∴∠ED F ＝90°﹣∠B D E ＝90°﹣48°＝42°．23．如图,A D 、A E 分别为△A B C 的高和角平分线,∠B ＝35°,∠C ＝45°,求∠D A E 的度数．[分析]根据三角形内角和定理求得∠B A C 的度数,则依据角平分线的定义求得角∠EA C ,然后在直角△AC D 中,求得∠D A C 的度数,则∠D A E ＝∠C A E ﹣∠D A C 即可求解．[解答]解：在△A B C 中,∵A E 平分∠B A C ,∴∠C A E ＝∠B A C , ∵∠B ＝35°,∠C ＝45°,21∴∠B A C ＝100°,∠D A C ＝45°,∴∠C A E ＝50°,∴∠D A E ＝∠C A E ﹣∠D A C ＝5°．24．(1)如图1,点P 为△A B C 的内角平分线B P 与C P 的交点,求证：∠B PC ＝90°+∠A ；(2)如图2,点P 为△A B C 内角平分线B P 与外角平分线C P 的交点,请直接写出∠B PC 与∠A 的关系；(3)如图3,点P 是△A B C 的外角平分线B P 与C P 的交点,请直接∠B PC 与∠A 的关系．[分析](1)先根据三角形内角和定理求出∠PB C +∠PC B 的度数,再根据角平分线的性质求出∠A B C +∠A CB 的度数,由三角形内角和定理即可求出答案．(2)根据角平分线的定义得∠PB C ＝∠A B C ,∠PC D ＝∠A C D ,再根据三角形外角性质得∠A C D ＝∠A +∠A B C ,∠PC D ＝∠PB C +∠P ,所以(∠A +∠A B C )＝∠PB C +∠P ＝∠A B C +∠P ,然后整理可得∠P ＝∠A ； (3)根据题意得∠PB C ＝(∠A +∠A C B ),∠PC B ＝(∠A +∠A B C ),由三角形的内角和定理以及三角形外角的性质,求得∠P 与∠A 的关系,从而计算出∠P 的度数．[解答]证明：(1)∵∠PB C +∠B C P +∠B PC ＝180°,∵∠B PC ＝120°,∴∠A B C +∠A C B ＝60°,∵B P 、C P 是角平分线,21212121212121∴∠A B C ＝2∠PB C ,∠A C B ＝2∠B C P , ∵∠A B C +∠A C B +∠A ＝180°, ∴∠B PC ＝90°+∠A ； (2)∠P ＝∠A (3)∠P ＝90°﹣∠A 212121。

第11章三角形一、选择题1．平行四边形的内角和为（）A．180°B．270°C．360°D．640°2．如图，正六边形的每一个内角都相等，则其中一个内角α的度数是（）A．240°B．120°C．60°D．30°3．五边形的内角和是（）A．180°B．360°C．540°D．600°4．如果一个多边形的内角和是720°，那么这个多边形是（）A．四边形B．五边形C．六边形D．七边形5．将一个n边形变成n+1边形，内角和将（）A．减少180°B．增加90°C．增加180°D．增加360°6．一个多边形的每个内角均为108°，则这个多边形是（）A．七边形B．六边形C．五边形D．四边形7．若一个多边形的内角和是900°，则这个多边形的边数是（）A．5 B．6 C．7 D．88．一个多边形的内角和是900°，这个多边形的边数是（）A．10 B．9 C．8 D．79．一个多边形的内角和是360°，这个多边形是（）A．三角形B．四边形C．六边形D．不能确定10．一个多边形的每个外角都等于60°，则这个多边形的边数为（）A．8 B．7 C．6 D．511．如图，在五边形ABCDE中，∠A+∠B+∠E=300°，DP、CP分别平分∠EDC、∠BCD，则∠P的度数是（）A．60°B．65°C．55°D．50°12．已知正多边形的一个外角等于60°，则该正多边形的边数为（）A．3 B．4 C．5 D．613．如果一个多边形的每一个外角都是60°，则这个多边形的边数是（）A．3 B．4 C．5 D．614．八边形的内角和等于（）A．360°B．1080°C．1440°D．2160°15．一个多边形的内角和是外角和的2倍，则这个多边形是（）A．四边形B．五边形C．六边形D．八边形二、填空题16．若一个正多边形的一个内角等于135°，那么这个多边形是正______边形．17．正多边形一个外角的度数是60°，则该正多边形的边数是______．18．正多边形的一个外角等于20°，则这个正多边形的边数是______．19．n边形的每个外角都等于45°，则n=______．20．一个多边形的内角和比外角和的3倍多180°，则它的边数是______．21．一个正多边形的一个外角等于30°，则这个正多边形的边数为______．22．五边形的内角和为______．23．四边形的内角和是______．24．若正多边形的一个外角为40°，则这个正多边形是______边形．25．内角和与外角和相等的多边形的边数为______．26．若正n边形的一个外角为45°，则n=______．27．四边形的内角和为______．28．如图，一个零件的横截面是六边形，这个六边形的内角和为______．29．某正n边形的一个内角为108°，则n=______．30．正多边形的一个外角是72°，则这个多边形的内角和的度数是______．第11章三角形参考答案一、选择题（共15小题）1．C；2．B；3．C；4．C；5．C；6．C；7．C；8．D；9．B；10．C；11．A；12．D；13．D；14．B；15．C；二、填空题（共15小题）16．八；17．六；18．18；19．8；20．9；21．12；22．540°；23．360°；24．九；25．四；26．8；27．360°；28．720°；29．5；30．540°；先制定阶段性目标—找到明确的努力方向每个人的一生,多半都是有目标的,大的目标应该是一个十年、二十年甚至几十年为之奋斗的结果,应该定得比较远大些,这样有利于发挥自己的潜能。

人教版数学八年级上学期《三角形》单元测试(时间:120分钟满分:150分)一、选择题(本题共12小题，每小题3分，共36分)1. 下列长度的三条线段能组成三角形的是( )A. 5，6，10B. 5，6，11C. 3，4，8D. 4a，4a，8a(a＞0)2. 如图，在△ABC中，D是BC延长线上一点，∠B＝40°，∠ACD＝120°，则∠A等于( )A. 60°B. 70°C. 80°D. 90°3. 如图，一扇窗户打开后，用窗钩AB可将其固定，这里所运用的几何原理是( )A. 两点之间线段最短B. 三角形的稳定性C. 两点确定一条直线D. 垂线段最短4. 能把一个三角形分成两个面积相等的三角形的线段是三角形的( )A. 中线B. 高线C. 角平分线D. 以上都不对5. 如图，已知BD是△ABC的中线，AB＝5，BC＝3，且△ABD的周长为11，则△BCD的周长是( )A. 9B. 14C. 16D. 不能确定6. 已知正多边形的一个外角等于60°，则该正多边形的边数为( )A. 3B. 4C. 5D. 67. 在△ABC中，已知∠A＝4∠B＝104°，则∠C的度数是( )A. 50°B. 45°C. 40°D. 30°8. 如图，∠AOB＝40°，OC平分∠AOB，直尺与OC垂直，则∠1等于( )A. 60°B. 70°C. 50°D. 40°9. 在下列条件中:①∠A＋∠B＝∠C;②∠A＝∠B＝2∠C;③∠A＝∠B＝a∠C;④∠A∶∠B∶∠C＝1∶2∶3，能确定△ABC为直角三角形的条件有( )A. 1个B. 2个C. 3个D. 4个10. 如图，在△ABC中，AD，CE分别是△ABC的高，且AD＝2，CE＝4，则AB∶BC＝( )A. 3∶4B. 4∶3C. 1∶2D. 2∶111. 一个正多边形的边长为2，每个内角为135°，则这个多边形的周长是( )A. 8B. 12C. 16D. 1812. 若a，b，c是△ABC的三边的长，则化简|a－b－c|－|b－c－a|＋|a＋b－c|的结果是( )A. a＋b＋cB. －a＋3b－cC. a＋b－cD. 2b－2c二、填空题(本题共6小题，每小题4分，共24分)13. 已知三角形两条边的长分别为3和6，第三边的长为奇数，则第三边的长为________．14. 若一个三角形的三个内角度数之比为5∶4∶3，则这个三角形是________三角形．15. 如图，平面镜A与B之间的夹角为120°，光线经过平面镜A反射后射在平面镜B上，再反射出去，若∠1＝∠2，则∠1＝________．16. 将一副三角板按如图所示的方式叠放，则角α＝________．17. 如图，在△ABC中，已知点D，E，F分别为边BC，AD，CE的中点，且S△ABC＝4cm2，则S阴影＝________．18. 科技馆为某机器人编制一段程序，如果机器人在平地上按照图中所示的步骤行走，那么该机器人所走的总路程为________米．三、解答题(本题共8小题，共90分．解答时应写出必要的文字说明、证明过程或演算步骤)19. 一个多边形的内角和是它的外角和的4倍，求这个多边形的边数．20. 已知三角形三边长分别为a，b，c，其中a、b满足(a－6)2＋|b－8|＝0，求这个三角形最长边c的取值范围．21. 如图:(1)在△ABC中，BC边上的高是________;(2)在△AEC中，AE边上的高是________;(3)若AB＝CD＝2cm，AE＝3cm，求△AEC的面积及CE的长．22. 如图，说明∠A＋∠B＋∠C＋∠D＋∠E＝180°的理由．23. 如图，△ABC中，BD是∠ABC的平分线，DE∥BC交AB于点E，∠A＝60°，∠BDC＝100°，求△BDE 各内角的度数．24. 如图，在△ABC中，∠ABC、∠BAC的平分线交于点O，且∠AOB＝135°.求证:△ABC是直角三角形．25. 如图，在△ABC中，AB＝AC，AC边上的中线BD把△ABC的周长分成12cm和15cm两部分，求△ABC 各边的长．26. 如图，在△ABC中，∠B＝∠C＝45°，点D在BC边上，点E在AC边上，且∠ADE＝∠AED，连接DE.(1)若∠BAD＝60°，求∠CDE的度数;(2)当点D在BC(点B，C除外)边上运动时，试写出∠BAD与∠CDE的数量关系，并说明理由．参考答案一、选择题(本题共12小题，每小题3分，共36分)1. 下列长度的三条线段能组成三角形的是( )A. 5，6，10B. 5，6，11C. 3，4，8D. 4a，4a，8a(a＞0)【答案】A【解析】试题解析:根据三角形任意两边的和大于第三边，得A中，5+6=11>10，能组成三角形;B中，5+6=11，不能组成三角形;C中，3+4=7<8，不能够组成三角形;D中，4a+4a=8a，不能组成三角形．故选A．2. 如图，在△ABC中，D是BC延长线上一点，∠B＝40°，∠ACD＝120°，则∠A等于( )A. 60°B. 70°C. 80°D. 90°【答案】C【解析】试题分析:根据三角形的一个外角等于与它不相邻的两个内角的和，可由∠B=40°，∠ACD=120°，得到∠A=∠ACD-∠B=120°-40°=80°．故选C考点:三角形的外角3. 如图，一扇窗户打开后，用窗钩AB可将其固定，这里所运用的几何原理是( )A. 两点之间线段最短B. 三角形的稳定性C. 两点确定一条直线D. 垂线段最短【答案】B【解析】分析:根据“三角形的稳定性”进行分析判断即可.详解:∵窗钩的两个端点A、B和窗户的下支点O刚好构成一个△AOB，而三角形具有稳定性，∴打开窗户后，用窗钩AB可以将该窗户固定.故选B.点睛;熟知“三角形具有稳定性”是解答本题的关键.4. 能把一个三角形分成两个面积相等的三角形的线段是三角形的( )A. 中线B. 高线C. 角平分线D. 以上都不对【答案】A【解析】试题分析:因为三角形的中线能把一个三角形分成两个等底同高的三角形，根据三角形的面积公式可得它们的面积相等，故选:A．考点:三角形的中线5. 如图，已知BD是△ABC的中线，AB＝5，BC＝3，且△ABD的周长为11，则△BCD的周长是( )A. 9B. 14C. 16D. 不能确定【答案】A【解析】根据BD是△ABC的中线，可得AD=CD，根据△ABD的周长为11，可得AB+BD+AD=11，可得BD+AD=11-5=6，而△BCD的周长=BC+BD+CD=BD+AD+BC=6+3=9.故选:A.6. 已知正多边形的一个外角等于60°，则该正多边形的边数为( )A. 3B. 4C. 5D. 6【答案】D【解析】分析:根据“正多边形的每个外角都相等和多边形的外角和为360°”进行分析解答即可.详解:设该正多边形的边数为n，∵正多边形的每个外角都相等，且多边形的外角和为360°，∴n=360°÷60°=6.故选D.点睛:解答本题有以下两个要点:(1)正多边形的每个外角都相等;(2)多边形的外角和都为360°.7. 在△ABC中，已知∠A＝4∠B＝104°，则∠C的度数是( )A. 50°B. 45°C. 40°D. 30°【答案】A【解析】∵4∠B=104°，∴∠B=26°，∴∠C=180°-∠A-∠B=180°-104°-26°=50°．故选A.8. 如图，∠AOB＝40°，OC平分∠AOB，直尺与OC垂直，则∠1等于( )A. 60°B. 70°C. 50°D. 40°【答案】B【解析】分析:如下图，由已知条件易得∠ODE=90°，∠AOC=20°，由此可得∠3=70°，结合直尺的对边相互平行可得∠2=∠3=70°，从而由对顶角相等可得∠1=70°.详解:∵OC平分∠AOB，∠AOB=40°，OC⊥DE，∴∠AOC=20°，∠ODE=90°，∴∠3=70°，∵直尺的对边是相互平行，∴∠2=∠3=70°，∴∠1=∠2=70°.故选B.点睛:“由已知条件根据三角形内角和定理求得∠3的度数，由直尺的对边相互平行得到∠2=∠3”是解答本题的关键.9. 在下列条件中:①∠A＋∠B＝∠C;②∠A＝∠B＝2∠C;③∠A＝∠B＝a∠C;④∠A∶∠B∶∠C＝1∶2∶3，能确定△ABC为直角三角形的条件有( )A. 1个B. 2个C. 3个D. 4个【答案】B【解析】分析:根据所给的4个条件分别求出4个条件下△ABC中的最大角的度数，再进行判断即可.详解:①∵∠A+∠B=∠C，∠A+∠B+∠C=180°，∴∠C=180°×=90°，∴此时△ABC是直角三角形;②∵∠A=∠B=2∠C，∠A+∠B+∠C=180°，∴5∠C=180°，解得∠C=36°，∴∠A=∠B=72°，∴此时△ABC不是直角三角形;③∵∠A＝∠B＝a∠C，∠A+∠B+∠C=180°，∴(2a+1)∠C=180°，解得∠C=，∴∠A=∠B=，∴此时△ABC中三个内角的度数是不确定的，∴不能确定△ABC是否是直角三角形;④∵∠A∶∠B∶∠C＝1∶2∶3，∠A+∠B+∠C=180°，∴∠C=180°×=90°，∴此时△ABC是直角三角形.综上所述，根据上述条件能够确定△ABC是直角三角形的有2个.故选B.点睛:本题的解题要点是:“根据已知条件结合三角形内角和是180°确定出△ABC的最大角的度数即可判断此时△ABC是否是直角三角形了”.10. 如图，在△ABC中，AD，CE分别是△ABC的高，且AD＝2，CE＝4，则AB∶BC＝( )A. 3∶4B. 4∶3C. 1∶2D. 2∶1【答案】C【解析】分析:由已知条件可得:S△ABC=AB·CE=BC·AD，再代入AD=2，CE=4即可求得AB:BC的值.详解:∵在△ABC中，AD、CE分别是△ABC的边BC和AB上的高，∴S△ABC=AB·CE=BC·AD∵AD=2，CE=4，∴2AB=BC，∴AB:BC=1:2.故选C.点睛:“由AD、CE分别是△ABC的边BC和AB上的高，得到S△ABC=AB·CE=BC·AD”是解答本题的关键.11. 一个正多边形的边长为2，每个内角为135°，则这个多边形的周长是( )A. 8B. 12C. 16D. 18【答案】C学.科.网...学.科.网...学.科.网...学.科.网...学.科.网...学.科.网...学.科.网...学.科.网...12. 若a，b，c是△ABC的三边的长，则化简|a－b－c|－|b－c－a|＋|a＋b－c|的结果是( )A. a＋b＋cB. －a＋3b－cC. a＋b－cD. 2b－2c【答案】B【解析】分析:根据三角形三边间的关系判断出原式中每个绝对值符号里面的式子的值的正负，再结合绝对值的代数意义进行化简即可.详解:∵a，b，c是△ABC的三边的长，∴a－b－c<0，b－c－a<0，a＋b－c>0，∴|a－b－c|－|b－c－a|＋|a＋b－c|=-(a-b-c)-[-(b-c-a)]+(a+b-c)=-a+b+c+b-c-a+a+b-c=-a+3b-c.故选B.点睛:解答本题有以下两个要点:(1)熟知三角形三边间的关系:三角形任意两边的和大于第三边，任意两边的差小于第三边;(2)熟知绝对值的代数意义:正数的绝对值是它本身，负数的绝对值是它的相反数，0的绝对值是0.二、填空题(本题共6小题，每小题4分，共24分)13. 已知三角形两条边的长分别为3和6，第三边的长为奇数，则第三边的长为________．【答案】5或7【解析】试题分析:首先设第三边长为x，根据三角形的三边关系可得6﹣3＜x＜6+3，再解不等式可得x的范围，然后再确定x的值即可．解:设第三边长为x，由题意得:6﹣3＜x＜6+3，解得:3＜x＜9，∵第三边的长为奇数，∴x=5或7．故答案为:5或7．考点:三角形三边关系．14. 若一个三角形的三个内角度数之比为5∶4∶3，则这个三角形是________三角形．【答案】锐角【解析】分析:根据已知条件结合三角形内角和为180°求出这个三角形的每个内角的度数即可作出判断.详解:∵三角形三个内角的度数之比为5:4:3，且三角形的内角和为180°，∴这个三角形的三个内角分别为:180°×=75°，180°×=60°，180°×=45°，∴这个三角形是锐角三角形.故答案为:锐角.点睛:“由已知条件结合三角形内角和为180°求得这个三角形每个内角的度数”是解答本题的关键.15. 如图，平面镜A与B之间的夹角为120°，光线经过平面镜A反射后射在平面镜B上，再反射出去，若∠1＝∠2，则∠1＝________．【答案】30°【解析】分析:根据“光的反射定律:反射角等于入射角”结合“三角形内角和为180°”和已知条件进行分析解答即可. 详解:如下图，由光的反射定律可知:∠1=∠OAB，∠2=∠OBA，∵∠1=∠2，∴∠OAB=∠OBA，又∵∠OAB+∠AOB+∠OBA=180°，∠AOB=120°，∴∠OAB=(180°-120°)=30°，∴∠1=∠OAB=30°.故答案为:30°.点睛:熟知:“光的反射定律:反射角等于入射角”是解答本题的关键.16. 将一副三角板按如图所示的方式叠放，则角α＝________．【答案】75°【解析】如图，根据三角板的特点，可知∠1=45°，然后根据三角形的外角，可求∠α=75°.故答案为:75°.17. 如图，在△ABC中，已知点D，E，F分别为边BC，AD，CE的中点，且S△ABC＝4cm2，则S阴影＝________．【答案】1cm2【解析】试题分析:根据三角形的面积公式，知△BCE的面积是△ABC的面积的一半，进一步求得阴影部分的面积是△BEC的面积的一半．解:∵点E是AD的中点，∴△BDE的面积是△ABD的面积的一半，△CDE的面积是△ACD的面积的一半．则△BCE的面积是△ABC的面积的一半，即为2cm2．∵点F是CE的中点，∴阴影部分的面积是△BCE的面积的一半，即为1cm2．考点:三角形的面积．18. 科技馆为某机器人编制一段程序，如果机器人在平地上按照图中所示的步骤行走，那么该机器人所走的总路程为________米．【答案】24【解析】试题分析:根据题意可得机器人每次都是旋转30°，则需要经过12次旋转才能回到起到，即所所走的总路程为12×1=12米.考点:多边形的外角和性质.三、解答题(本题共8小题，共90分．解答时应写出必要的文字说明、证明过程或演算步骤)19. 一个多边形的内角和是它的外角和的4倍，求这个多边形的边数．【答案】这个多边形的边数是10.【解析】试题分析:设这个多边形有n条边，根据内角和是它的外角和的4倍，列方程，然后解方程即可．试题解析:设这个多边形有n条边．由题意得:(n﹣2)×180°=360°×4，(2分)解得n=10．故这个多边形的边数是10．(2分)考点:多边形的内角和外角和．20. 已知三角形三边长分别为a，b，c，其中a、b满足(a－6)2＋|b－8|＝0，求这个三角形最长边c的取值范围．【答案】8＜c＜14.【解析】试题分析:根据算术平方根与绝对值的和为0，可得算术平方根与绝对值同时为0，可得a、b的值，根据三角形两边之和大于第三边，两边之差小于第三边，可得答案．试题解析:∵(a﹣6)2+|b﹣8|=0，∴a﹣6=0，b﹣8=0，∴a=6，b=8，b﹣a＜c＜a+b，这个三角形的最长边c，c＞b=8，8＜c＜14 .21. 如图:(1)在△ABC中，BC边上的高是________;(2)在△AEC中，AE边上的高是________;(3)若AB＝CD＝2cm，AE＝3cm，求△AEC的面积及CE的长．【答案】(1). AB(2). CD【解析】试题分析:根据三角形的高的定义，可得出三角形的高，然后根据三角形的面积公式可求解.试题解析:(1)AB(2)CD(3)∵AE＝3cm，CD＝2cm，∴S△AEC＝AE·CD＝×3×2＝3(cm2)．∵S△AEC＝CE·AB＝3cm2，AB＝2cm，∴CE＝3cm.22. 如图，说明∠A＋∠B＋∠C＋∠D＋∠E＝180°的理由．【答案】见解析.【解析】分析:如下图，连接BC，易得∠D+∠E=∠DCB+∠EBC，这样结合三角形内角和为180°即可得到所求结论了. 详解:如下图，连接BC，∵∠D+∠E+∠DOE=180°，∠OBC+∠OCB+∠BOC=180°，∴∠D+∠E+∠DOE=∠OBC+∠OCB+∠BOC，又∵∠DOE=∠BOC，∴∠D＋∠E＝∠OBC＋∠OCB，∴∠A＋∠ABE＋∠ACD＋∠D＋∠E＝∠A＋∠ABE＋∠EBC＋∠DCB＋∠ACD＝180°.点睛:“作出如图所示的辅助线，由三角形内角和定理证得∠D＋∠E＝∠OBC＋∠OCB”是解答本题的关键.23. 如图，△ABC中，BD是∠ABC的平分线，DE∥BC交AB于点E，∠A＝60°，∠BDC＝100°，求△BDE 各内角的度数．【答案】100°.【解析】解:如图因为∠BDC=∠A+∠ABD所以∠ABD=∠BDC-∠A=100°-60°=40°…………………………………3分因为BD平分∠ABC所以∠DBC=∠ABD=40°…………………………5分又因为DE∥BC所以∠BDE=∠DBC=40°…………………………7分(注:用其它解法正确的均给予相应的分值)24. 如图，在△ABC中，∠ABC、∠BAC的平分线交于点O，且∠AOB＝135°.求证:△ABC是直角三角形．【答案】见解析【解析】分析:详解:∵在△ABO中，∠AOB＝135°，∴∠ABO＋∠BAO＝180°－135°＝45°，∵BO，AO分别平分∠ABC，∠BAC，∴∠ABO＝∠ABC，∠BAO＝∠BAC.∴∠ABC＋∠BAC＝45°，∴∠ABC＋∠BAC＝90°，∴∠C=180°-90°=90°，∴△ABC是直角三角形．点睛:熟知“三角形内角和定理及角平分线的定义”是正确解答本题的关键.25. 如图，在△ABC中，AB＝AC，AC边上的中线BD把△ABC的周长分成12cm和15cm两部分，求△ABC 各边的长．【答案】△ABC各边的长为AB＝AC＝8cm，BC＝11cm或AB＝AC＝10cm，BC＝7cm.【解析】【试题分析】本题目需要分类讨论，设AB＝2x cm，BC＝y cm. (1)当AB＋AD＝12cm，BC＋CD ＝15cm，列方程组得: ,解得，从而得到AB＝AC＝8cm，BC＝11cm.(2)当AB＋AD＝15cm，BC＋CD＝12cm时，列方程组得解得，AB＝AC＝10cm，BC＝7cm.最后根据三角形的三边关系，进行验证.【试题解析】设AB＝2x cm，BC＝y cm.有以下两种情况:(1)当AB＋AD＝12cm，BC＋CD＝15cm时， ,解得即AB＝AC＝8cm，BC＝11cm，符合三边关系;(2)当AB＋AD＝15cm，BC＋CD＝12cm时，解得即AB＝AC＝10cm，BC＝7cm，符合三边关系．综上所述，AB＝AC＝8cm，BC＝11cm或AB＝AC＝10cm，BC＝7cm.【方法点睛】本题目三角形三边的综合题，体现分类讨论思想，方程思想，三角形的中线及三角形三边关系，难度有点大.视频26. 如图，在△ABC中，∠B＝∠C＝45°，点D在BC边上，点E在AC边上，且∠ADE＝∠AED，连接DE.(1)若∠BAD＝60°，求∠CDE的度数;(2)当点D在BC(点B，C除外)边上运动时，试写出∠BAD与∠CDE的数量关系，并说明理由．【答案】(1) 30°;(2)∠CDE＝∠BAD，理由见解析.【解析】试题分析:(1)先根据三角形外角的性质得出∠ADC=∠B+∠BAD=∠B+60°=105°，∠AED=∠C+∠EDC，再根据∠B=∠C，∠ADE=∠AED即可得出结论;(2)利用(1)的思路与方法解答即可．试题解析:(1)∵∠ADC是△ABD的外角，∴∠ADC=∠B+∠BAD=105°，∵∠AED是△CDE的外角，∴∠AED=∠C+∠EDC．∵∠B=∠C，∠ADE=∠AED，∴∠ADC-∠EDC=105°-∠EDC=45°+∠EDC，解得:∠CDE=30°;(2)∠CDE=∠BAD，理由:设∠BAD=x，∵∠ADC是△ABD的外角，∴∠ADC=∠B+∠BAD=45°+x，∵∠AED是△CDE的外角，∴∠AED=∠C+∠CDE，∵∠B=∠C，∠ADE=∠AED，∴∠ADC-∠CDE=∠45°+x-∠CDE=45°+∠CDE，得:∠CDE=∠BAD．点睛:本题考查的是三角形外角的性质，熟知三角形的外角等于与之不相邻的两个内角的和是解答此题的关键.。

人教版八年级上册数学全等三角形单元综合测试（Word版含答案）一、八年级数学轴对称三角形填空题（难）1．在平面直角坐标系xOy中，已知点A（2，3），在x轴上找一点P，使得△AOP是等腰三角形，则这样的点P共有_____个．【答案】4【解析】【分析】以O为圆心，OA为半径画弧交x轴于点P1、P3，以A为圆心，AO为半径画弧交x轴于点P4，作OA的垂直平分线交x轴于P2．【详解】解：如图，使△AOP是等腰三角形的点P有4个．故答案为4．【点睛】本题考查了在平面直角坐标系中寻找等腰三角形，掌握两圆一线找等腰三角形是解题的关键．2．如图，已知△ABC和△ADE都是正三角形，连接CE、BD、AF，BF=4,CF=7,求AF的长_________ .【答案】3【解析】【分析】过点A作AF⊥CE交于I，AG⊥BD交于J,证明CAE≅BAD ，再证明CAI≅BAJ，求出°7830∠=∠=，然后求出12IF FJ AF==，，通过设FJ x=求出x，即可求出AF的长.【详解】解：过点A作AF⊥CE交于I，AG⊥BD交于J在CAE和BAD中AC ABCAE BADAE AD=⎧⎪∠=∠⎨⎪=⎩∴CAE≅BAD∴ICA ABJ∠=∠∴BFE CAB∠=∠（8字形）∴°120CFD∠=在CAI和BAJ中°90ICA ABJCAI BJACA BA∠=∠⎧⎪∠=∠=⎨⎪=⎩∴CAI≅BAJ,AI AJ CI BJ ==∴°60CFA AFJ ∠=∠=∴°30FAI FAE ∠=∠=在RtAIF 和RtAJF 中°30FAI FAE ∠=∠=∴12IF FJ AF ==设FJ x = 7,4CF BF ==则47x x +=-32x ∴=2AF FJ =AF ∴=3【点睛】此题主要考查了通过做辅助线证明三角形全等，得出相关的边相等，学会合理添加辅助线求解是解决本题的重点.3．如图，△ABC 是等边三角形，高AD 、BE 相交于点H ，BC=43，在BE 上截取BG=2，以GE 为边作等边三角形GEF ，则△ABH 与△GEF 重叠（阴影）部分的面积为_____．53 【解析】试题分析：如图所示，由△ABC 是等边三角形，BC=433，∠ABG=∠HBD=30°，由直角三角的性质，得∠BHD=90°﹣∠HBD=60°，由对顶角相等，得∠MHE=∠BHD=60°，由BG=2，得EG=BE ﹣BG=6﹣2=4．由GE 为边作等边三角形GEF ，得FG=EG=4，∠EGF=∠GEF=60°，△MHE 是等边三角形；S △ABC =12AC•BE=12AC×EH×3EH=13BE=13×6=2．由三角形外角的性质，得∠BIF=∠FGE ﹣∠IBG=60°﹣30°=30°，由∠IBG=∠BIG=30°，得IG=BG=2，由线段的和差，得IF=FG ﹣IG=4﹣2=2，由对顶角相等，得∠FIN=∠BIG=30°，由∠FIN+∠F=90°，得∠FNI=90°，由锐角三角函数，得FN=1，IN=3．S 五边形NIGHM =S △EFG ﹣S △EMH ﹣S △FIN =223314231442⨯-⨯-⨯⨯=532，故答案为532．考点：1．等边三角形的判定与性质；2．三角形的重心；3．三角形中位线定理；4．综合题；5．压轴题．4．在锐角三角形ABC 中．BC=32，∠ABC=45°，BD 平分∠ABC ．若M ，N 分别是边BD ，BC 上的动点，则CM ＋MN 的最小值是____．【答案】4【解析】【分析】过点C 作CE ⊥AB 于点E ，交BD 于点M′，过点M′作M′N′⊥BC 于N′，则CE 即为CM+MN 的最小值，再根据32ABC=45°，BD 平分∠ABC 可知△BCE 是等腰直角三角形，由锐角三角函数的定义即可求出CE 的长．【详解】解：过点C 作CE ⊥AB 于点E ，交BD 于点M′，过点M′作M′N′⊥BC 于N′，则CE 即为CM+MN 的最小值，∵BC=32，∠ABC=45°，BD平分∠ABC，∴△BCE是等腰直角三角形，∴CE=BC•cos45°=32×2=4．∴CM+MN的最小值为4．【点睛】本题考查了轴对称最短路线问题，难度较大,根据题意作出辅助线，构造出等腰直角三角形，利用锐角三角函数的定义求解是解答此题的关键．5．如图,A,B,C三点在同一直线上,分别以AB,BC（AB>BC）为边,在直线AC的同侧作等边ΔABD和等边ΔBCE,连接AE交BD于点M,连接CD交BE于点N,连接MN. 以下结论：①AE=DC，②MN//AB，③BD⊥AE，④∠DPM=60°，⑤ΔBMN是等边三角形.其中正确的是__________（把所有正确的序号都填上）.【答案】①②④⑤【解析】【分析】①由三角形ABD与三角形BCE都为等边三角形，利用等边三角形的性质得到两条边对应相等，两个角相等都为60°，利用SAS即可得到三角形ABE与三角形DBC全等即可得结论；②由①中三角形ABE与三角形DBC全等，利用全等三角形的对应角相等得到一对角相等，再由∠ABD=∠EBC=60°，利用平角的定义得到∠MBE=∠NBC=60°，再由EB=CB，利用ASA 可得出三角形EMB与三角形CNB全等，利用全等三角形的对应边相等得到MB=NB，再由∠MBE=60°，利用有一个角为60°的等腰三角形为等边三角形可得出三角形BMN为等边三角形；可得∠BMN=60°，进行可得∠BMN=∠ABD，故MN//AB，从而可判断②，⑤正确；③无法证明PM=PN，因此不能得到BD⊥AE；④由①得∠EAB=∠CDB，根据三角形内角和和外角的性质可证得结论.【详解】①∵等边△ABD和等边△BCE，∴AB=DB，BE=BC，∠ABD=∠EBC=60°，∴∠ABE=∠DBC=120°，在△ABE和△DBC中，∵AB DBABE DBC BE BC⎪∠⎪⎩∠⎧⎨＝＝＝，∴△ABE≌△DBC（SAS），∴AE=DC，故①正确；∵△ABE≌△DBC，∴∠AEB=∠DCB，又∠ABD=∠EBC=60°，∴∠MBE=180°-60°-60°=60°，即∠MBE=∠NBC=60°，在△MBE和△NBC中，∵AEB DCB EB CBMBE NBC ∠∠∠⎧⎪⎪⎩∠⎨＝＝＝，∴△MBE≌△NBC（ASA），∴BM=BN，∠MBE=60°，则△BMN为等边三角形，故⑤正确；∵△BMN为等边三角形，∴∠BMN=60°,∵∠ABD=60°,∴∠BMN=∠ABD，∴MN//AB，故②正确；③无法证明PM=PN，因此不能得到BD⊥AE；④由①得∠EAB=∠CDB，∠APC+∠PAC+∠PCA=180°，∴∠PAC+∠PCA=∠PDB+∠PCB=∠DBA=60°，∵∠DPM =∠PAC+∠PCA∴∠DPM =60°，故④正确，故答案为：①②④⑤.【点睛】此题考查了等边三角形的判定与性质，以及全等三角形的判定与性质，熟练掌握判定与性质是解本题的关键．6．如图，在Rt ABC △中，AC BC =，D 是线段AB 上一个动点，把ACD 沿直线CD 折叠，点A 落在同一平面内的A '处，当A D '平行于Rt ABC △的直角边时，ADC ∠的大小为________．【答案】112.5︒或67.5︒【解析】【分析】当A D '平行于Rt ABC △的直角边时，有两种情况，一是当A D BC '时，二是当A D AC '时，两种情况根据折叠的性质及等腰三角形的性质进行角度的计算即可．【详解】 如图1，当点D 在线段AB 上，且A DBC '时，45A DB B '∠=∠=︒， 45180ADC A DC '∴∠+∠-=︒︒，解得112.5A DC ADC '∠=∠=︒.图1如图2，当A D AC '时，45A DB A '∠=∠=︒，45180ADC A DC '∴∠+∠+=︒︒，解得67.5A DC ADC '∠=∠=︒.图2【点睛】本题考查了翻折变换的性质，等腰直角三角形的性质，掌握折叠的性质是解题关键．7．如图，已知，点E 是线段AB 的中点，点C 在线段BD 上，8BD =，2DC =，线段AC交线段DE于点F，若AF BD=，则AC=__________.【答案】10.【解析】【分析】延长DE至G，使EG=DE，连接AG，证明BDE AGE∆≅∆，而后证明AFG∆、CDF∆是等腰三角形，即可求出CF的长，于是可求AC的长.【详解】解：如图，延长DE至G，使EG=DE，连接AG，∵点E是线段AB的中点，∴AE=BE,∴在BDE∆和AGE∆中，BE AEBED AEGDE EG=⎧⎪∠=∠⎨⎪=⎩,∴BDE AGE∆≅∆,∴AG=BD, BDE AGE∠=∠,∵AF=BD=8,∴AG=AF,∴AFG AGE∠=∠∵AFG DFC∠=∠,∴BDE DFC∠=∠,∴FC=DC,∴FC=2,∴AC=AF+FC=8+2=10.【点睛】本题考查了等腰三角形的性质与判定以及全等三角形的判定与性质，能利用中点条件作辅助线构造全等三角形是解题的关键.8．如图，△ABC 中， AB=11 ， AC= 5 ，∠ BAC 的平分线 AD 与边 BC 的垂直平分线 CD 相交于点 D ，过点 D 分别作 DE⊥AB ，DF⊥AC ，垂足分别为 E 、F ，则 BE 的长为_____．【答案】3【解析】【分析】连接CD，BD，由∠BAC的平分线与BC的垂直平分线相交于点D，DE⊥AB，DF⊥AC，根据角平分线的性质与线段垂直平分线的性质，易得CD=BD，DF=DE，继而可得AF=AE，易证得Rt△CDF≌Rt△BDE，则可得BE=CF，继而求得答案．【详解】如图，连接CD，BD，∵AD是∠BAC的平分线，DE⊥AB，DF⊥AC，∴DF=DE，∠F=∠DEB=90°，∠ADF=∠ADE，∴AE=AF，∵DG是BC的垂直平分线，∴CD=BD，在Rt△CDF和Rt△BDE中，CD BDDF DE⎧⎨⎩＝＝，∴Rt△CDF≌Rt△BDE（HL），∴BE=CF，∴AB=AE+BE=AF+BE=AC+CF+BE=AC+2BE，∵AB=11，AC=5，∴BE=12（11-5）=3．故答案为：3．【点睛】此题考查了线段垂直平分线的性质、角平分线的性质以及全等三角形的判定与性质，解题的关键是学会添加常用辅助线，构造全等三角形解决问题．9．如图，过边长为1的等边三角形ABC的边AB上一点P，作PE⊥AC于点E，Q为BC延长线上一点，当AP＝CQ时，PQ交AC于D，则DE的长为______．【答案】1 2【解析】过点Q作AD的延长线的垂线于点F.因为△ABC是等边三角形，所以∠A=∠ACB=60°.因为∠ACB=∠QCF，所以∠QCF=60°.因为PE⊥AC，QF⊥AC，所以∠AEP=∠CFQ=90°，又因为AP=CQ，所以△AEP≌△CFQ，所以AE=CF，PE=QC.同理可证，△DEP≌△DFQ，所以DE=DF.所以AC=AE+DE+CD=DE+CD+CF=DE+DF=2DE，所以DE=12AC=12.故答案为1 2 .10．如图，在△ABC中，AB=AC，D、E是△ABC内两点，AD平分∠BAC，∠EBC=∠E=60°，若BE=6cm，DE=2cm，则BC=_____cm．【答案】8cm.【解析】【详解】解：如图，延长ED交BC于M，延长AD交BC于N，作DF∥BC，∵AB=AC，AD平分∠BAC，∴AN⊥BC，BN=CN，∵∠EBC=∠E=60°，∴△BEM为等边三角形，∴△EFD为等边三角形，∵BE=6cm，DE=2cm，∴DM=4，∵△BEM为等边三角形，∴∠EMB=60°，∵AN⊥BC，∴∠DNM=90°，∴∠NDM=36°，∴NM=2，∴BN=4，∴BC=8．二、八年级数学轴对称三角形选择题（难）11．如图，在射线OA ，OB 上分别截取11OA OB =，连接11A B ，在11B A ，1B B 上分别截取1212B A B B =，连接22A B ，按此规律作下去，若11A B O α∠=，则1010A B O ∠=（ ）A ．102aB ．92aC ．20aD ．18a 【答案】B【解析】【分析】根据等腰三角形两底角相等用α表示出22A B O ∠，依此类推即可得到结论．【详解】解：1212B A B B =，11A B O α∠=，2212A B O α∴∠=， 同理332111222A B O αα∠=⨯=， 44312A B O α∠=， 112n n n A B O α-∴∠=， 101092A B O α∴∠=，故选：B ．【点睛】本题考查了等腰三角形两底角相等的性质，图形的变化规律，依次求出相邻的两个角的差，得到分母成2的指数次幂变化，分子不变的规律是解题的关键．12．如图，坐标平面内一点A(2，－1)，O 为原点，P 是x 轴上的一个动点，如果以点P 、O 、A 为顶点的三角形是等腰三角形，那么符合条件的动点P 的个数为( )A．2 B．3 C．4 D．5【答案】C【解析】以O点为圆心，OA为半径作圆与x轴有两交点，这两点显然符合题意．以A点为圆心，OA为半径作圆与x轴交与两点（O点除外）．以OA中点为圆心OA长一半为半径作圆与x 轴有一交点．共4个点符合，13．如图，在△ABC中，分别以点A和点B为圆心，大于12AB的长为半径画弧，两弧相交于点M、N，作直线MN，交BC于点D，连接AD，若△ADC的周长为14，BC=8，则AC 的长为A．5 B．6 C．7 D．8【答案】A【解析】【分析】根据题意可得MN是直线AB的中点，所以可得AD=BD，BC=BD+CD，而△ADC为AC+CD+AD=14，即AC+CD+BD=14，因此可得AC+BC=14，已知BC即可求出AC.【详解】根据题意可得MN是直线AB的中点AD BD∴=ADC的周长为14AC CD AD++=14AC CD BD++=∴BC BD CD=+14AC BC=∴+已知8BD=6AC∴=，故选B【点睛】本题主要考查几何中的等量替换，关键在于MN是直线AB的中点，这样所有的问题就解决了.14．在坐标平面上有一个轴对称图形，其中A （3，﹣52）和B （3，﹣112）是图形上的一对对称点，若此图形上另有一点C （﹣2，﹣9），则C 点对称点的坐标是（ ）A ．（﹣2，1）B ．（﹣2，﹣32）C ．（﹣32，﹣9） D ．（﹣2，﹣1） 【答案】A【解析】【分析】 先利用点A 和点B 的坐标特征可判断图形的对称轴为直线y=-4，然后写出点C 关于直线y=-4的对称点即可．【详解】解：∵A （3，﹣52）和B （3，﹣112）是图形上的一对对称点， ∴点A 与点B 关于直线y ＝﹣4对称， ∴点C （﹣2，﹣9）关于直线y ＝﹣4的对称点的坐标为（﹣2，1）．故选：A ．【点睛】本题考查了坐标与图形的变化，需要注意关于直线对称：关于直线x=m 对称，则两点的纵坐标相同，横坐标和为2m ；关于直线y=n 对称，则两点的横坐标相同，纵坐标和为2n ．15．如图所示，把多块大小不同的30角三角板，摆放在平面直角坐标系中，第一块三角板AOB 的一条直角边与x 轴重合且点A 的坐标为()2,0，30ABO ∠=︒，第二块三角板的斜边1BB 与第一块三角板的斜边AB 垂直且交x 轴于点1B ，第三块三角板的斜边12B B 与第二块三角板的斜边1BB 垂直且交y 轴于点2B ，第四块三角板斜边23B B 与第三块三角板的斜边12B B 垂直且交x 轴于点3B ，按此规律继续下去，则点2018B 的坐标为（ ）A ．()20182(3),0-⨯ B ．()20180,2(3)-⨯ C ．()20192(3),0⨯ D ．()20190,2(3)-⨯ 【答案】D【解析】【分析】 计算出OB 、OB 1、 OB 2的长度，根据题意和图象可以发现题目中的变化规律，从而可以求得点B 2018的坐标．【详解】 解：由题意可得， OB = 2242-= 23，OB 1= 3 OB= 233⨯ = 22(3)⨯，OB 2= 3 OB 1= 32(3)⨯，…∵2018÷4=504…2，∴点B 2018在y 轴的负半轴上，∴点B 2018的坐标为()20190,2(3)-⨯．故答案为：D ．【点睛】本题考查规律型：点的坐标规律及含30度角的直角三角形的性质，解答本题的关键是明确题意，找出题目中坐标的变化规律，求出相应的点的坐标．16．如图，△ABC 中，AB ＝AC ，且∠ABC ＝60°，D 为△ABC 内一点 ，且DA ＝DB ，E 为△ABC 外一点，BE ＝AB ，且∠EBD ＝∠CBD ，连DE ，CE. 下列结论：①∠DAC ＝∠DBC ；②BE ⊥AC ；③∠DEB ＝30°. 其中正确的是（ ）A ．①...B ．①③...C ．② ...D ．①②③【答案】B【解析】【分析】 连接DC,证ACD BCD DAC DBC ∠∠≅=得出①，再证BED BCD ≅，得出BED BCD 30∠∠==︒;其它两个条件运用假设成立推出答案即可.【详解】解：证明：连接DC ，∵△ABC 是等边三角形，∴AB=BC=AC ，∠ACB=60°，∵DB=DA ，DC=DC ，在△ACD与△BCD中，AB BC DB DA DC DC=⎧⎪=⎨⎪=⎩,∴△ACD≌△BCD （SSS），由此得出结论①正确；∴∠BCD=∠ACD=130 2ACB∠=︒∵BE=AB，∴BE=BC，∵∠DBE=∠DBC，BD=BD，在△BED与△BCD中，BE BCDBE DBCBD BD=⎧⎪∠=∠⎨⎪=⎩,∴△BED≌△BCD （SAS），∴∠DEB=∠BCD=30°．由此得出结论③正确；∵EC∥AD，∴∠DAC=∠ECA，∵∠DBE=∠DBC，∠DAC=∠DBC，∴设∠ECA=∠DBC=∠DBE=∠1，∵BE=BA，∴BE=BC，∴∠BCE=∠BEC=60°+∠1，在△BCE中三角和为180°，∴2∠1+2（60°+∠1）=180°∴∠1=15°，∴∠CBE=30，这时BE是AC边上的中垂线，结论②才正确．因此若要结论②正确，需要添加条件EC∥AD.故答案为：B.【点睛】本题考查的知识点主要是全等三角形的判定与性质以及等边三角形的性质，通过已知条件作出恰当的辅助线是解题的关键点.17．如图，C为线段AE上一动点（不与点A、E重合），在AE同侧分别作等边三角形ABC 和等边三角形CDE，AD与BE交于点O，AD与BC交于点P，BE与CD交于点Q，连接PQ．以下五个结论：①AD＝BE；②AP＝BQ；③PQ∥AE；④DE＝DP；⑤∠AOE＝120°；其中正确结论的个数为（）A．2个B．3个C．4个D．5个【答案】C【解析】【分析】①由于△ABC和△CDE是等边三角形，可知AC=BC，CD=CE，∠ACB=∠DCE=60°，从而证出△ACD≌△BCE，可推知AD=BE，故①正确；②由△ACD≌△BCE得∠CBE=∠DAC，加之∠ACB=∠DCE=60°，AC=BC，得到△ACP≌△BCQ （ASA），所以AP=BQ；故②正确；③根据②△CQB≌△CPA（ASA），再根据∠PCQ=60°推出△PCQ为等边三角形，又由∠PQC=∠DCE，根据内错角相等，两直线平行，可知③正确；④根据∠QCP=60°，∠DPC=∠BCA+∠PAC＞60°，可知PD≠CD，可知④错误；⑤利用等边三角形的性质，BC∥DE，再根据平行线的性质得到∠CBE=∠DEO，于是∠AOB=∠DAC+∠BEC=∠BEC+∠DEO=∠DEC=60°，由平角的性质可得∠AOE=120°，可知⑤正确；【详解】①∵△ABC和△CDE为等边三角形∴AC＝BC，CD＝CE，∠BCA＝∠DCB＝60°∴∠ACD＝∠BCE∴△ACD≌△BCE（SAS）∴AD＝BE，故①正确；由（1）中的全等得∠CBE＝∠DAC，且BC＝AC，∠ACB＝∠BCQ＝60°∴△CQB≌△CPA（ASA），∴AP＝BQ，故②正确；∵△CQB≌△CPA，∴PC＝PQ，且∠PCQ＝60°∴△PCQ为等边三角形，∴∠PQC＝∠DCE＝60°，∴PQ∥AE，故③正确，∵∠QCP＝60°，∠DPC＝∠BCA+∠PAC＞60°，∴PD≠CD，∴DE≠DP，故④DE＝DP错误；∵BC∥DE，∴∠CBE＝∠BED，∵∠CBE＝∠DAE，∴∠AOB＝∠OAE+∠AEO＝60°，∴∠AOE＝120°，故⑤正确，故选C．【点睛】本题考查了全等三角形的判定与性质，利用了等边三角形的判定与性质，全等三角形的判定与性质，平行线的判定与性质，综合性较强，题目难度较大．18．如图, 在△DAE中, ∠DAE＝40°, B、C两点在直线DE上，且∠BAE＝∠BEA，∠CAD＝∠CDA，则∠BAC的大小是（）A．100°B．90°C．80°D．120°【答案】A【解析】【分析】由已知条件，利用了中垂线的性质得到线段相等及角相等，再结合三角形内角和定理求解.【详解】解：如图，∵BG是AE的中垂线，CF是AD的中垂线，∴AB=BE，ACECD∴∠AED=∠BAE=∠BAD+∠DAE，∠CDA=∠CAD=∠DAE+∠CAE，∵∠DAE+∠ADE+∠AED=180°∴∠BAD+∠DAE+∠DAE+∠CAE+∠DAE=3∠DAE+∠BAD+∠EAC=120°+∠BAD+∠EAC=180°∴∠BAD+∠EAC=60°∴.∠BAC=∠BAD+∠EAC+∠DAE=60°+40°=100°；故选：A【点睛】本题考查了中垂线的性质、三角形内角和定理及等腰三角形的判定与性质；找着各角的关系利用内角和列式求解是正确解答本题的关键.19．如图，一张长方形纸沿AB对折，以AB中点O为顶点将平角五等分，并沿五等分的折线折叠，再沿CD 剪开，使展开后为正五角星（正五边形对角线所构成的图形）．则∠OCD 等于（ ）A ．108°B ．114°C ．126°D ．129°【答案】C【解析】【分析】 按照如图所示的方法折叠,剪开,把相关字母标上,易得∠ODC 和∠DOC 的度数,利用三角形的内角和定理可得∠OCD 的度数．【详解】解:展开如图,五角星的每个角的度数是,1805=36°. ∵∠COD =360°÷10=36°,∠ODC=36°÷2=18°,∴∠OCD =180°-36°-18°=126°,故选C ．【点睛】本题主要考查轴对称性质,解决本题的关键是能够理解所求的角是五角星的哪个角,解题时可以结合正五边形的性质解决．20．如图，在ABC △中，2B C ∠=∠，AH BC ⊥，AE 平分BAC ∠，M 是 BC 中点，则下列结论正确的个数为（ ）（1）AB BE AC += （2）2AB BH BC += （3）2AB HM = （4）CH EH AC +=A ．1B ．2C ．3D ．4【答案】D【解析】【分析】（1）延长AB 取BD=BE ，连接DE ，由∠D=∠BED ，2ABC C ∠=∠，得到∠D=∠C ，在△ADE 和△ACE 中，利用AAS 证明ADE ACE ≌，可得AC=AD=AB+BE ；（2）在HC上截取HF=BH,连接AF，可知△ABF为等腰三角形，再根据2ABC AFB C∠=∠=∠，可得出△AFC为等腰三角形，所以FC+BH+HF=AB+2BH=BC；（3）HM=BM-BH，所以2HM=2BM-2BH=BC-2BH，再结合（2）中结论，可得2AB HM=；（4）结合（1）（2）的结论，BC2BH BE BC BH BE BH CH EHAC AB BE=+=-+=-+-=+.【详解】解：①延长AB取BD=BE，连接DE，∴∠D=∠BED，∠ABC=∠D+∠BED=2∠D,∵2ABC C∠=∠，∴∠D=∠C，在△ADE和△ACE中，DAE CAED CAE AE∠=∠⎧⎪∠=∠⎨⎪=⎩，∴ADE ACE≌∴AC=AD=AB+BE，故（1）正确；②在HC上截取HF=BH,连接AF，∵AH BC⊥，∴△ABF为等腰三角形，∴AB=AF，∠ABF=∠AFB，∵2ABC C∠=∠，∴∠AFB=2∠C=∠C+∠CAF，∴FC=AF=AB，∴FC+BH+HF=AB+2BH=BC，故（2）正确；③∵HM=BM-BH，∴2HM=2BM-2BH=BC-2BH，由②可知BC-2BH=AB，∴2AB HM=④根据①②结论，可得:BC2BH BE BC BH BE BH CH EHAC AB BE=+=-+=-+-=+，故（4）正确；故选D.【点睛】本题主要考查了等腰三角形的判定和性质、三角形的外角以及全等三角形的判定和性质，结合实际问题作出合适辅助线是解题关键.。

人教版数学八年级上学期《三角形》单元测试时间:90分钟总分: 100一、选择题1.能将三角形面积平分的是三角形的..)A.角平分..B...C.中..D.外角平分线2.已知三角形的两边长分别为4cm和9cm, 则下列长度的四条线段中能作为第三边的是.. )A.13c..B.6c..C.5c..D.4cm3.三角形一个外角小于与它相邻的内角, 这个三角形是...)A.直角三角..B.锐角三角..C.钝角三角..D.属于哪一类不能确定4.若一个多边形每一个内角都是135º, 则这个多边形的边数是...)A...B...C.1..D.125.某商店出售下列四种形状的地砖:①正三角形;②正方形;③正五边形;④正六边形.若只选购其中一种地砖镶嵌地面, 可供选择的地砖共有( )A.4..B.3..C.2..D.1种6.一个多边形的外角和是内角和的一半, 则它是. )边形A...B...C...D.47.如图，DE是△ABC的中位线，F是DE的中点，CF的延长线交AB于点G，若△CEF的面积为12cm2，则S △DGF的值为. )学*科*网...学*科*网...A.4cm..B.6cm..C.8cm..D.9cm28.已知△ABC中, ∠A=20°, ∠B=∠C, 那么三角形△ABC是()A.锐角三角..B.直角三角..C.钝角三角..D.正三角形9.试通过画图来判定, 下列说法正确的是()A.一个直角三角形一定不是等腰三角形B.一个等腰三角形一定不是锐角三角形C.一个钝角三角形一定不是等腰三角形D.一个等边三角形一定不是钝角三角形10.如图，BD平分∠ABC，CD⊥BD，D为垂足，∠C=55°，则∠ABC的度数是()A.35..B.55..C.60..D.70°二、填空题11.如果点G是△ABC的重心.AG的延长线交BC于点D.GD=12.那么AG=________.12.如图，将三角尺的直角顶点放在直尺的一边上，∠1= ，∠2= ，则∠3=_____________°.13.若一个多边形的内角和比外角和大360°, 则这个多边形的边数为_______________.14.如图，△ABC中，∠ACB＞90°，AD⊥BC，BE⊥AC，CF⊥AB，垂足分别为D.E、F，则线段___是△ABC中AC边上的高.15.一个多边形的内角和是外角和的2倍, 则这个多边形的边数为___.16.十边形的外角和是_____°.17.若三角形的周长是60cm，且三条边的比为3:4:5，则三边长分别为__________．18.如图，⊿ABC中，∠..40°，∠..72°，CE平分∠ACB，CD⊥AB于D，DF⊥CE，则∠CD.=_________度。