浙江省宁波市第七中学2014-2015学年下学期八年级学习效果自我评估测试数学试题及答案

2024届浙江省宁波七中学教育集团数学八年级第二学期期末预测试题注意事项：1．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。

2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案标号。

回答非选择题时，将答案写在答题卡上，写在本试卷上无效。

3．考试结束后，将本试卷和答题卡一并交回。

一、选择题(每小题3分,共30分)1．如图，小颖为测量学校旗杆AB 的高度，她在E 处放置一块镜子，然后退到C 处站立，刚好从镜子中看到旗杆的顶部B ．已知小颖的眼睛D 离地面的高度CD ＝1.5m ，她离镜子的水平距离CE ＝0.5m ，镜子E 离旗杆的底部A 处的距离AE ＝2m ，且A 、C 、E 三点在同一水平直线上，则旗杆AB 的高度为（ ）A ．4.5mB ．4.8mC ．5.5mD ．6 m2．一个有进水管与出水管的容器，从某时刻开始4min 内只进水不出水，在随后的8min 内既进水又出水，每分钟的进水量和出水量是两个常数，容器内的水量y （单位：L ）与时间x （单位：min ）之间的关系如图所示．则8min 时容器内的水量为（ ）A ．20 LB ．25 LC ．27LD ．30 L3．一次函数y=2x ﹣1的图象大致是( )A ．B ．C ．D ．4．在矩形ABCD 中，4AB m BC H ==，，是BC 的中点，DE AH ⊥，垂足为E ，则用m 的代数式表示DE 的长为（）A ．255mB ．22444m m m ++C ．5mD ．522m 5．如图，在正方形ABCD 中，点P 在AC 上，PE ABPF BC ⊥⊥，，垂足分别为E ，3F EF =，，则PD 的长为( )A ．1.5B ．2C ．2.5D ．36．下列数据中不能作为直角三角形的三边长的是( )A ．1，3，2B ．7，24，25C ．111,,345. D ．1，2，37．用配方法解一元二次方程2610x x -+=，此方程可化为的正确形式是( )A ．2(3)10x +=B ．2(3)8x +=C ．2(3)10x -=D ．2(3)8x -=8．如图，将含30°角的直角三角尺ABC 绕点B 顺时针旋转150°后得到△EBD ，连接CD ．若AB=4cm ．则△BCD 的面积为（ ）A ．3B ．3C ．3D ．29．下列长度的三条线段能组成直角三角形的是() A ．3， 4，5 B ．2，3，4 C ．4，6，7 D ．5，11，1210．某交警在一个路口统计的某时段来往车辆的车速情况如表：车速（km/h ）48 49 50 51 52 车辆数（辆） 4 6 7 2 1则上述车速的中位数和众数分别是（ ）A ．49，50B ．49.5，7C ．50，50D ．49.5，50二、填空题(每小题3分,共24分)11．若平面直角坐标系内的点M 在第四象限，且M 到x 轴的距离为1，到y 轴的距离为2，则点M 的坐标为_________________．12．如图，在四边形ABCD 中，AB=BC=2，CD=1，AD=3，若∠B=90°，则∠BCD 的度数为____________________．13．在平行四边形ABCD 中，若∠A =70°，则∠C 的度数为_________.14．若1x +在实数范围内有意义，则x 的取值范围是_________．15．如图，在Rt ABC 中，90A ∠=︒，以顶点C 为圆心，适当长为半径画弧，分别交CB ，CA 于点M ，N ，再分别以点M ，N 为圆心，大于12MN 的长为半径画弧，两弧交于点P ，作射线CP 交AB 于点D ，若3AD =，12BC =，则DBC S △的值是__________．16．如图，在平行四边形ABCD 中，ABC ∠的平分线BF 交AD 于点F ，FEAB ．若5AB =，6BF =，则四边形ABEF 的面积为________．17．如图所示，△ABC 中，AH ⊥BC 于H ，点E ，D ，F 分别是AB ，BC ，AC 的中点，HF=10cm ，则ED 的长度是_____cm ．18．已知关于x 的方程x 2﹣kx ﹣6=0的一个根为x=3，则实数k 的值为_____．三、解答题(共66分)19．（10分）已知在▱ABCD 中，点E 、F 在对角线BD 上，BE ＝DF ，点M 、N 在BA 、DC 延长线上，AM ＝CN ，连接ME 、NF ．试判断线段ME 与NF 的关系，并说明理由．20．（6分）一组数据：1，1，2，5，x 的平均数是1．(1)求x 的值；(2)求这组数据的方差．21．（6分）如图，点C 在EF 上，90AEF EFB ACB ∠=∠=∠=︒，2AC =，3BC =，EF BF =，求EF 的长.22．（8分）已知直线y kx b =+的图象经过点(2,4)和点(2,2)--（1）求b 的值；（2）求关于x 的方程0kx b +=的解（3）若11(,)x y 、22(,)x y 为直线上两点，且12x x <，试比较1y 、2y 的大小23．（8分）如图，在Rt △ABC 中，∠C ＝90°，AC ＝5，AB ＝13，求BC ．24．（8分）如图，已知直线1l 的解析式为1y x b =-+，直线2l 的解析式为2 4y kx =+，1l 与x 轴交于点C ，2l 与x 轴交于点B ，1l 与2l 交于点()1,2A -.①,k b的值.②求三角形ABC的面积.25．（10分）如图，在平面直角坐标系中，点D是正方形OABC的边AB上的动点，OC＝1．以AD为一边在AB的右侧作正方形ADEF，连结BF交DE于P点．（1）请直接写出点A、B的坐标；（2）在点D的运动过程中，OD与BF是否存在特殊的位置关系？若存在，试写出OD与BF的位置关系，并证明；若不存在，请说明理由．（3）当P点为线段DE的三等分点时，试求出AF的长度．26．（10分）如图,一次函数y=kx+b的图象经过点A(8,0)，直线y=-3x+6与x轴交于点B,与y轴交于点D,且两直线交于点C(4,m).(1)求m的值及一次函数的解析式；(2)求△ACD的面积．参考答案一、选择题(每小题3分,共30分)1、D【解题分析】根据题意得出△ABE∽△CDE，进而利用相似三角形的性质得出答案．【题目详解】解：由题意可得：AE＝2m，CE＝0.5m，DC＝1.5m，∵△ABC∽△EDC，∴，即，解得：AB＝6，故选：D．【题目点拨】本题考查的是相似三角形在实际生活中的应用，根据题意得出△ABE∽△CDE是解答此题的关键．2、B【解题分析】试题分析：由图形可得点（4，20）和（12，30），然后设直线的解析式为y=kx+b，代入可得420{1230k bk b+=+=，解得5{415kb==，得到函数的解析式为y=54x+15，代入x=8可得y=25.故选：B点睛：此题主要考察了一次函数的图像与性质，先利用待定系数法求出函数的解析式，然后代入可求解.3、B【解题分析】根据一次函数的性质，判断出k和b的符号即可解答．【题目详解】由题意知，k=2＞0，b=﹣1＜0时，函数图象经过一、三、四象限．故选B．【题目点拨】本题考查了一次函数y =kx +b 图象所过象限与k ，b 的关系，当k ＞0，b ＜0时，函数图象经过一、三、四象限． 4、B【解题分析】如图连接DH ，根据面积和相等列方程求解.【题目详解】解：如图所示连接DH ，AB=m,BC=4,BH=2，则矩形面积24m +则矩形ABCD=三角形ABH+三角形AHD+三角形DHC ，则4m=m+12DE 24m ++m, 解得244m m +【题目点拨】本题考查勾股定理和矩形性质，能够做出辅助线是解题关键.5、D【解题分析】作辅助线PB ，求证BP DP =，然后证明四边形BFPE 是矩形，3PD EF BP ===【题目详解】如图，连接PB .在正方形ABCD 中，45AB ADBAC DAC =∠=∠=︒，. ∵45AP APBAP DAP AB AD =∠=∠=︒=，，， ∴()ABP ADP SAS ≌，∴BP DP =.∵90PE ABPF BC ABC ⊥⊥∠=︒，，， ∴四边形BFPE 是矩形，∴EF PB =.∴3PD EF ==.故选D.【题目点拨】本题考查了全等三角形的判定定理（SAS ）以及矩形对角线相等的性质，从而求出PD 的长度6、C【解题分析】根据勾股定理的逆定理：如果三角形有两边的平方和等于第三边的平方，那么这个三角形是直角三角形．如果没有这种关系，这个就不是直角三角形．【题目详解】解：A .2221(3)2+=，符合勾股定理的逆定理，故不符合题意；B . 72+242=252，符合勾股定理的逆定理，故不符合题意；C .222111()()()453+≠，不符合勾股定理的逆定理，故符合题意；D .222123+=（）（），符合勾股定理的逆定理，故不符合题意． 故选：C ．【题目点拨】本题考查了勾股定理的逆定理，在应用勾股定理的逆定理时，应先认真分析所给边的大小关系，确定最大边后，再验证两条较小边的平方和与最大边的平方之间的关系，进而作出判断．7、D【解题分析】方程常数项移到右边，两边加上9变形即可得到结果．【题目详解】解：方程移项得：x 2-6x=-1，配方得：x 2-6x+9=8，即（x-3）2=8,故选D ．【题目点拨】本题考查了解一元二次方程-配方法，熟练掌握完全平方公式是解题的关键．8、C过D点作BE的垂线，垂足为F，由∠ABC=30°及旋转角∠ABE=150°可知∠CBE为平角．在Rt△ABC中，AB=4，∠ABC=30°，则AC=2，BC=23，由旋转的性质可知BD=BC=23，DE=AC=2，BE=AB=4，由面积法：DF×BE=BD×DE求DF，则S△BCD=12×BC×DF．【题目详解】过D点作BE的垂线，垂足为F，∵∠ABC=30°，∠ABE=150°，∴∠CBE=∠ABC+∠ABE=180°．在Rt△ABC中，∵AB=4，∠ABC=30°，∴AC=2，BC=23，由旋转的性质可知：BD=BC=23，DE=AC=2，BE=AB=4，由DF×BE=BD×DE，即DF×4=23×2，解得：DF=3，S△BCD=12×BC×DF=12×23×3=3（cm2）．故选C．【题目点拨】本题考查了旋转的性质，解直角三角形的方法，解答本题的关键是围绕求△BCD的面积确定底和高的值，有一定难度．9、A【解题分析】利用勾股定理的逆定理：如果三角形两条边的平方和等于第三边的平方，那么这个三角形就是直角三角形．最长边所对的角为直角．由此判定即可．【题目详解】A、∵32+42=52，∴三条线段能组成直角三角形，故A选项正确；B、∵22+32≠42，∴三条线段不能组成直角三角形，故B选项错误；C、∵42+62≠72，∴三条线段不能组成直角三角形，故C选项错误；D、∵52+112≠122，∴三条线段不能组成直角三角形，故D选项错误；故选A．考查勾股定理的逆定理，如果三角形两条边的平方和等于第三边的平方，那么这个三角形就是直角三角形．10、D【解题分析】根据中位数的众数定义即可求出.【题目详解】车辆总数为：4+6+7+2+1=20辆，则中位数为：12（第10个数+第11个数）4950==49.52众数为出现次数最多的数：50故选D【题目点拨】本题考查了中位数和众数，难度低，属于基础题，熟练掌握中位数的求法是解题关键.二、填空题(每小题3分,共24分)11、 (2，-1)【解题分析】可先根据到x轴的距离为点的纵坐标的绝对值，到y轴的距离为点的横坐标的绝对值，进而判断出点的符号，得到具体坐标即可．【题目详解】∵M到x轴的距离为1，到y轴的距离为2，∴M纵坐标可能为±1，横坐标可能为±2，∵点M在第四象限，∴M坐标为(2，-1)．故答案为：(2，-1)．【题目点拨】本题考查点的坐标的确定；用到的知识点为：点到x轴的距离为点的纵坐标的绝对值，到y轴的距离为点的横坐标的绝对值．12、135°【解题分析】根据勾股定理求出AC，根据勾股定理的逆定理求出∠ACD=90°，进而得出答案．【题目详解】连接AC，在Rt△ABC中，由勾股定理得：2222AC AB BC=+=∵AB=BC，∴∠BAC=∠ACB=45°，∵CD=1，AD=3，2，∴AC2+CD2=AD2，∴∠ACD=90°，∴∠DCB=90°+45°=135°，故答案为：135°．【题目点拨】本题考查了勾股定理，勾股定理的逆定理的应用，能求出△ACD是直角三角形是解此题的关键．13、70°【解题分析】在平行四边形ABCD中，∠C=∠A，则求出∠A即可．【题目详解】根据题意在平行四边形ABCD中，根据对角相等的性质得出∠C=∠A，∵∠A=70°，∴∠C=70°.故答案为：70°.【题目点拨】此题考查平行四边形的性质，解题关键在于利用平行四边形的性质解答.14、x≥-1【解题分析】根据二次根式的性质即可求解.【题目详解】依题意得x+1≥0，解得x≥-1故填：x≥-1【题目点拨】此题主要考查二次根式的性质，解题的关键是熟知根号内被开方数为非负数.15、1【解题分析】过点D 作DE ⊥BC 于E ，根据角平分线的作法可知CD 平分∠ACB ，然后根据角平分线的性质可得DE=AD=3，然后根据三角形的面积公式求面积即可．【题目详解】解：过点D 作DE ⊥BC 于E由题意可知：CD 平分∠ACB∵90A ∠=︒∴DE=AD=3∵12BC =∴DBC S △=1182BC DE •= 故答案为：1．【题目点拨】此题考查的是用尺规作图作角平分线和角平分线的性质，掌握角平分线的作法和角平分线的性质是解决此题的关键． 16、1【解题分析】首先证明四边形ABEF 是菱形，然后求出AE 即可解决问题．【题目详解】解：连接AE ，交BF 于点O.∵四边形ABCD是平行四边形，∴AD∥BC，即AF∥BE，∵EF∥AB，∴四边形ABEF是平行四边形，∵AF∥BE，∴∠AFB=∠FBE，∵BF平分∠ABC，∴∠ABF=∠CBF，∴∠ABF=∠AFB，∴AB=AF，∴平行四边形ABEF是菱形，连接AE交BF于O，∴AE⊥BF，OB=OF=3，OA=OE，在Rt△AOB中，22AB OB，∴AE=2OA=8，∴S菱形ABEF=12•AE•BF=1．故答案为1.【题目点拨】本题考查菱形的性质和判定，平行四边形的性质和判定，勾股定理，等腰三角形的性质，平行线的性质等知识点的应用，能综合运用性质和判定进行推理是解此题的关键，难度适中．17、1【解题分析】分析中先利用直角三角形的性质，然后再利用三角形的中位线定理可得结果．【题目详解】∵AH⊥BC，F是AC的中点，∴FH=12AC=1cm，∴AC=20cm，∵点E，D分别是AB，BC的中点，∴ED=12AC ， ∴ED=1cm ．故答案为：1．【题目点拨】本题考查的知识点：三角形中位线定理和直角三角形斜边上的中线等于斜边的一半，是基础知识较简单．18、1【解题分析】本题根据一元二次方程的根的定义、一元二次方程的定义求解．【题目详解】∵x=3是方程的根，由一元二次方程的根的定义，可得32-3k-6=0，解此方程得到k=1．【题目点拨】本题逆用一元二次方程解的定义易得出k 的值．三、解答题(共66分)19、ME ＝NF 且ME ∥NF ，理由见解析【解题分析】利用SAS 证得△BME ≌△DNF 后即可证得结论．【题目详解】证明：ME ＝NF 且ME ∥NF ．理由如下：∵四边形ABCD 是平行四边形，∴AB ∥CD ，∴∠EBM ＝∠FDN ，AB ＝CD ，∵AM ＝CN ，∴MB ＝ND ，∵BE ＝DF ，∴BF ＝DE ，∵在△BME 和△DNF 中MB ND MBE NDF BE DF =⎧⎪∠=∠⎨⎪=⎩，∴△BME ≌△DNF （SAS ），∴ME ＝NF ，∠MEB ＝∠NFD ，∴∠MEF ＝∠BFN ．∴ME ∥NF ．∴ME ＝NF 且ME ∥NF ．【题目点拨】此题主要考查了平行四边形的性质以及全等三角形的判定与性质，熟练掌握全等三角形的判定方法是解题关键．20、（1）x=4；（2）2.【解题分析】（1）根据算术平均数定义列出关于x 的方程，解之可得x 的值；（2）根据方差计算公式计算可得．【题目详解】解：（1）根据题意知13255x ++++=1， 解得：x=4；（2）方差为15×[（1﹣1）2+（1﹣1）2+（2﹣1）2+（5﹣1）2+（4﹣1）2]=2． 【题目点拨】 考查方差的定义：一般地设n 个数据，x 1，x 2，…x n 的平均数为x ，则方差S 2=222121[]n x x x x x x n -+-+⋯+-（）（）（） ，它反映了一组数据的波动大小，方差越大，波动性越大，反之也成立． 2191010【解题分析】 首先证明AEC CFB △∽△，得到23AC EC CB FB ==，设EF BF x ==，于是得到2233EC FB x ==，13CF x =.在Rt FBC △中，利用勾股定理可得结果.【题目详解】解：∵ 90AEF EFB ACB ∠=∠=∠=︒∴∴∠ACE+∠BCF=∠CAE+∠ACE=90°，∴∠CAE=∠FBC ，∴AEC CFB △∽△.设EF BF x ==. ∴23AC EC CB FB ==. ∴2233EC FB x ==，13CF x =. 在Rt FBC △中，可得222133x x ⎛⎫+= ⎪⎝⎭.解得，1x =2x = 所以EF. 【题目点拨】本题考查相似三角形的判定与性质、勾股定理．利用三角形相似求出相似比是解决问题的关键．22、（1）b=1；（2）23x =-；（3）12y y <. 【解题分析】（1）将直线经过的两点代入原直线，联立二元一次方程组即可求得b 值；（2）求出k 值，解一元一次方程3102x +=即可； （3）根据k 的大小判断直线是y 随x 的增大而增大的，由此可知1y 、2y 的大小.【题目详解】解：（1）将（2，4），（-2，-2）代入直线得到：4222k b k b =+⎧⎨-=-+⎩， 解得：321k b ⎧=⎪⎨⎪=⎩，∴b=1；（2）已知32k，b=1， 令3102x +=， 解得23x =-， ∴关于x 的方程0kx b +=的解是23x =-；（3）由于32k>0，可知直线是y 随x 的增大而增大的， ∵12x x <，∴1y <2y . 【题目点拨】本题考查一次函数表达式，增减性，解题时要注意理解一次函数与方程的关系.23、12【解题分析】在Rt △ABC 中，∠C ＝90°，AC ＝5，AB ＝13，根据勾股定理，即可求出BC ．【题目详解】解：∵在Rt △ABC 中，∠C ＝90°，∴222AC BC AB +=∴222BC AB AC =-∴BC =又∵AC ＝5，AB ＝13，∴BC ==12【题目点拨】此题主要考查勾股定理的运用.24、①k=2，b=1；②1【解题分析】①利用待定系数法求出k ，b 的值；②先根据两个函数解析式计算出B 、C 两点坐标，然后再利用三角形的面积公式计算出△ABC 的面积即可．【题目详解】解：①∵l 1与l 2交于点A （-1，2），∴2=-k+4，2=1+b ，解得k=2，b=1；②当y=0时，2x+4=0，解得x=-2，∴B（-2，0），当y=0时，-x+1=0 解得x=1，∴C（1，0），∴△ABC的面积=12×（2+1）×2=1．【题目点拨】此题主要考查了待定系数法求一次函数解析式，关键是掌握凡是函数图象经过的点必能满足解析式．25、（1）A（1，0），B（1，1）；（2）OD⊥BF，理由见解析；（3）当P点为线段DE的三等分点时，AF的长度为2或2．【解题分析】（1）利用正方形的性质得出OA=AB=1，即可得出结论；（2）利用SAS判断出△AOD≌△BAF，进而得出∠AOD=∠BAF，即可得出结论；（3）先表示出BD，DP，再判断出△BDP∽△BAF，得出BD DPAB AF，代入解方程即可得出结论。

浙江省宁波市第七中学2014-2015学年八年级语文下学期学习效果自我评估测试试题满分为100分考试时间为100分钟一、书写（4分）本题根据卷面书写情况评分，请你在书写时努力做到正确、工整。

二、积累与运用（20分）1.读下面这段文字，根据拼音写汉字。

（4分）江南的雪，可是▲ (zī )润美艳之至了；那是还在隐约着的青春的消息，是极壮健的处子的皮肤。

雪野中有血红的宝珠山茶，白中隐青的单▲ ( bàn)梅花，深黄的▲ (qìng )口的蜡梅花；雪下面还有冷绿的杂草。

胡蝶确乎没有；蜜蜂是否来采山茶花和梅花的蜜，我可记不真切了。

但我的眼前仿佛看见冬花开在雪野中，有许多蜜蜂们忙碌地飞着，也听得他们▲ (wēngwēng )地闹着。

2.读下面这段文字，为空格处选择合适的词语，将其序号填在横线上。

（3分）结构是评价文章品质优劣的重要指标之一。

好的结构要求做到构思有▲，文势有▲，情节有▲，前有伏笔，后有照应，起承转合，自然得体。

A 跌宕 B新意 C 抑扬3.古诗文名句默写。

（6分）（④⑤两题任选一题作答。

）①怀旧空吟闻笛赋，▲。

（刘禹锡《酬乐天扬州初逢席上见赠》）②▲，松柏有本性。

（刘桢《赠从弟（其二）》）③王勃《送杜少府之任蜀州》中表达送别时豪迈气势，开阔意境的句子是：▲，▲。

④古诗词中有不少表达爱国之情的句子，请写出连续的两句。

▲，▲。

⑤古诗词中有不少蕴含哲理的句子，请写出连续的两句。

▲，▲。

4.下列表述不正确的一项是（▲）(2分)A 《海底两万里》的作家是法国的凡尔纳，他是现代科幻小说的重要奠基人。

B “诺第留斯号”是船长尼摩在大洋中一座荒岛上秘密建造的，它是用太阳能作为动力源的。

C 《海底两万里》中尼德·兰和尼摩在印度洋的珠场和鲨鱼展开搏斗，并手刃了它。

D 凡尔纳的小说构思巧妙、情节惊险，充满了异国情调和浓厚的浪漫主义色彩。

5.综合性学习。

（5分）仔细观察这幅漫画，回答下列问题。

宁波七中2011学年第二学期初二英语学习效果期中评估测试试题卷（2012.4）命题人：陈苏君一．听力部分（20%）I 、听句子：根据句子的内容和所提问题，选择符合题意的图画回答问题。

（5分）（ ）1、What has Ms James done in China since 2002?A B C( ) 2、How much money has the project raised?A B C( ) 3、Which does Sally like?AA B C( ) 4、 Who do some people s ay was the greatest European composer?A 、StraussB 、BeethovenC 、Mozart( ) 5、 What was her aunt doing at that time?A B CⅡ、听对话及问题选择最佳答案（5分）。

6.How is Mr Green?A.. He is illB. He is fine.C. He is sad7.What subjects will the boy work hard at next term？A. Maths and chemistry.B. English and history.C. Physics and Chinese.8. What day is it today ?A. TuesdayB. WednesdayC. Thursday.9. How long did the meeting last?A. One hour .B. Two hoursC. Three hours10. What change would Sally like to see in their school ?A. More clubsB. More booksC. More librariesⅢ、听长对话，根据问题选择最佳答案。

2014——2015学年度第二学期七年、八年级期末质量检测成绩统计分析2015年7月4日—6日，在教体局和教研室的统一安排下，七八年级进行了期末测试，通过对学生成绩的深入分析，现将有关情况进行总结，以便为本学期工作提供参考，进而提高各年级教学质量。

一、基本情况本次期末考试是在学校的组织下进行的，每个考场有两名教师监考，监考教师认真负责，考场秩序井然，没有发生舞弊抄袭情况；阅卷也是在学校的统一安排下进行的，实行流水作业，阅卷教师仔细认真，基本上杜绝了人为因素的干扰，可以说，本次考试真实反映我校七八年级的教学状况。

1、基本数据统计生边缘，教师要密切关注，严防学困生队伍扩大。

更要引起教师重视。

近四年最高分比对2、各学科平均分、及格率、优秀率及低分率率较低，不到30%，数学、英语学科低分率相对高些。

表二：八年级各科平均分、及格率、优秀率及低分率、物理平均分不及格，语文、数学、英语、物理优秀率较低，数学、物理学科低分率较高。

纵向比对：从平均分看，七年语文、英语、思品、历史低于八年，七年数学高于八年级。

综合表一和表二可知：三大主科中，语文学科成绩较好，但不排除自己阅卷时尺度把握因素的影响；数学和英语学科（相对语文来讲）是我校比较薄弱的学科，两个教研组要加强研讨和学习，最大限度的提高教学质量。

二、成绩统计对比分析1、两个年段班与班比较：50分左右，两班总平均分差近40分。

表四：八年级两班各项数据于八二，总平均分八一高于八二15.6分。

2、近四年各科平均分比对：走在前列，显示我校教师积极、向上的工作状态，排名靠后的教师不要气馁，要分析原因，改进方法，靠后只是暂时的，要相信自己。

三、问题与建议问题一：语文学科整体排名靠后。

和其他学科相比，语文学科的各项数据明显要高，但和其他兄弟学校相比，还是有一定差距的，七年语文和旗最高分差77分（149.9—227.2），八年语文和旗最高分差51分（185.9—237.1）。

究其原因一是学生汉字书写能力差，很多学生写的字老师不认识，潦草，错字别字多，乱勾乱抹现象严重，部分学生识字能力差，课文中的词语不会写；二是古诗默写不过关，很多学生给上句不会对下句，理解填空更是空白；三是课外积累少，名著不知梗概，阅读答题缺乏技巧。

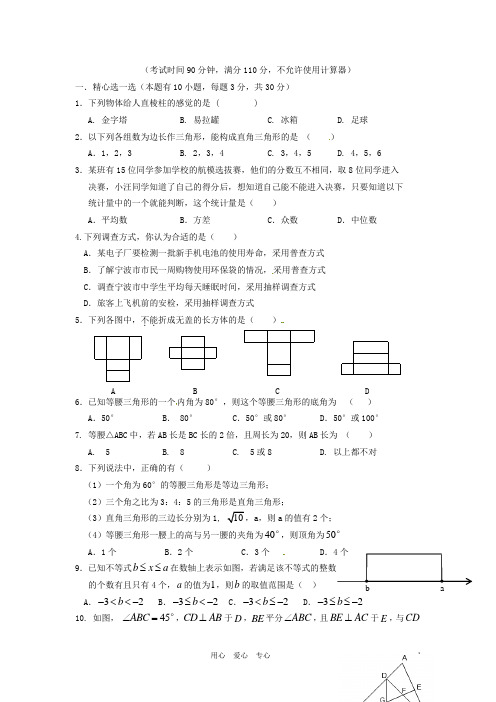
（考试时间90分钟，满分110分，不允许使用计算器）一．精心选一选（本题有10小题，每题3分，共30分）1．下列物体给人直棱柱的感觉的是 ( ) A. 金字塔B. 易拉罐C. 冰箱D. 足球2．以下列各组数为边长作三角形，能构成直角三角形的是 （ ） A ．1，2，3B. 2，3，4C. 3，4，5D. 4，5，63．某班有15位同学参加学校的航模选拔赛，他们的分数互不相同，取8位同学进入 决赛，小汪同学知道了自己的得分后，想知道自己能不能进入决赛，只要知道以下 统计量中的一个就能判断，这个统计量是（ ） A ．平均数B ．方差C ．众数D ．中位数4.下列调查方式，你认为合适的是（ ）A ．某电子厂要检测一批新手机电池的使用寿命，采用普查方式B ．了解宁波市市民一周购物使用环保袋的情况，采用普查方式C ．调查宁波市中学生平均每天睡眠时间，采用抽样调查方式D ．旅客上飞机前的安检，采用抽样调查方式5．下列各图中，不能．．折成无盖的长方体的是（ ）6．已知等腰三角形的一个内角为80°，则这个等腰三角形的底角为 （ ） A ．50°B ． 80°C ．50°或80°D ．50°或100°7. 等腰△ABC 中，若AB 长是BC 长的2倍，且周长为20，则AB 长为 （ ） A. 5 B. 8 C. 5或8D. 以上都不对8．下列说法中，正确的有（ ）（1）一个角为60°的等腰三角形是等边三角形； （2）三个角之比为3：4：5的三角形是直角三角形；（3）直角三角形的三边长分别为1, 10，a ，则a 的值有2个； （4）等腰三角形一腰上的高与另一腰的夹角为40°，则顶角为50° A ．1个 B ．2个 C ．3个 D ．4个 9．已知不等式b x a ≤≤ 的个数有且只有4个，a 的值为1，则b 的取值范围是（ ）A ．32b -<<-B ．32b -≤<-C ．32b -<≤-D ．32b -≤≤-10. 如图， 45ABC ∠=°，CD AB ⊥于D ，BE 平分ABC ∠，且BE AC ⊥于E ，与CD· ab · A B DC七 中学 子加 油（第15题）（第17题）4321DC BA（第14题）相交于点F H ，是BC 边的中点，连结DH 与BE 相交于点G ．以下结论中正确的个数有 （ ）（1）△ABC 是等腰三角形 （2）BF AC = （3）2CE BF =（4）BD:BC:DC =1:2:1（5）CE ≤ BG（6）222GE CE BG +=A ．3个 B. 4个 C. 5 个 D. 6个二．细心填一填（本题有10小题，每题3分，共 30分）11．如图，AB ∥CD ，∠A=∠B=90°，AB=3cm ，BC=2cm ，则AB 与CD 之间的距离为 cm ． 12．如图，把一块直角三角板的直角顶点放在直尺的一边上，若∠1=35o，则∠2= ．13. 如图是每个面上都标有一个汉字的立方体的表面展开图，在此立方体上与“子”字相对的面上的汉字是 ．14. 如图，不添加辅助线，请写出一个能判定AB ∥DC 的条件：______________． 15. 如图，将等边△ABC 的边BC 延长至D ，使得CD=AC ，若点E 是AD 的中点，则∠DCE 的度数为 ．16. 已知直角三角形斜边上的高与中线分别是5cm 和6cm ，则这个三角形的面积是 cm 217. 如图，在△ABC 中，已知AB=5，BC=6，∠ABC 和∠ACB 的角平分线BO 与CO 相交于点O ，OE ∥AB, OF ∥AC ，则△OEF 的周长为 ．18. 如图，折叠长方形ABCD 的一边AD ，使得点D 落在BC 边上的点F 处，已知AB=6cm ，D CA B（第11题）（第12题）ABCOE F（第13题）（第10题）ACEDFE D CBA BC=10cm ，则CE=_______cm ．19. 如图，△ABC 中，∠ABC=70°，在同一平面内，将△ABC ’绕点B 旋转到△A ’B ’C ’的位置，使得AA ’//CB ，则∠CBC ’度数为 _______．20. 如图，等腰直角△ABC 直角边长为2，以它的斜边上的高AD 为腰做第一个等腰直角△ADE ；再以所做的第一个等腰直角△ADE 的斜边上的高AF 为腰做第二个等腰直角△AFG ； ……以此类推，这样所做的第n 个等腰直角三角形的面积为_______．三．耐心做一做（本题有6小题，其中24,26题8分，其余各题6分共40分） 21. 如图所示的几何体由7个全等的小正方体组成，已知主视图如图，请补全该几何体的三视图。

宁波七中教育集团2023学年第二学期初二数学期中质量评估试题（2024.4）本试题卷分选择题和非选择题两部分，共6页，满分为110分，考试时间为90分钟。

考生注意：1．答题前，请务必将自己的姓名、准考证号用黑色笔迹的签字笔或钢笔分别填写在试题卷和答题纸规定的位置上。

2．答题时，请按照答题纸上“注意事项”的要求，在答题纸相应的位置上规范作答，在本试题卷上的作答一律无效。

选择题部分一、选择题（本题共10小题，每小题3分，共30分）1. 下列无理数中，大小在3与4之间的是（）．A. B. C. D.【答案】C【解析】【分析】根据无理数的估算可得答案，熟练掌握无理数的估算方法是解题的关键【详解】解：∵，，∴大小在3与4，故选：C．2. 下列图案是一些国产新能源车的车标，其中既是轴对称图形又是中心对称图形的是（）A. B. C.D.【答案】C【解析】【分析】根据轴对称图形和中心对称图形的概念，对选项逐个判断即可．【详解】解：A、该图形既不是中心对称图形，也不是轴对称图形，故此选项不合题意；B、该图形不是中心对称图形，是轴对称图形，故此选项不合题意；C、该图形既是中心对称图形，也是轴对称图形，故此选项符合题意；3=4==91316<<D 、该图形是中心对称图形，不是轴对称图形，故此选项不合题意．故选：C ．【点睛】本题考查了轴对称图形和中心对称图形的概念，熟练掌握如果一个图形沿着一条直线对折后两部分完全重合，这样的图形叫做轴对称图形，这条直线叫做对称轴，如果一个图形绕某一点旋转后能够与自身重合，那么这个图形就叫做中心对称图形，这个点叫做对称中心，是解答本题的关键．3. 正九边形的每一个外角的度数是（ ）A. B. C. D. 【答案】B【解析】【分析】根据正n 多边形的每一个外角的度数为，进行求解即可．【详解】解：正九边形的每一个外角的度数是,故选：B ．4. 用反证法证明命题“三角形中至少有一个内角小于或等于60°”时，首先应该假设这个三角形中（ ）A. 每一个内角都大于60°B. 每一个内角都小于60°C. 有一个内角大于60°D. 有一个内角小于60°【答案】A【解析】【分析】本题考查的是反证法的运用，反证法的一般步骤是：①假设命题的结论不成立；②从这个假设出发，经过推理论证，得出矛盾；③由矛盾判定假设不正确，从而肯定原命题的结论正确．反证法的步骤中，第一步是假设结论不成立，反面成立，据此进行判定．【详解】解：反证法证明命题“三角形中至少有一个内角小于或等于60°”时，首先应假设这个三角形中每一个内角都大于60°．故选：A ．5. 2023年4月23是第28个世界读书日，读书已经成为很多人的一种生活方式，城市书院是读书的重要场所之一，据统计，某书院对外开放的第一个月进书院600人次，进书院人次逐月增加，到第三个月末累计进书院2850人次，若进书院人次的月平均增长率为，则可列方程为（ ）A. B. C. D. 180︒30︒40︒60︒135︒360n ︒360409︒=︒x 600(12)2850x +=2600(1)2850x +=2600600(1)600(1)2850x x ++++=22850(1)600x -=【答案】C【解析】【分析】先分别表示出第二个月和第三个月的进馆人次，再根据第一个月的进馆人次加第二和第三个月的进馆人次等于2850，列方程即可．【详解】解：设进馆人次的月平均增长率为x ，则由题意得：．故选：C ．【点睛】本题属于一元二次方程的应用题，列出方程是解题的关键．本题难度适中，属于中档题．6. 八年级某班甲、乙、丙、丁四位同学准备选一人参加学校“跳绳”比赛．经过三轮测试，他们的平均成绩都是每分钟个，方差分别是，你认为派哪一个同学去参赛更合适（ ）A. 甲B. 乙C. 丙D. 丁【答案】D【解析】【分析】根据方差越小，成绩越稳定，进行判断即可．【详解】∵甲、乙、丙、丁四位同学的平均成绩相同，方差分别是，∴方差最小的为丁，∴派丁同学去参赛更合适．故选：D ．【点睛】本题考查利用方差作决策．熟练掌握方差越小，成绩越稳定是解题的关键．7. 如图，在四边形中，，添加下列条件，不能判定四边形是平行四边形的是（ ）A. B. C. D. 【答案】A【解析】2600600(1)600(1)2850x x ++++=180222265,56.5,53,50.5S S S S ====甲乙丁丙222265,56.5,53,50.5S S S S ====甲乙丁丙ABCD BC AD ∥ABCD AB CD=AB CD A C ∠=∠BC AD=【分析】本题主要考查了平行四边形的判定，熟知平行四边形的判定定理是解题的关键．【详解】解；添加条件，再由，不能根据一组对边相等，另一组对边平行证明四边形是平行四边形，故A 符合题意；添加条件，再由，能根据两组对边分别平行的四边形是平行四边形，证明四边形是平行四边形，故B 不符合题意；添加条件，由得到，进而得到，则，能根据两组对边分别平行的四边形是平行四边形，证明四边形是平行四边形，故C 不符合题意；添加条件，再由不能根据一组对边平行且相等的四边形是平行四边形，证明四边形是平行四边形，故D 不符合题意；故选；A ．8. 已知关于的方程，下列说法正确的是（ ）A. 当时，方程无解B. 当时，方程有一个实数解C. 当时，方程有两个相等实数解D. 当时，方程总有两个不相等的实数解【答案】C【解析】【分析】根据一元二次方程根的判别式求解即可．【详解】解：当时，方程为一元一次方程有唯一解，．当时，方程为一元二次方程，解的情况由根的判别式确定：∵，∴当时，方程有两个相等实数解，当且时，方程有两个不相等的实数解．综上所述，说法C 正确．故选：C ．【点睛】此题考查了一元二次方程根的判别式，解题的关键是熟练掌握一元二次方程根的判别式．当时，一元二次方程有两个不相等的实数根；当时，一元二次方程有两个相等的实数根；当时，一元二次方程没有实数根．的的AB CD =BC AD ∥ABCD AB CD BC AD ∥ABCD A C ∠=∠BC AD ∥180A B ∠+∠=︒180C B ∠+∠=︒AB CD ABCD BC AD =BC AD ∥ABCD x ()2110kx k x +--=0k =1k =1k =-0k ≠()()()221411k k k ∆=--⋅⋅-=+0k =10x -=1x =0k ≠()()()221411k k k ∆=--⋅⋅-=+1k =-0k ≠1k ≠-240b ac ∆=->240b ac ∆=-=24<0b ac ∆=-9. 如图，平行四边形的对角线相交于点的平分线与边相交于点是中点，若，则的长为（ ）A. 1B. 2C. 3D. 4【答案】B【解析】【分析】本题考查了平行四边形的性质，三角形中位线定理，根据平行四边形的性质可得，再根据平分，可得，从而可得，可得，进一步可得，再根据三角形中位线定理可得，即可求出的长．【详解】解：在平行四边形中，，∴，∵平分，∴，∴，∴，∵，∴，∵E 是中点，∴．故选：B ．10. 如图，在中，，斜边，分别以的三边长为边任上方作正方形，分别表示对应阴影部分的面积，则（）ABCD AC BD 、,O ADC ∠AB ,P E PD 12,16AD CD ==EO CDP APD ∠=∠DP ADC ∠CDP ADP ∠=∠APD ADP ∠=∠12AP AD ==4BP =EO ,,AB DC AB CD OD OB ==∥CDP APD ∠=∠DP ADC ∠CDP ADP ∠=∠APD ADP ∠=∠12AP AD ==16AB CD ==4BP =PD 122OE BP ==Rt ABC △60CBA ∠=︒2AB =ABC AB 12345,,,,S S S S S 12345S S S S S ++++=A. 2B. C. 4 D. 【答案】B【解析】【分析】本题考查勾股定理的应用和全等三角形的判定，根据题意过作于，连接，进而结合全等三角形的判定与性质得出进行分析计算即可.【详解】解：在中，，斜边，，，过作于，连接，在和中，，，同理，，，，，，，四边形是平行四边形，D DN BF ⊥N DI 123454ABC S S S S S S ++++= Rt ABC △60CBA ∠=︒2AB =BC ∴=121AB =AC==D DN BF ⊥N DI ACB BND 90ACB BND CAB NBD AD BD ︒⎧∠=∠=⎪∠=∠⎨⎪=⎩()AAS ACB BND ∴ ≌Rt MND Rt OCB ≌MD OB ∴=DMN BOC ∠=∠EM DO ∴=DN BC CI ∴== DN CI ∥∴DNCI，四边形是矩形，，、、三点共线，，，，图中，，在和中，，，同理，，．故选：B ．非选择题部分二、填空题（本题共8小题，每小题3分，共24分）11.的取值范围是________．【答案】##【解析】【分析】本题考查二次根式有意义的条件，根据题中二次根式列出不等式求解即可得到答案，熟记二次根式有意义的条件是解决问题的关键．【详解】解：有意义，90NCI ∠=︒ ∴DNCI 90DIC ∴∠=︒D ∴I H 90F DIO ∠=∠=︒ EMF DMN BOC DOI ∠=∠=∠=∠()AAS FME DOI ∴ ≌ 2Rt DOI BOC MND S S S S ==， ∴243ABC ABC S S S S S +==． Rt AGE Rt ABC AE AB AG AC =⎧⎨=⎩()Rt Rt HL AGE ACB ∴ ≌Rt Rt DNB BHD ≌∴12345S S S S S ++++13245()S S S S S =++++4ABCS = 1412=⨯⨯=x 3x ≥-3x-≤，解得，故答案为：．12. 若一组数据，，，，的众数是，则这组数据的方差是______．【答案】####【解析】【分析】首先根据众数的定义求出的值，进而利用方差公式得出答案．【详解】解：，，，，的众数是，，，，故答案为．【点睛】此题主要考查了方差以及众数的定义，正确记忆方差的定义是解题关键．13. 若a 是一元二次方程的一个根，则的值是______．【答案】8【解析】【分析】本题考查了一元二次方程的根的定义，整体思想的应用是本题的关键．根据一元二次方程解的定义可得，再整体代入求代数式即可．【详解】解：∵a 是一元二次方程的一个根，把代入得，，即，∴，故答案为：8．14. 已知菱形的周长为，其相邻两内角的度数比为，此菱形的面积为______．【答案】【解析】【分析】本题考查菱形性质，含度角的直角三角形的性质；根据相邻两内角的度数比为：，可求出一个角，根据周长为，求出菱形的边长，根据直角三角形里角的性质求出高，从而求出面积．【详解】解：作于点，的∴30x +≥3x ≥-3x ≥-02-81x 2-13.63135685x 02-81x 2-2x ∴=-1(02812)15x =-++-=2222221[(01)(21)(81)(11)(21)]13.65S =-+--+-+-+--=13.62240x x +-=224a a +224a a +=2240x x +-=x a =2240a a +-=224a a +=()222422248a a a a +=+=⨯=ABCD 241:518301530︒2430︒AE BC ⊥E其相邻两内角的度数比为：，，菱形的周长为，．．菱形的面积为：．故答案为：．15. 如图，在正方形ABCD 中，△ABE 为等边三角形，连接DE ，CE ，延长AE 交CD 于F 点，则∠DEF 的度数为_____．【答案】105°【解析】【分析】根据四边形ABCD 是正方形，可得AB =AD ，∠BAD =90°，△ABE 为等边三角形，可得AE =BE =AB ，∠EAB =60°，从而AE =AD ，∠EAD =30°，进而求得∠AED 的度数，再根据平角定义即可求得∠DEF 的度数．【详解】解：∵四边形ABCD 是正方形，∴AB =AD ，∠BAD =90°，∵△ABE 为等边三角形，∴AE =BE =AB ，∠EAB =60°，∴AE =AD ，∠EAD =∠BAD ﹣∠BAE =30°，∴∠AED =∠ADE=（180°﹣30°）=75°，∴∠DEF =180°﹣∠AED =180°﹣75°=105°．故答案为105°． 15180B ∴∠=︒⨯115+30=︒ ABCD 24AB BC ∴==14246⨯=AE ∴=1263⨯=∴6318BC AE ⨯=⨯=1812【点睛】本题考查了正方形的性质、等边三角形的性质，解决本题的关键是综合运用正方形的性质和等边三角形的性质．16. 如图，有5个形状大小完全相同的小矩形构造成一个大矩形（各小矩形之间不重叠且不留空隙），图中阴影部分的面积为16，且每个小矩形的宽为1，则每个小矩形的长为______．【解析】【分析】本题考查了一元二次方程的应用，结合图形建立方程是解题的关键．设小矩形的长为x ，根据“阴影部分的面积为16”列出方程求解．【详解】解：设小矩形的长为x ，根据题意，得，解得（负值舍去），故答案．17. 如图，点是平行四边形的对称中心，是边上的点，，是边上的点，且．若分别表示和的面积，则______．【答案】##【解析】【分析】本题考查了平行四边形的性质，连接，根据点是平行四边形的对称中心得到点是线段的中点，且，再由，进而可求解，熟练掌握平行四边形的性质是解题的关键．为(21)(2)516x x x ++-=x =O ABCD ,,AD AB E F >AB G H BC 42,79EF AB GH BC ==12,S S EOF GOH 12S S =18718:7,AC OB O ABCD O AC 14AOB BOC ABCD S S S ==平行四边形 47EF AB =29GH BC =【详解】解：如图，连接，点是平行四边形的对称中心，点是线段的中点，且，令 ， ，，，故答案为：．18. 如图，在矩形中，，点是的中点，将沿折叠后得到延长交射线于点，若，则的值为______．或【解析】【分析】本题考查了全等三角形的判定及性质、折叠的性质、勾股定理，连接，由折叠和线段中点的性质可得，，利用可得，可得，分两种情况：当点在线段上时，当点在的延长线上时，利用勾股定理即可求解，找准点的位置是解题的关键．【详解】解：由矩形的性质可知，，则，,AC OB O ABCD ∴O AC 14AOB BOC ABCD S S S ==平行四边形 AOB BOC S S S == 47EF AB = 29GH BC =47EOF S S =∴ 29GOH S S = 124187279S S ∴==187ABCD ,2AB m BC ==E AD ABE BE GBE BG DC F 2CD CF =m EF ,EG AE DE BG AB m ====90BGE A ∠=∠=︒HL Rt Rt EGF EDF △≌△DF GF =①F CD ②F DC F AB CD m ==1122CF CD m ==连接，如图：由折叠和线段中点的性质可得 ，，，（公共边），，，分两种情况：如图（1），当点在线段上时，易知，，，在中，由勾股定理得，，解得：或（舍去），如图（2），当点在的延长线上时， 易知，，，在中，由勾股定理，得，EF ,EG AE DE BG AB m ====90BGE A ∠=∠=︒90EGF D ∴∠=∠=︒EF EF = ()Rt Rt HL EGF EDF ∴ ≌DF GF ∴=①F CD 12GF DF CF m ===1322BF BG GF m m m ∴=+=+=Rt BCF 22213222m m ⎛⎫⎛⎫+= ⎪ ⎪⎝⎭⎝⎭m=②F DC 12CF m =1322GF DF m m m ==+=3522BF BG GF m m m ∴=+=+=Rt BCF 22215222m m ⎛⎫⎛⎫+= ⎪ ⎪⎝⎭⎝⎭解得：或（舍去），综上所述，，．三、解答题（19、20、21每题6分，22题8分，23、24每题10分，共46分）19. 计算．（1；（2）．【答案】（1）（2）1【解析】【分析】（1）先化成最简二次根式，再合并同类二次根式即可；（2）先化简二次根式并合并同类二次根式，再按照二次根式的除法进行即可．【小问1详解】；【小问2详解】解：．【点睛】本题考查了二次根式的加减运算及混合运算，关键是化为最简二次根式．20.解方程：m=m+÷6=-+=÷=-÷=÷1=（1）（2）【答案】（1）（2）【解析】【分析】本题考查了解一元二次方程；（1）根据直接开平方法解一元二次方程，即可求解；（2）根据因式分解法解一元二次方程，即可求解．【小问1详解】解：∴∴解得：【小问2详解】解：∴∴解得：，21. 如图，在的正方形网格中，小正方形的顶点叫做格点已知两点是格点仅用无刻度的直尺分别按下列要求画图保留画图痕迹，不写画法（1）如图，以线段为边长作菱形；（2）如图，以线段为边作一个面积为的正方形．2280x -=()2240x x -+=122,2x x =-=124,2x x ==-2280x -=228x =24x =122,2x x =-=()2240x x -+=228=0x x --()()420x x -+=124,2x x ==-106⨯．A B ，．(．)1AB ABCD 2AB 10【答案】（1）见解析（2）见解析【解析】【分析】（1）作一个边长为的菱形即可；（2的正方形即可．【小问1详解】如图所示，菱形即为所求；或【小问2详解】如图所示，正方形即为所求．【点睛】本题考查作图应用与设计作图，勾股定理，菱形的判定以及正方形的判定等知识，解题的关键是学会利用数形结合的思想解决问题．22. 每年的月日是我国全民国家安全教育日．某中学在全校七、八年级各名学生中开展“国家安全法”知识竞赛，并从七、八年级学生中各抽取名学生，统计这部分学生的竞赛成绩（竞赛成绩均为整数，满分分，分及以上为合格）八年级抽取的学生的竞赛成绩：．七年级抽取的学生的竞赛成绩条形统计图七、八年级抽取的学生的竞赛成绩统计表年级七年级八年级5ABCD ABC -415500201064466667778888889991010，，，，，，，，，，，，，，，，，，，平均数中位数众数合格率根据以上信息，解答下列问题：（1）填空：______；______；______．（2）估计该校八年级名学生中竞赛成绩不合格的人数；（3）在这次“国家安全法”知识竞赛中，你认为哪个年级的学生成绩更优异？请说明理由．【答案】（1），，（2）人（3）八年级的学生成绩更优异，理由见解析【解析】【分析】（）根据平均数、中位数、众数的定义即可求解；（）用乘以不合格率即可求解；（）根据平均数、中位数、众数比较即可判断；本题考查了条形统计图和统计表，平均数、中位数、众数，看懂统计图表是解题的关键．【小问1详解】解：由题意可得，，，，故答案为：，，；【小问2详解】解：（人），答：估计该校八年级名学生中竞赛成绩不合格的人数为人；【小问3详解】解：八年级学生成绩更优异，理由：七、八年级的平均分一样，但是八年级的中位数，众数和合格率都的a7.4b 87c 85%90%=a b =c =5007.47.58501250034152617685941017.420a ⨯+⨯+⨯+⨯+⨯+⨯+⨯==787.52b +==8c =7.47.58()500190%50⨯-=50050高于七年级的，所以八年级“国家安全法”知识竞赛的学生成绩更优异．23. 根据以下销售情况，解决销售任务．销售情况分析总公司将一批衬衫由甲、乙两家分店共同销售，因地段不同，它们的销售情况如下：店面甲店乙店日销售情况每天可售出20件，每件盈利40元．每天可售出32件，每件盈利30元．市场调查经调查发现，每件衬衫每降价1元，甲、乙两家店一天都可多售出2件．情况设置设甲店每件衬衫降价元，乙店每件衬衫降价元．任务解决任务1甲店每天的销售量 　（用含的代数式表示）．乙店每天的销售量 　（用含的代数式表示）．任务2当，时，分别求出甲、乙店每天的盈利．任务3总公司规定两家分店下降的价格必须相同，请求出每件衬衫下降多少元时，两家分店一天的盈利和为2244元．【答案】任务1：件，件；任务2：甲店每天的盈利为1050元，乙店每天的盈利为1040元；任务3：11元【解析】【分析】任务1，由题意即可得出结论；任务2，由盈利＝每件盈利×销售量，分别列式计算即可；任务3，设每件衬衫下降元时，两家分店一天的盈利和为2244元，列出一元二次方程，解方程即可．【详解】解：任务1，根据题意得：甲店每天的销售量为件，乙店每天的销售量为件，故答案为：件，件；任务2，当时，甲店每天的盈利为（元）；a b a b 5a =4b =()202a +()322b +m ()202a +()322b +()202a +()322b +5a =()()40520251050-⨯+⨯=当时，乙店每天的盈利为（元）；任务3，设每件衬衫下降元时，两家分店一天的盈利和为2244元，由题意得：，整理得：，解得：，即每件衬衫下降11元时，两家分店一天的盈利和为2244元．【点睛】本题考查了一元二次方程的应用、列代数式、有理数的混合运算，找准等量关系，正确列出一元二次方程是解题的关键．24. 已知平行四边形为边上的中点，为边上的一点．（1）如图1，连接并延长交的延长线于点，求证：；（2）如图2，若，求；（3）如图3，若为的中点，为的中点，，求线段的长．【答案】（1）见解析（2） （3【解析】【分析】（1）证明，即可得证；（2）连接并延长交的延长线于点，易得，进而得到，利用，得到，即可得解；（3）连接并延长交的延长线于点，易得，进而得到，从而得到，再利用勾股定理进行求解即可．【小问1详解】证明：四边形是平行四边形，，4b =()()30432241040-⨯+⨯=m ()()()()40202303222244m m m m -++-+=2221210m m +=-1211m m ==,ABCD E BC F AB FE DC G =FE GE ,36FB AB DF EDC +=∠=︒AFD ∠,FE DE P =AF Q FD 4,AQ DP ==BE 72︒FEB GEC ≌△△FE DC G =FE GE EDC EDF ∠=∠AB DC 2AFD FDC EDC ∠=∠=∠FE DC M FE DE ME ==90FDM EDF EDM ∠=∠+∠=︒90AFD FDM ∠=∠=︒ ABCD AB DC ∴，为边上的中点，，；【小问2详解】解：四边形是平行四边形，，连接并延长交的延长线于点，由（1）可得，∴，，即，∴；【小问3详解】解：连接并延长交的延长线于点，由（1）可得，,EFB EGC B ECG ∴∠=∠∠=∠E BC ,BE CE ∴=()AAS FEB GEC ∴ ≌FE GE ∴= ABCD AB DC ∴=FE DC G FEB GEC ≌△△FB GC =,FB AB DF += GC DC BF AB ∴+=+DG DF=,FE GE = EDC EDF ∴∠=∠,36AB DC EDC ︒∠= ∥272AFD FDC EDC ∠︒=∠=∠=FE DC M FE ME =，，为直角三角形，为的中点，为的中点，设，，，【点睛】本题考查平行四边形的性质，全等三角形的判定和性质，等腰三角形的判定和性质，勾股定理．熟练掌握平行四边形的性质，通过添加辅助线，证明三角形全等，是解题的关键．附加题部分25. 若，则的值为_______．【答案】【解析】【分析】根据换元法以及一元二次方程的解法即可求出答案．【详解】，,FE DE = ,FE DE ME ∴==,EFD EDF EDM EMD ∴∠=∠∠=∠180,EFD EDF EDM EMD ∠+∠+∠+∠=︒ 90FDM EDF EDM ︒∴∠=∠+∠=,AB DC 90,AFD FDM ∠=∠=︒∴,DF AB AFD ∴⊥△P AF Q FD ∴,AP FP x FQ DQ y ====222222,,4,PF DF DP AF FQ AQ AQ DP +=+=== ()()22222224,2x y x y ∴+=+=2210x y ∴+=222224440AD AF FD x y ∴=+=+=AD ∴=22BC AD BE ∴===2250a ab b +-=a b 52-±2250a ab b +-=．令，，，，．故答案为：【点睛】本题考查了用配方法解一元二次方程，解题的关键是熟练应用一元二次方程的解法，本题属于中等题型．26. 实数满足，且则______．【答案】##0.5【解析】【分析】本题考查了因式分解的应用，根据和可整理得，再进行因式分解得，进而可求得a 、b 、c 的值，则可求解，熟练掌握因式分解的方法是解题的关键．【详解】解：，，，，，22510a a b b∴+-=a tb =2510t t ∴+-=22529544t t ∴++=252924t ⎛⎫∴+= ⎪⎝⎭52t ∴=-52-±,,a b c 2a b =+25204ab c c +++=bc a =122a b =+25204ab c c +++=(()2122104b b c c ++++=()221102c ⎫+++=⎪⎭2a b =+ 25204ab c c +++=(()2122104b bc c ∴+++++=()2212104b c ⎛⎫∴+++= ⎪⎝⎭()221102c ⎫∴+++=⎪⎭10,102c +=+=，，，故答案为：．27. 如果菱形有一条对角线等于它的边长，那么称此菱形为“完美菱形”．如图，已知“完美菱形”的边长为是它的较短对角线，点分别是边上的两个动点，且，点为的中点，点为边上的动点，则的最小值为______．【答案】##【解析】【分析】本题考查轴对称最短路线问题，菱形的性质，勾股定理，用一条线段的长表示两线段和的最小值是解题的关键．连接，，易知，因为，所以求的最小值只要求出的最小值，然后减去1即可，再利用将军饮马模型构造出的最小值时的线段，利用勾股定理求出即可．【详解】解：设与的交点为，连接，，四边形是菱形，，，1b c ∴==-2a ∴=+=12bc a ∴==12ABCD 8,BD ,E F ,AC BD 4EF =G EF P AB PD PG +2-2-+-OG OP 122OG EF ==OG PG OP +≥PD PG +PD PO +PD PO +BD AC O OG OP ABCD BD AC ∴⊥122OG EF ∴==，的最小值为，作点关于的对称点，延长交于点，连接，，，，，的最小值为，四边形是菱形，，，四边形是“完美菱形”，∴菱形的边只能和较短对角线相等，∵的边长为8，，，，，，，由对称性和菱形的性质，知，，OG PG OP +≥ PG ∴2OP -O AB O 'O O 'CD H OP O P 'O D 'PO PO ∴'=222PD PG PD PO PD PO O D ∴+≥+-=+'-≥'-PD PG ∴+2O D '- ABCD O O AB '⊥O H CD ∴'⊥ ABCD ABCD 8AD AB BD ∴===4OD =60ODH ABD ∴∠=∠=︒30DOH ∠=︒122DH OD ==OH ==3O H OH '==O D '===的最小值为，故答案为：．PD PG ∴+22-。

某某七中2011学年第二学期初二科学学习效果期中评估测试试题卷满分：100分考试时间：90分钟一、单项选择题（每小题只有一个选项符合题意。

每小题2分，共50分）1、关于声音的说法，正确的是（）A.固体、液体、气体的振动都能发声B. 声音不能传递信息C. 声音是看不见的，所以声音没有能量D. 声音在固体、液体、气体中传播速度相同2、在下图所示的各电路中，两灯并联的是（）3、关于声学的下列说法中，错误的是（）A．利用回声可以探测海的深度B．回声是声音的一种反射现象C．控制噪声的措施有：防止噪声产生、阻断噪声传播、防止噪声进入耳朵D．闻其声知其人，是根据每个人发出的声音频率不同来判断的4、下列现象与对应知识的连线，正确的是（）A．小孔成像——光的折射B．河水看起来比实际浅——光的反射C.月球上寂静无声——声音不能在真空中传播D．先看到闪电后听到雷声——光的直线传播5、在两磁铁旁的小磁针的方向如图(小磁针右端是N极)，a、b两端的磁性是（）A．a端是N极，b端是S极B．a端是S极，b端是N极C．a、b两端都是N极D．a、b两端都是S极6、要增强电磁铁的磁性，可采用的方法是（）A．增大线圈中的电流B．减少线圈的匝数C．降低线圈两端的电压D．改变线圈中的电流方向7、科学家在实验的基础上进行合理的推理，建立了牛顿第一定律，下列物理规律的得出，也是运用了这种研究方法的是（）A．光的反射规律 B．真空不能传声C．并联电路中电流的规律 D．欧姆定律8、用焦距为5厘米的凸透镜做实验时，把光屏放在凸透镜前13厘米处，成一清晰像，像的特点是（）A．倒立、放大的实像B．倒立、缩小的虚像C．倒立、缩小的实像D．正立、放大的虚像9、将敲响的鼓面用手一按，声响马上消失了，这是因为（）A．鼓面振动停止了B．声音传到人体中去了C．鼓的振动频率变小了D．鼓面振动产生的声音无法传播了10、当你对着平面镜检查仪容仪表时，像的大小取决于（）A．镜的大小 B．人本身的大小 C．镜放置的高低 D．人离镜的距离11、太阳光直接垂直照到离地面高30厘米、水平放置的一X不透明的纸板上，如果纸板上有一个长方形小孔，则在地面上产生的光斑形状是（）A．方形 B．圆形 C．长方形 D．不确定12、高老师戴着眼镜正在批作业，听到远处有学生叫她，为了看清该学生的容貌，高老师立即摘下眼镜跟这位学生打招呼。

新世纪教育网精选资料版权全部@新世纪教育网第二次模拟考试数学参照答案一、（每 3 分，共36 分）号123456789101112答案D B A D B C C B A D C C二、填空（每小 3 分，共18分）13、114、5/1215、 -216、(4 π＋ 8)cm217、218、43三、解答 (19 ，20 各 6 分， 219 分， 228 分， 238 分， 247 分， 2510 分，26 12 分，共 66分 )19.（本小分 6 分）解：原式 =x+2 ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 3 分（取的x 的 x≠ 2 且 x≠ 0）⋯⋯⋯⋯⋯⋯⋯⋯⋯ 6 分20.（本小分 6 分）解：作CH⊥AB于H（1 分）Rt△中= ·sinAACH CH AC=43×sin30 °=23⋯⋯⋯⋯⋯（ 3 分）AH=· cosAAC= 4 3× cos30 °=6∴ BH=AB- AH=4⋯⋯⋯⋯⋯⋯⋯（ 4 分）∴ tan= CH233B42⋯⋯⋯⋯⋯⋯⋯（ 5 分 )BH∴ 部分内容内3⋯⋯⋯⋯⋯⋯⋯（ 6 分）221.（本小分9 分）答案不独一，略，每种画法 4 分，1 分22.（本小分8 分）解：（ 1） 1 28％38％34％⋯⋯⋯⋯⋯⋯⋯⋯⋯ 2 分（2）8160.342400 ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 3 分A2400(840816144)600 ⋯⋯⋯⋯⋯⋯⋯4分B 1 (0.340.25 0.06)0.35 ⋯⋯⋯⋯⋯⋯⋯⋯⋯ 5 分A 的 600，B 的 0.35⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 6 分（3）40834％1200 ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯7 分2400 12002⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯8 分校学生均匀每人 2 本外．23.（本小分 8 分）（ 1）明：∵△ ADC沿直 AD翻折后点 C落在点 E ，∴△ ADC≌△ ADE， ---------------1分∴CD=ED，∴∠ DCE=∠ DEC，∵AD中，∴ BD=DC，∴ BD=DE，∴∠ DBE=∠ DEB， --------------20 0∵∠ DBE+∠BEC+∠ ECB=180，即 2∠ DEB+2∠ CED=180，-----------------3∴∠ DEB+∠CED=90，∴ BE ⊥ EC（1） 绘图正确EAADBE 是平行四边形 ------------------- 4证明：∵△ ADC 沿直线 AD 翻折后点 C 落在点 E 处，∴△ ADC ≌△ ADE ，∴AE=AC ， DE=DC∵AC=DC ，∴ AE=AC=DE=DC ， BDC∴四边形 AEDC 是菱形 ---------------------------- 6∴AE//DC ，且 AE=DC------------------- 7∵AD 是中线，∴ BD=DC ，∴ AE//BD ，且 AE=BD∴四边形 ADBE 是平行四边形 -----------------------824. （本小题满分 7 分）(1)将 A( 3,0), B(1,0) 代入 yx 2 bx c ，得9 3b c 0b 21 b c，c3∴ yx 22x 3 --------------------------3 分(2)∵ yx 2 2x 3 ( x 1)2 4∴对称轴 x1， 而 A ，B 对于对称轴对称∴连接 BD 与对称轴的交点即为所求 P 点 .过 D 作 DF ⊥ x 轴于 F. 将 x2 代入 y x 22 x3 ，则 y 44 3 3 ∴ D （ -2， -3） ----------------4分∴ DF 3, BF 1 ( 2) 3Rt △ BDE 中， BD=32 323 2∵ PA=PB ∴ PA+PD=BD= 3 2 故 PA+PD 的最小值为 3 2--------------------------7 分25. ( 本小题满分 10 分 )解：（ 1）设 A 型 x 块， B 型（ 5000-x ）块23500≤ 5.2x+4.15(x-5000) ≤ 24000解得 26091x 3095 5------------------------- 2分2121X 取 100 的倍数，∴ x 为 2700， 2800，2900 ， 3000 ∴有 4 种方案① A 型 2700块，B 型 2300块② A 型 2800块，B 型 2200块 ③ A 型 2900块，B 型 2100块④A 型 3000 块， B 型 2000 块 ------------------------- 3分（2）设总花费为 W 元W=5.2x+4.15(x-5000)=1.05x+20750-------------------------- 5分当 x=2700 时，总花费为最少为 23585 元 --------------------------6分（3） W=(5+0.2-m)x+4.15(x-5000)=(1.05-m） x+20750 --------------------7分当 m>1.05 ，当 x=3000 用最少， 方案④ A 型 3000 ， B 型 2000 当 m<1.05 ，当 x=2700 用最少， 方案①A 型 2700， B 型 2300当 m=1.05 ，四种方案 用一 。

浙江省宁波市第七中学2014-2015学年八年级英语下学期学习效果自我评估测试试题听力部分Ⅰ. 听小对话, 选择图片（共5小题；每小题1分，满分5分）( )1. What are they talking about ?A. B. C.()2. What is the man speaker ’s job? A. B. C.()3. What does the woman still need?A. B. C.( )4. Where are the two speakers?A. B. C.( )5. Why didn ’t Laura go to the movie?A. B. C.Ⅱ. 听长对话，回答问题。

（共5小题;每小题1 分，满分5 分）听下面一段较长的对话，回答第6至7二小题。

( )6. What will Vivian bring?A. The net.B. The food.C. The camera.( )7. What will the weather be like on Sunday?A. Sunny .B. Rainy.C. Windy听下面一段较长的对话，回答第8至10三小题。

( )8. Where are the two speakers talking?A. In a club.B. In a bookstore.C. On the phone.( )9. When does the dialogue take place?A. In the morning.B. In the afternoon.C. In the evening.( )10. How does the woman speaker feel at last?A. Angry.B. Surprised.C. Bored.Ⅲ. 听短文，回答问题（共5小题; 每小题1 分，满分5 分）( ) 11.How long did the speaker volunteer at the local store?A. For a weekB. For one year.C. For a month( )12.What did the young lady want to buy for her son?A. A toy.B. Foods.C. Clothes( )13.What happened to the young lady’s wallet?A. She lost it somewhere.B. She left it at home.C. Someone took it away.( )14. What did the speaker do to help the young lady?A. She helped look after the baby.B. She helped to get the wallet for the young lady.C. She offered to pay for her toy.( )15.Who was surprised when the young lady returned the money?A. The speaker.B. The speaker’s husband.C. The speaker’s son.笔试部分Ⅳ. 完形填空（共15小题；每小题1分，满分15分）阅读下面短文，掌握其大意，然后从A、B、C、D四个选项中选出可以填入空白处的最佳选项。