第6章 组合体
- 格式:pdf
- 大小:3.94 MB
- 文档页数:174

广东技术师范学院天河学院教案单元教案首页第六章组合体的构形与表达一、本章重点:1.组合体表面间的过渡关系,平齐,不平齐,相切,相交;2.组合体的画法;3.读组合体。
4.轴测图二、本章难点:1.看组合体视图;2.由组合体的两个视图,补画第三视图;3.组合体的尺寸标注。
三、本章要求:通过本章的学习,能够根据轴测图,画组合体的三视图,并由组合体的两个视图画出组合体的第三视图,能够正确标注组合体的尺寸。
四、教学手段讲授法,演示法教学、习题集作业、模型演示、手工绘图五、本章内容:第一节组合体的构形与分析一、组合体的构形方式任何复杂的形体,都可以看成是由一些基本的形体按照一定的连接方式组合成的。
这些基本形体包括棱柱、棱锥、圆柱、圆锥、球和圆环等。
由基本形体组成的复杂形体称为组合体。
组合体的组成方式有切割和叠加两种形式。
常见的组合体则是这两种方式的综合。
二、相邻两基本体的表面连接关系无论以何种方式构成组合体,其基本形体的相邻表面都存在一定的相互关系。
其形式一般可分为平齐或错开、相切、相交等情况。
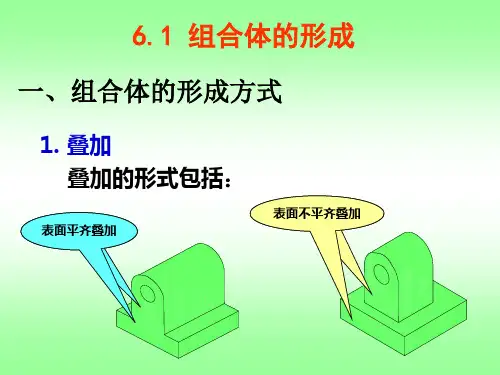
1.平齐或错开当相邻两基本体的表面平齐时,两表面为共面,因而视图上两基本体之间无分界线,如图6.2(a)所示。
如果两基本体的表面不共面,而是错开,如图6.2(b)所示,在主视图上要画出两表面之间的界线。
图 6.2(c)所示为两内表面共面,6.2(d)所示为两内表面不共面(错开)。
(a) (b)(c) (d)图6.2 两立体表面平齐或错开2.两基本体表面相交或相切两个基本体表面相交所产生的交线(截交线或相贯线),应在视图中画出其投影,如图6.3(a)所示。
相切是指两个基本体的相邻表面(平面与曲面或曲面与曲面)光滑过渡,相切处不存在轮廓线,在视图上一般不画出分界线,如图6.3(b)。
(a)(b)图6.3 两立体表面相交或相切第二节组合体的构形设计一、组合体的构形原则1、功能原则2、工艺性原则3、美学原则二、构形设计方法三、构形设计举例第三节组合体的视图表达叠加型组合体的三视图画法一、形体分析法所谓形体分析法就是假想把组合体分解为若干基本形体,并确定它们的形状、组合形式及其表面间相对位置的方法。

第6章组合体由两个或两个以上的基本体组成的类似机件的形体称为组合体。
本章着重研究组合体视图的画法、看图方法和尺寸标注,为今后学习零件图奠定基础。
6.1组合体的形体分析和组合形式6.1.1 组合体的形体分析任何复杂的物体都可以看成是由若干个基本几何体组合而成。
这些基本体可以是完整的,也可以是经过钻孔、切槽等加工。
如图6-1a所示的支座,可看成由圆筒、底板、肋板、耳板和凸台组合而成,如图6-1b所示。
在绘制组合体视图时,应首先将组合体分解成若干简单的基本体,并按各部分的位置关系和组合形式画出各基本几何体的投影,综合起来,即得到整个组合体视图。
这种假想把复杂的组合体分解成若干个基本形体,分析它们的形状、组合形式、相对位置和表面连接关系,使复杂问题简单化的思维方法称为形体分析法。
它是组合体的画图、尺寸标注和看图的基本方法。
a)图6-1b支座的形体分析圆筒肋板底板凸台耳板a)直观图b )分解图6.1.2组合体的组合形式及表面连接关系1.组合体的组合形式组合体可分为叠加和切割两种基本组合形式,或者是两种组合形式的综合。
叠加是将各基本体以平面接触相互堆积、叠加后形成的组合形体,如图6-2a 所示。
切割是在基本体上进行切块、挖槽、穿孔等切割后形成的组合体,如图6-2b所示。
图6-2c所示的组合体则是叠加和切割二种形式的综合。
a) b ) c )图6-2 组合体的组合形式a)叠加式组合体 b )切割式组合体 c )综合式组合体2.组合体的表面连接关系组合体表面连接关系有平齐、相交和相切三种形式。
弄清组合体表面连接关系,对画图和看图都很重要。
(1)当组合体中两基本体的表面平齐 (共面)时,在视图中不应画出分界线,如图6-3所示。
6.2组合体视图的画法画组合体的视图时, 首先要运用形体分析法将组合体合理地分解为若干个基本形体, 并按照各基本形体的形状、组合形式、形体间的相对位置和表面连接关系,逐步地进行作图。
下面结合实例,介绍组合体视图的画法。


第六章组合体的视图及尺寸标注由基本立体组合而成的立体称为组合体。
本章将学习组合体三视图的投影特性,组合体画图和读图和基本方法以及组合体的尺寸标注。
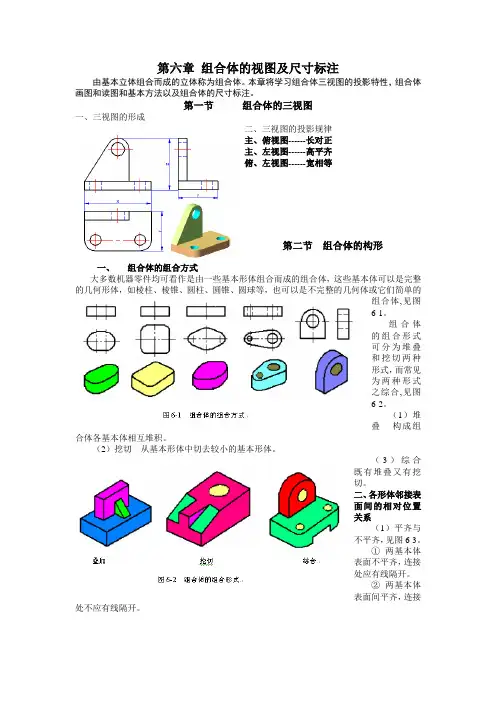
第一节组合体的三视图一、三视图的形成二、三视图的投影规律主、俯视图------长对正主、左视图------高平齐俯、左视图------宽相等第二节组合体的构形一、组合体的组合方式大多数机器零件均可看作是由一些基本形体组合而成的组合体,这些基本体可以是完整的几何形体,如棱柱、棱锥、圆柱、圆锥、圆球等,也可以是不完整的几何体或它们简单的组合体,见图6-1。
组合体的组合形式可分为堆叠和挖切两种形式,而常见为两种形式之综合,见图6-2。
(1)堆叠构成组合体各基本体相互堆积。
(2)挖切从基本形体中切去较小的基本形体。
(3)综合既有堆叠又有挖切。
二、各形体邻接表面间的相对位置关系(1)平齐与不平齐,见图6-3。
①两基本体表面不平齐,连接处应有线隔开。
②两基本体表面间平齐,连接处不应有线隔开。
(2)相交当两基本体表面相交时,其相交处交线一定要画出来,如图6-4所示,(3)相切当两基本体表面相切时,其相切处是圆滑过渡,应不画线,如图6-5所示,图中底板前端平面与圆弧面相切其平面上的棱线末端应画至切点为止。
切点位置由投影关系确定,相切处无线。
第三节组合体视图的画法一、形体分析画组合体视图之前,应对组合体进行形体分析,了解组合体的各基本体的形状、组合形式、相对位置以及在某个方向上是否对称,以便对组合体的整体形状有个概念,为画图做准备。
(a) 轴承座(b) 形体分析图6-6 画组合体视图从图6-6中可以看出,该组合体由四棱柱底板、空心圆柱体、等腰梯形柱的支承板、直角梯形柱和四棱柱叠合的肋板组成。
支承板与空心圆柱体外表面相切,叠放在底板上,它与底板后面平齐。
肋板叠放在底板上,其上与圆筒外面相结合,后面与支承板紧靠,两侧面与圆柱面相交。
整个组合体左右对称。
注意:画图时不要把组合体看成是由各零散的基本体“拼接”而成。

第6章组合体由两个或两个以上的基本体组成的类似机件的形体称为组合体。
本章着重研究组合体视图的画法、看图方法和尺寸标注,为今后学习零件图奠定基础。
6.1 组合体的形体分析和组合形式6.1.1 组合体的形体分析任何复杂的物体都可以看成是由若干个基本几何体组合而成。
这些基本体可以是完整的,也可以是经过钻孔、切槽等加工。
如图6-1a所示的支座,可看成由圆筒、底板、肋板、耳板和凸台组合而成,如图6-1b所示。
在绘制组合体视图时,应首先将组合体分解成若干简单的基本体,并按各部分的位置关系和组合形式画出各基本几何体的投影,综合起来,即得到整个组合体视图。
这种假想把复杂的组合体分解成若干个基本形体,分析它们的形状、组合形式、相对位置和表面连接关系,使复杂问题简单化的思维方法称为形体分析法。
它是组合体的画图、尺寸标注和看图的基本方法。
a) b)图6-1 支座的形体分析a)直观图 b)分解图6.1.2 组合体的组合形式及表面连接关系1. 组合体的组合形式组合体可分为叠加和切割两种基本组合形式,或者是两种组合形式的综合。
叠加是将各基本体以平面接触相互堆积、叠加后形成的组合形体,如图6-2a 所示。
切割是在基本体上进行切块、挖槽、穿孔等切割后形成的组合体,如图6-2b所示。
图6-2c所示的组合体则是叠加和切割二种形式的综合。
a) b) c)图6-2 组合体的组合形式a)叠加式组合体 b)切割式组合体 c)综合式组合体2. 组合体的表面连接关系组合体表面连接关系有平齐、相交和相切三种形式。
弄清圆筒底板肋板耳板凸台组合体表面连接关系,对画图和看图都很重要。
(1)当组合体中两基本体的表面平齐(共面)时,在视图中不应画出分界线,如图6-3所示。
(2)当组合体中两基本体的表面相交时,在视图中的相交处应画出交线,如图6-4、图6-5、图6-6所示。
图6-3 两表面平齐的画法 图6-4 平面与平面相交图6-5平面与曲面相交 图6-6 曲面与曲面相交(3)当组合体中两基本体的表面相切时,在视图中的相切处不应画线,如图6-7所示。



第6章立体几何第一节多面体与球的组合体问题纵观近几年高考对于组合体的考查,重点放在与球相关的外接与内切问题上.要求学生有较强的空间想象能力和准确的计算能力,才能顺利解答.从实际教学来看,这部分知识是学生掌握最为模糊,看到就头疼的题目.分析原因,除了这类题目的入手确实不易之外,主要是学生没有形成解题的模式和套路,以至于遇到类似的题目便产生畏惧心理.本文就高中阶段出现这类问题加以类型的总结和方法的探讨.一、球与柱体的组合体规则的柱体,如正方体、长方体、正棱柱等能够和球进行充分的组合,以外接和内切两种形态进行结合,通过球的半径和棱柱的棱产生联系,然后考查几何体的体积或者表面积等相关问题.1、球与正方体如图1所示,正方体1111ABCD A B C D -,设正方体的棱长为a ,,,,E F H G 为棱的中点,O 为球的球心.常见组合方式有三类:一是球为正方体的内切球,截面图为正方形EFGH 和其内切圆,则2a OJ r ==;二是与正方体各棱相切的球,截面图为正方形EFGH 和其外接圆,则22GO R a ==;三是球为正方体的外接球,截面图为长方形11ACA C 和其外接圆,则132A O R '==.通过这三种类型可以发现,解决正方体与球的组合问题,常用工具是截面图,即根据组合的形式找到两个几何体的轴截面,通过两个截面图的位置关系,确定好正方体的棱与球的半径的关系,进而将空间问题转化为平面问题.例1棱长为1的正方体1111ABCD A B C D -的8个顶点都在球O 的表面上,E F ,分别是棱1AA ,1DD 的中点,则直线EF 被球O 截得的线段长为()A.2B.1C.12+【强化训练】将棱长为2的正方体木块削成一个体积最大的球,则这个球的表面积为()A.π2B.π4C.π6D.π162、球与长方体长方体各顶点可在一个球面上,故长方体存在外切球.但是不一定存在内切球.设长方体的棱长为,,,a b c 其体对角线为l .当球为长方体的外接球时,截面图为长方体的对角面和其外接圆,和正方体的外接球的道理是一样的,故球的半径222.22l a b c R ++==例2在长、宽、高分别为2,2,4的长方体内有一个半径为1的球,任意摆动此长方体,则球经过的空间部分的体积为()A.10π3 B.4π C.8π3 D.7π3【强化训练】已知正四棱柱的底边和侧棱长均为32,则该正四棱锥的外接球的表面积为.3、球与正棱柱球与一般的正棱柱的组合体,常以外接形态居多.下面以正三棱柱为例,介绍本类题目的解法构造直角三角形法.设正三棱柱111ABC A B C -的高为,h 底面边长为a ,如图2所示,D 和1D 分别为上下底面的中心.根据几何体的特点,球心必落在高1DD 的中点O ,3,,,23h OD AO R AD a ===借助直角三角形AOD 的勾股定理,可求223()()23h R a =+.例3正四棱柱1111ABCD A B C D -的各顶点都在半径为R 的球面上,则正四棱柱的侧面积有最________值,为_______.【强化训练】直三棱柱111ABC A B C -的六个顶点都在球O 的球面上,若1AB BC ==,0120ABC ∠=,123AA =,则球O 的表面积为()A.4πB.8πC.16πD.24π二、球与锥体的组合体规则的锥体,如正四面体、正棱锥、特殊的一些棱锥等能够和球进行充分的组合,以外接和内切两种形态进行结合,通过球的半径和棱锥的棱和高产生联系,然后考查几何体的体积或者表面积等相关问题.2.1球与正四面体正四面体作为一个规则的几何体,它既存在外接球,也存在内切球,并且两心合一,利用这点可顺利解决球的半径与正四面体的棱长的关系.如图4,设正四面体S ABC -的棱长为a ,内切球半径为r ,外接球的半径为R ,取AB 的中点为D ,E 为S 在底面的射影,连接,,CD SD SE 为正四面体的高.在截面三角形SDC ,作一个与边SD 和DC 相切,圆心在高SE 上的圆,即为内切球的截面.因为正四面体本身的对称性可知,外接球和内切球的球心同为O .此时,,CO OS R OE r ===,23,,33SE a CE a ==则有2222233a R r a R r CE +=-=,=解得:66,.412R a r ==这个解法是通过利用两心合一的思路,建立含有两个球的半径的等量关系进行求解.同时我们可以发现,球心O 为正四面体高的四等分点.如果我们牢记这些数量关系,可为解题带来极大的方便.例4将半径都为1的四个钢球完全装入形状为正四面体的容器里,这个正四面体的高的最小值为() A.3263+ B.2+263 C.4+263 D.43263+2.2球与三条侧棱互相垂直的三棱锥球与三条侧棱互相垂直的三棱锥组合问题,主要是体现在球为三棱锥的外接球.解决的基本方法是补形法,即把三棱锥补形成正方体或者长方体.常见两种形式:一是三棱锥的三条侧棱互相垂直并且相等,则可以补形为一个正方体,它的外接球的球心就是三棱锥的外接球的球心.如图5,三棱锥111A AB D -的外接球的球心和正方体1111ABCD A B C D -的外接球的球心重合.设1AA a =,则32R a =.二是如果三棱锥的三条侧棱互相垂直并且不相等,则可以补形为一个长方体,它的外接球的球心就是三棱锥的外接球的球心.2222244a b c l R ++==(l 为长方体的体对角线长).例5在正三棱锥S ABC -中,M N 、分别是棱SC BC 、的中点,且AM MN ⊥,若侧棱3SA =,则正三棱锥S ABC -外接球的表面积是________.【强化训练】一个几何体的三视图如图所示,其中主视图和左视图是腰长为1的两个全等的等腰直角三角形,则该几何体的外接球的表面积为()A.12πB.43πC.3πD.123π2.3球与正棱锥球与正棱锥的组合,常见的有两类,一是球为三棱锥的外接球,此时三棱锥的各个顶点在球面上,根据截面图的特点,可以构造直角三角形进行求解.二是球为正棱锥的内切球,例如正三棱锥的内切球,球与正三棱锥四个面相切,球心到四个面的距离相等,都为球半径R .这样求球的半径可转化为球球心到三棱锥面的距离,故可采用等体积法解决,即四个小三棱锥的体积和为正三棱锥的体积.例6在三棱锥P-ABC 中,PA=PB=PC=3,侧棱PA 与底面ABC 所成的角为60°,则该三棱锥外接球的体积为()A.π B.3πC.π4D.34π【强化训练】已知正三棱锥ABC P -,点P,A,B,C 都在半径为3的球面上,若PA,PB,PC 两两互相垂直,则球心到截面ABC 的距离为____________.2.4球与特殊的棱锥球与一些特殊的棱锥进行组合,一定要抓住棱锥的几何性质,可综合利,OA OS OB OC ===用截面法、补形法等进行求解.例如,四个面都是直角三角形的三棱锥,可利用直角三角形斜边中点几何特征,巧定球心位置.如图8,三棱锥S ABC -,满足,,SA ABC AB BC ⊥⊥面取SC 的中点为O ,由直角三角形的性质可得:所以O 点为三棱锥S ABC -的外接球的球心,则2SC R =.例7矩形ABCD 中,4,3,AB BC ==沿AC 将矩形ABCD 折成一个直二面角B AC D --,则四面体ABCD 的外接球的体积是()A.π12125 B.π9125 C.π6125 D.π3125例8三棱锥A BCD -中,2,AB CD ====5AC AD BD BC ==则三棱锥A BCD -的外接球的半径是_______.三、球与球的组合体对个多个小球结合在一起,组合成复杂的几何体问题,要求有丰富的空间想象能力,解决本类问题需掌握恰当的处理手段,如准确确定各个小球的球心的位置关系,或者巧借截面图等方法,将空间问题转化平面问题求解.例9在半径为R 的球内放入大小相等的4个小球,则小球半径r 的最大值为()A.(2-1)R B .(6-2)R C.14R D.13R 四、球与几何体的各条棱相切球与几何体的各条棱相切问题,关键要抓住棱与球相切的几何性质,达到明确球心的位置为目的,然后通过构造直角三角形进行转换和求解.如与正四面体各棱都相切的球的半径为相对棱的一半:24r a '=.例10把一个皮球放入如图10所示的由8根长均为20cm 的铁丝接成的四棱锥形骨架内,使皮球的表面与8根铁丝都有接触点,则皮球的半径为()3B.10cm 2cm D.30cm 五、与三视图相结合的组合体问题本类问题一般首先给出三视图,然后考查其直观图的相关的组合体问题.解答的一般思路是根据三视图还原几何体,根据几何体的特征选择以上介绍的方法进行求解.例11某几何体的三视图如图所示,则该几何体的外接球的球面面积为()A.5πB.12πC.20πD.8π【强化训练】若一个底面是正三角形的三棱柱的正视图如图所示,其顶点都在一个球面上,则该球的表面积为()A.163π B.193π C.1912π D.43π第二节立体几何中折叠问题立体几何中的折叠问题主要包含两大问题:平面图形的折叠与几何体的表面展开。