重庆大学数理统计试题2

重庆大学全日制学术型硕士研究生 《数理统计》（A ）课程试卷2013-2014学年第一学期（秋）请保留四位小数，部分下侧分位数为：0.95 1.65u =，0.99 2.33u =，20.95(1) 3.841χ=，0.95(3,6)9.78f =一、（18分）设1X ，2X ，…，64X 是来自总体N （0，2σ）的样本，X ，2S 分别是样本均值和样本方差：（1）求参数c 满足{}0.1P X S c >⋅=；（2）求概率22122234{1}X X P X X +>+；(3)求322321(2)i i i D X X X +=⎡⎤+-⎢⎥⎣⎦∑。

(请写出计算过程)解：（1）~(1)t n-{}}0.1P X S c P c ∴>⋅=>=得0.95(63)c t = 故 1.650.20638c ==（2）2~(0,)X N σ22212(/)(/)~(2)X X σσχ∴+ 同理22234(/)(/)~(2)X X σσχ+2222223412122234(/)(/)(/)(/)/~(2,2)22X X X X X X F X X σσσσ+++∴=+ 22122234{1}{(2,2)1}X X P P F X X +>=>+ 且0.50.50.51(2,2)(2,2)1(2,2)F F F =⇒= 得2222121222223434{1}1{1}0.5X X X X P P X X X X ++>=-≤=++ (3)令2~(2,2)i i n i Y X X N μσ+=+，112n i i Y Y X n ===∑ 221()(1)ni Y i T Y Y n S =∴=-=-∑3232223211(2)[()]i i i i i D X X X DT D Y Y +==⎡⎤+-==-⎢⎥⎣⎦∑∑2~(0,2(11/))i Y YN n σ-+~(0,1)YN=3222422421[2(11/)4(11/)((32))256(11/32)i Y D n n D σσχσ=+=+=+∑二、（26分）设1X ，2X ，…，n X 是来自总体2~(2,)(0)X N σσ>的样本，{}0.95P X A <=。

()(){}{}()22222111221121221164~,~(8),89111,01(1)11~(0,1)1.28 1.280.281(2)0.261 1.8360.2619818ni i n X N S S X S n X X X X E X X n n n n n D X X DX DX DX X X N n n n P X X P U X P X S P μχσμ=-=--=--=---⎛⎫-=+==⇒- ⎪⎝⎭->=>=⎛ -⎧⎫ <-+<=<⎨⎬ ⎩⎭⎝∑解：由题可知（，）且与相互独立（）{}22222222241164. 1.836896464 = 2.08814.688=~(9)991188= 2.08814.688=0.90.01=0.89423948i i i S X X P S S P X X χχχμ=⎧⎫⎫⎪⎪⎪⎪⎪⎪+<⎨⎬⎪⎪⎪⎪⎪⎪⎭⎩⎭⎧⎫⎛⎫⎛⎫⎪⎪ ⎪ ⎪--⎪⎪⎪ ⎪<+<+⎨⎬ ⎪ ⎪⎪⎪⎪ ⎪⎪⎪⎝⎭⎝⎭⎩⎭<<-⎛⎫- ⎪⎝⎭=⋅∑，其中原式（）()()()(){}24882255448822554821584~(0,1)=~4998244~(4)8944 2.132= 2.132=0.1i ii i i i i i i i i ii i N X X X t t X XP X XP t μμχμμμμμμ======⎛⎫ ⎪⎛⎫⎛⎫ ⎪-- ⎪ ⎪ ⎪⎝⎭⎝⎭ ⎪⎝⎭⎛⎫⎛⎫⎛⎫-- ⎪⎪⎪⎝⎭⎝⎭==--⎧⎫⎛⎫⎪⎪-≤-≤⎨⎬ ⎪⎝⎭⎪⎪⎩⎭∑∑∑∑∑∑∑∑∑（）则，()()()(){}222222222891(4)=8~1~(1,8)6498911=(1,8)58.82(8,1)10.90.158.8258.82XXX F FSSXP P F P FSμμμχμ-⎛⎫⎪--==⎧⎫-⎪⎪⎧⎫<<=<=-=⎨⎬⎨⎬⎩⎭⎪⎪⎩⎭（），则也可以用T分布与F分布的关系.0020001111()()1ln(1)11,,ˆˆˆ1ln(1),,ln(1)ln(1)2(;,...,)(;)ln (;,...,)=01ˆ=（）（）似然方程：得到参数的极大似然估计，再由i A nnx n n xn i i i n P X A F A e p p A EX DX A EX p EX X A EX p X p L x x f x e e d L x x nnx d Xλλλλλλλλλλλλλλλ---==<==-=-=-===--=∴=--=--====-∏∏ 0000010000ln(1)ˆln(1)ˆln(1)ˆ(3)=ln(1)=ln(1)==ˆln (;,...,)ln(1){[ln(1)][]}ln(1)ˆ()ln(1)ˆˆ极大似然估计的不变性，推出的极大似然估计为是的无偏估计且是的无偏估计是有效n A p A X p p EA E X p p EX A AA d L x x p n n nx X p d p n AA p AA A λλλλλλ-=-=----⎡⎤----⎣⎦∴-=-=-----=--∴ ()202ˆlim ln(1)ˆlim lim 0ˆ估计又是相合估计量n n n EA A p DA n Aλ→∞→∞→∞⎧=⎪⎨-⎪==⎩∴221212121222122222222221222121.422,2~222(1)(1)~01~(2) (1)(1)(1)(1)2=222X YX Y X YX X X X Nn mX X n S m SU N n mn S m S n S m S X X Sn mX Xtωσσμμμμμμχχσσσσ+++++-+--==++----+-+++-+-+==的无偏估计为且（，+）（，）又且与独立,记则()()()()()()()121212212121211221212122222=22=22222=12122t n mP t t n mX XP t n m t n mP X X t n m S X X t n m SX X t n m Sαααααωαμμμμαμμα-----+-⎧⎫≤+-⎨⎬⎩⎭⎧⎫⎪⎪+-+⎪⎪+-≤≤+-⎨⎬⎪⎪⎪⎪⎩⎭⎧⎪+-+-≤+≤+++-⎨⎪⎩-+-+±+-因此构造的置信区间为{}{}121201212120121212121212.222=022,22=02=02=0=的无偏估计为，在：成立的条件下，大于某个常数应该是小概率事件，因此构造拒绝域：以下确定常数由X X H X X c K X X c cP X X c P P t t μμμμμμμμμμα+++++>+>+⎧⎫⎪⎪⎪=>+⎬⎪⎪⎭⎧⎫⎪⎪⎪⎪=>+=⎨⎬⎪⎪⎪⎪⎩⎭()()122n m c t n m S ααω--+-⇒=+-拒绝域为：3133011331122333333111~(1,).~(3)220.220.230.20.20.80.20.104220.4因为所以，类错误(弃真)：为真类错误(纳伪)：为真i i i i i i i i i i i i i i X B p X B p P X H P X p P X p P X p C C P X H P X p αβ=======I ⎧⎫⎧⎫=≥=≥=⎨⎬⎨⎬⎩⎭⎩⎭⎧⎫⎧⎫===+==⎨⎬⎨⎬⎩⎭⎩⎭=+=II ⎧⎫⎧=<=<=⎨⎬⎨⎩⎭⎩∑∑∑∑∑∑∑313311223333120.4120.430.410.40.60.40.648i i i i i i P X p P X p P X p C C ===⎫⎬⎭⎧⎫=-≥=⎨⎬⎩⎭⎧⎫⎧⎫=-==-==⎨⎬⎨⎬⎩⎭⎩⎭=--=∑∑∑()()221221111211=200ˆnE i i i n n nEi i i i i i i i i ni ii nii S y x dS y x x y x x d x yxββββββ======-=--=⇒-==∑∑∑∑∑∑解：（）利用最小二乘估计使残差平方和最小参数的最小二乘估计量为2211222111111221111ˆ2=~(,)ˆˆˆ~(,)111ˆ===11ˆ（），由正态分布的性质推知服从正态分布ni ii i i i ni ii nnni i iiiinnni i i i i ii i i ni i nn i i i i i x YY x N x xN E D E E x Y x EY x x x x xD D x Y x x ββεβσβββββββ============+⎛⎫ ⎪ ⎪= ⎪ ⎪⎝⎭⎛⎫⎛ ⎪ ⎪ == ⎪ ⎪⎝⎭⎝∑∑∑∑∑∑∑∑∑∑∑()()()()()222211221222111112211ˆ~(,)ˆˆˆ3=ˆˆˆ2(,)ˆ(,)(,)因此，（）nii ni ii n i i nnE i iiiiii i nni i i i i ii i ni ii ii i i i nniii i xDY xN x ES E Y x D Y x E Y x D Y x DY D x Cov Y x x Yx Cov Y x Cov Y x C xxσσβββββββββ==========⎫⎪⎪=⎪ ⎪⎭⎡⎤-=-+-⎣⎦⎡⎤=-=+-⎣⎦==∑∑∑∑∑∑∑∑∑∑()222221112222222222221111(,)(,)221则ni i i i i i i nni iii i nni i Enni i iii i x x ov Y x Y Cov Y Y xxx x ESn n n xxσσσσσσσσ==========+-=+-=-∑∑∑∑∑∑∑因素：车型水平：3种不同的车型A,B,C方差分析前提假设：正态性，方差齐次性，独立性对比分位数：0.95(2,9) 4.26F F >=，拒绝原假设0123:H μμμ==，认为这三种车型耗油量有显著差异。

重庆大学《概率论与数理统计Ⅱ》课程试卷2015 —2016 学年第二学期开课学院：数统学院课程号：10029930考试日期：2016.5.29考试方式：考试时间：120分钟分位数：0.975 1.96u =,0.9(9) 1.383t =,0.975(9) 2.262t =.一、填空题（每空3分，共42分）1. 已知()0.3,()0.5,()0.5,P A P B P AB ===则()P A B ⋃=；(|)P B A =.2. 某饮品连锁销售店有一款饮品销量很好，据统计调查有60%的人喜欢喝这款饮品。

某次在该销售店里随机抽查购买饮品的12人，问其中有4人购买了这款饮品的概率：；至少有2人购买这款饮品的 概率。

3. 某木质板材用于装修房子，假设一次该板材运往三个销售点，这三个销售点所占份额分别为30%，50%，20%，半年清点统计销售情况，发现这三个销售点销售该板材量各不相同，其概率分别为0.35,0.45,0.3，问销售该板材总销售量的概率：。

4. 设连续型随机变量的分布函数为20,02(),0131,1x F x Ax x x <⎧⎪⎪=+≤<⎨⎪≥⎪⎩，则A =，X 的密度函数()f x =，{||0.5}P X <=。

5. 设12,X X 独立同分布于泊松分布(1)P ，写出概率12{5}P X X +=的表达式： ，且212()E X X +=.6. 设随机变量~[0,2]X U ，~(0,3)Y N ，且,0.5X Y ρ=，则c o v (,)X Y Y-=；2(23)E X Y -=； 7. 设1210,,,X X X 是来自总体(0,1)N 的简单随机样本，则 ～，1021()i i E X =∑=。

二、（12分）假设随机变量(,)X Y 的联合分布律为命题人：组题人：审题人：命题时间：教务处制学院：专业：班年级：学号：姓名：考试教室：公平竞争、诚实守信、严肃考纪、拒绝作弊封线密且X Y 与独立。

数理统计习题答案习题5.1解答1. 设总体服从()λP 分布，试写出样本的联合分布律. n X X X ,,,12 解:()的分布律为：即X P X ~,λ ()!k e P X k k λλ-==, 0,1,2,,,n k =n X X X ,,,12 的联合分布律为：()n n P X x X x X x ===,,,1122 = ()()()n n P X x P X x P X x === 1122=nx x x x e x e x e nλλλλλλ---⋅2121=λλn n x x xe x x x n-+++!!!1212, n i n x i 0,1,2,,,1,2,, ==2. 设总体X 服从()0,1N 分布，试写出样本的联合分布密度. n X X X ,,,12 解：，即()~0,1X N X 分布密度为：()2221x p x e -=π，+∞<<-∞xn X X X ,,,12 的联合分布密度为：()∏==ni i n x x x p x p112*(),,...=22222221212121n x x x eee --⋅-πππ=()}212exp{122∑=--n i i x n π x i n i ,1,2,, =+∞<<∞-. 3. 设总体X 服从()2,μσN 分布,试写出样本的联合分布密度. n X X X ,,,12 解：()2~,μσX N ，即X 分布密度为：()p x =()}2exp{2122σμπσ--x ，∞<<∞-xn X X X ,,,12 的联合分布密度为：()∏==ni i n x xx p x p 112*,,...)(=)()}21exp{121222∑-⋅⋅-=-ni i n n x μσπσ, x i n i ,1,2,, =+∞<<∞-.4. 根据样本观测值的频率分布直方图可以对总体作什么估计与推断? 解：频率分布直方图反映了样本观测值落在各个区间长度相同的区间的频率大小，可以估计X 取值的位置与集中程度，由于每个小区间的面积就是频率，所以可以估计或推断X 的分布密度. 5. 略. 6. 略.习题5.2解答1. 观测5头基础母羊的体重(单位：kg)分别为53.2,51.3,54.5,47.8,50.9，试计算这个样本观测值的数字特征：(1)样本总和，(2)样本均值，(3)离均差平方和，(4)样本方差，(5)样本标准差，(6)样本修正方差，(7)样本修正标准差，(8)样本变异系数，(9)众数，(10)中位数，(11)极差，(12)75%分位数.解：设53.2,51.3,54.5,47.8,50.954321=====x x x x x()257.7151=∑=i ix，()51.54251==∑=i ix x(3) ss =()2512512xx xnx i ii i-=-∑∑===13307.84－5×51.542=25.982(4)=2s ()∑=-51251i i x x =51ss =5.1964, (5)s =2.28; (6) =s s *ss n 11-=6.4955(7)=2.5486; (8)*s cv =100⨯*xs =4.945;(9)每个数都是一个,故没有众数.(10)中位数为=51.3; (11)极差为54.5－47.8=6.7;(12)0.75分位数为53.2. 3x2. 观测100支金冠苹果枝条的生长量(单位：cm)得到频数表如下：组下限 19.5 24.5 29.5 34.5 39.5 44.5 49.5 54.5 59.5 组上限 24.5 29.5 34.5 39.5 44.5 49.5 54.5 59.5 64.5 组中值 22 27 32 37 42 47 52 57 62频数 8 11 13 18 18 15 10 4 3试计算这个样本观测值的数字特征：(1)样本总和，(2)样本均值，(3)离均差平方和，(4)样本方差，(5)样本标准差，(6)样本修正方差，(7)样本修正标准差，(8)样本变异系数，(9)众数，(10)中位数，(11)极差，(12)75%分位数.解：设组中值依次为,频数依次为,129,,,x x x 129,,,n n n +=++=912n n n n 100,()=∑=911i i in x 3950;()=+=∑=911912i i in xn n x 39.5;()()-=-==∑∑==29129123ss n x x n xnx i i ii i i 210039.5166300-⨯=10275;()==s ss 100142102.75; ()=s 510.137;()=-=*ss n s 1162103.788 ()=*s 710.188;()=⨯=*1008xs cv 25.79;()93742或众数是()50,210=n ;中位数为39.523742=+;()11极差为:62-22=40;()4783,0.7568,12612512分位数为+++=+++=∴n n n n n n .3.略.4. 设是一组实数，a 和是任意非零实数，n x x x ,,,12 b bx ay i i -=(i n 1,, =)，x 、y 分别为、的均值， =i x i y 2xs ∑-iixn(x 2)1，=2ys 1n(y y i i-)∑2，试证明：① b x a y -=；② 222b s s x y =. 解①：∑∑==-==ni i ni i b x a ny ny 1111= ()∑=-ni i x a bn11= ⎪⎪⎭⎫ ⎝⎛-∑=n i i x na nb 11= b x a -;②=2y s 1n∑-ii y y 2()=∑=⎪⎪⎭⎫⎝⎛---ni i b x a b x a n121=∑=⎪⎪⎭⎫⎝⎛-ni i b x x n 121=221x s b .1.求分位数（1），（2）()820.05x ()1220.95x 。

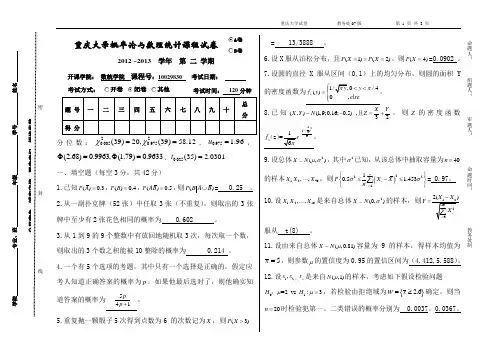
重庆大学概率论与数理统计课程试卷A卷B卷2012 ~2013 学年 第 二 学期开课学院： 数统学院 课程号：10029830 考试日期：考试方式：开卷闭卷 其他 考试时间： 120分钟分位数：220.0050.975(39)20,(39)58.12χχ==，0.975 1.96u =，(2.68)0.9963,(1.79)0.9633Φ=Φ=，0.025(35) 2.0301t =一、填空题（每空3分，共42分）1.已知()0.3P A =，()0.4P B =，()0.5P AB =，则()P B A B ⋃= 0.25 。

2.从一副扑克牌（52张）中任取3张（不重复），则取出的3张牌中至少有2张花色相同的概率为 0.602 。

3.从1到9的9个整数中有放回地随机取3次，每次取一个数，则取出的3个数之积能被10整除的概率为 0.214 。

4.一个有5个选项的考题，其中只有一个选择是正确的。

假定应 考人知道正确答案的概率为p 。

如果他最后选对了，则他确实知道答案的概率为541pp +。

5.重复抛一颗骰子5次得到点数为6 的次数记为X ，则(3)P X >= 13/3888 。

6.设X 服从泊松分布，且(1)(2)P X P X ===，则(4)P X ==0.0902 。

7.设圆的直径X 服从区间（0,1）上的均匀分布，则圆的面积Y 的密度函数为1//4()0 ,Y y f y elseπ⎧<<⎪=⎨⎪⎩。

8.已知(,)(1,9;0,16;0.5) ,32X YX Y N Z -=+且，则Z 的密度函数21()36z Z f --（z ）。

9.设总体2(,)X N μσ，其中2σ已知，从该总体中抽取容量为40n =的样本1,240,,X X X ，则()222110.5 1.453nii P X X n σσ=⎧⎫≤-≤⎨⎬⎩⎭∑= 0.97。

10.设1,210,,X X X 是来自总体2(0,)XN σ的样本，则Y =服从 t(8) 。

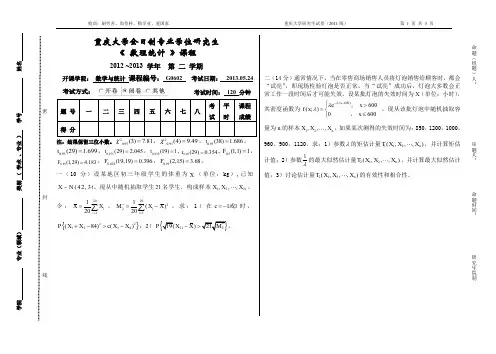
一、假设129,,X X X …，是来自总体2~,X N的简单随机样本，X 是样本均值，2S 是样本方差，求下列常数a 的值。

（1）0.78P Xa ；（2）922113.49()15.51ii P X X a ；（3）0.05X P aS。

解：（1）22~(,),~(0,1)xx N N Nn220.78{}xp ann即2{ 2.34},(2.34),0.99xp a a a n。

（2）222(1)~(1)n sn 992222119221221:()(1)()11{3.49()15.51}(1){3.4915.51}(15.51)(3.49)10.950.10.85ii i i ii s x x n s x x n p x x an sp aaaa（3）2222(1)~(0,1),~(1)Xn sN n n222()/~(1),(1)/(1)X n t n n sn即()~(1)3(){}0.053()1{}0.053(){}0.951.86n X t n s Xp a s Xp a s Xp a s a 二、设总体X 的密度函数2,0()00,0xxex f x x 其一个样本为12,,nX X X …，（1）求1g的最大似然估计量T ；（2）验证T是否为1g的有效估计量，若是，写出信息量I；（3）验证T 是否为1g的相合估计量。

解：（1）122111()(,)()()niii nnnx x ni i i I I i L f x x ex e1111ln ()2lnln 2ln ()01112212nniii i nii nii L n x x dn L x d x xn T X（2）由（1）121220211ln (,,,)2()21,()221111()()222nn ii xdnL X X X X n Xd TX c nE T E X EX x edxT 是1得无偏估计量因而T 是1的有偏估计量。

重庆大学概率论与数理统计课程试卷A卷B卷2012 ~2013 学年 第 二 学期开课学院： 数统学院 课程号：10029830 考试日期：考试方式：开卷闭卷 其他 考试时间： 120分钟分位数：220.0050.975(39)20,(39)58.12χχ==，0.975 1.96u =，(2.68)0.9963,(1.79)0.9633Φ=Φ=，0.025(35) 2.0301t =一、填空题（每空3分，共42分）1.已知()0.3P A =，()0.4P B =，()0.5P AB =，则()P B A B ⋃= 0.25 。

从一副扑克牌（52张）中任取3张（不重复），则取出的3张牌中至少有2张花色相同的概率为 0.602 。

从1到9的9个整数中有放回地随机取3次，每次取一个数，则取出的3个数之积能被10整除的概率为 0.214 。

4.一个有5个选项的考题，其中只有一个选择是正确的。

假定应 考人知道正确答案的概率为p 。

如果他最后选对了，则他确实知道答案的概率为541pp +。

5.重复抛一颗骰子5次得到点数为 6 的次数记为X ，则(3)P X > = 13/3888 。

6.设X 服从泊松分布，且(1)(2)P X P X ===，则(4)P X ==0.0902 。

7.设圆的直径X 服从区间（0,1）上的均匀分布，则圆的面积Y的密度函数为1//4()0 ,Y y f y elseπ⎧<<⎪=⎨⎪⎩。

8.已知(,)(1,9;0,16;0.5) ,32X YX Y N Z -=+且，则Z 的密度函数21()36z Zf --（z ）。

9.设总体2(,)X N μσ，其中2σ已知，从该总体中抽取容量为40n =的样本1,240,,X X X ，则()222110.5 1.453n i i P X X n σσ=⎧⎫≤-≤⎨⎬⎩⎭∑= 0.97。

10.设1,210,,X X X 是来自总体2(0,)XN σ的样本，则Y =服从 t(8) 。