关于网络等效电阻的研究

n阶电阻网络的等效电阻研究电阻网络是由多个电阻器按照一定的规则连接而成的电路。

在实际应用中，经常会遇到需要求解电阻网络的等效电阻的情况。

本文将介绍一种求解n阶电阻网络等效电阻的方法。

我们需要了解一些基本概念。

假设n阶电阻网络由n个电阻器组成，其中每个电阻器的阻值分别为R1，R2，...，Rn。

那么，n阶电阻网络的等效电阻可以表示为Rn，我们的目标就是求解Rn的值。

在求解等效电阻的过程中，我们可以利用串联和并联的电阻计算公式。

对于两个电阻器R1和R2，串联的电阻计算公式为R1 + R2，而并联的电阻计算公式为(1/R1 + 1/R2)^-1。

对于n阶电阻网络，我们可以使用递归的方法进行求解。

具体步骤如下：1. 当n=1时，电阻网络只有一个电阻器，等效电阻即为该电阻器的阻值。

2. 当n>1时，我们将电阻器R1与其他n-1个电阻器分成两组，分别记为G1和G2。

根据电阻器的连接方式，G1和G2可以是串联或并联。

- 如果G1和G2是串联关系，我们可以得到公式：R1 = R1' + R2，其中R1'为G1的等效电阻，R2为G2的等效电阻。

3. 我们可以根据上述公式递归计算出G1和G2的等效电阻。

当n=2时，我们可以直接使用串联和并联的电阻计算公式求解，从而得到G1和G2的等效电阻。

4. 接下来，我们再次根据G1和G2的等效电阻，按照步骤2的公式计算R1的值。

5. 重复步骤3和步骤4，直到n阶电阻网络的等效电阻被求解出来。

通过上述方法，我们可以求解出n阶电阻网络的等效电阻。

需要注意的是，以上方法仅适用于电阻网络中仅包含电阻器的情况，不适用于包含电容、电感等元件的网络。

在实际应用中，我们可以利用计算机编程进行求解。

通过编写递归函数，可以更方便地求解出n阶电阻网络的等效电阻。

求解n阶电阻网络的等效电阻需要利用串联和并联的电阻计算公式，并采用递归的方法进行计算。

这一方法在实际应用中非常有用，可以帮助我们更好地理解电阻网络的特性，并进行相关的电路设计和分析工作。

U OCI SC实验3。

3 有源二端网络等效参数的测量一、实验目的（1） 掌握有源二端网络的戴维南等效电路. （2） 验证戴维南定理，加深对该定理的理解。

（3） 掌握测量有源二端网络等效参数测量的方法. （4） 了解负载获得最大传输功率的条件。

二、实验仪器1台直流稳压电源、1块数字万用表、1块直流毫安表、电工试验箱 三、实验原理 1。

有源二端网络任何一个线性含源网络，如果仅研究其中一个支路的电压和电流，则可将电路的其余部分看做是一个有源二端网络。

有源二端网络包含线性电阻、独立电源和受控源. 2.戴维南等效电路及电路参数 戴维南定理指出：任何一个线性有源二端网络，总可以用一个电压源与一个电阻的串联来等效代替,此电压源的电动势U S 等于这个有源二端网络的开路电压U OC ，其等效电阻RO 等于该网络中所有独立源均置零时的等效电阻。

戴维南等效电阻如下图所示，电路参数为U OC (U S ）和R O .3。

有源二端网络等效电阻R O 的测量方法： （1)伏安法测R O 用电压表、电流表测出有源二端网络的外特性曲线，如图所示.根据外特性曲线求出斜率tg ϕ，则电阻为R O =tg ϕ=IU∆∆（2）半电压法4.负载获得最大功率的条件下图1可视为由一个电源向负载输送电能的模型，R O 可视为电源内阻和传输线路电阻的总和，R L 为可变负载电阻,负载R L 上消耗的功率P 可由下式表示：L L OS L R R R U R I P 22⎪⎪⎭⎫⎝⎛+==当R L =0或R L =∞时,电源输送给负载的功率均为零。

而以不同的R L 值代入上式，则可求得不同的P 值,其中必有一个R L 值，是负载能从电源处获得最大的功率。

R R L图1RL N 图2 U S根据数学求最大值的方法，令负载功率表达式的R L 为自变量,P 为应变量，并使0=LdR dP，即可求得最大功率传输的条件。

即RL=RO当满足RL=RO 时，负载从电源获得的最大功率为L SL L S L L O SR UR R U R RR U P 42222max =⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛+=这时，称此电路处于“匹配”状态. 四、实验步骤及数据 （一）伏安法测量戴维南等效电路参数（1）实验电路入图2所示.(2)调节直流稳压电源，使输出电压U 1=12V ，并保持不变. (3）将负载R L 开路,测网络a 、b 两端的开路电压U OC ，记录. (4）将负载R L 短路，测该支路短路电流I SC ，记录数据。

二端电阻网络的等效二端电阻网络的等效一、电阻的串联（ resistors in series ）串联n 个电阻相串联的二端电阻网络可以用一个等效电阻来等效，其等效电阻 R 等于串联的各电阻之和。

分压关系对于串联的电阻网络，电阻上分得的电压与其电阻值成正比，即电阻值越大，其分得的电压也越大。

第 j 个电阻上分得的电压为两个电阻串联时的分压公式为例 2.2-1 电路如图 2.2-1 所示，，，，求各电阻两端的电压。

解：图中 R1 、 R2 、 R3 电阻相串联，其等效电阻为则 10A 电流源两端的电压由分压公式，得到二、电阻的并联（ resistors in parallel ）并联n 个电导相并联的二端网络可用一个等效电导来等效，其等效电导 G 等于相并联的各电导之和，即两个电阻并联时，其等效电阻为分流关系对于并联电阻网络，电阻上分得的电流与其电导值成正比，即与其电阻值成反比。

电阻值越大，其分得的电流越小。

第 j 个电导上分得的电流为两个电阻串联时的分流公式为三、电阻的混联方法对于二端混联电阻网络的等效，关键是要抓住二端网络的两个端钮，从一个端钮出发，逐个元件地缕到另一个端钮，分清每个部分的结构是串联还是并联，再利用串联和并联的等效公式，最终求得该二端混联网络的等效电路。

例 2.2-2 ：求图 2.2-2 （ a ）所示电路 a 、 b 两端的等效电阻 Rab 。

解：电路为多个电阻混联，初一看似乎很复杂，但只要抓住端钮 a 和 b ，从 a 点出发，逐点缕顺，一直缕到另一端钮 b 。

为清楚起见，在图 2.2-4 （ a ）中标出节点 c 和 d 。

就得到图 2.2-4 （ b ），并可看出 5 Ω和 20 Ω的电阻是并联，两个 6 Ω的电阻也是并联，其等效电阻分别是这里，用符号“∥”表示两个电阻的并联关系。

由此，进一步得到图 2.2-4 （ b ）的等效电路图 2.2-4 （ c ）。

再对 2.2-4 （ c ）进行等效化简，得到 2.2-4 （ d ）。

n阶电阻网络的等效电阻研究电阻网络是电路中常见的一种元件，它由多个电阻组成，可以通过串联或并联的方式连接在一起。

而n阶电阻网络是一种特殊的电阻网络，它由多个电阻依据一定规律组成，具有较为复杂的结构和性能特点。

研究n阶电阻网络的等效电阻，不仅可以帮助我们更好地理解电路的工作原理，还可以为电路设计和性能优化提供重要参考。

本文将从n阶电阻网络的结构特点、等效电阻的计算方法和实际应用等方面进行探讨。

一、n阶电阻网络的结构特点n阶电阻网络是一种由n个电阻组成的网络结构，其中每个电阻都可以根据一定的规律连接在一起，形成一个整体。

这种网络结构通常具有较高的复杂度，需要通过一定的方法和技巧来进行分析和计算。

n阶电阻网络的结构特点主要包括以下几点：1. 多元件连接：n阶电阻网络中通常包含多个电阻元件，这些元件可以通过串联、并联或混合连接的方式组成。

不同的连接方式会影响整个网络的等效电阻值，需要进行分析和计算。

2. 多种结构形式：n阶电阻网络的结构形式多种多样，可以是线性结构、环形结构、树形结构等，而且不同的结构形式会对电阻网络的等效电阻产生重要影响。

3. 复杂的参数关系：n阶电阻网络中的每个电阻元件都有自己的参数，如电阻值、连接方式等，它们之间存在复杂的参数关系，需要通过适当的方法和模型进行描述和分析。

n阶电阻网络具有多个电阻元件、多种结构形式和复杂的参数关系等特点，这些特点决定了对n阶电阻网络的研究需要较为深入和全面的分析。

二、n阶电阻网络等效电阻的计算方法n阶电阻网络的等效电阻是指将整个电阻网络简化为一个等效电阻，其在电路中的作用和性能与原电阻网络相同。

对于n阶电阻网络的等效电阻计算方法，主要有以下几种常用的途径：1.串联/并联法：对于简单的电阻网络结构，可以通过串联和并联的组合方法来计算等效电阻。

对于串联电阻，等效电阻为各个电阻的总和；对于并联电阻，等效电阻为各个电阻的倒数之和再取倒数。

2.节点分析法：对于较为复杂的电阻网络结构，可以采用节点分析法来计算等效电阻。

n阶电阻网络的等效电阻研究电阻网络是电工电子学中的重要概念，用于描述电路中多个电阻元件之间的连接和电流流动关系。

当电路中存在多个并联或串联的电阻时，我们需要了解如何计算这些电阻的等效电阻，以便更好地分析电路性能和设计电路。

本文将重点研究n阶电阻网络的等效电阻，并探讨其计算方法和应用。

1. n阶电阻网络的概念n阶电阻网络是指电路中存在n个电阻元件连接成的网络。

这些电阻可以并联、串联或混合连接，构成了一个复杂的电路结构。

在实际电路中，我们经常需要分析这样的复杂电路，而了解其等效电阻将有助于简化分析和设计过程。

2. n阶电阻网络的等效电阻等效电阻是指一个电路中多个电阻元件合并后的一个电阻值，使得该电阻值对于该电路的某些特定电性质来说与原电路的行为完全相同。

对于n阶电阻网络，我们需要找到一个等效电阻值，使得用这个等效电阻替代原电路中的n个电阻后，整个电路的电阻特性保持不变。

3. n阶电阻网络的串联和并联在分析n阶电阻网络的等效电阻时，串联和并联是两个最基本的电路连接方式。

对于串联电路，n个电阻依次连接在一起，电流必须流过每个电阻才能到达电路的下一个部分。

而对于并联电路，n个电阻是平行连接的，电流可以选择不同的路径经过其中的任意一个电阻。

4. n阶电阻网络的等效电阻计算对于串联n阶电阻网络，其等效电阻可以通过简单的相加来计算：R_eq = R1 + R2 + R3 + ... + Rn。

而对于并联n阶电阻网络，其等效电阻则需要通过电阻的倒数相加再取倒数来计算：1/ R_eq = 1/R1 + 1/R2 + 1/R3 + ... + 1/Rn。

5. n阶电阻网络的混合连接在实际电路中，常常存在串联和并联混合连接的n阶电阻网络。

对于这种情况，我们可以采用分步骤的方法来计算其等效电阻：首先将串联和并联的电阻分别简化为一个等效电阻，然后再根据实际的连接方式进行相加或倒数相加计算。

6. n阶电阻网络的应用n阶电阻网络的等效电阻计算在电路设计和分析中有着广泛的应用。

电阻网络的等效电路分析电阻网络是电路中常见的一种电路元件组合形式，在电子电路设计和分析中扮演着重要角色。

通过等效电路分析，我们可以将复杂的电阻网络简化为一个等效电路，便于电路的计算和设计。

本文将详细介绍电阻网络的等效电路分析方法及应用。

一、电阻网络的基本概念电阻网络由多个电阻器按照一定的连接方式组成。

电阻器是一种被动元件，具有阻抗特性。

在电阻网络中，电阻器的连接方式可以是串联或并联。

1. 串联连接：当多个电阻器相互连接，电流依次经过每个电阻器后流入负载，称为串联连接。

图1为三个电阻器R1、R2和R3串联连接的电阻网络示意图。

```plaintext图1：串联连接示意图```2. 并联连接：当多个电阻器的一端或两端直接相连，电流在各个电阻器中分流，称为并联连接。

图2为三个电阻器R1、R2和R3并联连接的电阻网络示意图。

```plaintext图2：并联连接示意图```二、电阻网络的等效电路分析方法等效电路分析是指将复杂的电阻网络转化为简化的等效电路，以方便电路的计算和分析。

下面将介绍两种常用的等效电路分析方法：串并联电阻法和特殊电阻组合法。

1. 串并联电阻法串并联电阻法是将复杂的电阻网络通过串联和并联电阻的等效性，转化为简化的电阻网络。

具体步骤如下：步骤一：将电阻网络中的串联电阻进行合并。

若电阻网络中存在多个串联电阻，将其合并为一个等效电阻。

例如，图3为一个含有多个串联电阻的电阻网络。

```plaintext图3：含有多个串联电阻的电阻网络示意图```可以将R1和R2合并为一个等效电阻Req1，R3和R4合并为一个等效电阻Req2，得到简化的电阻网络。

```plaintext图4：等效电阻合并后的简化电阻网络示意图```步骤二：将电阻网络中的并联电阻进行合并。

若电阻网络中存在多个并联电阻，将其合并为一个等效电阻。

例如，图4中的电阻网络可以将Req1和Req2合并为一个等效电阻Req。

步骤三：根据需要，继续进行串并联电阻的合并，直到最终得到等效电路。

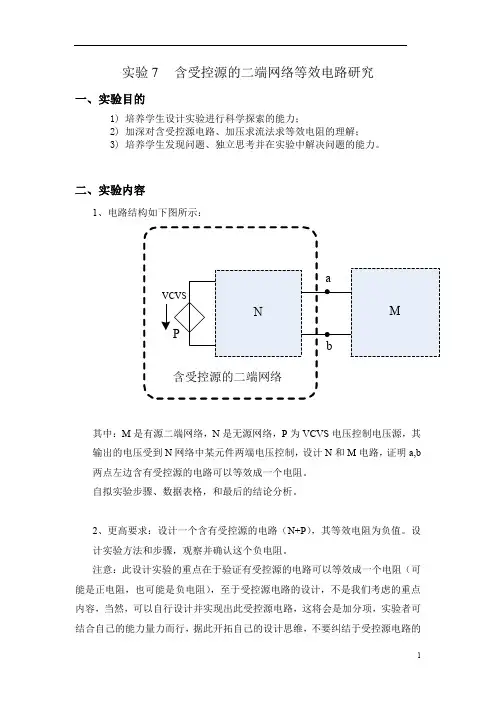
实验7 含受控源的二端网络等效电路研究一、实验目的1)培养学生设计实验进行科学探索的能力；2)加深对含受控源电路、加压求流法求等效电阻的理解；3)培养学生发现问题、独立思考并在实验中解决问题的能力。

二、实验内容1、电路结构如下图所示：其中：M是有源二端网络，N是无源网络，P为VCVS电压控制电压源，其输出的电压受到N网络中某元件两端电压控制，设计N和M电路，证明a,b 两点左边含有受控源的电路可以等效成一个电阻。

自拟实验步骤、数据表格，和最后的结论分析。

2、更高要求：设计一个含有受控源的电路（N+P），其等效电阻为负值。

设计实验方法和步骤，观察并确认这个负电阻。

注意：此设计实验的重点在于验证有受控源的电路可以等效成一个电阻（可能是正电阻，也可能是负电阻），至于受控源电路的设计，不是我们考虑的重点内容，当然，可以自行设计并实现出此受控源电路，这将会是加分项，实验者可结合自己的能力量力而行，据此开拓自己的设计思维，不要纠结于受控源电路的设计。

三、实验要求、步骤及提示1、自主决定N和M电路的复杂程度，建议在达到实验目的的前提下，尽量简单一些。

2、受实验条件限制，受控源类型为VCVS，电压转移比自定。

3、了解实验室所能提供的实验设备及元件，以备后续电路设计使用。

4、首先确定好含有受控源的电路（N+P），计算好其等效电路；5、设计测试电路M，其作用在于：在其辅助下，可以测试出含有受控源的电路（N+P）的等效电路。

6、拟定测试方案。

7、在MultiSim中，先对4、5中的电路进行搭建，按6的方案进行测试，从仿真角度验证其电路的正确性，以及方法的可行性。

8、在第一次实验课前，须完成以上的工作。

9、在仿真通过后，须在实验室进行实验验证，由于实验室没有提供相应的VCVS，故，此环节中，需重点考虑如何实现或是表现出VCVS这一功能。

10、在第一次实验课结束前，须完成出实物实验方案，并由老师确认方案的正确性及可行性。

n阶电阻网络的等效电阻研究引言电阻网络是电路中常用的元件，在实际的电路中经常会出现各种不同阶数的电阻网络。

对于n阶电阻网络而言，其等效电阻的计算是一个非常重要的问题。

在电路设计和分析中，需要通过等效电阻来简化电路，从而更方便地分析电路的性能和特性。

研究n阶电阻网络的等效电阻具有重要的理论和应用意义。

目前，关于n阶电阻网络的等效电阻的研究已经取得了一定的成果，但是在一些特殊情况下，如n阶电阻网络中电阻值不一致或者不规则排列等情况下，等效电阻的计算方法并不十分完善。

有必要对n阶电阻网络的等效电阻进行进一步的研究和探讨，以得到更加全面和深入的理解。

本文将围绕n阶电阻网络的等效电阻展开研究，首先介绍几种常见的n阶电阻网络结构及其等效电阻的计算方法，然后针对一些特殊情况进行讨论，最后通过实例分析验证所得结论的有效性，从而得出关于n阶电阻网络等效电阻的一些结论和启示。

一、n阶电阻网络的等效电阻的计算方法1.1 串联电阻网络首先考虑最简单的情况，即n个电阻按照串联的形式连接在一起。

对于串联电阻网络而言，其等效电阻可以直接通过电阻串联的性质进行计算，即等效电阻等于各个电阻之和，即R_eq=R1+R2+...+Rn。

这是一个非常简单和常见的计算方法，适用于一般的串联电阻网络。

1.3 混合电阻网络还存在一些混合的情况，即电路中同时存在串联和并联的情况。

对于这种情况，需要先将电路进行简化，将串联和并联的电阻分别合并成一个等效电阻，然后再对合并后的电路进行进一步的简化和计算。

二、特殊情况下的n阶电阻网络的等效电阻的计算2.1 电阻值不一致的情况首先考虑电阻值不一致的情况，如果n个电阻的阻值不同，那么直接使用上述的计算方法就不再适用了。

此时，可以利用电阻分压和电流分流的原理来进行计算。

具体而言，可以采用以下方法进行计算：1）将电阻网络进行分解，将其分解为若干个相互串联或并联的子电阻网络；2）对每个子电阻网络进行等效电阻的计算，可以采用上述介绍的计算方法；3）将各个子网络的等效电阻进行合并，最终得到整个电路的等效电阻。

一类n阶电桥电路网络的等效电阻研究李伟; 谭震; 王明君; 谭志中【期刊名称】《《大学物理》》【年(卷),期】2019(038)009【总页数】5页(P19-23)【关键词】电桥电路网络; 等效变换; 差分方程; 基尔霍夫定律【作者】李伟; 谭震; 王明君; 谭志中【作者单位】南通大学物理系江苏南通226019; 南通大学电子信息学院江苏南通226019【正文语种】中文【中图分类】O441.1; TN711.3170多年前的德国物理学家基尔霍夫(1824—1888)创立了两个基本定律(节点电流定律和回路电压定律)[1],人类在此理论基础之上建立了现代电气化文明社会,一系列复杂的科学问题通过建立电阻网络模型得以解决[1-18].电阻网络模型作为一种理论工具需要人们不断构建与创造,由此为人类的科学应用研究提供理论依据,因为许多实际问题可以通过构建电阻网络模型进行模拟研究[8-18].电阻网络模型是一种跨学科的问题其所涉及问题包括物理晶格问题、电路理论、数学中的图论、统计物理学、平均场理论等等学科问题,因而具有重要的理论研究意义与实践价值.电阻网络模型通常具有多种价值,每一个电阻元素的改变都将改变模型的电特性,因此,利用电阻网络模型研究的创新思想与方法开展基础物理实践创新活动具有较好的教学实践意义.经过科学家们的长期研究,已经建立了一些有效的研究电阻网络的方法,特别是文献[1,2]建立的等效变换方法,文献[9]建立的递推-变换方法,等等.因此不少电阻网络问题得到了比较好的解决[3-18].然而,实际研究中需要解决的问题通常比较复杂,寻找精确的等效电阻解析式通常是比较困难的事情.文献[6]研究了一类多功能n阶蜂巢型网络的等效电阻，文献[7]研究了一种含有交叉电阻的n阶电阻网络的电阻.尽管如此，科研中仍然会出现一些新的电路网络模型需要人们去解决，例如图1所示的内含双反馈电阻的n阶电阻网络模型，我们又称图1为n阶电桥电路网络模型(该名称在后文有详细解释).该模型的右边界上有一个独立的电阻R0并且另外有5个不同的电阻元素.这是本文提出的一个原创性的没有得到解决的问题，图1的网络模型包含了规则的梯形网络[1,2],三角形网络[3]等多个网络模型.本文考虑研究图1所示的n阶电桥电路网络的等效电阻,我们之所以称图1为n阶电桥电路网络模型,是因为当r1r2=r2时存在平衡桥电路,即在此条件下节点An、Bn之间的等效电阻与R0及n均无关,该问题在下文的情形1中给出了详细解释.图1网络模型的电阻参数已经标注在图形之中，含有n网络单元,含有5个不同的电阻，内部有2个不连接的交叉反馈线其电阻分别为r1、r2,这显然是一个之前没有解决的网络问题.本文的研究工作在于推导此网络左端An和Bn两节点间的等效电阻解析式，同时考虑它的一些应用.图1 一个n阶电桥电路网络模型,该网络含有5个不同的电阻元素.1 总的等效电阻公式图1网络的已知条件为: 网络单元数为n,上下水平线上的电阻均为r,竖直方向的电阻元素均为r0,内部交叉反馈线(不连接)上的电阻分别为r1、r2,右端的电阻为R0.在图1网络中,标注节点Ak从右端开始计数,右端的第一个节点记为A0,左边的节点为An,则得到n阶电桥电阻网络An和Bn之间的等效电阻：(1)式(1)中的参数定义为(2)同时(3)并且其中的常数为(4)利用式(3)、(4)计算得到(5)关于图1网络的等效电阻公式(1)为本文第一次发现,其研究是一次理论和方法上的创新.文章所采用的研究方法为文献[1,7]中建立的N-RT方法.2 等效模型和递推方程根据图1的结构特征能够将图1简化成为图2所示的一个简单模型，其中假设n 阶网络左端An和Bn节点间(从左向右看)的等效电阻为Rn,那么n-1阶网络两节点间(从左向右看)的等效电阻为Rn-1.图2 含有电流参数的二端电路网络模型研究发现利用基尔霍夫定律可以建立Rn和Rn-1之间的关系方程.假设分别在节点An和Bn之间输入和输出恒定电流I,并且在图2中分别给出其他的分支电流.在图2中应用基尔霍夫第二定律(回路电压定律)得到3个方程：I1r+I6r1-I3r0=0,I5r2+I4r-I3r0=0,I1r+I2Rn-1-I5r2=0(6)应用基尔霍夫第一定律(节点电流定律)得到3个方程：I5=I-I1-I3, I4=I2+I5, I6=I1-I2(7)解以上6个方程构成的方程组得到一个支路电流I3的解：(8)其中a和b分别由方程式(4)给出.将式(8)代入Rn=U/I=I3r0/I得到(9)至此我们建立了方程式(9)这样一个递推公式,这也是我们研究解决该问题的第一步.3 等效变换及其公式的推导为了推导方程式(9)的解，这里采用文献[1]建立的变量代换方法开展研究.假设一个未知数列{xn},建立以下变换：(10)对于一个未知数列{xn}可以规定其初始项x0=1,在式(10)中取n=0得到方程(11)即作为数列xn的初始条件.由方程式(10)递推之后可以得到Rn-1，以此代入式(9)进行化简，得到(12)此时，我们将一个分数阶方程式(9)转化成为一个线性化方程.设方程式(12)的2个特征根分别为α 和β,解之可以得到(3)的值.因此由式(12)变换得到xn+1=(α+β)xn-αβxn-1(13)利用文献[1,9]中建立的方法可以得到方程(13)的通解：(14)将等式(11)代入式(14),得到(15)另外利用方程式(12)和式(13) 得到(16)将方程式(16)代入式(15)化简得到xn=Fn+1+(R0-p)Fn(17)其中Fn=(αn-βn)/(α-β)定义在式(2)中.另外根据方程式(17)及(a+r0)/b=α+β-p可以将式(10)变形为将式(17)及其递推式xn-1代入式(18)即得到式(1).至此式(1)得到证明.4 特殊情形和比较情形1 考虑图1所示的网络,当r2r1=r2⟺r2=r2/r1 时, 由方程式(4)得到(19)将等式(19)代入式(2)得到将此代入式 (1) 得到(20)这是一个十分有趣的问题,因为式(20)与n和R0无关.为什么等效电阻会是常数,这正是平衡桥电路的必然结果.具体分析如下：不妨考虑一个图3所示的电路,将图3所示的电路实施拓扑变换可以得到图4所示的电路结构,很显然图4的电路存在一个常见的桥电路.如何识别图3与图4的电路等价,我们采用各节点之间所连接的电路来判断：在图3与图4的任何一个电路中,与A节点相连接的电阻有r、r0、r2,与B节点相连接的电阻有 r、r0、r1,与E节点相连接的电阻有r、r1、R0,与F节点相连接的电阻有r、r2、R0.众所周知,当r:r1=r2:r ⟺r1r2=r2时,称图4为平衡桥电路,此时当A与B之间通入电流时,电阻R0中无电流通过,也就是说节点AB之间的等效电阻与R0无关,又因为图3与图4的电路等价，这就解释了结论(20)的正确性(与第一个网孔右边的网络无关).正因为如此,我们称图1为n阶电桥电路网络.图3 一个简单的内含交叉(不连接)电阻的电路,该网络是一种桥电路图4 一个含有5个不同电阻元素的桥式电路情形2. 考虑图1所示的网络,当r1=r2时,根据等式(4)得到以及(22)那么,由式(3) 得到(23)以及(24)因此,根据公式(1)得到(25)其中a,b由式(21) 给出.情形3. 当r1→∞时,n阶电桥电路网络退化成为如图5所示的一种三角形的n阶电阻网络.下面依据公式 (1) 可以推导图5所示网络的等效电阻.图5 一个网格中内含2个三角形的n阶电阻网络模型.当r1→∞ 时,根据方程式(4) 得到(26)因此(27)(28)及特征根(29)其中d=2(r+r0)(r+r2).因此根据式(1)得到(30)文献[3]曾经研究了图6所示的网络问题,这里得到的结论式(30)与文献[3]中的结果完全一致,这说明本文得到的结论是完全正确的.情形4. 当r1、r2→∞ 时,网络图1将退化成图6所示的比较简单的n阶矩形电阻网络.在式(26)—(29)中取极限r2→∞，得到a=2r, b=1, p=r0(31)及(32)因此利用式(30)得到等效电阻(33)文献[1-7]曾经研究过图6所示的电阻网络,将文献[1-7]中的结果对比于式(33)可以发现所有结论完全相同.图6 一个含有任意右边界的n阶矩形电阻网络模型.情形5. 当n→∞时,根据式(4) 得到0<β/α<1,因此(34)根据式(1)得到(35)显然，在n→∞情形下的公式(1)是一个有限常数.情形6. 当R0=p-β时,将此代入(1)得到(36)因为Fn=(αn-βn)/(α-β),所以Fn-βFn-1=αn-1, Fn+1-βFn=αn(37)将方程式(37)代入式(36)得到(38)不难发现方程式(38)与方程式(35)完全相同,但是他们却来自不同的条件.公式(38)通常被称为电阻网络的特征电阻,其成立的条件是R0=p-β.这表明极限电阻值与特征电阻值相同，这是一个有趣的现象.5 小结本文提出了一种n阶电桥电路网络模型，分别采用构建等效模型和实施变量代换的方法(简称为N-RT方法)解决了一个n阶电桥电路网络的等效电阻问题,导出了An和Bn两节点间的等效电阻公式.特别地，文章推导出了一系列特殊情形下的等效电阻结论，同时将特殊结论与其他文献结论进行了比较使得本文的结论与其它结论得到了相互验证.本文的理论推导过程严密和精确，所得结论优美而简洁，是一次比较有意义的创新研究，其理论结果可以应用于未来相关的科学研究.本文的研究思想与方法有助于物理教学活动中开展科学探究教学,既能培养学生的创新实践能力,又能促进物理教学与科研协同相长,同时培养教师的教学与科研能力.【相关文献】[1] 谭志中.电阻网络模型[M].西安电子科技大学出版社,2011,3-230.[2] 陆建隆,谭志中.关于梯形网络等效电阻的普适研究[J].大学物理,2001,20 (10): 26-28.[3] 谭志中,杨建华.一类含有复杂电阻的n阶三角形网络的等效电阻公式[J].大学物理,2005,34 (6): 24-35.[4] 李建新,李保刚.2×n阶梯形电阻网络等效电阻研究[J].大学物理,2012,31 (6): 21-24.[5] 刘松山.基于对称性研究2×n 阶梯形电阻网络等效电阻[J].大学物理,2015,34 (1): 26-29.[6] 谭志中.多功能n阶蜂巢型电阻网络的等效电阻公式[J].首都师范大学学报(自然科学版) 2016,37(6): 34-40.[7] 谭志中.内嵌交叉电阻的N阶多功能电阻网络的等效电阻研究[J].南通大学学报(自然科学版),2016,15(1):49-56.[8] 谭志中,张庆华.基于递推-变换方法计算圆柱面网络的等效电阻及复阻抗[J].物理学报,2017,66,070501.[9] Tan Z-Z.Recursion-transform approach to compute the resistance of a resistor network with an arbitrary boundary[J].Chin Phys B，2015,24 (2): 020503.[10] Tan Z-Z,Fang J-H.Two-point resistance of a cobweb network with a 2rboundary[J].Commun Theor Phys,2015,63 (1): 36-44.[11] Tan Z-Z.Two-Point Resistance of a Non-Regular Cylindrical Network with a Zero Resistor Axis and Two Arbitrary Boundaries[J].Commun Theor Phys,2017: 67 (3),280-288.[12] Tan Z-Z.Two-point resistance of an m×n resistor network with an arbitrary boundary and its application in RLC network[J].Chin Phys B，2016,25 (5): 050504.[13] Tan Z-Z,Asad J H,Owaidat M Q.Resistance formulae of a multipurpose n-step network and its application in LC network[J].Int J Circ Theor Appl，2017,45(12): 1942-1957. [14] Zhou L,Tan Z-Z,Zhang Q-H.A fractional-order multifunctional n-step honeycomb RLC circuit network[J].Front Inform Technol Electron Eng,2017,18(8):1186-1196.[15] Tan Z-Z,Zhu H,Asad J H,et al.Characteristic of the equivalent impedance for an m×n RLC network with an arbitrary boundary[J].Front Inform Technol Electron Eng.2017,18(12): 2070-2081[16] Tan Z-Z.Recursion-transform method and pote ntial formulae of the m×n cobweb and fan networks[J].Chin Phys B,2017,26 (9): 090503.[17] Tan Zhen,Tan Z-Z,Zhou L.Electrical Properties of an m×n HammockNetwork[J].Commun Theor Phys,2018,69: 610-616[18] Tan Zhen,Tan Z-Z.Potential formula of an m×n globe network and itsapplication[J].Scientific Reports,2018,8: 9937.。